The main purpose of interval arithmetic is look into the uncertain-ties in the practical models with uncertain-but-bounded parameters, which only requires lower and upper bounds of uncertain parameters and with no in-formation about probability distributions. In this paper, an interval numerical method is proposed for solving the Hamilton Jacobi Bellman (HJB) Equations with uncertainties. An interval version of Adomian Decomposition Method is utilized for solving the interval model parameters in the partial differential equations of the HJB. This study assumes that the uncertainty can be happened in both differential coefficients and initial values. The proposed interval method is applied to solve the linear and nonlinear HJB equations in association with appropriate numerical solvers. A practical discussion problem is also solved to analyze the system robustness and to show that the proposed interval decomposition method is a powerful method for systems in the presence of uncertainties.

Keywords: interval arithmetic, Hamilton Jacobi bellman, partial differential equation, interval adomian decomposition method, nonlinear differential equation, optimal control

Optimal control is the policy of getting the optimized control value for minimizing a predefined cost function. Recently, several optimization methods have been introduced for achieving this purpose.^1–4 Among these methods, Pontryagins maximum principle⁵ and the Hamilton Jacobi Bellman equation⁶ are the most popular. In Pontryagins maximum principle, the optimal control problem will be converted to an ODE problem while the Hamilton Jacobi Bellman method converts the optimal control into a nonlinear partial differential equation. Hamilton Jacobi Bellman method can be utilized in different linear, non-linear and even distributed optimal control problems. Be-cause of difficulty in solving the HJB and the Pontryagins maximum principal method, it is usually necessary to employ the numerical methods to achieve the optimal solutions for the nonlinear practical models. One of the popular semi-numerical methods which is frequently used in the recent years is the Adomian decomposition method.⁷ Adomian decomposition method and its modifications have been efficiently employed to solve the ordinary and partial differential equations.^8–10 Because the method uses no linearization or smallness assumptions in solving the differential equations, it has been an effective method among the other techniques. Generally, in designing the optimal control problems for engineering and practical applications the parameters considered as deterministic, but there is a great deal of uncertain parameters which can greatly affect the system performance. Such an uncertainty can be made by model simplification, manufacture error, design tolerance etc. If the number of the system uncertainties becomes very small, deterministic methods can be employed to solve these problems with little errors. If the number of uncertain parameters has been increased or the ranges of these parameters have become large, the deterministic methods might give the wrong answer. Three different methods have been introduced for solving these uncertain problems: Probabilistic methods, fuzzy methods and interval methods.¹¹ The main purpose of this paper is to introduce an interval version of Adomian decomposition method to solve the Hamilton Jacobi Bellman equation. The proposed method is first applied on a linear optimal control with uncertainties. After that, it is utilized to solve a nonlinear optimal control with uncertain parameters. Finally, a practical distributed system is solved by the proposed method; in this problem, in addition to assuming the presence of uncertainty in parameters, the initial conditions are also considered with uncertainty.

This section describes the basic concepts of the interval arithmetic which is necessary to use the proposed method.¹² Generally, basic interval arithmetic operations have described to guarantee the interval results reliability. let: $X=\left[\underset{\_}{x},\overline{x}\right]$  and $Y=\left[\underset{\_}{y},\overline{y}\right]$  be interval numbers as: X, Y ∈ R, $\underset{\_}{x}<\overline{x},\underset{\_}{y}<\overline{y}$  and the symbol ⋄ illustrates the basic mathematical operations, i.e. addition , subtraction, multiplication and division for real numbers. In other words,
$\diamond \in \left\{+,-,\times ,÷\right\}]$ .
By assuming the assumption above, we have:
${\rm X}\diamond Y=\left\{{\rm X}\diamond Y|x\in {\rm X},y\in Y\right\}$ ,      (1)
where 0 $\notin$ Y for preventing the singularity in the division. We can easily prove that the set IR of real compact intervals is closed with respect to the illustrated operations.¹³ from the explanation above, the basic interval arithmetic operations between two interval numbers X and Y and can be defined as follows:
$X+Y=\left[\underset{\_}{x}+\underset{\_}{y},\overline{x}+\overline{y}\right]$ (2)
$X-Y=\left[\underset{\_}{x}-\overline{y},\overline{x}-\underset{\_}{y}\right]$  (3)
${\rm X}\times Y=\left[\min \left\{\underset{\_}{x}y,\overline{x}\underset{\_}{y},\underset{\_}{x}\overline{y},\overline{x}\overline{y}\right\},\max \left\{\underset{\_}{x}y,\overline{x}\underset{\_}{y},\underset{\_}{x}\overline{y},\overline{x}\overline{y}\right\}\right]$ (4)
${\rm X}/Y={\rm X}\times \frac{1}{Y}$ (5)
$\frac{1}{Y}=\left\{\frac{1}{y}|y\in Y\right\}$ , if $0\notin Y$ ,
${{\rm X}}^n=\{\begin{array}{c}\left[0,\max \left({\underset{\_}{x}}^n,{\overline{x}}^n\right)\right],n=2k,0\in {\rm X},\\ \left[\min \left({\underset{\_}{x}}^n,{\overline{x}}^n\right),\max \left({\underset{\_}{x}}^n,{\overline{x}}^n\right)\right]\\ \left[{\underset{\_}{x}}^n,{\overline{x}}^n\right],n=2k+1,\end{array},n=2k,0\notin {\rm X},$ (6)

If in mathematical operations, a real number like x gets into operations, it can be described as
$\underset{\_}{x}=\overline{x}=x$  and called degenerate interval ; in other words, the interval form for this constant number is X ≡ [x, x].

In this section, a brief illustration of the optimal control and how to use the Hamilton-Jacobi-Bellman for solving these problems are described. Consider a state space representation system as below:

  $\dot{x}\left(t\right)=F\left(x\left(t\right),u\left(t\right),t,\left[\delta \right]\right),$  (7)

where, x(t) is the space vector, u(t) is the control signal and $\left[\delta \right]=\left[\underset{\_}{\delta },\overline{\delta }\right]$ is a coefficient with interval uncertainties. The main purpose is to find a control signal to minimize the following index performance:
$J={\displaystyle \underset{0}{\overset{tf}{\int }}g\left(x\left(\tau \right),u\left(\tau \right),\tau ,\left[\widehat{\delta }\right]\right)}d\tau ,$  (8)
Here, g(.)is an arbitrary convex function, tf is final time of system operation
$\widehat{\delta }=\left[\widehat{\underset{\_}{\delta }},\overline{\widehat{\delta }}\right]$  is a coefficient with interval uncertainties and J = [J, J] is the lower and upper bounds of the optimized performance index. By supposing the dynamic programming approach, we have:14
$V\left(x\left(t\right),t\right)=J^{*}\left(x\left(t\right),t\right)=\underset{\begin{array}{c}u\left(\tau \right)\\ t\le \tau \le t_f\end{array}}{\min }{\displaystyle \underset{0}{\overset{t_f}{\int }}g\left(\pi x\left(\tau \right),u\left(\tau \right),\tau \left[\widehat{\delta }\right]\right)d\tau }$ (9)
Since,
$V\left(x\left(t\right),t\right)=J^{*}\left(x\left(t\right),t\right)=\underset{\begin{array}{c}u\left(\tau \right)\\ t\le \tau \le t_f\end{array}}{\min }\{{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}g\left(x\left(\tau \right),u\left(\tau \right),\tau ,\left[\widehat{\delta }\right]\right)d\tau +{\displaystyle \underset{t+\Delta t}{\overset{t_f}{\int }}g\left(x\left(\tau \right),u\left(\tau \right),\tau ,\left[\widehat{\delta }\right]\right)d\tau }\}}$ (10)
By considering the principle of optimality

$V\left(x\left(t\right),t\right)=\underset{\begin{array}{c}\left(\tau \right)\\ \le \tau \le t+\Delta t\end{array}}{\min }\{{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}g\left(x\left(\tau \right),u\left(\tau \right),\tau ,\left[\widehat{\delta }\right]\right)d\tau +\left[V\right]\left(x\left(t+\Delta t\right),t+\Delta t,\left[\widehat{\delta }\right]\right)\}}$ (11)

And with applying Taylor series, we have:

$V\left(x\left(t\right),t\right)=\underset{\begin{array}{c}\left(\tau \right)\\ \le \tau \le t+\Delta t\end{array}}{\min }\{{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}g\left(x\left(\tau \right),u\left(\tau \right),\tau ,\left[\widehat{\delta }\right]\right)d\tau +\left[V\right]\left(x\left(t\right),t,\left[\widehat{\delta }\right]\right)+\frac{\partial \left[V\right]}{\partial t}\Delta t+\frac{\partial \left[V\right]}{\partial x}\left[x\left(t+\Delta t\right)-x\left(t\right)\right]+H.O.T\}}$ (12)
By assuming $0<\Delta t\ll 1$ , then $\tau \to t$ [16]. Therefore:
$\left[V\right]\left(x\left(t\right),t\right)=\underset{u\left(\tau \right)}{\min }\{{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}\left[V\right]\left(x,t,\left[\widehat{\delta }\right]\right)+\frac{\partial \left[V\right]}{\partial t}\Delta t+\left[\delta \right]\frac{\partial \left[V\right]}{\partial x}f\left(x,u,t,\left[\delta \right]\right)\Delta x+O\left(\Delta t\right)}$  (13)

By applying the division operation into both sides, we obtain:
$-\frac{\partial V}{\partial t}=\underset{u\left(\tau \right)}{\min }\{{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}g}\left(x,u,t,\left[\widehat{\delta }\right]\right)+\frac{\partial \left[V\right]}{\partial t}f\left(x,u,t,\left[\delta \right]\right)\}$ (14)

The previous nonlinear time-variant differential equation forms the HJB equation. By using the Hamiltonian function, we have:
$H\left(x,u^{*}{V}_{x,t}\right)=\underset{u\left(\tau \right)}{\min }H\left(x,u,V_x,t\right)$  (15)
By substitution the Hamiltonian function into the Eq. (14), the nal interval HGB equation can be describes as below:
$-\frac{\partial V}{\partial t}=H\left(x,u^{*}{V}_{x,t}\right)$ (16)

In this section, a brief description of the interval Adomian method for HGB equation is introduced. Suppose that Lt = ∂t∂ . Let consider the HGB equation in the following form:

$L_{t}V=H\left(x,u^{*}\left(x,V_x,x,t\right),V_x,t\right)$  (17)
From Eq.15, we obtain:     
$u^{*}\left(x,V_x,x,t\right)=f\left(V_x,x,t,\left[\delta \right]\right)$ (18)
Substituting Eq.16 into Eq.17 yields:              
$L_{t}V=H\left(x,f\left(V_x,x,t,[\delta \right),V_x,t\right)$ (19)
Since, the main equation can be considered as:           
$L_{t}V=R\left(V_x\right)+N\left(V_x\right)$ (20)
where    
$R\left(V_x\right)=\left[\alpha \right]\times R\left(V_x\right)$ (21)
$N\left(V_x\right)=\left[\beta \right]\times N\left(V_x\right)$ (22)
Here, R (Vx) and N (Vx) are the linear and nonlinear terms of the Hamiltonian function, respectively and [α] and [β] are uncertain coefficients for linear and nonlinear terms, respectively. Using the Adomian decomposition method, the nonlinear term (N(Vx)), can be achieved by:
$N\left(V_x\right)={\displaystyle {\sum }_{n=0}^{\infty }{A}_n}$                 (23)
where, An = An(V0x(x), V1x(x), . . . , Vnx(x)) are the Adomian polynomials:
$A_n=\frac{1}{n!}\frac{d^n}{d{\lambda }^n}N{\left({\displaystyle {\sum }_{i=0}^{\infty }{\lambda }^i{V}_{ix}\left(x\right)}\right)}_{\lambda =0}n=0,1,2,\mathrm{...}$ (24)
By applying the inverse operator $\left(L_t^{-1}={\displaystyle \underset{0}{\overset{t}{\int }}[.]d\tau }\right)$ into the both sides of the Eq. 19
$L_t^{-1}{L}_{t}V=L_t^{-1}R\left(V_x\right)+L_t^{-1}N\left(V_x\right)$  (25)
Since, by considering the given conditions, the final equation can be achieved by:
$V=\Phi +L_t^{-1}R\left(V_x\right)+L_t^{-1}N\left(V_x\right)$  (26)
Where $\Phi =\left[\underset{\_}{\Phi },\overline{\Phi }\right]$  illustrates the initial condition interval by the presence of uncertainty. We consider the truncated V as:
$V={\displaystyle \sum _{i=0}^n{V}_i}$  (27)
By using Equation (28), we can compute Vi as follows:
$\{\begin{array}{l}{V}_0=\Phi ,\\ V_{n+1}=\left[\alpha \right]\times L_t^{-1}R\left(V_{nx}\right)+\left[\beta \right]\times L_t^{-1}{A}_n\end{array}$ (28)

The proposed interval method is studied by three examples to describe the robustness of the approach.

Example 1
Linear LQR system: In the first example, consider a linear system which has equal uncertainty in both control and state terms. Find the optimal control based on minimizing the performance index in below:
$J=\frac{1}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\left(U{\left(t\right)}^2+X{\left(t\right)}^2\right)}dt,0\le t\le 1$ (29)
Subject to
$\dot{X}=\delta X\left(t\right)+\widehat{\delta }U\left(t\right)$ (30)

Where $\delta =\widehat{\delta }=\left[\begin{array}{cc}0.1,& 0.9\end{array}\right]$ . The problem without uncertainty is solved in (14). From Eq. (15), the HJB equation is achieved as follows:
$\frac{\partial V}{\partial t}=\frac{1}{2}{\left[\widehat{\delta }\right]}^2{\left(\frac{\partial V}{\partial X}\right)}^2-\frac{1}{2}{\left[\delta \right]}^2{\left(\frac{\partial V}{\partial X}\right)}^2-\left[\delta \right]X\frac{\partial V}{\partial X}$ (31)

From the Eq. (27):

$\{\begin{array}{l}{V}_0=\frac{1}{2}{\displaystyle \underset{0}{\overset{t}{\int }}X{\left(\tau \right)}^{2}d\tau =\frac{1}{2}}{X}^{2}t=\left[-\frac{1}{2}{X}^{2}t,-\frac{1}{2}{X}^{2}t\right],\\ V_1=\frac{{\left[\widehat{\delta }\right]}^2}{2}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{\partial V_0}{\partial X}\right)}^2}d\tau -\left[\delta \right]{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{\partial V_0}{\partial X}\right)}d\tau =\left[0.0016,0.135\right]X^2{t}^3+\left[0.005,0.405\right]X^2{t}^2,\\ V_2=\frac{{\left[\widehat{\delta }\right]}^2}{2}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{\partial V_1}{\partial X}\right)}^2}d\tau -\left[\delta \right]{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{\partial V_1}{\partial X}\right)}d\tau =\left[64e-7,0.0437\right]X^2{t}^5-\left[0.001,0.2247\right]X^2{t}^4-\left[0.00035,0.255\right]X^2{t}^3,\\ .\\ .\\ .\\ V_{n+1}=\frac{{\left[\widehat{\delta }\right]}^2}{2}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{\partial V_1}{\partial X}\right)}^2}d\tau -\left[\delta \right]{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{\partial V_n}{\partial X}\right)}d\tau \end{array}$ (32)

Where, ${\left[\widehat{\delta }\right]}^2={\left[\delta \right]}^2=\left[\begin{array}{cc}0.1,& 0.9\end{array}\right]\times \left[\begin{array}{cc}0.1,& 0.9\end{array}\right]=\left[\begin{array}{cc}0.01,& 0.81\end{array}\right]$ . the closed form of this system for n=3 is shown as follows: Figure 1. A random value for $\delta =\widehat{\delta }$ is applied in the interval [0.1, 0.9] and the solution is stand between two interval. The intervals are characterized by grids.

Example 2
Non-linear quadratic regulation system: In this example, a non-linear LQR system with uncertainty is studied. The target is to find the optimal control based on minimizing the performance index is:
$J={\displaystyle \underset{0}{\overset{1}{\int }}\left(U{\left(t\right)}^2+X{\left(t\right)}^2\right)}dt,0\le t\le 1,$ (33)
subject to:
$\dot{X}=\frac{\delta }{2}{X}^2\left(t\right)\sin \left(X\left(t\right)\right)+U\left(t\right),$ (34)

where δ = [1, 2]. The HJB equation for this problem can be obtained as follows:

$\frac{\partial V}{\partial t}=\frac{\left[\delta \right]}{x}{X}^2\left(t\right)\sin \left(X\right)\left(\frac{\partial V}{\partial x}\right)-\frac{1}{4}{\left(\frac{\partial V}{\partial x}\right)}^2+X^2$  (35)

From the Eq.(27): 

$\{\begin{array}{l}{V}_0={\displaystyle \underset{0}{\overset{t}{\int }}X{\left(\tau \right)}^{2}d\tau =}{X}^{2}t=\left[X^{2}t,X^{2}t\right],\\ V_1=-\frac{1}{4}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{\partial V_0}{\partial X}\right)}^2}d\tau -\frac{\left[\delta \right]}{2}{\displaystyle \underset{0}{\overset{t}{\int }}{X}^2}sin\left(X\right)\left(\frac{\partial V_0}{\partial X}\right)d\tau =-\left[0.7,0.7\right]X^2{t}^3+\left[0.5,1\right]X^3\sin \left(X\right)t^2,\\ V_2=\left[-0.07,-0.07\right]X^2{t}^7+\left[-0.35,-0.17\right]X^{3}sin\left(X\right)t^6+\left[-0.35,-0.175\right]X^3\sin \left(X\right)t^4+\left[0.25,1\right]X^4{\sin }^2{t}^3,\\ .\\ .\\ .\\ V_{n+1}=\frac{1}{4}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\frac{\partial V_n}{\partial X}\right)}^2}d\tau -\frac{\left[\delta \right]}{2}{\displaystyle \underset{0}{\overset{t}{\int }}{X}^2\sin \left(X\right)\left(\frac{\partial V_n}{\partial X}\right)}d\tau \end{array}$ (36) 

So we can compute and plot the closed form Eq.(25) for n = 3 as follows: Figure 2. A random value for δ is applied in the interval [1, 2] and the solution stands between two intervals. The random value solution is characterized by stars.

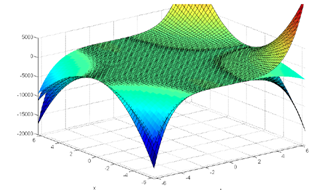
Figure 1 The Interval Adomian Solution for the linear LQR system with uncertainty by HGB method.

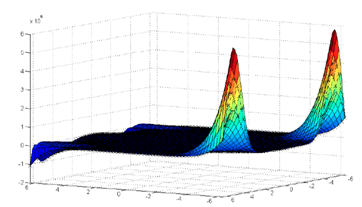
Figure 2 The Interval Adomian Solution for the nonlinear LQR system with uncertainty by HGB method.

Example 3
In this example, a class of nonlinear diffusion equations subject to initial and boundary conditions is studied which arises during Magnetic Resonance Imaging (MRI). The main reason for prosperity in diffusion MRI is in the powerful concept that during their diffusion-driven, random displacements molecules probe tissue structure at a microscopic scale well beyond the usual image res-olution.^15,16 Here, a class of diffusion problem is considered which arises in MRI frequently. The equation is given as below:
$\{\begin{array}{l}{\upsilon }_t={\left(\alpha \left(x\right){\upsilon }_x\right)}_x+\beta \left(x\right)F\left(\upsilon \right),\\ \upsilon \left(x,0\right)=f\left(x\right),0<x<1,\\ \upsilon \left(0,t\right)=p\left(t\right),0<t<t_f,\\ {\upsilon }_x\left(1,t\right)=q\left(t\right)0<t_f,\\ \left|\upsilon \left(x,t\right)\right|<K,\left(x,t\right)\in \left[0,1\right]\times \left[0,t_f\right].\end{array}$ (37)
Where f(x), $\alpha \left(x\right)$ and $\beta \left(x\right)$ are known functions with uncertainty parameters, K is a known constant and p(x) and q(x) are control variables. For generating a HGB problem, we can have considered the problem below:
$\{\begin{array}{l}{\upsilon }_t={\left(\alpha \left(x\right){\upsilon }_x\right)}_x+\beta \left(x\right)F\left(\upsilon +q\left(t\right)x+p\left(t\right)\right)-\dot{q}\left(t\right)x+\dot{p}\left(t\right),\\ \upsilon \left(x,0\right)=f\left(x\right)-q\left(0\right)x-p\left(0\right),0<x<1.\end{array}$ (38)
For instance, consider the equation below:
$\{\begin{array}{l}\frac{\partial V}{\partial t}=\frac{\left[\delta \right]}{x}\left(\frac{{\partial }^{2}V}{\partial x^2}\right)+\frac{\left[\delta \right]}{x}{V}^2,\delta =\left[0.8,1.2\right],\\ V\left(x,0\right)=\frac{x^4}{12}-\frac{x^3}{6},\\ V\left(0,t\right)=0,0<t<t_f\end{array}$ (39)

From the equation above, it can be seen that the initial condition has also uncertainty in this problem. From the Eq.27, the closed form solution can be achieved by $V={\displaystyle \sum _{i=0}^3{V}_i}$
$\{\begin{array}{l}{V}_0=\left[\frac{x^2}{12}-\frac{x^3}{6},\frac{x^2}{12}-\frac{x^3}{6}\right],\\ V_1=\left[0.8,1.2\right]\left[\left(x-1\right)+{\left(\frac{x^4}{12}-\frac{x^3}{6}\right)}^2\right]t,\\ V_2=\left[1.6,2.4\right][\left(\frac{x^2}{4}-\frac{x}{2}\right)\times \left(\frac{x^3}{4}-\frac{x^2}{2}\right)+\left(\frac{x^3}{2}-x\right)\times \left(\frac{x^4}{12}-\frac{x^3}{6}\right)+2\times V_0\times V_1\frac{t^2}{2},\\ .\\ .\\ .\\ V_{n+1}=\frac{\delta }{x}{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{{\partial }^2{V}_n}{\partial x^2}\right)d\tau +\frac{\left[\delta \right]}{x}{\displaystyle \underset{0}{\overset{t}{\int }}{A}_{n}d\tau ,A_n=V^2}}.\end{array}$ (40)

A random value for [δ] is applied in the interval [0.8, 1.2] and the solution is stand between two intervals. The intervals are characterized by grids (Figure 3).

Figure 3 The Interval Adomian Solution for distributed diffusion problem with uncertainty by HGB method.

In this paper, an uncertain analysis method is proposed for solving the Hamiltonian-Jacobi-Bellman, for systems involving uncertain parameters. The Adomian decomposition method is applied to deal with the interval method to handle the interval uncertainty. Three case studies including linear, nonlinear and a distributed nonlinear optimal control are studied for checking the system robustness. The main advantage of the proposed method over traditional numerical methods is that the proposed method is the first time which is used the interval arithmetic to provide a robust result for HGB equation with uncertain coefficients.

None.

The authors declare there is no conflict of interest.

1. Dehghan M, Allah Hamedi E, Khosravian-Arab H. A numerical scheme for the solution of a class of fractional variational and optimal control problems using the modi ed Jacobi polynomials. Journal of Vibration and Control. 2016;22(6).
2. Sabeh Z, Shamsi M Dehghan M. Distributed optimal control of the viscous Burgers equation via a Legendre pseudospectral approach, Mathematical Methods in the Applied Sciences. 2015;39(12):3350–3360.
3. Razmjooy N, Ramezani M. Analytical Solution for Optimal Control by the Second kind Chebyshev Polynomials Expansion. Iranian Journal of Science and Technology. 2016.
4. Lions, Louis J. Optimal control of systems governed by partial differential equations. Springer; 1971:170.
5. Pontryagin, Semenovich L. Boltyanskii VG. Mathematical theory of optimal processes. JSTOR. 1965;19(89):159–161.
6. Feldbaum AA. Optimal Control Systems. Mathematics in science and engineering. 1965.
7. Cherruault Y, Adomian G, Abbaoui K, et al. Further remarks on convergence of decomposition method. Int J Biomed Comput. 1995;38(1):89–93.
8. Wazwaz AM. Adomian decomposition for a reliable treatment of the EmdenFowler equation. Applied Mathematics and Computation. 2005;161(2):543–560.
9. Yucheng L. Adomian decomposition method with orthogonal polynomials: Legendre polynomials. Mathematical and Computer Modelling. 49(5-6):1268–1273.
10. Dehghan M, Hamidi A, Shakourifar M. The solution of coupled Burgers equations using AdomianPade technique. Applied Mathematics and Computation. 2007;189(2):1034–1047.
11. Wu J, Zhang Y, Chen L, et al. Uncertain analysis of vehicle handling using interval method, International journal of vehicle design. 2011;56(2011):81–105.
12. Tangaramvong S, Tin-Loi F, Yang C, et al. Interval analysis of nonlinear frames with uncertain connection properties, International Journal of Non-Linear Mechanics. 2016;86:83–95.
13. Alefeld G, Gnter M. Interval analysis: theory and applications. Journal of computational and applied mathematics. 121(1-2):421–464.
14. Fakharian A, HBMT, Davari A. Solving the Hamilton Jacobi Bellman equation using Adomian decomposition method., International Journal of Computer Mathematics, 2010;87:2769–2785.
15. Nouri K, Garshasbia J. Damirchi, Application of Adomian decomposition method to solve a class of di usion problem arises during MRI. Mathematical Sciences. 2014;2:207–218.
16. Frankowska H. Lower semi continuous solutions of Hamilton-Jacobi-Bellman equations. SIAM Journal on Control and Optimization. 1993;31:257–272.