Modern systems demand high computational power within limited resources. Approximate computing is a promising approach to design arithmetic units with tight resources for error-tolerant applications such as image and signal processing and computer vision. A floating-point multiplier is one of the arithmetic units with the highest complexity in such applications. Designing a floating-point multiplier based on the approximate computing technique can reduce its complexity as well as increase performance and energy efficiency. However, an unknown error rate for upcoming input data is problematic to design appropriate approximate multipliers. The existing solution is to utilize an error estimator relying on statistical analysis. In this paper, we propose new approximate floating-point multipliers based on an accumulator and reconfigurable adders with an error estimator. Unlike previous designs, our proposed designs are able to change the levels of accuracy at runtime. Thus, we can make errors distributed more evenly. In contrast to other designs, our proposed design can maximize the performance gain since reconfigurable multipliers are able to operate two multiplications in parallel once the low accuracy mode is selected. Furthermore, we apply a simple rounding technique to approximate floating-point multipliers for additional improvement. Our simulation results reveal that our new method can reduce area by 70.98% when error tolerance margin of our target application is 5%, and when its error tolerance margin is 3%, our rounding enhanced simple adders-based approximate multiplier can save area by 65.9%, and our reconfigurable adder-based approximate multiplier with rounding can save the average delay and energy by 54.95% and 46.67% respectively compared to an exact multiplier.

Keywords: approximate computing, multiplier, error tolerance, estimator, reconfigurable, floating-point

The computational demands of modern systems for scientific computing and social media have far exceeded the available resources.^1,2 To meet the computational demands within available resources, we are often struggling to reduce energy consumption and improve performance. However, we could stop struggling by using the approximate computing technique as long as our target applications are error-tolerant. Fortunately, many applications such as machine learning,³ image and signal processing,⁴ computer vision and big data analytics⁵ are intrinsically error-resilient. Without any shortcoming, we are able to apply the approximate computing technique to designing arithmetic units for error-resilient applications. Approximate arithmetic units are able to meet the computational demands of modern systems within the limited resources. Multipliers are the most-costly ones within arithmetic units regarding delay, area, power and energy consumption. In this paper, we propose efficient floating-point multipliers for error-resilient applications by using the approximate computing technique. To apply the approximate computing technique to arithmetic units, in advance, what we need to do is to break through a fundamental challenge. The approximate arithmetic units^6–12 alone cannot provide guarantees on error. kNN-CAM¹³ proposes to have an error estimator based on ML (Machine Learning) classifiers for upcoming input data. ML classifiers can guarantee error rates by estimating unknown input data error and help to determine the level of accuracy to minimize area and energy consumption while bounding to a maximum error rate. After training an error estimator based on ML classifiers with a large data set, the estimator can properly detect the number of mantissa bits (k, the level of accuracy) for an approximate floating-point multiplier. If k is large in the approximate multiplier, the level of accuracy is high. On the other hands, if k is small, the level of accuracy is lower than the multiplier with large k. Both can gain in performance and energy efficiency compared to an exact multiplier.

The error estimator based on ML classifiers can determine the best k values (optimal levels of accuracy) that are design clues, for any given input data with high accuracy. For bounding to a maximum error rate and relaxing the computational accuracy, each input pair has a different optimal level of accuracy. However, due to limits of hardware configurations, previous approximate multipliers cannot change the levels of accuracy at runtime. For a given data set, the optimal level of accuracy is determined simply by averaging over all best levels of accuracy.¹³ In other words, a single optimal level of accuracy for all input is fixed at design time regardless of upcoming input combinations. For various input pairs, all multiplications with the same level of accuracy cannot relax the computational accuracy as much as possible. Gains from approximate computing are restricted. Another problem is that having the fixed level of accuracy, which uses 3 as the universal level of accuracy for every input pair in¹³ could cause error biased when the optimal level of accuracy of input combinations are actually bigger than 3 for approximate multipliers. This problem can be solved by having multiple levels of accuracy at runtime. An approximate multiplier with multiple levels of accuracy makes errors distributed more evenly. Besides, having a single level of accuracy cannot be suitable for the applications such as CNNs (Convolutional Neural Networks), which requires different levels of accuracy in training and inference phases. Unless the approximate multiplier can alter the level of accuracy, an extra multiplier is required. Although ML classifiers are able to generate a dynamic quality control knob for each input pair, the existing approximate floating-point multipliers cannot deal with the dynamic quality control knob at runtime.

In this paper, a simple adder-based approximate multiplier with rounding is introduced. To alter the level of accuracy, an accumulator-based approximate multiplier and reconfigurable adder-based approximate multipliers are proposed. For our error estimator, the kNN algorithm is chosen due to its simplicity. The main characteristic of the kNN algorithm is high accuracy with a short computational time. Thus, the training phase is pretty shorter compared to other similar algorithms. By implementing the error estimator based on the kNN algorithm, we can prevent lengthy computational time in the training phase. In particular, our main contributions of this paper are as follows.

1. Present that a simple rounding technique for approximate multipliers reduces area, power, and delay further.
2. Present and compare an accumulator-based approximate multiplier and reconfigurable adder-based approximate multipliers, which deal with dynamic quality control knob at runtime.

A reconfigurable adder-based approximate multiplier does not have full flexibility like an accumulator-based approximate multiplier to choose the optimal level of accuracy for each input at runtime, but this design has the highest throughput and the lowest energy consumption among our proposed designs.

Cost function

To design the appropriate error estimator, it is necessary to have a cost function that relies on error rate, area, delay and power. The error rate is the percentage of the difference between the accurate and approximate results. The area, delay and power are extracted from Vivado 2015.2 of Xilinx.¹⁴ To obtain the optimal levels of accuracy of the given input data set, we need to customize the cost function. The customized cost function, Equation 1, should take into account the situation where the error rate is out of the error tolerance margin. It is fine to ignore the case where the error rate is lower than the lower bound that we determine. On the other hand, it is very critical that we force the cost function to infinite when we face the error rate higher than the error tolerance of target applications. By setting the cost function to infinite, we manage to eliminate this level of accuracy from the options of the optimal levels of accuracy. Based on the error tolerance margin of target applications, we choose the low and the up bounds in Eq. 1.

 A simple rounding

We want to show how a simple rounding technique can help our design reducing area, delay, and power. The conventional rounding method decides whether or not rounding occurs according to a fixed number of mantissa bits. To handle the number of mantissa bits that dynamically changes, the concept of a window is used. The window size indicates the maximum number of bits used for rounding. k is the number of mantissa bits considered in our approximate multiplier. To determine whether rounding up happens or not for dynamically changed k, k̂ is placed at the middle of the window. For window size 3, the least significant bit is used to determine whether or not rounding up occurs. For window size 5, the right-most two bits are considered. For example, when the right-most two bits are 10 or 11 in the window size 5, we execute the rounding up. When the two right-most bits are 01, rounding up does not happen since the maximum error increases in the worst case (i.e. the worst-case error is 000011 in mantissa when the optimal level of accuracy is set to 4).

An accumulator-based multiplier

An error estimator based on the kNN classifier can detect the optimal k value (the optimal level of accuracy) with high accuracy for each input data while bounding to a maximum error rate. However, because of the limits of its hardware configuration, as illustrated in Fig. 1a, for every input data, the universal level of accuracy is determined at design time. Fixing the level of accuracy at design time does not relax the computational accuracy for each input maximally to obtain performance gain. In contrast, if the optimal level of accuracy for each input can change at runtime, relaxing the computational accuracy can be maximized and then, the improvements can be amplified. To change the optimal level of accuracy for each input data at runtime, an accumulator-based multiplier, as illustrated in Figure 1B, is proposed.

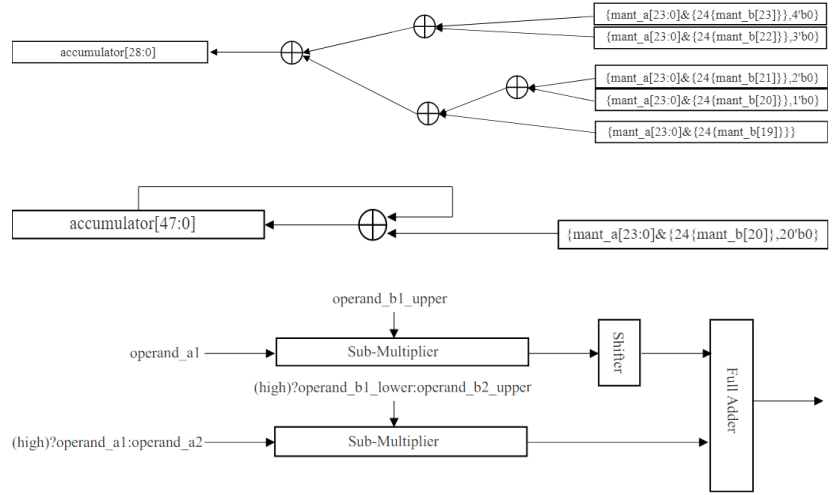
Figure 1 As examples, the level of accuracy is set to 4 in (a), the third iteration is shown in (b) and the reconfigurable adder-based multiplier is shown in (c).

Reconfigurable adder-based multipliers

An accumulator-based multiplier entirely utilizes the optimal levels of accuracy generated by the error estimator. However, it increases delay significantly for extra iterations improving accuracy. We propose reconfigurable adder-based multipliers, as illustrated in Fig. 1c, to suppress this problem by reducing flexibility of choosing the number of the optimal levels of accuracy at runtime. The reconfigurable adder-based multipliers have only two modes, high and low approximation modes. To implement reconfigurable adder-based multipliers, what we need to do first is to find an appropriate threshold. The proper threshold can be determined by the error tolerance margin of our target applications. When the error estimator predicts the optimal level of accuracy lower than a threshold for input data, the high approximate mode is selected in a reconfigurable adder-based multiplier. In parallel, two multiplications execute. On the other hand, if our estimator detects the best level of accuracy higher than a threshold for input data, the low approximation mode in a reconfigurable multiplier is determined. In this case, a single multiplication operates.

Furthermore, regardless of the error estimator, users can choose the levels of accuracy for some particular applications, which require higher or lower accuracy for every input pair. In this paper, we implement reconfigurable adder-based multipliers without and with rounding. The reconfigurable adders have k=1 & k=3, k=2 & k=5 and k=3 & k=7 (low & high accuracy modes).

A simple adder-based multiplier

Our input data set is created by using the uniform distribution. The input set consists of 2000 floating-point data randomly generated between 0 and100. To determine the level of accuracy of each input data pair, the error estimator based on kNN algorithm exploits the cost function from Equation 1. 90% of the given data set is for training the error estimator and the rest of them is used for testing the error estimator. According to our simulation, the accuracy of our error estimator is 93%. Figure 2 indicates the number of data belonging to a particular level of accuracy. From Figure 2, we find that for a simple adder-based multiplier, almost 30% of input pairs need higher accuracy (>3).

Figure 2 The number of data categorized into the optimal level of accuracy.

The average error rate of a simple adder-based multiplier is 3.26% and the average error rate of a simple adder-based multiplier with rounding is 3.15%. Figure 3a-3c summarizes the hardware characteristics of each design and Table 1 shows the error rate when the optimal level of accuracy (k) is fixed for all input data. When the error tolerance margin is 5%, we select either the simple k=3 or the simple k=2 with rounding. Choosing the simple k=2 with rounding can reduce the area by 7.57%, the delay by 2.91% and the energy by 9.45% compared to the simple k=3 without rounding. If the error tolerance margin is 1%, we select either the simple k=6 or the simple k=5 with rounding. Thus, by choosing the simple k=5 with rounding, we can save the delay by 3.47% and the energy by 4.27% compared to the simple k=6.

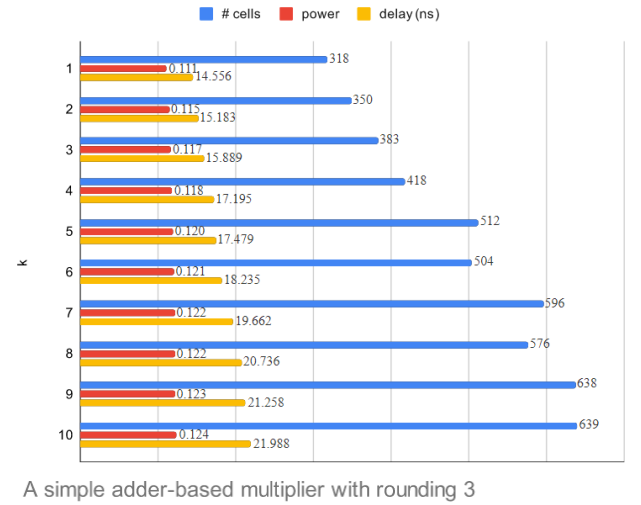
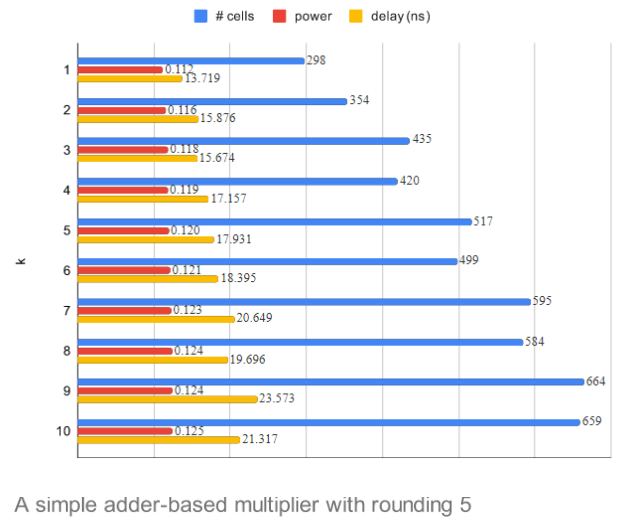
Figure 3 (a) is a simple adder-based multiplier, (b) is a simple adder-based multiplier with rounding (window size 3) and (c) is a simple adder-based multiplier with rounding (window size 5).

An accumulator-based multiplier

An accumulator-based multiplier is implemented to provide full flexibility to choose the optimal level of accuracy. The accumulator-based multiplier can alter the optimal levels of accuracy at runtime. Table 2 summarizes its hardware characteristics. The power and delay of the accumulator-based multiplier are much less than the simple adder-based multiplier. In the first iteration, it reduces the delay by 65% and energy by 48% when k=1. For the second iteration, it saves energy by 4.45% compared to the simple k=2 adder-based multiplier.

Reconfigurable adder-based multipliers

Reconfigurable k=1 & k=3, k=2 & k=5, and k=3 & k=7 adder-based multipliers without and with rounding are implemented. To realize reconfigurable adder-based multipliers, finding an appropriate threshold is indispensable. When the optimal level of accuracy predicted by the kNN error estimator is lower than a threshold, low accuracy mode is selected. Otherwise, high accuracy mode is determined. According to different thresholds, Fig. 4 illustrates average error rates and the number of data categorized into the specific level of accuracy. If the error tolerance of target applications is higher than the mean error of a reconfigurable adder-based multiplier, selecting the threshold with more data at lower levels of accuracy gives more opportunities to relax the computational accuracy, which results in high performance and high energy efficiency.

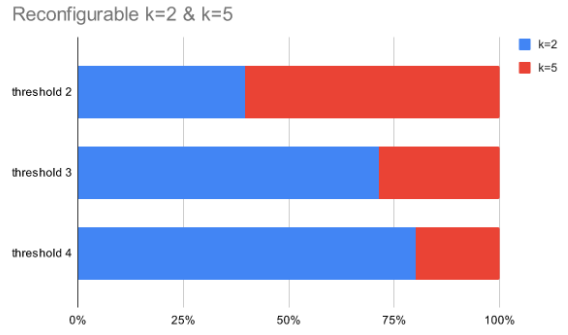
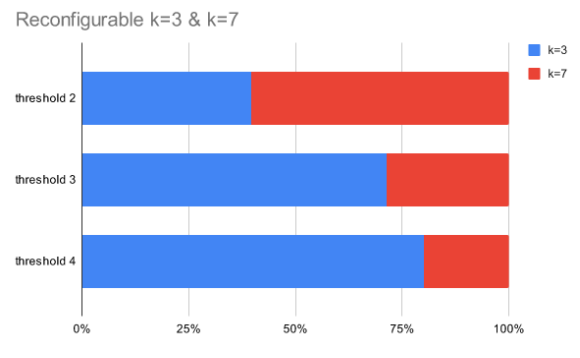
Figure 4 (a) is a reconfigurable adder-based multiplier (k=1 & k=3), (b) is a reconfigurable adder-based multiplier (k=2 & k=5), and (c) is a reconfigurable adder-based multiplier (k=3 & k=7).

Table 3 indicates the hardware characteristics of each design and the error rates when the error tolerance margin is 5%. A reconfigurable adder-based multiplier with rounding requires more area but the average delay is shorter than the simple one. The average delay of the reconfigurable adder-based multiplier (k=2 & k=5) with rounding is 30% less than the simple adder-based multiplier (k=2, delay=15.183ns), and the reconfigurable adder-based multiplier (k=3 & k=7) with rounding is 32% faster than the simple adder-based multiplier (k=3, delay=15.889ns). With regards to energy efficiency, the reconfigurable adder-based multiplier (k=2 & k=5) with rounding is 4.5% more efficient than the simple adder-based multiplier (k=2). When applications demand 3% as the error tolerance margin, feasible design choices are the reconfigurable adder-based multiplier (k = 2 & k = 5) without rounding and the reconfigurable adder-based multiplier (k = 3 & k = 7) without and with rounding. In terms of performance and energy efficiency, the reconfigurable adder-based multiplier (k = 3 & k = 7) with rounding is the best design option. It is 17.5% faster and 16.4% more energy-efficient than without rounding and 29.2% faster and 26.9% more energy-efficient compared to the reconfigurable adder-based multiplier (k = 2 & k = 5) without rounding.

In this paper, we develop runtime accuracy alterable approximate floating-point multipliers by using the different hardware configurations. Dissimilar to other designs, our proposed multipliers can change the level of accuracy at runtime. Our simulation results illustrate that the error estimator based on a machine learning algorithm can predict the optimal k values (levels of accuracy) with high accuracy for the input data set and while bounding to the maximum error rate, 5%, a simple adder-based multiplier (k=2) with rounding can save the area by 70.98%, the delay by 35.07%, and the energy by 44.6% compared to an accurate multiplier; while bounding to the maximum error rate, 3%, a simple adder-based multiplier (k=3) with rounding can reduce the area by 65.90%, and a reconfigurable adder-based multiplier (k=3 & k=7) with rounding can reduce the average delay by 54.95% and the energy by 46.67% compared to an accurate multiplier.

To achieve high performance and low energy consumption at the same time, it is mandatory that arithmetic units do not attempt to achieve unnecessary accuracy. Since every application does not require perfect accuracy, it is more than enough for arithmetic units to meet the required accuracy. Relaxing the computational accuracy with acceptable quality is the key to considerably improving performance and reducing energy consumption.

In future work, we should reflect on the potential improvement caused by approximating both operands. To realize this design, we need to find out a new hardware configuration that is suitable for altering the level of accuracy from both operands at runtime. We leave this for our possible future work.

None.

The authors declare there are no conflicts of interest.

1. Lu M. Arithmetic and logic in computer systems. 1st Ed. General & Introductory Computer Science. 2004:246.
2. Pathak R. A Review of Approximate Adders for Energy-Efficient Digital Signal Processing. IRJET. 2018;5(10):1895–1900.
3. Nazemi M, Pasandi G, Pedram M. Energy-efficient, low-latency realization of neural networks through Boolean logic minimization. IEEE. 2019:-6.
4. Huang J, Wang B, Wang W, et al. A surface approximation method for image and video correspondences. IEEE Transactions on Image Processing. 2015;24(12):5100–5113.
5. Sarwar SS, Srinivasan G, Han B, et al. Energy efficient neural computing: a study of cross-layer approximations. IEEE Journal of Emerging and Selected Topics in Circuits and Systems. 2018;8:796–809.
6. Miguel JS, Jerger NE. The Anytime Automaton. ACM/IEEE 43rd Annual International Symposium on Computer Architecture. 2016;44(3):545–557.
7. Rohani E, Xu J, Choi G, et al. Low-Power On-the-Fly Reconfigurable Iterative MIMO Detection and LDPC Decoding Design. Applied Mechanics and Materials Vols. 2014;496–500.
8. He C, Qin G, Lu M, et al. Group-Alignment based Accurate Floating-Point Summation on FPGAs. The European Regional Science Association. 2006;6:1–7.
9. Vahdat S, Kamal M, Afzali-Kusha A, et al. TOSAM: An Energy-Efficient Truncation- and Rounding-Based Scalable Approximate Multiplier. IEEE Transactions on Vary Large Scale Integration Systems. 2019;27(5):1161–1173.
10. Melchert J, Behroozi S, Li J, et al. SAADI-EC: A Quality-Configurable Approximate Divider for Energy Efficiency. IEEE Transactions on Vary Large Scale Integration Systems. 2019;27(11):2680–2692.
11. Imani M, Garcia R, Huang A, et al. CADE: Configurable Approximate Divider for Energy Efficiency. Automation & Test in Europe Conference & Exhibition. 2019.
12. Patel SK, B. Garg B, Rai SK. Power and Area Efficient Approximate Carry Skip Adder for Error Resilient Applications. Turkish Journal of Electrical Engineering & Computer Sciences. 2019;28(1):443–447.
13. Yan M, Song Y, Feng Y, et al. kNN-CAM: A k-Nearest Neighbors-based Configurable Approximate Floating-Point Multiplier. 20th Int’l Symposium on Quality Electronic Design. 2019.
14. Vivado Design Suite User Guide (UG910).