This paper considers a joint optimization problem of production and preventive maintenance for a serial production system subject to equipment degradations constrains. The system processes different job types to meet different customer demands. First, a joint optimization problem domain of the system with equipment degradations is formally introduced. A mathematic programming model is established with an optimal bi-objective function of minimizing the system makespan and preventive maintenance cost. Together with introducing an artificial bee colony theory, a novel bi-objective artificial bee colony algorithm is developed to pursue short production time and low preventive maintenance cost. To guarantee the algorithm convergence performance, a sorting rule of non-dominated sorting genetic algorithm II (NSGAII) is introduced into the proposed algorithm. Local Tabu search technology and probability criteria are involved. Finally, numerous experiments are conducted to evaluate the performance of the proposed algorithm. In comparison with the well-known NSGAII, the proposed algorithm performs significantly better in terms of finding the spread compromise solutions.

Keyword:scheduling, preventive maintenance, artificial bee colony algorithm, bi-objective

Over the years, enterprises are confronting an increasingly competitive market in price and quality of products with the quickening of the economic globalization contemporarily. Only by producing high-quality and low-cost products, can a manufacturing enterprise obtain an advantageous position under this situation. Therefore, production and fabrication, which directly determine the cost and quality of the products, are the key focus areas. A reasonable production schedule not only makes benefits to saving time and reducing unit cost, but also raises the production and energy efficiency. However, even if the products are processed according to an ideal optimal schedule, the machines could malfunction, which brings about quality defects. To lessen the failures occurring, preventive maintenance is introduced during the production processing.

With the due time limits of orders or jobs, how to schedule the production of jobs is always being the hot problem in the research field of production operation. Many real-world scheduling problems are naturally multi-objective.^1,2 Over years, efforts have been made in multi-objective flow shop scheduling problems (MOFSP) confronting a contradictory among different criteria.^3,4 More than that, an innovation or modification in algorithms springs up to solve the problem more efficiently,^5-8 and gains practical results.

It has been noted that an optimized production scheduling is hardly independent with preventive maintenance. However, with regards to preventive maintenance itself, it does not make the problem any easier.⁹ Taking no sufficient PM operations may lead to frequent machine failure, however, too much will increase total cost, both of which decrease the efficiency of production system. Therefore, making a rational decision for preventive maintenance is challenging but significant for manufactural enterprises. Studies can be summarized in term of their objects. Preventive maintenance policy is discussed for single machine,¹⁰ two-stage flow shop¹¹ or flowshop,^12,13 respectively.

It is worthy to note that almost all the literatures mentioned above adopt a perfect-maintenance policy, that is, the preventive maintenance measures make the condition or the age of machine as-good-as-new. However, in many cases, when machines operate in long-term orders, it is inevitably to result in the degradation of the machine, reflecting in the increase of its service age. Researchers have taken some imperfect maintenance in the manufacturing system into account. Considering manufacturing system in an excessive environment, the degradation of the machines cannot be neglected.^14,15 During the entire life cycle, reliability and availability of the machine decreases,¹⁶ so the preventive maintenance is apparently nonperiodic, which makes the problem complicated but practical.¹⁷ Moreover, combined with random shocks,¹⁸ deteriorations of machines often result in quality of products.¹⁹ It thus can be seen, under particular situations, deteriorations are non-negligible and significant.

While planning the scheduling in production system, a crucial issue should be noticed that machines may malfunction from time to time due to various of inducements, sometimes with non-negligible degradations. Breakdowns together with maintenance bring out loss of time and damage of the quality of products, even a stoppage of whole production system.²⁰ Thus, the proactive measure, preventive maintenance, must be adopted to reduce the breakdowns. Besides, either of productive processes or maintenance activities occupy machines running time, so both are supposed to be scheduled simultaneously. A great many efforts have been done in integrated scheduling. The study first begins with the single-machine problem. Researchers present integrated scheduling models considering both production scheduling and preventive maintenance planning for a single-machine problem,²¹ with the bi-objective aiming to minimize the maximum weighted tardiness, and flexible maintenance time is subjected to the degradation of the machine. Other bi-objectives, like robustness and stability,²² makespan and flow time²³ is also been studied. Correspondingly, models are built targetedly to be better fit for real problem. As the production processing is uncertainly, a random demand²⁴ or a random yield²⁵ may all occur. Meanwhile, with the uncertainty of the production system, it is effective to notice and apply the learning and forgetting effects.²⁶ Some studies emphasize the deterioration of machines due to various inducements and place a flexible interval between preventive maintenance within the integrated scheduling.^27,28 However, few of the real production systems is single machine, the most probable manufacturing system is flow shop. Two or more machines are installed in series in a certain order and each job is processed by each machine successively. This is what we called flow shop. Flow-shop system consists of single machines, so the studies of single machine are partly the basic. But it is not the simple pile of single machines, because some new factors emerge, like the interactions between machines, the impact of one machine to the whole system, and consideration of job sequencing. As its complexity and practicability, flow shop integrated scheduling problem gains a mass of attentions. The studies begin with the simplest form, two-machine flow shop, or two-stage flow shop. A perfect maintenance is adopted with periodic preventive maintenance,²⁹ while an imperfect maintenance is also concerned considering degradations of machines.³⁰ Furthermore, multi-machine flow shop problem is simultaneously investigated. Decision-making method for preventive maintenance is interchangeable in joint optimization. A condition-based maintenance policy is adopted with consideration of product quality.³¹ And heuristic algorithms for job sequencing can be applied and extended in integrated optimization to for job together with maintenance scheduling to gain an optimization like a minimum makespan.³² Some special situations are considered, like rush orders,³³ group production³⁴ or degradations of machines,³⁵ to correspond to reality. An integrated optimization combined with both production scheduling and preventive maintenance takes more elements into consideration and is proved to be more grounded.

As far as we know, till now, few of the latest investigations of integrated optimization concern the deterioration of machines. A few concerned without considering the inducement of deterioration, like processing speed of machines, and how it can influence the degrading process. But this procedure does exist in the real production processing, makes it practical to study the integrated scheduling under degradation subjected to processing speed.

This paper focuses on the integrated optimization of production and maintenance for serial production systems, subjected to the degradation resulting from processing speed. Based on reliability theory, two-parameter Weibull distribution is performed to simulate machine failure mode, a maintenance policy is provided on account of the period expectation value of preventive maintenance. Then an integrated scheduling model is built with bi-objective of minimizing makespan and maintenance cost. Based on artificial bee colony algorithm (ABC), a bi-objective artificial bee colony algorithm (BABC) is developed to solve decision-making problem of scheduling. Various problems scales are provided to evaluate the proposed algorithm, and several criteria are investigated to compare it with other algorithm. Numerical examples verify BABC is more efficient in finding non-dominated solutions compared with famous NSGAII and capable to get a superior result in finding Pareto front in quality and distributivity of solutions.

The rest of this paper is organized as following. In Section 2, the bi-objective model is formulated based on problem description and assumptions. Section 3 focuses on the construction of the algorithm step by step. An illustrative example and index analysis are given in Section 6 to verify the efficiency of the algorithm.

Assumptions

It is assumed that there are N jobs $\left(o_1,o_2,\dots ,o_n\right)$ during the scheduling, each of the jobs is processed by M machines $(M_1, M_2, \mathrm{....},M_n)$ successively. To describe the problem efficiently, some assumptions are summarized.

Assumption 1: The speed of processing is changeable due to actual conditions, which are simplified down to two different processing modes as follows.

Definition 1: Driving processing mode: The machines are processing at the top speed under the precondition of ensuring the quality. Accordingly, there are risks of high abrasion and failure rate.

Definition 2: Normal processing mode: The machines are processing at the standard speed under the precondition of ensuring the quality to meet the requirements.

Machines can freely switch their modes, of which time is negligible. Due to Assumption 1, actual machining process can be formulated as follows

$P_{ij}=p_{ij}^{*}\left(1-Z_{ij}\right)+p_{ij}^{\text{'}*}{Z}_{ij}$ (1)

$p_{ij}\ge p_{ij}^{\text{'}}$ (2)

Assumption 2: The processing operations are uninterruptible, each machine is preventively maintained at every interval between two consecutive operations.

Assumption 3: Machines are unreliable, whose failure intervals accord with Weibull distribution.

Assumption 4: Machines are not as-good-as-new after the PM is done but can be used immediately.

Assumption 5: A periodic expectation policy of preventive maintenance is adopted and defined as follows.

Definition 3: PM Expectation: in a PM interval, the optimal state of a machine ${\theta }_0$ gradually deteriorates to the state ${\theta }_t$ urgent to be maintained, while the states are discrete. Each state has a corresponding PM expectation $E(\theta ),$ i.e. $E\left({\theta }_0\right)=0$ , $E\left({\theta }_t\right)=1$ .

According to Assumption 3, the failure risk of the machine at normal processing mode can be formulated as follows.

$f(t)={\int }_0^t\lambda (t)dt={\int }_0^t[\frac{\beta }{\eta }{(\frac{t}{\eta })}^{\beta -1}]dt={(\frac{t}{\eta })}^{\beta }$ (3)

β Is Weibull shape parameter and η is Weibull scale parameter, both of which can be gained by statistical analysis of historical failure data. In the preventive maintenance interval τ, the time-to-repair of machine $M_j$ is assumed to be t_r, and the time of PM operation to be t_p. The optimal PM interval of machine under steady state can be derived (Zhou et al., 2007).

$T_o{}_p=\eta {[\frac{t_p}{t_r(\beta -1)}]}^{\frac{1}{\beta }}$ (4)

According to definition 3, the index of PM expectation of machine M_j in unit time is as follows.

${\theta }_j=\frac{1}{To{p}_j}$ (5)

Derived from Definition 1,2, machines deteriorate at different level under different processing modes. Accordingly, the PM expectation under driving processing mode in unit time is relatively high.

$\theta {\text{'}}_i={\theta }_j*K(K>1)$ (6)

Therefore, the increment of the PM expectation after process j is completed can be obtained by multiplying each PM expectation in unit time with corresponding processing time under different modes.

$E\left(\text{Δ}{\theta }_j\right)=\left\{{\theta }_j*T or {\theta }_j^{\text{'}}*T^{\prime }\right\}$ (7)

The expression (7) synthesizes the combined influence of processing state and processing time of the machines and can reflect various deterioration of machines under different processing speed. A sum is obtained by cumulative adding indexes of PM expectation among total processes of the machine. Derived from definition 3, the value of sum is 1 means confronting an urgent need of repairing, a PM should be operated. Moreover, one more assumption is given.

Assumption 6: If PM is strictly operated when the sum reaches 1 (or less than 1), therefore, no failure occurs between two consecutive PM; otherwise, if the value of the sum is more than 1 while maintaining, then a major failure may occur in the exceeding time. Figure 1 demonstrates the PM policy.

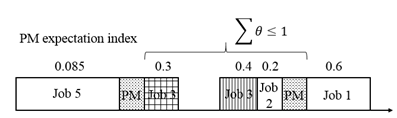
Figure 1 An example of the PM-index-based policy.

In Figure 1, blanks on the time axis indicate idle of the machine, at which the deterioration of the machine is neglected, so no index should be added as well. Moreover, as for assumption 4, a certain value of the index will be given in later study.

Mathematical modeling

Based on the definitions and assumptions above, a bi-objective productive maintenance and scheduling model is built in this section.

1. Objective function

Production objective: minimizing total completion time

$f_1=\min \left\{\max (c_{ij})\right\}$ (8)

Preventive maintenance objective: minimizing the cost of PM

$f2=\min \left\{c\right\}$ (9)

2. Productive constraints

$\{c_{(i+1)j}\ge c_{ij}+p_{ij}{c}_{ij}\ge o$ (10)

$C_{\left(j+1\right)i}\ge C_{ij}+P_{ij}{C}_{1j}\ge P_{i1}$ (11)

Equation (10) is machine constraint that each machine can’t process the next job unless the current job is completed. Equation (11) indicates the completion of the process, each job is processed according to the scheduled procedures with no preemption. The processing time P in Equation (10) and Equation (11) can be inferred by Equation (1). The completion time C can be obtained as follows.

Completion time:

$C_{ij}=S_{ij}+P_{ij}$ (12)

Start time:

$s_{ij}=\max \left\{c_{(i-1)j}+y_{ij}*t_p,c_{(j-1)i}\right\}$ (13)

3. Preventive maintenance constraints

According to assumption (4), after each PM operation, the residuary deterioration extent of machine increases with the increase of the times of PM operations. Thus, the assumption (4) is much more realistic compared with as-good-as-new. The residuary deterioration extent of machine after the Lth PM is expressed as follows.

$D_l=D_o+Num*a$ (14)

$D_0=0$ , $Num={\displaystyle {\sum }_{i=1}^l{Y}_i{}_j}$ , α is the parameter of one-time deterioration of PM.

The PM expectation index after each process is finished can be inferred from Equation (1) and Equation (7).

$E\left(\theta \right)=\theta *P_{ij}*\left(1-Z_{ij}\right)+{\theta }^{\prime }*p_{ij}^{\text{'}}\text{*}{Z}_{ij}$ (15)

Thereout, the expression of PM constraints can be formulated.

$D_l+\left(1-H_{lk}\right){\displaystyle \sum }_{m=l}^k{\displaystyle \sum }_{i=1}^n{X}_{im}E\left(\theta \right)\le 1$ (16)

4. Cost constraints

This paper considers cost factors including the fixed cost of PM, the tardiness cost due to PM operations and the penalty cost due to the wasted capacity by premature PM. If M_c expresses the left part of Equation (16).

$M_c=D_l+\left(1-H_{lk}\right){\displaystyle \sum }_{m=l}^k{\displaystyle \sum }_{i=1}^n{X}_{im}E\left(\theta \right)$ (17)

Then the total cost can be presented as follows.

$D_l+\left(1-H_{lk}\right){\displaystyle \sum }_{m=l}^k{\displaystyle \sum }_{i=1}^n{X}_{im}E\left(\theta \right)\le 1$ (18)

To solve a combinatorial optimization problem like flow shop sequencing, a heuristic algorithm is needed. A branch of algorithms that simulate natural phenomenon has been focused, like Ant Colony Algorithm or Genetic Algorithm. These algorithms utilize swarm intelligence that interactional individuals are able to organize themselves. Based on intelligent honey-gathering behaviors of honey bees,³⁶ proposed ABC (Artificial bee colony algorithm) to optimize multivariate functions.³⁷ It is developed promptly and being widely employed and practiced these years due to its simple actions, few control variables and convenient effectuation.³⁶ However, as efficient as it is for single objective optimization, ABC is not capable for bi-objective problems because a non-dominated solution sets are demanded. Thus, a bi-objective artificial bee colony algorithm (BABC) is proposed based on the frame of ABC and combined with non-dominated sorting principal, local Tabu algorithm and Probability acceptance criterion. The optimal Pareto solution sets are found aiming the characteristics of required problem.

The core operations of BABC mainly are encoding, honey source initialization, neighborhood structure and Tabu search, etc. Flow chart of BABC is shown in Figure 2 to make a clear demonstration. Specific steps are as follows

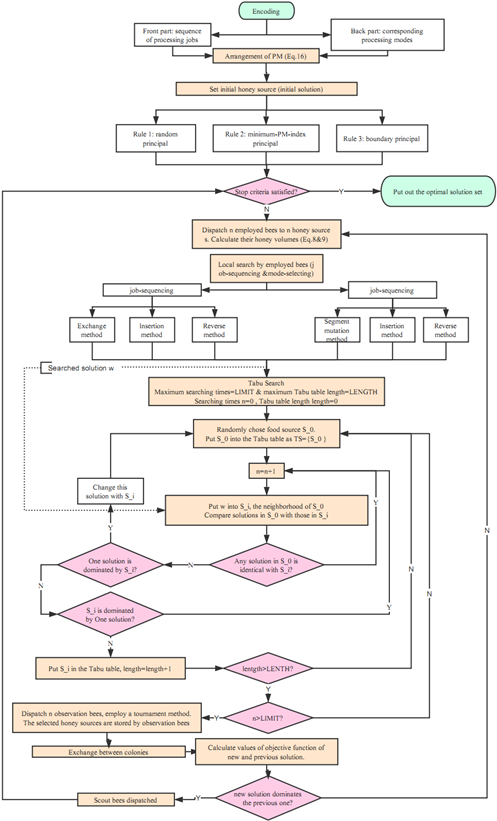
Figure 2 Flow chart of BABC.

Step 1 Encoding

The problem is a bi-objective problem, involving two parts of the decision variables including the productive part containing the processing sequence of the jobs and processing modes, and the maintenance part mainly containing arrangement of PM operations. For the former, a double nested encoding method is adopted, a real-value coding is adopted by the front part for the sequence of processing jobs, and a binary coding is adopted by the back part for choosing the processing modes in which value 0 means normal processing mode and value 1 means driving processing mode. A mapping is established between the front and back parts. Figure 3 demonstrates a job-processing sequence of 3-2-1-4-5 with the corresponding mode of 0-1-1-0-0.

Figure 3 An example for encoding the source.

For the latter, the arrangement of PM operations, a matrix is proposed to express. If there are N jobs processed on M machines, then the total amount of positions to arrange PM is M*N which can be expressed by the matrix as follows.

$PM=\left[\begin{array}{cc}\begin{array}{cc}p{m}_{11}& \dots \\ ⋮& \ddots \end{array}& \begin{array}{ccc}p{m}_{1j}& \dots & p{m}_{1n}\\ ⋮& \ddots & ⋮\end{array}\\ \begin{array}{cc}p{m}_{i1}& \dots \\ ⋮& \ddots \\ p{m}_{m1}& \dots \end{array}& \begin{array}{ccc}p{m}_{ij}& \dots & p{m}_{in}\\ ⋮& \ddots & ⋮\\ p{m}_{mj}& \dots & p{m}_{mn}\end{array}\end{array}\right]$

If $p{m}_i{}_j=1$ then there is a PM operation on the machine  after finishing processing job j; otherwise,$p{m}_{ij}=0$ means no PM is placed. The value of pm_ij is according to Equation (16).

Step 2 Honey source initialization

The initial solution has a significant impact on the searching of intelligent algorithm. Therefore, three rules are employed to generate the initial honey source.

Rule 1 random principal, the jobs is sorted randomly with a corresponding random processing mode.

Rule 2 minimum-PM-index principal, the PM expectation indexes of different modes are calculated respectively, the smaller index determines the value 0/1, then a SPT principal³⁸ is used for sequencing the jobs.

Rule 3 boundary principal, SPT and random principal are employed to sort the jobs, and value 0 or 1 are chosen for the modes respectively.

Step 3 Employed bees dispatched

 There are n employed bees dispatched and each one corresponds a honey source. The volumes of the honey under different objectives are recorded according to Equation (8) and Equation (9).

Step 4 Local search by employed bees

Three methods are employed to construct the neighborhoods while searching the present honey source area and sorting the jobs as follows.

1. Exchange method: two jobs are chosen randomly then exchange positions with each other.
2. Insertion method: two jobs are chosen randomly, all the jobs after the second job are inserted before the first job.
3. Reverse method: two jobs are chosen randomly, the jobs between them are arranged in reverse order.

As for the partial change for the processing modes, three similar methods are adopted as insertion method, reverse method and segment mutation method, which is choosing to positions randomly and mutating the value on the segment between the positions, that is, value 0 turns to 1 and value 1turns to 0.

Step 5 Tabu Search

Tabu search is proved to be successfully applied in the field of finding solutions for large combinatorial optimization problem.³⁹ Therefore, TS is adopted as local search to find new honey sources in the proposed algorithm.

1. The maximum times of searching LIMIT and maximum length LENGTH of the Tabu table are set.
2. A randomly chosen food source is the present solution and is put into the Tabu table as $TS=\left\{s_0\right\}$
3. The solution of Step 4 is put into the S_i, the neighborhood of S_o.
4. The solution in S_i is compared with the present solutions of TS respectively.
1. If there is an identical solution as S_i, then the times of searching n is added to (n+1). Then return to (3) and restructure the neighborhood.
2. If all the solutions differ from S_i, the dominance relations between S_i and the present table are considered. If there is one solution dominated by S_i, then change this solution with  and return to (2). If S_i is dominated by one solution, then the times of searching n is added to (n+1), then return to (3). If there is no dominance relation between S_i and all solutions in present table, then put S_i in the Tabu table, length is added to 1.
3. If length is larger than LENGTH, then go to (6); otherwise, return to (2).
5. If n is larger than LIMIT, then go to (6); otherwise, return to (2)
6. Search is complete, then put out solutions in Tabu table.

Step 6 Observation bees dispatched

There are n observation bees dispatched, and a tournament method is employed. Two pieces of randomly chosen honey-source information are calculated respectively on their value of objective. Non-dominated sorting principal is adopted to separate the honey sources by their quality.³⁹ If two honey sources belong to different layers, then the source in lower layer is selected. If two sources belong to the same layer, then a crowding distance is calculated and the source which has a larger distance is selected. The selected honey sources are stored by observation bees.

Step 7 Exchange between colonies

To structure new honey sources, a crossover operation is done between the honey sources carrying by two randomly chosen observation bees while exchanging information.

Due to enhance the search capability of bee colonies, probability acceptance criteria of simulated annealing algorithm (SA) is employed to update the optimal solution set. Firstly, the values of objective function of new and previous solution are calculated, if the new solution dominates the previous one, then the new solution is adopted, otherwise, the new solution is adopted by a probability $exp\left(-\text{Δ}E/T\right)$ , while $\Delta E=min\left(\text{Δ}{E}_i\right)$ , $\text{Δ}{E}_i=f_i\left(S^{\prime }\right)-f_i\left(S\right)$ indicating a different value under a certain objective, and Τ indicating a temperature parameter affected by time. If the solution is not adopted, then change the observation bees to scout bees and return to Step 8.

Step 8 Scout bees dispatched

Step 9 Judgments of breaking the loop

If the conditions are met to break the loop, then put out the optimal solution set. Otherwise, change the scout bees to employed bees and return to Step 3 continuing the loop.

A pseudo-code of BABC is given in Figure 4 to show its core operations. $X_1^G$ is one of n solutions in the Gth generation.$fitnes{s}_i$ is the criteria to evaluate current solution. ITERA is the current number of iterations, and maxITERA is the maximum number of iterations. A solution set $N_i^G$ is found in the neighbor of $X_1^G$ . limit is the current number of searching times in Tabu search, and LIMIT is the maximum number. rand(1,2,3) is a number selected from 1, 2 or 3 randomly. The final solution and current number of iterations are output.

Figure 4 Pseudo-code of BABC.

To prove the efficiency of the algorithm, the proposed BABC is analytically compared with classic NSGA-II. NSGA-II is a commonly used algorithm for solving multi-objective at present and is widely applied in many domains. We used MATLAB 2010b programming language to implement two algorithms, the simulation experiment was carried out on a PC with a memory of 4G and a main frequency of 2.5ghz.

Researchers investigate integrated scheduling of production and maintenance with a single objective.⁴⁰ In this paper, parameters are adjusted according to features of the problem, and are set as follows. The processing time of each procedure obeys distribution U(50,100), index k obeys distribution U(1.1,1.3), the time of operating preventive maintenance obeys U(15,20). Weibull parameters $\theta =U\left(100,150\right)$ and $\beta =U\left(2,4\right)$ . The deteriorated factor $\text{α}=U\left(0.002,0.005\right)$ . The unit cost of preventive maintenance $c_p$ is 8; unit cost of ability penalty $C_w$ is 30. Scale of the problem is as follows. The set of jobs is$\left\{5,10,20,50,100\right\}$ and the set of machines is $\left\{5,10,15,20\right\}$ . Thus, there are 20 kinds of problem scales with 15 numerical examples, 300 numerical examples in totally.

As for solving multi-objective optimization problem in engineering, it is often required a fast-convergent solution set with high quality, stability and uniformity. According to³⁶ different algorithms have different structure modes, so it is impractical and incomparable to contrast the algorithms by same iteration cycle.³⁶ Therefore, the following parameters of all the algorithms in this paper are contrasted using objective function vector under the condition of same calculating time.

C matrix

C matrix is a widely applied parameter to evaluate the Pareto curve.³⁶ The formulation, $C\left(A,B\right)=\frac{\left|\left\{b\in B|\exists A:B\prec a\right\}\right|}{\left|B\right|}$ , presents the proportion of the fronts of B which are dominated by at least one individual of A in overall B. If C=1, then every solution in B is dominated by at least one solution in A. If C=0 then no solution in B is dominated by any solution in A. Table 1 and Figure 5 indicates the comparison between the frontier curve presented by BABA and the one presented by NSGAII.

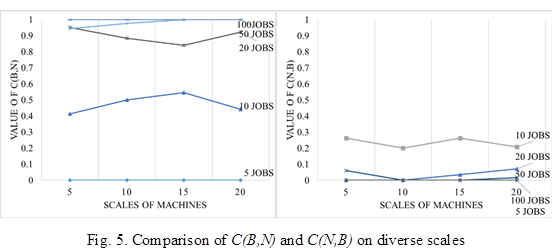
Figure 5 Comparison of C(B,N) and C(N,B) on diverse scales.

According to Table 1, both algorithms can obtain Pareto optimal fronts with small problem scales as values of C matrix are all 0. As is mentioned above, if C(A,B)=0, or tends to be 0, it means all solutions in B are non-dominated, that B performs more effective than A. Figure 5 indicates the tendency that, as the problem scales largen, BABC get more non-dominated solutions with respect to NSGAII. On the contrary, solutions gained by NSGAII tend to be dominated by BABC.

More numerical experiment results are shown in Figure 6. In small scales, a superposition between the Pareto fronts of those two algorithms indicates that the solution sets of those are mutual nondominated. Nevertheless, BABC manifests superiority with increase of problem scales. In the problem with 10 jobs, each algorithm has dominated solutions and a superposition is found between solution sets. With the enlargement of problem scales, all the front solution presented by NSGA2 are dominated by those presented by BABC. The effectiveness of the proposed algorithm BABC is verified.

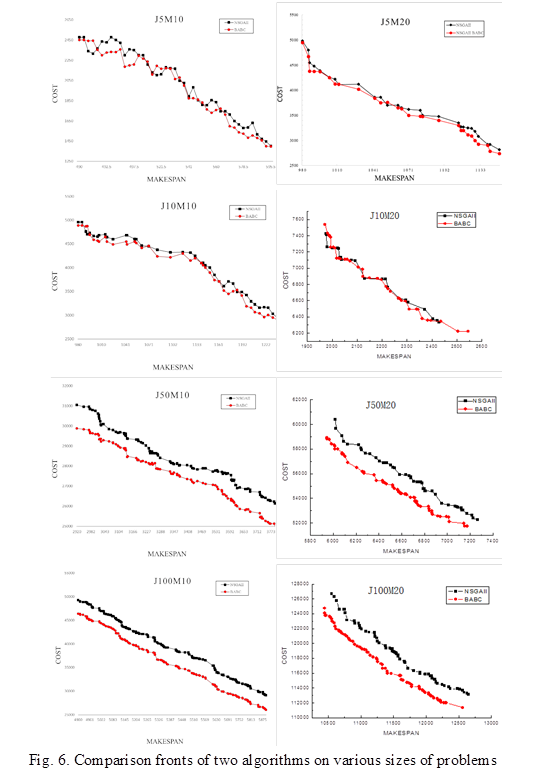
Figure 6 Comparison fronts of two algorithms on various sizes of problems.

${\sigma }_{sp}$

To evaluate distributivity of non-dominated solution set in Pareto front objective space, a parameter ${\sigma }_{sp}$ is adopted, and its formulation is as follows.

${\sigma }_{SP}=\sqrt{\frac{1}{n-1}}{\displaystyle {\sum }_{i=1}^n{(d_i-\overline{d})}^2}$ (19)

$d_i=mi{n}_{i,j\ne i}\left[{\displaystyle \sum }_{k=1}^K\left|f_k\left(x_i\right)-f_k\left(x_j\right)\right|\right],\stackrel{�}{d}={\displaystyle \sum }_{i=1}^n{d}_i/n$ (20)

n is the amount of non-dominated solutions presented by algorithms in Pareto front.$f_k\left(x_i\right)$ is the Kth objective function of individual x_i. K is the amount of total objective functions, K=2 in this paper. Therefore, the smaller is ${\sigma }_{SP}$ , the better is the distributivity of solution set. Table 2 indicates comparison of ${\sigma }_{SP}$ between two algorithms.

As is shown in Figure 7, all the solution sets compared have a good distributivity because they are Pareto front solutions gained after a considerable amount of calculations. Thus, a distinct difference can be seen that ${\sigma }_{BABC}$ is smaller than ${\sigma }_{NSGAII}$ . Thus, a better distributivity of BABC is proved.

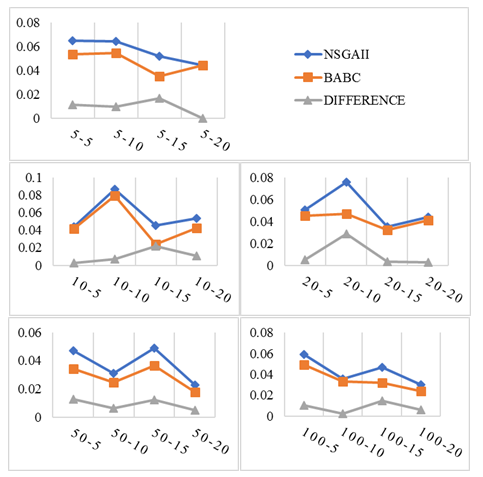
Figure 7 Comparison of σ_sp between two algorithms of various scales.

The solution sets of two algorithms are Pareto front solutions summarized respectively after multiple calculations, so both solution sets are equally distributed overall. However, ${\sigma }_{BABC}$ is smaller than ${\sigma }_{NSGAII}$ according to the table.

In general, the algorithm BABA proposed by this paper is superior to NSGAII in quality and distributivity of solutions and obtains satisfactory results to the raised problem. It also performs a well adaptation to scheduling model of the problem, brings steady solutions and proves its effectiveness.^41-44

In this paper, a mathematical programming model of flow shop scheduling with equipment degradations is proposed with objectives of minimizing makespan and preventive maintenance costs. Efforts have been made in the integrated model of job sequencing and preventive maintenance. Besides, variety of processing modes is considered and as one of the variables. A bi-objective algorithm, BABC, is developed and proved to be superior to NSGAII in the distributivity of Pareto front solutions. Satisfied results are gained by experiments in various scales of problems.

 Producers can select appropriate scheduling plans according to processing speed, degree of degradations, processing mode or size of order to achieve a demanded production processing, like minimum makespan or minimum preventive maintenance costs.

Researchers can be inspired by diverse inducements of machine degradations and minimize harmful impact for production instruction. In the research of this paper, the changeable speed is simplified discretely, and Weibull distribution is adopted to simulate equipment degradations. In future, a continuity of the speed, other degradation distribution and the robustness of results can be investigated in the following study.

None.

None.

The author declares there are no conflicts of interest.

1. Yenisey MM, Yagmahan B. Multi–objective permutation flow shop scheduling problem: Literature review, classification and current trends. Omega. 2014;45:119–135.
2. Talbi EG, Basseur M, Nebro AJ, et al. Multi–objective optimization using metaheuristics: Non–standard algorithms, International Transactions in Operational Research. 2012;19(1–2):283–305.
3. Geiger MJ. On operators and search space topology in multi–objective flow shop scheduling. European Journal of Operational Research. 2007;181(1):195–206.
4. Allouche MA, Aouni B, Martel JM, et al. Solving multi–criteria scheduling flow shop problem through compromise programming and satisfaction functions. European Journal of Operational Research. 2009;192(2):460–467.
5. Dhingra A, Chandna P. Multi–objective flow shop scheduling using hybrid simulated annealing. Measuring Business Excellence. 2010;14(3):30–41.
6. Satyanarayana D, Pramiladevi M. Multi–criteria M–machine SDST flow shop scheduling using modified heuristic genetic algorithm. International Journal of Industrial and Systems Engineering. 2016;22(4):409–422.
7. Spanos AC, Ponis ST, Tatsiopoulos IP, et al. A new hybrid parallel genetic algorithm for the job–shop scheduling problem. International Transactions in Operational Research. 2014;21(3):479–499.
8. Han YY, Gong DW, Jin YC, et al. Evolutionary multi–objective blocking lot–streaming flow shop scheduling with interval processing time. Applied Soft Computing Journal. 2016;42:229–245.
9. Percy DF, Alkali BM. Scheduling preventive maintenance for oil pumps using generalized proportional intensities models. International Transactions in Operational Research. 2007;14(6):547–563.
10. Hu JW, Jiang ZH, Liao HT. Preventive maintenance of a single machine system working under piecewise constant operating condition, Reliability Engineering & System Safety. 2017;168:105–115.
11. Seidgar H, Zandieh M, Mahdavi I. Bi–objective optimization for integrating production and preventive maintenance scheduling in two–stage assembly flow shop problem. Journal of Industrial and Production Engineering. 2016;33(6):404–425.
12. Xiao L, Song SL, Chen XH, et al. Joint optimization of production scheduling and machine group preventive maintenance. Reliability Engineering & System Safety. 2016;146:68–78.
13. Cui WW, Lu ZQ, Li C, et al. A proactive approach to solve integrated production scheduling and maintenance planning problem in flow shops. Computers and Industrial Engineering. 2018;115:342–353.
14. Zhou BH, Liu ZL. Optimizing preventive maintenance: A deteriorating system with buffers. Industrial Management & Data Systems. 2016;116(8):1719–1740.
15. Huang HF, He Y, Li D. EPQ for an unreliable production system with endogenous reliability and product deterioration. International Transactions in Operational Research. 2017;24(4):839–866.
16. Dohi T. Availability and performability analysis for a service degradation process with condition–based preventive maintenance I – formulation and optimization. International Journal of Strategic Engineering Asset Management. 2014;2(1):80–97.
17. Ben–Salem A, Gharbi A, Hajji A. Environmental issue in an alternative production–maintenance control for unreliable manufacturing system subject to degradation. International Journal of Advanced Manufacturing Technology. 2015;77(1–4):383–398.
18. Wang YP, Pham H, Imperfect preventive maintenance policies for two–process cumulative damage model of degradation and random shocks. International Journal of Systems Assurance Engineering and Management. 2011;2(1):66–77.
19. Chen Z, Li Y, Pan E. Joint optimization of degradation–based burn–in, quality, and preventive maintenance. IEEE International Conference on Industrial Engineering and Engineering Management. 2016;1397–1401.
20. Rahim A, Shakil M. A tabu search algorithm for determining the economic design parameters of an integrated production planning, quality control and preventive maintenance policy. International Journal of Industrial and Systems Engineering. 2011;7:477–497.
21. Pan ES, Liao WZ, Xi LF. Single–machine–based production scheduling model integrated preventive maintenance planning. International Journal of Advanced Manufacturing Technology. 2010;50(1–4):365–375
22. Lu ZQ, Cui WW, Han XL. Integrated production and preventive maintenance scheduling for a single machine with failure uncertainty. Computers and Industrial Engineering. 2015;80:236–244.
23. Xu SL, Wang LY. Single–machine production scheduling integrated preventive maintenance planning for minimizing makespan and flow time. 2016 IEEE International Conference on Industrial Engineering and Engineering Management. 2016;1513–1517.
24. Sloan TW. A periodic review production and maintenance model with random demand, deteriorating equipment, and binomial yield. Journal of the Operational Research Society. 2014;55:647–656.
25. Xiang YS, Cassady CR, Jin TD, et al. Joint production and maintenance planning with machine deterioration and random yield. International Journal of Production Research. 2014;52(6):1644–1657.
26. Pan ES, Wang GN, Xi LF, et al. Single–machine group scheduling problem considering learning, forgetting effects and preventive maintenance. International Journal of Production Research. 2014;52(19):5690–5704.
27. Wang SJ. Integrated model of production planning and imperfect preventive maintenance policy for single machine system. International Journal of Operational Research. 2013;18(2):140–156.
28. Cheng GQ, Zhou BH, Li L. Joint optimisation of production rate and preventive maintenance in machining systems. International Journal of Production Research. 2016;54(21):6378–6394.
29. Seidgar H, Zandieh M, Mahdavi I. An efficient meta–heuristic algorithm for scheduling a two–stage assembly flow shop problem with preventive maintenance activities and reliability approach. International Journal of Industrial and Systems Engineering. 2017;26(1):16–41.
30. Wang SJ, Liu M, Two–machine flow shop scheduling integrated with preventive maintenance planning. International Journal of Systems Science. 2015;47(3):672–690.
31. Lee S, Ni J. Joint decision making for maintenance and production scheduling of production systems. International Journal of Advanced Manufacturing Technology. 2013;66(5–8):1135–1146.
32. Khatami M, Zegordi SH. Coordinative production and maintenance scheduling problem with flexible maintenance time intervals. Journal of Intelligent Manufacturing. 2017;28(4):857–867.
33. Chiu YF, Shih CJ. Rescheduling strategies for integrating rush orders with preventive maintenance in a two–machine flow shop. International Journal of Production Research. 2012;50(20):5783–5794.
34. Liao WZ, Jiang M, Zhang XF. Group production scheduling model with due window and maintenance. 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM). 2017:588–592.
35. Hariga MA, Azaiez MN, Daya MB. A discounted integrated inspection–maintenance model for single deteriorating production facility. International Transactions in Operational Research. 2006;13(4):353–64.
36. Karaboga D, Akay B. A comparative study of Artificial Bee Colony algorithm. Applied Mathematics and Computation. 2009;214(1):108–132.
37. Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony(ABC) algorithm. Journal of Global Optimization. 2007;39(3):459–471.
38. Frutos M, Olivera AC, Tohme, F. A memetic algorithm based on a NSGAII scheme for the flexible job–shop scheduling problem. Annals of Operations Research. 2010;181(1):745–765.
39. Glover F, Tabu search: a tutorial. Interfaces. 1990;20:74–94.
40. Varnier C, Zerhouni N. Scheduling predictive maintenance in flow–shop. Proceedings of the IEEE 2012 Prognostics and System Health Management Conference. 2012
41. Liu BY, Chen WD. Single–machine scheduling with preventive periodic maintenance and both Preemptive and Non-preemptive jobs in remanufacturing system. Journal of Southeast University (English Edition). 2012;28:349–353.
42. Lu B, Zhou XJ, Li YT. Joint modeling of preventive maintenance and quality improvement for deteriorating single–machine manufacturing systems. Computers and Industrial Engineering. 2016;91:188–196.
43. Zhi SY, Yan S, Min X. Degradation–based burn–in with preventive maintenance. European Journal of Operational Research. 2012;221(2):360–367.
44. Zhou BH, Jiang SY, Wang SJ. Integrated production and preventive maintenance scheduling algorithm for flow shops. Journal of Dalian Maritime University. 2007;33:32–35.