This document explores the modeling and performance of the power train for a lower extremity exoskeleton during stair ascent and descent gait cycles. While the exoskeleton was optimized for walking gait cycles, the power train has not been evaluated under stair gaits. The power train for this exoskeleton is a novel design concept that locates torque motors at the back of the exoskeleton. After taking joint position data during stair gait ascent and descent cycles, joint velocities and accelerations of an unencumbered subject were found. Joint torque and power requirements of the unencumbered subject were scaled to include the effects of the extra mass and the position of the mass. After building a mathematical model to represent the power train, the output power of the motor for each joint was compared to the required joint power to actuate each joint across stair ascent and descent gait cycles. Overall it was found that the selected power train could provide assistance positive assistance to the operator under these loading conditions.

Keywords: Gait cycles; Descent cycles; Extra mass; Extremity exoskeleton; Motor Modeling

Standard mechanical methods for ground locomotion almost universally rely on wheels to translate rotational motion developed by a power train into linear motion. While the power trains used to provide this rotational motion vary significantly, it will still inevitably end up being transferred through a system of shafts and gears to end at a wheel. In recent years the use of legged locomotion has gained traction as a viable alternative to the wheel.^1–5 In certain types of rough terrain, traditional wheeled systems have trouble functioning. This project focuses specifically on designing and building a high efficiency lower extremity exoskeleton capable of enhancing the walking and load carrying abilities of a human operator. Traditional exoskeleton systems can achieve these load carrying goals, but generally, do not have the range to operate for more than a few hours away from an external power source.^6–10 This exoskeleton design will attempt to provide the similar load carrying capabilities of previous systems without requiring the operator to recharge the system during a typical shift (ex. A soldier carrying a load over the course of a full day).

A conceptual model of the exoskeleton is shown in Figure 1. This novel approach places torque motors on the back of the operator as opposed to the more traditional motor on joint design.¹¹ Rotational power is sent to the joints through a flexible transmission shaft. Harmonic drive gearboxes are located on the joints and transmit power from the driveshaft to the joint. While there are several exoskeletons that feature back mounted actuators these exoskeletons mostly use linear actuators to move the joints as opposed to torque motors. While the traditional motor on joint exoskeleton design has several advantages, our initial findings¹² show that the system experiences a decrease in efficiency due to an increased moment of inertia of the leg during the swing phase of the gait cycle. By offloading mass from the leg to the back of the operator the overall efficiency of the system can be increased. Torque motors are located at the backpack while their output is transmitted to the exoskeletons structure through flexible rotary driveshafts.

Figure 1 Conceptual model of our approach.

The paper is organized in the following manner: section II will give a brief overview of the exoskeleton for which the model was developed. Section III will explain the gait cycle model for ascending and descending a set of stairs. Section IV will cover how loading and joint position affects the torque and power requirements of each joint throughout the gait cycle. Section V will go over the equations used to build the mathematical model of the power train, and section VI will tie the previous sections together by showing the final evaluation of the motors for the stair ascent and descent gait cycles. Sections VIII and IX give the final conclusion and future work of this project. Lastly will be the appendix, which contains figures that further breaks down each inefficiencies for each gait cycle.

Joint position along with joint torque and power data from Bovi et al.¹³ were used to find the joints angular velocities and accelerations over stair ascent and descent gait cycles. Bovi et al.¹³ collected joint kinematic, ground reaction force, and surface EMG signals on 40 subjects split evenly into two groups of adults and youths using 9 SMART–E motion capture cameras, Kistler force plates, and an 8 channel electromyography. This data was collected for 5 different tests; walking over a range of speeds, toe walking, heel walking, stair ascending and stair descending. Subjects performed each test 5 times, and data was considered valid if a full gait was recorded else the set was discarded. Data was normalized against body mass, gait speed, stride length, step length and height.

Normalized joint velocity, acceleration, torque, and power data from the adult group’s stair ascent and descent experiments of Bovi et al.¹³ were scaled for the gait cycle period, dimensions, and weight of an average U.S male¹ to construct an approximated stair ascent and descent gait model of the exoskeletons intended user. The weight of the exoskeleton and a 30–kilogram load was included in this scaled model.

The ascent cycle (Figure 2) starts with one leg elevated above the other. The hip and knee are used to rotate the body up and over the load bearing leg. At the end of the stance phase, the load bearing leg is now at a lower elevation than the swing leg. During the beginning of the swing phase, the hip and knee rotate the leg up and onto the next step completing the ascent gait cycle. The descent cycle starts with the stance phase; similar to the ascent cycle the stance phase is used to rotate the upper body over the load bearing leg. The main difference being that at the end of the stance phase the load bearing leg is at a higher elevation than the stance leg.

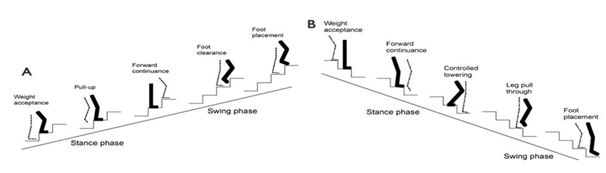
Figure 2 Parts A and B show the components of the stance and swing phase for the stair ascent and descent gait cycles.

Stair ascent joint position

During the stance phase of the stair ascent gait cycle the position of the hip and knee (Figure 3) follow each other almost perfectly; this motion keeps the hip joint position to the floor relatively constant as the knee rotates the body up and over the load bearing leg. The ankles motion doesn’t change until the end of the stance phase when it is used to rotate the body forward to catch the next step.

Figure 3 Relative degree of the hip, knee, and ankle joints during stair ascent.

Stair descent joint position

During descent (Figure 4) the hip has a much smaller range of motion. For the majority of the stance phase, it remains stationary as the other swing leg moves to the next lowest step. The knee and ankle articulate in concert to rotate the person’s center of mass down to the next step. The knee and ankle also rotate counter to each other; this keeps the upper body at a relatively perpendicular angle to the floor.

Figure 4 Relative degree of the hip, knee, and ankle joints during stair descent.

Stair ascent torque model

Contrary to the knees role as a passive damper during walking, during stair ascent the knee generates significant torque values. The weight of the upper portion of the stance leg, swing leg, and torso all act as a weight at the end of a moment arm that the knee must rotate up and over the load bearing stance leg. As the upper body is pivoted over the knee the torque seen at the knee drops, this is due a continuously shortening moment arm as the torsos center of gravity moves towards the knee. The average person ascends stairs with the ball of their foot placed on the stairs edge and the heel of the foot hanging over the edge. This puts a high torque on the ankle as it outputs a counter torque to hold up the entire weight of the body. The ankle sees torque spike as it is used to rotate the body of the person up and over the load bearing leg. Throughout the swing phase, torque generated by the ankle approaches 0. Looking to Figure 5, we can see that even though the ankle sees a large change in motion, once the ankle unloads there is no force acting against the moment arm of the foot. The hip sees a small torque spike at the beginning of the stance phase. This is a stabilizing force that the hip outputs in anticipation of the knee being used to rotate the body up and over the stance leg. This force keeps the upper body perpendicular to the ground. After the upper body stops accelerating this stabilizing force stops until a torque in the opposite direction is needed to de accelerate the upper body. The final torque spike in the hip occurs as the hip rotates the leg up and through the swing phase.

Figure 5 Scaled torque at each joint for stair ascent gait cycle.

Stair ascent power model

Across all gait cycles ascending stairs is one of the most power–intensive activities (Figure 6). The knee and hip see their largest power spike of any gait cycles and the ankle sees its second biggest power spike, second only to the power spike seen in the ankle at the end of the stance phase in a walk cycle.

Figure 6 Scaled power at each joint for the stair ascent gait cycle.

Stair descent torque model

The ankle sees a vast and constant torque throughout the majority of the stance phase. The knees torque spikes at around 55%. This is when the bulk of the weight of the torso, and the swing leg, are being lowered by the knee and ankle. At the end of the stance phase, torque about the knee and ankle fall while the hips torque jumps as it rotates the swing leg. Similar to the stair ascent cycle the hip sees small torques as it is being used to stabilize the upper torso throughout the stance cycle. As the swing cycle starts power spikes slightly as the hip is used to reposition the swing leg and to prepare for a stance phase.

Stair descent power model

The stair descent gait cycle is characterized by large negative power values (Figure 7). As the body’s center of mass is moved over the stance leg, the force of gravity will start to pull the body down towards the direction of motion. This action causes the knee and ankle joints to experience a negative power as they are used to slow down and control the descent of the body through this stance phase. The swing phase sees negligible power similar to the swing phase of the stair ascent cycle. As there is minimal weight acting against the joints, there are minimal torque values (Figure 8). The large negative power values experienced while descending stairs showcase a unique opportunity to increase the efficiency of an exoskeleton system. A properly designed system would allow the joint to back drive and pump energy into the system.

Figure 7 Scaled joint torque for the stair descent gait cycles at each joint.

Figure 8 Scaled joint powers of all joints for the stair descent gait cycle.

Moment of inertia

As a limb lengthens and shortens about the center of rotation of a joint throughout a walk cycle the moment of inertia will change as well. Therefore, for simplification, this system models the moment of inertia for each joint once during the swing phase and once during the stance phase for the stair ascent and descent cycles. By taking joint acceleration and torque data from Bovi et al.¹³ and using an empirical method for measuring the instantaneous moment of inertia across the gait cycle was found.

$I_i=\frac{{\tau }_i}{{\alpha }_i}$ (1)

After taking the average of the moment of inertia for the stance and swing¹⁴ gait cycles the resultant values were compared to the values computed by the created model. Modeling the system this way will overestimate the moment of inertia. This is acceptable as this system will be worn by operators of varying shapes and sizes, so a built-in factor of safety is desirable in this scenario. By running the motor through a gear reduction the moment of inertia that the motor sees is drastically reduced. The equivalent moment of inertia referenced to the motor is governed by (2).

$I_{Sys}=\left(I_A+I_B{\left(\frac{N_A}{N_B}\right)}^2\right)$  (2)

Where $I_{Sys}$ the moment of inertia of the geared system, $I_B$ is the moment of inertia about B, N_A is the number of teeth of gear A and N_B is the number of teeth of gear B.

Angular velocity and acceleration

The angular velocity and acceleration of the joint are governed by (3) and (4).

${\omega }_{j,n}=\frac{{\theta }_{j,n}-{\theta }_{j,n-1}}{t_n-t_{n-1}}$  (3)

${\alpha }_{j,n}=\frac{{\omega }_{j,n}-{\omega }_{j,n-1}}{t_n-t_{n-1}}$  (4)

      ${\omega }_m=N_g{\omega }_j {\alpha }_m=N_g{\alpha }_j$  (5)

Where, ${\omega }_{j,n}$  and ${\alpha }_{j,n}$ are the angular velocity’s and accelerations of the joint and ${\omega }_m$ , ${\alpha }_m$ are the angular velocities and accelerations of the motor. $N_g$ is the gear ratio of the gearbox, ${\theta }_j$ is the degree of the joint, and t is the time. These values are all taken at a gait percentage of n or n-1.

Joint position data from Bovi et al.¹³ was used along with the gait cycle time to find the angular velocity and acceleration of the joint throughout the gait cycle. Multiplying the angular velocity and angular acceleration of the joint by the ratio of the gearbox gives the velocity and acceleration the motor must achieve at minimum to match the operator’s movements.

Power

Power of the torque motor was found using (6)

$P_{motor}={\tau }_m{\omega }_m$  (6)

Where ${\tau }_m$ is the output torque of the motor at the motors angular velocity . Equation ${\omega }_m$ (6) gives us the maximum amount of mechanical power the motor can output at a given speed and torque output. By using the speed calculated from (3), and the torque the motor will output at a given speed, (this was taken directly from the manufacturer's torque vs speed curves), the total output power of the motor was calculated.

Inertial losses

Inertial power losses of this system are among the most important to consider for system design. Significant amounts of power are used to overcome the effects of inertia and accelerate the joint to a required velocity. If a motor is too slow to accelerate and mirror the operator's motion, the system can be rendered unusable. As the motors will constantly be accelerating and deaccelerating any unnecessary energy used to speed up or slow down the power train become efficiency drains.

$P_{Loss,\mathrm{Intertia}}=I_{sys}{\omega }_m{\alpha }_m$  (7)

Where $I_{sys}$ the moment of inertia referenced to the motor is, ${\omega }_m$ is the angular velocity of the motor, and ${\alpha }_m$  is the required angular acceleration of the motor. Equation (7) is used to calculate this inertial power loss. Any excess speed or acceleration of the joint will cause large inertial losses. The knee-jerk reaction upon looking (7) would be to keep the gear ratio as low as possible to reduce the speed and accelerations the motor must achieve. But looking to (2) we can see that as we increase the gear ratio the moment of inertia when referenced to the motor decreases. Across a certain speed range for each gait cycle, there exists a point where the increasing gear ratio decreases the moment of inertia faster rate than the angular velocity and acceleration of the joint increase. This result in an overall reduction in power lost due to inertial effects. The rate at which systems moment of inertia decreases is a decaying function. At some point, the rate of inertial change will be outstripped by the linearly increasing rate of change of angular velocity and acceleration.

Friction loss

Friction loss of the motor is governed by equation

$P_{Loss,Friction}=D{\omega }_m{}^2$ (8).

Where $P_{Loss,Friction}$ is the power loss from the friction of the power train, D is the motors viscous damping coefficient, and ${\omega }_m$ is the motors angular velocity. As the motors viscous damping coefficient remains constant throughout the gait cycle for a particular motor the only variable is the overall gear ratio of the system. The power lost from friction, therefore, will increase exponentially with an increasing gear ratio. Choosing a motor with a very low viscous damping coefficient allows for a higher system gear ratio before the extra friction losses outstrip the benefits of lower inertial losses.

Gearbox loss

Tying into losses from friction, significant power losses occur through the selected harmonic drive gearbox. Harmonic drive gearboxes employ strain wave gear reduction. Strain wave gear units have several positive attributes such as the ability to fit extremely high reductions in small spaces. They have no backlash and are employed where extreme precision is required. However, because they physically deform a gear during operation, the no-load running torque and overall efficiency of the system is poor.

$P_{Loss,Gearbox}={\omega }_M\left({\tau }_{Nl}+\left|{\tau }_i\right|\left(1-{\in }_G\right)\right)$  (9)

Where $P_{Loss,Gearbox}$ the power lost due to inefficiencies of the gearbox, ${\omega }_M$ is the angular velocity of the motor, ${\tau }_{Nl}$ is the no load running torque of the motor, ${\tau }_i$ is the torque input to the gearbox, and ${\in }_G$ is the efficiency of the gearbox. Power losses through this gearbox are speeding dependent. The efficiency of the gearbox and the no-load running torque change based upon the motors output speed and the ambient temperature.¹⁵ The manufacturers no load torque and efficiency to speed curves were used to obtain the appropriate values as a function of the speed of the motor. These losses were then added to the power loss from friction to find the overall mechanical loss of power.

Heat Generation loss

While heat generation plays a smaller component in power loss than friction or inertial losses, it is still an important inefficiency to analyze. As shown by equation (10) power losses from heat generation are highly dependent upon the characteristics of the chosen motor and thus there most optimization for minimizing power losses from heat generation take place while selecting the motor¹⁶

$P_{Loss,HeatGen}=\frac{{\tau }_m^2}{{{\rm K}}_m^2}$ (10)

Where, is the power lost due to heat generation i $P_{Loss,HeatGen}$ n the motors windings T is the motors output torque, and ${{\rm K}}_m$ is the motor constant. The motor constant ${{\rm K}}_m$ is a function of the output torque of the motor and the motors resistive power loss. The general trend is that larger motors will produce larger torque values because they have more windings. Because they have more windings the resistive losses and thus the power loss from heat generation will be more substantial as well.¹⁷

$P_{Net}=P_{Motor}-P_{ActurateJo\mathrm{int}}-P_{Inefficiencies}$ (11)

Where $P_{Net}$ is the net power of the motor, $P_{Motor}$ is the motors theoretical power output found using (6), $P_{ActurateJo\mathrm{int}}$ is the power required to actuate the joint as shown in Figure 6 & 8 and $P_{Inefficiencies}$ are the combined power losses due to the inertial, frictional, mechanical, and thermal losses.

Using (11), the net power of the motor could be determined at every point along the ascent and descent gait cycles. These values where mapped against gait cycle percentage in Figure 9, Figure 10. Any positive power values in Figure 9, Figure 10 are either the result of the system being back driven, or as a result of reserve power left in the motor. It is shown that across the stair ascent and stair descent gait cycle there is never a point during which an average sized male carrying a load of the exoskeleton and 30 kilograms will have to exert more power into the exoskeleton than would be required if he were just transporting the weight itself.

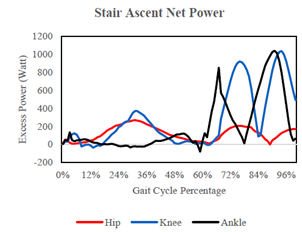
Figure 9 Graph showing the net power in each joint for the stair ascent gait cycle, positive values indicate power that is not needed to power the joint while negative values indicate that the motor is not strong enough to power the joint.

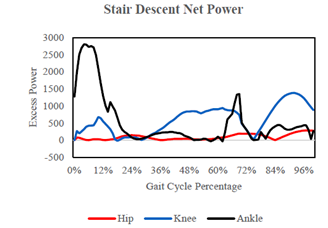
Figure 10 Graph showing the net power in each joint for the stair descent gait cycle, positive values indicates power that is not needed to power the joint while negative values indicate that the motor is not strong enough to power the joint.

Appendix A contains figures that break down the inefficiencies of each motor through the stair ascent and stair descent gait cycle. Overall it was found that mechanical losses and inertial losses dominated power losses. A significant reduction in mechanical losses could be achieved by finding a gearbox with a higher efficiency and lower no–load running torque. Although several alternatives were considered, no gearboxes commercially available can provide the needed gear reductions in such a lightweight package. Using a larger gear head with a higher efficiency actually ends up hurting performance, the extra weight of the gear head increases inertial losses beyond the current mechanical system losses (Figures 11–16).

Figure 11 Graph showing the inefficiency loss of the hip motor for the stair ascent gait cycle.

Figure 12 Graph showing the inefficiency loss of the hip motor for the stair descent gait cycle.

Figure 13 Graph showing the inefficiency loss of the knee motor for the stair ascent gait cycle.

Figure 14 Graph showing the inefficiency loss of the knee motor for the stair descent gait cycle.

Figure 15 Graph showing the inefficiency loss of the ankle motor for the stair ascent gait cycle.

Figure 16 Graph showing the inefficiency loss of the ankle motor for the stair descent gait cycle.

After constructing a complete gait cycle model scaled for a male of average height and weight wearing an exoskeleton and a carrying a 30–kilogram load, a model of the power train of the exoskeleton system was constructed. While this system was fully optimized for walking, this model shows that the optimizations made for walking carry over and improve the efficiency of the stair ascent and descent gait cycles. Furthermore, if an operator needed to ascend or descend a set of stairs the exoskeleton would easily cope with the extra power requirements with a faster gait cycle time and lower overall exertion from the operator than if the operator were transporting a 30–kilogram load without assistance. Friction, inertia and gearbox losses have been all accounted in the optimization modeling. The result showed that much of the energy losses will happen within the gearbox as the ratio increased. This implies the need for lower gear ratio to enhance the efficiency of the exoskeleton’s power terrain. The significance of the presented work is geared toward valuable insights into how moving the center of mass above the hip joint would result in minimizing energy consumption in different locomotion scenarios, such as stair ascending and descending. This key result will advance development of future exoskeleton through a more efficient, modular and user friendly design approach. As for the future work, we will realize the backpack actuated exoskeleton and will experimentally test the results on custom made walkway and step way with embedded force plates. The joint trajectories will be tracked by motion capture system in order to show the effect of having actuators at the backpack on the locomotion mechanics. The experimental result will be used to calibrate and validate the numerical result of this work in order to establish a forward and predictable model.

None.

Author declares that there are none of the conflicts.