The main component of the gyroscopic devices is the spinning rotor, which design can be different and represented by the disc, cylinder, ring, etc. forms. These rotating objects manifest gyroscopic effects which action is increased proportionally with the intensification of the angular velocity of their spinning. Recent publications demonstrate the applied torque on gyroscopic devices generates internal resistance and precession torques based on the action of the centrifugal, common inertial, and Coriolis forces, as well as the change in the angular momentum. This internal inertial torques act simultaneously and interdependently around axes of gyroscopic devices. This paper presents mathematical models for the internal inertial torques generated by the mass elements and centre mass of the spinning ring. These models enable for the computing the forces acting on the supports of the spinning ring and describe the motions of the gyroscopic devices in space. The content of the manuscript presents novelty for machine dynamics and engineering.

Keywords: gyroscope theory, property, torque, ring, centrifugal

Since the Industrial Revolution, researchers paid attention to the remarkable gyroscope properties of gyroscopic devices and tried to develop the gyroscope theory. The simplified theories of gyroscopes started to publish a hundred years ago.^1–4 numerous publications described gyroscopic effects and applications in engineering but none of them explained the physics of gyroscope properties.^5–7 the action of the gyroscopic effects is an important aspect of the science of classical mechanics. Fundamental textbooks and manuals have chapters of gyroscope theory.^8,9 Many simplified approaches to gyroscope theory are dedicated to gyroscopic effects.^10,11 All publications based on assumptions and described gyroscopic effects in terms only of the angular momentum.^12–14 Researchers focused attention on the action of inertial forces on the gyroscope but did not represent mathematical models.^15,16 The known theories of gyroscopic effects do not adequate to actual motions of rotating objects.^17,18 Unsolved gyroscopic problems generated artificial terms as gyroscope resistance, gyroscopic effects and attributed fantastical properties to rotating objects.^19,20 Still, gyroscopic effects attract researchers to find true theory.^21,22 New investigations in the area of gyroscope theory discovered the action of the system of inertial torques on rotating objects. This work describes the application of new mathematical models for the system of inertial torques generated by the rotating mass of the spinning ring.

Centrifugal torques acting on a rotating ring

The ring is a typical component of gyroscopic devices that manifest the gyroscopic effects presented in Figure 1. For computing of the inertial torques acting on the narrow spinning ring with the mass M and a constant angular velocity of ω in a counter-clockwise direction around axis oz. is accepted locations of its mass elements m on the middle radius R. The centrifugal forces are generated by the mass elements of a spinning ring and resisted to the action of an external torque. The scheme for computing the resistance torque generated by the centrifugal forces is the same as presented for the spinning disc²².

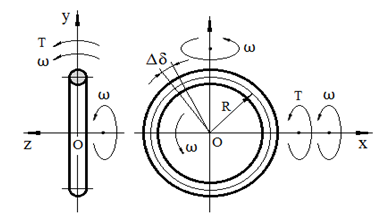
Figure 1 Schematic of the spinning ring.

The resistance torque ΔT_ct produced by the centrifugal force f_ct.z of the mass element m is expressed by the following:

$\Delta T_{ct}=-f_{ct.z}{y}_m=-m{a}_z{y}_m$             (1)

Where a_z is the acceleration of the mass element and y y_m = Rsinα _m is the distance of the disposal of the mass element along axis oy.

The change in the centrifugal force of the mass element is expressed by the following equation:

$f_{ct.z}=f_{ct}\sin \alpha \sin \Delta \gamma =\left(\frac{MR{\omega }^2}{2\pi }\right)\Delta \delta \sin \alpha \sin \Delta \gamma =\frac{MR{\omega }^2}{2\pi }\Delta \delta \Delta \gamma \sin \alpha$              (2)

where $f_{ct}=\frac{MR{\omega }^2}{2\pi }\Delta \delta$ is the centrifugal force of the mass element m; $m=\frac{M}{2\pi R}\Delta \delta R=\frac{M}{2\pi }\Delta \delta$ ; Δδ is the sector’s angle of the mass element’s location; α is the angle of the mass element’s location; Δγ is the angle of turn for the ring’s plane (sinΔγ=Δγ for the small values of the angle) around axis ox.

The resistance torque produced by the centrifugal forces of the mass element is expressed by substituting the defined parameters into Eq. (1).

$\Delta T_{ct}=-\frac{MR{\omega }^2}{2\pi }\times \Delta \delta \times \Delta \gamma \times \sin \alpha \times y_m$                     (3)

Where all components are as specified above.

The integrated torque produced by a change in the centrifugal forces is defined by the presentation of components of Eq.(3) in a form appropriate for integration. The axial component of the centrifugal forces is applied to the pseudo centroid at the ring’s semi-circle, which is calculated by the known integrated equation.

$y_A=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}{y}_{m}d\alpha }}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}d\alpha }}$                                                                        (4)

Substituting Eq. (4) into Eq. (3) and transformation yields the following.

$\begin{array}{l}{y}_A=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}{y}_{m}d\alpha }}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}d\alpha }}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{2\pi }\Delta \delta \times \Delta \gamma \times R\sin \alpha \sin \alpha d\alpha }}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{2\pi }\Delta \delta \times \Delta \gamma \sin \alpha d\alpha }}=\\ \frac{\frac{MR{\omega }^2}{2\pi }\Delta \delta \Delta \gamma {\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}R{\sin }^{\text{2}}\alpha d\alpha }}{\frac{MR{\omega }^2}{2\pi }\Delta \delta \Delta \gamma {\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}=\frac{\frac{R}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\alpha )d\alpha }}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}\end{array}$             (5)

Where the expression $\frac{MR{\omega }^2}{2\pi }\Delta \delta \Delta \gamma$ is accepted as constant for the Eq.(5); the expression ${\sin }^2\alpha =(1-\cos 2\alpha )/2$ is a trigonometric identity that replaced in the equation, and other parameters are as specified above.

Substituting Eq. (5) into Eq. (3), replacing $\sin \alpha ={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \alpha d\alpha }$ by the integral expression and converting by the integral form, the following equation emerges:

${\displaystyle \underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}}=-\frac{MR{\omega }^2}{2\pi }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}d\delta }\times {\displaystyle \underset{0}{\overset{\gamma }{\int }}d\gamma }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }\times \frac{R{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\alpha )d\alpha }}{2{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}$                            (6)

Where the first integral of the cosines is increased twice due to limits of integration, for the second integral of the cosines remains the same due to the symmetrical location of the centroid.

Integral Eq.(6) is solved and yields the following result

$T_{ct}|{}_0^{T_{ct}}=-\frac{MR{\omega }^2}{2\pi }\times \left(\delta |{}_0^{\pi }\right)\times \left(\gamma |{}_0^{\gamma }\right)\times 2\left(\sin \alpha |{}_0^{\pi /2}\right)\times \frac{R\left(\alpha -\frac{1}{2}\sin 2\alpha \right)|{}_0^{\pi /2}}{-2\cos \alpha |{}_0^{\pi }}$

Thus giving rise to the following:

$T_{ct}=-\frac{MR{\omega }^2}{2\pi }\times (\pi -0)\times (\gamma -0)\times 2(1-0)\times \frac{R\left(\frac{\pi }{2}-0\right)}{-2(-1-1)}=-\frac{M{R}^2{\omega }^2\pi }{8}\times \gamma$                (7)

The components of Eq.(7) is expressed by the differential equation of time derivative

$\frac{d{T}_{ct}}{dt}=-\frac{M{R}^2{\omega }^2\pi }{8}\frac{d\gamma }{dt}$                              (8)

where $t=\alpha /\omega$ , $dt=\frac{d\alpha }{\omega }$ ; $\frac{d\gamma }{dt}={\omega }_x$ is the angular velocity of the ring’s precession around axis ox.

The defined components are substituted into Eq(8) and yield the following differential equation:

$\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\omega }^2{\omega }_x\pi }{8}$                              (9)

Separating variables of Eq.(9) and presenting by the integral form yield the following equation:

$\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\omega }^2{\omega }_x\pi }{8}$                     (10)

The integral solution of Eq.(10) yields the following

$T_{ct}|{}_0^{T_{ct}}=-\frac{M{R}^2\omega {\omega }_x\pi }{8}\alpha |{}_0^{\pi }$

Substituting limits and increasing the result twice because of centrifugal forces act on the upper and lower sides of the ring, yield the expression of the total resistance torque T_ct

$T_{ct}=-\frac{2{\pi }^{2}M{R}^2\omega {\omega }_x}{8}=-\frac{1}{4}{\pi }^{2}J\omega {\omega }_x$                  (11)

Where J = MR² is the thin ring’s mass moment of inertia.

Common inertial forces acting on the spinning ring

The solution for the common inertial forces acting on the spinning ring that generates the element of the precession torque ΔT_in is similar as for the rotating disc²² and represented by the following equation:

$\Delta T_{in}=f_{in}{x}_m=m{a}_z{x}_m$                        (12)

Where f_in is the inertial force of the spinning ring’s mass element_, x_m is the distance to the mass element’s location along with axis ox, other components are as specified above.

The distance x_m is expressed by Eq.(3) with a change in the index of axis. The acceleration a_z is defined by the first derivative of the change in tangential velocity and is expressed by the following.

${\alpha }_z=\frac{d(-V_z)}{dt}=\frac{d[-V\cos \alpha \sin \Delta \gamma ]}{dt}=V\cos \alpha \frac{d\gamma }{dt}=R\omega {\omega }_x\cos \alpha$               (13)

where V_z=-VcosαsinΔγ is the change in tangential velocity V, V=Rω, ω_x=dγ/dt, t is time, and the other components are as specified above.

The element of torque ΔT_in is defined by substituting defined parameters into Eq.(12).

$\Delta T_{in}=\frac{M}{2\pi }\times \Delta \delta \times R\omega {\omega }_x\sin \alpha \times x_m$                   (14)

Equation (14) is similar to Eq.(3) and x_m is the same as y_m. The following solution yields the equation for precession torque.

$T_{in}=\frac{1}{4}{\pi }^{2}J\omega {\omega }_x$                             (15)

where all parameters are as specified above.

Coriolis forces acting on the spinning ring

The torque generated by the Coriolis force of the rotating mass elements is acting on the ring. The equation for the integrated torque should be defined. The solution to this problem is the same as for the spinning disc.²² The element of the resistance torque generated by the Coriolis force is expressed by the following

$\Delta T_{cr}=-f_{cr}{y}_m=-m{a}_z{y}_m$                   (16)

Where all components are represented above

Coriolis acceleration a_z is defined by the time derivative of the change in tangential velocity and presented by the following equation.

${\alpha }_z=\frac{d{V}_z}{dt}=\frac{d(-V\cos \alpha \sin \Delta \gamma )}{dt}=V\cos \alpha \frac{d\gamma }{dt}=R\omega {\omega }_x\cos \alpha$         (17)

Where all components are as specified above.

The element of the torque generated by Coriolis force is defined by substituting parameters into Eq. (16) that yields the following.

$\Delta T_{cr}=-\frac{M\Delta \delta }{2\pi }\times R\omega {\omega }_x\cos \alpha \times y_C=-\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha \times y_C$            (18)

The resulting torque of Coriolis forces acting on the centroid calculated by substituting defined parameters into Eq.(5) and expressed by the following.

$\begin{array}{l}{y}_C=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}{y}_{m}d\alpha }}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{f}_{ct.z}d\alpha }}=\frac{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha \times R\sin \alpha d\alpha }}{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha d\alpha }}=\frac{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha \times R\sin \alpha d\alpha }}{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha d\alpha }}=\\ \frac{\frac{M{R}^2\omega {\omega }_x\Delta \delta }{2\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \alpha \sin \alpha d\alpha }}{\frac{M{R}^2\omega {\omega }_x\Delta \delta }{2\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \alpha d\alpha }}=\frac{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{1}{2}\sin 2\alpha d\alpha }}{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \alpha d\alpha }}\end{array}$                     (19)

Where the expression $\frac{MR\omega {\omega }_x\Delta \delta }{2\pi }\cos \alpha$ is constant for Eq.(19), $2\sin \alpha \cos \alpha =\sin 2\alpha$ is a trigonometric identity that is replaced and other parameters are as specified above.

Substituting Eq.(19) into Eq.(18), the component $\cos \alpha ={\displaystyle \underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha }$ is replaced and presented by the integral form that yields the following equation:

${\displaystyle \underset{0}{\overset{T_{cr}}{\int }}d{T}_{cr}}=\frac{M{R}^2\omega {\omega }_x}{2\pi }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}d\delta }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha \times }\frac{\frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin 2\alpha d\alpha }}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }}$                             (20)

The solution of integral Eq.(21) yields the following:

$T_{cr}|{}_0^{T_{cr}}=\frac{M{R}^2\omega {\omega }_x}{2\pi }\times \left(\delta |{}_0^{\pi }\right)\times \left(\cos \alpha |{}_0^{\pi }\right)\times \frac{-\frac{1}{2\times 2}\cos 2\alpha |{}_0^{\pi /2}}{\sin \alpha |{}_0^{\pi /2}}$                         (21)

Where the limits taken for the quarter of the circle are due to its symmetrical location and the value is the same.

The resultant torque generated by Coriolis forces increased twice due to the action on the upper and lower sides of the ring.

$T_{cr}=-2\times \frac{M{R}^2\omega {\omega }_x}{2\pi }\times (\pi -0)\times (-1-1)\times \frac{[-\left(-1-1\right)]}{4(1-0)}=-M{R}^2\omega {\omega }_x=-J\omega {\omega }_x$           (22)

The inertial torque generated by the change in the angular momentum of the ring is presented by the equation:

$T_{am}=M{R}^2\omega {\omega }_x=J\omega {\omega }_x$                         (23)

Where all components are specified as above.

Attributes of inertial torques acting on the spinning ring

The resistance torques generated by the centrifugal (Eq.(12)) and Coriolis forces²²)

act around axis ox in the same direction. The total initial resistance torque acting around axis ox generated by the external torque presented as their sum, whose equation is as follows

$T_r=T_{ct}+T_{cr}=\left(\frac{{\pi }^2+4}{4}\right)J\omega {\omega }_x$                      (24)

Where T_r is the total initial resistance torque acting around axis ox.

The torques generated by the common inertial forces (Eq.(16)) and by the change in angular momentum (Eq. (23)) are acted around one axis oy and present a total initial precession torque generated by the external torque presented as their sum, whose equation is as follows

$T_p=T_{in}+T_{am}=\left(\frac{{\pi }^2+4}{4}\right)J\omega {\omega }_x$                        (25)

where T_p is the total initial precession torque acting around axis oy.

Table 1 presents the torques generated by the inertial pseudo forces of the spinning ring. The inertial torques acting on the spinning ring demonstrates differ in the results compare with a spinning disc.²²

Working example

The ring has a mass of 1.0 kg and a mean radius of 0.1 m, spinning at 3000 rpm and precessing with an angular velocity of 0.05 rpm. It is determined the values of the components for resistance and precession torques. This problem is solved based on the equations in Table 1.

1. The torque generated by the centrifugal T_ct and common inertial T_in forces

$T_{ct}=T_{in}=\frac{1}{4}{\pi }^{2}J\omega {\omega }_x=\frac{1}{4}{\pi }^2\times 1.0\times {0.1}^2\times \frac{3000\times 2\pi }{60}\times \frac{0.05\times 2\pi }{60}=0.04058712Nm$

2. The torque generated by Coriolis T_cr forces and the change in the angular momentum T_am

$T_{cr}=T_{am}=J\omega {\omega }_x=1.0\times {0.1}^2\times \frac{3000\times 2\pi }{60}\times \frac{0.05\times 2\pi }{60}=0.016449340Nm$

3. The initial resistance T_r and precession T_p torques

$T_r=T_p=\left(\frac{{\pi }^2+4}{4}\right)J\omega {\omega }_x=\left(\frac{{\pi }^2+4}{4}\right)\times 1.0\times {0.1}^2\times \frac{3000\times 2\pi }{60}\times \frac{0.05\times 2\pi }{60}=0.057036461Nm$

Where J=MR² is the mass moment of inertia of the ring.^8,9

The spinning ring is the typical part of movable mechanisms that manifest gyroscopic properties. The gyroscopic effects are dependent on the action of the system of internal torques generated by the rotating mass the spinning ring. The mathematical models for internal torques acting on the spinning ring are derived and now can be used for engineering computing of gyroscopic effects. The inertial torques acting on the spinning ring are generated by known four components presented in publications that acting on other rotating objects. The equations of the inertial torques have different expressions than for the spinning disc and reflect the geometry of the narrow ring. New mathematical models for the inertial torques enable for describing all gyroscope properties and are useful for modeling the behavior of the spinning ring.

The known mathematical models for the theory of gyroscopic effects are presented mostly by the expression of the change in the angular momentum of the rotating objects. Such analytical models do not respond to practical motions of the gyroscopic devices and do not respond to engineering requirements. The new investigations in the area of gyroscopic effects solved this long-time problem presented the equation of the inertial torques and described the physics of gyroscopic defects. The new analytical approach enables for solving gyroscopic problems without application of the complex numerical modeling. The mathematical models for the inertial torques acting on the spinning ring can be used for the computing of forces and motions of mechanisms. The new analytical approach clearly describes gyroscope properties in a new light while setting forth new challenges for future studies of the gyroscope theory.

f_ct, f_cr., f_in.–centrifugal, Coriolis and inertial forces, respectively, generated by mass elements of a spinning ring

J–mass moment of inertia of a ring

M–mass of a ring

m–mass element of a ring

R–radius of a ring

T–load external torque

T_ct, T_cr., T_in. T_a –torque generated by centrifugal, Coriolis and inertial forces and a change in the angular momentum, respectively

t–time

y_c, y_m–centroid and distance of the location of the mass element along axis

Δα, α–increment angle and angle of the turn for a ring respectively

Δδ–angle of the ring’s a mass element

Δγ–angle of inclination of a ring’s plane

ω–angular velocity of a ring

ω_x–angular velocity of precession around axes ox

None.

The author declares there are no conflicts of interest.

None.

1. Armenise MN, Ciminelli C, Dell'Olio FV et al. Advances in gyroscope technologies. Berlin, Springer-verlag berlin and heidelberg gmbh & co. kg; 2010.
2. Deimel RF. Mechanics of the gyroscope. New York: Dover Publications Inc; 2003.
3. Greenhill D. Report on gyroscopic theory. London: General Books LLC; 2010.
4. Scarborough JB. The gyroscope theory and applications. UK: Interscience Publishers Ltd; 1958.
5. neil b. gyroscope. the charles stark draper laboratory inc. Massachusetts: Cambridge; 2014.
6. Acar C, Shkel A. MEMS vibratory gyroscopes: structural approaches to improve robustness. New York, Springer science & business media; 2009.
7. Weinberg H. Gyro mechanical performance: the most important parameter, technical article ms-2158, analog devices. Norwood: MA. 2011; p.1–5.
8. Hibbeler RC. Dynamics. 12th ed. Singapore: Prentice Hall. 2010.
9. Gregory DR. Classical mechanics. Cambridge University Press. 2006.
10. Dicker JJ, Pennock GR, Shigley JE. Theory of machines and mechanisms. 3rd ed. New York: Oxford university press. 2002.
11. Aardema MD. Analytical dynamics–theory and applications. Springer. 2005.
12. Jonsson RM. Gyroscope precession in special and general relativity from basic principles. American journal of physics. 2007;75(5):463.
13. Liang WC, Lee SC. Vorticity, gyroscopic precession, and spin-curvature force. Physical review D. 2013;87:044024.
14. Butikov E. Inertial rotation of a rigid body. Europien journal of physics. 2006;27(4):913–922.
15. Tekinalp O, Elmas T, Yavrucuk I. Gimbal angle restricted control moment gyroscope clusters. Proceedings of 4th International Conference on Recent Advances in Space Technologies (RAST). 2009;585–590.
16. Quinn TJ, Picard A. The mass of spinning rotors: no dependence on speed or sense of rotation. Nature international journal of science. 1990;343:732–735.
17. Zyga L. Gyroscope's unexplained acceleration may be due to modified inertia. PhysOrg.com. 2011.
18. Faller JE, Hollander WJ, Nelson PG, et al. Gyroscope-weighing experiment with a null result. Physical Review Letters. 1990;64: 825–826.
19. Zhang Z, Sun J, Wum K. Error analysis and test study of fibre optic gyroscope north-finder. Advanced sensor systems and applications II, proceedings of SPIE. 2005;5634:611–618.
20. Kodama  K, Adachi M, Kamimura K. Gyroscopic force measuring system. Transactions of SICE. 2002;38(2):117–123.
21. Ferrari JA. Gyroscope's precession and the principle of equivalence. Annalen der physik. 1989;501(5):399–400.
22. Usubamatov R. Inertial forces acting on gyroscope. Journal of mechanical science and technology. 2018;32(1):101–108.