In system-informational culture (SIC) man is occupied by inter discipline activity proceeding in computer instrumental systems (S_I). So, natural intellect (I_N) and artificial intelligence (I_A) must achieve semantic level of communication. It becomes possible due to deep learning of the partners both. Meanings as the utmost mathematical abstractions have been already applied in computer sciences and human mind is backward. By authors’ opinion person’s subjectization in SIC can be accomplished with the help of rational educational model (E_R), system axiomatic method (AM_S) usage, and technology of universal I_N tutoring (T_U) implementation in the form of I_A.

Keywords: artificial intelligence, universal (deep) tutoring, rational consciousness, axiomatic method, language of categories, ontological knowledge base, functor

SIC, I_N, I_A, E_R, T_U, AM_S, S_I, I_I, SI, , L_N, L_C, M_DL_E, , , , C_R, , ATD

Man has transcendental abilities presented in the form of knowledge without premises ().¹ Human mind exists also in co-evolution with anthropogenic environment. There is de docta ignorantia (scientific ignorance – SI) in metaphoric forms of natural languages (L_N) and tools of SIC. Internet, S_I, and multidisciplinary electronic libraries became means of cognition. It means that I_N has at least humanitarian scope of view on system world which is insufficient for inter discipline semantic activity proper to SIC. The matter is that determinate knowledge in SIC is sophisticated natural sciences one (). Narrow professional trend of T_T can’t guaranty student’s subjectization in SIC and does not even occupy by trans-disciplinary theoretical meanings clarifying. It is difficult to understand complex semantic without study of the utmost universal mathematical constructions. The learning needs serious assistance in order to do breakthroughs to whole theories meanings understanding. Universalities problem solution on personal level becomes now direct problem of education. To cope with corresponding educational difficulties it is impossible to do without deep learned super computer I_A as lifelong tutoring partner.² Universal laws of human mind functioning must be used to help man to mold his rational part of consciousness (C_R).Authors contributed ER for I_N tutoring for achieving the aim. On the basis of  and SI principles and AMS lifelong partner I_A will find adequate ways of teaching adapted to every student. AM_S gives systems description, comparison, and investigation means. Natural language (L_N) glottogonia in direction of thinking in categories becomes general aim of E_R securing I_N development so as ideas of mathematical glottogenesis for semantic expression play here the most important role.³ Mathematics clarifies scientific meanings achieving mathematical sense  of  apperception. On the eve of SIC language of categories (L_C) was discovered.⁴ Meanings of the whole theories can be described in L_C exposing inter connections. I_A will perfect I_N by T_U method developing subject’s super natural sense of knowledge ().Each indexed abbreviation here denotes a functor  acting between any categories. This correspondence maps morphisms (m) structure of  into the one of . It conserves domain  laws, presented by commutative diagrams in, see Figure 1.^4,5 Functor  transforms empirical facts (N) in scientific form (S). Data base (B) becomes knowledge base.

Figure 1 Functors as means of any systems synthesis and comparison (); compression and identification of K

(K) due to functor realization. In full measure, K is presented by  theories. Functor Ont implemented in L_C compresses knowledge. Functor P_Ont gives it personal form. That is why tutor I_A can find out reasons of student’s incomprehension and render him an adaptive prompt help in his studies.²

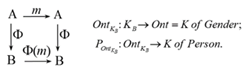
Figure 1 Functors as means of any systems synthesis and comparison ($\Phi$ ); compression and identification of K.

(K) due to functor$K_B:B\to K$ realization

Rational education by axiomatic method implementation

Problem of education in SIC is to develop C_R answering for meanings understanding. Essence of the latter can be expressed in L_C in exact and concise form. L_C is functional language destined for semantic expression and study.

Definition 1 Meaning is phenomena understanding in the unity of idea-fact), intention-theory), and design-ideal. Understanding happens as result of these components synthesis. Meanings are present in mathematical theories and are to be identified and comprehended under special study. Scientific problems solution occurs by generalizations. Thinking development proceeds according to the scheme: geometry (G)→algebraic G→G of algebra. It answers to three levels of AM - initial, modern, and system one.

Example 1 Meanings of equivalence relation. Next descriptions use set A elements, relations algebra , and any systems A,B comparison with the help of function f – level AM_S, see Figure 1&2.

Figure 2$A{M}_S\text{}:$ equivalence relation $\rho =R_f$ as inverse image of f.

$A{M}_I:\rho \subset A\times A;a,b,c\in A:\left\{a\rho a,(a\rho b)\Rightarrow (b\rho a),(a\rho b)\wedge (b\rho c)\Rightarrow (a\rho c)\right\};$

$A{M}_M:\langle P\left(A\times A\right)|È,Ç,Í,\overline{},\AE ,\widehat{},o,{}^{-1},\tau \rangle :\{\tau Í\rho ,{\rho }^{-1}Í\rho ,{\rho }^2Í\rho \}Û\{\tau Í\rho ,{\rho }^{-1}=\rho ,{\rho }^2=\rho \};$

Approaches AM_M and AM_S can be applied to different categories not only to SET. Eucleidus’s AM_I leans on  and issues from building of “real” world self obvious models. It deals also with real tools – compasses, a ruler, and gnomon. “Imaginative” instruments of AM_M are much more diverse. It gives possibility to use different ways of teaching leaning on modern tools - theories. Then new “intellectual reality” is achieved. Theory supplies knowledge with obviousness on mathematical level  thus solving more general cognitive problems. Human in SIC reality needs real grounds of AM_I in order to balance sophistication and even change of initial concepts meaning. The latter are complicated by outstanding scientific discoveries. Thinking in L_C as AM_S application allows doing it on the basis of universal mathematical tools. Deep learned I_A can apply T_U starting at once from AM_S level to support the meaning unity,⁶ see def. 1, thus ensuring knowledge self obviousness (). Any non-contradictory assumptions (axioms) are reality of system world. Open mathematical theories can be studied by adequate axioms introduction. Axioms can be regarded on as properties of abstract tools (ATD). Then theories comparison becomes possible on the apperception level. Reality of these super sensitive models is maintained by L_C and practice in computer S_I. It gives stability to new presentations and restores lost self obviousness of system meanings.

SIC gave trans-disciplinary scientific environment where cognitive function of thinking consciousness deals with trans-fundamental meanings. It is time for transition from view perception and experience observation to synthesis of theories on the base of self obvious speculation. New horizons of I_A consist of smoothing misbalance of clever machines and men. Robot sophistication will serve to person’s inter discipline horizon enlarging. It will ensure human leading role in long life partnership with I_A. Universalities are core problem of C_R formation. Its solution is achieved by AM as inherited activity of semi gods (geniuses) studying intellectual possibilities of human tools.

None

The author declares there is no conflict of interest.

1. Husserl A. From idea to pure phenomenology and phenomenological philosophy. General introduction in pure phenomenology. Book 1 Acad Project; Russia. 2009. 220 p.
2. Gromyko VI, Kazaryan VP, Vasilyev NS, et al. Artificial intelligence as tutoring partner for human intellect. J AISC. 2018;658:238‒247.
3. Pinker S. Thinking substance. Language as window in human nature. Librokom, Russia. 2013. 560 p.
4. McLane S. Categories for working mathematician. Phys Math; Russia. 2004. 364 p.
5. Goldblatt R. The categorical analysis of logic. N.-H. Publ Comp; Amst, USA, Oxford; 1979. 485 p.
6. Gromyko VI, Vasilyev NS. From automatization to neurophenomenology of artificial intelligence in robotics. Int Rob Auto J. 2018;4(1):1‒2.