Despite its introduced superiority in pattern recognition, the conventional neural network is yet to cope with the model uncertainty. To tackle this issue, Bayesian neural network, which allows the predictions to equip with model uncertainty, is succinctly reviewed. However, the misspecification of the model prior can lead the posterior to be of no avail. For this, contrast with the conventional informative priors, e.g., Normal and Laplace priors, the suggestion of employing weakly informative priors in Bayesian neural network is put forward for their tolerance of prior misspecification. For empirical datasets with available semantic annotations, the consideration of hierarchical weakly informative priors is further introduced in order to boost the discriminability of the model. A conducted evaluation experiment revealed the effectiveness of hierarchical weakly informative priors over other priors in a hand-written digit classification task.

Keywords: neural network, bayesian neural network, weakly informative prior

The recent renaissance of deep neural network, aka, DNN, has made leap forward in algorithmic innovations in image and nature language processing tasks.¹ However, the boosted discriminability in DNN does not belie its intrinsic inferiority in outputting the probabilistic prediction, i.e., the model uncertainty. The introduction of Bayesian neural network, aka, BNN, which models the distribution of the weights rather than the single estimate of the weights in conventional neural network allows DNN to make probabilistic inferences.^2,3 For the illustrative purpose, a simulated simple BNN with its produced model uncertainty is depicted below in Figure 1. In the nutshell, the BNN is merely a neural network with a properly defined prior distribution on its weights.⁴ The distinction between DNN and BNN is not superficial, as the former targets on the stacked multiple non-linear extrapolations of input-output relations, whereas the latter aims for a chain of inferential processes from setting up the prior to applying the likelihood (evidence) to correct the prior in yielding the posterior.

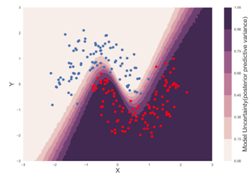
Figure 1 Model Uncertainty, is measured via the posterior predictive variance from defined prior to posterior of weights. In this BNN simulation, the model is less certain about the predictions in the shaded(middle) area compare to the predictions in dark area for the classification of one datum as class 1(colour red).

It is clear that given the pre-determined likelihood function, different priors that reflect our heterogeneous prior beliefs towards the to-be-modelled task, should result in diversity of posterior weight distributions. Unfortunately, previous researches in BNN uniformly focused on one specific type of prior, i.e., the informative prior, such as a zero mean, spherical Gaussian for its conjugacy between prior and posterior and its computational convenience.⁵ The issue of such standard informative prior lies on its assumed assumption of proper specification of the model as its relative small variance and the fixed prior shape in constraining the variability of posterior distributions of weights. However, in a practical problem, where the specification of a model is commonly sub-optimal in the first place, hence, a prior that is defaulted with some amount of information but not as overwhelmed as an informative prior is demanded. To fulfil this research enquiry, we resort on the weakly informative priors, which assert controlled influence towards the posterior compare to the informative ones (see⁶ for detailed review). However, previously documented weakly informative priors, such as the uniform prior, is not ideal for BNN due its yielded improper posterior distribution in outputting biased and less interpretable probabilistic predictions. As a result, we are gravitated towards the usage of weakly informative priors that belong to Cauchy distributions for their flexibility. Moreover, it is advisable to place weakly informative priors in a hierarchical order to penalise the large weights in BNN.

For empirical evaluation of above mentioned hierarchical weakly informative priors in BNN, an experiment on Digits dataset⁷ was conducted. Consider a three-layer neural network with one densely connected hidden layer, and both input and output variables are in the classification setting. The likelihood function for this BNN is defined as equation (1):

$p\left(y_n|w,x_n,{\sigma }^2\right)=Normal\left(y_n|NN\left(x_n;w\right),{\sigma }^2\right)$  (1)

Where NN stands for the conventional neural network whose weights and biases from the latent weight variable w (assumed known ${\sigma }^2$ this case). To verify whether the proposed hierarchical weakly informative priors produce more robust performance in Digits classification compare to other ordinary used Normal and Laplace priors, we explicitly compare among the performance of BNNs with three corresponding priors. The parameterisations of three priors are expressed in following equation (2) to (4):

Normal Prior: $f\left(x|\mu , b\right)=\frac{1}{2b}exp\left\{-\frac{\left|x-\mu \right|}{b}\right\}$  (2)

Laplace Prior:   $f\left(x|\mu , \tau \right)=\sqrt{\frac{\tau }{2\pi }}exp\left\{-\frac{\tau }{2}{\left(x-\mu \right)}^2\right\}$     (3)

Cauchy Prior: $f\left(x|\mu , \tau \right)=\sqrt{\frac{\tau }{2\pi }}exp\left\{-\frac{\tau }{2}{\left(x-\mu \right)}^2\right\}$    (4)

In this experiment, we set the $\mu$ as 0, b as 1 for implementing the Normal prior, then define $\mu$ as 0, $\tau \left({\sigma }^2\right)$  as 1 for the Laplace prior. For the hierarchical weakly informative priors, we placed the two Cauchy priors with both centered $\left(\alpha \right)$  at 0 and scale $\left(\beta \right)$  at 2.5 and 1.0, respectively. The demonstration of these applied priors is shown in Figure 2. Posterior to the parameter estimations, we resorted on the scalar valued metrics to access the performance of trained models. From (Table 1), it is lucid that our proposed hierarchical weakly informative priors, i.e., stacked Cauchy priors with gradually constrained variances, improved the discriminability of BNN in the largest extent compare to other informative priors, e.g., Normal and Laplace priors.

Figure 2 Demonstration of applied priors, e.g., the Normal, Laplace, and hierarchical weakly priors (different Cauchy priors for weights in different layers).

As briefly reviewed in this article, Bayesian neural network can compensate the vanilla neural network with its induced model uncertainty. Contrast with ordinarily applied informative priors, such as Normal and Laplace priors, the adoption of hierarchical weakly informative priors, i.e., stacked Cauchy priors, leads to flexible model specification and consequently gives arise to superior discriminative performance reflected in an empirical experiment. However, the current practical implementation of BNN is still suffered from the prolonged and biased approximation to the intractable posterior.⁸ This calls for future researches on improving the posterior inferences process.

This study is partially supported by the Okawa Foundation for Information and Telecommunications, and National Natural Science Foundation of China under Grant No.61472117.

No conflict of interest exists.