This section briefly introduces the attitude kinematics and dynamic models of a flexible spacecraft. The model of the actuator faults is also established. The attitude kinematic equation of spacecraft can be expressed by unit quaternion as
(1)
Where
is the angular velocity of the spacecraft with respect to an inertial frame and expressed in body frame, Q is the unit quaternion with the unit norm constraint Q,
given by
(2)
and
are the vector part and the scalar part of the unit quaternion Q, respectively,
3 and
denote the Euler axis and Euler angle, respectively, I is the identity matrix with appropriate dimension, and the superscript X is an operator which is denoted by
(3)
a is a three dimensional vector with elements a1 , a2 and a3 . Obviously,
is a skew-symmetric matrix.
The dynamic equations of a flexible spacecraft can be written as12
(4)
(5)
where Js
represents the inertia matrix of the whole spacecraft,
denotes the model coordinate vector with is the model number,
denotes the coupling matrix between the elastic and rigid structure,
N is the actual control torque,
is disturbance torques,
and
are the damping and stiffness matrices, respectively,
is the corresponding damping ratio, and
is the natural frequency. When considering actuator faults, the actual control torque u can be modeled as
(6)
Where
is the actuators distribution matrix,
with
being the fault switch factor,
is the struck fault of actuators,
denotes the input torque of actuators,
represents effectiveness matrix of actuators. F (t) can be modeled as19
Where
denotes the magnitude of the actuator effectiveness and,
and
are the amplitude and frequency of the high-frequency component, respectively, with
. Therefore, we have
, i=1,2,…,L.
Remark 1: Note that
and
, i=1,…, L , can be constant or time-varying. From (6) we can conclude that, for the i th actuator, in the case of
and
, the actuator occurs stuck fault; In the case of
and
, the actuator experiences partial loss of actuator effectiveness; In the case of
,
=0 or
,
, the actuator undergoes outage; In the case of
,
=1, the actuator is fault-free . If all the actuators are fault-free in the whole attitude control process, the dynamic system (4) become the nominal system where
. In the following controller designs, the fault system and nominal system are considered, respectively.
In practice, due to fuel consumption, out-gassing during operation, onboard payload motion and rotation Of flexible appendages and so on, the inertial matrix Js of the whole spacecraft structure is time varying and uncertain. We divide it into two parts, that
, where J and
represent the nominal value component and the parameter perturbation component of the inertial matrix
, respectively. As
is time-varying and unknown, the terms
and
are also time-varying and unknown. Therefore we can treat them as the disturbance to be tackled in the controller design. When considering
,
and
as the total disturbance d ,(4) can be rewritten as
(7)
Where
.
The following assumptions are taken throughout this paper.
Assumption 1: Both J and
are known positive definite symmetric and bounded constant matrices.
Assumption 2: The actuators distribution matrix
, fault switch matrix
and actuator effectiveness matrix F satisfy
.
Assumption 3: The stuck faults
are bounded, i.e.,
.
Assumption 4: The total disturbance d is bounded with a bound constant
, i.e.,
for
, where
denotes the norm of vector or matrix.
Assumption 5: The control input torque of actuators
satisfies
(8)
Where
max is a known constant.
Remark 2: Assumption 2 is used to guarantee that the remaining actuators can still achieve the designed control aims even though some actuators undergo outage or stuck. From Assumption 2 and the fact
, we have
. From Assumption 5, we have c
when all actuators are fault-free. The rest-to-rest maneuver of the spacecraft is considered in this work. The control aim is to design a controller c u for the system in (1), (4)-(6) such that for all initial conditions the desired rotations are achieved in the presence of model uncertainty, external disturbances, inputs saturation or ever actuator faults under Assumptions 1-5, that is
Mathematical preliminaries
This section includes some important mathematical preliminaries required for the rest of the paper. Consider the nonlinear dynamic system
(9)
Where
is the state,
is the input,
is the disturbance, and
are smooth vector- or matrix-valued function, respectively. System (9) is said to be input-to-state stable (ISS)27,28 from d to x if the following property is satisfied:
Where
is a class
L functions and
is a class
function.
Definition 1:27,28 A smooth function positive definite and radically unbounded
is called an input-to-state stabilizable control Lyapunov function (ISS-CLF) for (9) if there exists some class
function
such that the following implication holds for all x
0 and all d
(10)
Definition 2:27 For system (9), let V is an ISS-CLF with the control law
, where
is positive definite symmetric matrix and
V is Lie derivative defined as
, then the stabilizing control law
(11)
Is
inverse optimal with respect to the cost functional
Where
is the set of locally bounded functions of x and
>0
Remark 3: A necessary and sufficient condition for system being ISS is the existence of an ISS-CLF.28 The main characteristic of the inverse optimal approach is that the meaningful cost function is a posteriori determined from the stabilizing feedback control law. The inverse optimal controller
(x) in (11) can achieve
level of
disturbance attenuation for all
. Compared with nonlinear
control, the inverse optimal method solves the nonlinear optimal-assignment problem with respect to a meaningful cost functional without solving the HJIPD equation explicitly.
Robust controller design for flexible spacecraft
For simplicity, we denote the following variable v by
differentiating the variable v yields
. Let
, and then (5) can be written as
(12)
Where
. Since matrix
has all its eigen values in the left-hand plane, there exists a symmetric and positive-definite solution
satisfying
(13)
Where
is positive definite symmetric matrix In view of (7), one has
(14)
Define
(15)
Where
and
. as a result, the subsystem (14) becomes
(16)
Amplitude constrained attitude controller design: In this section, one controller is presented by constructing control Lyapunov function and using inverse optimal method for normal system in (1) and (4)-(6) with actuator fault-free in the presence of inertia matrix uncertainty, external disturbance and amplitude constraint of actuator. A compensator is proposed and embedded into the feedback controller to eliminate the effect of input saturation. And then a fault-tolerant version is designed to deal with the stuck faults and loss of effectiveness of actuators by employing two parameter update laws with e-modifications to estimate the unknown parameters caused by actuator faults. For convenience, we firstly define the two saturation functions as
(17)
Where
and
, and
(18)
Where
With
and
,
>0,
.
In the follows, in order to propose the fault-tolerant constrained controllers, a significant Lemma is proposed.
Theorem 1: For flexible spacecraft system in (1), (12) and (16), under Assumptions 1-5, given
, let
,
, where
and
be positive definite symmetric matrices. If
, K and satisfy the following inequality
(19)
Where
denotes the minimum singular value of matrix A , then the dynamic feedback control law
(20)
Where
(21)
(22)
(23)
(24)
Renders the resulting closed loop system in (1), (12) and (16) ISS from the total disturbance d to the state
furthermore, the control law
(25)
Where
(26)
(27)
(28)
, and
is defined in (22), is inverse optimal in the sense that it minimizes the meaningful functional
(29)
(30)
Proof: Consider the smooth positive-definite radically unbounded function
(31)
The time derivate V along (1), (12) and (16), substituting (21), (23)-(24) into (20) and based on the definition
in (17), using (13), (19)-(21), (22), (31) and the fact
, we have
(32)
Choosing
, then when
we have
, which implies that V in (31) is ISS-CLF for system in (1), (12) and (16) based on Definition 1.Therefore the resulting closed loop system in (1), (12) and (16) is ISS from the total disturbance d to the state
based on Remark 3. In addition, from the definition of
in (30) and the proof above, it is not difficult to yield
(33)
Which implies that
is positive definite. From Definition 2 we get that control law u in (25) is
inverse optimal control with respect to (u). To this end, from the controller in (25) and the definition in (17), the inequality
can be obtained. The proof of Theorem 1 is completed. From (28) we have
(34)
Solving the above inequality, we can obtain
, , which implies that system in (28) is ISS with input
.
Remark 4: The proposed control law in (25) involves parameters
and
which should be determined by designing in advance before it is implemented. Here, we can first determine the parameters
and matrix K, for example
and
, and then
,
,
and
can be determined accordingly based on the constraint condition
. Finally, an appropriate gain matrix K1 can be selected to make the matrix inequality (19) satisfied. The given parameter
in (22) represents the disturbance attenuation level of the resulting closed system in (1), (12) and (16). As discussed in,26 any level of
disturbance attenuation can be achieved by choosing
sufficiently small at the expense of a larger control effort.
From Theorem 1, we can obtain the amplitude constrained attitude controller (ACAC) for normal system in (1) and (4)-(6):
(35)
with (25)-(28). Based on Theorem 1 and equation (35), the overall structure of the ACAC is shown in Figure 1, and the design procedure for ACAC is given as follows.
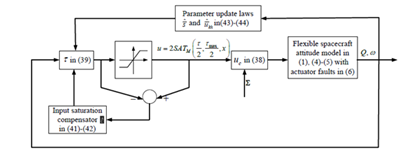
Figure 1 The overall structure of FTACAC.
Step 1: Given
and select the parameter,
, K and K1 based on Remark 4 such that the matrix
inequality in (19) is satisfied;
Step 2: Select compensator parameter diagonal matrix
, set
and construct the saturation compensator l in (27)-(28), where the input of the saturation compensator can be obtained by the feedback loop as shown in Figure 1;
Step 3: Obtain the controller u in (25);
Step4: Further get the ACAC controller uc based on (35).
The proposed amplitude constrained attitude controller in (35) with (26)-(28) achieves asymptotical stability of the resulting closed-loop attitude system with fault-free actuators. However, when actuator faults occur, it no longer ensures the stabilization and accuracy for the attitude control system. Therefore, to guarantee the stability of the system, a controller that can accommodate the actuator faults is needed for flexible spacecraft during actuator fault occurrence. In the follows, in order to propose the fault-tolerant constrained controllers, a significant Lemma is proposed.
Lemma 1:For the actuator distribution matrix
, fault switch matrix
and actuator effectiveness matrix F under assumption 2, there exists a function matrix S(t) and a constant
, such that the following equation holds:
(36)
Proof: Because
, therefore
is a positive definite symmetric matrix. Let
, we have
. As rank
,
, without loss of generality, suppose
with
and then there exists a constant
such that
Let
with
and
being
and
orders, respectively, and then
.
As
therefore we have
based on the fact
. Let
be a row vector. As
system of linear equations
only has zero solution. So, we have
for
. As
which implies that
is a positive definite symmetric matrix. Therefore we have
this proof is completed.
As the fault switch matrix
and the actuator effectiveness matrix F are unknown, the constant
is also unknown, which needs to be estimated in the following control design. From Assumption 3 and the fact
we have
(37)
Based on Theorem 1 and Lemma 1, we propose the following fault-tolerant amplitude constrained attitude controller (FTACAC) in (38) with (39)-(44).
Theorem 2: Consider the flexible spacecraft system that consists of (1), (12) and (16) under actuator faults in (6) for which Assumptions 1-5 hold. Given
, let
,
, where
,
and
be positive definite symmetric matrices. If
, K and
satisfy the inequality in (19), then the dynamic feedback control law
(38)
Where
(39)
(40)
(41)
(42)
(43)
(44)
Denotes the maximum singular value of matrix
,
,
are the estimates of
and
respectively,
and
re positive constants, renders the closed loop system in (1), (12) and (16) under actuator faults in (6) ISS from the input
to the state
Proof: Define the estimation errors of
and
as follows:
and
. Following the same steps as the proof in Theorem 1, we consider the smooth positive-definite radically unbounded function as follows
(45)
The time derivate V1 along (1), (6), (12) and (16) is given by
(46)
From update law in (43), we can obtain that
>0 if choosing
> 0. Therefore, we have the following
Inequality hold based on Lemma 1:
The last inequality in (47) is based on the fact that
. In order to prove
, we first prove the following inequality holds
(48)
So from Theorem 1 and (46)-(48) we can obtain
(49)
Choosing
, then when
we have
=0 , which implies that V1 in (45) is ISS-CLF based on Definition 1. Therefore, the resulting closed loop system in (1), (12) and (16) under actuator faults in (6) is ISS from the input
to the state
. The proof of Theorem 2 is completed.
Remark 5: The second terms of parameter update laws in (43)-(44) are the e-modifications, which guarantee bounded parameter estimates. Based on Theorem 2, the overall structure of the FTACAC is shown in Figure 2, and the design procedure for FTACAC is given as follows
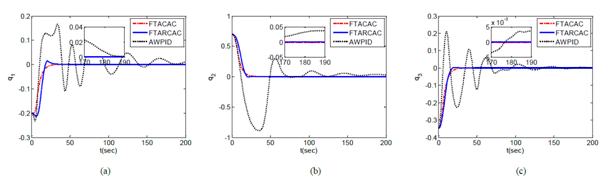
Figure 2 Quaternion with faulty actuators.
Step1: Given
and select the parameter
, K and K1 based on Remark 4 such that the matrix inequality in (19) is satisfied;
Step 2: Select compensator parameter diagonal matrix
, set
and construct the saturation compensator l in (41)-(42), where the input (
) of the saturation compensator can be obtained by the feedback loop as shown in Figure 2;
Step 3: Select parameters,
and
, set
and
, and construct the parameters update laws in (43)-(44);
Step 4: Obtain the FTACAC controller
in (38).
A fault-tolerant amplitude and rate constrained attitude controller design: Control law in (38) only accounts for actuator amplitude constraint. In fact, many cases we require not only the amplitude constraint but also rate constraint of actuators to limit the possible excitation of high-frequency UN modeled dynamic of spacecraft as discussed in.9 However, there are still few results that take both actuator amplitude and rate constraints into account in the attitude control of spacecraft. To account for the amplitude and rate constraints, we proposed the fault-tolerant amplitude and rate constrained attitude controller (FTARCAC) in (50) with (51)-(58) based on the following Theorem 3.
Theorem 3: Consider the flexible spacecraft system that consists of (1), (12) and (16) under actuator faults in (6) for which Assumptions 1-5 hold, given
>0 let
,
, where
and
be positive definite symmetric matrices. If
, K and K1 satisfy the inequality in (19), then the dynamic feedback control law
(50)
With the time derivative of
defined as
(51)
Where
,
(52)
(53)
(54)
(55)
(56)
(57)
(58)
Renders the closed loop system in (1), (12) and (16) under actuator faults in (6) ISS from the input
to the state
.
Proof: following Theorem 1 and Theorem 2, the proof can be completed and therefore we omit it. Finally, we prove control law u in (50) satisfying
Define
. From (51) and the and the
in (18), we can obtain
. Therefore
So the inequality in (8) is satisfied.
Remark 6: The overall structure of the FTARCAC is shown in Figure 3. Equation (51) can be considered as a linear, stable and low-pass filter, where
is the natural frequency of the filter. By employing the filter in (51), the robust controller in (50) with (51)-(58) accounts for not only amplitude constraint but also rate constraint, as well as actuator faults in the presence of inertia matrix uncertainty and external disturbance.


