A concept of equivalence of soft sets is introduced in the article. Concepts of correct operations and correct relationships for soft sets are introduced on the basis of equivalence. Examples of correct and incorrect operations and relations are presented.

Keywords: soft sets, equivalenceforsoftsets, correct operations, correct relationships

The rapid development of the soft sets theory began with the appearance of.^1,2 Later many authors have introduced new operations and relations for soft sets and used these structures in various areas of mathematics and in applied science. Unfortunately in some works the introduction of operations and relationships for soft sets were carried out without due regard to the specific of soft set definition. The purpose of current work is discussion of these problems.

The formal definition of soft sets is following. Let A Bea set of parameters that can have an arbitrary nature (numbers, functions, sets of words, etc.). Let X Bea universal set.

Definition

A pair $\left(S,A\right)$ will be called a soft set over X if S is a mapping from set A to the set of all subsets of X, i.e. $S:A\to 2^X$ . In fact a soft set is a parameterized family of subsets. For better understanding of the specifics of this formal definition, we should discuss the meaning of a notion "soft set". Although mathematics is usually described by science with precisely defined concepts and objects, but the practical application of mathematics is almost always associated with some blurring of the concepts or objects. This is the so-called approximate solutions. For objective reasons it is not possible to find the exact solution in many problems. For example, if the differential equation has no solution in the form of quadrature, it is necessary to use grid solution methods, which basically cannot give exact solution. Even if there is an analytical form of the solution, for example $y=x^2$ we still can't accurately calculate the solution at any point due to the fact that we use real numbers.

A similar situation exists for many other areas of mathematics. For practical work with objects and concepts, we are forced to introduce a collection of sets that define an approximate understanding of these objects and concepts. A concept of soft sets is a mathematical tool for dealing with such objects and concepts. The family $\Im \left(S,A\right)=\left\{S\left(a\right), a\in A\right\}$ defines subsets, which may be an approximate description, and the set of parameters $A$ is chosen for reasons of convenience by the person who introduces the definition of these soft sets. Of course, when you specify a soft set, you have some semantic interpretation of this soft set. However, the mathematical formalism of soft sets does not imply any semantic sense on family of subsets or on the parameters. The parameters serve only the purpose to indicate a specific subset. This situation is very close to defining vicinities of a point in the topology. To determine topology we have to define only the family of vicinities of a point. No comparison of vicinities and no other properties of these subsets are needed. The situation is quite similar for soft sets, as the soft set is a family of vicinities of a point except that the initial point (as in topology) may not exist. Thus, the role of parameters in definition of soft sets is only auxiliary. Parameters are used only as names of subsets. Therefore, the introduction of the notion of equivalence of soft sets $\left(S,A\right)$ and $\left(S^{\prime },A^{\prime }\right)$ should be based on equality of families of sets $\Im \left(S,A\right)$ and $\Im \left(S^{\prime },A^{\prime }\right)$ , but not on equality of point-to-set mappings $S$ and $S^{\prime }$ .

It is necessary to clarify now what we mean by a family of sets $\left\{S\left(a\right),a\in A\right\}$ . This family is considered without repetitions, i.e. if the set belongs to the family, this family has only one such set.
Consider an illustrative example. Let $X=\left\{1,2,3\right\}, A=\left\{1,2,3\right\}, B=\left\{a,b,c\right\}, C=\left\{\alpha ,\beta ,\gamma ,\delta \right\}$ ,

$\begin{array}{l}S\left(1\right)=\left\{1\right\},S\left(2\right)=\left\{2\right\},S\left(3\right),\\ F\left(a\right)=\left\{1\right\},F\left(b\right)=\left\{2\right\},F\left(c\right)=\left\{3\right\},\\ G\left(\alpha \right)=\left\{1\right\},G\left(\beta \right)=\left\{2\right\},G\left(\gamma \right)=\left\{3\right\},G\left(\delta \right)=\left\{3\right\}.\end{array}$

From our point of view, soft sets $\left(S,A\right)$ , $\left(F, B\right)$ and $\left(G, C\right)$ should be considered equivalent, despite the fact that mapping S, F and G are defined on disjoint sets. Let us proceed to the formal definitions.

Definition

Two soft sets $\left(S,A\right)$ and $\left(S^{\prime },A^{\prime }\right)$ , defined over a universal set X are called equal, and written $\left(S, A\right)=\left(S\text{'},A^{\prime }\right)$ if $S=S^{\prime }$ and $A=A^{\prime }$ .

Definition

Two soft sets $\left(S,A\right)$ and $\left(S^{\prime },A^{\prime }\right)$ , defined over a universal set X are called equivalent, and written $\left(S,A\right)\cong \left(S^{\prime },A^{\prime }\right)$ if $\Im \left(S,A\right)=\Im \left(S^{\prime },A^{\prime }\right)$ . Each soft set is a representative of its equivalence class. The difference between equivalent soft sets consists only in the selection of the names for the subsets (including the use of multiple names for a single subset). Therefore, the construction of the theory of soft sets should be produced considering the fact that the replacement of soft set to equivalent does not lead to any changes in results. Let us formulate this notion more formally for operations and relationships with the soft sets.

We first consider the operations with soft sets. We will consider only unary and binary operations with soft sets. It is easy to transfer all of the proposed constructions and operations to a more complex structure. A unary operation on a soft set $\left(S, A\right)$ , defined over the universal set $X$ is the mapping $\Phi$ ,that for any soft set $\left(S, A\right)$ corresponds the soft set $\left(H, B\right)$ , defined over the universal set $X$ , $\Phi \left(S, A\right) = \left(H, B\right)$ .

Definition

A unary operation $\Phi$ is called correct if for any pair of equivalent soft sets $\left(S, A\right) ,\left(S^{\prime }, A^{\prime }\right)$ defined over the universal set $X$ , the results of this operation are also equivalent, i.e. $\Phi \left(S, A\right) \cong \Phi \left(S^{\prime }, A^{\prime }\right)$ . The naturalness of this requirement in the theory of soft sets is obvious. A result of the correct operation on the soft set should not depend on the parameterization method (giving names to the subsets) of a family of sets. A binary operation on a pair of soft sets $\left(S,A\right)$ , $\left(F, D\right)$ ,defined over a universal set $X$ ,is the mapping $\Theta$ , that for any pair of soft sets $\left(S,A\right)$ , $\left(F, D\right)$ corresponds the soft set $\left(H, B\right)$ , defined over the universal set $X$ , $\Theta \left(\left(S, A\right)\left(F,D\right)\right) = \left(H,B\right)$ .

Definition

Binary operation $\Theta$ is called correct if for any four pair wise equivalent soft sets $\left(S, A\right) \cong \left(S^{\prime }, A^{\prime }\right) ,\left(F, D\right) \cong \left(F^{\prime }, D^{\prime }\right)$ , defined over the universal set $X$ , the results of this operation are also equivalent, i.e. $\Theta \left(\left(S, A\right),\left(F,D\right)\right) \cong \Theta \left(\left(S^{\prime },A^{\prime }\right),\left(F^{\prime },D^{\prime }\right)\right)$ . Only correct operations with soft sets are natural for the soft sets theory. When considering incorrect operations, a detailed explanation of the meaning of these operations and reasons for their introduction appears to need. A relationship $\Omega$ for two soft sets $\left(S, A\right),\left(F,D\right)$ , defined over a universal set $X$ , is a mapping $\Omega \left(\left(S, A\right),\left(F,D\right)\right) \to \left\{0,1\right\}$ . If the relation $\Omega \left(\left(S, A\right),\left(F,D\right)\right) =1$ is true, then we will write $\left(S, A\right) \Omega \left(F,D\right)$ .

Definition

The relationship $\Omega$ is called correct if for any four pair wise equivalent soft sets $\left(S, A\right) \cong \left(S^{\prime }, A^{\prime }\right)$ , $\left(F, D\right) \cong \left(F^{\prime }, D^{\prime }\right)$ , defined over the universal set $X$ , the equality $\Omega \left(\left(S, A\right),\left(F,D\right)\right) = \Omega \left(\left(S^{\prime },A^{\prime }\right),\left(F^{\prime },D^{\prime }\right)\right)$ Is true.

It seems reasonable to build correctly all relationships for soft sets.

Consider first the operations with soft sets proposed in.^2,3 The unary operation "complement" $C\left(S,A\right)=\left(CS,A\right)$ has a following definition. The set of parameters is the same, and the mappingis given by the formula $CS\left(a\right)=X\backslash S\left(a\right)$ for all $a\in A$ . Binary operation "intersection" $\cap \left(\left(S,A\right),\left(F,D\right)\right)=\left(W,A\times D\right)$ and "union" $\cup \left(\left(S,A\right),\left(F,D\right)\right)=\left(H,A\times D\right)$ for a couple of soft sets $\left(S,A\right),\left(F,D\right)$ , defined on a universal set $X$ is defined as follows. The set of parameters is chosen to be the direct product of a sets of parameters of arguments, that is equal to $A\times D$ , and the corresponding mappings are given by

$W\left(a,d\right) = S\left(a\right)\cap F\left(d\right), H\left(a,d\right)=S\left(a\right)\cup F\left(d\right), \left(a,d\right)\in A\times D$

Statement: Operations complement $C\left(S,A\right)$ , intersection $\cap \left(\left(S,A\right), \left(F,D\right)\right)$ and union $\cup \left(\left(S,A\right), \left(F,D\right)\right)$ are correct. The proof is obvious. Consider now therelationshipfor softsets introduced in.³ This relationships are defined similarly to topology comparison. Suppose we havea pair of soft sets $\left(S,A\right), \left(F,D\right)$ .

Definition

1. Softset $\left(S,A\right)$ is an internal approximation for soft set $\left(F,D\right)$ , notation $\left(S,A\right)\subseteq \left(F,D\right)$ ,iffor any $d\in D$ , such that $F\left(d\right)\ne \varnothing$ , there exists $a\in A$ which satisfies inclusion $\varnothing \ne S\left(a\right)\subseteq F\left(d\right)$ .

2. Soft set $\left(S,A\right)$ is an external approximation for soft set $\left(F,D\right)$ , notation $\left(S,A\right)\supseteq \left(F,D\right)$ ,iffor any $d\in D$ , such that $F\left(d\right)\ne X$ ,there exists $a\in A$ which satisfies inclusion $X\ne S\left(a\right)\supseteq F\left(d\right)$ On the basis ofinternal and external approximations for softsets we can introduce relevant concepts of equivalence.

Definition

1. Soft set $\left(S,A\right)$ is internally equivalent to a soft set $\left(F,D\right)$ ,notation $\left(S,A\right)\stackrel{\subset }{\approx }\left(F,D\right)$ , if $\left(S,A\right)\subseteq \left(F,D\right)$ and $\left(F,D\right)\subseteq \left(S,A\right)$ .
2. Soft set $\left(S,A\right)$ is externally equivalent to a soft set $\left(F,D\right)$ notation $\left(S,A\right)\stackrel{\supset }{\approx }\left(F,D\right)$ , if $\left(S,A\right)\supseteq \left(F,D\right)$ and $\left(F,D\right)\supseteq \left(S,A\right)$ .
3. Soft set $\left(S,A\right)$ is weakly equivalent to a soft set $\left(F,D\right)$ , notation $\left(S,A\right)\approx \left(F,D\right)$ , if $\left(S,A\right)\stackrel{\subset }{\approx }\left(F,D\right)$ and $\left(S,A\right)\stackrel{\supset }{\approx }\left(F,D\right)$ . Here is the simples properties of these relations.

Statement

1. Relationships $\left(S,A\right)\cong \left(F,D\right)$ , $\left(S,A\right)\approx \left(F,D\right)$ , $\left(S,A\right)\stackrel{\subset }{\approx }\left(F,D\right)$ , $\left(S,A\right)\stackrel{\supset }{\approx }\left(F,D\right)$ , are reflexive, symmetric, and transitive.
2. The relationships $\left(S,A\right)\subseteq \left(F,D\right)$ , $\left(S,A\right)\supseteq \left(F,D\right)$ , are reflexive and transitive.

The caseof a finite family of sets $\Im \left(S,A\right)$ is most interesting for the practical use. Therefore,we will examine which kind of softsets canbe internally and externally equivalent in this case.We introduce notation forthe minimum and maximum for the inclusion for the sets in $\Im \left(S,A\right)$

$MIN\left(S,A\right)=\left\{B \in \Im \left(S,A\right) | B \ne \varnothing , \neg \exists B^{\prime }\in \Im \left(S,A\right) : B^{\prime }\subset B \ne B^{\prime } \ne \varnothing \right\},$

$MAX\left(S,A\right)=\left\{B \in \Im \left(S,A\right) | B \ne X, \neg \exists B^{\prime }\in \Im \left(S,A\right) : B^{\prime }\subset B \ne B^{\prime } \ne X\right\}$ .
We say thata family $\Im \left(S,A\right)$ is nontrivial if it contains at least one non-empty subset distinct from the universal set. Obviously, for the finite and non trivial family $\Im \left(S,A\right)$ sets $MIN\left(S, A\right)$ and $MAX\left(S, A\right)$ are not empty.

Statement : Let the family $\Im \left(S,A\right)$ be finite and nontrivial.

1. The relationship $\left(S,A\right)\stackrel{\subset }{\approx }\left(F,D\right)$ is true if $MIN\left(S, A\right)=MIN\left(F,D\right)$ .
2. The relationship $\left(S,A\right)\stackrel{\supset }{\approx }\left(F,D\right)$ is true if $MAX\left(S, A\right)=MAX\left(F,D\right)$ .
3. The relationship $\left(S,A\right)\approx \left(F,D\right)$ is true if $MIN\left(S, A\right)=MIN\left(F,D\right)$ and $MAX\left(S, A\right)=MAX\left(F,D\right)$ .

Proof. Item 1.Suppose $\left(S,A\right)\stackrel{\subset }{\approx }\left(F,D\right)$ andthere exists a non-empty set $B\in MIN\left(S,A\right)$ and $B\notin MIN\left(F,D\right)$ . Because $\left(F,D\right)\subseteq \left(S,A\right)$ there exists aset $B^{\prime }\in MIN\left(F,D\right)$ such that $B^{\prime }\subseteq B$ . We can assume that $B^{\prime }\ne B$ , because $B\in MIN\left(F,D\right)$ . Now, since $\left(S,A\right)\subseteq \left(F,D\right)$ there exists a non-emptyset $C\in MIN\left(S,A\right)$ such that $C\subseteq B^{\prime }\subset B$ , and $C\ne B$ . It follows that $B\notin MIN\left(S,A\right)$ . This contradiction completes the proof of the necessity. Sufficiency is obvious. Items 2 and 3are proved similarly.

Statement: Relationships: internal approximation, external approximation, internal equivalence, external equivalence and weak equivalence-are correct. The proof is obvious.

Statement

1. If $X\in \Im \left(S,A\right)$ , then $\cap \left(\left(S,A\right),\left(F,D\right)\right)\subseteq \left(F,D\right)$ .
2. $\cup \left(\left(S,A\right),\left(F,D\right)\right)\supseteq \left(F,D\right)$ , $\cup \left(\left(S,A\right),\left(F,D\right)\right)\supseteq \left(S,A\right)$ .

Theproofisobvious. Let us now considersome of the conceptsfor softsetsintroduced in.¹ Authors introducethe following definition.

Definition

For two soft sets $\left(F,A\right)$ and $\left(G,B\right)$ over a commonuniverse U, wesaythat $\left(F,A\right)$ is a soft sub set of $\left(G,B\right)$ if

1. $A\subset B$ , and
2. $\forall \epsilon \in A$ , $F\left(\epsilon \right)$ and $G\left(\epsilon \right)$ are identical approximations.

We write $\left(F,A\right)\tilde{\subset }\left(G,B\right)$ .

$\left(F,A\right)$ is said to be a soft superset of $\left(G,B\right)$ , if $\left(G,B\right)$ is a soft sub set of $\left(F,A\right)$ . We denote it

by $\left(F,A\right)\tilde{\supset }\left(G,B\right)$ .»It is obvious that the condition of (i) leads to a lackof correct ness of the relation $\left(F,A\right)\tilde{\subset }\left(G,B\right)$ , and thus the relation $\left(F,A\right)\tilde{\supset }\left(G,B\right)$ is notcorrect. The authorsof¹ introduced the operation of complement for softsets,based on the mysterious operation with parameters, which hasthe following definition.

Definition

Not Set of A Set of Parameters. Let $E=\left\{e_1,e_2,e_3,\mathrm{....},e_n\right\}$ be a set of parameters. The NOT stof E denoted by $\neg E$ is defined by $\neg E=\left\{\neg e_1,\neg e_2,\neg e_3,\mathrm{....},\neg e_n\right\}$ where $\neg e_i= not e_i, \forall i$ . When defininga softset there are no restrictions on the set of parameters. Different objects may play role of parameters. It can be numbers, words, sentences, subsets - generally speaking everything that will choose the authorintroducinga softset.Therefore expression $\neg e_i= not e_i, \forall i$ looks a completely mystery. Authors¹ introduced two more operations for softsets.

Definition

Union of two soft sets of $\left(F,A\right)$ and $\left(G,B\right)$ over the common universe U is the soft set $\left(H,C\right)$ , where $C=A\cup B$ , and $\forall e\in C$ ,

$\begin{array}{l}H\left(e\right)=F\left(e\right), if e\in A-B,\\ =G\left(e\right), if e\in B-A,\\ =F\left(e\right)\cup G\left(e\right), if e\in A\cap B.\end{array}$

Definition

 Intersection of two soft sets $\left(F,A\right)$ and $\left(G,B\right)$ over a common universe U is the soft set $\left(H,C\right)$ , where $C=A\cap B$ , and $\forall e\in C$ , $H\left(e\right)=F\left(e\right)$ or $G\left(e\right)$ , (asbotharesameset). Firstly, it is not necessary that $F\left(e\right)$ and $G\left(e\right)$ are samesetsin determining 6.1. Secondly, even ifin definition 6.2. instead writing $H\left(e\right)=F\left(e\right)$ or $G\left(e\right)$ ,write $H\left(e\right)=F\left(e\right)\cap G\left(e\right)$ , these two operations are not correct anyway. We make one more comment.¹ Itsauthors introduce the concept of absolute and null soft sets.

Definition

 NULL SOFT SET. A soft set $\left(F,A\right)$ over U is said to be a NULL soft set denoted by $\Phi$ , if $\forall \epsilon \in A$ , $F\left(\epsilon \right)=\varnothing$ , (null-set,).

Definition

ABSOLUTE SOFT SET. A soft set $\left(F,A\right)$ over U is said to be absolute soft set denoted by $\tilde{A}$ , if $\forall \epsilon \in A$ , $F\left(\epsilon \right)=U$ . Each of these definitions does not define a singlesoft set, and determines the class of soft sets and number of soft sets in this class can be as many as different sets of parameters can be imagined. So you can get to the set of all sets that carries a contradiction. It is much more convenient and easier to introduce the concepts required by using the equivalence of soft sets. In fact, the null soft set is the class of equivalencefor relation $\cong$ , which is determined by the condition $\Im \left(S,A\right)=\{\varnothing \}$ . Similarly, for the absolute soft set we have condition $\Im \left(S,A\right)=\left\{X\right\}$ . These are incorrect operations with soft sets and other incorrect operations and relations are found in many papers.The list of such papers is too large to bring it here. It would certainly be useful for the theory of soft sets to try to restructure all such results on the basis of correct operations and relationships.

A fuzzy set over the universal set X is described by membership function $\mu :X\to \left[0,1\right]$ . Thismembership functioncan be associated withthe soft set $\left(M_{\mu },\left[0,1\right]\right)$ , over the universal set $X$ where $M_{\mu }\left(a\right)=\left\{x\in X/\mu \left(x\right)\ge a\right\}$ , $a\in \left[0,1\right]$ . Iffor two fuzzy sets $\mu$ and $\lambda$ the relationship $\left(M_{\mu },\left[0,1\right]\right)\cong \left(M_{\lambda },\left[0,1\right]\right)$ is true, then from the standpoint ofthe softsetstheory, thesefuzzy setsare equivalent.The question naturally arises: will alsobe naturally equivalentfuzzy sets $\mu$ and $\lambda$ in terms ofthe theory of fuzzysets? Let us consider an example. Let $X=\left[0,1\right],\mu =x^n,\lambda =x^{\frac{1}{n}},x\in \left[0,1\right]$ and n– big natural number. Graphs of the functions $\mu$ and $\lambda$ have the form shownin Figure 1. It is easy to see that the relation $\left(M_{\mu },\left[0,1\right]\right)\cong \left(M_{\lambda },\left[0,1\right]\right)$ holds, but the fuzzy sets $\mu$ and $\lambda$ , can hardly be equivalent in terms of the theory of fuzzy sets. Fuzzy set $\mu$ - is “almost the only one point 1” and a fuzzy set $\lambda$ - is “almost the entire segment [0,1]”. If our interpretation of fuzzy sets $\mu$ and $\lambda$ is true, then it indicates that the values of the membership functions have a significant importance. This fact is yet another distinction of soft sets theory and fuzzy sets theory. This difference suggests that the concept of equivalence of soft sets and the equivalence of fuzzy sets are fundamentally different, and therefore the generation of hybrid approaches twisting soft sets and fuzzy sets should be carried out very carefully, taking into account differences between the concepts of equivalence.

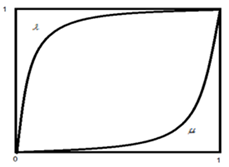
Figure 1 Graphs of the functions $\mu$ and $\lambda$ .

The notion of equivalence for soft sets and concepts of the correct operations and relationsfor soft sets area fundamental conceptsof the theory of soft sets.It seems necessary todevelop the theoryof soft sets using onlythe correct operations and relationships. Using the incorrect operations and relationsto be justified by weighty practical necessity.

None.

Author declares that there is none of the conflicts.