The immiscibility of vegetable oil in methanol provides a mass transfer challenge in the early stages of Transesterification reaction in the production of biodiesel. It is of a great significance to design high–performance nonlinear controllers for efficient control of these nonlinear processes to achieve closed–loop system’s stability and high performance of a biodiesel CSTR. A mathematical model capable of predicting the performance and behaviour of a CSTR has been developed and evaluated. In this work, a comprehensive design procedures based on model predictive control (MPC) have been proposed to efficiently deal with the design of gain–scheduled controllers, controller tuning, optimal controllers and time–varying for nonlinear systems. Since all the design procedures proposed in this work rely strongly on the process model, the first difficulty addressed in this paper is the identification of a relatively simple model of the nonlinear processes under study. The second major difficulty is the analysis of stability and performance for such models using nonlinear control theory of a robust control approach. In the current work, the nonlinear model is approximated by a nominal linear model combined with a mathematical description of model error (due to nonlinearity) to be referred to (in this work) as model uncertainty. The robust control theoretical tools developed are used for the design of gain–scheduled Proportional–Integral–Differential (PID) control and gain–scheduled Model Predictive Control (MPC) in which the MPC method achieves the steady–state optimal set–points of the biodiesel Transesterification reactor.

Keywords: CSTR, mathematical model, predictive control, gain–scheduled controllers, transesterification

MPC, model predictive control; PID, proportional–integral–differentia; MG, mono glycerides; DG, di glycerides

With the world’s depletion of fossil fuels and global environmental degradation, the development of alternative fuels from renewable resources has received considerable attention. Biodiesel has become the foremost alternative fuel to those refined from petroleum feedstock. It can be produced from renewable sources, such as vegetable and animal oils, as well as from wastes, such as used cooking oil. Transesterification is the primary method of converting these oils to biodiesel.^1–3 Transesterification is the chemical reaction between triglyceride and alcohol in the presence of a catalyst to produce biodiesel and glycerol. Transesterification process can be classified as homogenous and heterogeneous. Marchetti et al.,⁴ investigated the possible methods for biodiesel production. The catalysts used in the process can also be classified as homogeneous and heterogeneous. In both groups of catalyst there are several kinds; alkali catalyst, acid catalyst, lipases (biocatalyst). You et al.,⁵ conducted a research into the biodiesel production using an alkali catalyst and discovered it is quite common due to its low temperature and pressure operation. Production of biodiesel using homogeneous catalysts offers high conversion rapid reactions. However associated problems such as saponification reaction as well as the difficulty in separation between the produced biodiesel and catalyst often results in the use of heterogeneous catalyst which when used results in an easy separation of the biodiesel from glycerol (glycerin). Transesterification consists of three steps in series with two intermediates namely diglycerides (DG) and monoglycerides (MG). As shown in Equation 1 the three consecutive reversible reactions of Transesterification include;

1. Conversion of triglycerides to diglycerides,
2. Conversion of diglycerides to monoglycerides,
3. The conversion of monoglycerides to glycerol.

Overall, the three fatty acids bound to the glycerol bond of triglyceride are combined to CH₃–group of methanol, yielding three fatty acid methyl esters. The alcohol used in Transesterification is a short type such as methanol, ethanol, propranolol and butanol. However, methanol is the favorite choice because of its low cost, physical and chemical advantages (polar and shortest chain alcohol). For the stoichiometry of Transesterification, the ratio of alcohol to oil is 3:1 but an excess of alcohol is usually used in order to shift the reaction for more production of biodiesel.

$\begin{array}{l}Triglyceride(TG)+ROH\stackrel{Catalyst}{\leftrightarrow }Diglyceride(DG)+RCOO{R}_1\\ Diglyceride(DG)+ROH\stackrel{Catalyst}{\leftrightarrow }Monoglyceride(MG)+RCOO{R}_2\\ Monoglyceride(MG)+ROH\stackrel{Catalyst}{\leftrightarrow }Glycerol(GL)+RCOO{R}_3\end{array}$ (1)

The chemical reaction with methanol is shown schematically in Figure 1.

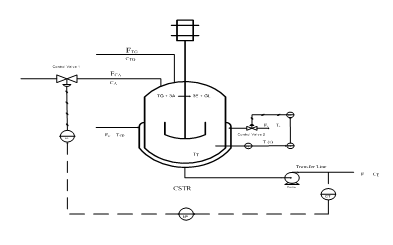
Figure 1 Control diagram for two inputs - two outputs.

$\begin{array}{l}C{H}_{2}O\stackrel{\begin{array}{l}O\\ \end{array}}{C}{R}_1{R}_1\stackrel{\begin{array}{l}O\\ \end{array}}{C}OR\text{'}C{H}_{2}OH\\ ⋮⋮\\ CHO\stackrel{\begin{array}{l}O\\ \end{array}}{C}{R}_2+3R\text{'}OH\stackrel{Catalyst}{\rightleftarrows }{R}_2\stackrel{\begin{array}{l}O\\ \end{array}}{C}OR\text{'}+CHOH\\ ⋮⋮\\ C{H}_{2}O\stackrel{\begin{array}{l}O\\ \end{array}}{C}{R}_3{R}_3\stackrel{\begin{array}{l}O\\ \end{array}}{C}OR\text{'}C{H}_{2}OH\\ TriglyceridesAlcoholEstersGlycerol\end{array}$ (2)

The Parameters which greatly influences the Transesterification reaction include: temperature, methanol: oil molar ratio, mixing rate, catalyst type and amount of catalyst. Catalysts and feedstock are closely related to each other and affect the economic profitability of biodiesel production. Therefore, intensive research is dedicated to finding pertinent feedstock and establishing optimum reaction conditions. Biodiesel can be used directly in diesel engines but is commonly mixed with petroleum–based diesel.

This section presents the development of a mathematical model algorithm to generate the controller behaviour. The simulation, which is done using ASPEN–Plus® Version 20.0 and the model predictive toolbox in MATLAB/SIMULINK motivated by the prediction and control of future inputs and outputs based on the present data/model and comparing with that of conventional PIDs as used by Mjalli et al.,⁶

Development of the mathematical models

The modeling of trans–esterification reactors starts with the understanding of the complex reaction kinetic mechanism. The stoichiometry of vegetable oil methanol sis reaction requires three moles of methanol (A) and one mole of triglyceride (TG) to give three moles of fatty acid methyl ester (E) and one mole of glycerol (glycerin) (GL).The overall reaction scheme for this reaction is:

$\text{TG + 3A }\to \text{ 3E + GL}$  (3)

Accordingly, the model predictive controller is designed to handle a 2×2 system of inputs and outputs as shown in Figure 1. The controlled output variables include biodiesel concentration (CE) and reactor temperature (T); the manipulated variables include reactant flow rate (F_o) and coolant flow rate (F_c). It is very important for a reactor to handle the disturbances in the feed concentration and initial temperatures, as these disturbances heavily change the system performance. The reactions in the reactor during biodiesel production may be modelled as a scheme of multiple reactions of the consecutive‐competitive/series‐parallel type. The forward reactions are said to be second order, referring to the overall order of the proposed forward reaction step. When the molar ratio of alcohol to triglyceride is very high, the concentration of alcohol can be assumed constant. The rate of reaction, then, depends solely on the concentration of triglyceride, a condition which Freedman et al.,⁷ referred to as pseudo–homogeneous first order kinetics. Finally, where the data does not fit the sequential model, Freedman et al.,⁷ proposed a “shunt reaction” in which three alcohols simultaneously attack the triglyceride. The shunt reaction is said to be of fourth order, presumably proportional to [TG] [ROH].^3,8 The catalytic effect is also captured here. The stepwise reactions are modelled as follows;

$\begin{array}{l}\text{TG }+\text{ ROH }\underset{k_2}{\overset{k_1}{\rightleftarrows }} \text{ DG }+\text{ E}\\ \text{DG }+\text{ ROH }\underset{k_4}{\overset{k_3}{\rightleftarrows }} \text{ MG }+\text{ E}\\ \text{MG }+\text{ ROH }\underset{k_6}{\overset{k_5}{\rightleftarrows }} \text{ GL }+\text{ E} \end{array}$  (4)

Where E – (FAME) and GL – Glycerol. The first–order kinetic model can be explained through the following set of differential:

$\begin{array}{l}\frac{d{C}_{TG}}{dt}=-k_1{C}_{TG}{C}_A+k_2{C}_{DG}{C}_E\\ \frac{d{C}_{DG}}{dt}=k_1{C}_{TG}{C}_A-k_2{C}_{DG}{C}_E-k_3{C}_{DG}{C}_A+k_4{C}_{MG}{C}_E,\\ \frac{d{C}_{MG}}{dt}=k_3{C}_{MG}{C}_A-k_4{C}_{MG}{C}_E-k_5{C}_{MG}{C}_A+k_6{C}_{GL}{C}_E,\\ \frac{d{C}_E}{dt}=k_1{C}_{TG}{C}_A-k_2{C}_{DG}{C}_E+k_3{C}_{DG}{C}_A-k_4{C}_{MG}{C}_E+k_5{C}_{MG}{C}_A-k_6{C}_{GL}{C}_E,\\ \frac{d{C}_{GL}}{dt}=k_5{C}_{MG}{C}_A-k_6{C}_{GL}{C}_E,\\ \frac{d{C}_A}{dt}=-\frac{d{C}_E}{dt}\end{array}$  (5)

Where $C_{TG},C_{DG},C_{MG},C_E,C_A,C_{GL}$ are the concentrations of triglyceride, diglycerides, monoglycerides, methyl ester, methanol, and glycerol respectively $k_1,k_3,and{k}_5$ are the effective rate constants foe the forward reactions, and $k_2,k_4,and{k}_6$ are the effective rate constants for the reverse reactions. It is assumed that the initial concentration of triglycerides is C_TG0 and that of diglycerides, monoglycerides, and glycerol is zero at time zero. This is an example of three‐step reaction where the final GL, glycerol and E (FAME) are desired.

A second-order decomposition reaction occurs in the continuous stirred tank reactor, the reactor is equipped with a heat transfer surface that contains a condensing fluid, so that it remains at uniform temperature. The outlet composition and temperature may vary as a result of disturbances in inlet temperature, inlet composition, and coolant temperature. Material and energy balances, plus supplementary equations, are the basis of the model of the reactor system and a mechanistic approach proposed by Mjalli et al.⁶ is used. The equations are nonlinear, so that numerical solution is necessary to predict how the reactor will behave from arbitrary initial conditions. However, because we desire to operate the reactor at steady state, it may be sufficient to examine the dynamics in the vicinity of a steady state; hence linear approximations are useful. In order to realize the optimization and control of continuous biodiesel production process, the model used in this work are based on the second-order kinetic model joining the material and energy balance equations as well as the dynamic equation of the coolant temperature, thus giving us the equations.

The material balance of the reactor for each component reactant is expressed as:

$V\frac{d{C}_i}{dt}=F_{i0}{C}_{i0}-F_i{C}_i-{\displaystyle \sum _{j=1}^n{r}_{j}V}$  (6)

The reactor energy balanced is expressed as:

$\begin{array}{l}V{\displaystyle \sum _{i=1}^{ni}{C}_i{C}_{p_i}}\frac{dT}{dt}=(F_{TG0}{C}_{TG0}{C}_{P_{TG}}+F_{A0}{C}_{A0}{C}_{P_A})(T_0-T)\\ -(V{\displaystyle \sum _{i=j}^n{r}_j\Delta H_j})-(U{A}_H\Delta T)\end{array}$  (7)

The coolant fluid energy balance is expressed as:

$\frac{d{T}_C}{dt}=\frac{F_{C_0}}{V_C}(T_{Cin}-T_C)+\frac{U{A}_H\Delta T}{{\rho }_C{V}_C{C}_{P_C}}$  (8)

The function equation of heat transfer coefficient is approximately expressed as:

${\text{U = αF}}_{\text{C}}{}^{\text{β}}{\text{N}}^{\text{γ}}\text{ = 735}{\text{.5F}}_{\text{C}}{}^{\text{1}\text{.095}}{\text{N}}^{\text{0}\text{.405}}$  (9)

On linearization of Equations (5) and (6), we have:

For material balance,

$V\frac{d{C}_A}{dt}=F{C}_{Ain}-F{C}_A-V{k}_s{C}_{A_s}^2-V\frac{E}{R{T}_s^2}{k}_s{C}_{A_s}^2(T-T_s)-2V{k}_s{C}_{A_s}(C_A-C_{A_s})$  (10)

The energy balance must account for the reaction and heat transfer

$\begin{array}{l}\Im (F,T,T_{in},C_A,F_c)=\\ V\rho C_P\frac{dT}{dt}=F\rho C_P(T_{in}-T_{ref})-F\rho C_P(T-T_{ref})-\Delta H_{r}V{k}_o{e}^{-\frac{E}{RT}}{C}_A^2-UA(T-T_c)\end{array}$  (11)

In the process vegetable oil was Trans–esterifies in the reactor, followed by downstream purification, which consisted of: methanol recovery by distillation; glycerol separation; and methyl–ester purification by distillation. The final purity of the methyl–ester product was quantified by reporting the product stream composition, which was determined by thermodynamic calculations in ASPEN. Mono–and di–glycosides were neglected as reaction intermediates. Plant capacity, unit block operating conditions, and chemical components (except the catalyst) were selected based on the previous heterogeneous acid catalyst (Styrene divinely benzene copolymer) simulation.⁹ For the present simulation styrene divinely benzene copolymer was chosen as the catalyst, as it has been shown to effectively catalyze both the trans–esterification and esterification reactions by several authors.^10,11 Although the properties for triolein were available in the ASPEN data banks, different values of the boiling point and critical temperature were obtained from the literature and used to Re–estimate the Antoine’s vapor pressure coefficients since initial estimates and the results were unsatisfactory. The NRTL model was selected as the thermodynamic model. Since no kinetic data were available for the styrene divinely benzene copolymer reaction, the reactor was modeled as a stoichiometry reactor representing a packed bed reactor, eliminating the catalyst removal step. The conversion was set at 90%. It was assumed that no side reactions involving glycerol occurred, since there had been no reports of such reactions in the literature. ASPEN–Plus flow sheet of the process is presented in Figure 2; conditions and reactor specifications are outlined in Table 1. Catalyst characteristics such as density and porosity have not been included in the reaction scheme since they have not been reported in the literature and are likely to change with each method of synthesis. Additionally, since the reactor is modeled as a batch reactor, including such parameters would not have affected the results. The operating values and calculated data of each component are obtained from literatures^12–15 The reaction rate constant, k, is taken from.¹⁶ Cooling water flow rate, Fc, overall heat transfer coefficient times transfer area, UA, products and reactants values are obtained from.⁶ Model of the reactor is written in MATLAB–MPC by using Equations 5–10.

Figure 2 ASPEN-Plus process flow diagram of the biodiesel production.

Model identification

Figures 3–7 shows that the biodiesel process is a two–input two–output multivariable process. The process nonlinear model was programmed and simulated in Mat lab. Simulation results shows system as an open stable process achieved the parameters of the controller by incrementally adjusting the parameters until the error was reduced to zero.

Figure 3-7 Output response curves under F₀ and F_c actions.

Controller design and simulations

The controller did not attempt to regulate the measured reactor temperature directly. However it varies since it needed to regulate the concentration. Thus, its MPC weight is zero. Each of these parameters was chosen carefully to attain the best controller performance and the least controller moves. Plant inputs C_Ai and T_i are unmeasured disturbances as shown in Figures 4–6. By default, the controller assumes integrated white noise with unit magnitude at these inputs when configuring the state estimator and increasing the state estimator signal–to–noise by a factor of 10 to improve disturbance rejection performance. The MPC Controller block was configured to look ahead the set–point changes in the future, i.e., anticipating the set–point transition which improves set–point tracking as shown in Figure 8, Figure 9. Testing the response to a 5% increase in feed concentration, the closed–loop response is satisfactory to the desired set–point transition.

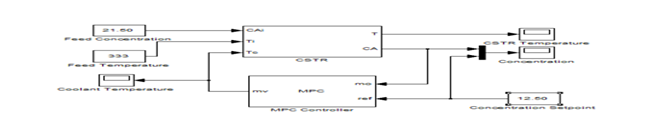
Figure 8 The CSTR MPC controller design with a set-point.

Figure 9 A closed-loop response with a step disturbance in feed concentration.

After a 10minute warm–up period, ramp the concentration set point downward at a rate of 0.25per minute until it reaches 2.0kmol/m³. Removing the 5% increase in feed concentration used previously gives an unacceptable closed–loop response. Performance along the full transition is improved when other MPC controllers are designed at different operating conditions along the intermediate and final transition stages respectively as shown in Figure 10.

Figure 10 A closed-loop controller response using full transition.

Biodiesel Transesterification reactor control has become a very important issue in recent times due to the difficulty in controlling the complex and highly nonlinear dynamic behavior. Nonlinear models have a lot of advantages over linear models for control and estimation and at the same time, they also present new difficulties that must be addressed to guarantee their usefulness. This study demonstrates both the features and caveats of nonlinear models in MPC and presents simple and effective methods for analyzing and avoiding these problems. The research shows the proposed model of the control scheme for the continuous biodiesel Transesterification reactor and also, the transformation of the model in time domain presents the results of the model which shows that it achieved optimal output set–points according to the optimal control scheme goal of the actual production process, and the MPC realized the dynamic tracking control and it was observed that the choice of disturbance models is an important issue for nonlinear plants. The choice of disturbance model can determine whether a system can be stabilized. In general, the input disturbance model is appropriate for cases of plant/model mismatch, although it is ineffective for a specific class of systems. We further demonstrate poor performance of linear MPC on this class of system.

The control system design of the biodiesel Transesterification reactor is different from plant to plant. This depends mainly on the specific production technology adopted. For example, biodiesel production plants based on the MPOB (Malaysia Palm Oil Board) technology have the Transesterification reactor operating pressure higher than atmospheric pressure. For this project, the reactor flow rate is used as a controlled variable and is maintained at a certain level in order to keep methanol in the liquid phase constant. Meanwhile, the temperature of tank is chosen as another controlled variable, rather than the feed temperature itself. A cooling jacket system is utilized to manipulate this controlled variable to maintain the reactor temperature below 65°C (right below the boiling point of methanol at atmospheric pressure). Alternatively, the temperature of reactant feed is chosen as another controlled variable, rather than the temperature of the reactor itself using dynamic simulation software such as MATLAB, Simulink and Aspen Plus.

None.

Author declares that there is none of the conflicts.