A novel design of an artificial soft robot similar to motions of an elephant trunk is presented. The proposed soft undulating robot is a combination of several sections. Each section is an assembly of cylindrical/tubular helical IPMC soft robotic manipulators. The IPMC elements are made of bending IPMC cylindrical/tubular helical elements distributed symmetrically around a cylindrical mantle. This paper further introduces some models and special cases the proposed IPMC soft actuators and sensors in cylindrical/tubular helical form. Experimental results relating the bending deformation to the axial deformations of slit cylinders are also presented.

Keywords: ionic polymer–metal composites, electro active polymers, electrophoretically, spectacular, osmotic pressures

IPMCs or Ionic polymer–metal composites are electro active polymers (EAPs) and are capable of actuation, energy harvesting, and sensing capabilities among other properties. Thus, they are multi–functional smart materials that can be used in biomimetic soft robotics. They normally require a small electric field of a few V/mm and generate spectacular bending and flexing under small electric fields and generate transient voltage and currents output due to dynamic interaction with the environment. Environmental dynamics, like wind or ocean waves, makes them generate an output voltage and transient current of a few mVs for small samples (10mm x 40mm x 0.2mm). IPMCs are capable of operating in or under water or other polar liquids, like blood. Due to the imposed electric field, the conjugated cations electrophoretically migrate towards the cathode and thus expand the cathode side of the ionic membrane and thus bending towards the anode electrode is observed. Osmotic pressures are also instrumental in the migration of cations towards the cathode electrode. Shahinpoor, Bar–Cohen, Xue, Simpson, and Smith^1–2 published an early version and review of IPMCs in 1998.^1–2 See the pioneering works of Osada, Oguro, Kawami, Asaka, Takenaka and Shahinpoor,^3–14 in the 1992–93periods. The electrodynamics of cations generation and transportation in IPMCs are governed by the Poisson–Nernst–Planck field equations^15–24 Biomimetic soft robotic actuation like artificial muscles and sensing of these materials display artificial muscle behavior. For example, an applied voltage of 1 to 4 volts for a typical sample of the size 10mm x 80mm x 0.2mm typically produces spectacular bending (Figure 1).

Figure 1 IPMC strip spectacular bending under 4 volts (A), IPMC strip bending & twisting due to the eccentric placement of electrodes (A).

Different kinds of deformation can be generated in IPMCs by various forms of cationic migration under an imposed dynamic electric field across a strip of IPMC. Conversely, physical deformation of IPMCs can generate an output voltage signal, thus serving as energy harvesters and sensors.

IPMCs, as shown in the following Figure 2, undergo similar cation migrations and rearrangements when subjected to either an electric field or a deformation field. Small samples of IPMC cantilevered strips (0.5cmx3cmx0.2mm) are capable of generating a tip blocking force density of 40. This capability means they can lift an object 40 times their weight^12,23 For example, if the weight of an IPMC strip with a density 2gm/cm³ is 0.1gmf, then it can produce a tip blocking force of about 4gmf.

Figure 2 Essential mechanisms of actuation and sensing in IPMCs.

Several water molecules tend to attach or bond with cations. This number is called the hydration number, 4 for Na+ and 6 for Li+. Poisson–Nernst–Planck phenomena^23,24 govern such ion dynamics, which we will not dwell upon theoretically in this short paper.

The idea of designing and operating a soft biomimetic highly maneuverable robotic arm like an elephant trunk is highly desirable for many soft biomimetic robotic applications.

If we assemble the IPMC strips bend and rolled around a cylindrical/tubular mantle in the form a slit cylindrical assembly, we begin to observe some highly maneuverable undulation similar to an elephant trunk. Some of the configurations of slit IPMC strips around a cylindrical/tubular mantle are shown below in Figures 3a through 3h.

Figure 3 Basic elements of IPMCs with hinge endings (A), clamped-clamped endings (B).

The expansion and contraction undulations of the artificial elephant trunk are performed by the elements shown in Figures 3a through 3h arranged pair wise in a chain, as shown in Figure 4.

In Figure 4 note the combination of movements 1 and 2, the device is capable of 3–D undulating an object like an elephant trunk or a slithering snake–like flexible robotic manipulator. 

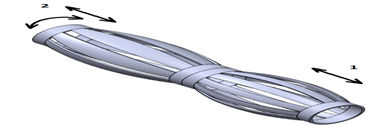
Figure 4 Basic pairs of undulating IPMC strips in a helically slit tubular configuration capable of bending, twisting, expansion, contraction, and undulation.

Note that in the IPMC slit tubular configurations, slit IPMC cylindrical strips have two major forms of boundary condition for this type of the actuator/sensor family in the forms of simple hinges or clamps. Twisting the IPMC slip cylinder then allows for rolling and twisting motion of the slip tubular elements. The twisted and helically wound around the cylindrical mantle will provide more complex manipulation and maneuver possibilities similar to movements of an elephant trunk capable of undulating motion including internal deformation in compression, expansion, twisting, rolling, bending, or twirling.

From another point of views, soft biomimetic artificial elephant trunk robotic actuators and sensors configurations of IPMC as shown in Figures 5a&5b, can be employed for the design and fabrication of the biomimetic robotic artificial elephant trunk.

Figure 5A Helical form of slit IPMC actuators and sensors.

Consider a rectangular cartesian coordinate systems x, y and z (Figure 5b) such that $x=rcos\phi ,y=rsin\phi$ and $z=c\phi for\phi ϵ\left[0,2\pi \right]$ . Here r is the radius of the helix and c is a constant giving the vertical separation of the helix's loops, and φ is an independent parameter. The $tan\alpha =c/r$ is the value of the slope of the strip sample. The curvature of the helix is given by $\kappa =r/\left(r^2+c^2\right)$ , arc length is given by $s=\phi {\left(r^2+c^2\right)}^{0.5}$ , the torsion of a helix is given by $\tau =c/\left(r^2+c^2\right)$ such that $\kappa /\tau =r/c$ .

Figure 5B Helical geometry of axial and twisting slit tubular IPMC strips.

Here the initial form of the device considered for the tubular actuators/sensors is a combination of axial and rotary movements that resemble slithering snakes, as shown in Figure 4 above.

Referring to Figure 6a, in case of having more combinations of these actuation configurations, the possibility of having a more complex soft robotic undulating elephant–like trunk can be expected as it is depicted in Figure 6b.

Figures 6a, 6b depict various forms of artificial elephant trunk type undulation with a variety of boundary conditions. Under suitable feedback control, the artificial elephant trunk can be robotically manipulated to move the soft snake–like, worm–like, or elephant trunk–like soft robots. For the rotary movement in the direction denoted by I, actuators 1 and 2 are helically arranged and can produce a combined rotation and slithering movement.

Figure 6A worm/snake/elephant trunk soft robot made of tubular IMPC actuators.

The actuation unit number 3 in Figure 6b can produce bending and twisting if we apply a voltage to generate helical and planar movements in the direction denoted by II. Furthermore, other types of undulating movements can be generated by actuator unit number 3 in Figure 6b in the direction denoted by III. Thus, the combinations of cylindrically and helically arranged slip IPMC actuators are capable of generating elephant–trunk–like motions and undulations.

Figure 6B worm/snake/elephant trunk soft robot made of tubular IMPC actuators.

Figure 7 depicts electrical wiring of each modular unit. The anode/cathode electrodes will be placed either at the proximal, distal, or in the middle of the each IPMC strip to enable moving and controlling each modular unit.
As can be seen in Figure 7, the wire bundle of electrical lead wires is networked to enable IPMC actuation as well as energy harvesting and sensing.

Figure 7 Electrical wiring of each modular unit.

Preliminary design and development of an artificial biomimetic soft robotic elephant trunk were presented. The design used a cylindrical tubular arrangement of helically twisted slit cylinders made with IPMC strips. This family of soft biomimetic artificial elephant trunk robotic actuators and sensors actuator and sensors were designed with bending/twisting slit IPMC elements that were symmetrically arranged and placed around a cylindrical/tubular mantle with either hinged or clamped ends. These types of soft actuators and sensors are capable of generating a combination of actuation, energy harvesting and sensing consisting of linear expansion, contraction, bending, twisting and rotating action similar to a slithering snake or an elephant trunk. The next steps in the development of advanced elephant–trunk–like soft biomimetic robotic actuators and sensors are to further explore various cylindrically and helically arranged IPMC strips. Currently, we are further exploring such possibilities towards fabrication an artificial soft biomimetic robotic elephant–trunk.

The author declares there are no conflict of interest.

None.

None.

1. Shahinpoor M, Bar–Cohen Y, Simpson JO, et al. “Ionic Polymer-Metal Composites (IPMCs) As Biomimetic Sensors, Actuators and Artificial Muscles-A Review”. Smart Materials and Structures. 1998;7(6):R15–R30.
2. Shahinpoor M, Bar–Cohen Y, Xue T, et al. “Ionic Polymer-Metal Composites (IPMCs) As Biomimetic Sensors, Actuators and Artificial Muscles”. California: Proceedings of SPIE's 5th Annual International Symposium on Smart Structures and Materials. 1998. p. 3324–3327.
3. Osada Y, Okuzaki H, Hori H. A polymer gel with electrically driven motility. SAO/NASA ADS Physics Abstract Service. 1992;355(6357):242–244.
4. Oguro K, Kawami Y, Takenaka H. “Bending of an Ion-Conducting Polymer Film Electrode Composite by an Electric Stimulus at Low Voltage”. Trans. J Micro–Machine Society. 1992;5:27–30.
5. Segalman D, Witkowski W, Adolf D, et al. “Theory of Electrically Controlled Polymeric Muscles as Active Materials in Adaptive Structures.”Int. Journal of Smart Material and Structures. 1992;1:95–100.
6. M. Shahinpoor. Conceptual Design, Kinematics and Dynamics of Swimming Robotic Structures Using Ionic Polymeric Muscles. Int. Smart Material and Structures. 1992;1(1):91–94.
7. Doi M, Marsumoto M, Hirose Y. Deformation of Ionic Gels by Electric Fields. Macromolecules. 1992;25:5504–5511.
8. Oguro K, Asaka K, Takenaka H. Polymer film actuator driven by low voltage. Nagoya: In Proceedings of the 4th International Symposium of Micro Machines and Human Science. 1993;38–40.
9. Adolf D, Shahinpoor M, Segalman D, et al. Electrically Controlled Polymeric Gel Actuators. US Patent Office. US Patent No.5,250,167. 1993.
10. Oguro K, Kawami Y, Takenaka H. Actuator Element. US Patent Office. US Patent No. 5,268,082. 1993.
11. Shahinpoor M, Kim KJ. Ionic Polymer-Metal Composites – I. Fundamentals, Smart Materials and Structures. 2001;10(4):819–833.
12. Shahinpoor M, Kim KJ, Mojarrad M. Artificial Muscles: Applications of Advanced Polymeric Nano–Composites. 1st edn. USA: Great Britain: CRC Press, Taylor & Francis Group. 2007.
13. Kim KJ, Shahinpoor M. Ionic Polymer-Metal Composites – II. Manufacturing Techniques. Smart Materials and Structure. 2003;12(1):65–79.
14. Kim KJ, Shahinpoor M. A Novel Method of Manufacturing Three-Dimensional Ionic Polymer-Metal Composites (IPMC's) Biomimetic Sensors, Actuators and Artificial Muscle. Polymer. 2002;43(3):797–802.
15. De Gennes PG, Okumura K, Shahinpoor M, et al. Mechanoelectric Effects in Ionic Gels. Europhysics Letters. 2007;50(4):513.
16. Asaka K, Oguro KJ. Bending of polyelectrolyte membrane platinum composites by electric stimuli: Part II. Response kinetics. Journal of Electroanalytical Chemistry. 2000;480(1–2):186–198.
17. Shahinpoor M. Ionic Polymer-Conductor Composites as Biomimetic Sensors, Robotic Actuators and Artificial Muscles-A Review. Electrochimica Acta. 2003;48(14–16)2343–2353.
18. Shahinpoor M, Kim KJ. Novel Ionic Polymer-Metal Composites Equipped with Physically-Loaded Particulate Electrode as Biomimetic Sensors, Actuators and Artificial Muscles. Sensors and Actuators A Physical. 2002;96(2–3):125–132.
19. Shahinpoor M, Kim KJ. A Solid-State Soft Actuator Exhibiting Large Electromechanical Effect. Applied Physics Letters. 2002;80(18):3445–3447.
20. Bahramzadeh Y, Shahinpoor M. Charge Modeling of Ionic Polymer-Metal Composites for Dynamic Curvature Sensing. California : Proceedings of SPIE 18th Annual International Symposium on Smart Structures and Materials. 2011. p. 6–10.
21. Bahramzadeh Y, Shahinpoor M. Dynamic Curvature sensing employing Ionic Polymer-Metal Composite Sensors. Smart Materials and Structures. 2011;20(9):7.
22. Shahinpoor M. Biomimetic Robotic Venus flytrap (Dionaea Muscipula Ellis) Made with Ionic Polymer Metal Composites (IPMCs). Bioinspir Biomim. 2011;6(4).
23. Shahinpoor M. “Ionic Polymer-Metal Composites (IPMCs): Smart Multi-Functional Materials and Artificial Muscles. UK: Volume II, Royal Society of Chemistry Publishers. 2016
24. M.Shahinpoor, “Ionic Polymer–Metal Composites (IPMCs): Smart Multi–Functional Materials and Artificial Muscles”. Volume I. UK:  Royal Society of Chemistry Publishers. 2016. p. 1.