In this study, in order to increase manufacture efficiency and improve machining precision of heavy-duty spiral bevel gear CNC (Computerized Numerical Control) machine tool, an innovative cutter spindle feed mode replacing the traditional work piece or spindle box feed mode used for heavy-duty spiral bevel gear CNC machine tool is proposed. The method is described as follows. Firstly, a three-dimensional structural model of heavy-duty spiral bevel gear CNC machine tool adopting the proposed cutter spindle feed mode is designed. Then, the numerical control machining model of heavy-duty spiral bevel gear CNC machine tool using the cutter spindle feed mode is constructed, including determining cutter location parameters, establishing machining coordinate system and calculating motion parameters. An example is consequently demonstrated to verify the established numerical control machining model. Finally, a virtual simulation model and an experimental model of heavy-duty spiral bevel gear CNC machine tool adopting the proposed cutter spindle feed mode are established and the validation of the proposed cutter spindle mode is conducted . Both the virtual simulation and experimental results show that the proposed cutter spindle feed mode used for heavy-duty spiral bevel gear CNC machine tool is feasible and effective with improved machining efficiency and accuracy.

Keywords: cutter spindle feed mode, spiral bevel gear, heavy-duty, cnc machine tool, virtual simulation

Due to the smoothly meshing characteristics, spiral bevel gear is still a hot topic of research and has been widely used to various kinds of intersecting or crossed-axes power transmissions in many industry fields, such as aerospace, armament, metallurgy and refineries.^1-3 Over the past few decades, many researchers have studied spiral bevel gear and its machine tool, especially on optimization of machine tool settings and modification of tooth surface based on tooth contact analysis (TCA).

Optimization of machine tool settings can improve the machining accuracy and meshing characteristics of spiral bevel gears.⁴ Used an optimization approach to systematically define the optimal head-cutter geometry and machine tool settings to minimize the tooth contact pressure and the transmission error simultaneously, by which the sensitivity of face-hobbed spiral bevel gears to the misalignments can be reduced.⁵ The author investigated the combined influence of machine tool settings for pinion teeth finishing and misalignments of the mating members on load distribution and transmission errors in mismatched spiral bevel gears.⁶ Presented a method to determine the optimal machine tool settings for manufacturing modified hypoid gears based on improved load distribution and reduced transmission errors. Cao, et al.⁷ developed an approach to design the pinion machine tool settings for spiral bevel gears by controlling contact path and transmission errors.

Tooth contact pressure, area and pattern directly influence meshing characteristics of spiral bevel gears. To improve meshing performances, TCA has been frequently used to investigate the modification of tooth surface. Litvin, et al.⁸ Used a local synthesis of spiral bevel gears to provide improved conditions of meshing within the neighborhood of the mean contact point. Sobolewski &Marciniec⁹ described a tool for analyzing tooth contact and transmission errors of spiral bevel gear sets with tooth flanks represented as CAD free-form surfaces. Vimercati¹⁰ proposed a mathematical model for spiral bevel gear tooth surface representation by face-hobbing method based on TCA under light and heavy loads and stress analysis. Argyris, et al.¹¹ adopted an integrated computerized method to perform the synthesis, analysis and stress analysis of enhanced spiral bevel gear drives by application of computerized methods of local synthesis and simulation of meshing and contact of gear tooth surfaces. Simon¹² investigated the influence of misalignments and tooth errors on load distribution, stresses and transmission errors in mismatched spiral bevel gears with the method of loaded TCA. Fang et al.¹³ developed an accurate and convenient edge TCA method of spiral bevel gears to determine the contact points on tooth edges and resolved the tooth edge contact problem successfully. However, the above studies are mainly focused on traditional spiral bevel gear machine tool. Recently, more and more researchers turn to apply their methods to CNC (Computerized Numerical Control) machine tool due to its greater manufacturing precision, better transmission characteristics, and higher efficiency.

Simon¹⁴ developed an algorithm for execution of motions on CNC hypoid generating machine tool for the manufacture of spiral bevel gears. Deng et al.¹⁵ presented a machining method of face milling using a disk cutter with a concave end to solve some common problems of CNC-machined spiral bevel gears. Suh, et al.¹⁶ adopted a CNC milling machine controlled by the 3/4-axis control mode to manufacture spiral bevel gears and ascertained the validity and effectiveness of the method by experimental cuts. Shih and Fong¹⁷ proposed a flank-correction method obtained directly from a six-axis Cartesian-type CNC hypoid generator in which high-order correction can be easily achieved through direct control of the CNC axis motion, and validation of this method was demonstrated by a numerical study. Liu et al.¹⁸ applied an adaptive acceleration-deceleration control method to spiral bevel gear CNC machining and its effectiveness was verified through related experimental study. Fan^19,20 adopted a generic model of tooth surface generation for spiral bevel and hypoid gears produced by face-milling and face-hobbing processes conducted on free-form CNC hypoid gear generators.

Studies on modification of tooth surface are also conducted on CNC machine tool,²¹ as it is a preferred method to improve meshing characteristics of spiral bevel gears. Shih²² proposed a novel ease-off flank modification methodology for spiral bevel and hypoid gears made by a modern Cartesian-type hypoid gear generator. Simon^23,24 used a method for the determination of optimal tooth modifications of spiral bevel gears for CNC machine tool, based on improved load distribution and reduced maximum tooth contact pressure and transmission errors. Su and He²⁵ employed an ease-off based modification method of spiral bevel gear tooth surface, and the CNC machine-tool setting parameters approaching the target surface can be obtained.

The up-to-date literatures on spiral bevel gear and its machine tool are focused on TCA, transmission error analysis, optimization of machine-tool settings and multi-axis CNC machine tool. However, little attention has been paid to design of gear CNC machine tools for heavy-duty spiral bevel gears, especially those with the diameter bigger than 1000 mm. Heavy-duty spiral bevel gear machine tool is a typical representative of heavy-duty complex manufacturing equipment, and its performance directly influences spiral bevel gear’s manufacturing efficiency, machining precision, movement accuracy and transmission efficiency. Improving the manufacturing efficiency and machining accuracy of heavy-duty spiral bevel gears is of great importance. However, the efficiency and precision of heavy-duty spiral bevel gear machine tools with traditional feed mode by work piece or spindle box moving is relatively poor because of the huge weight of work piece or spindle box.

This paper proposes an innovative cutter spindle feed mode used for heavy-duty spiral bevel gear CNC machine tools to solve the problem of low efficiency and accuracy of heavy-duty spiral bevel gear machine tools with the traditional work piece or spindle box feed approach. The rest of the paper is organized as follows. Section 2 describes the basic theory of machining principle of spiral bevel gears. In section 3, structural model of heavy-duty spiral bevel gear CNC machine tool are first established and consequently the numerical control machining model of heavy-duty spiral bevel CNC machine tool using the proposed feed mode is constructed, including determining cutter location parameters, establishing machining coordinate system and calculating motion parameters. And the numerical control machining model is verified by an illustrative computation example. In section 4, a virtual simulation model and an experimental model of heavy-duty spiral bevel gear CNC machine tool adopting the proposed spindle feed mode are established and the validation of the proposed feed mode is conducted . Finally, Conclusions are drawn in section 5.

In this section, firstly, the basic theory of machining principle of spiral bevel gears is presented. And then the diagram of the proposed cutter spindle feed mode used for heavy-duty spiral bevel gear CNC machine tool is also illustrated.

Machining principle of spiral bevel gears

Spiral bevel gears are usually manufactured through generating method for face milling by means of the virtual crown gear principle as shown in Figure 1.^19,20 The blade edges of the rotating cutter, whose axis is offset from the axis of the virtual crown gear and imagined to be fixed to the virtual crown gear, function as a tooth of the virtual crown gear. During the machining process of a spiral bevel gear, the virtual crown gear and the gear work piece mesh and rotate around their respective axes at a predetermined ratio of rotation; therefore, the cutter will gradually cut out a tooth groove in the gear work piece. After cutting a tooth groove, the virtual crown gear returns to its original position and the gear work piece rotates to the next indexing position to prepare to cut the next tooth groove. The above procedure repeats until all the teeth are generated. Machining process for spiral bevel gears is illustrated in Figure 2.

Figure 1 Schematic illustration of the generating principle of face milling of spiral bevel gear.

Figure 2 Machining process for spiral bevel gears.

Diagram of the proposed cutter spindle feed mode for heavy-duty spiral bevel gear CNC machine tool

The cutter spindle feed mode is proposed for heavy-duty spiral bevel gear CNC machine tool to overcome the low precision and accuracy of heavy-duty spiral bevel gear machine tool with traditional workpiece or spindle box feed mode. The diagram of the proposed cutter spindle feed mode for heavy-duty spiral bevel gear CNC machine tool is described and illustrated in Figure 3.

Figure 3 Diagram of the proposed feed mode for heavy-duty spiral bevel gear CNC machine tool.

Structural model of heavy-duty spiral bevel gear CNC machine tool

Heavy-duty spiral bevel gear CNC machine tool has a similar structure, machining principle and movement pattern with traditional mechanical spiral bevel gear machine tool. For the traditional spiral bevel gear machine tool or CNC spiral bevel gear machine tool, feed amount and feed speed are accurately controlled by the movement of work piece box moving left and right with the bed saddle or the movement of slippery pedestal type spindle box moving back and forth with the machine column. Due to the heavy weight of work piece or spindle box, it is very difficult to precisely control the feed speed of heavy-duty spiral bevel gear machine tool, and the manufacture efficiency will become relatively low if the traditional feed amount and feed speed are used on the heavy-duty spiral bevel gear machine tool. Therefore, the cutter spindle feed mode is proposed and adopted to control the feed amount and feed speed in the heavy-duty spiral bevel gear machine tool. In this way, feed movement can be easily achieved through machine tool spindle’s rectilinear stretching motion, completely replacing the traditional work piece or spindle box feed approach, and the manufacture efficiency and accuracy can be greatly improved with this new feed mode. Three-dimensional structural mode of heavy-duty spiral bevel gear machine tool is shown in Figure 4. The basic machining process is illustrated in Figure 5 and is described as follows. After machining one tooth space, the machine tool spindle retracted, the cradle reverts to its original position, and the work piece rotates one dividing angle at the same time, then to machine next tooth space. After finishing one machine cycle, the feed amount is changed by the machine tool spindle’s rectilinear stretching motion, and moves to the next machining cycle. This process repeats until the whole work piece gear is finished.

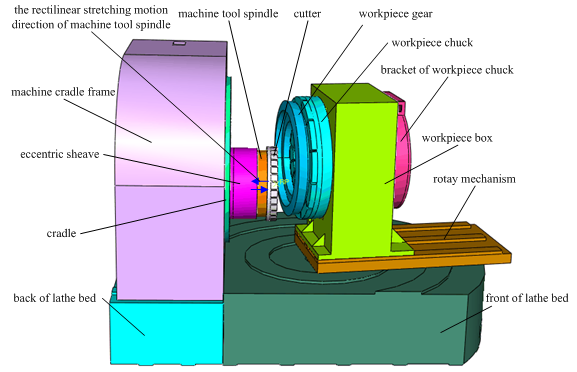
Figure 4 Structure of heavy duty spiral bevel gear machine tool.

Figure 5 The basic machining process of heavy-duty spiral bevel gear CNC machine tool.

Numerical control machining model of heavy-duty spiral bevel gear CNC machine tool

1. Determining cutter location parameters

Before the process of machining on spiral bevel gear with the principle of imaginary crown generating gear, the first step is to determine the cutter’s nominal radius ${\text{r}}_{\text{k}}$ through related calculation according to the geometric parameters of workpiece gear, and then to determine the cutter’s location parameters, which is the cutter’s center ${\text{O}}_{\text{k}}$ in the machine coordinate systems. In this paper, the eccentric method is adopted to determine the cutter’s location parameters of the heavy-duty spiral bevel gear machine tool. The schematic diagram for calculation of the cutter’s location parameters is shown in Figure 6.

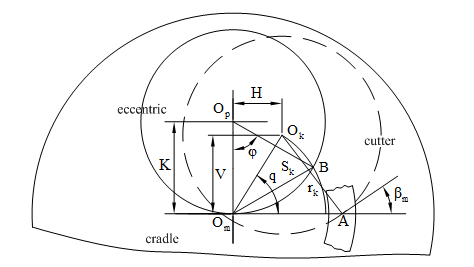
Figure 6 schematic diagrams of calculation the cutter’s location parameters.

When adjusting the cutter location parameters of heavy-duty spiral bevel gear machine tool, the vertical coordinate V and horizontal coordinate H of the tool center ${\text{O}}_{\text{k}}$ in the coordinate plane ${\text{X}}_{\text{m}}{\text{O}}_{\text{m}}{\text{Y}}_{\text{m}}$ are expressed as

$V=r_k\cdot \cos {\beta }_m$ (1)

$H=L_m-r_k\sin {\beta }_m$ (2)

Where ${\text{β}}_{\text{m}}$ is helical angle and ${\text{L}}_m$ refers to cone distance. Then, the radial cutter spacing ${\text{S}}_{\text{k}}$ and the angular cutter spacingare described as

$S_k=\sqrt{V^2+H^2}$ (3)

$q=\arctan \frac{V}{H}$ (4)

Before adjusting the cutter location parameters, cutter’s center ${\text{O}}_{\text{k}}$ coincides with the center of the machine too ${\text{O}}_{\text{m}}$ . When adjusting the cutter location parameters, the eccentric rotates an angle $\text{φ}$ and drives the cutter’s center ${\text{O}}_{\text{k}}$ to move from the machine tool center to ${\text{O}}_{\text{m}}$ point B (shown in Figure 6) so that the distance between the cutter center ${\text{O}}_{\text{k}}$ and machine tool center ${\text{O}}_{\text{m}}$ is equal to the radial cutter spacing ${\text{S}}_{\text{k}}$ . Then, rotate the cradle an angleto make sure that the angle from the horizontal line to the line between machine tool’s center ${\text{O}}_{\text{m}}$ and cutter’s center ${\text{O}}_{\text{k}}$ is equal to the angular cutter spacing q. The eccentric angle $\text{φ}$ and the cradle angleare formulated as

$\varphi =2\arcsin \frac{S_k}{2K}$ (5)

$\begin{array}{l}Q=q\pm \frac{\phi }{2}\\ \{\begin{array}{l}\text{+ = }left\text{-}handhelicalbevelgear\\ -\text{= } right\text{-}handhelicalbevelgear\end{array}\end{array}$ (6)

whereis the distance between cutter’s centerO_k and eccentric’s center O_p.

2. Establishing machining coordinate system

In this section, the principle of imaginary crown generating gear to machining spiral bevel gears is used, and the machining coordinate system is similar to the traditional mechanical spiral bevel gear machine tool as shown in Figure 7. The coordinate systemsΣ_m,Σ_c,Σ_kand Σ_ware rigidly connected to the machine, cradle, cutter and workpiece gear respectively, and O_m,O_c,O_k andO_ware the corresponding origins. The origin O_c coincides with the origin O_m, and O_w is the design intersection point of workpiece gear. The origins of coordinate Σ₁ and Σ₂ coincide with the origins O_k and O_w respectively. The origin O_k is the center of the knifepoint plane, and the knifepoint plane ${\text{X}}_{\text{k}}{\text{O}}_{\text{k}}{\text{Y}}_{\text{k}}$ coincides with the machine plane ${\text{X}}_{\text{m}}{\text{O}}_{\text{m}}{\text{Y}}_{\text{m}}$ . During the process of machining spiral bevel gear, the coordinate system Σ_c and cradle turn around the axes Z_m together, and ${\phi }_{\text{c}}$ is the current rotation angle of cradle. The coordinate systemΣ_w and the workpiece gear turn around the axes Z_mtogether, and ${\phi }_{\text{w}}$ is the current rotation angle of workpiece gear, which is relative to ${\phi }_{\text{c}}$ .β is the angle between the line from cutter’s center O_kto machine tool’s center O_mand horizontal line S_k.Refers to the distance between cutter’s center O_k and machine tool’s center O_m.${\delta }_{\text{m}}$ is machine root angle.refers to the work head offset. When machining the heavy-duty spiral bevel gear,E is equal to zero.X_bis sliding base, refers to the distance of the cutter going or falling back along the cradle’s center line relative to a certain standard position, which directly influences the cut tooth depth of work piece gear.X_pis machine center to back, referring to the distance between workpiece gear’s design intersection point O_w and machine tool’s center point O_m.

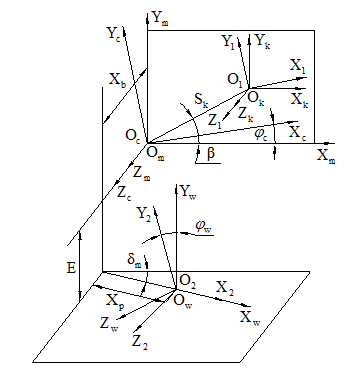
Figure 7 Machining coordinate system of heavy duty spiral bevel gear machine tool.

3. Calculating motion parameters

The essence of machining heavy-duty spiral bevel gear is to achieve the relative movements between cutter and workpiece gear. It needs to transform the coordinate systems of cutter and workpiece gear to a same coordinate system so as to calculate the relative movement and relative position between cutter and workpiece gear during the process of machining heavy-duty spiral bevel gear.

In the schematic of alternate blade cutter (shown as Figure 8), the ${\text{r}}_{\text{ki}}$ indicates the cutter point radiu of inner cutting edge, and ${\text{α}}_{\text{i}}$indicates the pressure angle of inner cutting edge. The element of cone through point P on the circular conical surface of inner cutting edge intersects the knifepoint plane at point $\text{P'}$ . Assuming $\left|\text{PP'}\right|$ is equal to $s$ , and ${\text{θ}}_{\text{k}}$ indicates the phase angle at point P on the cutter. therefore, the radius vector of point P can be presented as ${\text{r}}_{\text{p}}{\text{(θ}}_{\text{k}}\text{,s)}$ in the cutter coordinate system by the parameters $s$ and ${\text{θ}}_{\text{k}}$ .

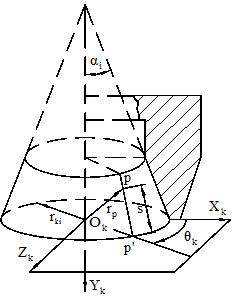
Figure 8 The schematic diagram of alternate blade cutter of heavy duty spiral bevel gear machine tool.

$\begin{array}{l}{r}_p({\theta }_k,s)=\left[\begin{array}{c}(r_{kn}\pm s_n\sin {\alpha }_n)\cos {\theta }_k\\ (r_{kn}\pm s_n\sin {\alpha }_n)\sin {\theta }_k\\ -s_n\cos {\alpha }_n\end{array}\right]\\ \{\begin{array}{l}+=\text{ inner cutting edge}\\ -=\text{ outside cutting edge}\end{array}\end{array}$ (7)

The unit vector of the normal through pointcan be presented by the parameters ${\text{θ}}_{\text{k}}$ as

$\begin{array}{l}{n}_p({\theta }_k)=\left[\begin{array}{c}\pm \cos {\alpha }_n\cos {\theta }_k\\ \pm \cos {\alpha }_n\sin {\theta }_k\\ -\sin {\alpha }_n\end{array}\right]\\ \{\begin{array}{l}+=\text{ inner cutting edge}\\ -=\text{ outside cutting edge}\end{array}\end{array}$ (8)

According to the machine coordinate system of heavy-duty spiral bevel gear machine tool, the coordinate-transformation matrix from cutter coordinate system to machine coordinate system can be expressed as

$M_{mk}=M_{mc}{M}_{c1}{M}_{1k}$ (9)

where $M_{1k}$ is the coordinate-transformation matrix from coordinate system Σ_k to auxiliary coordinate system Σ₁,

$M_{1k}=\left[\begin{array}{cccc}\cos {\theta }_k& \sin {\theta }_k& 0& 0\\ -\sin {\theta }_k& \cos {\theta }_k& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (10)

$M_{c1}$ is the coordinate-transformation matrix from auxiliary coordinate system Σ₁ to coordinate system Σ_c,

$M_{c1}=\left[\begin{array}{cccc}1& 0& 0& s_k\cos \beta \\ 0& 1& 0& \mp s_k\sin \beta \\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (11)

$M_{mc}$ is the coordinate-transformation matrix from coordinate system Σ_c to coordinate system Σ_m,

$M_{mc}=\left[\begin{array}{cccc}\cos {\phi }_c& -\sin {\phi }_c& 0& 0\\ \sin {\phi }_c& \cos {\phi }_c& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (12)

The radius vector of pointand the unit vector of the normal through point P is described as

$r_p{}^{(m)}=M_{mk}=M_{mc}{M}_{c1}{M}_{1k}{r}_p({\theta }_k,s_k)$ (13)

$n_p{}^{(m)}=L_{mc}{L}_{c1}{L}_{1k}{n}_p({\theta }_k)$ (14)

where L is 3×3 coordinate-transformation matrix which is obtained from the corresponding M in which the last line and the last column are removed. In the same way, the radius vector ${\text{r}}_{\text{q}}{}^{\text{(m)}}$ of point G on the work piece gear which meshes with the pointis shown as

$r_q{}^{(m)}=M_{m2}{M}_{2w}{r}_q$ (15)

where ${\text{r}}_{\text{q}}{}^{\text{(m)}}$ is the radial vector of pointin the coordinate system of workpiece gear.

During the process of machining spiral bevel gears, the speed of relative movement between point P on cutting edge’s surface and point G on work piece gear is expressed as

$v^{(kw)}=v_k^{(m)}-v_w^{(m)}=\frac{\text{d}{r}_k^{(m)}}{\text{d}t}-\frac{\text{d}{r}_w^{(m)}}{\text{d}t}$ (16)

Generating gear and workpiece gear should be satisfied with the meshing equation and the transmission ratio

$n_p{}^{(m)}\cdot v^{(kw)}=0$ (17)

$m_{cw}=\frac{{\omega }_c}{{\omega }_w}$ (18)

where ${\text{ω}}_{\text{c}}$ and ${\text{ω}}_{\text{w}}$ refers to rotational angular velocity of generating gear and workpiece gear respectively, and ${\text{m}}_{\text{cw}}$ is the transmission ratio between the generating gear and work piece gear.

Suppose the initial rotor angles of imaginary crown generating gear and work piece are ${\phi }_{\text{c0}}$ and ${\phi }_{\text{w0}}$ , then the motion parameters of cradle’s rotating axesand work piece’s rotating axesare described as

$\angle C={\phi }_c={\phi }_{c0}+{\displaystyle {\int }_0^t{\omega }_c}\text{d}t$ (19)

$\angle A={\phi }_w={\phi }_{w0}+{\displaystyle {\int }_0^t{\omega }_w}\text{d}t$ (20)

If the modified-roll method is applied to machining pinion spiral bevel gear, the third ordered modification function needs to be considered for the instantaneous variation transmission ratio.

${\phi }_w=\frac{1}{m_{cw}}\left[{\phi }_c-D{\left({\phi }_c\right)}^2-E{\left({\phi }_c\right)}^3\right]$ (21)

where D is second order modified roll coefficient, andis third order modified roll coefficient. The motion parameter of work piece gear box’s rotating axes B on the heavy duty spiral bevel gear machine tool is usually equal to workpiece gear’s root angle.

$\angle B={\delta }_m$ (22)

During the process of machining of the heavy duty spiral bevel gear with the heavy duty spiral bevel gear machine tool, feed motion is achieved by the cutter spindle’s concertina movement along the axes Z_k to change the distance between the knifepoint plane and work piece’s root cone.

$Z_k=F(t)$ (23)

Based on the above discussions, we can obtain the heavy duty spiral bevel gear machine tool’s motion parameters or instantaneous relatively position of generating gear and workpiece gear during the process of machining heavy duty spiral bevel gear.

Verification of numerical control machining model

An example of calculating machining parameters of a given heavy-duty spiral bevel gear with the diameter 1600 mm is presented to verify the numerical control machining model of heavy-duty spiral bevel gear CNC machine tool adopting the proposed cutter spindle feed mode . The specifications of the heavy duty-spiral bevel gears are shown in Table 1. The adjusting parameters of the heavy duty-spiral bevel gear machine tool are illustrated in Table 2, and the partial NC code used to drive the motion parameters of numerical control machining model of heavy-duty spiral bevel gear CNC machine tool is described in Table 3.

To validate the feasibility and effectiveness of the proposed cutter spindle feed mode, a virtual simulation machining model and an experimental model for heavy-duty spiral bevel gear CNC machine tool are established. The virtual simulation machining model is constructed using simulation machining software VERICUT and the experimental model is built on a bull heavy-duty spiral bevel gear CNC machine tool. Virtual simulation machining on a given pair of heavy-duty spiral bevel gears has been conducted using motion parameters which are derived from the methods expressed in section 3. Virtual machining simulations on a bull heavy-duty spiral bevel gear and a pinion spiral bevel gear are illustrated in Figure 9A & 9B respectively. The practical machining is performed on a bull heavy-duty spiral bevel gear using the CNC machine tool adopting cutter spindle feed mode as shown in Figure 10. Both the virtual simulation machining and practical machining results indicate that the proposed cutter spindle feed mode used for heavy-duty spiral bevel gear CNC machine tool is feasible and effective and meet the expected design requirements.

Figure 9 The virtual simulation machining of heavy duty spiral bevel gears. (A) Virtual simulation machining on bull gear. (B) virtual simulation machining on pinion gear.

Figure 10 Machining on one bull heavy duty spiral bevel gear.

1. A novel cutter spindle feed mode replacing the traditional workpiece or spindle box feed mode for heavy-duty spiral bevel gear CNC machine tool is proposed.
2. Structural model and numerical control machining model of heavy-duty spiral bevel gear CNC machine tool adopting the proposed cutter spindle feed mode are established respectively. In the numerical control machining model, cutter location parameters are first determined, and then the machining coordinate system is established and the motion parameters are calculated. The numerical control machining model is verified by an illustrative example.
3. A virtual simulation machining model and an experimental machining model are established respectively. And the feasibility and effectiveness of the proposed cutter spindle feed mode is validated through conducting machining heavy-duty spiral bevel gears with diameter 1600 mm on both the virtual simulation machining model and the experimental machining model. Both the virtual simulation machining and practical machining results show that the proposed cutter spindle feed mode is feasible and effective with improved machining efficiency and accuracy.

The authors are grateful for the financial support of the National Natural Science Foundation of China under grant No. 51305127 and youth backbone teacher in Colleges and Universities training program of Henan Province of China No. 2016GGJS-040.

The author declares there are no conflicts of interest.

1. Litvin FL, Alfonso F. Gear’s geometry and applied theory. 2th ed.Cambridge University Press; 2004. p. 633–644.
2. Zeng T. Design and machining of spiral bevel gear. China:Harbin Institute of Technology Press; 1989. p. 90–91.
3. Takayuki N. Computerized Modeling and Loaded Tooth Contact Analysis of Hypoid Gears Manufactured by Face Hobbing Process. Journal of Advanced Mechanical Design, Systems, and Manufacturing. 2009;3(3):224–235.
4. Simon VV. Optimal machine-tool settings for the manufacture of face-hobbed spiral bevel gears. Journal of Mechanical Design. 2014;136(8).
5. Simon VV. Machine-tool settings to reduce the sensitivity of spiral bevel gears to tooth errors and misalignments. J Mech Des. 2008;130(8):0826031–08260310.
6. Simon VV. Optimal machine tool settings for hypoid gears improving load distribution. Journal of Mechanical Design. 2001;12(4):557–582.
7. Cao XM, Fang ZD, Xu Hao. Design of Pinion Machine Tool-settings for Spiral Bevel Gears by Controlling Contact Path and Transmission Errors. Chinese Journal of Aeronautics. 2008;21(2):179–186.
8. Litvin FL, Zhang Y, Handschuh RF. Local Synthesis and Tooth Contact Analysis of Face-Milled Spiral Bevel Gears. NASA Contractor Reports. 1991;4342:184.
9. Sobolewski B, Marciniec A. Method of spiral bevel gear tooth contact analysis performed in CAD environment. Aircraft Engineering and Aerospace Technology. 2013;85(6):467–474.
10. Vimercati M. Mathematical model for tooth surfaces representation of face-hobbed hypoid gears and its application to contact analysis and stress calculation. Mechanism and Machine Theory. 2007;42(6):668–690.
11. Argyris J, Fuentes A, Litvin FL. Computerized integrated approach for design and stress analysis of spiral bevel gears. Computer Methods in Applied Mechanics and Engineering. 2002;191(11-12):1057–1095.
12. Simon VV. Head-cutter for optimal tooth modifications in spiral bevel gears. Mechanism and Machine Theory. 2009;44(7):1420–1435.
13. Fang ZD, Deng XZ, Ren DF. Loaded tooth contact analysis of spiral bevel gears considering edge contact. Chinese Journal of Mechanical Engineering. 2002;38(9):69–72.
14. Simon VV. Advanced manufacture of spiral bevel gears on CNC hypoid generating machine. Journal of Mechanical Design. 2010;132(3):0310011–0310018.
15. Deng XZ, Li GG, Wei BY. Face-milling spiral bevel gear tooth surfaces by application of 5-axis CNC machine tool. The International Journal of Advanced Manufacturing Technology. 2014;71(5-8):1049–1057.
16. Suh SH, JihWS, Hong HD. Sculptured surface machining of spiral bevel gears with CNC milling. International Journal of Machine Tools and Manufacture. 2001;41(6):833–850.
17. Shih YP, Fong ZH. Flank correction for spiral bevel and hypoid gears on a six-Axis CNC hypoid generator. Journal of Mechanical Design. 2008;130(6):0626041–06260411.
18. Liu K, Lu YH, Zhao DB. Application of adaptive acceleration-deceleration control method of parametric curve interpolator in spiral bevel gear NC machining. Journal of Mechanical Engineering. 2009;45(12):198–204.
19. Fan Q. Computerized modeling and simulation of spiral bevel and hypoid gears manufactured by gleason face hobbing process. Journal of Mechanical Design. 2006;128(6):1315–1327.
20. Fan Qi. Enhanced algorithms of contact simulation for hypoid gear drives produced by face-milling and face-hobbing processes. Journal of Mechanical Design. 2007;129(1):31–37.
21. Chao Lin, Yu Fan, Yao Wang, et al. A five-axis CNC machining method of orthogonal variable transmission ratio faces gear. Journal of Advanced Mechanical Design, Systems, and Manufacturing. 2014;8(3):1–12.
22. ShihYP. A novel ease-off flank modification methodology for spiral bevel and hypoid gears. Mechanism and Machine Theory. 2010;45(8):1108–1124.
23. Simon VV. Loaded tooth contact analysis and stresses in spiral bevel gears. ASME 2009 International Design Engineering Technical Conferences &Computers and Information in Engineering Conference. 2009;271–279.
24. SimonVV. Influence of tooth modifications on tooth contact in face-hobbed spiral bevel gears. Mechanism and Machine Theory. 2011;46(12):1980–1998.
25. Su JZ, He ZX. High-precision modification of tooth surface for spiral bevel gears. Journal of South China University of Technology (Natural Science). 2014;42(4):91–96.