
Review Article Volume 4 Issue 2
About method which increases efficiency of motion control of orbital spacecraft
MV Levskii
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Khrunichev State scientific & production Space Center, Moscow, Russia
Correspondence: MV Levskii, Khrunichev State scientific & production Space Center, Moscow, Russia
Received: March 16, 2018 | Published: April 30, 2018
Citation: Levskii MV. About method which increases efficiency of motion control of orbital spacecraft. Int Rob Auto J. 2018;4(2):146-152. DOI: 10.15406/iratj.2018.04.00112
Download PDF
Abstract
Aspects of increase of efficiency of spacecraft’s motion control are discussed. It is supposed that basic means of control for change of spacecraft position are jet engines. The combining of control regimes of orientation and orbit correction, as perspective way of problem solution, is considered. New specific index of optimality is entered for estimate of a quality of motion control. Then, the problem of combining terminal orientation with correction of orbit altitude maintenance by optimal way is solved. Concrete control algorithm of spacecraft reorientation combined with orbit correction, in application to large massive spacecrafts and, in particular, orbital station, is presented. Results of mathematical simulation of motion control which uses the designed method are given. Also, estimation of efficiency indices is made for the mount scheme of motionless micro-engines. High efficiency of combining regimes of attitude control and correction of spacecraft’s orbit altitude is shown.
Keywords: spacecraft motion, jet engines, criterion of optimality, control law, combining regime
Introduction
Angular stabilization and reorientation of a spacecraft are the most frequently used dynamic regimes. The research programs conducted during the flight and the related stringent requirements for precision and efficiency of control over the spacecraft angular motion motivate the interest in the problem of optimization of the process of spacecraft reorientation. The significant increase in size, mass and active lifetime of orbital spacecraft supplied with systems of attitude control and correction leads to a sharp increase in the relative propellant load necessary for operation of the executing devices of the motion control system. The conception of the control of motion as the center of mass, as well as of the motion with respect to the center of mass of the spacecraft by means of non-central jet force is successfully used in designing the control system of rockets. Using and developing the above idea, one can economize a significant amount of fuel when designing systems of control of spacecraft motion. Such economy can be achieved by combining the regimes of attitude control and correction, accomplished through applying to the spacecraft the non-central force produced by the jet engine of the attitude control system whose thrust vector does not pass through the spacecraft's center of mass. The goal of optimally combining the regimes of correction and attitude control is advisable only for a certain class of spacecraft for which the condition
, holds true; here
and
are the propellant loads intended for the orbit correction and the spacecraft attitude control, respectively. If inertial actuators (powered gyroscopes1 or gyro dynes) are used, then
represents the fuel consumption necessary to compensate the inadmissible increase of angular momentum of the gyro-system. The considered class of spacecraft includes the long-term orbital stations also. In this paper, the problem of the optimal programmed turn of the spacecraft combined with correction of its orbit is considered in the general form. Let us assume that jet micro-engines are used as main actuators of the motion control system. In this case, possibilities to increase the efficiency of the spacecraft turn are related to three main directions:
- efficient arrangement of the attitude control engines on the spacecraft body;
- synthesis of the optimal, with respect to fuel consumption, laws of control of spacecraft reorientation, and
- Combining the process of attitude with a correction of the spacecraft orbit altitude.
Development of the first theme leads us to a transition from control with respect to the principal central axes of a spacecraft to control with respect to the axes bound to its angular momentum vector. For this type of control, provisions must be made for shifting the point of attachment of the control engines with respect to the spacecraft body, which requires some special design features. The second subject is well known, and the largest number of works on optimization of spacecraft rotations (though without requiring the simultaneous correction of the orbit) has been dedicated toil.1-14 In particular, kinematical problem of a slew maneuver is studied in detail2 where solution was resulted for variant when angular velocity vector is limited by modulus. The problems of solid body rotation, optimal in fast response and minimum energy expenditures, were considered.3 An analytic solution was obtained using the Pontryagins maximum principle. In some cases, construction of attitude control is based on fuzzy logic or on the method of inverse problem of dynamics4,5 (the majority of solutions1,2,4-7 corresponds to spacecraft rotation around motionless axis or instantaneous Euler axis). The combined control of the motion around the center of mass and of the motion of the spacecraft center of mass itself permits us to significantly reduce total stocks of propellant, necessary for all dynamic regimes of attitude control of the spacecraft and correction of its orbit. This domain is relatively new, but it is very promising nevertheless. Now, combining of terminal orientation and orbit correction of spacecraft by optimal way is considered in detail. Numerical realization of the algorithm with prognostic model15 is proposed. The peculiarity of the model in use is the prediction of the “free” motion in the class of spacecraft rotations along the trajectory where the vector of angular momentum of spacecraft body is constant in inertial coordinate system. This allows us to change over from the continuous synthesis of controls to their determination and action onto the spacecraft at discreet instants of time.
General statement of the problem, and introduction of efficiency index
Increase of control efficiency by motion of the orbital spacecraft is possible at the expense of combination of regimes of orientation and correction of spacecraft orbit. Let, in the course of the combined control increase in the required direction of the correcting impulse of velocity
be transmitted in the center of spacecraft mass; in the process, an amount of working medium
is spent for the turn and orbit correction. Had the processes of the spacecraft reorientation and correction of its orbit been independent, the total fuel consumption would have been
. To estimate the efficiency of the control, we introduce function
. Here,
denotes the minimum fuel expenditure for the independent turn of the spacecraft,
is the fuel expenditure for the orbit correction, and
is the fuel expenditure for the combined control. The absolute fuel economy is determined by the value
. It is obvious that the turn that is optimal for fuel expenditure corresponds to the maximum value of the target function E. Only in this case is the effect of combining the regimes of control revealed to the fullest extent. Thus, when optimizing laws of the combined control of spacecraft motion, first determine the value of the minimum fuel expenditure for the rotation independent of orbit correction, which requires in its turn, the prior solution of the traditional problem, i.e., the problem of optimization of control of the spacecraft reorientation. Therefore, we formulate the problem of combined control of the spacecraft reorientation as follows: one should determine the control providing, with the prescribed accuracy
, the spacecraft turn from the arbitrary initial position
to the required final position Lf within the fixed time T, with the minimum fuel expenditure: the increment of velocity
transmitted to the spacecraft center of mass during the turn should be maximum. It is accepted that the initial and final angular velocities are equal to zero. When solving the formulated problem, we made some assumptions:
- The spacecraft is considered to be a perfectly rigid body,
- Possible misalignment of the principal central axes of the spacecraft's ellipsoid of inertia with the axes of the bound coordinate system is ignored;
- The time of action of the controlling moment is small compared to the time of the turn;
- The angular momentum imparted by the attitude control engines to the spacecraft body significantly exceeds the angular momentum acquired during the turn from external disturbances,
- The influence of the projection of thrust impulse of the attitude control engines on the normal to the spacecraft orbital velocity is negligible small.
For an estimation of a control efficiency by a turn, are used three indicators:
- Absolute economy of fuel
,
where
is minimum possible (theoretically) the expense of fuel for a turn at independent control;
is the expense of fuel for a turn combined with correction of maintenance of orbit height (it is obvious,
);
is the expense of the fuel necessary for orbit correction creating the same effect of orbit's raising (height increase) as after the turn which is executed using the investigated method;
corresponds to two-impulse control for a turn;16
is a difference between the expense of fuel for motion control at the independent and combined control of orientation and orbit correction of the spacecraft;
- Efficiency of the combined control of a turn
;
- An indicator of a combining
,
Where
is the expense of fuel for a turn (it is agreed with the developed method) at independent control of orientation and orbit correction. If control of spacecraft motion is made by the engines established motionlessly concerning the spacecraft body then
, and
, where
is an increment of orbital (linear) speed of the spacecraft, got during a turn (the correcting impulse);
is the coefficient of proportionality connecting the speed increment created by the correcting engine and the fuel expense necessary for giving the additional speed to the spacecraft in value
. More efficient control of motion corresponds to more value of indicators
and
(when the control of a turn is more effective, the values
,
are closer to 2). However, more capacious (and fairly) an indicator for an estimation (and comparisons with other analogues) of method of turn control combined with orbit correction is the rating
Obviously, the volume of fuel equal
is necessary to spend in any case (irrespective of turn method and its optimality) as the effect of speed increment
for orbit correction can be reached only at the expense of jet thrust. At independent control, is required at least
fuel (it is the minimum level); at the combined control of considered method of a turn, the fuel expense is
or
. We can consider the quantity
as a payment for necessity of spacecraft turn but not just correction of its orbit. The difference between minimal possible expenses of fuel at independent control of a turn and the expense for that what the spacecraft has accepted the given angular position
as a result of motion control is the economy received for the account of combination of control regimes. The absolute economy
also is coordinated with earlier accepted indicator:
. At independent control, is spent
, at the combined control we have
. From here we receive the difference
. At an ideal turn (the bottom lath) as pattern, is required GR min fuel, and at combined turn
(as from
whole GC goes for orbit correction, and remains
for the rotation). For efficient control of spacecraft motion, is necessary that the value I corresponding to control method was as small as possible (in an ideal case it comes nearer to zero). The planar turn is a special case (it meets seldom), and its separate studying is not so actually. We will note only, what even in case of planar rotation of a spacecraft for a combination indicator is fairly
(it easily to demonstrate). Even by the example of this particular case (the planar rotation of the spacecraft around the principal central axis of inertia) one can clearly see that the use of the idea of regulation of the spacecraft’s angular position by means of the non-central jet force allows us to gain significant fuel economy. The general case of a spatial turn (three-dimensional rotation of the spacecraft when Euler's axis does not coincide with one of axes of body-fixed coordinate system) represents interest. Let's consider this case more in detail.
Solution of the problem of combined control of spacecraft’s spatial motion
At first, let's solve the problem of optimal control of spacecraft's three-dimensional reorientation independent of orbit correction. Turn of a spacecraft around the Euler axis and the turn in the form of the regular precession (simultaneous rotation around the longitudinal axis of the spacecraft and the motionless axis in inertial space) we not consider because they obviously are not optimum (the fuel expense in these cases much more of the optimal value, at least, in 1.4-1.6 times). The method proposed below belongs to a group of algorithms of the combined synthesis of optimal control with predicting.15 As the prognostic models we take the model of the rotational motion of a dynamically symmetric spacecraft. Prediction of the "free" motion corresponds to the regular precession of the spacecraft. We chose the parameters of the prognostic models on the basis of the condition of maximum symmetry of the predicted motion to the actual motion of the spacecraft. The spacecraft’s rotational motion is described by the following equations1,2
,
,
,
,
Here, w1 , w2 , and w3 are the projections of the spacecraft’s angular velocity on the hound axes;
,
, and
are the principal central moments of inertia of the spacecraft;
,
, and
are the moments of external forces;
,
,
and
are components of the quaternion L describing the relative orientation of the bound and inertial coordinate systems. For the sake of definiteness, we assume that the OX-axis is the longitudinal axis of the spacecraft,
, and
,
. Note that the chosen spacecraft class satisfies the condition of quasi-symmetry:
, but
, and
. Hence, the moment
is small, and we can consider it as a perturbation. Further, we select the moment of inertia with respect to the transverse axis
on the basis of the condition of invariance of the characteristic equation of the dynamic system:
, where
, and
.
In the accepted notation is, the dynamics of real spacecraft will be described by the system:
,
In the determination of the motion by prediction, the controlling moments are taken to be zero. Therefore,
, and
include only the perturbing moments. Analysis of this system shows that the right-hand sides of the equations are the small values (the perturbations); thus, in the prognostic model, we neglect them. Finally, the equations of the prognostic model assume the form:
Solving the boundary value problem
with allowance for last system, we obtain the required angular velocities:
Angles
and
and vector
are determined by the following system of relationships:
, where
are components of the quaternion of the turn
. Taking into account the fact that the true motion of the spacecraft differs only slightly from the predicted motion, we will use the method of iterative guidance in order to form the control commands in the process of rotation. According to this method, the trajectory is divided into several legs where the control is absent (M = 0). The transition from one leg to another is accomplished by the correcting pulses. There is only one requirement for the legs: they must pass through
and
. The objective of the control consists in providing such initial conditions for the legs without control that the motion by prediction passes through the final position
. To do this, for the beginning or each leg
, the quaternion of the turn is determined,
, by which the required initial conditions for the next leg,
and
are determined. The spacecraft motion on the stages of acceleration and retardation coincide with the predicted trajectories (since
), and their duration
is determined by the prescribed time T of the turn, the available value of the controlling moment M, and the rotation angle
arccos
, by which it is necessary to rotate the spacecraft. Duration of the motion along the spacecraft’s free motion legs is determined from the condition of minimization of fuel expenditure G and depends on the logic of formation of the commands on execution of the angular momentum correction. Usually, several (depending on the rotation angle4–6) impulses of correction of the angular momentum are sufficient. The optimization is reduced to determination of the durations of gain and cancellation of the spacecraft angular velocity. The controlling moments
,
and
on the legs of acceleration and retardation are determined by two conditions:
and
for all
and at the same time,
- For the leg of acceleration,
and K is the calculated value of the angular momentum:
; and
- For the leg of retardation,
and K is the actual angular momentum of the spacecraft at the beginning of retardation. On both legs, M = const in the inertial coordinate system.
Thus, control of the spacecraft reorientation is reduced to the execution of the following operations13:
Calculation of the turn quaternion
and determination of the initial conditions for the free motion leg
,
, and
; determination of the calculated value of the angular momentum
and the controlling moments
,
, and
; Spacecraft acceleration with the maximal controlling moment to the required value of the angular momentum
during the process, the controlling moment direction being constant in the inertial coordinate system:
Free rotation of the spacecraft, M = 0, up to the instant
of the spacecraft motion correction; At time instant
, determination of the error signal quaternion
, and calculation of the boundary conditions corresponding to it (the new hitting trajectory),
and
, for the next leg of the motion without control. Determination of the required impulse of the angular momentum <
for
. We calculate the controlling moments on the basis of the requirement
for all
according to the
, where
. Then, one should assume that
, and repeat operation 3) and 4) until the time instant when the spacecraft can be rotated through the remaining error angle
within the time
necessary to cancel the angular velocity. Braking of the spacecraft with the maximal controlling moment:
at this phase, controlling moment is directed strictly opposite to the actual angular momentum. Correction of the trajectory of spacecraft motion can be made at regular intervals
or at regular decrements of the remaining error angle
. The time instants
can be formed by the logarithmic scale as well, in the direction of lowering
or
as time passes. The smaller the remaining angular distance to the prescribed position
, the more frequently are corrections made of spacecraft angular momentum. The choice of a particular program for determination of the sequence of times
during the spacecraft rotation (the cyclogram of the output of the correcting impulses of spacecraft angular momentum) depends on the priorities of accomplishing the planned tasks. The proposed algorithm is based on the method of iterative guidance with the use of prognostic model. Therefore, it needs no continuous formation of the controls and is reduced to moderate correction of the trajectory of the spacecraft rotational motion at certain instants of time. It is known, that the minimum fuel expenditure is reached at two-impulse control of a turn.3 And for increase of accuracy of spacecraft reorientation into the required angular position we offer to correct rotary motion of the spacecraft during time interval between acceleration and braking. Corrections make at time moments
when equalities
are carried out, where
, i is correction number,
. Such law of formation of correction moments is possible also
, where q < 1 (for example, q = 1/2 or q = 3/5). The designed method of control is invariant to the external as well as to the parametric disturbances and provides high efficiency and accuracy of the spacecraft reorientation.
The index of efficiency of the synthesized law of control of a single spatial turn of the spacecraft can be naturally represented in the form
. We form the control commands for the attitude control engines on the basis of the assumption that the main purpose of control is to minimize fuel expenditures on the spacecraft reorientation,
, and the orbit correction is the consequence of this process. Hence, it is reasonable to assume that
; i.e., the fuel is not consumed specially for increase of the orbit altitude. According to this approach,
represents the fuel expenditures necessary to provide the same effect of orbit altitude increase for the independent control:
, where
is the spacecraft velocity increase obtained as the result of the reorientation,
, m is the spacecraft mass, and W is the gas exhaust velocity of the altitude control engines. The values
and
depend on the pattern of mounting the attitude control engines. For spacecraft’s planar rotation, the optimal combining of the regimes of attitude and orbit correction require the possibility to turn the jet engine thrust in an arbitrary way. It is obvious that, for the case of spacecraft’s spatial rotation combined with orbit correction, the optimal control also necessitates orienting the engine thrust P in the required direction with respect to the bound spacecraft axes. However, such a method of control implies a mounting the attitude control engines in gimbals mounts, which involves non-small (and even considerable) constructive difficulties. Because of this, we consider pattern of the rigid mounting of the attitude control engines, which is expedient from the practical point of view Figure 1. The reorientation control law becomes rather simple: in order to create the prescribed controlling moment M providing the spacecraft transition from the initial angular position
to the required final position
within the prescribed time T,we switch on only those engines whose thrust makes the acute angle with the velocity V. It can be easily seen that this is always possible, since, in order to create the required controlling moment one of two oppositely directed attitude control engines can be chosen. Values of the optimized fuel expense GCOM and of the index of optimality were determined by the method of mathematical shooting using a personal computer.17 When considering the problem of combining the regimes of attitude and correction, we make one important assumption: the velocity vector V is constant in inertial space (we have neglected the spacecraft’s orbital motion during the rotation time T and have not taken into account the rotation of the orbital coordinate system with respect to the inertial basis). For the new generation orbital stations where the rotation time T is large, this simplification might be too restrictive (and even inadmissible for exact estimations of the index of efficiency of combining). Hence, in the mathematical simulation, we take account of all factors of the spacecraft’s real flight including the variation in space of the direction of velocity V during the rotation. According to the notations in left part of Figure 1, we have
, where
the controlling moment in cross-section is;
is longitudinal component of controlling moment M. In the calculations, the following simplifications ere accepted; all the engines are situated at equal stances from the longitudinal axis OX and are symmetrically located with respect to the plane YOZ, and point O coincides with the center of mass of the spacecraft. Let us introduce the notations
, where
is the time of action of the thrust impulse.
Similarly,
,
. Let,
,
, and
are the projections of the unit vector of velocity V on the bound axes
,
is the fuel economy due to combining control per one impulse (one switching on of the attitude control engines); and
is the fuel expenditure per one impulse. Then,
,
, where N is the number of impulses of the spacecraft angular momentum per one turn. Omitting the detailed reasoning, we present the final logic of the calculations of
and
for presented pattern of mounting the attitude control engines (the pattern with 32 attitude control engines, see right part of Figure 1):
if
, then
and
;
if
, then
and, at the same time:
if
, then
;
if
, then
if
, then
.
For basic modes of a turn, indicators of a combining Q are known (after mathematical simulation of virtual turn), as a rule. Dependence between other characteristics (E and I) is expressed by formulas:
Relation
is fair for indicators Е and Q (parity Е = Q only for the two-impulse control accepted as a standard).
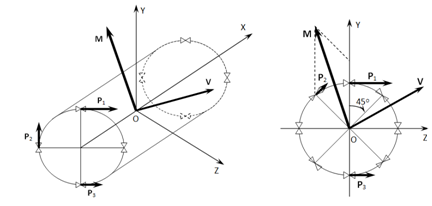
Figure 1 The schemes of mounting the controlling engines (16 at the left and 32 on the right).
Example of computational modeling the spatial motion under optimized control
Now, we give numerical illustrating the results of solving the problem of optimal rotation. For example, let us consider three-dimensional maneuver of some spacecraft (as solid body) from position
into position
(the quaternion’s
and
give initial and final attitude). It was assumed that initial and final angular velocities are zero:
. In the considered case the quaternion
is
, and the elements of the quaternion
are
,
, and
. Also, we assume that duration of maneuver should be not more than 360 seconds, and spacecraft have following characteristics:
;
;
; values
are equal
,
,
. After computational modeling we have: durations of acceleration and braking are 23.68 s and 23.64 s, accordingly; the entire turn is completed in a time T = 357.25 s, optimal control satisfies the condition
(because
= 360 s). It means that perturbations (including asymmetry of the spacecraft) helped rotation into required position. Visual illustration of rotation dynamics is given in Figure 2. The upper and the middle parts of this figure correspond to phase variables of motion: the upper part shows graphs of the variation of the angular velocities in the body coordinate system
,
,
; the middle part shows graphs of the variation of the components of the quaternion L(t), which specifies the current attitude of the spacecraft during the rotation maneuver:
,
,
and
. The variables
are smooth functions of time. Finally, the lower part of Figure 2 presents the dynamics of the variation of the variables
,
and
which are components of the ort of the angular momentum. The following rule is observed for the functions
and p1(t): for any combinations of the boundary values of
and
, these functions are always sign-invariant and of the same sign. From Figure 2, we see that number of motion corrections is four. Corrections of spatial motion are formed by following law:
, where i is number of correction. First correction of spacecraft motion carried out at instant
when
, where
is discrepancy angle in current instant of time t;
arccos
is initial angle of discrepancy. In this example of controlled rotation, we have following durations of correction:
= 0.68 s,
= 1.16 s,
= 0.64 s,
= 0.64 s. Notice that the quaternion of the turn
corresponds to the case when the final rotation vector (Euler’s axis) makes the same angle with the longitudinal axis OX as with the plane perpendicular to OX, and initial angle of discrepancy
is 180 degrees. This is most difficult case of reorientation of solid body. The presented results of solving the reorientation problem demonstrate what the characteristics of designed method of spacecraft control are very good (and the best from known modes).
Data of mathematical simulation
As an example, we present modeling results of a series of virtual turns of the spacecraft as the orbital station type, which has
, and the coefficients of expenditure by channels
,are equal:
= 8.74 kg×s ,
= 11.59 kg×s , and
= 7.09 kg×s. The simulation was accomplished for a large number of turns, while the initial find final angular positions of the spacecraft were chosen at random and the reorientation time was assumed to be proportional to the angle of turn. The mathematical simulation results in estimations of the average fuel consumption per one rotation G and the location accuracy, as well as of the performance of combining the regimes of attitude and orbit correction for considered scheme of mounting of the control engines. For 16 engines, we have the average fuel consumption per one rotation G = 5.24 kg, the index of combining the control Q = 1.59 and the index of optimality I = 0.418. The reorientation precision was equal to
. Values of the optimized functional G and of the index of combining Q were determined by the method of mathematical shooting using a personal computer.17 For the new family of orbital stations where the rotation time T is large, in the mathematical simulation, we take account of all factors of the spacecraft’s real flight including the variation in space of the direction of spacecraft’s linear velocity V during the rotation. One can clearly see that the use of the idea of regulation of the spacecraft’s angular position by means of the non-central jet force allows us to gain significant fuel economy.
For the purpose of comparison, we present the results of modeling of spacecraft reorientation by the two-impulse control pattern,16 which provides the absolutely minimum fuel consumption for the rotation, independent of the orbit correction. For the pattern with 16 attitude control engines, we have: G = 5.14 kg, Q = 1.43 and I = 0.570. They well demonstrates what the characteristics of method of spacecraft control designed by us are the best. To increase an efficiency of motion control of orbital spacecraft is possible at the expense of number increase of control jet-engines (by distribution or "a smearing" them onboard of a spacecraft). The number increase of the all-possible directions of thrusts of a included jet-engines for creation of a necessary moment of the controlling forces decreases a time of engines work for achievement of a required impulse of angular momentum, it decreases volume of fuel expense for control of motion around a centre of mass, on the one hand, and, on the other hand, it increases a probability of this that a thrust of working engines makes with a vector of spacecraft velocity minimal angle (obviously less than 90 degrees), and it will increase the increment
of orbital velocity (
is result of motion control during time of maneuver) and, as consequence, will increase the value
which is necessary for creation of same correcting impulse
at independent control of spacecraft motion of a centre of mass. As a result, at more number of control engines, the coefficient of a combining will be more, and the control efficiency index (or the index of optimality) is less. As an example, the scheme with 32 control engines which are established onboard of a spacecraft is possible (it is shown in Figure 2). For this scheme, we received following values of basic indexes reflecting an efficiency of motion control: Q =1.72; I =0.286 (and, E =1.70). At this, absolute values have turned out equal:
= 3.30 kg,
= 4.58 kg (and,
= 4.48 kg). For comparison, we give the values of the same indexes for the two-impulse control pattern: Q =1.51; I = 0.490 (and, E =1.51), and absolute volumes:
= 4.48 kg ,
= 2.28 kg,
= 4.48 kg. An analysis of these data distinctly shows what even having 16 engines, our designed control method of spacecraft motion using iterative (multi-impulse) principle of control will be more preferable than the two-impulse scheme of spacecraft's rotation control at the presence of 32 engines, because
,
=1.57 >
=1.51,
.
Summary conclusion
It is supposed that the control efficiency of a motion of the orbital spacecraft may be raised by simultaneous control of spacecraft rotation and motion of the centre of mass. In this research, optimal control of a spacecraft turn combined with correction of maintenance of the orbit altitude is considered. An algorithm of the control of reorientation combined with orbit correction for orbital spacecraft (in particular, for spacecraft of the long-term orbital station’s type) is synthesized in this paper. Designed by us algorithm uses measurements of angular velocity and information about angular position of a spacecraft. Data of angular velocity vector is necessary for control of the angular momentum and determination of required correcting impulse at the moments of rotation correction (and at the phases of acceleration and braking also). The feedback organization over position allows to increase the accuracy of spacecraft reorientation (at the expense of the control of the remained turn angle before required position, of determination of the moments of correction of spacecraft motion and calculation of the angular momentum necessary at the beginning of phases of uncontrolled rotation). The high efficiency of the combining of the regimes of attitude and maintenance of the spacecraft orbit altitude is shown. A numerical simulation of spatial rotations of a spacecraft (as the orbital station) using the designed algorithm of control was executed. As a result, the practically attainable values of fuel expenditure and the indices of efficiency of combining the regimes which can be reached were obtained. The practical application of the proposed method of control of spacecraft’s spatial motion allows us to lower significantly the fuel consumption for the dynamic operations as a whole. The results of mathematical simulation show that this economy reaches no less than 60%. For sufficiently frequent changes of spacecraft attitude, the value of the velocity impulse necessary to maintain the orbit altitude can be achieved through control over the spacecraft angular position only. The operating experience of the orbital scientific complex Mir (before a joining with the reusable transport spacecrafts of Space Shuttle system) shows the approximate equality of the actual fuel consumption for attitude control and orbit altitude maintenance. The ratio of the considered consumptions Gc / Ga varies between 0.68 and 0.75, which corresponds to the range of the index variation of a combining
. These data confirm the real possibility of practical use of the combined regimes of control over motion of the orbital spacecraft by means of jet micro-engines. It may be possible in the future to abandon the executing special corrections of the orbit in order to increase its altitude (or, at least, to reduce sharply the number of such corrections).
Acknowledgements
Conflict of interest
The author declares there is no conflict of interest.
References
- Raushenbakh BV, Tokar’ EN. Spacecraft orientation control. Russia; 1974, 600c.
- Branets VN, Shmyglevskii IP. Use of quaternion in the problems of orientation of solid bodies. Russia; 320c.
- Levskii MV. Optimal control of a programmed turn of a spacecraft. Cosmic Research 2003;41(2):178–192.
- Alekseev KB, Malyavin AA, Shadyan AV. Extensive control of spacecraft orientation based on fuzzy logic. Flight. 2009;1:47–53.
- Ermoshina OV, Krishchenko AP. Synthesis of programmed controls of spacecraft orientation by the method of inverse problem of dynamics. Journal of Computer and Systems Sciences International. 2000;39(2):313–320.
- Zubov NE. Optimal control over terminal reorientation of a spacecraft based on algorithm with a prognostic model. Cosmic Research. 1991;29(3):291–300.
- Van’kov AI. Adaptive robust control of attitude motion of a spacecraft using prognostic models. Cosmic Research. 1994;32(4–5):359–366.
- Levskii MV. A solving the problem of optimal control over turn of a spacecraft within the class of regular motions. Cosmonautics and rocketry-constructing. 1999;16:22–36.
- Levskii MV. Control of a spacecraft’s spatial turn with minimum value of the path functional. Cosmic Research. 2007;45(3):234–247.
- Levskii MV. Some issues of time-optimal control over a spacecraft programmed turn. Cosmic Research. 2011;49(6):521–533.
- Levskii MV. A special case of spacecraft optimal attitude control. Journal of Computer and Systems Sciences International. 2012;51(4):587–601.
- Levskii MV. Kinematically optimal spacecraft attitude control. Journal of Computer and Systems Sciences International. 2015;54(1):116–132.
- Levskii MV. Method of control of spacecraft reorientation and control system of spacecraft reorientation. Russian Federation Patent No. 2076833. Bulletin “Inventions. Statements and Patents. 1997. p.133–134.
- Levskii MV. Method of Controlling a Spacecraft Turn. Russian Federation Patent No. 2093433. Bulletin “Inventions. Applications and Patents.1997. p. 271.
- Handbook on the Automatic Control Theory. Krasovskii AA editor. Russia; 1987. 712c.
- Levskii MV. Control system of spatial turn of a spacecraft, Russian Federation Patent No. 2006431. Bulletin “Inventions. Statements and Patents”, 1994. p. 49–50.
- Vasil'ev FP. Numerical Methods of Solving Extremal Problems. Russia; 1988. 374c.

©2018 Levskii. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


