The planar rigid-body motion of a body is a classical topic of textbooks of engineering mechanics. This planar rigid-body motion considers its rotation about an axis and a curvilinear motion. The textbooks of classical mechanics describe only the radial acceleration and centrifugal force acting on the rotating body. Detailed analysis of the rotation of a body about a fixed point discovered the action of the two inertial torques and the angular acceleration. This inertial torques acting on the rotating bodies are not considered by lecturers, engineers, and practitioners. None of the less, this inertial torques are fundamental as the centrifugal force acting on the rotating body and should be computed in engineering with the aim to enhance the quality of machine work. This manuscript presents the physical interpretation of the angular acceleration of a rotating body that generates the two inertial torques acting about its center mass and fixed point.

Keywords: rotating body, radial and angular acceleration, inertial force and torque

Classical mechanics describes the planar rigid-body motion with its rotation about its centre mass and curvilinear motion about the fixed point.^1–3 The planar rigid-body motion generates its radial acceleration and the radial force that depends on the values of the angular velocityunder the action of the external torque and radius of gyration.^2–5 The textbooks of engineering mechanics present the mathematical model for the radial acceleration of rotating body about the fixed point by the expression $a=r{\omega }^2$ where a is the radial acceleration, r is the radius of gyration of the body, and ω is the constant angular velocity of the body rotation about a fixed point.^6–9 The textbooks present the expression $ma=mr{\omega }^2$ , where m is the mass of the body, as the centrifugal $F_{ct}=ma$ and centripetal $F_{cp}=mr{\omega }^2$ forces respectively and other components are as specified above.^10–13 Analysis of two expressions for the radial force demonstrates the dual presentations of the one physical term which has different physical interpretations.^14–16 This dualism contradicts mathematical rules that do not allow ambiguous interpretations due to the mathematical logic of the exact science. The physics of the rotation of the body about the fixed point manifests the turn of the body about its center mass and the turn about the fixed point. It means the rotating body is under the action of the two inertial torques. This manuscript gives the physical interpretation and mathematical proof of the action of the inertial torques on the body at the process of its rotation about the fixed point.

The textbooks of engineering mechanics derive the mathematical model for the radial acceleration of the rotating body about the fixed point based on the schematic of Figure 1a & 1b. The radial acceleration of the rotating body is presented by the following expression:

$a_r=r{\omega }^2$                                                  (1)

where $a_r$  is radial acceleration; r is the radius of rotation of the body about the fixed point $o$ , $\omega$  is the constant angular velocity of rotation of the body. The radial acceleration a is obtained by the time derivative of the change of the tangential velocity $\Delta V$ of the rotation of the body about the fixed point. The right side of Eq. 1 presents the scalar product of the constant angular velocity $\omega$ that expresses the angular acceleration, i.e., ${\omega }^2=\epsilon$ . This angular acceleration $\epsilon$ relates to the change of the tangential velocity of rotation of the body about its center mass $p$ . It means the body rotates about its center mass with acceleration under the action of the inertial torque $T_p=J_b\epsilon$  where $J_b$  is the mass moment of inertia of the body about its center mass, other parameters are as specified above. The second mathematical proves of the inertial torque $T_p$ acting on the rotating body is presented by the following. The equation of the circular motion of the body under the action of the external torque T that rotates it about the fixed point is presented by the following:

$T=J\epsilon =\left(J_b+m{r}^2\right)\epsilon$                 (2)

Where $J=J_b+m{r}^2$  is defined by the parallel axis theorem, other parameters are as specified above.

The right side of Eq. (2) can be rewritten by the following expression:

$T=J_b\epsilon +m{r}^2\epsilon$                   (3)

Where $J_b\epsilon =T_p$  that is the torque acting on rotating the body about its center mass.

The second item of Eq. (3) is presented by the following expression:

$T_o=mr\left(r\epsilon \right)=m{a}_{t}r=Fr$                  (4)

where $r\epsilon =a_t$  is the tangential acceleration of the rotating body about the fixed point $o$ , $m{a}_t=F$  is the inertial force, and $T_o$  is the inertial torque acting on the body about the fixed point.

The obtained result demonstrates the rotating body about the fixed point is subjected to the action of the inertial torque $T_p$  that turns the body about its center mass, and inertial torque $T_o$  acting on the body about the fixed point  $T=T_p+T_o$ . These inertial torques do not consider in the textbooks of engineering mechanics but they are fundamental as the centrifugal force in physics mechanics. Generalization of the conducted analysis enables stating that all rotating bodies about the fixed point always submerged by the action of the centrifugal force $F_{ct}$ of the radial direction and two inertial torques. The one inertial toque turns the body around its center mass and the second one turns about the fixed point Figure 1c. This statement is validated by the practice and by the circular motion of the moon about the earth that always shows its one side.

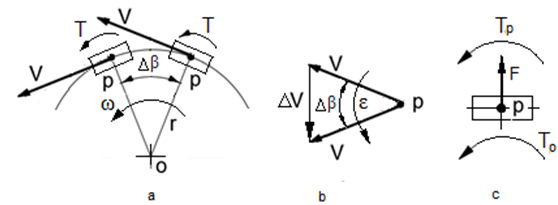
Figure 1 Schematic of the rotating of the body about the fixed point.

The disc of the radius 0.02 m, the mass of 0.1 kg that located on the length 0.4 m from the fixed point rotates with the constant angular velocity of 5 rad/s. Determine the values of the centrifugal force and the inertial torque acting on the disc.

Solution

The value of the centrifugal force is as follows:

$F=ma=mr{\omega }^2=0,1\times 0,4\times 5^2=1,0N$

The disc turns around its center mass under the action of the inertial torque of the value:

$T=J{\omega }^2=(m{l}^2/2+m{r}^2\text{)}{\omega }^2=(\text{0,1}\times {\text{0,02}}^{\text{2}}\text{/2 + 0,1}\times {\text{0,4}}^{\text{2}}\text{)}\times 5^{\text{2}}=\text{ 0,4005}\underset{}{}\text{Nm}$

where J is the disc mass moment of inertia about the fixed point.

Mathematical analysis of the rotation of the body about the fixed point yields the two inertial torques and the centrifugal force are acting on the body. The inertial torqueses turn the body about the centre mass and fixed point at the process of its circular motion. These inertial torques are fundamental as the centrifugal force acting on the body rotating around the fixed point. These inertial torques are the missed components in the analytical approach and interpretation of the mathematical models for the rotating body in the textbooks. The kinetic energy of the rotation of the body around the fixed point generates the inertial torques. The textbooks and manuals should consider the mathematical models for the inertial torques acting on the rotating body.

The textbooks of classical mechanics consider the planar motion of the rigid body which curvilinear motion generates the centrifugal force acting on the body rotating about the fixed point. The analysis of the rotation of the body at this condition demonstrated the action of the two inertial torques. The first inertial torque turns the body about its center mass and the second torque turns about the fixed point of its rotation. The physics of the two inertial torques acting on a rotating body about the fixed point originated from the kinetic energy of its curvilinear motion. This inertial torques are fundamental as the centrifugal force of classical mechanics and should be presented in the textbooks and manuals.

None.

The author declares that they have no conflicts of interest.

None.

1. Taylor JR. Classical mechanics. Sausalito CA: University Science Books. 2004.
2. Gregory DR. Classical mechanics. Cambridge University Press, New York. 2006.
3. Hibbeler RC. Engineering mechanics -statics and dynamics. 12th ed. Prentice Hall, Pearson, Singapore. 2010.
4. Dreizler R. Theoretical mechanics: theoretical physics 1. Springer, Boca Raton. 2010.
5. Jewett, J, Serway RA. Physics for scientists and engineers. Cengage Learning, 10 ed. USA, Boston, 2018.
6. Smith PF, Longley WR. Theoretical mechanics. Franklin Classics, Boston. 2018.
7. Germain P, Piau M, Caillerie D. Theoretical and applied mechanics. Elsevier, 2012.
8. Nolting W. Theoretical physics 1: classical mechanics. Springer, Cham, Switzerland, 2016.
9. Aardema MD. Analytical dynamics. theory and application. Academic/Plenum Publishers, New York, 2005.
10. Thornton M. Classical dynamics of particles and systems (5th ed.). Brooks/Cole. 2004.
11. Baumann G. Mathematica for theoretical physics. Springer, New York, 2005.
12. Millard BF. Principles of engineering mechanics: dynamics-the analysis of motion. Springer, 2006.
13. Kevin R, Qiong S, Rajpal SS. Kinematics and dynamics of mechanical systems. 2nd ed. Implementation in MATLAB and Sim mechanics, Taylor & Francis, Boca Raton. 2019.
14. Müller-Kirsten, Harald JW. Classical mechanics and relativity. World Scientific. 2008.
15. Knauf A. Mathematical physics: classical mechanics. Springer. 2018.
16. https://www.scientificamerican.com/article/is-it-just-a-coincidence/