A Review on stability and passivity analysis of haptic devices

doi:10.15406/iratj.2023.09.00258

eISSN: 2574-8092

International Robotics & Automation Journal

Mini Review Volume 9 Issue 1

A Review on stability and passivity analysis of haptic devices

Ahmad Mashayekhi,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Behnam Akhoundi,¹ Vahid Modanloo¹

¹Mechanical Engineering Department, Sirjan University of Technology, Sirjan, Iran
¹Mechanical Engineering Department, Sirjan University of Technology, Sirjan, Iran

Correspondence: Ahmad Mashayekhi, Mechanical Engineering Department, Sirjan, Kerman, Iran, Tel +98912643502, +3441522089

Received: February 14, 2023 | Published: March 9, 2023

Citation: Mashayekhi A, Akhoundi B, Modanloo V. A Review on stability and passivity analysis of haptic devices. Int Rob Auto J. 2023;9(1):26-28 DOI: 10.15406/iratj.2023.09.00258

Download PDF

Abstract

Haptic devices are robots that are used for simulating virtual objects for their operators. Since most real objects can be modelled by spring and dampers, the virtual object is also a (discrete) spring and damper. The discretization is done with a constant sampling time, while a time delay may exist in the control loop, due to do different sources. Simulating stiff objects is a challenging problem since severe vibrations occur in the body of the haptic device and may damage itself or even its operator. The stable operation of a haptic device is a key problem in all haptic applications. It is shown that using smaller values of sampling time and time delay, can make an increase in the stability domain; while increasing effective mass and friction has the same result. In this paper, a review of the stability and passivity of haptic devices is presented and helps the readers to know better recent activities in this field.

Keywords: Haptic device, stability, passivity, time delay, sampling time

Introduction and related works

A haptic system is a combination of a haptic device (either a serial type manipulator such as VirSense haptic device,¹ or a parallel type such as Omega haptic device,² which is in contact with an operator for feeling and sensing the virtual objects.³ This virtual object can be simulated graphically in a 3D format on a monitor. Most the real objects can be modelled by spring-damper elements, thus most of the time the virtual object is modelled as a spring and damper in the discrete domain. In some papers such as^4‒7 the virtual object is also modelled as mass-spring and damper elements. Simulating stiff virtual objects is a challenging problem in many studies, and lots of ways are used for this purpose, such as.⁸

The paper is structured in the following manner: in the next section a system description is presented and control model of the haptic device is described. A short review in the field of passivity in haptic devices is the next section; while the section after that one is stability analysis of these systems. The paper ends with a discussion.

System description

Haptic devices are mostly several degrees of freedom (DOF) manipulators with large workspaces. Thus, in general, haptic devices have multi-DOF and nonlinear dynamics. While simulating a virtual object for an operator, the end effector of the haptic device (called stylus) has very small movements around a fixed point. Thus this complex dynamic, can be simplified to a 1-DOF dynamic with fixed values of mass, viscous friction, and Coulomb friction. The accuracy of this simplification is studied in⁹ and used in¹⁰ for redundant haptic devices. Thus a simplified model of a haptic device can be seen in Figure 1.

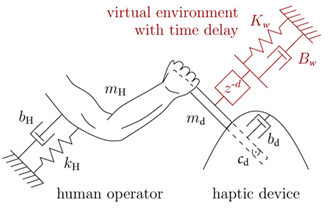
Figure 1 Schematic view of a haptic device.¹¹

The haptic device has position sensors and velocity is determined using numerical backward difference. Considering the Coulomb friction, zero-order-hold, time delay, and effect of sensor quantization, the 1-DOF nonlinear model of a haptic device can be depicted in Figure 2.

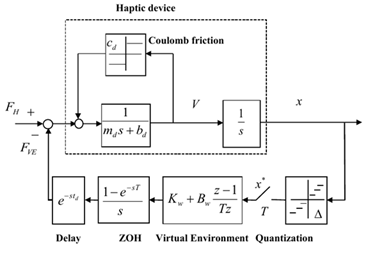
Figure 2 A 1-DOF nonlinear model of a haptic device.¹²

Viscous and Coulomb friction always dissipates energy and makes the haptic device more stable. Sensor quantization and sampling data can insert energy into the system due to the uncertainity of position. In references such as^13,14 and later improved in¹⁵ it is shown that minimum dissipated energy due to Coulomb friction is more than the maximum generated energy due to quantization and sampling, in most of the famous haptic devices. Thus these nonlinear phenomena can be removed by each other, leading to Figure 3, as used in many references such as.^16‒18

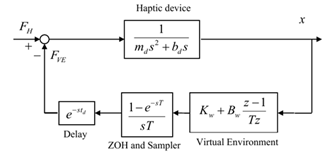
Figure 3 A 1-DOF linear model of the haptic device in discrete domain.¹²

Passivity analysis

When a haptic device is passive, no net energy is generated in it.¹⁴ It means that generated energy inside the haptic system is less than dissipated energy. Passivity analysis of a 1-DOF system was studied in,¹⁹ without considering the time delay. A more accurate passivity criterion is determined in¹⁴ and later improved in.¹⁵ These mentioned criteria are derived mathematically, verified by simulations and experiments.

Stability analysis

The stability of haptic devices is first studied by Minsky et al.²⁰ They assumed the haptic device as a 1-DOF continuous system and reached a linear formulation for predicting the stable operation of a haptic device. Gil. et. al improved the stability criterion by considering time delay, the effect of the operator, and verifying by experiments in.^21-23 All of these studies are valid for small values of virtual damping and time delay. Studies show that increasing the physical damping of the haptic device in any shape, makes it more stable.^16,24‒26 The effect of the operator’s hand on the stability of haptic devices is studied in references such as,^11,27,28 and concluded that the operator’s hand can reduce the instability in haptic devices. Somehow new study of stability in haptic devices,^12,27 lead to new equations for predicting the stable region of a haptic device without any limitation on the time delay and virtual damping. The effect of the LuGre friction model on the stability of haptic rendering was studied in,²⁹which shows using describing function of the LuGre friction model, allows one to predict the stability boundary with good accuracy. The stability of dual-rate haptic devices is the subject of some researches such as.^30,31

Also these mentioned criteria are derived mathematically, verified by simulations and experiments. Most of the time a 1-DOF haptic device is used for experiments, (like^13,14) or one joint of a several-DOF haptic system is used, such as.^12,23

Discussion

In this brief, a short history of stability and passivity analysis in haptic devices is presented. References such as^{8,12,27,32,33} proved (theoretically or experimentally) that using a faster sampling rate (i. e. using smaller values of the sampling time), makes the stability region larger. The effect of small values of time delay was studied in^{11,21‒23,28} while effect of large values of time delay was studied in,^12,27 and all of them show that increasing time delay makes the stable operation smaller. The effect of haptic device mass is studied well in.^12,27 The limitation of the mentioned methods is using a 1-DOF haptic device with a linear dynamic. There is no closed-form stability/passivity criteria for a nonlinear multi-DOF haptic device.