Abstract
A numerical study is carried out to investigate the effect of different heating sections on the rate of heat and mass transfer of a fluid contained in a trapezoidal cavity with partially thermally active right side wall. The active part of the right side wall has a higher temperature and concentration than the left side one. The length of the thermally active right part is equal to half of the inclined wall. The top and bottom of the cavity as well as the inactive part of the right side wall are considered to be adiabatic and impermeable to heat and mass transfer. The species diffusivity of the fluid is assumed to be constant but the density of fluid is assumed to vary linearly with the temperature and concentration. The coupled differential equations are discredited by the Finite Difference Method. The Successive- Over-Relaxation (SOR) method is used in the solution of the stream function equation. The results are presented graphically in terms of flow patterns, isotherms and are concentrations. The results reveal that the location of heating zones has a significant effect on the flow pattern and the corresponding of heat and mass transfer in the cavity.
Keywords: double diffusive natural convection, trapezoidal cavity, various angles, partially heated, heat and mass transfer
List of symbols
Introduction
In nature and many industrial applications, there is a diversity of transport processes where simultaneous heat and mass transfer is a common phenomenon. Fluid flows which are formed due to the combination of temperature and concentration gradients are referred to as double-diffusive convection. Double diffusion convection (D.D.C) occurs in a wide range of scientific fields such as oceanography, astrophysics, geology, biology as well as in many engineering applications such as solar ponds, natural gas storage tanks, crystal manufacturing, material processing, food processing and etc. In order to have an overview of this phenomenon see some relevant fundamental works such as Turner et al.1-3 Double diffusive natural convection in enclosures has enormous industrial and geophysical applications, such as petrochemical process, fuel cells, pollutant dispersions in soil and underground water, design of heat exchangers, channel type solar energy collectors, and thermo-protection systems. Therefore, the characteristics of natural convection heat and mass transfer are very important. In recent years, a considerable number of analytical, numerical and experimental studies have been performed in order to analyze such interesting phenomenon in different enclosures. Ostrach et al.,4,5 have reported complete reviews on the subject. Gebhart6 were among the first ones to study D.D.C numerically for the cases of vertical laminar fluid motions along surfaces or in plumes. In this study, special attention was paid to the influence of non-dimensional parameters relevant to double-diffusion, on the heat and mass transport processes; transition to turbulence was mentioned. Bejan7 has reported a fundamental study of scale analysis relative to heat and mass transfer within cavities submitted to horizontal combined and pure temperature and concentration gradients. Pure thermal convection, pure solutal convection, heat transfer driven flows, and mass transfer driven flows were taken into account. Mobedi et al.,8,9 analyzed double diffusive convection in partially heated cavities. Nikbakhti and Rahimi10 studied numerically the flow, heat and mass transfer in a rectangular cavity with partially thermal active walls. They found the rate of heat and mass transfer will be a maximum when heating section located at the bottom and the cooling one on the top. A careful review of the existing literature reveals that D.D.C. have been mainly analysed in rectangular cavities and only a minority of studies have considered non-rectangular cavities and in particular the trapezoidal geometry, which is encountered in several practical applications, such as attic spaces in buildings11, greenhouses12 or sun drying of crops.13 Dong and Ebadian14 were the first did a preliminary investigation on double diffusive convection in trapezoidal cavity. They considered a cavity with 75° inclined side walls and horizontal top and bottom and steady numerical solutions were obtained with lateral thermal and solutal gradients for Pr=7 and Le = 100 (water) with both opposing and assisting buoyancy forces. Boussaid et al.15 studied double diffusive convection in the laminar-flow regime in a trapezoidal enclosure. Papanicolaou & Belessiotis16 analysed double diffusive natural convection in an asymmetric trapezoidal enclosure. The present study investigates double-diffusive natural convection phenomenon in a trapezoidal cavity with partially thermally active right side wall for three different heating locations. That is, for the hot region located at the top, middle and bottom and the left wall is cooling. The main objective of this work is to determine the region where the heat and mass transfer rate is maximum/minimum in the cavity. The results are displayed graphically in terms of the streamlines, isotherms and isconcentration. Teamah & Shehata17 conducted a numerical investigation to analyse double diffusive natural convection within a trapezoidal cavity submitted to the magnetic field. They found that the rate of heat and mass transfer experienced a decrease when the inclination angle increased from 0° to 75°. In addition, heat and mass transfer decreased as Hartman number increased from 0 to 15. Al-Mudhaf et al.,18 carried out an analysis of the influences of Soret and Dufour on the transient double-diffusive natural convection inside trapezoidal enclosures filled with isotropic porous medium with exponential variation of boundary conditions. The results revealed that the local Nusselt number decreased with increasing either D for 𝜏. However, the increase in Sr led to reduce the average Sherwood number and to increase the average Nusselt number. Borhan Dddin et al.,19 studied double diffusive mixed convection flow in a trapezoidal enclosure in the presence of the uniform magnetic field effect applied in negative horizontal direction. They concluded that Heat transfer rate was not significant for lower values of Ri but increases rapidly for higher value of Ri for all values of Le in both cases which shows the dependency of Ri on heat transfer.
Physical model and governing equations
A schematic diagram of the two-dimensional trapezoidal cavity with two walls of length L inclined at an angle s
with the x axis and height H is shown in Figure 1. Considering that the enclosure is filled with moist air, with a low concentration of water vapor, it can be taken Pr=0.71, Sc=0.63. The active right side wall of the cavity is partially heated at
with a high concentration
and the left one is cooled at
with a low concentration,
where
The length of the thermally active right part of the cavity is equal to half of the length
are considered. In Case I, the hot region is located at the top wall, in Case II it is located in the middle and in Case III it is located adjacent to the bottom wall. In this study, it is considered that the fluid is incompressible, Newtonian, and viscous. The viscous dissipation is assumed negligible and the gravity acts in the downward direction. The Boussinesq approximation with opposite thermal and solute buoyancy forces is used for the body force terms in the momentum equations. The heat flux driven by concentration gradients (thermal diffusion or Soret effect) and the mass flux driven by temperature gradients (diffusion thermo or Dufour effect) are also neglected. The mixture density is assumed to be uniform over the cavity, exception made to the buoyancy term, in which it is taken as a function of both the temperature as well as concentration levels through the Boussinesq approach;
With these descriptions and assumptions of the problem, and representing the position through Cartesian coordinate system in two dimensions, the governing equations could be written in non-dimensional form as the following:
(1)
(2)
(3)
(4)
The initial and boundary conditions in the dimensionless form are
side walls,0≤Y≤1,
on the hot part of the right wall,
on the left wall,
at inactive parts of the right wall,
at Y=0 and 1
Where the non-dimensional variables and parameters are
,
,,
,
,
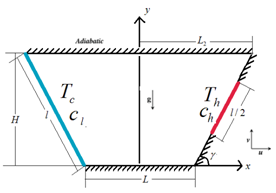
Figure 1 Physical configuration.
Method of solution
The governing equations along with the boundary conditions are solved numerically, employing finite-difference techniques. The vorticity transport, energy and mass equations are solved using the ADI (Alternating Direction Implicit) method and the stream function equation is solved by SOR (Successive Over Relaxation) method. The over-relaxation parameter is chosen to be 1.8 for stream function solutions. The buoyancy and diffusive terms are discretized by using central differencing while the use of upwind differencing is preferred for convective terms for numerical stability. Starting from arbitrarily specified initial values of variables, the discretized transient equations are then solved by marching in time until an asymptotic steady-state solution is reached. Convergence of iteration for stream function solution is obtained at each time step. The following criterion is employed to check for steady-state solution
(5)
Where
stands for either
or
n refers to time and i and j refer to space coordinates. The value of
is chosen as
.
The time step used in the computations is varied between 0.0001 and 0.000001 depending on Grashof number and the angle
.The numerical solutions are found for different grid systems from
to
for
as well as for
and it is observed that a further refinement of grids from
,
,and
for γ=〖90〗^°,γ=〖60〗^°, and γ=〖30〗^°respectively to
does not have a significant effect on the results in terms of average Nusselt and Sherwood number and the maximum value of the stream function. Consequently, according to this observation, a uniform grid of
points is used for all of the angles in this work.
Results and discussion
Numerical study is conducted for different heating sections, inclination angles, thermal Grashof numbers, and Buoyancy ratio number. The results are presented in the form of streamlines, isotherms and isoconcentration to show the fluid flow, heat and mass transfer phenomena in steady states. The rate of heat and mass transfer in the enclosure is measured in terms of the average Nusselt number and average Sherwood number.
Effect of heating locations
Figures 2-4 demonstrate the flow pattern, the temperature and concentration distributions for three different mentioned cases by plotting the contours of stream lines, isotherms and iso-concentrations for angle with following characteristics: Pr=0.71, Sc=0.63, GrT=106, N=0.2. Figure 2 shows the flow patterns inside the cavity for three different cases. In the first case, when the heating zone is placed on the top of the right sidewall of the cavity (Figure 2(a)) there exist two inner cells each at the top-right near the heating zone and in the middle near the cold wall and the remaining parts of the cavity are less activated. In Figure 2(b) where the heating section is in the middle, there is a principal cell occupied almost the whole cavity. In the last case, when the heating zone moves to the bottom of the right side wall, there are two inner cells grown in strength. In comparison with the other cases, velocity and circulation rate of this section is a maximum. Figure 3 illustrates the temperature distribution inside the cavity for these cases by plotting the contours of isotherms. Figure 3(a) displays isotherms for top active heated section and convection near the active section is converted to conduction. In contrast to the other cases, in this case the rate of heat transfer contributes to the least. When heating section moves to the bottom part of the side wall a thermal boundary layer forms near the active zone, and convection can be seen from isotherms, Figure 3(c). It is important to note that in this case heat transfer rate is a maximum. The distribution of concentration is shown in Figure 4(a-c). As it can be seen, the isopleths of concentration has similar behaviour as that of temperature and this is mainly because of the similarity of energy and mass transfer equations. It is also significant to mention that due to Prandtl number which is almost equal to Schmidt number (Le=1), the mass and the thermal diffusivity have similar effect on fluid.

Figure 2 Streamlines for all heating locations
,N = 0.2 and
.

Figure 3 Isotherms for all heating locations,
N = 0.2 and

Figure 4 Isoconcentrations for all heating locations,
N = 0.2 and
Effect on heat and mass transfer
The average Nusselt and Sherwood numbers which quantify the amount of heat and mass transfer in the enclosure are the significant quantities in double diffusive natural convection phenomenon. The average Nusselt and Sherwood numbers have been depicted in Figure 5 & 6, respectively as a function of Grashof number for different active heated zones and angle with following characteristics: Pr=0.71, Sc=0.63, N=0.2. The average Nusselt and Sherwood numbers are increased by increasing the Grashof number which led to the increase in the rate of heat and mass transfer in the cavity. Also, the average Nusselt and Sherwood numbers are increased when the heated zone moves from the top to the bottom of the right side wall in each Grashof number. As a result, the maximum rate of heat and mass transfer in the enclosure is when the active heated section is located on the bottom of the right side wall.

Figure 5 Average Nusselt number vs. Grashof number for different locations.

Figure 6 Average Sherwood number vs. Grashof number for different locations.
Conclusion
A numerical investigation of double diffusive natural convection in a two-dimensional trapezoid enclosure with a partial heated wall has been studied. With moving the heating zone toward the bottom of the cavity the heat and mass transfer rate is found to increase and it is the highest for the bottom thermally active location while the heat and mass transfer rate is poor when the heated section is located at the top of the cavity for N=0.2. In addition, Grashof number has a direct effect on the average Nusselt and Sherwood numbers so that the rate of heat and mass transfer in the cavity is increased by increasing Grash of number.
Acknowledgements
Conflict of interest
The author declares there is no conflict of interest.
References
- Turner JS. Double diffusive phenomena. Annu Rev Fluid Mech. 1974;6:37–56.
- Huppert HE, Sparks RSJ. Double-diffusive convection due to crystallization in magmas. Annu Rev Earth Planet Sci. 1984;12:11–37.
- Schmitt RW. Double diffusion in oceanography. Annu Rev Fluid Mech. 1994;26:255–285.
- Ostrach S. Fluid mechanics in crystal growth–the 1982 Freeman Scholar Lecture. J Fluids Eng. 1983;105(1):5–20.
- Viskanta R, Bergman TL, Incopera FP. Double-diffusive natural convection. In: Kakac S, Aung W, Viskanta R, editors. Natural Convection: Fundamentals and Applications, Hemisphere.Washington, DC, 1985. p. 1075–1099.
- Gebhart B, Pera L. The nature of vertical natural convection flows resulting from the combined buoyancy effects of thermal and mass diffusion. Int J Heat Mass Transfer. 1971;14(12):2025–2050.
- Bejan A. Mass and heat transfer by natural convection in a vertical cavity. Int J Heat Fluid Flow. 1985;6(3):149–59.
- Mobedi M, Özkol Ü, Sunden B. Visualization of diffusion and convection heat transport in a square cavity with natural convection. Int J Heat Mass Transfer. 2009;53(1-3):99–109.
- Nithyadevi N, Yang R. Double diffusive natural convection in a partially heated enclosure with Soret and Dufour effects. Int J Heat and Fluid Flow. 2009;30(5):902–910.
- Nikbakhti R, Rahimi AB. Double-diffusive natural convection in a rectangular cavity with partially thermally active side walls. J Taiwan Inst Chem Eng. 2012;43(4):535–541.
- Moukalled F, Acharya S. Natural convection in trapezoidal cavities with baffles mounted on the upper inclined surfaces. Numer Heat Transfer. 2000;37(6):545–565.
- Boulard T, Kittas C, Roy JC, et al. Convective and ventilation transfers in greenhouses, part 2: determination of the distributed greenhouse climate. Biosyst Eng. 2002;83(2):129–147.
- Oosthuizen PH. Free convective flow in an enclosure with a cooled inclined upper surface. Comput Mech. 1994;14(5):420–430.
- Dong ZF, Ebadian MA. Investigation of double-diffusive natural convection in a trapezoidal enclosure. J Heat Transfer Trans ASME. 1994;116(2):492–495.
- Boussaid M, Djerrada A, Bouhadef M. Thermosolutal transfer within trapezoidal cavity. Num Heat Transfer. 2003;43(4):431–448.
- Papanicolaou E, Belessiotis V. Double-diffusive natural convection in an asymmetric trapezoidal enclosure: unsteady behavior in the laminar and the turbulent-flow regime. Int J Heat Mass Transfer. 2005;48(1):191–209.
- Teamah MA,Shehata AI. Magnetohydrodynamic double diffusive natural convection in trapezoidal cavities. Alexandria Engineering Journal. 2016;55(2):1037–1046.
- Al-Mudhaf F, Rashad A, Ahmed SE, et al. Soret and Dufour effects on unsteady double diffusive natural convection in porous trapezoidal enclosures. International Journal of Mechanical Sciences. 2018;140:172–178.
- Uddin MB, Rahman M, Khan M, et al. Hydromagnetic double-diffusive mixed convection in trapezoidal enclosure due to uniform and nonuniform heating at the bottom side: Effect of Lewis number. Alexandria Engineering Journal. 2016;55(2):1165–1176.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


