In order to obtain robust and measurable data from the marine environment, citizen science projects need user-friendly tools that, during dives, autonomously gather information in an easy, low-cost and integrated way. Data collected from different devices and by different untrained divers must have good estimation of the position where the information has been acquired. With this goal, in the context of the Green Bubbles project, a novel platform, called DocuScooter has been designed and developed. DocuScooter implements all the algorithms to filter and merge data with correct timestamp and position preparing the complete mission report. After the mission, the diver can upload the report on an appropriate web service to produce a 3D documentation. In order to obtain the underwater position during the dive, a tailored device compatible with the platform is also presented. Result of the prototype of the platform and the first results of the position estimation algorithm are presented and discussed.
Keywords: citizen science, underwater robotics, underwater positioning systems, marine documentation
The preservation of the marine environment provides benefits for the whole society and constitutes a basic need for the mankind. These habitats are extremely complex systems, characterized by strong links between their physical and chemical processes and biological population. A great part of the work carried out by scientists involved in this field consists in the acquisition and analysis of robust and measurable data, in order to detect threats and take actions to contrast them. Unfortunately, this kind of activity has been proven to be very costly in terms of people and instrumentation1–3 to be carried out by a single research team with the goal to gather an amount of historical data that can allow a fully interpretation of phenomenon in this kind of environment. As a partial solution to these issues, in the last years there has been an increasing exploitation of the citizen science in marine monitoring projects, helped by the fact that in the last decades there is also a major assessing of scuba diving as a mass leisure activity, with millions of divers from all around the world. Because non-experts are involved in the research process through the citizen science, in literature there is a debate on the usefulness of this kind of researches, specifically on the quality of the data collected.4–6
Despite the advantages previously mentioned, the use of volunteers is often criticized on the basis that the information collected is unreliable as a result of either insufficient training or a lack of consistency due to the large numbers of different observers. Several research teams tried to answer to these doubts organizing training days before the missions and finding out that the data collected by the general public are consistent with those collected by the scientists.5,7,8 At a higher level of cooperation and engagement, recreational and professional divers can team up with researchers and managers to identify issues that need to be addressed, and design strategies to do so.9 Besides this aspect, the design, development and adoption of new technologies can increase the outcomes of this type of cooperation. In fact, in the recent years there is an increasing interest from the robotic community in the realization of user-friendly technologies and tools to carry out efficiently activities in the underwater environment.10–15 What the marine community is lacking is an integrated system where all the processes of acquisition, processing, analysis and output representation are gathered in a unique solution. In literature there are different examples about improving the collection or the analysis steps,16–21 where advanced low-cost techniques like structure from motion and digital photogrammetric are involved in order to estimate structural complexity of large reef areas. Anyway all these advances do not take in consideration the whole process from data acquisition to output visualization.
For this reason, a low-cost and flexible IT tool that allows professionals and/or citizen science volunteers to collect, analyze and archive different types of information simultaneously from the marine environment during a unique diving session could very helpful and useful to the marine community. Starting from this need, in the present work authors present the DocuScooter: an innovative device that allows scuba divers to automatically collect, analyze and visualize data from the ocean during their leisure activity. This latter data-processing system is called DiRAMa and the results can be stored in the most common three-dimensional formats. The system can provide ad-hoc outputs for different types of applications like data mining, Gamification and 3D printing. With the use of this system it is possible to create a wide photo database of the seabed worldwide oriented to different types of end users. In order to have more useful information that can be used for research purposes the estimation of the position of the acquired data is mandatory. In this context an additional peripheral of the Docu Scooter has been designed and developed and its operation will be introduced in this article. This component is capable to estimate the position of the diver during the mission using its on-board sensors. At the moment of writing the realization of the DocuScooter is at the first prototype step. In this paper authors present the global project, the main Mechatronic features of the developed architecture and a discussion about implemented algorithms for the position estimation. Authors are working and starting validation of the general multi-agent system structure for the scooter NGC system22 and for its hydrodynamic parameters estimation.23
The green bubbles project
The Green Bubbles project (www.greenbubbles.eu), Figure 1 funded by the EU’s H2020 Research and Innovation programme under the Marie Sklodowska-Curie grant agreement N. 643712 take care of sustainability diving. Diving nowadays has become a mass leisure activity with millions of divers all around the world. By a way it is well known that this phenomenon produces direct and indirect earnings that are able to sustain the coastal communities and the MPAs, increases the awareness to the marine environment and can help the scientific research community by interacting through the citizen science. On the other hand, a badly executed dive can lead to tangible and irreparable impacts and damages to the habitat. The main objective of the project is to maximize the benefits of the diving activities while minimizing the negative impacts to the marine environment, in order to achieve the environmental, social and economic sustainability of the whole system. One topic in particular regards the development of tailored IT tools to support citizen science projects to acquire, gather and analyze data from the marine environment.

Figure 1 The Green Bubbles logo.
In order to accomplish the need of environmental monitoring in an autonomous or semi-autonomous way, in the past years Università Politecnica delle Marche team developed DiRAMa,24 a platform designed for image acquisition and three-dimensional reconstruction of submarine environments. The principal innovation brought by DiRAMa is the integration of multiple heterogeneous knowledge concerning the marine and underwater habitats using tested and reliable COTS component. This project aimed at providing greater data processing, implementing 3D reconstruction algorithms on an external server; this expands the list of possible results with a three-dimensional model of the area explored. The outcomes can be stored in the most common three-dimensional formats like PLY (Polygon File Format), OBJ + MTL, DAE (Collada), and PDF, due to the importance of letting reconstruction being modifiable with software suites of common use or open source, even directly from the mobile device employed for taking mission data. In Figure 2 a schematic representation of DiRAMa system is presented.

Figure 2 Architecture of DiRAMa.
It is possible to recognize five different components:
- Mobile acquisition device: any suitable technology (smartphones, tablets, smart cameras etc.) capable of sending information to DiRAMa web server.
- PHP/HTML5 Web server: it manages the internal user database, displays the results to end-users and communicates with the 3D Engine Module.
- 3D Engine module and database: it implements complex reconstruction algorithms and shares information with the Web Server. The module makes use of the database where info and elaboration results are stored.
- Cloud manager: it implements a notification server in order to inform the users about elaboration success or eventual errors.
- Home navigator: after the data elaboration is successful, end-users can download the results in order to visualize them remotely.
For further implementation details of each component, the reader can refer to.25
In the context of the Green Bubbles projects Università Politecnica delle Marche (a university from Italy), Innovasub (a SME from Turkey) and Ubica (a SME from Italy) are cooperating together in order to bring innovation to the diving industry by designing and developing an innovative modular low-cost platform called DocuScooter capable to acquire heterogeneous data from the marine environment. This device is structured as an array of different devices (commercial sport cameras, lights, sensors etc.) connected to a main central unit and to an underwater Android tablet (that is optional). All the equipment is designed to equip different commercial underwater scooters that the diver can use to gather data from the marine environment while performing his leisure activity. In the recreational scuba diving there is a great employment of underwater scooters. Using this type of equipment, the capability of exploration of the marine environment by the divers is greatly increased. For this reason, the development of an add-on for an underwater scooter to gather data from this environment autonomously can be considered a great tool to help the study and monitoring of MPAs.
Aims
Main ideas behind the DocuScooter platform are:
- Modularity: different missions require a different sensor payload so it is necessary to have a system that allows the hot plug of different components (also during the diving activity itself) without compromising the entire system.
- Low cost: in order to be easily adopted by the diving industry, the platform must be low-cost and tailored to different available COTS. For example, all the cameras that can be connected to the system are sports cameras from well-known manufacturers (like GoPro or Kodak). This helps to lower the costs of the whole structure because a diver could use his/her own instrumentation.
- Highly extensible: it must be easy to add new compatible devices to the system with less effort as possible. To obtain this goal, in order to add a new compatible component, it is only mandatory to respect the communication protocol used to transit the data and the cable connector type.
- Works up to 50mt: this specification derives from the maximum depth that can be achieved by waterproof housings of commercial sports cameras.
System architecture
The architecture of the platform is presented in Figure 3. The DocuScooter is divided in three Units.
- User Interface Unit: It is consisting of two components: an underwater Android tablet and a subsystem. In the tablet a custom application is installed: it allows performing some basic or advanced tasks like start and following the mission, capture photos, recording video and so on. After the mission the application allows the diver to review the acquired data and upload them to the external DiRAMa service to perform data analysis. The subsystem is composed by a COTS and configurable Wi-Fi hotspot that allows the data transmission between the tablet and the rest of the system and a COTS and configurable Video Server that allows the streaming of one camera connected to the system through the screen of the tablet. It is important to notice that to perform some simple data acquisition missions this unit is optional.
- Motherboard unit: This unit can be considered the main communication node of the system. This unit is capable to discover, monitor and communicate with all the payload units connected to the system, receive commands from the User Interface Unit, acquire some specific data from onboard sensors (like depth and temperature) and allows to operate and monitor the state of the whole system easily through an embedded LCD screen and buttons.
- Payload unit: A Payload Unit is any compatible device that the diver wants to control through the User Interface Unit Android application or through the embedded screen and buttons of the Motherboard Unit. In the Figure 4 it is possible to see five different payloads (two different Wi-Fi cameras, one sensor, one light and one battery) these peripherals are a sort of intelligent devices; in fact, the single component or sensor is not directly connected to the communication bus but through a microcontroller that receives the commands and executes them.
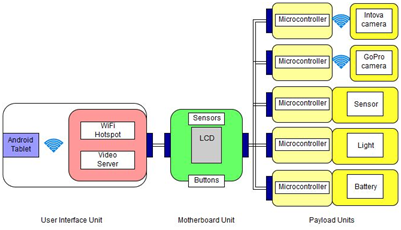
Figure 3 The DocuScooter architecture.

Figure 4 DocuScooter prototype.
The communication between the elements of the system (with the exception of the Android tablet that uses Wi-Fi to communicate with the system) is performed by an underwater 8 pin cable.
As stated before, in order to obtain the position of the DocuScooter underwater while performing the survey, a specific payload unit has been designed and developed. This unit implements an estimation algorithm based on a multi-rate Unscented Kalman Filter that uses a high-rate data from an onboard IMU at fixed rate of 50Hz and slow-rate depth information from an onboard depth sensor and the position from a GPS and an USBL (when available) systems at a fixed rate of 1Hz.
Model
The state estimation is based on a discrete-time non-linear state space description:
Where the equations describe the dynamic and the measurement model of the system
, is the model uncertainty and
is the measurement noise, which, for the hypothesis based on the central limit theorem, is white zero-mean Gaussian noise with respectively Q and R covariance matrices. The state is composed by position p referred to the inertial frame, velocity v and acceleration a referred to the body frame, quaternion q and angular velocity w. Moreover, the state contains the bias of accelerometer
and gyroscope
.
(2)
The position dynamic26 is modeled by the equation of the uniformly accelerated motion:
Where
and
are, respectively, identity and 3 all-0 matrices, and
is the rotation matrix from body frame to the inertial frame and is the sample time. The quaternion dynamic27 is the following:
Where
is the module of the angular velocity
Angular velocity, accelerometer and gyroscope bias are modeled as a linear system with dynamic matrix. The measures are the acceleration, angular velocity from the IMU, the quaternion’s calculated from the accelerometer and magnetometer inside the IMU and the position obtained from a GPS/USBL system or a vision system. The measurement model, inclusive of gravity and bias compensation, is:
Where
is the gravity acceleration vector.
Unscented Kalman Filter (UKF):
The UKF28,29 is based on the propagation of the sigma points, calculated from the state and the state covariance matrix, on non-linear equations of the model. This algorithm needs to run recursively starting from the initial condition:
Where
the expected value of initial state is,
is the covariance matrix related to the initial state error. Three scaling parameters
and the state dimension L are used to calculate the fixed weights
The sigma points are calculated from the square root of the covariance matrix.
Where
is the Cholesky Decomposition method
The dynamic equation is evaluated in the sigma points to calculate the predicted state
and covariance matrix
.
The same operation is used to calculate the predicted output
and covariance
The Cross Covariance of the state and of the output vector
is calculated as:
The Kalman gain
is calculated from the Covariance and Cross Covariance matrices:
Hence, the estimated state
and error Covariance
are calculated as:
Presently the realization of the DocuScooter is at the first prototype step. The electronics of the User Interface Unit, the whole Motherboard unit and multiple microcontrollers of the Payload unit have been inserted in a unique watertight box in order to perform the preliminary tests. The underwater tablet that has been employed during the validation was an Alleco AllTab2. Three underwater action cameras of different brands (GoPro Hero 3 Black, Kodak PixPro Sp360 and Intova EdgeX) have been used as payloads in order to perform the 3D reconstruction. Figure 4 presents the first prototype of DocuScooter. After the system has been verified to correctly work out of water, a series of test have been conducted in water. Specifically, the system was proved in different missions by the marine biologists of Hopkins Marine Station of Stanford University in the Monterey Bay, CA. The aim of the mission was to evaluate the functionality of the system and the inspection of a semi-submerged pipe located at the bottom of the seabed. The diver was instructed to survey the pipe different times in order to have images redundancy for the 3D reconstruction process of an area of about 2 x 14 meters.
After the dive the gathered data set is uploading to the DiRAMa servers. The time for obtaining the 3D model depends mainly on two factors: the number of the photos and the quality requested. A low quality model can be available with few hours of elaboration and this means that the researchers can better organize another survey for the same day or the day after analyzing the site models obtained with the feedback. The high quality model is instead available in 1 month, together with the possibility of having also its 3D print. In Figure 5 the low quality model resulted from the mentioned missions is shown. It was obtained from the elaboration of about 200 photos in four hours. The high quality output can be produced in different formats, so manageable with different kind of software and for different kind of usages. It can be imported in virtual environments like common game engines (the authors use Unity) or common GIS (the authors use QGIS) which makes its fruition easier. In parallel to the reconstruction process, from the cameras alignment and correspondence steps, is possible to recover also the trajectory followed by the diver. An example of this output related to the pipe inspection is illustrated in Figure 6. It can be noticed that the diver started the survey from the middle of the pipe and the continued along its length. In this phase the filtering algorithm was implemented on a National Instrument MyRIO and tested on the DocuScooter which was moved only on the surface to allow acquiring the GPS data. Due to the particular nature of this test, no depth sensor has been involved in the algorithm. The IMU used during this test was an Xsens MTi-3-8A7G6, installed on center of gravity of the vehicle. The Ad fruit Ultimate GPS v3 has been used to receive the GPS signal with an active antenna. The accuracy of this sensor is about 3 meters. These two sensors have been used to feed the data to the UKF algorithm.

Figure 5 Low quality 3D model.

Figure 6 Path followed by the diver.
Table 1 gathers quantitative results regarding five tests that have been performed. The maximum and the mean error are related to the real GPS position. As the table shows, the algorithm is able to satisfactorily estimate the position of the device during the test. For sake of brevity only the results and graphs related to Test 1 will be analyzed and discussed. In any case, comparable considerations could be done with the data acquired during the other tests.
|
Test Time (s) |
Max Error (m) |
Mean Error (m) |
Test 1 |
421 |
0.9154 |
0.0966 |
Test 2 |
877 |
0.7151 |
0.1034 |
Test 3 |
244 |
0.8519 |
0.1466 |
Test 4 |
414 |
0.7268 |
0.0797 |
Test 5 |
719 |
0.6153 |
0.0847 |
Table 1 Quantitative results of the five tests performed
It is possible to observe that only in the first seconds the filtered position doesn’t track perfectly the GPS because the accelerometer bias wasn’t compensated, as confirmed by position error (Figure 8). Confirming a good behavior of the UKF, Figure 9 shows the track of the estimated heading compared to heading computed by the GPS. In this case the gyro bias is very small, so the filter works well also in the first’s instants.
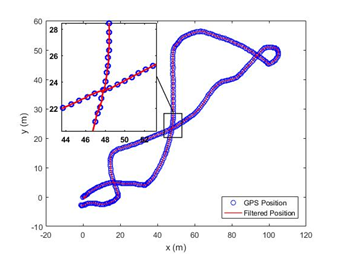
Figure 7 GPS and filtered position Figure 7 show device position measured from GPS and filtered by the UKF algorithm.
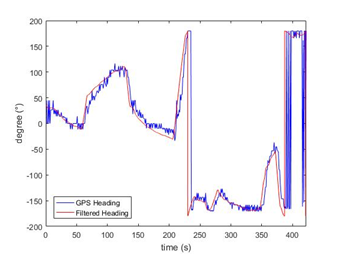
Figure 9 GPS and filtered heading.


