One of the main challenges of watershed hydrology is the calculation of the variation of the depth of water storage in a watershed. To address this question this paper presents a methodology for calculating the watershed water storage based on watershed water balance over a period of infinite time. The results obtained through this methodology have been applied to the Mount Hope River watershed in Connecticut and had been tested by applying the equation of Hughes and Murrel for discharge and storage.

Keywords: analytical method, water balance, discharge, evapotranspiration, precipitation

The estimate of the watershed water storage is perhaps one of the most important problems in hydrology and has an added difficulty due to the inability to measure the flow of water storage into the watershed soil, besides that the variation of water stored in a watershed can have a direct impact on the flow of the river, important enough to diminish or exacerbate the consequences of a storm¹ furthermore, Coutagne² considered that the recession and the streamflow are conditioned by the water storage in the watershed and the meteorological factors. Jakeman & Hornberger³ assume that it is possible to classify water storage models in two ways: using empirical relationships taking observations of the stream characteristics like discharge, channel geometry, and vegetative cover along the stream; or using the energy and water balance in the stream. However there are other physically based models to estimate the parameters related with the storage of water.³ For example, the groundwater module of the ARNO model represents the overall response of storage through a cascade of linear reservoirs, the storage of soil moisture and other components which control the hydrograph recession.⁴ Several watershed functions response has been developed to predict the rate of water storage in a watershed, for example, Chapman⁵ was testing recession functions in 11 different streams, during periods of no recharge and he found that for most of the catchments, the storage-discharge relationship is more strongly non-linear than the quadratic form.⁵

For example the NERC⁶ model uses the Equations 1 originally deduced from Hughes & Murrel⁷ for the calculation of the discharge as part of the model structure. Equation (1) calculates the water storage in the watershed in function of the discharge and use two parameters storage constant (AC) and n, but the traditional analytical solution of Equation 1 is n = 0.5.

Where:

$S\text{ =}AC*Q^n$ [1]

S, Depth of water storage [m/day];

AC, Storage constant [(mm.h)^0.5];

Q, Discharge [m³/day];

N, Parameter, 0<n<1 [-]

Castro & Hornberger⁸ created a physically-based model using time series analysis to predict transport and storage in alluviated mountain catchments, their model consist of three major zones that affect storage and transport properties (1) the stream; (2) the coarse gravel bed associated with the active stream and (3) the less coarse alluvial material adjacent to and underlying the stream. They found that water storage models in a watershed may have to account for interactions between the stream and large portions of its floodplain and that the short term storage may result from small mixing of water with stagnant surface pools and movement of water into and out of the gravels and cobbles in the streambed.⁸

Also for Castro & Hornberger⁸ long term storage may occur as result of mixing of water into the reservoir of water in the extensive alluvium surrounding the active stream channel and during times of low streamflow, all of these mechanism may be important. After the research conducted by Klaassen et al.⁹ In the area of Speulderbos (Netherlands), he arrived to the conclusion that the common methods for water storage calculation have systematic errors that neglect the drainage before saturation and systematically underestimate water storage and overestimate evaporation during rain. Klaassen et al.⁹ considered that the water storage is better simulated assuming an exponential saturation of a larger storage capacity, and that a small evaporation can be simulated using an appropriate resistance to vapor transport. The observations in dense coniferous forest showed that water storage is the dominant process in rainfall interception, but this conclusion should not be generalized to other forests and climates.⁹

Hodnett et al.¹⁰ conducted research in the Amazonia (Brazil) to compare changes in seasonal soil water storage with a depth of 2 meters in pasture and rainforest vegetative cover, they arrived at the conclusion that the spatial variability of soil water storage was significantly greater under the pasture than under the forest, especially after rainfall events in the dry season. The conclusion was that the forest has more capacity than the pasture to utilize all of the available water at the depth studied, and this was largely due the result of redistribution of rainfall as local surface runoff.¹⁰ Harvey & Bencala¹¹ applied a hydrologic simulation model at St. Kevin Gulch (USA) west of the Rocky Mountains to test the water exchange between stream channels and adjacent aquifers by streambed topography. They arrived to the conclusion that the subsurface hydraulic gradients indicated that stream water was locally recharged into well-defined flow paths through the alluvium and return of substream flow paths to the stream occurred where stream water slope decreased during the transition from steeper channel units to pools¹¹ and a sequential increase and decrease in stream stage is required to reverse the direction of water exchange from stream to subsurface¹² and.¹³

Beside rural areas the water storage in an urban environment remains a little researched topic, with a few studies such as Grimmond & Oke,¹⁴ Lerner,¹⁵ Cawley & Cunnane,¹⁶ Mitchel et al.,¹⁷ Van Rooijen et al.¹⁸ and Mitchel et al.¹⁹ Urban water storage calculation has the complexities of the city and the lack of data can lead to high uncertainties. Lerner¹⁵ recommend holistic approaches in for the calculation of water storage in an urban environment whenever possible, for example by investigating the overall water balance or calibrating a groundwater flow model. Also Lerner¹⁵ arrived to the conclusion that recharge in urban areas is now widely recognized to be usually as high or higher than in equivalent rural areas. Other estimates of water storage in a watershed have a simplistic approach that divides the impermeable and permeable soil, but with urbanization the grassed areas probably will not have the same pre-urban development runoff characteristics altered by landscaping, changes in soil drainage and the topography flattened.¹⁶

The satellite Gravity Recovery and Climate Experiment (GRACE) provides data describing monthly changes in the geoid, which are closely related to changes in vertically integrated terrestrial water storage.²⁰ Swenson et al.²⁰ In their research described techniques for constructing spatial averaging kernels, with which the average change in vertically integrated water storage within a given region can be extracted from a set of Stokes coefficients. Swenson et al.²⁰ research focused in North America river basins to find monthly water storage variations. Swenson et al.²⁰ arrived to the conclusion that GRACE is capable of estimating monthly changes in water storage with an accuracy better than 1 cm of water thickness for regions with areas smaller than 100 square kilometers, with better accuracies for larger regions. GRACE can be applied in regional or global scale for water balance analysis and direct measure of seasonal water storage for river-basin water balance analyses.²⁰ Lettenmaier & Famiglietti²¹ also applied GRACE in the Congo basin to measure precisely where and in what quantities the watershed stores water and how the water moves between those stores.²¹ Other way to know the water storage is to make a water balance in the watershed. Water balance techniques were initially developed in the 1940s and 1950s²² to evaluate the importance of different hydrological parameters under a variety of hydrological conditions.²³ Thornthwaite & Mather²² applied the water balance to gain information in periods of moisture surplus or deficit. Milly²⁴ found out that the long-term water balance is determined only by precipitation and potential evapotranspiration, mediated by water storage in the soil. Assuming the hypothesis of a finite land area having and under stationary climate Milly²⁴ developed and tested without calibration a simple model of the water balance east of the Rocky Mountains (USA). Milly²⁴ worked with a storage model of local water balance of the plant root zone of the soil, the average water storage (which includes storage on the soil profile, groundwater aquifers and above surface storages of local scale) is obtained by integration of a continuous water balance equation with respect to time (Equation 2).

Where:    

$\frac{\text{dS}}{\text{dt}}=\text{P-ET-Q}$ [2]

S, Depth of water storage [mm]

t, Time [day]

P, Precipitation [mm]

ET, Evapotranspiration [mm]

Q, Discharge [mm]

Grimmond & Oke¹⁴ applied a model to calculate the daily, monthly, and annual water balance components for a suburban catchment in Vancouver (Canada), the water balance was compared with that for a rural area in the region. The results shows that the temporal pattern of external water use is related to prevailing weather conditions, in particular, closely related to evapotranspiration. The model was run with, and without, an irrigation input to gauge its impact on the water budget. The results provide both quantitative and qualitative support for the idea that irrigation is the source of water supporting the relatively large rates of suburban evapotranspiration reported in energy balance studies.¹⁴ Mitchel et al.¹⁷ applied a daily model to quantify the components of the total urban water balance of the Curtin catchment, Canberra (Australia). Seasonal and annual variations in climate exert a very strong influence over the relative magnitude of the water balance components; this needs to be accounted for when assessing the potential for utilizing stormwater and wastewater within an urban catchment.¹⁷

Cawley & Cunnane¹⁶ considered that depending upon the focus of the analysis in the water balance, each sub-system can be modeled separately, details of the atmospheric water balances component are normally excluded from watershed based hydrologic models, and the atmospheric variables are measured and often treated as input parameters. Surface water, soil water and groundwater water systems are closely linked, and are often treated together in water budget modeling.¹⁶ The most simple version of water balance (Equation 3) can be viewed as the simple frameworks of water inputs and outputs.²⁵

Where:

                        $\Delta S=P+I-Q-ET$ [3]

∆S, Relative water storage [mm];

I, Water supply [mm]

Another possible way to obtain a water storage over time of one watershed is searching for water balance over a long time. The Fenton River study²⁶ was conducted to determine streamflow variations in the Fenton River watershed. Peak flow and recessions studies were conducted especially during the low-flow period of the summer, and the amount of induced infiltration caused by the wells.²⁶ As part of this study, research in the neighbor watershed, the Mount Hope River watershed was conducted to predict the future water storage level in the Fenton River based on Mount Hope River flows, evapotranspiration and precipitation in order to manage the well field and minimize the potential impacts in the Fenton river pump area.

The specific objectives of the study reported here were: Find a mathematical methodology to calculate the water storage in the Mount Hope River watershed using Oke²⁵ water balance equation (Equation 3) as initial approach and test the results with the discharge and storage equation of Hughes & Murrel,⁷ Equation 1, in the Mount Hope River watershed.

Study site and data used

The Mount Hope River, Figure 1, has a total length of 23 km, and the drainage area at the USGS gage # 01121000 is 74.0 km² and is located at Latitude 41°50'37" and Longitude 72°10'10" North American Datum 1927 (NAD27).²⁷ The Gage datum is 102.3 meters above sea level National Geodetic Vertical Datum of 1929 (NG5D29).²⁷ The Table 1 shows the hydrologic and vegetative cover of the Mount Hope river watershed, discharge attributes (1), percentages of land use in the watershed (2) and the stratified drift (3), calculated by Bighinatti.²⁸ Data for the calculation and testing of the water storage methodology were obtained from 1997 to 2006. Flow data were obtained from USGS gage # 01121000 for the Mount Hope River and precipitation data were obtained from the University of Connecticut, Agronomy Farm Latitude 41°47'42" N and Longitude 72°13'42" W approximately 11.26 km from the Mount Hope gage. The precipitation data were available for 30 minutes increments, while the stream discharge was in 15 minute increments. Therefore, the 15 minute streamflow data and 30 minutes increments precipitation data were combined into daily increments to directly compare rainfall and streamflow.

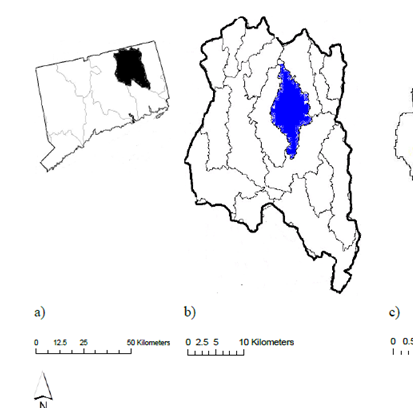
Figure 1 (a) West branch of the Thames River watershed in black color in the State of Connecticut; (b) the east branch of the Thames River watershed with the Mount Hope River watershed in blue color; (c) Mount Hope river watershed.

Methodology for the calculation of the rate of water storage

First, Equation 3, is applied in the Mount Hope watershed for daily values of precipitation, evapotranspiration and discharge from 01/01/1997 to 10/31/2006, Figure 2, shows the result of the relative water storage ( ΔS ) between precipitation, evapotranspiration and discharges, water supply equal to zero (I=0) for this period of time. Figure 2 shows that a it is not possible to find a water storage trend like the evapotranspiration or discharge have in the watershed at any moment of the year. To find the water storage trend a mathematical development of the Equation 3 was done assuming the hypothesis that:

Figure 2 Relative water storage in the Mount Hope river watershed from 01/01/1997 to 10/31/2006.

A generalization of Equation 3 for the relative water storage can be used to obtain the water storage in a watershed using as approach Equation 4, assuming:

1. Water supply equal to zero (I=0).
2. The relative water storage (ΔS) between the initial (So) and the final water storage (Sf) obtained fromthis equation is the results of the water balance between the precipitation, evapotranspiration and the discharge of the watershed, plus a residual (R) that is the water not accounted with these parameters, such as the errors in the measurements of precipitation, discharge and evapotranspiration, groundwater aquifers, surface storages and all the groundwater inflows and outflows that cannot be measured, the residual can be positive or negative depending of the direction of the residual

Where:

                                                                  $\Delta S={\text{S}}_{\text{f}}{\text{-S}}_{\text{o}}\text{=}P-ET-Q-R$ [4]

R, Residual [mm];

S_f, Final water storage for the period [mm];

S_o, Initial water storage for the period [mm].

3. Transform the parameters precipitation, evapotranspiration and discharge of the Equation 4 in series in function of the time, relative water storage (ΔSi), precipitation (Pi), evapotranspiration (ETi), discharge (Qi) and the residual (Ri), that means for example that for time step 10 (later in theapplication the time step will be one day) we have that the relative water storage is: , resulting in the Equation

                                                                                                      $\Delta S_i=P_i-E{T}_i-Q_i-R_i$ [5]

Where:

S_i, Water storage in function of time [mm];

P_i, Precipitation in function of time [mm];

ET_i, Evapotranspiration in function of time [mm];

Q_i, Discharge in function of time [mm];

R_i, Residual in function of time [mm]

Making a summation of the parameters of the relative water storage (ΔS_i), precipitation (P_i), evapotranspiration (E_i), discharge (Q_i) and the residual (R_i), of the Equation 5, for the total period of time or number of time steps (n), we have Equation 6.

${\displaystyle \sum _0^n\Delta S_{{}_i}}={\displaystyle \sum _0^n{P}_{{}_i}}-{\displaystyle \sum _0^{n}E{T}_{{}_i}}-{\displaystyle \sum _0^n{Q}_{{}_i}}-{\displaystyle \sum _0^n{R}_{{}_i}}$ [6]

Where:

n # of time steps [-].

We assume that the summation of every parameter for the whole period of time calculated is equal to the average of every parameter multiplied the number of time steps n (${\displaystyle \sum _0^n{P}_{{}_i}}=n.\overline{P}$ ,${\displaystyle \sum _0^{n}E{T}_{{}_i}}=n.\overline{ET}$ ,<math >
<semantics>
<mrow>
<mtext>&#x00A0;</mtext><mstyle displaystyle='true'>
<munderover>
<mo>&#x2211;</mo>
<mn>0</mn>
<mi>n</mi>
</munderover>
<mrow>
<msub>
<mi>Q</mi>
<mrow>
<msub>
<mrow></mrow>
<mi>i</mi>
</msub>
</mrow>
</msub>
</mrow>
</mstyle><mo>=</mo><mi>n</mi><mo>.</mo><mover accent='true'>
<mi>Q</mi>
<mo>&#x00AF;</mo>
</mover>
</mrow>
<annotation encoding='MathType-MTEF'>MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcfaieaaaaaa
aaa8qacaqGGaWaaabCaeaacaWGrbWaaSbaaeaalmaaBaaajuaGbaqc
LbmacaWGPbaajuaGbeaaaeqaaaqaaiaaicdaaeaacaWGUbaacqGHri
s5aiabg2da9iaad6gacaGGUaGabmyuayaaraaaaa@4312@
</annotation>
</semantics>
</math>
and ${\displaystyle \sum _0^n{R}_{{}_i}}=n.\overline{R}$ ) and the result of the summation of the relative water storages () is equal to the final water storage (S_f) minus the initial water storage (S_o) of the whole period of time because the other water storage are

eliminated between each other $(S_f-So=S1-S_o+S_2-S_1\dots \dots \dots S_{n-1}-S_{n-2}+S_f-S_{n-1})$ , Equation 7.

$S_f-So=n.\overline{P}-n.\overline{ET}\text{ -}n.\overline{Q}-n.\overline{R}$ [7]

, Average precipitation during n time steps [mm];

, Average evapotranspiration during n time steps [mm];

, Average discharge during n time steps [mm];

, Average residual during n time steps [mm].

Joining the parameters that have number of time steps (n) in common lets, Equation 8.

$S_f-So=n.(\overline{P}-\overline{ET}\text{ -}\overline{Q}-\overline{R})$ [8]

Equation 5 is divided by the number of time steps (n) in both sides of the equation, Equation 9.                       

$\frac{S_f-So}{n}=\frac{n.(\overline{P}-\overline{ET}\text{ -}\overline{Q}-\overline{R})}{n}$ [9]

n Then is assumed that the number of time steps trend to infinite (n→∞) and the limit of the equation 9 is calculated, Equation 10.

$\underset{n\to \infty }{\lim }\frac{S_f-So}{n}=\text{ lim}(\overline{P}-\overline{ET}\text{ -}\overline{Q}-\overline{R})$ [10]

Equation 11 shows the result of the limit calculation when the number of time steps trend to infinite, the difference between the final and initial water storage over the time step is zero because a finite number over a number that trend to infinite is equal to zero, therefore the water balance between the averages of precipitation, evapotranspiration, discharge and the residual is equal to zero.

$\underset{n\to \infty }{\lim }\frac{S_f-So}{n}=0\Rightarrow \text{ lim}(\overline{P}-\overline{ET}\text{ -}\overline{Q}-\overline{R})=0$ [11]

Therefore, from Equation 11, is obtained the Equation 12 that shows that the trend of the average residual () for a long period of time is equal to the average precipitation () minus average evapotranspiration () minus average discharge () of the whole period of time.

$\overline{R}=\overline{P}-\overline{ET}\text{ -}\overline{Q}$ [12]

From the result obtained in the Equation 12, the average residual ( R ) is included in the Equation 5, obtaining the Equation 13.

$S_f-So={\displaystyle \sum _0^n{P}_{{}_i}}-{\displaystyle \sum _0^{n}E{T}_{{}_i}}-{\displaystyle \sum _0^n{Q}_{{}_i}}-n.\overline{R}$ [13]

To find the average residual is necessary to find a regression function for the average precipitation minus average evapotranspiration minus average discharge of the whole period of time. That means a regression function for the summation of precipitation minus evapotranspiration minus discharge of the whole period of time. The square-R of the regression will test the goodness of this approach, then the trend is used as long trend correction for the accumulated relative water storage. The first step to obtain the water storage during a period of time is the Equation 14.

$S_f\text{= }So\text{ +}{\displaystyle \sum _0^n{P}_{{}_i}}-{\displaystyle \sum _0^{n}E{T}_{{}_i}}-{\displaystyle \sum _0^n{Q}_{{}_i}}-n.\overline{R}$ [14]

The final step to obtain the depth of storage (S_f) is with the calibration of the parameter S_o to satisfy the condition that the depth of water storage (S_f) always must be a positive number, Equation 15.

$So\text{ +}{\displaystyle \sum _0^n{P}_{{}_i}}-{\displaystyle \sum _0^{n}E{T}_{{}_i}}-{\displaystyle \sum _0^n{Q}_{{}_i}}-n.\overline{R}\underset{\_}{>}0$ [15]

The results of the mathematical develop were applied to the Mount Hope River watershed to obtain the water storage in this watershed from 01/01/1997 to 12/31/2006. The inputs for the water budget are discharges, precipitations and evapotranspiration. Discharges were obtained from the Mount Hope River where there is a USGS station,²⁷ precipitation data were obtained from the Agronomy Farm at the University of Connecticut and, equation 16 and 17 were used for the calculation of the evapotranspiration as a function of Julian Day by Brenham(com. pers. 2007) from 01/01/1997 to 12/31/2006.

PredictedET=

0.4208114930830774

- 8.575993091953963. Sin(JR)

+95.32701397086473. Sin(JR)² [16]

-398.34483201433795.Sin(JR)³

+782.1931080407808.Sin(JR)⁴

-708.4279629693772.Sin(JR)⁵

+240.86032253834992.Sin(JR)⁶

Where:

JR: Julian Radians

$\text{JulianRadians}=(\frac{\Pi }{365}\text{)* JulianDays}$ [17]

Where:

JDays, Yearly Julian day [-].

Applying Equation 6 of the water balance assuming the residual equal zero (R=0), then it will be calculated, the result for the daily summation of the relative water storage (ΔS ) shows a definite declining trend in the amount of water in the watershed, Figure 3.

By the second law of thermodynamics, it is impossible that an isolated system such as the Mount Hope river watershed, if not already in its state of equilibrium, evolves towards it, therefore perpetual loss of water from the watershed as shows the accumulated water balance of the Figure 3, it is impossible. Therefore exist a non accounted input of water that we called residual R. Applying the mathematical demonstration made above, a correction of the accumulated water Storage was applied using Equation 12, that means that the average residual R trend is used as long trend correction for the accumulated relative water storage as first step to obtain the depth of water storage.

A trend line () for the average accumulated values of the relative water storage shown in Figure 3, is given by the equation obtained from a linear regression over the accumulated values of the relative water storage with a coefficient of correlation equal to 0.91, Equation 18.

$\overline{R}=\text{- 0}\text{.3496* t}+1\text{2264}$ [18]

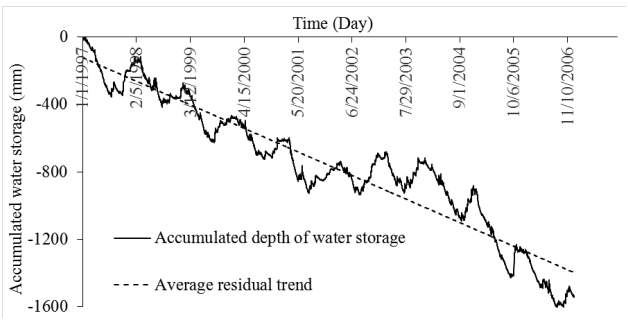
Figure 3 Depth of accumulated water storage and Residual calculated in the Mount Hope River watershed from 01/01/1997 to 12/31/2006.

Then making a correction in the accumulated relative water storage (applying Equation 13), the Equation 19 is obtained.

$S_f\text{= }So\text{ +}{\displaystyle \sum _0^n{P}_{{}_i}}-{\displaystyle \sum _0^{n}E{T}_{{}_i}}-{\displaystyle \sum _0^n{Q}_{{}_i}}-(-\text{0}\text{.3496* t}+1\text{2264)}$ [19]

Finally the initial water storage (S_o) in the Equation 19 is calibrated to satisfy the condition that the depth of water storage (S_f) is always positive (applying Equation 15), the value obtained for S_o is 253.79. Therefore with the outputs of Equation 19 it is possible to calculate the daily water storage for the period from 01/01/1997 to 10/31/2006, Figure 4.

Due to the lack of measured data to test the methodology for the calculation of the watershed water storage, the values of the depth of water storage found above were tested against the equation of Hughes & Murrel⁷ for discharge and storage (Equation 1) in the Mount Hope River watershed. Equation 1 was tested during 10 recession periods between 01/01/1997 and 12/31/2006. The resulting relationship is shown in Figure 5, results in values of AC=0.0231 and n=The power regression obtained from the plot of the Discharges versus the water storage in the Mount Hope River watershed has a coefficient of regression of 0.61. This coefficient of regression can be explained by the lack of other parameters such as evapotranspiration, soil properties in the equation of Hughes & Murrel⁷ Equation 1.

Figure 4 Depth of water storage in the Mount Hope River watershed, from 01/01/1997 to 12/31/2006.

Figure 5 Discharge and water storage in the Mount Hope River, from 01/01/1997 to 10/31/2006.

This investigation created a simple and mathematically proven methodology for the calculation of watershed water storage that is a step forward for the study of watershed scale hydrology due to the inability to measure the flow of water storage into the watershed soil,. For this calculation it is necessary to have available daily data of discharge, evapotranspiration and precipitation of the watershed for a considerable period of time. In the event that an extremely long period of data is available, say 100 years, the methodology can help to study hydrologic phenomenon that includes droughts and flooding.

None.

The author declares that there is no conflicts of interest.

1. Faulkner B. The control of surface water runoff from new development – UK national policy in need of review. Urban Water. 1999;1(3):207‒215.
2. Coutagne A. Les variations de debit en periode non influence par les precipitations. La Houille Blanche. 1948;3:416‒436.
3. Jakeman AJ, Hornberger GM. How much complexity is warranted in a rainfall‐runoff model? Water Resources Research. 1993;29(8):2637‒2649.
4. Chapman T. A comparison of algorithms for streamflow recession and baseflow separation. Hydrological Process. 1999;13(5):701‒714.
5. Todini E. The ARNO rainfall‒runoff model. Journal of Hydrology. 1996;175(1‒4):339‒382.
6. NERC. Flood Studies Report. Natural Environment Research Council. 1975;1(5):527‒534.
7. Hughes DA, Murrell HC. Non‒Linear runoff routing, a comparison of solution methods. Journal of Hydrology. 1986;85(3‒4):339‒347.
8. Castro N, Hornberger GM. Surface‒subsurface water interactions in an alluviated mountain stream channel. Water Resources Research. 1991;27(7):1613‒1621.
9. Klaassen W, Bosveld F, De Water E. Water storage and evaporation as constituents of rainfall interception. Journal of Hydrology. 1998;212:36‒50.
10. Hodnett MG, da Silva LP, Da Rocha HR, et al. Seasonal soil water storage changes beneath central Amazonian rainforest and pasture. Journal of Hydrology. 1995;170(1‒4):233‒254.
11. Harvey JW, Bencala KE. The effect of streambed topography on surface‒subsurface water exchange in mountain catchments. Water Resources Research. 1993;29(1):89‒98.
12. Cooper HH, Rorabaugh MI. Groundwater movements and bank storage due to flood stages in surface streams. US Geological Survey. Water Supply. 1963;1536(5):343‒363.
13. Pinder GF, Sauer SP. Numerical simulation of flood wave modification due to bank storage effects. Water Resources Research. 1971;7(1):63‒70.
14. Grimmond CSB, Oke TR. Urban Water Balance 2: Results From a Suburb of Vancouver, British Columbia. Water Resources Research. 1986;22(10):1404‒1412.
15. Lerner DN. Identifying and quantifying urban recharge: a review. Hydrogeology Journal. 2002;10(1):143‒152.
16. Cawley AM, Cunnane C. Comment on estimation of greenfield runoff rates. Proceedings of National Hydrology Seminar. 2003;1:29‒43.
17. Mitchell VG, McMahon TA, Mein RG. Components of the total water balance of an urban catchment. Environmental Management. 2003;32(6):735‒746.
18. Van Rooijen DJ, Turral H, Wade Biggs T. Sponge city: water balance of mega‐city water use and wastewater use in Hyderabad, India. Irrigation and drainage. 2005;54(S1):S81‒S91.
19. Mitchell VG, Cleugh HA, Grimmond CSB, et al. Linking urban water balance and energy balance models to analyse urban design options. Hydrological processes. 2007;22(16):2891‒2900.
20. Swenson S, Wahr J, Milly PCD. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resources Research. 2003;39(8):13.
21. Lettenmaier DP, Famiglietti JS. Hydrology: Water from on high. Nature. 2006;444(7119):562‒563.
22. Thornthwaite CW, Mather JR. The water balance. Drexel Institute of Technology, Publications in Climatology. Drexel Institute of Technology. 1995;8(1):104.
23. Gleick PH. The development and testing of a water balance model for climate impact assessment: modeling the Sacramento Basin. Wafer Resources Research. 1987;23(6):1049‒1061.
24. Millу PСD. Climate, soil water storage, and the average annual water balance. Water Resources Research. 1994;30(7):2143‒2156.
25. Oke TR. Boundary Layer Climates. Routledge. 1978;327.
26. Warner GS, Ogden FL, Bagtzoglou AC, et al. Long Term Impact analysis of the University of Connecticut’s Fenton River Water supply Wells on the Habitat of the Fenton River, Special Report # 39. Connecticut Institute of Water Resources. Connecticut. 2006. p. 211.
27. USGS. Daily Streamflow for Connecticut. 2005.
28. Bighinatti. Investigations of flow‒duration curves and application to estimating discharge on ungauged streams. Master’s Thesis, University of Connecticut, Connecticut. 2006.