In recent years, the problems associated with water use have sharply escalated worldwide. One of the main methods used for these purposes is ion exchange. In turn, the most promising ion-exchange materials are inorganic ion exchangers - substances with exceptionally high selectivity concerning ions of certain elements. In connection with life, it is necessary to understand ion exchange mechanisms on inorganic ion exchangers since they have significant differences in the unit vector of classical ion exchange resins. A theoretical analysis was conducted, which made it possible to reveal some features of the sorption kinetics of inorganic ion exchange materials. It has been found that when working in the region of concave isotherms, a significant slowdown of the mass transfer process is possible even on very sorbent granulates. This effect is associated with reversing sorption processes involving highly selective sorbents. In this regard, difficulties can be encountered when using displacement desorption, which is associated with maintaining high concentrations of the displacing agent and the low rate of the ion exchange process. The rate of sorption on inorganic ion exchange materials depends in a certain way on the concentration of sorbed ions in an external solution. This dependence manifests itself even in the absence of external diffusion inhibition. In this case, the determining factor is the distribution of electrolytes between the pore space of the granule and the free volume of the solution. The rate of mass transfer processes with the participation of inorganic sorbents can be affected not only by the permeability of granulates but also by inhibition at the level of homogeneous sections of the solid phase. The simplest way to detect such deceleration is to compare the data of the kinetic experiment with the theoretical results related to the model that ignores deceleration at the level of homogeneous sections of the solid phase. In such a comparison, it is necessary to consider possible distortions due to the finite width of particle size fractions, the discrepancy between the particle shape and the calculated one, etc.

Keywords: kinetics, ion exchange, inorganic sorbents, inorganic ion exchangers, diffusion, ion exchange isotherms, modeling of ion exchange processes

In recent years, the problems associated with water use have increased dramatically worldwide. These problems include such environmental issues as the purification of natural and wastewater from various polluting components. Also, such areas as extracting rare, trace elements and other valuable components from waters associated with surface and underground sources began to develop intensively. These factors contributed to the development of research on seawater processing - its desalination and used as an inexhaustible source of various mineral resources. One of the main methods used for these purposes is ion exchange. In turn, the most promising ion-exchange materials are inorganic ion exchangers - substances with exceptionally high selectivity for ions of certain elements. The phenomenon of ion exchange is widespread in animate and inanimate nature. In turn, ion exchange processes play a significant role in chemical technology, hydrometallurgy, and industrial ecology.^1,2 Recently, inorganic ion exchangers have been increasingly used in ion exchange technologies. In contrast to organic ion exchange resins, inorganic ion exchangers have increased radiation and chemical resistance, high selectivity, and low cost. Effective use of any ion exchangers in technology is impossible without knowledge of their sorption-kinetic properties. Currently, ion exchange kinetics for organic ion exchange resins has been studied much more than inorganic ion exchangers. The current situation is because organic ion exchangers have better kinetic properties than known inorganic ion exchangers and are more widely used in modern technological processes.^1,2,3–29 The main reason for the poor kinetic properties of inorganic ion exchangers is most often the slow diffusion of ions in crystallites.^30,31 In this case, the features of the exchange of ions inside the crystallites are primarily responsible for the high selectivity of inorganic ion exchangers.

However, by now, the situation is improving. Inorganic sorbents³² with small crystalline blocks have been created, making it possible to raise their functional properties to the required level. But many essential characteristics are missing for the synthesized ion exchangers: the sorption-kinetic properties have not been quantitatively characterized, the influence of various factors on the ion exchange kinetics has not been determined, and the optimal operating conditions have not been established. The variety of ion exchange mechanisms and their inherent kinetic features are not sufficiently studied. The need for systematic information on these issues becomes a severe obstacle in applying existing and developing new inorganic ion exchange materials. During the exchange of various ions, the course of the process in time depends on factors: the electric field (diffusion potential), changes in the separation factor, and gradients of the activity coefficients. Proper consideration of these factors seems impossible. Considering these systems, we must assume that even the most significant effects lead to nonlinear differential equations; such equations' analytical solutions are found only in individual cases. Nevertheless, these solutions make it possible to reveal regularities, the qualitative conclusions of which can also be applied to other issues. Of the above effects, the electric field has the most significant effect. Maintaining electrical neutrality in the system requires a "stoichiometric" flow of the exchange process, i.e., the counterflows of both counterions participating in the exchange (in equivalents) must always be equal in total.

The "stoichiometric" exchange required by the condition of electrical neutrality means that the counter diffusion fluxes (in equivalents) of counterions A and B are equal in magnitude at any time and in any section of the ion exchanger. For quantitative consideration, studying how flow equalization occurs is especially important. If one of the two counterions is more mobile, then its flux must initially be large; due to this, a short-term space charge arises and creates an electric field (diffusion potential), slows down the faster ion, and accelerates the slower one. Thus, there is an alignment of flows. The fluxes of both types of counterions are related to each other by electrical neutrality, just as the fluxes of cations and anions are connected during the diffusion of electrolytes in a free solution. The appearance of a space charge is equivalent to the violation of electrical neutrality. Therefore, in the literal sense, it is illogical to explain the conservation of electrical neutrality, as was done above, by the influence of space charges. As an additional condition, one should not consider electrical neutrality in all system parts but apply the Poisson-Boltzmann equation, which establishes the relation between the space charge and the electric field.^32–61,62 But it turns out that even a minor violation of electrical neutrality leads to a powerful electric field, which, by the above considerations, counteracts this violation. An accurate calculation shows that the deviations from electrical neutrality cannot be so large that they can be determined analytically. In addition to the space charge, there are only electric double layers at the ion exchanger/solution interface, which do not affect the kinetics since they are purely equilibrium phenomena. We can assume that applying the electrical neutrality condition as an additional condition is also valid when diffusion potentials arise.

As a "force" (in the meaning used by the thermodynamics of non-equilibrium processes), the ions are affected by the concentration gradient and the electric field resulting from diffusion processes. It follows that the electric field is an essential property of the system, which any theory should not neglect. Calculations that consider the influence of the electric field differ significantly from views in which this effect was not considered.⁶³ We restrict ourselves to quantitatively considering the effect of the electric field as the principal factor and consider the ideal limiting cases for ion exchange. Discussing other aspects should be conducted qualitatively since the corresponding theories still do not exist. In this regard, an important task is to study the kinetic properties of inorganic ion-exchange materials. The complexity of solving this problem is related to the peculiarities of their structure. Such materials have a rigid crystalline structure of primary particles forming granules. They are characterized by a specific pore space, the void between the particles that form the material's structure. These pores are filled with a solution under ion exchange conditions. In this regard, inorganic ion exchangers can be classified as biporous sorbents.¹ A mathematical apparatus has been developed to describe the kinetics of ion exchange on such materials. However, the application of this apparatus to natural ion-exchange systems is currently limited because of its complexity and difficulties in obtaining initial data.

The main difference between inorganic and organic ion exchangers is manifested in the crystal structure and, consequently, the presence of the stage of ion effluent into the solid phase of crystallites. Inorganic ion exchangers, in this case, can be divided into the following three groups according to the location of ion-exchange centers in crystallites and, accordingly, the implemented mechanism:^33,34

1. Ion exchangers whose sorption centers are located only on the surface of crystallites. There is no stage of ion sink into the solid phase. Kinetic difficulties associated with the process of sorption of ions on the surface of crystallites are most likely absent or are due to the chemical exchange reaction.
2. Ion exchangers that have sorption centers are distributed in the volume of crystallites. In this case, during ion exchange, there is a stage of diffusion of ions deep into the crystallites; if it is slow, it should manifest itself kinetically.
3. Ion exchangers, where sorption centers are located on the phase interface. During the ion exchange process, a new phase is formed on these materials through a heterogeneous exchange reaction.

In general terms, the ion exchange kinetics for ion exchangers of all presented groups will be described by the mathematical model described below, supplemented by various initial and boundary conditions for different types of external diffusion. The stage of internal diffusion is the transfer of ions inside the granule from ion-exchange centers to its surface and vice versa. Since inorganic ion exchangers are usually used in granular form, ion exchange processes on inorganic ion exchangers controlled by internal diffusion are relatively common, for example, in.^25,26 Granules of crystalline inorganic ion exchangers are agglomerates of primary crystallites, the space between which is filled with a liquid solution. This pore space plays an essential role in ion-exchange processes on these materials since almost the entire transport of ions deep into the granule occurs through it. Consequently, the granules' pore structure will significantly affect the rate of diffusion processes.^35–38

If we assume that the solution in the pores of the granule has the same properties as in the free volume, then the observed diffusion coefficients related to the volume of the granule decrease due to geometric factors. For a granule with a known structure, a decrease in the value of the diffusion coefficient can be estimated both purely mathematically^41,42 and based on statistical modeling methods,⁴³ among which the random walk method^44,45 is most widely used. These studies have shown that the diffusion coefficient decreases with a decrease in the specific pore volume. In loose structures, the diffusion coefficient decreases mainly due to the limited volume available for diffusion. In denser structures, the diffusion coefficient also decreases due to the tortuosity of the channels and the appearance of closed pores. However, in natural porous systems, the properties of the solution differ from the free volume. The smaller the pore size, this difference is more significant, which was experimentally shown in⁴⁶ using NaCl diffusion in glass as an example. The main reason for the unique properties of the solution in the pores is the formation of an electrical double layer. In the electric double layer, the ion concentration is increased, but its viscosity also increases, which can lead to an increase in the observed diffusion coefficient and its decrease. Thus, comparing the values of the diffusion coefficients of ions in solution and ion exchanger granules can provide a lot of information about the pore structure of granules and the mechanism of transfer within them.

In addition, there is information about the possibility of the diffusion mechanism of ions in the adsorbed state over the surface of crystallites.^47–49 Although the diffusion coefficients of ions, in this case, should be much smaller than in the free volume of the solution, a large concentration of ions on the surface can provide sufficient driving force for this process. Granules of ion exchangers with a fractal pore structure have unique properties. In these systems, the diffusion equations contain fractional derivatives,⁵⁰ and their solutions can lead to the so-called cases of anomalous diffusion⁵¹ when the Einstein-Smoluchowski equation is violated. This circumstance must be considered when analyzing experimental data on the kinetics of ion exchange in ion exchangers with a fractal structure. The observed fractal effects for inorganic ion exchangers are described in.⁵¹ In this work, we exclusively analyze the kinetic regularities of ion exchange processes on inorganic ion-exchange materials. Since these regularities, we do not consider the dynamics of ion-exchange sorption in column-type apparatuses. However, related sorption kinetics are associated explicitly with their technological design.

Statement and solution of diffusion problems of ion exchange

The object closest to inorganic ion-exchange materials, for which the theoretical issues of the kinetics of mass-transfer processes have been studied sufficiently, are ion-exchange resins. For these objects, the mass transfer process is described as a nonstationary diffusion of several charged particles.⁵⁷ The flux ${\left({\Phi }_i\right)}_{el}$ of ions of the ith type, created in a homogeneous solution due to the applied electric field, is proportional to the gradient of the electric potential $\phi$ , the concentration C_i, and the electrochemical charge of the ion z_i:

${\left({\overrightarrow{\Phi }}_i\right)}_{el}=-u_i{Z}_i{C}_i \text{ grad} \phi$   (1)

The coefficient of proportionality u is the electrochemical mobility of the ion. When deriving the equation for the ideal limiting case, we apply the Einstein relation, which gives the relationship between the electrochemical mobility and the individual diffusion coefficient D_i of the ion:

$u_i=\frac{D_iℱ}{RT}$   (2)

Where: $ℱ$  — Faraday number, R — gas constant, T — absolute temperature. Equation (2) is strictly applicable only to ideal systems. However, from the experimental material, it is also suitable with some approximation to ion exchange. This situation is likely due to the ion exchanger having narrow pores that prevent the formation of ion clouds, and their deformation does not play a significant role.

If, in addition to the electric field, there is an ion i-th kind concentration gradient in the solution, then the pure diffusion flux ${\left({\overrightarrow{\Phi }}_i\right)}_{diff},$ described by first Fick's law, is superimposed on the transfer of electricity (1). According to this law, the diffusion flux ${\overrightarrow{\Phi }}_i$  of particles of the i-th kind is expressed as follows (3):

${\left({\overrightarrow{\Phi }}_i\right)}_{diff}=-D_i \text{grad} C_i$   (3)

The resulting flow will be described by the Nernst-Planck equation:^58,60,61

${\overrightarrow{\Phi }}_i={\left({\overrightarrow{\Phi }}_i\right)}_{di ff} +{\left({\overrightarrow{\Phi }}_i\right)}_{el}=-D_i\left(\text{grad} C_i+-z_i{C}_i\frac{ℱ}{RT} \text{grad} \phi \right)$   (4)

Equation (4) does not consider convection phenomena, the influence of activity and pressure gradients, and the mutual influence of ion fluxes, except for what is considered by the term describing the electric field. Equation (4) applies to mobile ions of all available varieties. The system of such equations that appears instead of equation (3) must be solved under the appropriate boundary and additional conditions.

A rigorous description of such a problem is given by the system of equations (5):³⁹

$\{\begin{array}{l}\frac{\partial C_1}{\partial t}=\text{div} \left[D_1\left(grad \left(C_1\right)+\frac{z_{1}F{C}_1}{RT}grad \left(\phi \right)\right)\right]\\ \mathrm{......................................................................}\\ \frac{\partial C_i}{\partial t}=\text{div} \left[D_i\left(grad \left(C_1\right)+\frac{z_{i}F{C}_i}{RT}grad \left(\phi \right)\right)\right]\end{array}$   (5)

Where: C_i and z - concentration and charge of ions, respectively; D_i - diffusion coefficient; φ - potential.

To determine the potential, we used the Poisson-Boltzmann equation (6)

$\text{div}\left(grad\left(\phi \right)\right)=-\frac{4\pi }{\epsilon }{\displaystyle \sum _{}{z}_i}{C}_i$   (6)

Where: ε - dielectric constant of the medium.

When solving this problem, a simplifying assumption is used that there is no spatial separation of electric charges during ion exchange (7):

${\displaystyle \sum _{}{z}_i}grad\left(C_i\right)=0$   (7)

This equation allows us to express the potential gradient in terms of ion concentration gradients (8):

$grad\left(\phi \right)=\frac{RT}{F}\frac{{\displaystyle \sum Z_i{D}_i} \text{grad}\left(C_i\right)}{{\displaystyle \sum Z_i{D}_i} C_i}$   (8)

The value of the gradient of the electric potential in equation (8) is determined based on the Poisson-Boltzmann equation; however, if we accept the conditions of electrical neutrality of the granule and the absence of an electric current in it, then the electric potential can be excluded from equation (8) by introducing the interdiffusion coefficient. This value is not constant during the ion exchange process.

Kinetic model of the ion exchange process in a gel matrix

First, we will again consider the case of ideal gel kinetics. In an idealized consideration, the presence of coions in the ion exchanger is neglected, the concentration and flow of which are, as a rule, negligible compared to the concentration and flow of counterions. In addition, the concentration of fixed ions and the individual diffusion coefficients are taken constantly $\overline{D}A$  and ${\overline{D}}_B$ . Additional conditions will be the following:

$z_A{\overline{C}}_A+z_B{\overline{C}}_B=-\omega \overline{C}=const$  electrical neutrality

$z_A{\overrightarrow{\Phi }}_A+z_B{\overrightarrow{\Phi }}_B=0$  no electric current

Where: — i-th ion charge value, $\omega$  — fixed ion charge sign. After combining these equations and equations (4) for counterions A and B,² we obtain:

${\overrightarrow{\Phi }}_A=-\left[\frac{{\overline{D}}_A{\overline{D}}_B\left(z_A^2{\overline{C}}_A+z_B^2{\overline{C}}_B\right)}{z_A^2{\overline{C}}_A{\overline{D}}_A+z_B^2{\overline{C}}_B{\overline{D}}_B}\right] grad {\overline{C}}_A$   (9)

The expression in square brackets, as shown by comparison with equation (7), is the interdiffusion coefficient for the ion exchange process. As applied to the problem of the simplest case of exchanging a pair of ions, this approach makes it possible to determine the interdiffusion coefficient by an expression determined from the equation obtained by Tunitsky and Helfferich (10).^2,59 This process is also called coion diffusion.

$D_{AB}=-\left[\frac{D_A{D}_B\left(z_A^2{C}_A+z_B^2{C}_B\right)}{z_A^2{D}_A{C}_A+z_B^2{D}_B{C}_B}\right]$   (10)

Where: D - diffusion coefficient of diffusing ions; C - diffusing ion concentration; z - charge of diffusing ions.

However, it is by no means a constant value but depends on the individual diffusion coefficients $\overline{D}A$ and ${\overline{D}}_B$ , on the ratio of the concentration of ions A and B (Figure 1) and therefore is a function of time and distance from the center of the grain. For ${\overline{C}}_A\ll {\overline{C}}_B$ , the parenthesized expression becomes $\overline{D}A$ , for ${\overline{C}}_A\gg {\overline{C}}_B$  is equal to ${\overline{D}}_B$ . As can be seen from formula (10), the value of the interdiffusion coefficient turns out to be dependent on the concentrations of diffusing ions. Coionic diffusion can influence the rate or even be the only step in controlling the ion exchange rate. Many existing theories of ion exchange kinetics assume that exchanged ions retain their identity and are not consumed in accompanying chemical reactions. This fundamental assumption is hardly acceptable, especially if the ions undergo neutralization reactions, association, complexation, or changes in the state of hydration during the ion exchange. The value of the interdiffusion coefficient is strongly influenced by an ion whose concentration is lower. This general rule² follows directly from the Nernst-Planck equation (4), in which the concentration of the i-th ion is included in the term containing the electric potential gradient. This rule can be easily explained: the electric field acts on each ion separately; it, therefore, causes a significant transport of ions present in a higher concentration and, at the same time, has little effect on ions present in a lower concentration. Analytical solutions to the problems of ion exchange kinetics have been obtained only for the case of a constant diffusion coefficient. These solutions correspond to a partial differential equation of the form (11):

Figure 1 Dependence of the interdiffusion coefficient in the ion exchanger on the relative content of ion A during the exchange of ions of the same charge. The family of curves calculated by equation (9) corresponds to different values of the mobility ratio ${\overline{D}}_B/{\overline{D}}_A$ . At vanishingly low ion concentrations A, the interdiffusion coefficient is equal to ${\overline{D}}_A$ , and at vanishingly small ion concentrations B, to ${\overline{D}}_B$ .²

$\frac{\partial \overline{C}}{\partial t}=D\left(\frac{{\partial }^2\overline{C}}{\partial x^2}+\frac{{\partial }^2\overline{C}}{\partial y^2}+\frac{{\partial }^2\overline{C}}{\partial z^2}\right)$   (11)

Where: $\overline{C}$ - concentration of a sorbed ion in the ion exchanger phase.

Equation (11) is a boundary value problem, and the initial and boundary conditions must be determined for its solution. As the initial conditions, expression (12) is usually used, the meaning of which is that the concentration of the sorbed ion at the initial moment is equal to zero at all internal points of the granule:

$\overline{C}\left(x,y,z,0\right)=0$   (12)

The so-called conditions of the first and third kinds are considered boundary conditions.^4,19 Conditions of the first kind are determined by expression (13), the meaning of which is that the capacitance at points belonging to the surface of the granule remains unchanged during the entire time of the sorption process:

$\overline{C}\left(x_0,y_0,z_0,0\right)=\overline{C}0$   (13)

Where: $\overline{C}\left(x_0,y_0,z_0,0\right)$ - capacitance at the points of the granule belonging to its surface.

This definition of boundary conditions corresponds to the so-called problem of internal diffusion kinetics. Conditions of the third kind are determined by expression (14), the meaning of which is that the magnitude of the ion flux through the boundary layer that occurs at the interface between the grain of the ion exchanger and the solution is equal to the flux of these ions through the outer surface of the granule.

$D\frac{\partial \overline{C}}{\partial l}=\beta \left(C_0-C_n\right)$   (14)

Where: D - diffusion coefficient; β - external mass transfer coefficient; $\frac{\partial \overline{C}}{\partial l}$  - capacitance gradient on the surface of the granule in the direction normal to this surface; C₀ - sorbed ion concentration in the free volume of the solution; C_n - sorbed ion concentration at the surface of the granule.

This definition of boundary conditions corresponds to the so-called problem of mixed diffusion kinetics, which makes it possible to consider the influence of hydrodynamic conditions on the rate of the mass transfer process. Several empirical dependencies are proposed to determine the value of the external mass transfer coefficient. For example, in,⁶¹ it is suggested to use formula (15):

$\beta =0.009\frac{\omega V^{0.53}}{d^{1.47}}\left[\frac{1}{\sec }\right]$   (15)

Where: β - mass transfer coefficient; ω - individual constant for each pair of exchanging ions; V - filtration rate; d - granule diameter.

In,^6,20 a more general equation (16) is proposed:

$\beta =5.39\frac{{\left(1-k\right)}^{1.53}}{k}\frac{D^{\frac{2}{3}}}{d^{1.53}}{V}^{0.47} {\left(\frac{\rho }{\mu }\right)}^{0.14}$   (16)

Where: k - filter layer porosity; D - diffusion coefficient; ρ - liquid density; μ - fluid viscosity. Other notations in equations (15) and (16) are the same.

The self-diffusion coefficient is a constant value inside the ion exchanger and the film. It does not depend on time and distance since the concentration of ions in both phases does not change depending on time or distance. Time changes in the concentration of the i-th ion are related to its flow by the continuity condition (second Fick's law):

$\frac{\partial C_i}{\partial t}=-div{\overrightarrow{\Phi }}_i$   (17)

For the system of interest to us with spherical symmetry and the case of constant diffusion coefficients, from equations (3) and (17), we can derive the following equation:

$\frac{\partial C_i}{\partial t}=D_i \left(\frac{{\partial }^2{C}_i}{\partial r^2}+\frac{2}{r}\frac{\partial C_i}{\partial r}\right)$   (18)

To understand the process of filling primary particles in a sorbent granule, let us consider the approximation of this problem in the version of spherically symmetric particles. For this case, equation (18) can be simplified by reducing it to form (19), with boundary conditions (20) for dimensionless time (t) and unit scattering (l) from the surface to the center of a spherical particle:

$\frac{\partial \overline{C}\left(l,t\right)}{\partial t}=D \left(\frac{{\partial }^2\overline{C}\left(l,t\right)}{\partial l^2}\right)$   (19)

$\overline{C}\left(0,t\right)=1$

$\overline{C}\left(l,0\right)=0$

$\frac{\partial }{\partial l}\overline{C}\left(1,t\right)=0$   (20)

The equation (19) solution for various diffusion coefficients D will have the form shown in Figure 2.

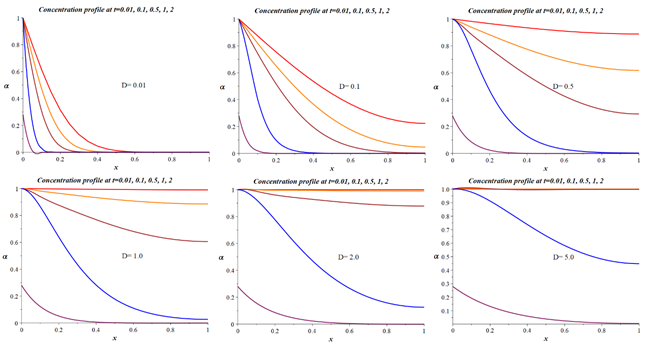
Figure 2 Dependence of the concentration profile of the degree of filling of the primary particles in the sorbent granule for cases of different diffusion coefficients calculated following the model (19).

The equation (19) solution for a fixed diffusion coefficient can also be represented in the 3D form in Figure 3.

Figure 3 Change in time of the concentration profile of the degree of filling of the primary particles in the sorbent granule following equation (19). l - is the dimensionless coordinate of a point inside a spherical particle.

From the data presented in Figure 2 and 3, there is no front of its filling inside the particle. There is a gradual filling of ion-exchange positions inside the primary particle, and the rate of this filling increases with an increase in the diffusion coefficient. In this case, inside the particle, the degree of its filling has an S-shaped character and is like a second-order reaction. The solution of equations (18) and (19) determines the dependence of the capacitance on the contact time and spatial coordinates inside the granule. In the practical use of solutions of this equation, the sorbent's integral capacity or the conversion's degree is usually determined since it is this value; as a rule, that is the result of a kinetic experiment. These quantities are determined by expressions (21) and (22), respectively, and in expression (21), integration is carried out over the entire volume of the granule at a fixed contact time.

$\overline{C}\left(t\right)={\displaystyle \underset{v}{\overset{}{\int }}\overline{C}\left(x,y,z,t\right)}dv$   (21)

$\alpha =\frac{\overline{C}\left(t\right)}{\overline{C}\left(\infty \right)}$   (22)

Where: $\overline{C}\left(t\right)$  - integrated capacitance; $\overline{C}\left(\infty \right)$  - capacitance at infinite contact time; α - degree of conversion.

This problem formulation obtained analytical solutions for several bodies of a simple geometric configuration, for example, a ball, a cylinder, and a parallelepiped.^7,19 We present the solutions obtained for a sphere with a linear sorption isotherm as examples of such solutions. By substituting equation (9) into the continuity condition (17), one more differential equation describes the mutual diffusion of ions A and B in the ion exchanger. For a system with spherical symmetry, the equation written in dimensionless form has the following form:²

$\frac{\partial {\overline{\gamma }}_A}{\partial \tau }\frac{1}{{\rho }^2}\frac{\partial }{\partial \rho }\left[{\rho }^2\left(\frac{1+b{\overline{\gamma }}_A}{1+a{\overline{\gamma }}_A}\right)\frac{\partial {\overline{\gamma }}_A}{\partial \rho }\right]$   (23)

It contains the following variables:

${\overline{\gamma }}_A\equiv \frac{z_A{\overline{C}}_A}{\overline{C}}; \tau \equiv \frac{{\overline{D}}_{A}t}{r_0^2}; \rho \equiv \frac{r}{r_0}$

and (constant) parameters

$a\equiv \frac{z_A{\overline{C}}_A}{z_B{\overline{C}}_B}-1; b\equiv \frac{z_A}{z_B}-1$

For ions with the same mobility a=b, equation (23) goes into equation (18). Analytical solutions of Eq. (23) have not yet been obtained. Numerical solutions are available only for the case of the exchange of ions with different mobility ratios ${\overline{D}}_A/{\overline{D}}_B$  under the initial and boundary conditions corresponding to the exchange between an ion exchanger completely saturated with A ions and a solution containing no ions A and in which the concentration of ions A can be neglected at all times compared to the concentration of ions B (a large volume of solution that satisfies the condition $\overline{C}\overline{V}\ll CV$ , or a constantly renewing flowing solution). Figure 4 shows the dependence of the conversion fraction U on the dimensionless time parameter \tau for various values of the ratio ${\overline{D}}_A/{\overline{D}}_B$ . The process completion measure is the dimensionless Fourier criterion (Fo) defined by expression (24):

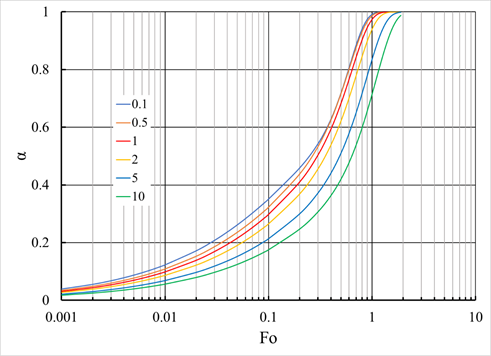
Figure 4 Exchange of ions with different mobility in the case of pure gel kinetics. The figure shows the dependence of the conversion fraction on the logarithm of the dimensionless time parameter of the Fourier criterion $Fo=\frac{{\overline{D}}_{A}t}{r_0^2}$ . The family of curves calculated by equation (23) corresponds to different values of the mobility ratio ${\overline{D}}_A/{\overline{D}}_B$ . The ions are assumed to have the same charge, and the solution is constantly renewed. The red line marks the boundary case for ions with the same mobility.²

$Fo=\frac{D \cdot t}{r^2}$   (24)

Where: D - diffusion coefficient; t - contact time; r - granule radius.

The dependence shown in Figure 4 with some approximation can be expressed as follows:²

$U={\left\{1-e^{\left(f_1\left(\alpha \right)\tau +f_2\left(\alpha \right){\tau }^2+f_3\left(\alpha \right){\tau }^3\right)}\right\}}^{\frac{1}{2}}$   (25)

Moreover, for ions with the same number of charges, the coefficients have the following values:

$\frac{1}{f_1\left(\alpha \right)}=-0.570 - 0.430{\alpha }^{0.775}$

$\frac{1}{f_2\left(\alpha \right)}=-0.260 - 0.782\alpha$       $\alpha =\frac{{\overline{D}}_A}{{\overline{D}}_B}$

$\frac{1}{f_3\left(\alpha \right)}=-0.165 - 0.177\alpha$       $0.1\le \alpha \le 10$

The conversion fraction depends only on the dimensionless time parameter $\tau =Fo=\frac{{\overline{D}}_{A}t}{r_0^2}$ and mobility ratios $$\alpha =\frac{{\overline{D}}_A}{{\overline{D}}_B}$$ $\alpha =\frac{{\overline{D}}_A}{{\overline{D}}_B}$ . As can be seen from Figure 4, the curves for different values of ${\overline{D}}_A/{\overline{D}}_B$  cannot be aligned when the time axis is stretched linearly. Consequently, with a decrease in the concentration of ions A during the exchange, the interdiffusion coefficient increases if A is a faster ion and decreases if A is a slower ion. Since m contains the value ${\overline{D}}_A$ , a direct comparison of the curves in Figure 4 is possible only if the ion A initially located in the ion exchanger is the same in all cases. For the case of internal diffusion kinetics, the dependence of the degree of transformation on the contact time is determined by expression (26), and for mixed diffusion kinetics, by expression (27).

$\alpha =1-\frac{6}{{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }\frac{e^{-{\pi }^2\cdot n^2\cdot Fo}}{n^2}}$   (26)

$\alpha =1-\frac{2}{3.K_d}{\displaystyle \sum _{i=1}^{\infty }\frac{e-{\mu }_i^2.Fo}{1+\frac{{\mu }_i^2}{9.K_d.\left(K_d+1\right)}}}$   (27)

Where: α - conversion degree; ${\mu }_i$ - parameter represents the roots of the solution of the transcendental equation (28) and (29); $K_d$ – distribution ratio.

${\mu }_{i}ctg({\mu }_i)-\frac{{(\mu i)}^2}{3.k_d}-1=0$   (28)

$\frac{{(\mu i)}^2}{3({\mu }_{i}ctg({\mu }_i)-1)}-K_d=0$   (29)

Dependence graphs (26) for granules of various sizes are shown in Figure 5.

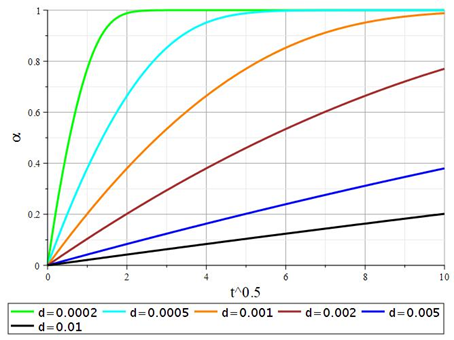
Figure 5 Dependence of the degree of conversion in equation (26) on √t at different values of the diameter of the sorbent granules (d, m).

The initial sections of the kinetic curves have noticeable linearity $\alpha =a_1\sqrt{t}$  in the coordinates $\alpha \propto \sqrt{t,}$ , which is typical for internal diffusion processes. To test this assumption, the first derivatives of the degree of conversion concerning the parameter $\sqrt{t}$  were calculated. The resulting dependencies are shown in Figure 6. The data obtained show that this assumption is valid to a certain extent for sorbent granules of large sizes d > 2 mm. However, this dependence is not correct for sorbent granules of smaller sizes. In this case, deceleration of the rate of the exchange process is observed, although, in the initial sections of the curves, the decrease in the process also has a linear character$\frac{da}{d\sqrt{t}}=b_1\sqrt{t}+b_0.$  This inhibition is due to deeper factors, such as internal diffusion within the crystallites that form the overall structure of the sorbent granule. Note that in solutions (26) and (27), the diffusion coefficient is determined only by the ion exchange properties and is not related to the concentration of ions in the external solution. To carry out calculations using equation (26), it is necessary to find the roots of the transcendental equation (28). To understand what roots equation (28) can have, it is essential to transform it into form (29) and analyze its behavior. This function is shown in Figure 7.

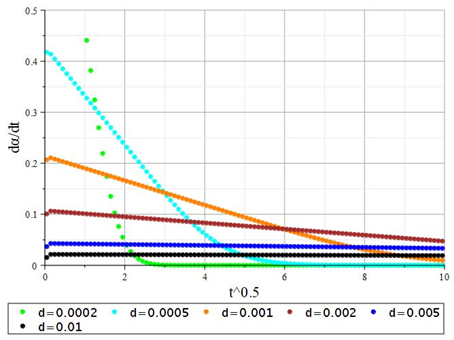
Figure 6 Time dependence of the first derivative $\left(\frac{d\alpha }{dt}\right)$ of the conversion degree (Eq. (26)) on $\sqrt{t}$ for various sorbent granule diameters (d, m).

Figure 7 View of function (29).

Based on the form of function (29), one can approximately estimate the value of an infinite number of its roots. In the case of a concave isotherm, that is, for small values of the exchange constants, they are respectively approximately equal to ${\mu }_i\sim [\mathrm{...},-2\pi ,-\pi ,\pi ,2\pi ,\mathrm{...}].$  With an increase in the exchange constant, the values of the roots shift in absolute value upwards. This makes it possible to estimate them for the subsequent calculation of the degree of exchange according to equation (26). The results of these calculations are presented in Figure 8. From the data obtained, in the exchange process, an induction period occurs, which increases with a decrease in the exchange constant. In addition, the exchange process proceeds to the end only at very large exchange constants. All the solutions presented above correspond well to the physical situation for organic ion exchangers, which can be considered homogeneous polyelectrolytes; however, for inorganic ion-exchange materials, the physical representations underlying the original model are far from fully fulfilled. Mass transfer within a granule of inorganic ion-exchange materials can occur through the solid phase's pore space and homogeneous areas. In working conditions, the pore space of the sorbent is filled with a solution. Given that the diffusion coefficients in solutions are much higher than in the solid phase, it seems logical to assume that the transfer of ions over relatively long distances (within the granule) is carried out through the solution. However, in the end, sorbed ions are placed in homogeneous areas of the solid phase. The mass transfer equation takes the form (30) in this case. To solve equation (30), as in the case of equation (11), it is necessary to determine the initial and boundary conditions; however, in this case, they will concern not the capacity of the sorbent but the concentration of the sorbate in the pore space:

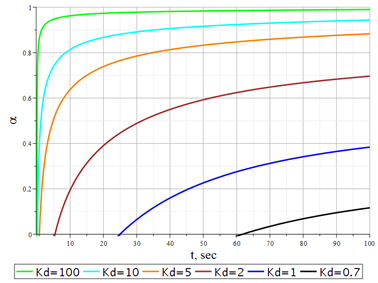
Figure 8 Dependence of the degree of conversion for mixed-diffusion kinetics in equation (26) on t for various values of the exchange constant (Kd).

$\frac{\partial C}{\partial t}=D.\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}+\frac{{\partial }^{2}C}{\partial z^2}\right)+F(x,y,z,t)$   (30)

Where: C - concentration of the collected ion in the pore space of the granule; D - diffusion coefficient; F(x,y,z,t) - the intensity of ion transfer from the pore space to the solid phase.

Let us consider one case of solving Eq. (30), namely, a solution based on the assumption that the rate of ion transfer from the pore space of the granule to homogeneous areas of the solid phase is much faster than the process as a whole. With a known concentration of ions at a certain point in the pore space, the capacity of the homogeneous section of the solid phase conjugated with this point can be determined through the isotherm equation (31):

$F(x,y,z)=G\left[C(x,y,z)\right]$   (31)

Where: C - concentration of the collected ion in the pore space of the granule; E - capacity of a homogeneous section of the solid phase of the sorbent at a point with coordinates inside the granule x, y, z. Suppose the distribution of a substance between two liquid phases is a purely physical process and is not accompanied by other physical or chemical processes. In that case, it obeys the Nernst law: “at equilibrium, the ratio of the concentrations of a component contained in two liquid states is a constant value”.⁴⁰ A similar situation is typical for the equilibrium between the liquid and solid phases:

$\frac{E}{C}=K=const$   (32)

Where: C – the equilibrium concentration of an ion in the liquid phase; E – the equilibrium capacity of the solid phase of the sorbent. K – called the distribution coefficient or exchange constant. Equation (32) is correct, provided that the concentrations are small, and one can ignore the interactions of molecules and ions with each other. Therefore, for most real conditions in equation (32), the distribution coefficient becomes dependent on concentration, i.e., the isotherm becomes non-linear. Strictly speaking, the exchange constant K depends on temperature, the exchanging ions, on the concentration of counterions; it can change with a change in the concentration of the gathering ions themselves, and it can also change with a difference in the degree of filling of the sorbent with sorbent ions and is determined by the properties of the sorbent itself. During sorption from complex solutions, the exchange constant can also be affected by other ions in the solution, both due to the buffering of the solution, the formation of complex ions, and changes in the structure of water in the solution because of salting in and salting out. The main types of isotherms are shown in Figure 9. The behavior of the concentration curve in the sorbent in dynamics depends on the type of isotherms. Studies in the field of kinetics have shown a predominantly diffusion character with the influence of the hydrodynamics of the porous layer of the sorbent. Four stages were identified that limit mass transfer: external diffusion is the flow of a substance to the surface of a sorbent granule; internal diffusion is a flow of a substance inside the pore space of a grain; diffusion of ions through a double electric layer near the surface of a crystallite in the sorbent phase; crystal chemistry positions. The last three types of diffusion processors are often considered integrally as one interdiffusion process.

Figure 9 The main types of ion exchange isotherms depend on the value of the exchange constant by the Langmuir equation for exchanging equally charged ions (equation (36)). Capacity (E) and concentration (C) are relative values. The numerical values correspond to the exchange constant (K) value.

The flow rate in equation (30) is the rate of change in the capacity of a homogeneous section of the solid phase (33).

$F(x,y,z,t)=\frac{\partial E}{\partial t}$   (33)

Since the isotherm equation relates the values of capacitance and concentration, the change in capacitance can be expressed in terms of the change in concentration (34).

$\frac{\partial E}{\partial t}=\frac{dG\left(C\right)}{dC}.\frac{\partial C}{\partial t}$   (34)

Expression (34) allows us to write equation (30) in the following form (35)

$\left(1+\frac{dE}{dC}\right).\frac{\partial C}{\partial t}=D.\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}+\frac{{\partial }^{2}C}{\partial z^2}\right)$   (35)

For the convenience of understanding and simplification of mathematical transformations, (36) can be used as an isotherm (the Langmuir equation for the exchange of equally charged ions):

$E=\frac{E_0.K.C}{1+(K-1).C}$   (36)

Where: E₀ - maximum exchange capacity; K - exchange constant; C - concentration of sorbed ions.

In this case, equation (35) is transformed into (37):

$\left(1+\frac{E_0.K}{{(1+(K-1).C)}^2}\right).\frac{\partial C}{\partial t}=D.\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}+\frac{{\partial }^{2}C}{\partial z^2}\right)$   (37)

In particular, at K=1 (linear exchange isotherm), equation (37) is reduced to the form (38), that is, to an equation with a constant diffusion coefficient:

$\frac{\partial C}{\partial t}=\frac{D}{1+E_0}.\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}+\frac{{\partial }^{2}C}{\partial z^2}\right)$   (38)

The solutions of equations (38) and (11) are identical; however, in the case of equation (38), the value of the Fourier criterion is determined by expression (39)

$Fo=\frac{D.t}{\left(1+\frac{E_o}{C_o}\right).{\text{ r}}^{\text{2}}}$   (39)

Where: E₀ - maximum exchange capacity; C₀ - total concentration of exchanging ions in the pore space.

Thus, the rate of mass transfer processes on porous ion-exchange granules is dependent not only on the geometric dimensions of the granule and the diffusion coefficient but also on the sorbent capacity's ratio to the exchangeable concentration ions in the pore space. We note one more solution to the problem of mixed diffusion on porous ion-exchange materials, related to the case of an L-shaped isotherm defined by expression (40):

$\{\begin{array}{l}E=E_o\text{, C > 0}\\ E=0,\text{ C = 0}\end{array}$   (40)

Where: E - exchange capacity; E₀ - maximum exchange capacity; C - concentration of sorbed ions.

In this case, the sorbent granule is divided into two zones - the outer one, where the sorbent is completely saturated with the absorbed ion, and the inner one, completely free from these ions. In this case, the rate of the process is determined by the diffusion of sorbed ions through the growing layer of the reaction product. According to,⁸ for spherical particles, the solution to this problem has the form (41):

$t=\frac{\alpha }{\beta }+\frac{E_o}{C_o}\cdot \frac{3-3{(1-\alpha )}^{\frac{2}{3}}-2\alpha }{D.K}$   (41)

Where: t - the time required to reach the degree of conversion equal to α; β - external mass transfer coefficient; E₀ - ion exchanger capacity; C₀ - concentration of sorbed ions in the free volume of the solution; D - diffusion coefficient; K - coefficient of distribution of sorbed ions between the pore space and the free volume of the solution.

Note that for the problem of internal diffusion with an L-shaped isotherm, there is an explicit solution that determines the dependence of the degree of transformation on the Fourier criterion (42):⁹

$\alpha =\{\begin{array}{l}1-\left(0.5+\sin \left(\frac{\arcsin \left(1-12. Fo\right)}{3}\right)\right){,}^3 Fo<\frac{1}{6}\\ , Fo\ge \frac{1}{6} \end{array}$   (42)

As follows from expression (42), in the case of an L-shaped isotherm, the process of internal diffusion is completed in a finite period. Solutions to the problem of internal diffusion for Eq. (37) were numerically obtained for various values of the exchange constants. These solutions, as dependences of the degree of transformation on the Fourier criterion calculated by the formula (39), are shown in Figure 10. As the calculation results showed, at the value of the exchange constant equal to unity, the obtained dependence of the degree of conversion on the Fourier criterion coincided with the support determined by the formula (26). With an increase in the values of the exchange constants, it asymptotically approached the dependence determined by the formula (42). Thus, there was a significant slowdown in the exchange process for exchange constants less than unity. These differences in the rate of techniques for the convex and concave isotherms are explained by the different speeds of the concentration fronts and the degree of conversion inside the granule, as seen in Figure 11. From the data analysis presented in Figure 11, with convex sorption isotherms, the front of the conversion degree (E/E₀) lags the concentration front (C/C₀). With concave ones, on the contrary, it is ahead of it. This effect is due to the higher rate of transition of sorbate ions from the liquid phase to the solid phase at convex isotherms, that is, at K_ij=10. On the contrary, with concave isotherms at K_ij=0.1, the transition of sorbed ions into the solid phase from the liquid slows down due to the shift of the corresponding equilibrium.

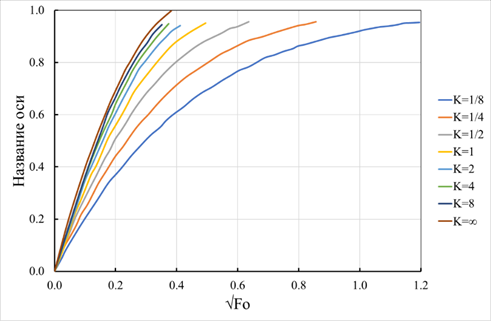
Figure 10 Kinetic curves at various exchange constants, as solutions of equation (26) in the form of dependences of the degree of conversion (α) on the root of the Fourier square criterion (Fo), calculated by the formula (39).

Figure 11 Fronts of the degree of conversion and concentration at 50% capacity development.

Kinetic model of the ion exchange process with the transfer of matter through the surface film of the liquid phase

Pure film kinetics should be considered in a slightly different way. In the case of pure gel kinetics, the selectivity of the ion exchanger does not play a role since only the B ion is constantly supplied to the phase boundary. In film kinetics, this does not happen even if the solution does not contain A ions; these ions will appear at the ion exchanger/film interface. They leave the ion exchanger and diffuse very slowly through the film. In addition, the presence of coions in the film cannot be neglected. Only two solutions exist for the ideal limiting cases for pure film kinetics. One of them allows the presence of ions with different mobilities, but it is assumed that the ion exchanger does not have selectivity and that the ions have the same charge. In another case, selectivity is considered, but the ions are considered to have the same mobility. Interdiffusion in a film is considered a quasi-stationary process in a flat layer. For the case of ions with different mobilities, it is necessary to solve the Nernst–Planck equations (4) for counterions of both types A and B and coions of type Y. Additional conditions in the film can be expressed as follows (for ions with the same charge):

$C_A+C_B=C_Y$   Electrical neutrality (43)

$\overrightarrow{{\Phi }_A}+\overrightarrow{{\Phi }_B}=\overrightarrow{{\Phi }_Y}=0$   No electric current (44)

The condition $\overrightarrow{{\Phi }_Y}=0$  follows from the assumption of the existence of a quasi-stationary state. In contrast to gel kinetics, the film's total concentration is not constant with film kinetics. The electric field acts on the coions in the film (the concentration of coions is equal to the total concentration), increasing or decreasing the number of coions until a quasi-stationary state is reached, in which the “force” of the electric field acting on the coions is balanced by the resulting concentration gradient. An analytical solution was found for ions with the same number of charges (z_A=z_B=-z_Y) with a boundary condition corresponding to the condition of a constantly renewing solution. In addition, it is limited to an ion exchanger that does not have selectivity $\left(T_B^A=1\right).$  For this case, the following condition is satisfied at the phase boundary:

${C^{\prime }}_A=\frac{{\overline{C}}_A{C}^{\prime }}{\overline{C}}$   (45)

The time dependence of the interdiffusion flux is also described here by equation (46).

$-\frac{d{C^{\prime }}_A}{dt}=\frac{3C}{r_{o}C}{\Phi }_A$   (46)

Where: F — total grain surface of the ion exchanger; $C{\text{'}}_A$ — ion concentration A at the ion exchanger/film interface. Equation (46) includes the equilibrium condition at the phase boundary $\overline{C}/C{\text{'}}_A=\overline{C}/C.$  As the initial conditions, we choose an ion exchanger completely saturated with A ions and a solution containing no A ions; the concentration of A ions in the ion exchanger is equal to ${\overline{C}}_A^0.$  In general, for film kinetics, the initial conditions are formulated as follows:

$r=r_o;t=0;{C^{\prime }}_A=\frac{{\overline{C}}^o{}_{A}C}{C}$

$r\ge r_o;t=0;C_A(r)=0$   (47)

For the case under consideration, an additional condition is introduced

$C{\text{'}}_A\left(t=0\right)=C\text{'}$

Since the value of $C\text{'}\left(t\right)$  is unknown from the beginning, the initial and boundary conditions at the phase boundary cannot be precisely specified. The joint solution of three equations (4) for particles of types A, B, and Y under the indicated conditions has the form:²

$U=\frac{D_B{y}^2\left(t\right)-D_A}{D_B+D_A}$

$\ln \left\{\frac{y\left(t\right)-1}{{\left(\frac{D_A}{D_B}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-1}\right\}+\frac{1}{2}\left(y^2\left(t\right)-\frac{D_A}{D_B}\right)+y\left(t\right)-{\left(\frac{D_A}{D_B}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-\frac{3D_{A}C}{r_0\delta \overline{C}}t$   (48)

U and t are related by a common dependence on the mathematical parameter y(t). The parameter y(t) is defined as follows:

$y\left(t\right)\equiv \frac{\left[D_A{C^{\prime }}_A\left(t\right)+D_B{C^{\prime }}_B(t)\right]}{D_{B}C}=\frac{C^{\prime }(t)}{C}$   (49)

Where $C\text{'},C{\text{'}}_A$ and $C{\text{'}}_B$  refer to the ion exchanger/film interface, and C denotes the total concentration in the solution.

If the ion exchanger is initially saturated not only with A ions but with a mixture of A and B ions, then the conversion fraction can be expressed as follows:

$U\left(t\right)=\frac{U\text{'}\left(t+t_0^{\text{'}}\right)-{\overline{\gamma }}_B^0}{1-{\overline{\gamma }}_B^0}$ (50)

Where $U\text{'}$  denotes the function (6.40) and ${\overline{\gamma }}_B^0$  — an equivalent fraction of ions B for time t=0, t₀ — the time required, according to equation (48), to saturate the ion exchanger (containing initially only A ions) with B ions to an equivalent fraction ${\overline{\gamma }}_B^0.$  When exchanging ions with the same mobility, an electric field does not arise. Therefore, instead of the Nernst–Planck equation (4), the first Fick law (3) can be used. The consideration of isotopic exchange differs from the latter only in that, due to the selectivity of the ion exchanger, the equilibrium condition at the phase boundary has the following form:

$\frac{C_B^{\text{'}}}{C_A^{\text{'}}}=\frac{{\overline{C}}_B^{\text{'}}}{{\overline{C}}_A}{T}_B^A$   (51)

In this case, the separation factor $T_B^A$  is assumed to be constant. In connection with this, equation (46) and the boundary condition at the phase boundary will be modified. For a solution of limited volume between U and t, the following relation is obtained:

$\left(1-aN\right)\ln \left(1-U\right)-\left(1-aN-ab\right)\ln \left(\frac{U}{1+\frac{b}{N}}\right)=-ct$   (51)

in which connection

$a\equiv 1-T_B^A;b\equiv {\left[{\left(\frac{1+\omega }{1+\frac{b}{N}}\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.};c\equiv \frac{3ab\overline{V}D}{r_0\delta V}; \omega \equiv \frac{\overline{C}\overline{V}}{CV};N\equiv \frac{{\overline{Q}}_B^{\infty }}{\overline{Q}}=\frac{1+\omega }{2a\omega }-\frac{b}{2}$   (52)

Where N – is the relative content of the ion B in the ion exchanger after equilibrium has been established. For a flowing solution or a solution whose volume satisfies the condition $\overline{C}\overline{V}\ll CV\left(\omega \ll 1\right)$ , connection (51) occurs, and the form (53) occurs.

$\ln \left(1-U\right)+\left(1-\frac{1}{T_B^A}\right)U=-\frac{3DC}{r_0\delta \overline{C}{T}_B^A}t$   (53)

Equation (53) is a limiting case in the theory developed by Adamson,⁵⁷ assuming ions of specific mobility and not considering the occurring field. Equation (51) is also a limiting case of the Dickel theory,⁵⁹ a development of the Adamson theory. The Dickel relation is restricted to the state $\overline{C}\overline{V}=CV.$  Equation (53) yields the given expression for the half-time exchange:

$t_{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=\left(0.167+0.067T_B^A\right)\frac{r_0\delta \overline{C}}{DC}$   (54)

Thus, the exchange is slower the more selective the ion exchanger about the ion A initially located in the ion exchanger compared to the ion B. This fact is obvious. As expected, Deviations are most important in exchanging two ions with different mobilities (for example, Li⁺/H⁺).

Comparison of sorption and desorption processes

Based on general considerations, it can be assumed that the rates of ion-exchange reactions depend on the mobility of the ions involved in them. Data on the mobility of the primary ions in aqueous solutions are presented in Table 1. As can be seen from the data presented, for example, in the series Li⁺, Na⁺, and K⁺, the actual radii of the ions increase, and the mobilities should decrease. However, the mobilities increase by almost a factor of two when going from Li⁺ to K⁺. This effect is because ions in the solution and the ionic lattice have different radii. In this case, the smaller the ion's crystal-chemical radius, the larger the effective radius in the electrolyte. The current situation is because the ions are not free but are hydrated in solution. Then the effective radius of an ion moving in an electric field will be determined mainly by the degree of its hydration, i.e., by the number of water molecules associated with the ion. In turn, at the interface between the surface of the sorbent and the solution, due to the presence of uncompensated charges on the surface of the crystalline phase of the sorbent, a specific electric field strength arises, which in turn is the driving force for the movement of the corresponding cations.

The bond of an ion with solvent molecules, particularly water molecules, is ion-dipole since the field strength on the surface of a lithium-ion is much greater than on the surface of a potassium ion. This effect is because the surface of the former is smaller than the surface of the latter, and the radius, i.e., the distance of the water dipoles from the practical point charge at the center of the ion, is smaller. Thus, the degree of hydration of the lithium-ion is greater than the degree of hydration of the potassium ion. Based on these considerations, multiply-charged ions should have greater mobility than singly-charged ones. As can be seen in Table 1, the movement rates of multiply charged ions differ little from the movement of singly charged ions, obviously due to the greater degree of their hydration due to the greater field strength created by the multiply charged ions. This table also shows the anomalously high mobility of hydronium and hydroxyl ions. Since the solution contains not hydrogen ions H⁺, but hydroxonium ions H₃O⁺, like all ions, they are hydrated, and their effective radii are in the same order as the radii of other ions. Consequently, if the mechanism of charge transfer by these ions were expected, then their mobility would not even differ significantly from the mobilities of other ions. The anomalously high mobility of H₃O⁺ and OH^־ manifests itself mainly in aqueous solutions, which is associated with the features of charge transfer by these ions. They differ from other ions because they are ions formed by the solvent - water. Thus, the charge is transferred mainly not by hydronium ions. However, they also participate in the charge transfer by protons jumping from one water molecule to another along the field lines at the interface between the sorbent and solution. It is also necessary to consider the need to rotate the newly formed water molecule, which has an orientation that does not allow it to accept, in turn, the hydronium ion's proton from the molecule's other side. Kohlrausch derived an empirical equation relating the equivalent electrical conductivity (λ) of strong electrolytes to concentration (c):

$\lambda ={\lambda }_{\infty }-A\sqrt{c}$   (55)

Where ${\lambda }_{\infty }=U_{\infty }+V_{\infty }$ ; A – constant.

Debye and Hueckel attributed the decrease in ion mobility and equivalent electrical conductivity for strong electrolytes with increasing concentration to the presence of an ionic atmosphere. Indeed, each ion is surrounded by an ionic atmosphere, consisting mainly of ions of the opposite sign to the central ion, the density of which increases with increasing electrolyte concentration. When an electric field is applied, the ion moves in one direction, and the ionic atmosphere in the opposite direction. The movement of ions of different charges, at the same time solvated, in opposite directions creates, as it were, additional friction, which reduces the absolute speed of ion movement. This braking effect is called the electrophoretic effect. As the concentration increases, the density of the ionic atmosphere rises; therefore, the inhibitory electrophoretic effect also increases. It should not be thought that during the random motion of an ion, its ionic atmosphere moves along with it. When moving, the ion leaves its ionic atmosphere and continuously creates a new one in the way of its movement. This process of destruction of the old and formation of new ionic atmosphere proceeds, although rapidly, but not instantaneously; because of this, when the ion moves, the symmetry of the ionic atmosphere is violated, and its density is more significant behind the moving ion. The appearance of an asymmetry in the ionic atmosphere also causes some deceleration of the translational motion of the ion, which is called the effect of asymmetry or relaxation. Thus, due to the presence of an ionic atmosphere, two decelerating effects arise during the movement of an ion: an electrophoretic effect, due to the action of the ionic atmosphere in the direction opposite to the direction of movement of the ion, and a relaxation effect, due to the asymmetry of the ionic atmosphere.

Similar effects are also observed when ions enter the crystal structure of an inorganic ion exchanger. However, no electrophoretic effect occurs in the ion exchanger's solid phase due to the ionic atmosphere's stability, which is the polyanionic framework of the crystal lattice of the ion exchanger. When an ion moves in the ion exchanger phase, only relaxation effects are observed when the ion jumps from one position to another. In this case, the driving force determining its movement is the osmotic pressure due to the difference in ion concentrations in different parts of the ion exchanger phase. The transfer of ions from the liquid phase to the solid phase of the ion exchanger is due to the so-called Wien effect. Therefore, the decrease in the mobility of ions with increasing concentration is explained by an ionic atmosphere. Then, the latter's destruction should lead to an increase in the mobility of ions to a limiting value. Since the speed of the ion movement is proportional to the voltage. The rate of formation of the ionic atmosphere is a finite value; then, with an increase in the electric field strength, it is possible to achieve such a high speed of movement of the ions, at which the ionic atmosphere will no longer have time to form. In this case, the ions, having left their ionic atmospheres, will move without them and, consequently, will have the maximum speed of movement and mobility. Considerable field strengths arise at the interface between the sorbent's solid phase and the solution's liquid phase in contact with it due to uncompensated charges on the surface of the crystalline phase sorbent. Thus, the ions shed their ionic atmosphere and pass into the solid phase of the sorbent. In this regard, the effect of the difference in the rates of the sorption and desorption processes should arise, especially for hydrated oxides of polyvalent metals, which act as inorganic ion exchangers and on which a reversible exchange reaction occurs between hydronium ions and ions of the exchanged metal in solution.

Based on equation (9) and equation (17), which describe the interdiffusion of ions A and B in the grain of an inorganic ion exchanger:

$\frac{\partial u\left(x,t\right)}{\partial t}=\frac{\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}}{1+au\left(x,t\right)}-{\frac{a\left(\frac{\partial u\left(x,t\right)}{\partial x}\right)}{{\left(1+au\left(x,t\right)\right)}^2}}^2$   (56)

$u\left(0,t\right)=1,u\left(x,0\right)=0$   (57)

${\left(\frac{\partial u\left(x,t\right)}{\partial x}\right)}_{x=1}=0$   (58)

$a=\frac{D_A}{D_R}-1$   (59)

$u\left(x,t\right)={\overline{C}}_A$   (60)

$x=\frac{r}{r_0}$   (61)

$t=\frac{D_A\tau }{r_0{}^2}=F_0$   (62)

The equation (56) solution for various diffusion coefficients D will have the form shown in Figure 12.

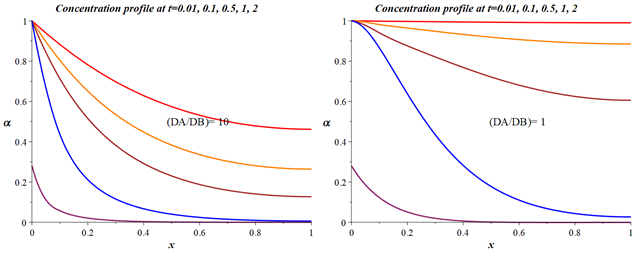
Figure 12 Dependence of the concentration profile of the degree of filling of the sorbent granule for cases of different diffusion coefficients calculated following the model (56). x - is the dimensionless coordinate of a point inside a spherical particle. t - is the dimensionless time according to equation (62).

The solution to equation (19) for fixed diffusion coefficients can also be represented in the 3D form in Figure 13.

Figure 13 Change in time of the concentration profile of the degree of filling of the sorbent granule by equation (56). l - is the dimensionless coordinate of a point inside a spherical particle.

$A-\frac{D_A}{D_B}=10.B-\frac{D_A}{D_B}=1$

From the presented data, a decrease in the ratio of the diffusion coefficients of the ions involved in the process of mutual diffusion leads to an increase in the saturation rate of the granule of the inorganic ion exchanger. As an example of direct and reverse ion exchange processes, consider the following process, which is of great practical importance:

${\overline{H}}^{+}+L{i}^{+}\to \overline{L}{l}^{+}+H^{+}$

$\overline{L}{l}^{+}+H^{+}\to {\overline{H}}^{+}L{i}^{+}$

and

A comparison of these processes is shown in Figure 14, which offers both curves for the same time parameter, expressed through the Fourier criterion Fo. Based on the data presented in Table 1, it can be assumed that the ratio of the diffusion coefficients of hydrogen and lithium ions will be approximately equal to the ratio of their limiting mobilities in water $U_{\infty }^H/U_{\infty }^{Li}\approx {\overline{D}}_H/{\overline{D}}_{Li}=9.06$ . Figure 14 shows that the exchange occurs faster if there are more mobile ions in the ion exchanger; the time of their half-exchange differs by about a factor of two, while the time required for the exchange by 90% varies by more than three times. Also, essential conclusions can be drawn when considering the radial concentration profiles in the grain, which are presented in Figure 12–14 for two extreme values of the mobility ratios and, accordingly, the diffusion coefficients $\left({\overline{D}}_A/{\overline{D}}_B=10 H {\overline{D}}_A/{\overline{D}}_B=1\right)$ .

Figure 14 Comparison of direct and reverse processes of exchange of ions with different mobility. The exchange rate of H⁺/Li⁺ and Li⁺/H⁺ was calculated using equation (23) for the case of pure gel kinetics and the mobility ratio $U_{\infty }^H/U_{\infty }^{Li}\approx {\overline{D}}_H/{\overline{D}}_{Li}=9.06$ . The exchange is faster if there is a speedier ion initially H⁺.²

And it follows from Figure 12–14 that if the A ions initially located in the ion exchanger move much faster than the B ions, then a rather sharp front moves to the center of the grain in the exchange process. In another case, the front is rapidly washed out, and the grain is relatively uniformly depleted of A ions. This phenomenon can also be easily explained by the fact that the diffusion coefficient of an ion in a lower concentration has a more substantial effect on the value of the interdiffusion coefficient. In the first case, the interdiffusion coefficient in the outer shells of the grain is significant and decreases towards the middle; therefore, the outer shell is rapidly depleted, while closer to the center of the grain, the exchange remains slow. In the second case, the interdiffusion coefficient in the outer shells of the granule is minimal and increases towards the middle of the sorbent particle; therefore, after the depletion of the outer layers, the process rapidly propagates toward the center of the grain. Let us again compare the exchange of ${\overline{H}}^{+}+L{i}^{+}\to \overline{L}{l}^{+}+H^{+}$  ions with the reverse process. Calculation by equation (56), like pure gel kinetics, leads to different exchange rates for both processes. However, with film kinetics, in contrast to gel kinetics, the exchange in the initial stage proceeds faster if the ion exchanger initially contains a slower ion. It seems it is easy to explain. During interdiffusion, an electric field arises in the film. Suppose initially. The ion exchanger contained only the more mobile H⁺ ion. In that case, the electric potential at the film/solution interface will be more positive than the potential at the ion exchanger/film interface. The electric field, therefore, causes the coions to move from the film into the solution until the electric force balances the concentration gradient of the coions. Since the ion exchanger cannot replace the departed coions, the film becomes depleted in electrolytes compared to the solution. The electric field has the opposite sign if the ion exchanger initially contains only Li⁺ ions. As a result, an excess of coions is created at the phase boundary, and the film becomes richer in electrolyte than the solution. The concentration gradients are, therefore, more significant in the second case than in the first. For the H⁺/Li⁺ exchange and the reverse process, the initial mutual diffusion fluxes differ by about a factor of three, while the half-exchange time differs by only about 3%.

Ion exchange steps

Ion exchange is a heterogeneous process associated with transferring ions from a liquid phase to a solid one. Therefore, ion exchange kinetics can be described regarding the mechanism of heterogeneous processes.^{1,2,14,20–22,39,40} For any heterogeneous process, two stages are characteristic: the transfer of a substance to the reaction zone and the actual chemical reaction. When describing the kinetics of heterogeneous processes, it is necessary to consider both stages simultaneously. In natural systems, each step is complex, and although it can often be represented in terms of simpler components, describing the kinetics of ion exchange is a rather difficult task. Thus, as a rule, the chemical stage of ion exchange consists sequentially of the desorption of one ion and the sorption of another. It is often complicated by the influence of coions and the solvent on the process, such as the pH value. The transfer of a substance from the solution to the ion exchanger phase can be represented as a sequence of the following stages:¹

1. Diffusion of ions from the depth of the solution to the granule.
2. Diffusion through a fixed film near the surface of the granule, the so-called. External diffusion.
3. Entry of ions into the pore space of the granule.
4. Internal diffusion - the transfer of ions in the pore space of the granule.
5. For biporous sorbents, the following stages are possible:^35,40
6. Adsorption of ions on the surface of crystalline blocks
7. Diffusion of ions deep into crystallites.

A chemical exchange reaction completes the transfer process, and the same stages, only in reverse order, are characteristic of desorbed ions. It should be noted that when describing the processes of ion transfer, it is necessary to consider the emerging electric potential due to the difference in the mobilities of the exchanged ions.^23,24 Introducing the electrodiffusion potential into the transport equations leads to their non-linearity concerning the value of the interdiffusion coefficient. The diffusion problem becomes even more complicated in the case of multicomponent exchange.²⁵ Considering that, in most cases, the equilibrium of ion exchange processes is also non-linear, their exact mathematical description encounters specific difficulties. Thus, attempts to construct a mathematical ion exchange model that considers all the features of the ion exchange process lead to a complex system of differential equations, often nonlinear, with many parameters that are sometimes difficult to determine experimentally. Therefore, the mathematical description of ion exchange processes is usually carried out, assuming some stages do not significantly affect the process's kinetics. The kinetics of organic gel sorbents has been relatively well studied.¹ The ion exchange processes on these materials are usually satisfactorily described within the framework of internal diffusion kinetics; the solution of inverse kinetic problems makes it possible to find the effective diffusion coefficient of ions in the ion exchanger gel matrix.²⁶ Nevertheless, even to describe these processes, approximate equations are often used, mainly those of Boyd-Adamson.² The kinetics of ion exchange on inorganic ion exchangers has been studied in less detail. In many ways, this situation is because the crystalline nature of inorganic ion exchangers²⁷ manifests itself in low rates of ion exchange processes.^22,28,29 Therefore, there is a need for a more detailed consideration of the stages of ion exchange on inorganic ion exchangers, their possible mathematical description, and methods for their study.

Experimental study of sorption kinetics under conditions of rapid equilibrium between pore solution and homogeneous regions of the solid phase

An experimental study of the sorption kinetics under conditions of rapid establishment of equilibrium between the pore solution and homogeneous areas of the solid phase was carried out on granular samples of various inorganic sorption materials. These sorbents seemed to be very convenient objects for studying those features of the kinetic characteristics of inorganic ion-exchange materials that were considered above. In particular, the effects associated with the influence of the type of isotherm on the rate of sorption processes, the rate's dependence on the sorbate's concentration, and the granules' size were studied. An experimental setup was created to conduct kinetic experiments, the schematic diagram of which is shown in Figure 15. The operation of the installation was carried out as follows. The test solution and the weighed portion of the sorbent were placed in a reaction vessel (1) equipped with a mechanical stirrer (2). Air purified from carbon dioxide was supplied above the solution layer to avoid the latter's influence on the pH of the solution. The same vessel contained an electrode system (3) consisting of a measuring electrode (glass or ion-selective), an auxiliary electrode (calomel), and a resistance thermometer. The signal from the ion-selective electrode, containing information about the pH (pX) and the temperature of the solution, was processed by a measuring transducer (pH meter) (4) and fed to the control computer (5). An experimental setup for studying the sorption kinetics was created based on TitroLine-7000 from SI Analytics, using a thermostated cell TZ 1759. The view of the experimental setup is shown in Figure 15 B and C. A computer operating under the control of a pre-created program, depending on the data coming from the pH meter, can send a signal to turn on the heater (7) to the temperature control unit (6) or a signal to turn on the automatic titration burette (8). Thus, it is possible to maintain quasi-constant conditions in the solution during the kinetic experiment. The accuracy of maintaining the temperature on this installation is ±0.2°C. The error in maintaining the pH depends on its value, and at pH>10 does not exceed ±0.1 of the pH unit. The data on the duration of titrations and their distribution over the time of the experiment makes it possible to judge the rate of the ion exchange process. Thus, kinetics studies were carried out under a constant concentration of ions (sorption from a solution of infinite volume).

Figure 15 Experimental setup for studying the kinetics of ion exchange. A - general installation scheme; C – TitroLine-7000 titrator from SI Analytics; C - temperature-controlled cell TZ 1759. 1 - reaction vessel; 2 - the mechanical stirrer; 3 - electrode system with temperature compensator; 4 - measuring transducer (pH meter); 5 - control computer; 6 - thermostat control unit; 7 – thermometric measuring element; 8 - automatic titration burette.

Influence of the type of isotherm on the rate of mass transfer processes

The influence of the type of isotherm on the rate of mass transfer processes was studied using the example of an inorganic ion exchanger FS-3,¹⁰ a composite material based on mixed zinc-potassium hexacyanoferrate and silica gel. The exchange rate was studied for the following pairs of K-H, Cs-K, and Li-H ions. A granulate fraction with sizes from 0.6 to 0.75 mm was used in all cases. The sorbtive concentration was 0.025 mol/dm³. The experiments were carried out on an automated setup that maintains a constant sorbate concentration in the reaction volume and fixes the reagent consumption over time. The results of these experiments are shown in Figure 16.  As can be seen from Figure 16, the exchange process in the Li-H system is much slower than in the Cs-K and K-H systems. In the case of Li-H, the value of the exchange constant was K=0.11, and in the cases of exchange in the Cs-K and K-H systems, the importance of the exchange constants exceeded the value K>10. Thus, the exchange constants are directly related to the kinetics of the ion exchange process. Considering the difference in exchange isotherms, processing experimental data led to relative values of the diffusion coefficients presented in Table 2.

Figure 16 Kinetics of ion exchange on the FS-3 sorbent.

Thus, the difference in the rates of the processes is explained not by the difference in the permeability of the granulates (the same sorbent was used in all experiments) but by the difference in the isotherms. The influence of the sorbent concentration on the rate of ion-exchange processes involving inorganic sorbents was also studied using the FS-3 sorbent as an example. Before experiments, the sorbent was converted into a hydrogen ion-exchange form by washing with a sulfuric acid solution with a concentration of 12 mol/dm³ under dynamic conditions until the filtrate was free of potassium ions. For experiments, a sorbent fraction with granule sizes from 0.6 to 0.75 mm was taken. Potassium chloride was used as a sorbate, and the concentration in various experiments varied from 0.00125 to 0.0125 mol/dm³. The kinetic curves were recorded on the automatic setup described at the beginning of this section. Since, in this case, the sorption isotherm had a strongly convex character, equation (63) was used to process the results.

$t=\frac{\alpha }{\beta }+\frac{E_0}{C_0}\cdot \frac{3-3{\left(1-\alpha \right)}^{\frac{2}{3}}-2\alpha }{D\cdot K}$   (63)

The result of this processing was the estimation of the mass transfer coefficient (15) and the product of the diffusion coefficient, and the coefficient of electrolyte distribution between the pore space of the granule and the free volume of the solution (K×D). The time of full completion of the sorption process was calculated from the value of the last parameter. Figure 17 shows the dependence of the time for the full completion of the internal diffusion process, calculated from estimates of the K×D values obtained by processing the kinetic curves of sorption of cesium ions on the composite ferrocyanide-silica gel sorbent FS-3. The experiments were carried out at various concentrations of the sorbate. As seen in Figure 17, as the concentration of the sorbate increases, the time for the full completion of the internal diffusion process decreases. A characteristic feature is that the process rate was much higher than follows from the general theoretical concepts.¹¹ These ideas assume that the transfer of ions inside the granule occurs through the volume of the pore space and lead to the following expression for the diffusion coefficient (64).

Figure 17 Effect of sorbent concentration on the completion time of the internal diffusion process. Dots are experimental data. The red curve is the calculated dependence according to formulas (32) and (33).

$D=\frac{D_e}{1+\frac{K_d}{1-\epsilon }}$   (64)

Where: D - diffusion coefficient in the ion exchanger; D_e - diffusion coefficient in water; K_d - coefficient of distribution of the sorbed ion between the ion exchanger and the solution; ε - sorbent layer porosity. Note that this approach to determining the diffusion coefficient is based on the hypothesis that the properties of the solution in the free volume and the pore space of the granule are identical. In addition, the above data indicate that the ions adsorbed on the pore surface determine the rate of mass transfer processes on inorganic ion exchange materials.

The dependence of the process completion time on the concentration of the sorbate, calculated by the formula (64) for the value De=10^-9 m²/sec, which seems to be a somewhat overestimated estimate for the diffusion coefficient of monovalent ions in an aqueous solution and ε=0.5, is shown in Figure 17 together with the experimental data. As can be seen, these dependencies differ in order of magnitude. Based on this, the hypothesis about the identity of the properties of the solution in the free volume and the pore space of the granule cannot be considered correct. The higher rates of mass transfer processes can be explained based on the assumption that the sorbed ions concentration in the sorbent's pore space exceeds the concentration of these ions in the free volume of the solution due to adsorption in the double electric layer. If we proceed from the fact that the concentration of the electrolyte in the pore space occurs due to adsorption on the surface of the pores and the isotherm of this adsorption has the character of the Langmuir isotherm, then the dependence of the distribution coefficient on concentration can be represented by the expression (65)

$K\left(C\right)\cdot D=\frac{K_0\cdot D}{b+C}$   (65)

Where: K₀ - partition coefficient at infinite dilution; C - electrolyte concentration; b - isotherm parameter having the dimension of concentration. Experimental estimates of the parameter K×D on the concentration of the sorbate and their approximation by expression (65) are shown in Figure 18. As can be seen from the data presented in Figure 18, the K×D product decreases with increasing sorbate concentration. We attribute this decrease to a change in the electrolyte distribution coefficient between the pore space and the free volume of the solution. The curve in Figure 18 corresponds to just such a relationship. It should be emphasized that only the product of the electrolyte distribution coefficient and the diffusion coefficient can be determined from the kinetic experiment. At the same time, there is no reason to believe that the diffusion coefficient in the pore space of the granule is equal to this value in the free volume of the solution. Thus, for a separate assessment of the diffusion and electrolyte distribution coefficients, some independent method must determine one of these values. The fact that diffusion in the pore space of the granule proceeds somewhat differently than in the free volume of the solution is also evidenced by the temperature dependence of K×D. As the results of experiments have shown, the temperature dependence of the K×D value for the same pair of exchanging ions is different for different sorbents. As an example. Figure 10 shows the activation energies for the exchange of cesium ions for potassium and some other parameters characterizing the properties of the FS-3 and FS-10 sorbents.^10,12 Note that the activation energy values turned out to be close in order of magnitude to the equivalent values for the activation energy of diffusion of ions in ion-exchange resins. As can be seen in Table 3, there is a significant difference between the studied samples' activation energy values and pre-exponential factors. An exciting feature of the obtained results is that the value of the pre-exponential factor correlates well with the value of the specific surface area of pure ferrocyanide phases. Thus, the results presented in Table 3 suggest that the surface of the active phase of the composition plays an essential role in the transport of ions within the granule. At the same time, the size of the surface is not a factor that ultimately determines the rate of the mass transfer process. This rate is also affected by the mobility of ions adsorbed on the pore surface.

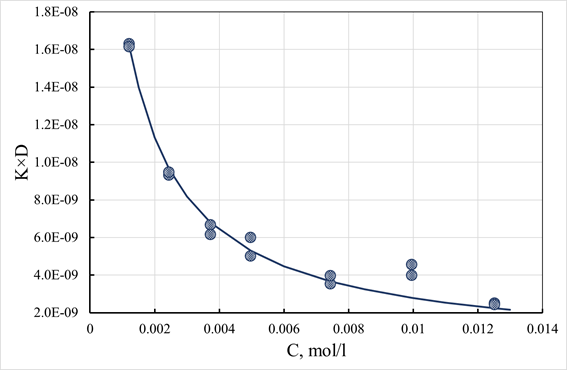
Figure 18 Dependence of K×D parameter estimates on sorptive concentration.
K₀×D= 2.95∙10^-8, b=0.611.

Inhibition effects at the level of homogeneous sections of the solid phase

The problems considered earlier concern diffusion inhibition of the sorption process at the granule level. When the mass transfer process is retarded at the level of a homogeneous particle of the solid phase, as already noted, the usual size is the size of this region. The other characteristics of the pore space should not play any role in limiting the sorption rate. A change in the size of homogeneous sections of the solid phase almost always accompanies one very common process for synthesizing selective inorganic sorbents, namely, thermochemical modification. Considering the great practical significance of this process, let us consider the influence of the effects of growth in the size of homogeneous regions of the solid phase on the kinetic characteristics of sorbents.

In the processes of thermochemical modification, the growth of the linear dimensions of homogeneous sections of the solid phase is due to the heating of the modified materials to temperatures close to the crystallization temperature. In this case, the purpose of such processing is not the actual crystallization of the material but the ordering of its structure. Moreover, even this ordering is partial since samples synthesized in this way always retain a certain proportion of nonselective ionogenic centers. Let us consider the influence of the growth of the linear dimensions of homogeneous sections of the solid phase on the example of a model system - cadmium sulfide. We chose this compound to ensure the chemical homogeneity of the material. To obtain samples of cadmium sulfide with different linear sizes of homogeneous areas of the solid phase, they were calcined at different temperatures, using specific measures to prevent their oxidation. The sample's crystallization degree was estimated from the size of the region of coherent X-ray scattering. This site, in turn, was determined by analyzing the line profile in the diffraction pattern. The samples were used to study the kinetics of copper sorption from a CuSO4 solution. The results of the experiments are shown in Figure 19.

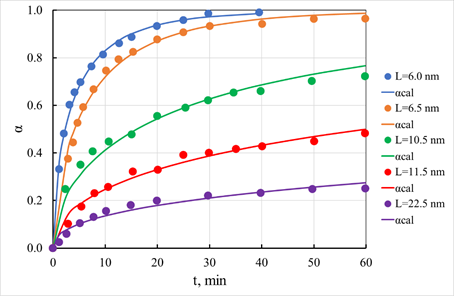
Figure 19 Sorption kinetics of copper ions on cadmium sulfide. Points - experimental data, curves - calculated.

The icons in Figure 19 correspond to the experimental points, the solid lines correspond to the calculated values of the degrees of conversion, and the numbers near the solid lines correspond to the sizes of crystalline blocks in angstroms. The experimental data were processed using equation (42). It was assumed that the granule material could be conditionally divided into crystallized and non-crystallized. The calculations proceeded because only the non-crystallized part of the granule material participates in the sorption process. Thus, because of processing the kinetic curves, we obtained estimates of the proportion of the non-crystallized part of the sample and the diffusion coefficient, the value of which was used to determine the time for the full completion of the process. The dependence of these parameters on the size of crystalline blocks is shown in Figure 20. It can be seen from these data that as the size of crystalline blocks increases, the value of the estimate of the fraction of non-crystallized material decreases, and the time required for the complete completion of the process associated with sorption on this part of the granule material increases. The latter effect is associated, in our opinion, with a reduction in the specific surface of the pore space, which occurs as the granule structure is compacted. It should be noted that the absorption of copper ions continues even after saturation of the non-crystallized part of the samples. Thus, after the contact of these samples with a solution of copper sulfate for a day, the total capacity exceeded the values obtained from assessing the fraction of non-crystallized material. The value of this additional capacitance, related to the fraction of crystallized material, is shown in Figure 20. As expected, this value decreases sharply with the increasing size of the crystalline blocks.

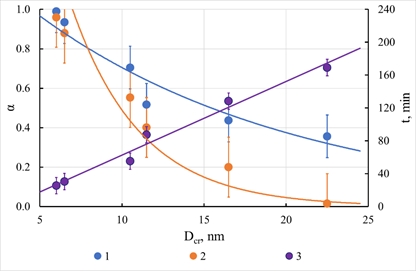
Figure 20 Estimates of the proportion of the sample's non-crystallized part, the diffusion coefficient, and the time to complete the process. Results of a kinetic experiment obtained on cadmium sulfide. 1 - The proportion of non-crystallized material. 2 - The proportion of crystallized material. 3 - Time of full completion of the process.

Effect of granule size

To study the effect of the size of sorbent granules on the stage of ion diffusion in the pore space, we investigated the dependence of the sorption rate on the granule size. The experiments were carried out with cationic fractions obtained by sieving. The experimentally obtained curves for the case of sorption of lithium ions Li⁺ from a solution with a lithium concentration of 0.001 M at pH 9.5 and 25 °C are shown in Figure 21 (indicated by dots). As seen in Figure 21, the ion exchange process rate increases significantly with a decrease in the granules' size. Under these conditions, the influence of the polyfunctionality of the cation exchanger does not significantly affect the kinetics of ion exchange. The exchange isotherm may be represented in the form corresponding to the Langmuir isotherm. Previous studies have shown that the exchange constant in the Langmuir isotherm equation for these conditions is 4.07, i.e., the isotherm has a convex form. The process was a controlled stage of internal diffusion. The sorbent granules were assumed to be spherical. Like the model used to describe the kinetics of ion exchange on nickel hydroxide, the difference in the self-diffusion coefficients of ions was considered. Therefore, the kinetics of the exchange of lithium ions on a cation exchanger with a lithium-manganese spinel structure, as well as of halide ions on granular nickel hydroxide, is described by equation (23) with initial and boundary conditions of the form (12)-(14). Since the obtained granulate fractions were characterized by a significant width (Δ≈0.47 for a fraction of 0.088–0.25 mm), the polydispersity of the material within the fractions was considered when processing the experimental data. The distribution within the fractions was assumed to be uniform, except for the fraction smaller than 0.088 mm, where a uniformly decreasing distribution was used. Such an assumption was made reasonably based on the relative weights of the obtained fractions. Approximation of experimental data (shown in Figure 21 by solid lines) confirms that the process is controlled by internal diffusion under these conditions. The effective diffusion coefficients obtained for each fraction are close to each other and lie within the experimental error. Studies of the sorption kinetics of sodium and potassium cations depending on the size of the granules also confirmed the mechanism of the ion exchange process corresponding to internal diffusion. Therefore, under these conditions, the stage of ion sink into the solid phase does not manifest itself kinetically.

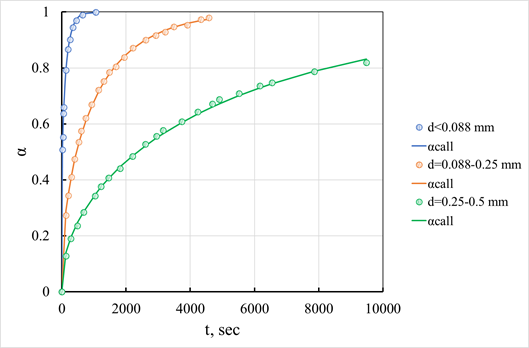
Figure 21 Kinetic curves of lithium sorption by cation exchanger depend on the granules' size. Points are experimental data, and curves are calculated. Granule size: 1 – less than 0.088 mm; 2 - 0.088-0.25 mm; 3 - 0.25-0.5 mm

The influence of the shape of the granules

Granulates of inorganic sorbents often have a shape different from that of simple bodies (spheres, cylinders, disks, etc.), for which the analytical solutions of the equations discussed in the previous section were obtained. Approximation of kinetic curves for such granules is possible using solutions obtained for particles of any simple shape. The most natural choice, in this case, seems to be spherical particles since their geometric dimensions are characterized by only one parameter - the radius. However, this raises the question of how suitable these solutions are to them and how the equivalent size should be determined to minimize the systematic errors that arise when determining the diffusion coefficient. According to,¹³ the equivalent diameter of a particle can be defined as the diameter of a sphere having the same volume as the given particle or as the diameter of a sphere having the same surface area. In the first case, the equivalent diameter is expressed by formula (66), and in the second - (67). Another definition of the equivalent diameter is also possible as the diameter of a sphere, the specific surface of which is equal to the particular surface of the particle (68).

$d_v=\sqrt[3]{\frac{6V_g}{\pi }}$   (66)

$d_s\sqrt{\frac{S_g}{\pi }}$   (67)

$d_{sv}=\frac{6V_g}{S_g}$   (68)

Where: Vg and Sg - volume and surface of the granule, respectively.

We used the shape factor value (69), which determines the degree of deviation of the particle shape from spherical. The shape factor was determined through the ratio of effective diameters by the methodology described in:¹³

$\Phi =\frac{d_v^2}{d_s^2}$   (69)

In the approximation of the kinetic curve obtained for a non-spherical particle by the equation of the calculated curve calculated for a spherical particle, the value of the effective radius should be substituted into the latter. On the other hand, having an analytical solution of the diffusion equation for some non-spherical particles can be approximated by a solution for a spherical particle with an appropriate selection of the radius of this particle. Let us consider the results of such approximations by comparing the solutions of the internal diffusion equation for a cylinder with permeable bases and a sphere. The equation for the kinetics of internal diffusion for a cylinder with permeable bases is given by equation (70):¹⁴

$\alpha =1-8{\displaystyle \sum _{m=1}^{\infty }\frac{1}{{\mu }^2}} {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\sigma }_n^2}ex}p\left(-\left(x^2\cdot \mu +{\sigma }^2\right)\cdot F{o}_{cil}\right)$   (70)

Where: $\mu =\frac{\pi \left(2m-1\right)}{2}$  – number expansion parameter; ${\sigma }_n$ - positive roots of the first-order Bessel function; $Fo=\frac{D\cdot t}{r^2}$  - Fourier criteria; α - conversion degree; D - diffusion coefficient; T - time; m, п - summation indices; χ- the ratio of the height of a cylinder to its diameter; R - cylinder radius.

As a parameter that determines the shape of the cylinder, we used relation (71), which varied from 0.05 to 0.95 with a step of 0.05.

$\gamma =\frac{D}{D+H}$   (71)

Where: D, H - diameter and height of the cylinder, respectively.

For these parameters, the values of the Fourier criteria were calculated, which provide conversion values from 0.05 to 0.95 with a step of 0.05. The grid of values of the Fourier criteria obtained in this way was used to calculate the degrees of conversion according to formula (72), and the proportionality coefficient was chosen in such a way as to ensure the best match between the degrees of modification calculated by equations (70) and (72).

${\alpha }_{sph}=1-\frac{6}{{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}exp\left(-{\pi }^2\cdot n^2\cdot \gamma \cdot F{o}_{cil}\right)}$   (72)

Where: ${\alpha }_{sph}$ - degree of transformation for sphere; $F{o}_{cil}$ - Fourier criterion for a cylinder; γ – shape factor (71).

It should be noted that the range of change in the value of the particle shape coefficient obtained in this case covers these values, characteristic of many granular materials (Table 4). The dependence of the root-mean-square deviation of the curves calculated by equations (70) and (72) on the value of the parameter $\frac{D}{D+H}$ is shown in Figure 22. As seen from Figure 22, for parameter values α less than 0.8, the root-mean-square error of approximating the kinetic curve for a cylinder by the equation for a sphere does not exceed 1% of the maximum degree of conversion. The most significant errors are observed for flat discs (large D/H ratios). At the same time, the approximation error is minimal for elongated cylinders and even fibers, and in many cases of practical analysis of kinetic results, it can be neglected. This situation is especially actual for granules of irregular shape or having a shape close to ellipsoidal. The value of the coefficient of proportionality in equation (41) determines the ratio between the radius of the cylinder, for which the initial kinetic curve was calculated, and the sphere's radius corresponding to the approximating curve. In this case, we can speak of an effective radius determined from the kinetic curve. The ratio between this radius and the radius of the corresponding cylinder is determined by expression (73).

Figure 22 The efficiency of approximation of the kinetic dependence through the shape factor.

$R_k=R_c\sqrt{\gamma }$   (73)

Where: R_k - effective radius determined from the kinetic curve; R_c - cylinder radius; γ - coefficient in the equation (71).

At the same time, the values of the effective radius for the cylinder can also be calculated using formulas (66) - (68). The ratios of the radii determined by equations (66) - (68) and calculated by expression (73) depending on the value of the parameter α are shown in Figure 23.

Figure 23 Radius ratios and shape factors depend on the parameter α.

As can be seen from this figure, from the point of view of the interpretation of the kinetic experiment, equation (37) gives an adequate estimate of the effective radius of the granule. It can be recommended for universal evaluation of the results of kinetic experiments on natural objects. Overall, the data obtained indicate that the solutions to the diffusion problem obtained for spherical particles can be a reasonably effective approximation for non-spherical granules, at least in those cases where the unevenness of the particles is not too large.

Influence of polydispersity effects

Almost all methods of manufacturing granular ion-exchange materials lead to the production of granulates of a polydisperse composition with a greater or lesser degree of heterogeneity. In this section, we consider how the polydispersity of the granulometric composition of granules affects their kinetic characteristics. We used the Gamma distribution (74) as a model distribution:

$\phi \left(d\right)=\{\begin{array}{l} 0, d<0\\ d^{\alpha -1}\frac{-\frac{d}{\beta }}{{\beta }^{\alpha }\Gamma \left(\alpha \right)\text{'}} d\ge 0\end{array}$ (74)

Where: d – sorbent particle size, gamma distribution argument (d>0); α, β - distribution parameters (α>0, β>0); Г(α) - full Euler gamma function.

The distribution width was defined as the ratio of the distribution variance to the square of its mean value. The values of the parameters α and β, corresponding to different distribution width values, and the same average values of these distributions, equal to one, are presented in Table 5. Differential density curves for these model distributions are shown in Figure 24.

Figure 24 Model Gamma distributions according to Table 12.

The degree of conversion for polydisperse samples was calculated by the formula (75):

${\alpha }_{pd}\left(T\right)=\frac{{\displaystyle {\int }_0^{\infty }p\left(R\right)\cdot \alpha \left(R,T\right)dR}}{{\displaystyle {\int }_0^{\infty }p\left(R\right)dR}}$   (75)

Where: α_pd(T) - degree of conversion for a polydisperse sample; α(R,T) - degree of transformation for a sphere of radius R, p(R) - distribution density.

The calculation results are shown in Figure 25. As can be seen from this figure, with an increase in the distribution width for polydisperse systems with the same value of the average particle radius, the rate of the initial stage of the process increases, and the final stage decreases.

Figure 25 Influence of distribution width (D) on sorption kinetics for polydisperse materials.

The initial segments of the kinetic curves, just as in the case of spherical particles (Figure 5 and 6), are more or less linear in the coordinates $\alpha =a_1\sqrt{t}$ , which is a characteristic feature of internal diffusion processes. As shown by our calculations, the slope  of this dependence at α→0 turned out to be proportional to the value determined by relation (76):

$\frac{1}{R_{av}}=\frac{{\displaystyle {\int }_0^{\infty }\frac{1}{R}\cdot p\left(R\right)dR}}{{\displaystyle {\int }_0^{\infty }p\left(R\right)dR}}$   (76)

The correlation between the slope of the experimental dependence of α on $\sqrt{t}$  and the value from relation (76) is shown in Figure 26. The data obtained show that at kinetics corresponding to the mechanism of internal diffusion, the shape of the kinetic curve obtained for a set of particles with a wide size distribution differs significantly from the kinetic curves for monodisperse fractions. Using the kinetic equation for a monodisperse sorbent with a particle size averaged by formula (76) can be effective only for the initial section of the kinetic curve shown in Figure 27.

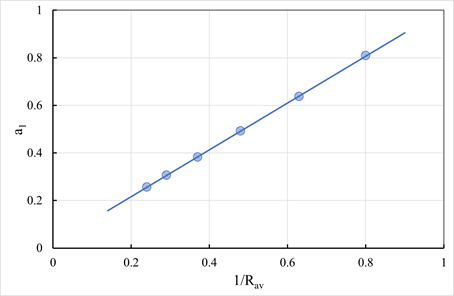
Figure 26 The ratio of the initial slope of the kinetic curve a1 to $\frac{1}{R_{av}}$ for polydisperse and monodisperse sorbent.

Figure 27 Kinetic curves for different particle size distribution widths.

Let us consider one more aspect related to the polydispersity of samples of sorption materials and the methodological problems of determining their kinetic characteristics. The granule size is necessary to calculate the diffusion coefficient from experimental data. Since granulometric fractions of finite width are always used for the kinetic experiment, estimating the average size is very important. Indeed, if determining the average size leads to a biased estimate, then the analysis results will be distorted due to a systematic error. The results show that granulates with a narrow granulometric composition are the most preferable in terms of ensuring the completeness of the sorbent loading. The simplest way to isolate narrow fractions of granular material is sieving. However, even in this case, one must deal with a polydisperse sample, the dimensions of which are distributed within the sizes of the cells of fine and coarse sieves between which the selection was made. Even in the simplest case of a unimodal granule size distribution in a narrow fraction, the fraction of particles of the minimum size can be less than the fraction of particles of the maximum size and vice versa, depending on the position of the fraction relative to the distribution mode shown in Figure 28.

Figure 28 Granule size distribution.

The arithmetic mean of the sieve mesh sizes can be used to determine the average granule size. However, such a solution leads to specific errors, the magnitude of which we will try to estimate in this section. The kinetic curve obtained in the experiment can be considered the result of averaging the kinetic curves for granules of a specific size, feeling the weight of their fractions (77).

$a\left(t\right)=\frac{{\displaystyle {\int }_{r_{min}}^{r_{ma[}}a\left(r,t\right)\cdot P\left(r\right)dr}}{{\displaystyle {\int }_{r_{min}}^{r_{max}}P\left(r\right)dr}}$ (77)

Where: α(t)- experimental kinetic curve; α(r,t) - kinetic curve for particle size r; P(r) - a mass fraction of particles of size r in the investigated fraction; $r_{min},r_{max}$ - minimum and maximum fraction sizes, respectively. This integral curve can be more or less accurately approximated by a curve for a monodisperse sample with some effective size $\alpha \left(r_{eff}\text{'}t\right)$ . An estimate of the effective radius can be obtained in various ways. For example, as such an estimate, you can use the average value of the minimum and maximum granule size $R_{mun,max}$  (78). Another estimate corresponds to the averaging of the specific surface of the granulate, which can be obtained using the formula (79).

$R_{mun,max}=\frac{R_{min}+R_{max}}{2}$   (78)

$\frac{1}{R_{ssav}}=\frac{{\displaystyle {\int }_{R_{min}}^{R_{max}}\frac{P\left(r\right)}{r}}dr}{{\displaystyle {\int }_{R_{min}}^{R_{max}}P}\left(r\right)dr}$   (79)

Where: R_min and R_max - minimum and maximum sieve size, respectively; P(r) - distribution function.

To resolve the issue of the most efficient methods for estimating the effective radius, consider the results of model calculations. The size distribution of granules in the narrow sieve fraction of the granulate was characterized by the relative width of this fraction $\left(\Delta R_{rel}\right)$  determined by expression (80) and the asymmetry (Asym) of the distribution defined by expression (81).

$\Delta R_{rel}=\frac{R_{max}-R_{min}}{R_{min}+R_{max}}$ (80)

$Asym=\frac{P\left(R_{max}\right)-P\left(R_{min}\right)}{P\left(R_{max}\right)+P\left(R_{min}\right)}$ (81)

Where: R_min and R_max - maximum and minimum sieve size; P(r) - particle size distribution function.

The P(r) dependence in the range from r_min to r_max was considered linear. It is easy to see that the relative width of the distribution can vary from 0 to 1, with smaller values corresponding to more homogeneous fractions. The asymmetry value can range from -1 to 1, and the equality of the mass fractions of fractions corresponding to the minimum and maximum sizes is achieved when the value of the asymmetry factor is 0. The image of such distributions is shown in Figure 29.

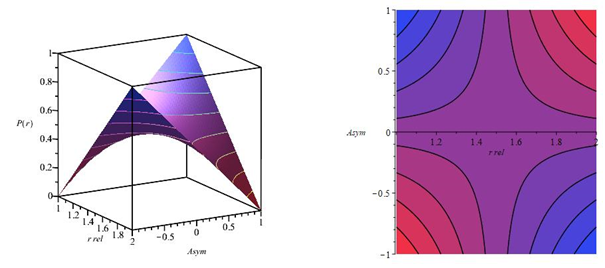
Figure 29 Mass distribution depends on the skewness factor. a - 3D plot of particle size distribution function P(r). b – contour plot of particle size distribution function P(r). rrel - relative particle radius: R_min=1.0; R_max=2.0. Asym - distribution asymmetry, according to expression (81).

The use of a polydisperse sorbent fraction in a kinetic experiment can lead to two consequences:

1. As a result of averaging according to formula (77), some distortions of the experimental kinetic curve may occur compared to the calculated one, even if the model fully corresponds to the system under study.
2. Estimating the kinetic parameters, for example, the diffusion coefficient, may be biased due to the inequality of the average size of the fraction and the effective size of the particles in it.

We carried out a series of model calculations to determine the quantitative estimates of these effects. The equation of the kinetics of internal diffusion on spherical sorbent grains for a linear isotherm was chosen as a model. The dependence of the degree of conversion on time, in this case, is given by formula (82):

$\alpha \left(R,t\right)=1+\frac{6}{{\pi }^2}\cdot {\displaystyle \sum _{n=1}^{\infty }\frac{e\frac{{}^{-{\pi }^2{n}^{2}Dt}}{R^2}}{n^2}}$   (82)

Where: α(R,t) - degree of conversion; D - diffusion coefficient; t - contact time; R - granule radius; n - summation index. Using this formula, we calculated the averaged kinetic curves using equation (77) for various relative fraction width and distribution asymmetry values. These curves were approximated by equation (82). The parameter R in this equation was varied to ensure the minimum discrepancy between the averaged kinetic curve and that calculated from this equation. The results of these calculations are shown in Table 6 and 7. As seen from Table 6, the root-mean-square relative approximation error, expressed in fractions of the degree of conversion, only exceeds 1% for a large distribution width. In addition, the maximum relative approximation error is achieved for symmetric distributions. It follows that averaging over particle sizes does not lead to a significant distortion of the shape of the kinetic curve. At the same time, for comprehensive and asymmetric distributions, there may be significant discrepancies between the estimates of the effective radius and the average sieve size (Table 7), which can exceed 10% under certain conditions. Moreover, this situation is typical for distributions where the proportion of small particles is higher than that of large particles. One more feature related to the asymmetry of distributions should be kept in mind. The fact is that when selecting fractions of small size (less than the most probable size of granules), the asymmetry factor will be positive (P(r_max)>P(r_min)), and for large fractions, it will be negative. Consequently, for small granule sizes, the estimate of the diffusion coefficient will be overestimated, and for large granules, it will be underestimated. To recalculate the average sieve sizes into effective ones, considering the nature of the distribution of the granulate, we propose an empirical expression (83)

$R_{kin}=R_{ssav} \cdot \left(1+0.06375\cdot S \cdot \left(1+6.2807\cdot Asym\right)\right)$   (83)

Where: $R_{kin}$  - “kinetic” radius; $R_{ssav}$  - average network radius; S - distribution width (formula (80)); Asym - distribution skewness (formula (81)).

A comparison of the kinetic radii obtained by approximating the kinetic curves for polydisperse samples with the calculation results by formula (83) is shown in Figure 30. Thus, the empirical equation (83) is a reasonably effective tool for calculating corrections to the effective particle radius due to polydispersity.

Figure 30 The ratio of kinetic radii to average sieves.

Fractal and hierarchical structure of porous sorption materials

The basis of the structure of sorption materials is colloidal gels. According to its structure, the gel is a system of interconnected solid particles, and the volume occupied by the particles is a small part of the volume of the gel. Almost all its volume falls on voids - pores. The characteristic size of individual gel particles is usually 2÷200 nm. The simplest gel model can be built from spherical particles of the same size, and the connection between them is carried out where the particles practically touch each other. Any piece of gel that includes many individual particles within the framework of the model under consideration is a fractal cluster.⁵² The term "fractal" was introduced by Benoit Mandelbrot in 1975 and became widely known with the release of his book "The Fractal Geometry of Nature" in 1977.⁵³ The word "fractal" is used not only as a mathematical term. A fractal can be called an object with at least one of the following properties and a non-trivial structure at all scales. This is the difference between fractals from regular figures (such as a circle, an ellipse, or a graph of a smooth function). A small fragment of a familiar figure on a large scale will look like a fragment of a straight line. For a fractal, zooming in does not lead to a simplification of the structure; that is, on all scales, we will see an equally complex picture:

1. The fractal material is self-similar or approximately self-similar.
2. It has a fractional dimension or a metric dimension that is superior to the topological dimension.

In the synthesis of sorbents, such a structure is determined by its formation mechanism. The formation and growth of the gel are due to the adhesion of individual particles moving in solution, which leads to the formation of growing aggregates. Following one of the properties of a fractal aggregate, the average mass density of a substance in a sphere of radius R is equal to:

$\overline{\rho }\left(R\right)={\rho }_0{\left(\frac{r_0}{R}\right)}^{3-Df}$   (84)

Where: ${\rho }_0$ - the density of the material of the particles that make up the aggregate; $r_0$ - the average radius of the particles that formed the aggregate; $D_f$ - fractal dimension of the aggregate.

The presented dependence means that with an increase in the allocated volume, voids of an ever larger size will appear, leading to a decrease in the total relative volume occupied by the substance. In an actual sample, the fractality of the structure will manifest itself at limited sizes $r\ll \overline{R}$ . The boundary size can be recovered from formula (85):

$\overline{R}\sim r_0{\left(\frac{{\rho }_0}{\overline{\rho }}\right)}^{\frac{1}{\left(3-D_f\right)}}$   (85)

Where: $\overline{\rho }$ - average density of a substance in a gel.

This pattern is determined by the nature of transforming particles into a gel. In the first stage, they form small clusters, which, when combined, grow. If the aggregates are small, their association is determined by the nature of the motion in the solution, and they have the lowest dimensional fractal structure. However, when aggregates' sizes become close to $\overline{R}$ , they will occupy the entire space. The subsequent association of aggregates will be associated with their proximity and not with the nature of the movement. Therefore, at distances $r\gg \overline{R}$ , the fractal aggregative structure disappears, and a large aggregate becomes, on average, homogeneous. However, scale invariance remains, and the formed gel retains its fractal character at the level of primary particles. Consider as an example a purely geometric model of filling space with points represented as two variables, x and y. At any point in time, the instantaneous values of these variables define a point on the XY plane. The appearance of new points over time forms a specific structure. The relationship between variables will determine the form and type of this structure. For example, if the x variable is unrelated to the y variable and time, we will not see any stable structure. With enough points, they will evenly fill the XY plane (Figure 31).

Figure 31 Lack of interaction and correlation between x and y - uniform filling of the plane.

If there is a relationship between x, y, and time, then some regular structure will be visible: in the simplest case, it will be some curve or maybe a more complex structure (Figure 32).  The same is true for three- and more-dimensional space. If there is a connection or dependence between all variables, the points will form a curve; if there are two independent variables in the set, then the points will form a surface; if there are three, then the points will fill the three-dimensional space, etc. Without the connection between the variables, the points will be uniformly distributed across all available dimensions. It follows that having determined how the points fill the space. We can judge the nature of the connection between the variables. Moreover, the shape of the resulting structure (lines, surfaces, three-dimensional figures, etc.), in this case, does not matter. The fractal dimension of this structure is essential: a line has a dimension equal to 1, a surface has a dimension of 2, a volume structure has a dimension of 3, etc. It can usually be considered that the value of the fractal dimension corresponds to the number of independent variables in the data set. The size can be a fractional value, which can happen if the resulting structure turns out to be a fractal - a self-similar set with a non-integer dimension. Hence, in the case of gel formation during the synthesis of sorbents, it can be concluded that the value of the fractal dimension makes it possible to determine how the gel structure was organized. If, for a three-dimensional space, the experimentally determined fractal dimension is within $1<Df<2$ , then a branched chain structure is formed. A porous openwork frame is formed if its value falls within the range of $2<Df<3$ . The fractal dimension $Df\cong 2$  indicates the formation of layered structures.

Figure 32 There is some correlation between x and y.

Let us determine the possible values for the fractal dimension during the formation of gels from colloidal solutions formed during the synthesis of sorbents. The above equations (84) and (85) reduce to the pattern described in,^54,55 which relates the number of particles in a fractal aggregate to the ratio of its radius and the radius of the particles that formed it. For calculations, it is more convenient to use an equation that relates the properties of sols to the fractal dimension of aggregates and gels formed during synthesis. We represent this equation in the following form:

$n={\left(\frac{D_{agr}}{d_p}\right)}^{Df}$   (86)

Where: n – the number of monodisperse particles in a sphere with a diameter $D_{agr}$ - inside a sphere circumscribed around one of the emerging aggregates. In the case of the formation of an infinite aggregate, $D_{agr}$ - corresponds to the size of the whole system. $d_p$ – sol particle diameter. $Df$ – fractal dimension. To estimate the maximum fractal dimension that can be formed in the ash of a given mass of particles (M) in a volume with a diameter $D_{agr}$  and a given mass of a sol particle $\left(m_p\right)$ , we write an expression for calculating the number of particles per unit volume of the colloid solution. After substituting the values of the corresponding quantities, we obtain the following:

$n=\frac{M}{m_p}=\frac{m}{\rho }{\left(\frac{D_{agr}}{d_p}\right)}^3$ (87)

Where: m – mass concentration of sol. $\rho$  – sol particle density. Combining equations (86) and (87), we obtain:

$\frac{m}{\rho }={\left(\frac{D_{agr}}{d_p}\right)}^{D_{f-3}}$ (88)

This equation is very similar to equation (84). However, equation (88), in contrast to equation (84), does not describe the structure of the formed gel. It describes the asymptotic structure that can be formed from a given sol during its gelation. Thus, it illustrates that asymptotic structure with a fractal dimension, above which no other structure can start from a sol with provided properties. That is, this fractal dimension, being a function of time t, is the value to which it tends during the formation of the gel structure, during the aggregation of the colloid solution, and the formation of the gel structure, after passing the sol-gel transition point:

$D_f(\infty )=\underset{t\to \infty }{\lim }{\text{ D}}_f(t)$   (89)

Thus, the fractal dimension can differ for the same system at different scales and times, which is also clearly seen from the analysis of formal kinetic models of particle aggregation processes presented in.^54,55 It can be seen from these data that by the time of gelation, only about half of the sol particles entered the structure of the infinite aggregate formed because of this process. That is, the fractal dimension of the gel at the time of gelation has not yet reached the critical value that the formed gel will have - equation (89).  From equation (88), one can obtain an equation describing the dependence of the limiting value of the fractal dimension of the gel structure that can be formed from a given sol:

$D_f=3+\frac{\lg m-\lg \rho }{\lg D_{agr}-\lg d_p}$   (90)

The results of calculations carried out according to equation (88) for sols with different particle sizes and mass concentrations are shown in Figure 33–36. The results obtained indicate the relationship between the structural parameters of the gels. They apply to wet, freshly obtained gels and materials that have undergone syneresis and drying, that is, to the structure of directly inorganic ion-exchange materials. Figure 34 shows that for coordination numbers from 3 to 12, there is an almost direct relationship between the coordination number of particles in the structure and its fractal dimension. Moreover, this dependence is much weaker for coordination numbers less than n<2.6. The fractal dimension drops catastrophically when approaching the critical value of the coordination number (equation (94)). Therefore, using equations (91) and equation (93), we can calculate the dependence of the limiting value  of the fractal dimension on the coordination number of particles in globular packing. The results of such calculations for particles of different diameters are presented in Figure 35, 36. In,⁵⁶ the relationship between the packing porosity of spherical particles in a globular structure was demonstrated, depending on the coordination number of these particles. Based on this, the dependence (91) of porosity α (%) on the coordination number n of spherical particles was calculated:

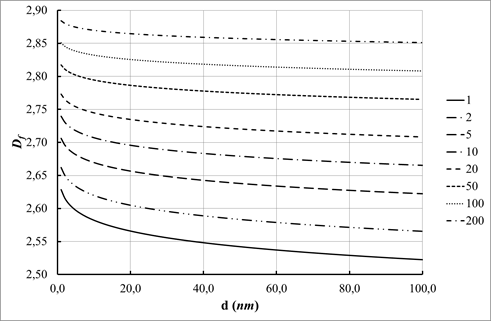
Figure 33 Dependence of the limiting value $\left(D_f\right)$ of the fractal dimension on the sol particles' diameter at different sol mass concentrations (g/l).

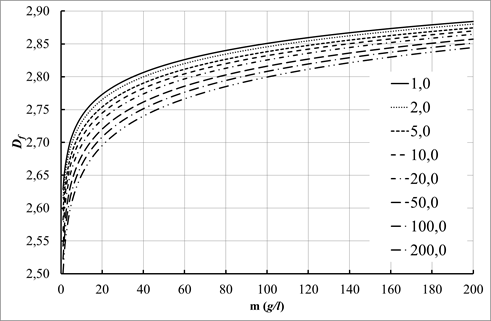
Figure 34 Dependence of the limiting value $\left(D_f\right)$ of the fractal dimension on the mass concentration of the sol for sol particles of different diameters (nm).

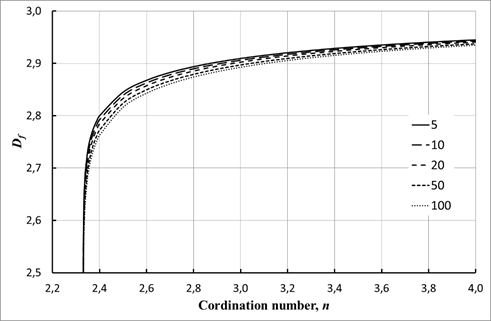
Figure 35 Dependence of the limiting value of the fractal dimension $D_f$ , on the coordination number of particles, in globular packing, for sol particles of different diameters (nm).

$\alpha ={\alpha }_{\infty }+\frac{B}{n}$   (91)

The coefficients in equation (91), for the dimension dim(α)=%, have the following values: α_∞=7,763±0,016; B=221,95±0,45, R²=0,9959. Since the equation of this curve has a singular point, it is possible to calculate the limiting value of the coordination number at which the volume of voids will be equal to 100%:

$n_{100}=\frac{100-{\alpha }_{\infty }}{B}$   (92)

Value n₁₀₀=2.406±0.010. The physical meaning of this value lies in the fact that in the structures of dispersed nanosystems with a coordination number less than this value, there is no rigid structure of the framework of the material assembled from individual particles. Below this coordination number, the particles are assembled only into separate chain structures that are not interconnected, in which coordination number 2 is realized. We carried out calculations on the selection of a correlation dependence to describe the dependence of porosity on the coordination number of packing of spherical particles, which gives the maximum correlation coefficient. The maximum correlation coefficient was obtained for the dependence of the following form:

$\alpha ={\alpha }_{\infty }^{\text{'}}+\frac{B^{\prime }}{(n-n_0)}$   (93)

The coefficients in equation (93), with the conditions, as in the previous case, were: ${\alpha }_{\infty }^{\text{'}}$ =0,14964± 0,00019, $B\text{'}$ =310,10±0,40, $n_0$ =-0,7750±0,0010, $R^2$ = 0,9975. For this dependence, it is also possible to calculate the limiting value of the coordination number, at which the volume of voids will be equal to 100%:

$n_{100}=n_0+\frac{B^{\prime }}{(100-{\alpha }_{\infty }^{\text{'}})}$   (94)

Hence, substituting the values obtained for expression (93), we get the following value n₁₀₀=2.331±0.006. It is more difficult to interpret these results. However, they give a more accurate result and somewhat expand the range of coordination numbers, up to which forming a rigid framework is still possible, with an openwork packing of spherical particles. The values of the fractal dimensions of the gels, obtained from the measurement of the gelation time of the sols, show that during gelation, first, chain structures are formed, which form the pore structure of the sorption material. The dependence on the limiting value of the fractal dimension  on the diameter of the sol particles for packings of globules with different coordination numbers. Figure 35 indicates a weak effect of particle sizes on the geometry of their packing during the sol-gel process, which is especially true for particles larger than 10 nm, which can be associated with large particles' inertia and steric hindrances in their interaction. The data thus obtained can be further applied to analyzing the structural features of various sorption materials having a spherical structure.

Influence of fractality effects on the kinetics of sorption processes

We note one more feature concerning determining the size of irregularly shaped granulates. As shown above, the most successful estimate of the effective size of the granules is the value calculated by the formula (37), which includes the surface of the granule and its volume. With sieve classification, granules are selected based on linear size. If we assume that the surface is proportional to the second power of the linear size and the volume is proportional to the third. The classification according to the linear size seems sufficient. However, there are objects for which the relationships between linear dimensions, surface, and volume differ. It was shown in [15] that the relationship between the linear size of an aggregate (cluster) composed of particles of finite size is generally determined by expression (64):

$N=\rho {\left(\frac{R}{R_0}\right)}^D$   (95)

Where: N - cluster mass characteristic; ρ - density per particle; R - linear cluster size; R₀ - the linear size of a single particle; D – fractal dimension of the cluster. Aggregation processes can lead to the formation of clusters of fractional dimensions. For example, the processes of aggregation of proteins,¹⁶ colloidal particles of gold,¹⁷ and silicon dioxide¹⁸ lead to the formation of just such particles. We also observed similar effects for granulates of inorganic sorbents. For example, Figure 36 shows the dependence of the average granule mass on the average sieve fraction size for the FS-3 sorbent. The slope of this dependence in logarithmic coordinates is 2.39±0.01. Thus, the mass of granules does not grow in proportion to the third power of the linear size but much more slowly. Similar fractal connections also exist between other geometric characteristics of the granulate of a given sorbent. For example, consider the results of measurements of the perimeters and areas of projections performed for the FS-3 sorbent (Figure 38) and the approximation of these results by a power law. As the regression analysis of the data presented in Figure 37 showed, the value of the projection area increases in proportion to the perimeter growth to the power of 1.67 ± 0.24 and not in proportion to the square of this value. Thus, the fractality effect can be a source of systematic errors in determining the diffusion coefficients. The effective particle size, by analogy with formula (77), can be calculated using the data on the perimeter and area of their projection by expression (96):

Figure 36 Dependence of the limiting value ( $D_f$ ) of the fractal dimension on the diameter of the sol particles for packings of globules with different coordination numbers.

Figure 37 Correlation of a granule's average mass (mav) and its average sieve size (Rssav).

Figure 38 Dependence of the particle projection area on its perimeter.

$D_{eff}=\frac{4. S}{L}$   (96)

Where: S - granule projection area; L - granule projection perimeter.

These estimates lead to a quadratic dependence of the time of complete mining of the granule on the square of its diameter, in contrast to average sieve sizes (Figure 39). The regression analysis of the data presented in Figure 39 showed that the slope of the dependence ln(T_k) on ln(D) using the average sieve size is 1.47 ± 0.16. In the case of estimates using formula (96), we obtain 1.85 ± 0.28; in the first case, there is a significant deviation from the quadratic dependence. In the second case, such a deviation is absent.

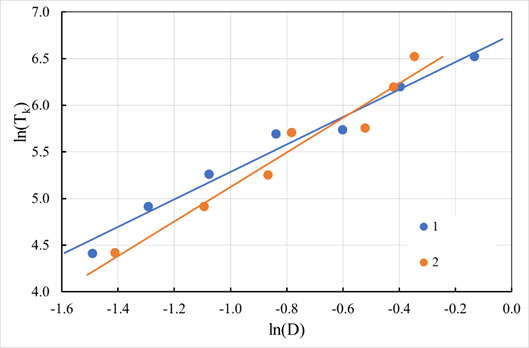
Figure 39 Dependence of the time of full completion of the exchange process on the linear dimensions of the granules for the FS-3 sorbent.Dependence of the time of full completion of the exchange process on the linear dimensions of the granules for the FS-3 sorbent.
1 - Average sieve size. 2 - Estimate by formula (96).

The theoretical analysis makes it possible to reveal some features of the sorption kinetics of inorganic ion exchange materials. Firstly, the above results indicate that when working in the region of concave isotherms, a significant slowdown of the mass transfer process is possible even on very permeable granules. This conclusion suggests that reversing sorption processes involving highly selective sorbents using displacement desorption may encounter difficulties associated with maintaining high concentrations of the displacing agent and the low rate of the exchange process. Second, the rate of sorption on inorganic ion exchange materials depends in a certain way on the concentration of absorbed ions in the external solution. This dependence should manifest itself even in the absence of external diffusion inhibition. In this case, the question of the distribution of electrolytes between the pore space of the granule and the free volume of the solution is fundamental. Thirdly, the rate of mass transfer processes with the participation of inorganic sorbents can be affected not only by the permeability of granulates but also by inhibition at the level of homogeneous sections of the solid phase. The simplest way to detect such deceleration is to compare the data of the kinetic experiment with the theoretical results related to the model that ignores deceleration at the level of homogeneous sections of the solid phase. However, in such a comparison, it is necessary to consider possible distortions that arise due to the finite width of particle size fractions, the discrepancy between the particle shape and the calculated one, etc. This work expands the existing knowledge about the mechanisms of implementing ion-exchange processes on inorganic ion-exchange materials of various types. One of the promising applications of inorganic ion exchange materials is their use for direct lithium extraction (DLE) from lithium-poor natural and technological brines. Researchers can use the data and techniques used in this work to model and predict the modes of conducting current technical processes for extracting lithium and other rare and trace elements from natural and industrial waters.

None.

The author declares there is no conflict of interest.

1. Kokotov Yu A, Pasechnik VA. Equilibrium and kinetics of ion exchange - L., Chemistry, Leningrad branch. 1970. p. 335.
2. Helfferich FG. Ion Exchange. McGraw-Hill, New York. 1962. p. 615.
3. Chernova EP, Nekrasov VV, Tunitsky NN. Study of the kinetics of ion-exchange sorption. I. Kinetics of total ion exchange. Journal of Physical Chemistry. 1956;30(10):2185.
4. Paskonov VM, Polezhaev VI, Chudov LA. Numerical heat and mass transfer process modeling. - M, Science, 1984. p. 82.
5. Nikashina VA, Rubinstein RN. Determination of the external diffusion kinetic coefficient from dynamic experience. Journal of Physical Chemistry.1971;45:1177.
6. Senyavin MM, Rubinstein RN, Komarova IV. Theoretical foundations of freshwater demineralization. Acad. Sciences. In: VI Vernadsky, et al., editors. USSR, Institute of Geochemistry. 1975. p. 325.
7. Lykov AV, Mikhailov Yu A. Theory of heat and mass transfer. M-L, State Energy Publishing House. 1963. p. 535.
8. Helfferich FG, Hwang YL. "6.2 Ion Exchange Kinetics". Ion Exchangers, edited by Konrad Dorfner, Berlin, New York: De Gruyter, 2011. p. 1277–1310.
9. Helfferich F. Ion-Exchange Kinetics. V. Ion Exchange Accompanied by Reactions. The Journal of Physical Chemistry. 1965;69(4):1178–1187.
10. TU 6-09-40-570-84, Electron-ion exchanger FS-3.
11. Dolgonosov AM, Senyavin MM, Voloshchin IN. Ion exchange and ion chromatography. In: M Nauka editor. 1993. p. 30.
12. TU 6-09-40-212-84, Electron-ion exchanger FS-10.
13. Aerov ME, Todes OM, Narinsky DA. Apparatus with a stationary granular layer. L Chemistry, 1979. p. 12.
14. Kokotov Yu A, Zolotarev PP, Elkin GE. Theoretical foundations of ion exchange. L Chemistry, 1986. p. 280.
15. Feder, J. Fractals, Plenum Press, New York, 1988. p. 305.
16. Feder J, Jossang T, Rosenqvist E. Scaling behavior and cluster fractal dimension determined by light scattering from aggregation protein. Phis Rev Lett.1984;53:14031406
17. Weitz DA, Oliveria M. Fractal structures formed by kinetic aggregation of aqueous gold colloids. Phis Rev Lett. 1984;52:1433–1436.
18. Schaefer DW, Martin JE, Wiltzins P, et al. Fractal geometry of colloidal aggregates. Phis Rev Lett. 1984;52:2371–2374.
19. Bennett CO, Myers JE. Momentum, Heat, and Mass Transfer. N-Y, McGraw-Hill chemical engineering series. 1962. p. 697.
20. Venitsianov EV. Application of mathematical methods for describing and optimizing sorption and chromatography processes (on the centenary of M.M. Senyavin). Sorption and chromatographic processes. 2017;17(6):844–856.
21. Ionites in chemical technology. In: BP Nikolsky et al., editors. L Chemistry, 1982. p. 416.
22. Melikhov IV, Berdonosova DG, Sigeikin GI. Sorption and prediction of the behavior of sorbents in physical and chemical systems. Uspekhi khimii. 2002;71(2):159–179.
23. Tunitsky HH. Diffusion and random processes. Novosibirsk: Science. 1970. p. 120.
24. Kalinichev AI, Kolotinskaya EV. Modeling the kinetics of interdiffusion binary exchange of different-valence ions in nonlinear selective systems. Journal of Physical Chemistry. 2000;74(3):473.
25. Karpov S, Matveeva MV, Selemenev VF. Kinetic parameters of ion sorption during multicomponent exchange. Journal of Physical Chemistry. 2001;75(11):2016.
26. Dolgonosov AM, Garbar AM. Calculation of coefficients of internal diffusion of ions in polymeric ionites. Journal of Physical Chemistry. 1986;40(1):199.
27. Barrer RM, Bartholomew RF, Rees LVC. Ion exchange in porous crystals part I. Self- and exchange-diffusion of ions in chabazites. Journal of Physics and Chemistry of Solids. 1963;24(1):51–62.
28. Vol’khin VV, Pogodina OA, Leont’eva GV. Nonstoichiometric Compounds Based on Manganese(III, IV) Oxides with the Birnessite Structure. Russian Journal of General Chemistry. 2002;72(2):173–177.
29. Yang X, Kanoh H, Tang W, et al. Synthesis of Li1.33Mn1.67O4 spinels with different morphologies and their ion absorptivities after delithiation. J Mater Chem. 2000;10:1903.
30. Chitrakar R, Kanoh H, Miyai Y, et al. Recovery of lithium from seawater using manganese oxide adsorbent (H1.6Mn1.6O4) derived from Li1.6Mn1.6O4. Ind Eng Chem Res. 2001;40(9):2054–2058.
31. Keay J, Wild A. The kinetics of cation exchange in vermiculite. Soil Science. 1961;92:54.
32. Feng Q, Kanoh H, Ooi K. Manganese oxide porous crystals. J Mater Chem. 1999;9:319–333.
33. Kolyshkin AS, Volkhin VV. Determining the limits of applicability of the intra- and external diffusion approximation for mixed-diffusion processes with frontal sorption dynamics. Collection of scientific works "Chemistry, technology and industrial ecology of inorganic compounds", Perm, PSU. 2001;4:55–60.
34. Kolyshkin AS, Volkhin VV. Investigation of the possibility of an approximate description of ion exchange processes characterized by a nonlinear diffusion coefficient in the framework of a model with an effective diffusion coefficient. Proceedings of the international scientific conference "Prospects for the development of natural sciences in higher education" V.2, Perm, PSTU, 2001. p. 126–131.
35. Kolyshkin AS, Saenko EV, Nagorny OV. Study of the kinetics of ion exchange of lithium-manganese spinel // Collection of scientific papers "Problems and prospects for the development of the chemical industry in the Western Urals", Perm, 2003. T. 1, p. 80–86.
36. Kolyshkin AS, Nagorny OV, Volkhin VV. Kinetics of exchange of halide ions on nickel hydroxide. Journal of Physical Chemistry. 2004;78(2):335–339.
37. Nagorny OV, Kolyshkin AS, Volkhin VV. Sorption of hexacyanoferrate(II, III) ions by nickel(II) hydroxide. Journal of Applied Chemistry. 2003;76(8):1277–1280.
38. Nagorny OV, Kolyshkin AS, Volkhin VV. Sorption of mercury (II) by nickel (II) hydroxide: influence of the concentration of halide ions and pH of solutions. Journal of Applied Chemistry. 2004;77(7):1112–1115.
39. Zilberman MV. Scientific bases for synthesizing highly filled composite inorganic sorbents / Dissertation for the account competition. Doctorate degrees. Chem. Sciences. Perm GTU. 2000.
40. Kolyshkin AS. Kinetics of ion exchange on inorganic ion exchangers. Dissertations for the degree of candidate of chemical sciences, Perm, 2005.
41. Popov Yu A. Quasi-homogeneous transport model in a chaotic porous medium. Journal of Physical Chemistry. 2001;75(12):2266.
42. Popov Yu A. Stephen A. Diffusion model in a porous medium with reactions on the pore walls. Journal of Physical Chemistry. 2001;75:12:2273.
43. Bhattacharya A, Mahanti SD, Chakrabarti A. Diffusion and magnetic relaxation in porous media. Phys Rev B. 1996;53:17.11495.
44. Watanabe Y, Nakashima Y. RW3D.m: three-dimensional random walk program for the calculation of the diffusivities in porous media. Computers & Geosciences. 2002;28(4):583–586.
45. Bhattacharya A. Random walk for interacting particles on a Sierpinski gasket. Phys Rev B. 1994;49(6):4947.
46. Voloshina OS, Burkat TM, Pak VN. Dependence of the diffusion coefficient on the pore radius in the process of sodium chloride transfer in porous glass membranes. Journal of Physical Chemistry. 2000;74(6):1099.
47. Markovska L, Meshko V, Noveski V, et al. Solid diffusion control of the adsorption of basic dyes onto granular activated carbon and natural zeolite in fixed bed columns. J Serb Chem Soc. 2001;66(7):463.
48. Stenina I, Golubenko D, Nikonenko V, et al. Selectivity of Transport Processes in Ion-Exchange Membranes: Relationship with the Structure and Methods for Its Improvement. Int J Mol Sci. 2020;21:5517.
49. Cremers AE, Laudelout H. Surface Mobilities of Cations in Clays. Soil Science Society of America Journal. 1966;30(5):570–576.
50. Koltsova EM, Vasilenko BA, Tarasov VV. Numerical methods for solving transport equations in fractal media. Journal of Physical Chemistry. 2000;74(5):954.
51. Sukhanov AD, Timashev SF. On the fractal nature of anomalous diffusion. Journal of Physical Chemistry. 1998;72(11):2073.
52. Smirnov BM. Aerogels. Uspekhi fizicheskikh nauk. 1987;152(1):133–157.
53. Mandelbrot B. Fractal geometry of nature - M., IKI, 2002, 656 p.
54. Kudryavtsev P., Figovsky O. Simulation of hardening processes in silicate systems. International Letters of Chemistry, Physics and Astronomy. 2015;5(1):1–49.
55. Kudryavtsev P, Figovsky O. Simulation of Hardening Processes in Silicate Systems. Journal "Scientific Israel - Technological Advantages". 2015;17(1–2):122–159.
56. Kudryavtsev P, Figovsky O. The sol-gel technology of porous composites. Monograph. LAP Lambert Academic Publishing, 2015. p. 466.
57. Adamson AW, Grossman JJ. A Kinetic Mechanism for Ion‐Exchange. The Journal of Chemical Physics. 1949;17(10):1002–1003.
58. Nernst W. Die elektromotorische wirksamkeit der jonen. Zeitschrift für physikalische Chemie. 1889;4(1):129–181.
59. Dickel G, Meyer A. Zur kinetik des ionenaustausches an harzaustauschern. Zeitschrift für Elektrochemie, Berichte der Bunsengesellschaft für physikalische Chemie. 1953;57(10):901–908.
60. Nernst, W. Zur Kinetik der in Lösung befindlichen Körper. Zeitschrift für Physikalische Chemie. 1888;2U(1):613–637.
61. Planck M. Ueber die Erregung von Electricität und Wärme in Electrolyten. Annalen der Physik. 1890;275(2):161–186.
62. Oel H. Diffusion von Ionen und Elektronen. Zeitschrift für Physikalische Chemie. 1957;10(3-4):165–183.
63. Zagorodni AA. Ion Exchange Materials: Properties and Applications. Elsevier: 2006.
64. Gerasimov Ya I, Dreving VP, Eremin EN. Course of physical chemistry. Chemistry M. 1974;2:624.