The development of Intensity-Duration-Frequency (IDF) models for storm drain design and related flood mitigation structures requires rainfall amount and corresponding duration records. To achieve this purpose, three short duration downscaling methods from 24-hourly rainfall amount data were selected for improvement, namely: IMD, AIMD and MCIMD, with the CAMS method used as the experiment control. Three types of general PDF-IDF models (GEVT-1, LPT-3 and ND) were developed based on the downscaling methods yielding goodness of fit (R²) with very high correlation of 0.995–0.999 and model accuracy with mean square error (MSE) of 4.123–7.85. The PDF-IDF models predicted intensities plotted against durations for different return periods of 2, 5, 10, 25, 50 and 100 years, showed visual differences in the predictive performance of the intensities derived from the downscaling methods. Kruskal-Wallis non-parametric test of significance at 5% level carried out showed that no-significant difference exist for 15-60 minutes duration, while the difference was significant for durations between 90–300 minutes. The LPT-3 based on MCIMD yielded higher improved performance in prediction of intensities relative to the IMD. The level of improvement ranges from 35.17 to 52.26% and 25.0 to 39.89%; while that of AIMD ranges from 10.97 to 20.87% and 3.33 to 12.53% for 10 and 100 year return periods, respectively. The use of the IMD downscaling method with the LPT-3 PDF-IDF model for design purposes will be justified if modified with some percentage improvement or adjustment factor.

Keywords: 24-hourly rainfall amount, short duration downscaling, IMD, AIMD, MCIMD, PDF- IDF model, predicted intensities

A major proven tool for the design of flood mitigation structures for urban, semi-urban and rural settlement in a typical watershed is the intensity-duration-frequency (IDF) models. The efficiency in performance of IDF models in prediction of rainfall intensity are dependent on the quality of the measured precipitation records which serve as input data for calibration of the IDF models. Records of rainfall amount and their corresponding durations are used for IDF modeling. Automated rain-gauge provides information on rainfall amount and its corresponding duration while the manual rain-gauge can only provide information on accumulated daily rainfall amount. Historical time series can be evaluated based on the rainfall Annual Maximum Series (AMS). The AMS daily rainfall is defined as an extreme instance with critical durations for a water- shed, catchment area or river basin which has some consequences to agriculture and soil conservation, roads, dams and drainage.¹ AMS include the highest value(s) that occur for each year spanning through the period of record. The AMS method is often preferable in frequency analysis because the resulting values can be converted to partial series values using conversion factors.

The emergence of the extreme value theory as one of the most important disciplines of applied science in the last 50 years has been of immense contribution in its application in various fields of science and engineering. Thus, by recording daily or 24 hourly rainfall values the extreme value records can be obtained. Extreme value theory is a probability science that studies the stochastic behavior of the extremes of a set of random variables.² Two different approaches exist for the construction and analysis of daily ams rainfall data, namely, the application of highest precipitation amount for different durations, and the Indian Meteorological Department (IMD) method for shorter duration rainfall downscaling. Both methods are briefly discussed herein:

Conventional annual maximum series (CAMS) method

The conventional annual maximum series is the use of records of highest precipitation amount with corresponding durations. This is the most common approach used for construction of AMS that is applied in rainfall frequency analysis and consequently in Intensity-Duration-Frequency (IDF) modeling. The analysis is anchored on ground-based observations of precipitation extremes being the annual maxima. The annual maxima series is constructed by the extraction of the averages of the highest precipitation amount for different durations. Thus, numerical analysis are performed on AMS for storm durations such as 10, 15, 30 and 45 minute which are typical time of concentration for small urban catchments and 1, 2, 6, 12, and 24 hour, also typical time of concentration for larger rural watersheds. In the USA, Adamowski et al.³ adopted the CAMS rainfall analysis method to develop a scaling model of a rainfall IDF relationship; Cheng et al.⁴ used the CAMS construction method to develop a generalized framework for estimating IDF curves and their uncertainties using Bayesian inference. Like in USA and other Countries, the CAMS method as the most prevalent rainfall analysis method has been of immense usage by Nigerian scholars to develop IDF models for major cities.^5–10 

Indian meteorological department (IMD) Method

The IMD method is simply the application of an empirical formula for downscaling of daily or 24– hourly precipitation amount into precipitations of shorter durations. The availability of observed hourly rainfall data is limited due to very poor network of such rain gauges. By analyzing data at some locations where both hourly and daily rainfall data are available Ramaseshan¹¹ proposed an empirical relationship adopted by Indian Meteorological Department (IMD), to disaggregate daily rainfall to a given hourly values. The daily rainfall data commonly available in both urban and rural areas especially in non-automated rain gauge stations can be converted to peak hourly rainfall as may be required for analysis. Thus, from the daily rainfall records the AMS data can be obtained for any gauge station by the use of the IMD empirical formula by its reduction to shorter durations such as 0.25, 0.50, 0.75, 1, 2, 6 and 12 hours. The derived rainfall values of shorter durations serve as representative values of the various durations having been derived from the annual daily extreme values from a common statistical population. Burgess et al.¹² applied a modified version of the IMD empirical formula for frequency analysis, infilling and trends for extreme precipitation for Jamaica (1895-2100). Rasel¹³ adopted the IMD method to derive rainfall IDF equations and curves for seven divisions in Bangladesh, while the IMD method was similarly applied by Dakheel¹⁴ and Hamaamin¹⁵ to develop IDF models for Cities in Iraq. Diwan et al.¹⁶ also used the IMD method to investigate practices such as roof water harvesting and artificial recharge to be evaluated as alternative intervention to undertake such restoration of natural conditions in urban areas for proper restoration of declining groundwater levels. The IMD method of rainfall analysis can be applied in stations where there exist no automated rain gauges to record both rainfall amount and duration simultaneously, but has rain gauges to record cumulated 24-hourly rainfall amount data. Therefore, the purpose of this study is to develop PDF-IDF models from rainfall amounts with corresponding durations extracted from downscaled daily (24-hourly) precipitation records from an automated gauge station using the IMD method. The PDF-IDF model adopted as control experiment was developed using the same data for IMD which were sorted (amount versus duration) for model calibration. It is here-in taken as Conventional Annual Maximum Series (CAMS) model. Thus, correction factor can be determined if necessary, to enhance a pragmatic universal application of the IMD method for construction of rainfall amount versus duration for IDF modeling for gauge stations that does not have automated rain gauges but can measure 24-hourly rainfall amount only which are very common especially in developing countries.

Study area

The study area is Uyo metropolis located in the state of Akwa Ibom, South-Eastern Nigeria, with GPS coordinates of Latitude: 5^o 2’ 20’’N and Longitude: 7^o 54’34’’E, (Figure 1). The elevation above sea level is 45m. Uyo has a topography that is characterized by undulating sandy plain terrain that is well drained to the Atlantic Ocean in the Southern end. Uyo metropolis has mean daily maximum and minimum temperatures of 34 ⁰C and 23 ⁰C with average humidity of 72% especially during the month of January. The annual rainfall ranges from 1599.5mm to 3855.5mm in 1983 and 1977, respectively. The mean annual rainfall value is 2466.6mm with rainfall concentration occurring in the months of April to October which exhibits mostly high intensity of prolonged rainstorm.¹⁷ 

Figure 1 Google map showing Uyo metropolis.

Data collection

Historical rainfall records for Uyo were obtained from the meteorological gauge station of Department of Oceanography and Regional Planning of the University of Uyo, for the period of1986-2015 (30 years inclusive). The rainfall records collected were recorded as rainfall amounts in mm against corresponding durations in minutes. These records were sorted out by extraction of the daily (24-hourly) annual maximum for the rest of the 30 years (Table 1) (Figure 1).

Construction of short duration rainfall

The 30 year 24 - hourly AMS sorted out were downscaled into shorter durations of 15, 30, 45, 60, 120, 360, and 720 minutes. The reduction of sorted AMS into time scale of shorter values less than 24 hour was achieved using scaling relationships in Equation (1) originally proposed by Ramaseshan¹¹ to the Indian Meteorological Department (IMD),

$R_t=R_{24}{\left(\frac{t}{24}\right)}^n$      (1)

And, $I=R_t/t$    (2)

Where: $R_t$  is the required rainfall depth in mm for durations less than 24 hours, $R_{24}$ is the daily rainfall depth (mm), t is required duration (hours), n is an exponential constant =1/3 and I = rainfall intensity (mm/hr). The corresponding values of downscaled rainfall intensities in Table 1 were converted to their logarithmic (base 10) values for the development of Probability Distribution Function (PDF)-IDF models. Equation (1) is an empirical equation that requires calibration of the model to obtain a modified exponent n to capture the true physiographic features dominant in the catchment for a new amended version of Equation (1). Another IMD empirical reduction formula adopted for estimation of rainfall depths, (mm) for various durations (t) from AMS values was that of Modified Chowdhury Indian Meteorological Department (MCIMD) method¹⁸ shown in Equation (3):

$R_t=R_{24}{\left(\frac{t}{24}\right)}^{n }+C$       (3)

Where n and C are constants for determination. The basis for the Chowdhury model also remains the use of 24-hour event rainfall depth, $R_{24}.$

Statistical parameter estimates and frequency distribution analysis of rainfall intensities

The determination of the probability distribution requires the application of method of moments on the sorted data in Table 1 to calculate their statistical parameters such as mean $\left(\overline{x}\right),$  standard deviation (S), and coefficient of skewness (C_S) using Equations (4) to (6).²²

Mean,   $\overline{x}={\displaystyle \sum }_{i=1}^n\frac{x}{n}$      (4)

Standard deviation,     $S=\sqrt{\frac{{\left(x- \overline{x}\right)}^2}{n-1}}$           (5)

Coefficient of Skewness, $C_s=\frac{n{{\displaystyle \sum }}_{i=1}^n{\left(x- \overline{x}\right)}^3}{\left(n-1\right)\left(n-2\right)S^3}$      (6)

Extreme value theory was adopted in the probability distribution assumption of the rainfall sample data in determination of their frequency distribution and for computing their magnitude of occurrence. Therefore, some of the commonly used probability distribution function (PDF) are the Gumbel Extreme Value Type –1 (GEVT-1), Log Pearson Type -3 (LPT-3) and Normal distributions (ND). In order to determine the rainfall intensity value on the basis of the PDF, selected the formula proposed by Chow (1951) (Equation (7)) or its logarithmic equivalent (Equation (8)) was applied.

$X_T= \overline{x}+K_{T}S$     (7)

Or,    $\log X_T=\log \overline{X}+K_T{S}_{logx}$     (8)

Where, $\log \overline{X}$ = logarithmic mean; $S_{logx}$ = standard deviation and K_T =distribution factor. And the required rainfall intensity, X_T is found by taking the antilog of $\log X_T.$  The frequency factor K_T and the PDF type are both function of the return period, T. Hence to calculate the rainfall intensity applying either Equation (7) or its Log equivalent of Equation (8) frequency factors K_T, can be generated using the following formula given in Equations (9) to (12) thus;

For ND frequency factor;

$K_T = z = w–\frac{2.515517+0.802853\text{w}+0.010328{\text{w}}^2}{1+1.432788\text{w}+0.189269{\text{w}}^2+0.001308{\text{w}}^3}$      (9)

Where   $w={\left[In\left(\frac{1}{P^2}\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$   for $(0<p\le 0.5)$  (10)

 And, z = standard normal variate; and probability function, p =1/T

Also, for GEVT-1 distribution, frequency factor;

$K_T=\frac{-\sqrt{6}}{\pi }\left\{0.5772+In \left[In\left(\frac{T}{T-1}\right)\right]\right\}$      (11)

And for LPT-3 distribution, the frequency factor using Kite (1977) approximation formula as given in Equation (12);

$K_T=Z+\left(Z^2-1\right)K+\frac{1}{3}\left(Z^3-6\right)K^2-\left(Z^{2 }-1\right)K^{3 }+Z{K}^4+\frac{1}{3}{K}^5$     (12)

For, $C_s\ne 0,K=\frac{C_s}{6}$ , normal variate, $\text{Z}=K_T$ for coefficient of skewness of sample, $C_s=0.$

Calibration of IDF models

The modified Sherman empirical equation is selected for calibration as given in Equation (13),¹⁹ which shows probabilities that are functions of rainfall intensities average over durations that are typical of intervals of the storm;

Intensity   $I=\frac{c{T}_r{}^m}{T_d{}^a}$    (13)

Where; I = rainfall intensities (mm/hr); T_r = return period (years); T_d = duration of rainfall in minutes; and c, a, and m = physiographic constants. Thus, the calibration of Equation (13) including the evaluation of the coefficient of determination (R²) and the mean squared error (MSE) followed the optimization technique or non-linear regression method as reported by Zakwan²⁰ The method uses Excel Solver in Microsoft to estimate the parameters of IDF models.²⁰ The procedure requires feeding into the spreadsheet, 48 PDF computed intensities from Table 4 as observed intensity values with their durations (15, 30,...,1440 min) and return periods (2, 5,…, to 100 years). Intensities corresponding to each duration and return period were calculated using the selected equation based on the assumed values of parameters of the IDF equation. To obtain the values of optimum IDF parameters sum of square error between observed intensity and predicted intensity were set to minimization as shown in Equation (14). The equation was solved using Generalized Reduced Gradient (GRG) solver as the objective function:

$MinSSE={\displaystyle \sum }_{i=1}^n{\left(I_{obs}- I_{pred}\right)}^2$    (14)

Where: $I_{obs}$  = computed or observed rainfall intensity, $I_{pred}$  = IDF model predicted rainfall intensity, n =number of data sets and I is a counter. Therefore, solving Equation (14) gives the optimum values for the constants, a, b, m and c achieved through iterative process that produced the least squared error. The coefficient of determination (R²) and the mean squared error (MSE) were also calculated from Equations (15) and (16) applying optimization technique:²⁰

$R^2=\frac{{{\displaystyle \sum }}_{i=1}^n{\left(I_{obs}- I_{avg}\right)}^2- {{\displaystyle \sum }}_{i=1}^n{\left(I_{obs}- I_{pred}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(I_{obs}- I_{avg}\right)}^2}$     (15)

$MSE=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(I_{obs}- I_{avg}\right)}^2$    (16)

Where: $I_{avg}$  = average of observed or computed PDF rainfall intensity.

Results

Evaluation of PDF rainfall intensities

Downscaled 24 hourly rainfall amounts with the IMD method applying Equation (1) are presented in Table 1. The statistical parameters were estimated to obtain the sample mean, standard deviation and coefficient of skewness using Equations (4), (5) and (6) respectively. These results are recorded in the last three rows of the same table. Following are the generation of frequency factor values calculated using either of Equations (9), (10), (11) or (12), as presented in Nwaogazie et al.²¹ The frequency factors calculated were substituted into Equation (7) to obtain the PDF intensities for GEVT-1 and ND. Using the converted logarithmic equivalent of Table 1 intensity values including LPT-3 generated frequency factors, substitution were similarly made into Equation (8) to produce LPT-3 PDF intensities presented in Table 2.

Calibration of general PDF-IDF model

Most existing IDF models are return period specific (RPS) which means that input data are required to be limited to specific duration with corresponding PDF intensity values for a specified return period. However, the calibration of a general PDF-IDF model remains different as non-return period specific (NRPS), because they require larger size of input data that are more encompassing than as in the RPS model calibration. This is because the calibration of the general PDF-IDF model requires that the values of all the durations and their corresponding intensity for each of the 6 return period equating to 48 data set as contained in Table 2 serve as input data for the calibration of the selected Sherman’s quotient-power Equation (13) to produce PDF-IDF models presented in Table 4 for LPT-3, and similarly repeated for GEVT-1 and ND model types. The optimization technique was applied for evaluation of the calibration processes.

Improved IMD rainfall downscaling and CAMS modeling

In order to achieve improved performance in rainfall intensity prediction of the PDF- IDF models obtained from the IMD short duration downscaling methods, Equation (1) was subjected to modification to obtain a new exponent values consistent with the physiographic factors of the catchment locality. The amended Indian Meteorological Department (AIMD) method relies on the substitution of the IMD Equations (1) and (2) into the intensity probability distribution frequency formula (see Equation (7)) of the 24-hourly and any other durations, which are summed-up for each return period and integrated. Existing PDF-IDF models established for the study station – Uyo metropolis were achieved using CAMS method herein referred to as the control experiment.²² The parameter values for the exponent in the IMD model were optimized for the least square error by comparing the initial derived intensities of the PDF-IDF model from the IMD method (observed) with those of the existing CAMS PDF-IDF model intensities (predicted). The mean square error (MSE) of their differences were subjected to optimization and reduced to the least minimum. New parameter values for the exponent of IMD model were obtained for the AIMD for each PDF as presented in Table 3. Similarly, for the MCIMD, the optimizing functions were applied to obtain the best fit values for its exponent (n) and constant (C). Thus, using Equation (3) the downscaling formula for the MCIMD was calibrated to obtain the constant values for the GEVT-1, LPT-3 and ND PDFs as shown in Table 3. From the results obtained of the IMD, AIMD and MCIMD short duration downscaling models calibration for the various PDFs short duration intensities were obtained to serve as input data for the corresponding IDF models calibrated and presented in Table 4. Furthermore, a power model as adjustment factor based on Equation (17) was calibrated to serve as an alternative approach to apply the achieved improvements directly to the original IMD method predicted intensities:

$R_a=C{t}^a$       (17)

Where; R_a =adjustment factor ratio, t =duration (minutes), while C and a are parameters. The calibration was carried out by regression of the ratio of MCIMD and IMD method as dependent variable for any given duration (t) as independent variable. Optimization of this inputted values gave the values of the parameters Canda. For example, the calibrated adjustment factor ratio (R_a) for LPT-3 PDF-IDF models yielded adjustment parameters of; C=0.9896, a=0.0761 with =0.999, and C=0.9094, a=0.0761 with =0.9291 for 10 and 100 year return periods, respectively. Thus, adjustment factor was calculated for any given duration to obtain the equivalent intensity values as that of the MCIMD improved downscaling method for PDF-IDF models for any given catchment area.

Distribution and comparison of various predicted rainfall intensity curves

Consequent to the development of the general PDF-IDF models listed in Table 4 based on the different short duration downscaling methods applied, the predicted rainfall PDF-IDF curves were generated for GEVT-1, LPT-3 and ND, respectively. Figure 2 are typical family of curves for return periods of 2, 5, 10, 25, 50 and 100 years plotted for intensity versus duration obtained from the general PDF-IDF model with respect to the IMD method. This is to verify if the curves or intensity distributions are in conformity with those in literature. For comparative analysis, plots of predicted rainfall intensity against duration were made on same graph sheets for various PDF-IDF models derived as per CAMS, IMD, AIMD and MCIMD methods (of short duration downscaling) for different return periods (2, 5, 10, 25, 50 and 100 years) as shown in Figure (3­–5). The skewness test computed for the downscaled intensity in Table 1 served as the Normality test. The positive skewness values of the results are evidence that non-parametric analysis could be applied for test of significance at confidence level of 5% (Table 6). Kruskal-Wallis non-parametric analysis of variance (ANOVA) was carried out for two segments, that is, 15-60 minutes and 90-300 minutes durations to ascertain the null hypothesis that there exist no significant difference amongst the rainfall intensity distribution curves for the plots. Further to the plots, the predicted intensities of the PDF-IDF models developed for each of the short duration downscaling methods were analyzed for differences in predicted intensities performance between the CAMS and the IMD, AIMD and the MCIMD methods (Table 5). This is for determination of the degree of bias. Also, the percentage improvements of the intensity distributions of the AIMD and MCIMD over the original IMD were equally computed (Table 5).

Derived PDF rainfall intensities

The purpose of this study is to develop PDF-IDF model from 24 hourly AMS rainfall measurement collected for Uyo metropolis, and develop strategies for its application as alternative approach for data generation for IDF modeling. In order to achieve this purpose, the IMD empirical formula as Equation (1) originally proposed by Ramaseshan¹¹ was adopted to reduce the 24-hourly rainfall amount to shorter durations (0.25, 0.5, 0.75. 1, 2, 6 and 12 hours) to produce result in Table 1. Descriptive statistical parameters such as mean, standard deviation and coefficient of skewness were derived and presented in the last three rows of Table 1. The results of the mean and standard deviation indicate variations from lower to higher durations in line with the trend of rainfall downscaling. The downscaled intensities had a constant positive skewness value of 1.211458 confirming that the rainfall intensities data are non-parametric. Table 2 shows typically the summary of LPT-3 PDF computed rainfall intensities, derived via Equation (8), while Equation (7) was used to compute GEVT-1 and ND PDF rainfall intensities. A visual examination of the derived PDF rainfall intensity values indicates that there are no large noticeable difference among the various PDF types selected. 

Calibrated general PDF-IDF models with short duration downscaling methods

Based on the different short duration downscaling methods applied and the GEVT-1, LPT-3, and Normal PDFs selected, the Sherman’s quotient-power equation was calibrated to develop general PDF-IDF models shown in Table 4. The downscaled values of computed PDF intensity values as shown in Table 2 obtained from the original IMD Equation (1) with exponent constant value of 1/3 produced PDF-IDF models with goodness of fit (R²) of 0.999, indicative of very high correlation amongst the various variables of the models. The mean square error (MSE) were 4.58, 5.68 and 7.13 for GEVT-1, LPT-3 and ND general PDF-IDF models, respectively. The MSE of the derived models were very low value. Likewise for the LPT-3 it had a very low bias that ranged from 24.16–50.75 mm and 7.54–62.42 mm for 10 and 100 years return period, respectively when compared to the existing CAMS method predicted intensity values.   The AIMD model maintained the same range of goodness of fit (R²) of 0.999 and also produced an improved lower MSE values of 4.123, 5.119 and 7.0 for GEVT-1, LPT-3 and ND, respectively. Similarly, the MCIMD model had very high goodness of fit (R²) values of 0.996, 0.997 and 0.995 with MSE values of 4.64, 10.26 and 7.85 for the GEVT-1, LPT-3 and ND, respectively. The AIMD produced improved exponents for Equation (1) presented in Table 3 as 0.2359, 0.2596 and 0.2457 for the GEVT-1, LPT-3 and ND, respectively. On the other hand, the modified Chowdhury IMD (MCIMD) model in Equation (3) was similarly optimized, thus, producing improved exponent (n) and additive constant (C) values of 0.252 and 6.0; 0.295 and 14.4; and 0.259 and 6.0 for the GEVT-1, LPT-3 and ND, respectively (Table 3).               

The LPT-3 PDF-IDF model for 60 minute duration with respect to the MCIMD produced higher improved performance in prediction of intensities relative to the original IMD model (Table 5). That is the improvement ranges from 35.17 to 52.26% and 25.0 to 39.89%, for 10 and 100 year return periods, respectively. Similarly, AIMD showed improvement in the range of 10.97 to 20.87% and 3.33 to 12.53% for 10 and 100 year return periods, respectively. Additionally, MCIMD equally displayed the least bias from the CAMS (control experiment). The bias ranges from 14.02 to 15.34 mm/hr and 13.463 to 17.965 mm/hr for 10 and 100 year return periods, respectively. For AIMD the bias ranges from 22.398 to 25.662 mm/hr and 24.061 to 30.193 mm/hr for 10 and 100 year return periods, respectively. In order to implement the application of the improvements shown by the MCIMD method of PDF-IDF models, an adjustment factor was developed for direct multiplication to the original IMD computed rainfall intensities as indicated in Equation (17). Therefore, the introduction of the adjustment factor to the original IMD enabled the improvement of its predictive capability and promote its universal adoption for development of PDF-IDF models comparable to PDF-IDF models constructed from CAMS methods for any given catchment area.

Distribution of predicted rainfall intensity curves

Using the original IMD general PDF-IDF models predicted rainfall intensities were plotted against various durations in a log-log graph paper as shown in Figure 2 with each containing a total of six plots for different return periods (2, 5, 10, 25, 50 and 100). The observed common features of the IDF curves were that: an increase in duration produced a corresponding decrease in intensity, and, for any given duration, an increase in the return period also produced a corresponding increase in intensity. These observed features were in agreement with those of IDF theory in literature.^23,24 However, the predicted intensity values of the IMD PDF-IDF models were consistently higher than those of the PDF-computed intensity values (Table 2).

Figure 2 Intensity curves of rainfall predicted from general PDF-IDF models based on IMD method.

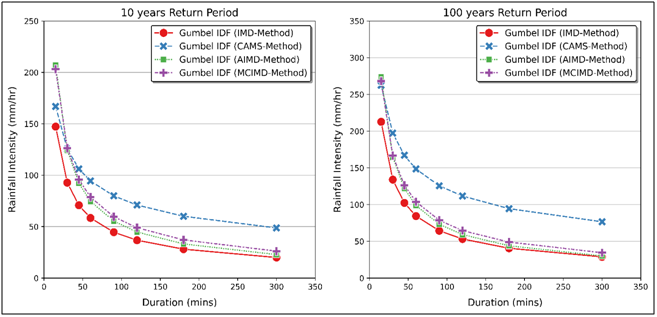
Figure 3 Distributions of IMD, AIMD, MCIMD and CAMS methods for GEVT-1 IDF predicted intensity curves for 10 and 100 years return period.

Performance analysis of PDF-IDF models predicted intensity distributions for the various short durations per downscaling methods

The PDF-IDF models in Table 4 developed predicted intensities versus durations were plotted together for different return periods of 2, 5, 10, 25, 50 and 100 years for the GEVT-1, LPT-3 and ND as presented in Figure 4,5. The figures are showing noticeable visual differences in the predictive performance of the intensity distributions of the models derived from the IMD, AIMD and MCIMD short duration downscaling methods along with the CAMS method (control experiment). The CAMS method derived PDF-IDF models used for the experimental control produced intensities with corresponding durations from an automated rain gauge for the study station. Therefore, the plots of the IMD, AIMD and MCIMD methods derived PDF-IDF models were compared against that of the CAMS method.

Figure 4 Distributions of IMD, AIMD, MCIMD and CAMS methods for LPT-3 IDF predicted intensity curves for 10 and 100 years return period.

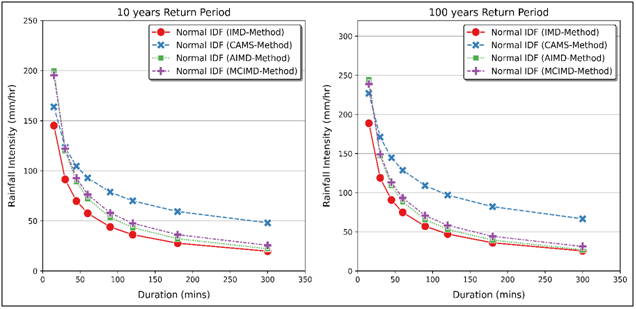
Figure 5 Distributions of IMD, AIMD, MCIMD and CAMS methods for Normal IDF predicted intensity curves for 10 and 100 years return period±.

A cursory look at Figure 4,5 indicates that the distribution of the intensities for the IMD model showed lower intensities prediction closely followed by the AIMD model with the MCIMD model consistently higher as proved by earlier scholars.^12,18 Furthermore, the LPT-3 PDF-IDF model type out-performed the GEVT-1 and ND PDF-IDF models as the best-fit, high intensity prediction and least bias distributed model type. However, the PDF-IDF models obtained from the downscaling methods predicted intensities for short durations less than or equal to 60 minutes were very good match with the CAMS method (control experiment) for all return periods. The intensity distribution of the plots in Figures 4 to 6 for two segments of the durations: 15–60 minutes and 90–300 minutes were subjected to Kruskal-Wallis non-parametric test of significance at 5% level. The test was carried out for the selected PDFs and return periods as shown in Table 6. For 15-60 minutes duration the K (observed) values were lower than the K (critical) and the p-values were higher than alpha value of 0.05. Thus, the null hypothesis that no-significant difference exist is accepted. Interestingly, researchers^3,4 gave the short durations of 60 minutes or less as the reliable but typical time of concentration for small urban catchment storm drain design. Therefore, it will suffice to state that the short duration downscaling using either of the IMD, AIMD or better the MCIMD methods will be appropriate for IDF modeling for urban storm drain where there are no automated rain gauges to record both rainfall amount and duration concurrently.

Hence, confirming the merit in the application of 1 hour duration in various storm design investigations.^11,25 For durations between 90–300 minutes, the result shows that for the GEVT-1 and ND the K (observed) maintained lower values over the K (critical) and slightly higher p-values except at 100 year return period where the K (observed) was 8.4485 with also a lower p-value of 0.0376 for both distributions. In contrast, the case of the LPT-3 was different as the K (observed) of 7.8750 at 2 year return period was higher than the K (critical) with a lower K (observed) value for the rest of return periods. Similarly, the p-value exhibited the same trend of being slightly lower at 2 year return period while being slightly higher value for other return periods than the alpha value (0.05). Thus, amongst the three model types it is the LPT-3 that showed better distribution and performance at 90–300 minutes duration, and this result agrees with the report in literature.^14,15,26 Wherein, for design purposes the LPT-3 model type ranks 1^st, the GEVT-1 came 2^nd, and ND occupied the 3^rd position; where either the 1st or 2^nd general PDF-IDF model type can be used along with any of the improved short duration downscaling methods.^27–29

The objective of improvement in predictive performance of the IMD method was achieved by integration of the probability of distribution into the original IMD and re-evaluated by optimization technique to obtain improved exponent and constant values contained in the IMD, AIMD and MCIMD formula. Three type of general PDF-IDF models (GEVT-1, LPT-3 and ND) were developed based on the downscaling methods yielding goodness of fit (R²) of 0.995 – 0.999 and model accuracy with mean square error (MSE) of 4.123 – 7.85. For LPT-3 PDF-IDF model based on MCIMD model for 60 – 300 minutes duration had higher improved performance in prediction of intensities relative to the original IMD. The range of improvements were from 35.17 to 52.26% and 25.0 to 39.89% for 10 and 100 year return periods, respectively. The AIMD level of improvement ranges from 10.97 to 20.87% and 3.33 to 12.53% for 10 and 100 year return periods, respectively. However, it was also observed that the predicted intensity values of the IMD PDF-IDF models were consistently higher than their PDF-computed intensity values. Also, intensities derived from the original IMD model can be adopted by multiplying with an adjustment factor and this approach can subsequently be applied in any catchment area. A comparison of the downscaling models indicates that the distribution of the intensities for the IMD model showed lower intensities prediction closely followed by the AIMD model with the MCIMD model consistently higher. Also, the LPT-3 PDF-IDF model type performed better than GEVT-1 and ND PDF-IDF models in terms of best-fit and high intensity prediction with least bias. However, the general PDF-IDF models developed, predicted intensities for short durations less than or equal to 1 hour matched that of the control experiment for all return periods. Kruskal-Wallis non-parametric test of significance at 5% level conducted for 15 - 60 minutes duration confirmed that no-significant difference exists, but was rejected for 90 – 300 minutes. Therefore, short duration downscaling methods are adequate and hereby recommended for IDF.

None.

The author declares there is no conflict of interest.

1. Willems P, Arnbjerg-Nielsen K, Nguyen VTV. Climate Change Impact Assessment on Urban Drainage: Methods and Shortcomings. Amos Res. 2012;103:106–118.
2. Heaton MJ, Katzfuss M, Ramachandar S, et al. Spatio-temporal Models for Large- scale Indicators of Extreme Weather. Environmetrics. 2011;22(3):294–303.
3. Adamowski K, Bougadis J. Detection of Trends in Annual Extreme Rainfall. Hydrological Processes. 2006;17:3547–3560.
4. Cheng L, A AghaKoucak, Gilleland E, et al. Non-stationary Extreme Value Analysis in a Changing Climate. Climate Change. 2014;127(2):353–369.
5. Akpan SU, Okoro BC. Developing Rainfall Intensity – Duration – Frequency         Models for Calabar City, South-South, Nigeria. American Journal of Engineering Research (AJER). 2013;2(6):19–24.
6. Ologhadien I, Nwaogazie IL. Rainfall Intensity-Duration-Frequency Models for Selected Cities in Southern Nigeria. Standard Scientific Research and Essays. 2014;2(10):509– 515.
7. Nwaogazie IL, Ekwueme MC. Rainfall Intensity – Duration – Frequency (IDF) Models for Uyo City, Nigeria. International Journal of Hydrology. 2017;1(3):63–66.
8. Akpen GD, Aho MI, Musa AA. Rainfall Intensity – Duration – Frequency Models for Lokoja Metropolis, Nigeria. Global Journal of Pure and Applied Sciences. 2018;24:81–90.
9. David AO, Nwaogazie IL, Agunwamba JC. Modeling Rainfall Intensity by Optimization Technique in Abeokuta, South-West, Nigeria. Jour of Engg Research and Reports. 2019;6(4):1-10.
10. David AO, Nwaogazie IL, Agunwamba JC. Development of Models for Rainfall Intensity-Duration-Frequency for Akure, South-West, Nigeria. Inter Jour of Env And Climate Change. 2019;9(8):457–466.
11. Ramaseshan S. Urban Hydrology in Different Climate Conditions. Lecture Notes of the International Course on Urban Drainage in Developing Countries, Regional Engineering College, Warangal, India. 1996.
12. Burgess CP, Taylor MA, Stephenson T, et al. Frequency Analysis, Infilling, and Trends for Extreme Precipitation for Jamaica (1895-2100). Journal of Hyrdology: Regional Studies. 2014;3(2015):424–443.
13. Rasel MM, Hossain SM. Development of Rainfall Intensity Duration Frequency (R-IDF) Equations and Curves for Seven Divisions in Bangladesh. International Journal of Scientific and Engineering Research. 2015;6(5):95–101.
14. Dakheel AA. Drawing Curves of the Rainfall Intensity Duration Frequency (IDF) and Assessment Equation Intensity Rainfall for Nasiriyah City, Iraq. Journal of Thi-Qar University. 2017;12(2):63–78.
15. Hamaamin YA. Developing of Rainfall Intensity - Duration – Frequency Model for Sulaimi City. Journal of Zankoy Sulaimani. 2017;26(5):3–4.
16. Diwan PC, Karanam HK. Hydrological Analysis for Planning Rooftop Rainwater Harvesting of Urban Area. SSRG International Journal of Civil Engineering (SSRG-IJCE). 2020;7(1):1–15.
17. Udosen CE. Rainfall Trends in Uyo-Akwa Ibom State and its Implication on Urban Flooding. Journal of Engineering and Applied Sciences. 2012;7(1):79–85.
18. Rashid M, Faruque S, Alam J. Modelling of Short Duration Rainfall Intensity Duration Frequency (SDRIDF) Equation for Sylhet City in Bangladesh. ARPN J Sci Technol. 2012;2:92–95.
19. Chow VT, Maidment DR, Mays LW. Applied Hydrology. 1st ed. McGraw-Hill, New York. 1988.
20. Zakwan Mohammad. Application of Optimization Techniques to Estimate IDF Parameters. Water and Energy Research Digest (Water Resources Section). 2016;1–3.
21. Nwaogazie IL, Sam MG. Probability and non-probability rainfall intensity-duration-frequency modeling for Port Harcourt metropolis, Nigeria. International Journal of Hydrology. 2019;3(1):66–75.
22. Nwaogazie IL, Sam MG, David AO. Predictive Performance Analysis of PDF-IDF Model Types Using Rainfall Observations from Fourteen Gauged Stations. International Journal of Environment and Climate Change. 2021;11(1):125–143.
23. Chow VT. A General Formula for Hydrologic Frequency Analysis. Trans American Geophysics Union. 1951;32:231–237.
24. Chen WF, Richard JY. The Civil Engineering Handbook. 2nd ed. CRC Press LLC, New York. 2003.
25. Cheng L, Agha Kouchak A. Nonstationary Extreme Value Analysis (NEVA) Software Package: User Guide. Centre for Hydrology & Remote Sensing, University of California, Irvine. 2014a.
26. AlHassoun SA. Developing an Empirical Formulae to Estimate Rainfall Intensity in Riyadh Region. Journal of the King Saud University – Engineering Sciences. 2011;23:81–88.
27. Kite GW. Frequency and risk analyses in hydrology. Water Resources Publication, Fort Collins, Colorado, US. 1977.
28. Nwaogazie IL. Probability and Statistics for Science and Engineering. 3rd edn. De-adroit Innovation, Enugu – Nigeria. 2011.
29. Nwaogazie IL, Okonkwo SC. Rainfall Intensity-Duration –Frequency Modeling and Comparative Analysis Development Models for Abakiliki, Ebonyi State, Nigeria. International Journal of Trend in Research and Development. 2017;4(2):2394–9333.