Flooding is a significant impact that regularly affects the majority of cities/towns in developing countries due to inadequate drainage systems that were designed without considering hydrological-hydraulic efficiency caused by design rainfall intensity. Design rainfall intensity is essential to urban stormwater management systems; however, obtaining long-term, short-term design rainfall in developing countries such as Ethiopia is challenging. As a result, this study is conducted to derive short-term design rainfall intensity from daily rainfall data for Robe town using three empirical equations for urban drainage design: Indian Meteorological Method (IMD), Modified Indian Meteorological Method (MIMD), and Ethiopian Road Authority Method (ERAM). The results show that the estimated design rainfall by IMD is greater than other methods; the relationship between IMD, MIMD, ERAM, and existing ranges from 0.57 to 1.001, 1.015 to 1.218, and 0.890 to 1.027, respectively. According to the findings of this study, the design rainfall intensity of all empirical equations is not the same in all return periods and durations. Furthermore, the peak stormwater that caused flooding will vary due to variations in rainfall intensity. Thus, this study strongly suggested that the experts consider each empirical equation and select the accurate design rainfall to design adequate stormwater drainage systems for Robe Town. To manage unexpected urban inundation caused by urban development, short-duration design rainfall and other sub-catchment characteristics will need to be considered.

Keywords: daily rainfall data, design rainfall intensity, empirical equation, IMD, MIMD, ERA

The stormwater quantity in the worldwide city/town increased as the impervious surface cover, such as buildings, roads, and other paved surface areas, increased over time due to urban growth. This resulted in urban flooding problems in developing countries with inadequate drainage systems not designed considering different factors. These problems had a significant impact on cities on a regular basis, disrupting the regular activity of households on an hourly basis and causing infrastructure damage and flooding on the main pavement.^1,2 Furthermore, it disrupts the city's service line by causing damage to the water supply, poorly constructed sewerage, power transmission lines, communication, transportation, and other community infrastructure, requiring early waring systems.³ Therefore, as previously noted, the relationships between rainfall intensity-duration-frequency (IDF) and its impact on urban hydrological response are required to alleviate this challenge. For example, Nwaogazie et al.⁴ highlighted that shorter durations of rainfall intensity are essential to designing flood mitigation structures for urban, semi-urban and rural settlements. Saraswat et al.⁵ and Elsebaie⁶ also stated that IDF relationships are the most important tools engineers use when designing flood management structures like culverts, sewers, control and routing structures, ponds, street curbs, and other structural mitigation measures. However, due to a lack of long years of short-term rainfall data at specific locations, it isn't easy to analyse the hydrological response of urban catchments and design engineering structures such as stormwater management systems.⁷ Furthermore, different hourly/sub-hourly time scales (e.g., 5, 15, 30, 45, 60, 120, 360 minutes, etc.) for long consecutive years must be available to obtain accurate and precise IDF relationships that can be used for design purposes.⁸

Inundation has recently become a significant risk in developing countries such as Ethiopia cities/towns such as Robe, Dire Dawa, Adama, and Dodola due to inadequate drainage systems.^9–11 Robe Town, in particular, requires new adequate hydrological-hydraulic drainage systems to reduce flooding. However, due to instrumentation limitations, short-term rainfall is unavailable in most Ethiopian cities; data is only measured daily. Several studies have been done to overcome this challenge and develop different experimental and analytical equations for other areas worldwide.^12,7 As Allard et al.¹³ demonstrated, some of these equations are simple and have appropriate accuracy, while others are complex in calculating short-duration rainfall and parameter estimation. Hershfeld (1961) proposed one of the earliest equations for estimating rainfall depth (P_tT) in the United States, with t-duration (minute) and T-year return period (year), which was later modified and extended by Bell (1969). This equation is still widely used in water resource projects, but it is only applicable for rainfalls lasting 5 to 120 minutes with return periods lasting 5 to 100 years.⁸ Many researchers modified and calibrated the Hershfeld equation to derive short-term rainfall from 24-hour data in different regions of the world other than the United States.¹⁴

In spite of derivation of short-term design rainfall intensity from daily rainfall data by relating different parameters such as near-surface temperature, wind, humidity, geospatial height, and sea level pressure is very difficult and time-consuming.^15–18 Other studies attempted to estimate short-duration rainfall using various statistical methods such as multivariate regression,¹⁹ logarithmic graph fitting,⁷ L-moment method,²⁰ and statistical distribution fitting techniques.²¹ Though, these statistical methods require effort and more time. Other researchers used a non-paramteric method (K-nearest neighbour resampling), method of the fragment, and random cascade for converting daily rainfall data to sub-daily. These methods are not easy, and the methods' accuracy differs for different rainfall resolutions.^22–24

Later, the India Meteorological Department (IMD) developed one of the simplest and most straightforward empirical equations, which is widely used in India and other parts of the world.^12,8,25,26 Due to the power of this equation caused different accuracy at different rainfall stations, many other researchers improved this equation for different regions than India by changing its power.^4,27 Furthermore, the Ethiopian Road Authority (ERA) equation was recently used to design an urban drainage network in Ethiopia.^28–30 It is simple and widely used to calculate design rainfall intensity from daily rainfall data. However, each method has limitations that make urban drainage systems inadequate. As a result, this study compared the estimated short-duration design rainfall intensities using three empirical equations: IMD, MIMD, and ERAM from daily rainfall data. As a result, this study's output would enable quick development of short IDF relations used for designing urban stormwater infrastructures.

Study area and data used

The Robe town is situated in South-Eastern Ethiopia. Figure 1 illustrates the location of the study area, land-use, and slope. The study area is located between 7°5'20" to 7°10'40"N latitude and 39°56'00" to 40°6'40"E longitude, with elevations ranging from 2413 to 2520 meters above mean sea level. The cross-country road from Addis Ababa to Goba town crosses the city. It is surrounded by agricultural farms, ongoing land development, and on the northern side, surrounded by the Shaya River. According to the slope map shown in Figure 1, the mean slope ranges from 0 to 16%, with most of the area covered by gentle and sloping slopes covering 20% and 40%, respectively. The total catchment area of the study area is approximately 6680 ha. The town has mean maximum and minimum temperatures 28 ^oC and 14 ^oC, with an average rainfall of 712 mm, especially during April. Based on the quality of the data, historical rainfall data from five stations obtained from the Ethiopian National Metrological Agency were included in this study from 1989 to 2020 (30 years). Table 1 presents the locations, record lengths, and geographical coordinates of selected stations in and around Robe town.

Figure 1 Study area location maps a) land-use map, and b) slope maps.

A long period and short-duration rainfall intensity are required to design stormwater management systems; however, obtaining this data in the study area is difficult. Therefore, after analysis and the data quality was checked, the daily rainfall data were used to derive design rainfall intensity from daily data. The obtained rainfall data from the stations may be incomplete due to various factors such as the absence of an observer, instrument failure, and shifting of the gauge station location. However, there are different most commonly used methods by earlier reserachers for filling the missed data, such as arithmetic mean, Normal ratio, Inverse distance, Regression, and Power.^31,32

The missing rainfall (Px) was estimated in this study using the normal ratio method (Eq. 1) because the percent difference between the annual rainfall of the missing data station and each of the annual precipitation of the nearby stations was greater than 10%.³³ This demonstrates significant variations in rainfall data from gauge station to gauge station. The majority of the stations are in the same climate zone. Robe station, for example, has long continuous records and is located in the center of Robe town, the capital city of the Bale zone, with nearly 78.3% of its surface covered by impervious surface area. The rain gauges at Ali and Dinsho are about 9 and 21 kilometers west of town, respectively. The station's altitude ranged from 2130 m to 2563 m in this study. The highest altitude in the study area is at Robe (2563 m), while the lowest is at Ali (2130 m) (Table 1).

$Px= \frac{Nx}{m}x\left(\frac{P1}{N1}+ \frac{P2}{N2}+\frac{P3}{N3}\dots +\frac{Pn}{Nn}\right)$    (1)

Where P_x is missing rainfall data at station x, and P₁, P₂, and Pn are precipitation at particular times and stations. m is the number of neighboring stations, Nx is the missing data station's normal annual rainfall, and N₁, N₂, and N_n are the neighboring stations’ normal annual rainfall.

The consistency of a station's rainfall record was checked using the double mass curve, the most commonly used method of checking consistency, before using the data in this study.³⁴ The ratio was calculated as the slope of the straight lines before and after the graph change to correct inconsistencies in station rainfall records. The Grubbs and Beck (G-B) test then identifies outliers in rainfall data.³⁵

Estimation of short-duration rainfall

In this study, rainfall depth for various short durations (i.e., 5, 15, 30, 45, 60, 120, 360, and 720 minutes) was estimated from annual maximum values using Indian Meteorological Department (IMD), Modified Indian Meteorological Department, and Ethiopian Road Authority empirical formula. Numerous researchers used these equations to estimate short-term rainfall from 24-hour rainfall data in different locations and found that these formulas give the best short-term rainfall estimation. For example,²⁷ used IMD to model a short-duration isopluvial map for Raichur district, Karnataka, and Rashid et al.³⁶ also used the same equation to derive sub-hourly rainfall from daily data in Sylhet city. Furthermore,⁸ used MIMD to calculate sub-daily rainfall for five selected stations from daily rainfall data. They noticed that the power of these equations differed at each corresponding rainfall station.

Similarly,²⁸ used ERAM to analyze the hydraulic efficiency of stormwater drainage systems in Alamata town, Ethiopia. According to the suggestion of earlier studies, the accuracy of each method varies from station to station; this means there is no more accurate equation to estimate at each selected rainfall station. This study compared the results of these selected empirical equations (Eqs. 2-4). First, the maximum daily rainfall for each year was extracted.

$Pt=24{{\displaystyle \left(\frac{t}{24}\right)}}^{1/3}$   (2)

$Pt=P24 {\left(\frac{t}{24}\right)}^m$   (3)

$Pt=P24x\left(\frac{t}{24}\right){{\displaystyle \left(\frac{b+24}{b+t}\right)}}^n$   (4)

Where: P_t is the required rainfall depth in mm at t-hr duration, P₂₄ is the daily rainfall in mm, t is the duration for depth of rain required in hr, and m is the regional coefficient which can vary in various regions and obtain by calibration.^28,4

Frequency distribution analysis of rainfall intensity

The rainfall intensity (I_T) for selected return periods with different short-term durations can be estimated using a chosen probability distribution. These estimated rainfall intensities are used for developing the rainfall intensity-duration-frequency (IDF) curves needed to calculate design rainfall for stormwater management systems. Different probability distribution methods, such as Normal, Log-normal, Gumbel maximum Log-Pearson III, Generalized extreme value, Wake by distribution, and others, were compared to determine the best-fit probability distribution method for Robe town rainfall data. The researchers used the widely used L-moment ratio diagram to select an appropriate probability distribution method to estimate different return period rainfall depth and intensity; then, three goodness-fit tests were used to confirm the method obtained from the graph. The basic steps outlined by Ahmad et al.,³⁷ were used.

After determining the quality of the rainfall, maximum daily data were ranked in ascending order of magnitude.

Determine the probability-weighted moment parameters (bo, b1, b2, and b3) for each probability distribution method using Eq. 5.

${{\displaystyle b}}_r=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[\frac{(i-1)(i-2)\mathrm{...}(i-r)}{(n-1)(n-2)\mathrm{...}(n-r)}\right]}X(i)$   (5)

Where X_(i) represents the arranged rainfall, with X_n being the smallest observation and X₁ the largest.

The calculation of the first four L-moment ratios of each probability distribution is defined as follows:

${{\displaystyle L}}_1=\beta o$   (6)

${{\displaystyle L}}_2=2\beta 1-\beta o$   (7)

${{\displaystyle L}}_3=6\beta 2-6\beta 1+\beta o$   (8)

$L4=20\beta o-30\beta 2+12\beta 1-\beta o$   (9)

Based on the and, the L-coefficient of variation (), L-coefficient of skewness (), and L-moment ratio diagrams were plotted. From the diagram, the ratio of  and  goes near the most appropriate probability distribution in the diagram.

$\tau 2=\frac{L2}{L1}$   (10a)

$\tau 3=\frac{L3}{L2}$   (10b)

$\tau 4=\frac{L4}{L2}$   (10c)

The best-fitted probability distribution method from the graphical judgement was re-checked and confirmed using the statistics tests: Kolmogorov-Smirnov (KS), Anderson-Darling (AD), and Chi-Square (x²). According to Alam et al.³⁸ and Ghosh et al.³⁹ no distribution method was ranked first in all tests. According to the X² value, the Pearson Type III probability distribution function provides the best estimation of the distributed predicted rainfall data because it has the smallest value, i.e., 9.82, compared to other distribution functions. However, based on the Anderson-Darling test value, Generalized Pareto is the best-fitted method. Based on the L-moment ratio diagram and the lowest sum of three statistical goodness-fit tests, the GP method is the best probability distribution of rainfall data in the study area.⁴⁰ Therefore, the GP method was used to estimate the rainfall depth P_T (mm) and intensity I_T (mm/hr) for each duration with the return period of 2-yrs, 5-yrs, 10-yrs, 25-yrs, 50-yrs, and 100-yrs.

Derivation of short-term design rainfall from IDF curves

The IDF curves allow for deriving short-term design rainfall for a given return period over a range of duration times. Design engineers and hydrologists widely use the IDF curves to estimate the design rainfall required to design safe and cost-effective flood mitigation measures and flood control structures. Peak runoff for a given catchment is typically calculated using short-term IDF relationships in combination with empirical methods or hydrological models. Also, stormwater management systems such as trunk lines, manholes, culverts, sewer networks, and flood control structures are typically designed using IDF curves. However, in the absence of long-term hourly or sub-hourly rainfall IDF relationships, the expert designed infrastructures that are frequently inadequate and vulnerable to flooding, as seen more regularly in recent years in Robe, Ethiopia. To solve the problem, this study used three empirical equations to compare the design rainfall at various return periods with different short-term durations.

Moreover, the hydrological models such as SWMM and PCSWMM require design rainfall to be estimated using selected formula format as input data for the simulation of the hydrological-hydraulic analysis. As suggested by Krvavica et al.,⁴¹ Berggren et al.,⁴², and Takele et al.,^43,44 there are various equations widely used in literature, such as the Talbot equation, Sherman formula, Bernard equation, Kimijima equation, and Chicago equation, that estimate the design rainfall for various duration and return periods.^45,46 This study used the Sherman equation (Eq. 11) to estimate the inputted design rainfall from IDF curves, as recommended in the literature.⁴⁷ Later, the estimated design rainfall from three empirical equations was compared with existing rainfall intensity to design an adequate drainage network.

$i\left(d,T\right)= \frac{a\left(T\right)}{{\left(b\left(T\right)+td\right)}^{c\left(T\right)}}$   (11)

Where i(d, T) is the intensity of rainfall (mm/hr) corresponding to a return period of T-years and to a duration of t_d-hours. In addition, 'a' is a coefficient in mm/hr units, 'b' is a time constant in hours, and 'c' is an exponent that is usually less than one.

One of the most important factors in determining peak stormwater in urban areas and designing stormwater management infrastructure such as conduits, culverts, stormwater drains, and flood mitigation measures is design rainfall. The inundation disrupts normal working activities because Robe Town has inadequate drainage networks. Inundation is caused by a lack of adequate drainage systems with urban development, as observed in the study area. As a result, the relationships of rainfall IDF estimated using three empirical equations were compared in this study. Because the designer requires design rainfall to re-design sustainable flood mitigation measures to mitigate the significant impacts of inundation, as presented.^43,44

Short-term rainfall estimated using empirical equations

The various short-duration rainfall depths like 5, 15, 30, 45, 60, 120, 240, 360, and 720 were estimated from 24-hourly rainfall using IMD, MIMD, and ERAM equations presented in Table 2. The Table 2–4 results revealed that each equation estimates no similar rainfall depth at each rainfall duration in each recorded year. This demonstrates how the outcomes of various empirical equations might affect the estimated short-term rainfall required to design flood management structures in specific areas. As Galoie et al.⁸ suggests, the first step is to compare its values before selecting any equation. For example, the estimated rainfall at 5 minutes by IMD, ERA, and MIMD, and is 7.2, 8, and 11.4 mm, respectively, and at 720 minutes by the same method is 37.8, 45.9, and 39.8 mm, respectively. In most cases, the MIMD empirical equation's rainfall estimate is greater than other methods. The rainfall estimated by the IMD equation is lower than that calculated by other empirical formulas. The results of both equations are not the same because the regional coefficient (m) of MIMD (0.259) is not equal to the power of IMD (0.333). This showed that the value of the exponent (m) that varies rainfall intensity is influenced by physiographic factors in the catchment area. Consistent with this study,⁴ downscaled 24 hourly rainfall to a shorter duration and improved the IMD equation by changing its power (n) for the Uyo metropolis.

Similarly,⁸ compared the n value for five selected stations located in different regions with different climatic conditions. They highlighted as due to the power of the IMD equation varied by ±15%, the estimated rainfall depth was also affected by the variation of the coefficient of the equation. Therefore, they improved this equation and got other MIMD that can be estimated with more accurate values. These revealed that the results of each equation could be affected by the geographic condition of the catchment and climatic conditions that can affect the power of each equation. This confirmed that the results of short-term rainfall estimated using considered equations differ in the study area at similar rainfall patterns. Estimation of the short-duration rainfall intensity for any specific area requires minimum effort as suggested by;^7,36 however, to get accurate results, a comparison of estimated findings should be required.

Comparison of various estimated rainfall intensity curves

The statistical variables (average and standard deviation) at the selected short durations (10, 20, 30, 60, 120, 180, 360, 720, 1440 min) were calculated from the raw data using the empirical reduction formulas of the MIMD, IMD, and ERA methods. These estimated statistical parameters were used to calculate rainfall intensity for selected return periods of 2, 5, 10, 25, 50, and 100 years using Eq. 2-4. Plots of estimated rainfall intensity versus short durations were made on the same graph sheets for the ERA, IMD, and MIMD methods for comparison, as shown in Figure 2–4. The findings show no discernible difference between the empirical methods used in this study; however, results revealed a significant difference between existing and predicted rainfall intensities.

Figure 2 The Existing, E.R.A, IMD & M.I.M.D estimated intensity curves for 2 and 5 years return period.

Figure 3 The Existing, E.R.A., IMD & M.I.M.D estimated intensity curves for 10 and 25 years return period.

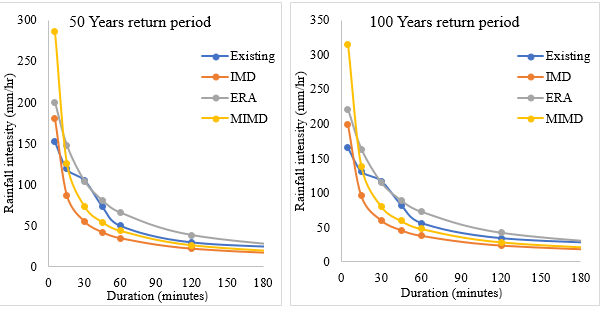
Figure 4 The Existing, E.R.A., IMD & M.I.M.D estimated intensity curves for 50 and 100 years return period.

IMD, ERA, and MIMD estimate the highest rainfall intensity at a 5-min duration and 100-year return period are 198.7 mm/hr, 220.6 mm/hr, and 315 mm/hr, respectively. Similarly, using the same method, the rainfall intensity at 720-minutes and 2 years is 3.1 mm/hr, 3.8 mm/hr, and 3.3 mm/hr, respectively. This demonstrated that it is essential to identify and select the best empirical equations that estimate rainfall intensity for the selected return periods at specific catchments. Overall, the IMD equation can estimate greater rainfall intensity than the other equation methods. Table 5 show the ratios that show the relationships between existing and computed rainfall intensity using empirical equations. Compared to existing rainfall intensity values, the IMD method had a very low bias ranging from 0.495-13.799 mm/hr and 2.346-15.586 mm/hr for 2 and 100 years return periods, respectively. Similarly, compared to the existing IDF, the MIMD has a high bias ranging from 2.129-34.123 mm/hr to 2.074-26.325 mm/hr for 2 and 100 years return periods, respectively. However, the difference between existing and estimated rainfall intensity using ERA ranges between 3.25-17.837 mm/hr and 2.346-15.586 mm/hr for 2 and 100 years return periods, respectively.

As a result, understanding the relationships between rainfall IDF by selected empirical equations, i.e., the formula has a low bias, is the first step to design adequate drainage to address the risk of flooding. The inundation has posed significant risks to human life and infrastructure in various areas of Robe town. It will be impossible to manage amplified floods using only the existing drainage systems with increasing impervious surface areas. The flooding in the study area hindered human movement and social activities. The existing drainage networks in most cities of Ethiopia are designed based on the experts' assumptions without considering urban growth and design rainfall of specific areas.⁴⁸ Due to this, flooding frequently happened in cities, as noted by Erena et al.⁴⁹. Hence, experts/designers must estimate accurate rainfall intensity to design safe and sufficient drainage systems such as culverts, sewers, drains, and other conveyance systems to mitigate the effects of current and future flooding.

Developing empirical IDF formula for estimation of design rainfall

It is essential to develop the mathematical equation of the rainfall IDF relationships, which allows for a more accurate estimation of rainfall intensity at each return period. The parameters of the Sherman equation considered in this study were estimated using MIDUSS and presented in Table 6. Due to the peak runoff exceeding the adequacy of drainage systems, the town frequently flooded and caused community complaints. Due to increased runoff from rapidly expanding new settlements, the constructed ditches along the main asphalt are heavily inundated during the rainy season. Particularly, the main asphalt from Welmal Cafe (518141.5E, 772125.8N) to Madda Walabu University (519359.2 E, 771266.3N) and from the city roundabout (519501.6E, 771241.5N) to the Siko Mando hotel (520355E, 771362.8N) was frequently flooded, resulting impeded transportation and community activities. As a result, the responsible body must respond quickly to the design of new adequate stormwater infrastructures and assess potential flooding risks in Robe town.

The parameters results show an increasing or decreasing trend with an increase in the return period. In all empirical equations, the coefficient parameter "a" values and the corresponding return periods have a statistically significant direct linear relationship. However, the value of "b" constant and "c" exponent increases and decreases as the return period increases. In some cases, all the values of a, b, and c increase with increases in return periods. No generalised pattern exists between the parameters ‘b’ and ‘c’ and the return periods. Overall, short-term design rainfall is required for designing safe and cost-effective urban drainage systems using statistical equations such as the Rational method and other hydrological models such as SWMM and PCSWMM.^50,51 The computed parameters were used to estimate rainfall intensity at various durations.^52,53

Rainfall analysis is one of the most common processes in most water engineering projects, particularly in urban stormwater management systems. In many developing countries, including Ethiopian rainfall stations, the rainfall depths are only available daily. To estimate an IDF relationship, the daily rainfall data should be converted to Sub-hourly and sub-daily, such as 1-, 2-, 6-, and 12-h. Several researchers have proposed various simple methods for converting daily to sub-daily rainfall depth, but the accuracy of these methods is not acceptable in some regions. Five stations were chosen to analyse the Robe town rainfall data because short-duration rainfall was not available. The study area's short-duration rainfall was estimated using three empirical reduction formulas: Indian Meteorological Method (IMD), Modified Indian Meteorological Method (MIMD), and Ethiopian Road Authority (ERA.) Method from 24-hourly rainfall data from 1990 to 2019. The Generalized Extreme Value method calculated the depth and intensity of sub-daily and sub-hourly rainfall at selected return periods. The IDF results of these three empirical equations were compared with the existing rainfall intensity. The findings showed that the accuracy of the MIMD method in estimating sub-daily (especially 6- and 12-h) rainfall depths was considerably increased compared to the IMD method. Overall the results of rainfall intensity estimated using the Ethiopian Road Authority downscaling method was relatively higher than other methods. Safe and cost-effective stormwater management systems based on accurate rainfall design will be required to mitigate the effects of increased flooding risks, which hampered community movement and disrupted transportation activities. For further studies, it is suggested that more station data near the catchment verify the results obtained or increase the accuracy for converting the daily to 1-hour or less duration rainfall.

None.

The author declares there is no conflict of interest.

1. Manawi SMA, Nasir KAM, Shiru MS, et al. Urban flooding in the northern part of Kabul City: causes and mitigation. Earth Systems and Environment. 2020;4:599–610.
2. Wang X, Xia J, Zhou M, et al. Assessment of the joint impact of rainfall and river water level on urban flooding in Wuhan City, China. Journal of Hydrology. 2012;613:128419.
3. Singh P, Sinha VSP, Vijhani A, et al. Vulnerability assessment of urban road network from urban flood. International Journal of Disaster Risk Reduction. 2018;28:237–250.
4. Nwaogazie IL, Sam MG, Ikebude C. Improving Indian meteorological department method for 24- hourly rainfall downscaling to shorter durations for IDF modelling. International Journal of Hydrology. 2021;5(2):72–82.
5. Saraswat C, Kumar P, Mishra BK. Assessment of stormwater runoff management practices and governance under climate change and urbanization: An analysis of Bangkok, Hanoi and Tokyo Chitresh. Environmental Science and Policy. 2016;64(1):101–117.
6. Elsebaie IH. Developing rainfall intensity--duration--frequency relationship for two regions in Saudi Arabia. Journal of King Saud University-Engineering Sciences. 2012;24(2):131–140.
7. Al Mamun A, bin Salleh MN, Noor HM. Estimation of short-duration rainfall intensity from daily rainfall values in Klang Valley, Malaysia. Applied Water Science. 2018;8(7):1–10.
8. Galoie M, Kilanehei F, Motamedi A, et al. Converting Daily Rainfall Data to Sub-daily—Introducing the MIMD Method. Water Resources Management. 2021;35(11):3861–3871.
9. Adisu M, Hailemikael M. An Approach to Drainage System Sustainability in Wolaita Soddo Town: A Case Study from Southern Ethiopia. Int J Waste Resour. 2007;7(271):2.
10. Bulti DT, Mekonnen B, Bekele M. Assessment of Adama city flood risk using multicriteria approach. The Ethiopian Journal of Science and Sustainable Development (EJSSD). 2017;4(1):6–23.
11. De Risi R, Jalayer F, De Paola F, et al. From flood risk mapping toward reducing vulnerability: the case of Addis Ababa. Natural Hazards. 2020;100:387–415.
12. Palaka R, Prajwala G, Navyasri KVSN, Anish IS. Development of Intensity Duration Frequency Curves for Narsapur Mandal, Telangana State, India. International Journal of Research in Engineering and Technology. 2016;05(06):109–113.
13. Allard D, Bourotte M. Disaggregating daily precipitations into hourly values with a transformed censored latent Gaussian process. Stochastic Environmental Research and Risk Assessment. 2015;29(2):453–462.
14. Ghahraman B Abkhezr H. Improvement in intensity-duration-frequency relationships of rainfall in Iran. JWSS-Isfahan University of Technology. 2004;8(2):1–14.
15. Ali H, Mishra V. Contributions of dynamic and thermodynamic scaling in subdaily precipitation extremes in India. Geophysical Research Letters. 2008;45(5):2352–2361.
16. Lepore C, Allen JT, Tippett MK. Relationships between hourly rainfall intensity and atmospheric variables over the contiguous United States. Journal of Climate. 2016;29(9):3181–3197.
17. Schröer K, Kirchengast G. Sensitivity of extreme precipitation to temperature: the variability of scaling factors from a regional to local perspective. Climate Dynamics. 2018;50:3981–3994.
18. Utsumi N, Seto S, Kanae S, et al. Does higher surface temperature intensify extreme precipitation? Geophysical Research Letters. 2011;38(16).
19. Koutsoyiannis D, Onof C, Wheater HS. Multivariate rainfall disaggregation at a fine timescale. Water Resources Research. 2003;39(7).
20. Galoie M, Zenz G, Eslamian S. Application of L-moments for IDF determination in an Austrian basin. International Journal of Hydrology Science and Technology. 2013;3(1):30–48.
21. Haddad K, Rahman A, Green J, et al. Design rainfall estimation for short storm durations using L-moments and generalised least squares regression-application to Australian data. Int J Water Res Arid Environ. 2011;1:210–218.
22. Bakhshi M, Al Janabi F. Disaggregation the Daily rainfall dataset into sub-daily resolution in the temperate oceanic climate region. International Journal of Marine and Environmental Sciences. 2019;13(1):11–16.
23. Li X, Meshgi A, Wang X, et al. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. International Journal of Climatology. 2018;38:e1119–e1138.
24. Park H, Chung G. A nonparametric stochastic approach for disaggregation of daily to hourly rainfall using 3-day rainfall patterns. Water. 2020;12(8):2306.
25. Rasel MMHS. Development of Rainfall Intensity Duration Frequency (R-IDF) Equations and Curves for Seven Divisions in Bangladesh. International Journal of Scientific & Engineering Research. 2015;6(5):96–101.
26. Rosbjerg D, Madsen H. Initial design of urban drainage systems for extreme rainfall events using intensity--duration--area (IDA) curves and Chicago design storms (CDS). Hydrological Sciences Journal. 2019;64(12):1397–1403.
27. Parvez MB, Parvez MB, Parvez MB. Modelling of Short Duration Isopluvial Map for Raichur District Karnataka Modelling of Short Duration Isopluvial Map for Raichur District Karnataka. IJSART. 2019;5(4).
28. Zinabie A, Kebede B. Hydraulic Analysis of Storm Water Drainage System in Alamata Town, South Tigray, Ethiopia. Journal of Energy & Environment. Journal of Energy & Environment. 2020;11(1):40–50.
29. FUPCoB. Urban stormwater drainage design manual of Ethiopia. Ministry of Works and Urban Development Federal Urban Planning Coordinating Bureau. 2008.
30. ERA. The Federal Democratic Republic of Ethiopia Ethiopian Roads Authority Route Selection Manual. 2013.
31. Sattari MT, Rezazadeh-Joudi A, Kusiak A. Assessment of different methods for estimation of missing data in precipitation studies. Hydrology Research. 2017;48(4):1032–1044.
32. Jahan F, Sinha NC, Rahman MM, et al. Comparison of missing value estimation techniques in rainfall data of Bangladesh. Theoretical and Applied Climatology. 2019;136(3–4):1115–1131.
33. Nadiatul Adilah AAG, Hannani H. Comparison of Methods to Estimate Missing Rainfall Data for Short Term Period at UMP Gambang. IOP Conference Series: Earth and Environmental Science. 2021;682(1):012027.
34. Gebreigziabher ET. Analysis Rainfall Intensity-Duration-Frequency relationships Under Climate Change for Mekele City, Ethiopia. International Journal of Technical Research & Science. 2020;05(02):1–11.
35. Ramachandra Rao KHH. Flood frequency analysis. CRC press. 2019. p. 376.
36. Rashid MM, Faruque SB, Alam JB. Modeling of Short Duration Rainfall Intensity Duration Frequency (SDR- IDF)Equation for Sylhet City in Bangladesh. ARPN Journal of Science and Technology. 2012;2(2):92–95.
37. Ahmad I, Khan DA, Almanjahie IM, et al. At-site rainfall frequency analysis using partial duration series and annual maximum series: A case study. Applied Ecology and Environmental Research. 2019;17(4):8351–8367.
38. Alam A, Emura K, Farnham C, et al. Best-fit probability distributions and return periods for maximum monthly rainfall in Bangladesh. Climate. 2008;29(1):141–150.
39. Ghosh S, Roy MK, Biswas SC. Determination of the best fit probability distribution for monthly rainfall data in Bangladesh. American Journal of Mathematics and Statistics. 2016;6(4):170–174.
40. Overeem A, Buishand A, Holleman I. Rainfall depth-duration-frequency curves and their uncertainties. Journal of Hydrology. 2008;348(1–2):124–134.
41. Krvavica N, Rubinić J. Evaluation of design storms and critical rainfall durations for flood prediction in partially urbanized catchments. Water. 2020;12(7):21–44.
42. Berggren K, Packman J, Ashley R, et al. Climate changed rainfalls for urban drainage capacity assessment. Urban Water Journal. 2014;11(7):543–556.
43. Takele SB, Kara KG, Bedada HJ, et al. Application of PCSWMM for assessing the impacts of urbanization and climate changes on the efficiency of stormwater drainage systems in managing urban flooding in Robe town, Ethiopia. Journal of Hydrology: Regional Studies. 2023;45:101291.
44. Takele SB, Kefale GK. Evaluation of climate change, urbanization, and low-impact development practices on urban flooding. Heliyon. 2023;9(1):e12955.
45. Lin GF, Chen LH, Kao SC. Development of regional design hyetographs. Hydrological Processes: An International Journal. 2005;19(4):937–946.
46. Te Chow V, Maidment DR, Mays LW. Applied hydrology. Journal of Engineering Education. 1962;308:1959.
47. Bui Thi Thu Trang, Nguyen Thi Hong Hanh, Nguyen Thi Hoai Thuong, et al. Analysis of Storm Pattern for Design Urban Drainage System in the Monsoon Areas of Vietnam. Journal of Environmental Science and Engineering A. 2018;7(2):5–8.
48. Bulti DT, Abebe BG. Analyzing the impacts of urbanization on runoff characteristics in Adama city, Ethiopia. SN Applied Sciences. 2020;2(7):1–13.
49. Erena SH, Worku H. Dynamics of land use land cover and resulting surface runoff management for environmental flood hazard mitigation: The case of Dire Daw city, Ethiopia. Journal of Hydrology. 2019;22(1):598–611.
50. Grafius DR, Corsanje R, Warren PHKL, et al. The impact of land use land cover scale on modeling urban ecosystem services. Landscape Ecology. 2016;31(7):1509–1522.
51. Hossain S, Guna Alankarage Hewa SWH. A comparison of continuous and event-based rainfall–runoff (RR) modelling using EPA-SWMM. Water. 2019;11(3):611–625.
52. Palaka R, Prajwala G, Navyasri KVSN. Development of intensity duration frequency curves for Narsapur Mandal, Telangana state, India. International Journal of Research in Engineering and Technology. 2003;11(6):2321–2346.
53. Parvez MB, Inayathulla M. Modelling of short duration isopluvial map for Raichur district Karnataka. International Journal for Science and Advance Research in Technology (IJSART). 2009;5(4):973–976.