Probable Maximum Precipitation (PMP) is used for estimating Probable Maximum Flood (PMF) which, in turn, is used for design of major hydraulic structures, such as dams and spillways, flood protection works, and nuclear power plants. One of the commonly used methods for estimating PMP is the statistical method, also called Hershfield method that entails computation of frequency factor, adjustment of the frequency factor, construction of an enveloping curve of the frequency factor, estimation of PMP, choosing a probability distribution of PMP, and determination of the return period of PMP. There are, however, uncertainties associated with the PMP values estimated using the statistical method. This study determined the PMP values for different durations using the statistical method with data from the Brazos River basin, Texas. It was found that significant uncertainty in the PMP estimates can occur with the use of enveloping curve of the frequency factor and the number of stations involved in its construction. Hershfield’s curve yielded higher frequency factor values by 16% for 1 hour duration, by 17.9% for 6 hour duration, and by 22.1% for 24 hour duration. In comparison with basin-specific values, the PMP values from the Hershfield enveloping curve were 16.8% higher for 1-hour duration, 18.5% for 6-hour duration, and 23.4% for 24-hour duration. For most of the Brazos River basin the return period of the PMP values was in the range of 1000 to 3000 years which was less than the range of 10³ to 10⁶ years reported in HMR 51, showing the degree of risk associated with the PMP values. Therefore, a basin specific-enveloping curve is suggested. From 24 commonly used statistical distributions and 5 goodness of fit tests, the Burr Type XII distribution was found to be the best frequency distribution for describing PMP. It was observed that the return period obtained from the Burr type XII frequency distribution was not significantly higher than that obtained from the hydreometeorological reports (HMRs) of National Weather Service and other studies.

Keywords: probable maximum precipitation, statistical method, frequency factor, enveloping curve, uncertainty, hershfield method, burr xii distribution

Probable Maximum Precipitation (PMP) is termed as “theoretically the greatest depth of precipitation for a given duration that is physically possible over a given size storm area at a particular geographic location at a given time of the year”.¹ Originally PMP was defined as the Maximum Possible Precipitation (MPP), the value of precipitation that could not be exceeded. However, MPP values have been exceeded² and because of the complex atmospheric interactions contributing to extreme precipitation its name was changed to PMP. Since the 1940s, the National Weather Service has published a series of Hydrometeorological Reports (HMRs) that describe procedures for deriving the PMP values for the majority of United States. The main assumption in these procedures for PMP calculation is that there is the optimum combination of available moisture in the atmosphere and efficiency of the causative mechanism in the storm that will cause maximum precipitation. PMP is used for the calculation of Probable Maximum Flood (PMF) which is then used for the design of hydraulic structures, such as large dams and spillways, flood control works, levees, and nuclear power plants. PMF is used to size the hydraulic structures such that the risk of their failure is minimized.³ There are, however, uncertainties involved in the PMP estimation regardless of the method used to calculate it. An upper bound with zero risk is not realistic, as there have been instances where storms in USA have exceeded the PMP estimates.⁴ and the recorded floods have exceeded the estimated PMFs.⁵

PMP has been used to predict the volume, timing, and peak flow of extreme flood events all around the world. Designers obtain PMP values from hydrometeorological reports (HMRs) produced by the U.S. Bureau of Reclamation (USBR) and National Weather Service (NWS). However, these HMR documents provide generalized precipitation values that are not basin specific. Hence, they tend to represent the largest PMP values across broad regions. Many site-specific studies in the past have produced different PMP values compared to HMR published values.⁶ There is therefore a need to determine basin-specific PMP which can then be used for the calculation of PMF. Such PMP can incorporate basin characteristics that are specific to the local topography and climate. Hence, to quantify the uncertainty with PMP, frequency analysis of extreme precipitation is needed. The objective of this study therefore was to estimate PMP values for different durations and locations in the Brazos River basin using the statistical method and determine the associated uncertainty. To achieve this objective, specific objectives were to:

1. Construct a basin-specific enveloping curve of frequency factor for the Brazos River basin and calculate the PMP values by using it and construct the Isohyetal maps of PMP values;
2. Determine the best-fit probability distribution for extreme precipitation and the probability of exceedance of PMP values for the Brazos River basin; and
3. Compute the uncertainties associated with the statistical estimates of PMP values arising from the uncertainties due to the choice of probability distribution, number of stations, and frequency factor, and calculate the return periods of calculated PMP values.

The paper is organized as follows. With the introduction in this section, methods of computing PMP are discussed in section 2, followed by a discussion of uncertainty in PMP in section 3. The methodology of estimating PMP is discussed in section 4 and computation of the return period of PMP is outlined in section 5. The paper is concluded in section 6.

There are different methods used for PMP estimation which can be categorized as hydrometeorological and statistical. Common hydrometeorological methods^7‒9 include moisture maximization method,¹⁰ storm transposition method, generalized method, storm separation method¹¹ and depth-area-duration method. Common statistical methods include the Hershfield method and its variants and multifractal method. In moisture maximization the storm precipitation is increased to such a value that is consistent with the maximum moisture in the atmosphere for the storm location and the month of occurrence.¹² The basic assumptions in this method are that precipitation is linearly related to precipitable water. Storm transposition is associated with the relocation of storm precipitation within a region that is homogeneous relative to terrain and meteorological features important to the particular storm rainfall. The basic assumption here is that a meteorologically homogeneous region exists such that a major storm occurring somewhere in the region could occur anywhere else in the region. In the generalized method, the maximum recorded rainfall depths of rainstorms over a large area and adjustment source are made in applying the maximum recorded rain depths to a particular catchment.¹³ The generalized method has an advantage of using the maximum recorded rain depths for all combinations of area and duration and allowing for almost free transposition in space.^14,15 used the generalized method to estimate the PMP values for catchments of four large dam basins in India. It was assumed that the PMP values would result from the optimum combination of the available moisture in the atmosphere and the storm mechanism efficiency which was indirectly measured by observed precipitation.

Storm separation method is used particularly in orographic regions where the storm transposition method is inappropriate. It assumes that orographic and convergence rainfall amounts can be explicitly determined. The convergence rainfall is referred to as the free-atmospheric forced precipitation (FAFP) (HMR, 57). It develops PMP in terms of orographic and convergence components, and HMR 36 is one of the earliest reports which discusses this method. Recently, multifractal analysis has been used for PMP estimation. Multifractal, also known as multiscaling, is widely used to describe the scaling behavior of precipitation and streamflow. Douglas & Barros¹⁶ used this technique to calculate the physically meaningful estimates of maximum precipitation from observations in the eastern United States. The multifractal approach has an advantage in that it provides a formal framework to infer the magnitude of extreme events, called the fractal maximum precipitation (FMP), independently of empirical adjustments, at a site specific application of FMP in orographic regions. The method is constrained by the length of record, the spatial resolution of raingauge network, and the lack of uncertainty estimates. Of all the methods the statistical method, often called Hershfield¹⁷ method is more commonly used and can be applied, if long term precipitation data is available.^18,19 Bruce & Clark²⁰ in Canada and Myers²¹ in the U.S. have shown that the PMP estimates obtained by the Hershfield method are too far from those obtained by the moisture maximization and storm transposition methods. Wiesner²² argued that this method expressed the entire rainfall data set in terms of statistical parameters. Papalexiou & Koutsoyiannis¹⁴ showed that the statistical method for estimating extreme precipitation values was more consistent with natural behavior and provided a better basis for estimation than did moisture maximization. Since the Hershfield method is based on average precipitation and standard deviation of precipitation, it is similar to the Chow²³ frequency factor method, expressed as:

$P=\overline{X}+k_m{S}_n$ (1)

Where n is the number of annual maximum precipitation values corresponding to a given duration, is the sample mean,  is the sample standard deviation, and  is the frequency factor. Hershfield¹⁷ used 15 as the maximum value of  for computing PMP. Later in 1965, Hershfield³ found that an upper envelope of  had a tendency to decrease with increasing precipitation amount. In other words, the frequency factor decreases with increasing mean annual maximum precipitation. The value of  varies from 5 to 20, depending upon the precipitation duration and average precipitation.²⁴ This method was also used in this study. Hershfield³ analyzed over 95,000 station-years of annual maxima belonging to 2,645 stations, about 90% data was from the United States and 10% from other parts of the world which included some of the heaviest precipitation regions. He then produced an empirical nomograph ranging from 5 minutes to 24 hours that have been standardized by WMO¹⁹ as a basis for estimating PMP.²⁵ Using this method, enveloping curves were derived for particular areas and durations and these have been used to calculate the PMP values.^26,27 The enveloping frequency factor serves the purpose of transposition. Casas et al.²⁶ used the Hershfield method to estimate the PMP values for one-day duration and their return periods, and spatial resolution over the Catalonia region. The Gumbel distribution with parameters estimated by the L-moments method was used to determine the return periods of calculated PMP values. They showed that 90% of the PMP values had return periods of 10⁴ to 10⁸ years.

The fundamental element in the Hershfield method is the parameter k_m and different variants of this method estimate this parameter differently. For example, Koutsoyiannis & Papalexiou¹⁴ proposed nomographs for estimating the k_m value. Lan et al.⁹ used a standardized variable, defined as the maximum deviation from the mean of a sample scaled by the standard deviation of the sample to replace the k_m factor and found it to be more reasonable., Koutsoyiannis²⁵ fitted a generalized extreme value (GEV) to the frequency factor values for the same data set as used by Hershfield and found that the k_m value of 15 corresponded to a 60,000 year return period PMP. This shows that there can be a large variation in the value of PMP resulting from the frequency factor value. Therefore, this study revisits the PMP estimation and its uncertainty.

The uncertainty with different methods for estimating PMP has been investigated by several researchers who were mainly concerned with maximizing and transposing actual storms using in-place moisture maximization.^10,14 Studies focusing on uncertainties in the PMP estimates using the statistical method or more specifically Hershfield method have been limited. There can be two ways to quantify uncertainty in the PMP estimates. First, uncertainty can be determined due to uncertainties in the frequency factor, and mean and standard deviation of extreme precipitation values. Second, frequency analysis of PMP can be used to quantify uncertainty.

There exist uncertainties in the frequency factor () which is accounted for by using an enveloping function of the highest frequency factor values. Koutsoyiannis²⁵ pondered whether the extreme precipitation data used in the Hershfield method suggested a deterministic upper limit of precipitation. He suggested unifying all classes of record length and adding the number of occurrences of all classes after ignoring the effect of record length on . Considering  as a random variable, the probability of its non-exceedance can be estimated using the Weibull formula, assuming all records of standardized annual maximum precipitation  represented practically the same population. There are also uncertainties in the sample mean and sample standard deviation which can affect the PMP estimation.²⁸ On the other hand, the uncertainty of PMP values can be quantified by frequency analysis of the annual maximum precipitation series. The first step is to determine the best fit probability distribution for the extreme precipitation series and return periods of PMP values. The exceedance probability of PMP values can be used to analyze uncertainty. Although the definition of PMP assumes an upper bound of precipitation, there are, however, no assigned probability level and return period to ‘probable’ events which might exceed the upper limits.²⁹ There is the uncertainty of occurrence of such extreme events. However, by selecting an appropriate distribution for extreme precipitation values and ignoring the concept of upper limit, the return period can be calculated for the estimated PMP value. Various probability distributions can be used to calculate the return periods of maximum precipitation of different durations or calculate the return period of extreme precipitation. The Gumbel distribution has been commonly used for extreme frequency analysis, because maximum annual precipitation series are relatively short, especially in developing countries, and outliers are observed. The traditional fitting method with the conventional moments, such as mean and standard deviation, can result in return periods shorter than the ones corresponding to a longer sample containing a large number of years of data.²⁶ The coefficient of variation (CV) of the annual maximum precipitation series can be adjusted to compensate for the effect of outlier.³⁰

There is a considerable amount of uncertainty associated with finding the best-fit distribution for doing frequency analysis. Stations having limited quantity of data for frequency analysis introduce sampling uncertainty, in particular, due to the presence of outliers, which make the estimates of higher order moments (like skewness) become unstable.³¹ For daily time series, Koutsoyiannis³² found that the Generalized Extreme Value (GEV) type II (EV2) better described hydrological extremes than did the Gumbel distribution. Assuming the shape parameter of the EV2 distribution as constant (=0.15) across Europe and North America, the distribution fitting was simplified. More recently Papalexiou & Koutsoyiannis³³ used a three-parameter Generalized Gamma (GG) distribution and a four-parameter Generalized Beta distribution of the second order (GB2) to 11,519 daily precipitation records across the globe. Results showed that these distributions described almost all empirical records satisfactorily. Determining the best fit probability distribution is important to quantify the uncertainty in the PMP estimates. Asquith³⁴ analyzed frequencies of annual maximum precipitation for durations of 15, 30, and 60 minutes; 1, 2, 3, 6, 12, and 24 hours; and 1, 2, 3, 5, and 7 days using L-moments, like mean, L-scale, L-coefficient of variation, L-skew, and L-kurtosis. He found that the generalized logistic distribution, using L-moment ratio diagrams, was an appropriate probability distribution for modeling the frequencies of annual maxima for durations of 15 minutes to 24 hours; whereas the generalized extreme-value distribution was appropriate for durations of 1 to 7 days.³⁴ However, the results were only based on the L-moments ratio and included only a few distributions, like generalized logistic distribution and generalized extreme value (GEV) distribution, generalized Pareto distribution, and Pearson Type III distribution. To our knowledge, the best-fit probability distributions for different durations like 2, 3, 6, 12, 24 hours have not been determined for the Brazos River basin.

Therefore, the question arises: “What are the PMP estimates for Brazos River basin and what is the uncertainty associated with those values.” Our study calculated PMP for 1, 2, 3, 6, 12, and 24 hour durations and focused on uncertainties due to the use of frequency factor enveloping curve, return period of PMP values, and uncertainty in the selection of best fit probability distribution. It is also important to see how PMP values vary with the given duration and if there is any relation between the PMP values and the mean of extreme values, PMP values and the highest observed precipitation, or the mean and the standard deviation for different stations and durations. If there exists a strong correlation between these statistics then one statistic can be substituted for the other.

The methodology for PMP estimation is comprised of 5 steps:

1. Selection of precipitation data;
2. Estimation of frequency factor;
3. Determination of uncertainty in frequency factor;
4. Computation of PMP; and
5. Determination of uncertainty in the PMP values. Each of these steps is described in what follows.

Precipitation data             

Precipitation data for 1-hour duration were taken from the NCDC NOAA website (https://www.ncdc.noaa.gov/cdo-web/). Shapefiles of rain gauge stations to be imported into GIS were prepared using the latitude and longitude of stations. Using the locations of stations and the boundary of Brazos River basin, it was determined that the basin had more than 90 stations. The stations were selected, based on the criteria of having at least 30 years of record length and 9-month observations for each year.³⁵ Then 39 stations were selected that had an average record length of 50 years and 17 of these stations had record lengths of more than 60 years. The recording period varied from 1940 to 2013. Figure 1 shows the locations of 1-hour duration rain gauges. From the data of 1-hour duration the data for other durations 2, 3, 6, 12, and 24 hours were generated. Time series of stations with different durations was plotted to see if there was any trend in the precipitation records corresponding to time. No time series plot showed any significant non-stationarity. Then, annual maximum precipitation series, based on different durations, were compiled for each station.

Figure 1 1-hour duration rain gauge station locations.

Estimation of frequency factor

The values of mean, standard deviation  and highest observed precipitation were calculated for annual maximum series of each station corresponding to each duration. Mean and standard deviation were adjusted for sample size and maximum observed event.⁷ The mean and standard deviation of the annual maximum series tend to increase with the length of record, because the frequency distribution of precipitation extremes is skewed to the right so that there is a greater chance of getting a larger value of mean for a longer length of record. Hence, for smaller series of extreme precipitation n, adjustments were made to the mean and standard deviation for the length of record.⁷ The coefficient of variation (CV), the ratio of standard deviation and mean of the annual maximum series, was calculated for each station. Sometimes the inclusion of an outlier or an extraordinarily extreme precipitation event, with a recurrence period much longer than the series, could cause an anomalous effect in the calculated mean and standard deviation values.¹⁷ CV for each station was calculated and checked whether it differed too much from that of the neighboring stations. For stations whose CV value was found to be too much different from neighboring stations, it was adjusted to the nearest value as compared to the neighboring stations.¹⁵

 The frequency factor  was calculated as:

_{$k_m=\frac{X_m-{\overline{X}}_{n-1}}{S_{n-1}}$ ;}(2)

where is the mean and is the standard deviation for the annual maximum precipitation series excluding the highest value from the series. The highest value of  for 1 hour duration was found to be 10.1 at Santa Anna, Texas. A similar procedure was applied to the maximum precipitation series for other durations. Since each station had its own value, depending upon the magnitude of the mean, the values of 39 stations were plotted against the adjusted mean in order to consider an appropriate enveloping curve that would give reliable estimates of 1-hour PMP rather than using the observed highest value. As there were only 39 stations in the study area hence, only a single enveloping curve was constructed rather than constructing regional enveloping curves for different areas within the basin. Also, there was not any considerable topography difference which could yield to unreliable frequency factor values. Enveloping curve was drawn with the help of upper points for different durations. Figure 2 shows the enveloping curves for different durations. The curve seemed to be more sensitive for lower durations of precipitation, meaning changing the mean changed the value of the corresponding  by a considerable amount. However, all of the curves followed the same trend.

Figure 2 Enveloping curves of for different durations.

Uncertainty in frequency factor

Figure 3 shows the enveloping curve of  based on 39 stations in the Brazos River basin and the enveloping curve provided by Hershfield for computing PMP on an hourly basis. From Figure 3, it is seen that both curves generally followed the same trends but did not match properly. Brazos River basin has a smaller number of stations as compared with 2645 stations that Hershfield used, hence the frequency factor markedly depends on number of stations used. The enveloping curve specific for the Brazos River basin is lower than the Hershfield curve, which was constructed using some of the highest precipitation producing regions with long term records. The Hershfield enveloping curve seems to give higher values of  as the mean increases. Hence, it is more conservative than the basic-specific one for one hour duration. The same can be said for other durations, as the basin-specific curves followed the same trend and Hershfield’s  was higher for other durations as compared to the basin-specific one. Figure 4 shows the difference between the  values for each station for 1-hour duration in dimensionless terms based on the formula:

$\frac{k_{mH}-k_{mB}}{k_{mH}}$ (3)

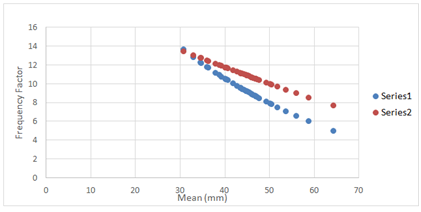
Figure 3 Comparison of Hershfield’s enveloping curve of with Brazos River basin enveloping curve.

Series 1– Basin-specific curve; Series 2- Hershfield curve.

Figure 4 Uncertainty in the values of frequency factor in dimensionless terms.

Where is the Hershfield frequency factor value and  is the basin specific frequency factor value. This difference is an indication of uncertainty that can be introduced when using the Hershfield curve rather than the basin-specific curve. The same procedure was applied for 6-, and 24-hour durations and the same trend was observed. Using Hershfield’s curve rather than basin specific can increase  by 16% for 1 hour duration, by 17.9% for 6 hour duration and by 22.1% for 24 hour duration.  was also calculated by using the PMP values published in HMR documents (HMR, 51). The range of PMP values varied from 863.6 mm (station at Pep) to 1198.8 mm (station at Houston Alife) for 24-hour duration. The value of  was calculated as:

$k_{m_{}}=(\frac{PM{P}_{HMR}-\overline{X}}{S_n})$ (4)

Where  is the PMP values from the HMR documents. Using the PMP values and the mean and standard deviation of stations, the range of  was from 22.2 to 26.6. The value of k_m was high but had a range from the lowest to the highest value. It was because the PMP values published in HMR are too high as compared to the average precipitation amount and the PMP estimated using basic-specific enveloping curve. This shows the significance of constructing the basin-specific enveloping curve and then calculating PMP. In order to quantify the uncertainty due to the number of stations, the enveloping curve was constructed by removing the top two stations (Lexington and Briggs) on an hourly basis. The curve changed, giving lower values of  that gave lower PMP values (Figure 5). The frequency factor, on an average basis, decreased by 8.1%. Hence, accurate data of stations and the number of stations are important in constructing the curve. Otherwise, uncertainty can be introduced in the curve. Also, the inclusion of any outlier can increase the value of  which can change the shape of the curve.

Figure 5 Comparison of the original enveloping curve and the curve made upon removing top two stations.
Series 1- Original enveloping curve; Series 2- Curve made upon removing top two stations.

Computation of PMP

The PMP values for each station and duration were calculated using equation (1). The calculated PMP values were then adjusted for the fixed observational time interval based on the procedure described in WMO (2009). As precipitation data are usually given for fixed time intervals, for example, 3 AM to 4 AM (hourly data), 6 AM to noon (6-hour), or 8 AM to 8 PM (daily). The adjustment will yield values closely approximating those to be obtained from analysis based on true maxima.^7,15 However, less adjustment is required when maximum observed amounts for various durations are determined from two or more fixed time intervals.^36,37 Table 1 shows the PMP values for the study area using the basin-specific enveloping curve.

Uncertainty in PMP values

To quantify the uncertainty that can be introduced in PMP estimates by using Hershfield’s enveloping curve, basin-specific PMP values were also calculated. Figure 6 compares the PMP values based on both methods and shows that PMP from the Hershfield enveloping curve was higher than the basin-specific curve. For 1 hour duration the PMP values were 16.8% higher using Hershfield’s curve than basin-specific values, 18.5% for 6 hour duration, and 23.4% for 24 hour duration. Plots between PMP values and mean of extreme values, PMP values and highest observed precipitation and mean and standard deviation were also made. There was an increasing correlation between mean and standard deviation, highest observed precipitation and PMP but not that significant. However, there was no significant correlation between the mean and PMP for different stations. It may be because the frequency factor comes in the multiplication with standard deviation which has a more effect on the values of PMP. Plots were also made for different durations for Eastland station (Figure 7), showing increasing correlation between PMP values and the mean of extreme values, PMP values and the highest observed precipitation, and the mean and standard deviation. However, it may be noted that a highest observed precipitation for one duration can be the same as for another duration.

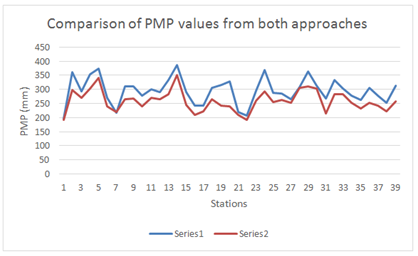
Figure 6 Comparison of Hershfield’s PMP estimates against PMP estimates for Brazos River basin based on 1-hour duration (mm).

Series 1– Hershfield’s PMP; Series 2- Own PMP

Figure 7A Plots between PMP values and mean of extreme precipitation.

Figure 7B Plot between mean and the standard deviation of extreme precipitation.

Figure 7C Plot between PMP values and the highest observed precipitations.

Return period of PMP from frequency analysis of extreme precipitation

It is important from the standpoint of hydrologic design to compute the return period of a PMP value. The computation entailed four components:

1. Frequency analysis
2. Frequency analysis of extreme precipitation
3. Factors affecting frequency distributions
4. Return period of PMP values and uncertainty due to the choice of a probability distribution. Each of these components is discussed below.

Frequency analysis

For extreme precipitation frequency analysis, the same 39 stations were used as for calculating the PMP values. Stations were checked for stationarity and independence. Time series for the stations with all durations of precipitation were plotted to see if there was any trend in the precipitation records corresponding to time. No time series plot showed any significant non-stationarity. For frequency analysis of extreme precipitation for all durations and stations, 24 probability distributions (Table 2), were used. Three goodness of fit (GOF) tests, Kolmogorov-Smirnov (K-S) test, Anderson-Darling (A-D) test and Chi-square (C-S) test, were employed to check whether a hypothesized distribution function fitted the sample data.³⁸ The hypothesis of the GOF tests was:

H₀=The precipitation data followed the specific distribution; and H₁=The precipitation data did not follow the specific distribution.

These tests were performed at the significance level (α=0.05) for choosing the best fit probability distribution.³⁹ Q-Q plot and Root Mean Square Error (RMSE) were also used to find the best fit probability distribution. Extreme precipitation data were fitted to all the distributions and parameters of the distributions were estimated by the maximum likelihood estimation. The probability density functions (PDFs) were determined and plotted. Matlab and R-statistics were employed for fitting the probability distributions.

Frequency analysis of extreme precipitation

To find the best fit probability distribution for each station and different durations a three-step process similar to Olofintoye et al.⁴⁰was used. It may be noted that our focus was on the right tail of the distribution where extreme precipitation occurs. In the initial processing all 24 common statistical distributions were used in this step. For each station and duration the test statistic values of Kolmogorov-Smirnov, Anderson Darling, and Chi-square were calculated for every distribution. For each of the three tests the distributions were ranked according to the lowest test statistic value. The distribution having the 1^st rank was assigned a score of 24, 2^nd rank distribution a score of 23, and so on. The total scores from the three tests of each distribution were added to see which distribution had the highest score, the second highest, and so on. At least 5 to 6 distributions were considered for further analysis. The stations were ranked according to the least RMSE value and best Q-Q plot (Here best means Q-Q plot is linear or the specified theoretical distribution is the correct model.). The PDFs of the selected 5 or 6 distributions were compared to see if our results were consistent with the PDF graph or not. In the last step, for those stations and durations for which the difference in the PDF graphs of selected distributions was not too much or there were contradicting results by observing the quantiles of the distributions with the observed values against the MSE and Q-Q plot results, the ranking system was used again. The top 5 or 6 distributions from step 1 were selected. The distributions were ranked according to the test statistic value from K-S, A-D, C-S, RMSE tests and visually seeing Q-Q plots. A score of 5 or 6 was assigned to the best distribution for a particular test and so on. The distribution having the highest combined score from the 5 tests was regarded as the best distribution. After the best distribution was selected, it was analyzed to see which distribution fitted most of the stations and for different durations overall.

Table 2 shows the overall best distributions for each station and 1-, 6-, and 24-hour durations, based on different GOF tests. The Anderson-darling GOF test performed better than the other tests. It is because it focuses more on the tail of the distribution than the K-S test. The K-S test is distribution free in the sense that the critical values do not depend on the specific distribution being tested. The Anderson-Darling test makes use of the specific distribution in calculating critical values. The log-logistic (3parameter) distribution performed good in the right tail for higher quantiles for 1-, 2-, 3-, and 6-hour durations. But overall it did not perform as well as Burr XII or GEV for 2-, 3-, and 6 hour durations. For 12 and 24-hour durations of extreme precipitation, the generalized gamma (4parameter) and Johnson SB performed better in the right tail.

Factors affecting frequency distributions

Next, the effect of duration and distance from the Gulf on the histogram and best-fit distribution was analyzed. It was observed that there was a general tendency for higher skewness for shorter durations of precipitation than for longer durations, as shown in Figure 8 for station at Evant, Texas, for 2-, 6-, and 24-hour durations. It is because for short durations such as 1-hour, a large amount of precipitation may occur within a short time in certain cases exhibiting large skewness, while for long durations, such as 24-hour, precipitation is averaged and thus exhibits less skewness. Burr type 12 performed better for less skewed distributions and log-logistic (3-parameter) performed better for more skewed distributions. Within Brazos River basin there exist different climate producing mechanisms for different areas. For example, in the eastern part of Texas or near the Gulf of Mexico there is fairly uniform seasonal precipitation, with slight maxima occurring in the summer season, because the influence of the Gulf of Mexico is dominant.⁴¹ Hence, the effect of the distance from Gulf was analyzed. There was no systematic pattern but still it was observed that for stations close to the Gulf of Mexico, the histogram was smooth but had more variation. As the distance from the Gulf increased the histogram began to become sharp with less variation. Figure 9 shows histograms for stations at Thompson and Lubbock for 2 hour duration. Thompson lies close to the gulf, whereas Lubbock lies in the north-western part of Texas. The reason for this pattern may be due to the moderating influence of the Gulf of Mexico. As we go farther from the Gulf, in the northwest direction we come close to regions of High Plain division in which maximum precipitation comes from thunderstorms during the summer season. However, there was no preferable distribution which performed best near the Gulf or far away from it. However, Burr XII and GEV performed better for smooth histograms. Overall Burr type 12 distributions were chosen to be the best distribution for the Brazos River basin covering 30 to 40% of the stations for different durations. For other stations also, it was in most of the cases one of the top three best distributions.⁴²

Figure 8A Histogram at Evant, TX for 2-hour duration.

Figure 8B Histogram at Evant, TX for 6-hour duration.

Figure 8C Histogram at Evant, TX for 24-hour duration.

Figure 9A Histogram at Thompson, TX, for 2-hour duration.

Figure 9B Histogram at Lubbock, TX, for 2-hour duration.

Return period of PMP values and uncertainty due to choice of probability distribution

For quantifying uncertainty, return periods of the PMP values were determined for each duration. For our study we used the PMP values derived from the basin-specific enveloping curve of  as it was made only by using the data for the Brazos River basin and is more accurate.^43,44 The return period was less than expected. For most of the Brazos River basin the return period of the PMP values was in the range of 1000 to 3000 years which was less than the range of 10³ to 10⁶ years reported in HMR 51. It shows the amount of risk associated with the PMP values. The difference between the two sets of values points to the uncertainty associated with the PMP values. To evaluate the uncertainty in the return period due to the choice of distribution, return periods for stations and durations were also calculated from the 4^th best distribution. Table 3 shows the return period from the best and the 4^th best distribution. On an average basis the return period from the 4^th best distribution was 55.1% lower than that from the best distribution. Figure 10 shows the difference between the return period of the 24-hour PMP values for selected stations from the best and the 4^th best distribution in dimensionless terms as:

$\frac{T_{best}-T_{4thbest}}{T_{best}}$ (5)

Figure 10 Difference between the return period of the 24-hour PMP values for selected stations from the best and 4th best distribution in dimensionless terms.

Where is the return period from the best distribution, and  is the return period from the 4^th best distribution. As can be seen from the figure return periods were different, showing the importance of accurately determining the best-fit probability distribution. Figure 11 & Figure12 show the spatial distribution of the 1- hour PMP values and return period for those values calculated based on the best fit probability distribution. The GIS spatial interpolation tool was employed for performing it. The spatial interpolation was done on the basis of inverse distance weighted interpolation. The depth-duration-frequency curve was also constructed for PMP values. Log of 1, 2, 3, 6, 12, and 24 hour of precipitation and log of PMP values of different return period was taken. Figure 13 below shows the relation between PMP values and duration on log-log paper. It was observed that there was an increasing correlation between log of PMP values and log of duration for different return periods. The chosen return was the return period of different duration PMP values and for the same return period the depth of rainfall was calculated for different durations.⁴⁵

Figure 11 Spatial distribution of the PMP values in Brazos River Basin for 1-hour duration.

Figure 12 Spatial distribution of the Return period of 1-hour PMP values in Brazos River basin.

Figure 13 Depth-Duration-Frequency curve of PMP values.

It is seen from this study that the PMP values are subject to uncertainty. The PMP estimates obtained from the statistical method depend largely on the frequency factor. Removing or adding any one station can change the shape of the curve which can result in highly uncertain PMP values. Hershfield’s statistical method can approximate the PMP values generally but for a specific area priority should be given to using the specific precipitation data for the area and deriving the enveloping curve for the specific area. For the Brazos River basin, the PMP values are lower than those calculated using Hershfield’s curve. Also we should have at least 20-30 stations which can be used in the construction of the curve. It is important to find the best fit probability distribution as uncertainty can be introduced due to the choice of probability distribution. Frequency analysis was done using five goodness-of-fit tests and different distributions. It was observed that for stations close to the Gulf of Mexico, the histogram was smoother but had more variation. As the distance from the Gulf increased the histogram began to become sharp with less variation. There was also a general tendency for higher skewness of precipitation data of shorter duration than of longer duration. The Burr distribution XII was the best distributions for different durations on an average basis. The return periods of PMP values were less than those published in the HMR documents.

This study was supported in part by the project “Quantifying Uncertainty of Probable Maximum Flood (PMF),” contract No. DOD-USACE contract W912HZ-16-C-0027, funded by U.S. Army Engineer-Engineer Research Development Center, Vicksburg, Mississippi.

The authors declare there is no conflict of interest.

1. US National Weather Service. Probable Maximum Precipitation–United States between the Continental Divide and the 103rd Meridian. Hydrometeorological Report No. 55A (HMR‒55A), Silver Spring, MD, USA. 1988.
2. Benson MA. Thoughts on the Design of Design Floods. Floods and Droughts, Proc 2nd Intern Symp in Hydrology. 1973;7‒33.
3. Hershfield DM. Method for Estimating Probable Maximum Precipitation. American Water Works Association. 1965;57(8):965‒972.
4. Dooge JCI. Looking for Hydrologic Laws. Water Resour Res. 1986;22(9):46S‒58S.
5. Dawdy DR, Lettenmaier DP. Initiative for Risk‒based Flood Design. ASCE J Hydrau Eng. 1987;113(8):1041–1051.
6. Tomlinson EM, Kappel WD. Dam Safety. Revisiting PMPs. 2009.
7. World Meteorological Organization. Manuel on Estimation of Probable Maximum Precipitation. WMO‒No 1045, Geneva, Switzerland. 2009.
8. Lin B, AECOM. 24h PMP updating study, technical report, study of landslides occurring in Kowloon and the new territories in 2012 and 2013. Feasibility study Hong Kong. Hong Kong. 2014.
9. Lan P, Lin B, Zhangm Y, et al. Probable maximum precipitation estimation using the revised Km value method in Hong Kong. Journal of Hydrologic Engineering. 2017;22(8):05017008.
10. Micovic Z, Schaefer MG, Taylor GH. Uncertainity Analysis for Probable Maximum Precipitation Estimates. Journal of Hydrology. 2014;521(2015):360‒373.
11. Collier CG, Hardaker PJ. Estimating probable maximum precipitation using a storm model approach. J Hydrol. 1996;183(3‒4):277–306.
12. Schreiner LC, Riedel JT. Probable Maximum Precipitation Estimates, United States East of the 105th Meridian HMR No. 51. National Weather Service, National Oceanic and Atmospheric Administration, United States Department of Commerce, Washington, DC. 1978.
13. Kulkarni BD. Generalized Physical Approach of Estimating Areal Probable Maximum Precipitation for Plain Region of the Godavari River Basin (India). Journal of Spatial Hydrology. 2010;2(2).
14. Koutsoyiannis D, Papalexiou SS. A Probabilistic Approach to the Concept of Probable Maximum Precipitation. Advances in Geosciences. 2006;7:51‒54.
15. Rakhecha PR, Deshpande NR, Soman MK. Probable Maximum Precipitation for a 2‒day duration over the Indian Peninsula. Theory of Applied Climatology. 1992;45(4):277–283.
16. Douglas EM, Barros AP. Probable Maximum Precipitation Estimation Using Multifractals: Application in the Eastern United States. Journal of Hydrometeorology. 2003;4:1012‒1024.
17. Hershfield DM. Estimating the Probable Maximum Precipitation. Journal of Hydraulics Division. 1961;87(HY5):99‒106.
18. National Research Council. Safety of dams, flood and earthquake criteria. National Academy Press: Washington DC. 1985.
19. World Meteorological Organization. Manual for Estimation of Probable Maximum Precipitation. Operational Hydrology Report 1, Publication 332, World Meteorological Organization, Geneva. 1986.
20. Bruce JP, Clark RH. Introduction to Hydrmeteorology. Pergamon Press: New York. 1966.
21. Myers VA. Meteorological estimation of extreme precipitation for spillway design floods. Weather Bureau Technical Memoranda WBTMHYDRO‒5. US Dept of Commerce, Environmental Science Services Administration, Weather Bureau, Boulder, CO. 1967.
22. Wiesner C. Hydrometeorology 232. Chapman and Hall. Londres. 1970.
23. Chow VT. A General formula for Hydrologic Frequency analysis. Transactions‒American Geophysical Union. 1951;32:231‒237.
24. Casas MC, Rodriguez R, Redano A, et al. Estimation of the Probable Maximum Precipitation in Barcelona (Spain). Int J Climato. 2012;31(9):1322‒1327.
25. Koutsoyiannis D. A Probabilistic view Of Hershfield’s Method for Estimating Probable Maximum Precipitation. Water Resources Research. 1999;35(4):1313‒1322.
26. Casas MC, Rodriguez R, Nieto R, et al. The Estimation of Probable Maximum Precipitation: The Case of Catolonia. Annals of the New York Academy of Sciences. 2008;1146:291–302.
27. Tessier Y, Lovejoy S, Schertzer D. Universal multifractals: Theory and observations for rain and clouds. J Appl Meteor. 1993;32: 223–250.
28. Salas JD, Gavilan G, Salas FR, et al. Uncertainty of the PMP and PMF. Handbook of engineering hydrology. Ch 57, 2014;2.
29. Kite GW. Frequency and Risk analysis in Hydrology. Water resources publications, Littleton, CO, USA. 1988.
30. Rakhecha PR, Kennedy MR. A Generalized Technique for the Estimation of Probable Maximum Precipitation in India. Journal of Hydrology. 1985;78(3‒4):345‒359.
31. Mamoon AA, Rahman A. Uncertainty in Design Precipitation Estimation: A Review. Journal of Hydrology and Environment Research. 2014;2(1);1‒7.
32. Koutsoyiannis D. Statistics of Extremes and Estimation of Extreme Precipitation II: Empirical Investigation of Long Precipitation Records. Hydrological Sciences Journal. 2004;49(4):591–610.
33. Koutsoyiannis D, Papalexiou SS. Battle of Extreme Value distributions: A Global Survey on Extreme Daily Precipitation. Water resources research. 2012;49(1):187–201.
34. Asquith WH. Depth‒Duration Frequency of Precipitation for Texas. Water‒Resources Investigations Report. 1998;98–4044.
35. Hao Z, Singh VP. Entropy‒based Method for Extreme Precipitation Analysis in Texas. Journal of Geophysical research: Atmospheres. 2013;10:1‒11.
36. Weiss LL. Ratio of True to Fixed‒Interval Maximum Precipitation. Journal of Hydraulics Division.1968;90:77–82.
37. Miller JF. Two‒to Ten‒Day Precipitation for Return Periods of 2 to 100 Years in the Contiguous United States. Technical Paper No. 49. 1964.
38. Chakravarti Laha, Roy. Handbook of Methods of Applied Statistics. John Wiley and Son. 1967;392‒394
39. Sharma MA, Singh JB. Use of Probability Distribution in Precipitation Analysis. NY Sci J. 2010;3(9):40‒49.
40. Olofintoye O, Sule BF, Salami AW. Best‒fit Probability distribution Model for Peak Daily Precipitation of Selected Cities in Nigeria. NY Sci J. 2009;2(3);1‒12.
41. National Fibers Information Center. The Climate of Texas Counties. Univ of Texas, Austin and Texas A&M University, College Station, Texas. 1987.
42. Koutsoyinannis D, Papalexiou SM. Extreme rainfall: Global perspective. In: Singh VP, editor. Handbook of Applied Hydrology. McGraw‒Hill: New York. 2016.
43. US Department of Commerce. Generalized Estimates of Probable Maximum Precipitation for the United States West of the 105th Meridain. Technical Paper number 38. 1960.
44. US Department of Commerce, National Oceanic and Atmospheric Administration. Probable Maximum Precipitation‒ Pacific Northwest States. Hydrometeorogical Report number 57, 1994.
45. Brebbia CA. River Basin Management VII. Ashurust Lodge, Ashrust, Southampton, SO40 7AA, UK: WIT press. 2013.