The objective of this review is to highlight the need for an integrated approach to the understanding of the major processes controlling the hydrochemical composition of water bodies in drylands using multivariate statistics, water quality index and heavy metal pollution index. The integrated approach to the hydrochemical investigation of streams and aquifers in drylands is essential owing to their distinctive climate, notably, low rainfall and high temperature. Studies on water quality in arid and semi-arid areas using multivariate analysis and water quality indices were scrutinized. Results showed that the hydrochemistry of streams and aquifers is controlled by both the natural geogenic processes and anthropogenic activities. However, in-depth understanding of geochemistry and land use types, as well as climatic vagaries, is required, to be able to discriminate these processes, since several ions of rock minerals origin are increasingly being added into the environment through human activities. While the sources of solutes and processes controlling the hydrochemistry of streams and aquifers can be established through application of multivariate analysis, this technique is limited in water quality investigations since it cannot measure the suitability of water for domestic, agriculture and industrial uses. Thus, an integrated approach incorporating water quality indices in conjunction with multivariate analysis is required. This is essential owing to the fact that the suitability of water for various uses is central to any hydrogeochemical investigation in arid and semi-arid environments. Thus, it is expected that future hydrochemical studies would apply this approach.

Keywords: natural geogenic and anthropogenic processes, correlation analysis, principal component analysis, hierarchical cluster analysis, water quality index, heavy metal pollution index

Arid and semi-arid areas (Figure 1), draining wide basins and overlying extensive aquifer(s), e.g., Iullemedden basin, West Africa,^1,2 Saladin Province, Iraq,³ Goshen Valley, UT, USA,⁴ Northwest China,⁵ and Hamedan-Bahar plain, Iran.⁶ These areas are largely fortified with irrigation facilities that, combined with the application of agrochemicals, make possible areas of intensive irrigation farming. The survival and throughput of these arid areas depend on the availability of water of acceptable quality. A decline in the accessibility or quality of water will consequently affect human health and wellbeing as well as agricultural output which, given the position of these areas for food production could have detrimental effects to the immediate environment and beyond.⁷ Arid and semi-arid areas cover approximately 40% of the global landmass and are occupied by 37% of the global population.⁷ Though there is no general definition of the term dryland, FAO⁸ classifies drylands into four categories based on their precipitation (p) and associated potential evapotranspiration (ETP). The four types of drylands are: (1) p/ETP below 0.03 (hyper-arid), comprised of areas of barren land and precipitation below (pb) 100 mm; (2) p/ETP varying between 0.03 to 0.2 mm (arid) and pb ~300 mm; (3) p/ETP 0.2 to 0.5 (semi-arid) and p fluctuating between 300 and 500 mm and rising to 800 mm in tropical regions with very short rain season; and (4) p/ETP oscillating between 0.5 to 0.75 mm - sub-humid.⁷

Figure 1 World map of aridity zones. Retrieved from http://www.unesco.org/mab/ doc.html, 22/07/2019.

In this review, all four subtypes of drylands are counted in within the term “semi-arid and arid areas” or drylands. The climatic features common to all drylands largely include uneven distribution of annual rainfall, drought phases, rate of evaporation greater than annual precipitation, a dry and wet season within a year, and scanty dispersal of native vegetation.^9,10 Freshwater resources in these regions are over-exploited as a result of low rainfall and slight aquifer recharge consequent of the growing demand of water from industry, domestic water supply, and dry season farming.^9,11,12 Water scarcity has become endemic in arid and semi-arid areas, particularly in developing countries.^13–15 Thus, groundwater occupies a central role in the water supply of these areas and is increasingly gaining ground in the supply of water to both rural and urban centres.^16,5 For instance, estimates show that at least one-third of the global population relies on groundwater for drinking.¹⁷ Thus, understanding of the hydrogeochemical characteristics of sources of water supply plays a vital role in water resources management, especially as it relates to water quality from aquifers and streams. This allows for water classification for various uses. Thus, it is essential to understand the hydrochemical composition of streams and aquifers and its evolution under environmental processes for effective management and sustainable utilization of water resources.

The quality of water basically depend on diverse hydrogeochemical and biological processes that take place over space and time in a stream or groundwater aquifer.^18–20 The variation of stream or groundwater quality is the joint effect of anthropogenic and natural geogenic processes, such as leaching of organic and inorganic fertilizers, biogeochemical processes, mixing of surface and groundwater, dissolution of minerals/precipitation, cation exchange, reduction/oxidation, composition of precipitation and geological formation underlying groundwater aquifers or channels over which streams pass. Other anthropogenic activities affecting water quality include mining, urbanization, industry and improper sewage disposal (Figure 2). Consequently, different water types are produced as a result of the interaction of these factors.¹⁷ Generally, studies on water quality of streams and aquifers are deemed beneficial in detecting processes that govern the hydrochemical composition of streams and groundwater aquifers.^22–24,17

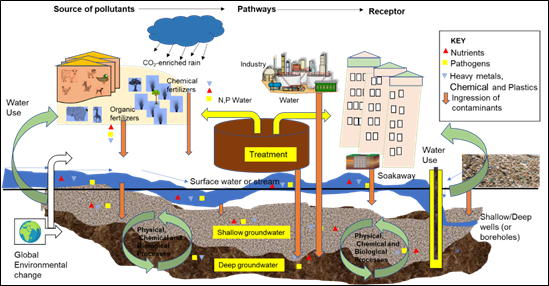
Figure 2 Geogenic and anthropogenic controls on water quality. After Andrade.²¹

Hydrochemical transformation in surface and groundwater in drylands present a thought-provoking topic,^25–27 owing to difficulties involved in understanding the interaction between surface and groundwater. Though pollutant wash-off,²⁸ municipal and industrial sewage,^29,30 agriculture and mining dominate pollutants pools;^31,32 streams and catchments, floodplain inundation and infiltration of water during and after rainfall event, initiate pollutant load to groundwater aquifers.^33–35 Therefore, understanding the factors controlling the hydrochemical composition of streams and aquifers is necessary for the overall management of water resources. This can be achieved by the application of simple statistical techniques, which enable understanding the types of natural and anthropogenic processes controlling water chemistry.^36,22 Likewise, numerous indices such as water quality index (WQI) and heavy metal pollution index (HPI),^37,38 are used to evaluate the water quality and determine its suitability for drinking, agriculture and industrial uses.

Conversely, simple statistical techniques such as correlation, PCA, FA and HCA,^39,40 can be used to identify the origin of salinity in streams and aquifers (Table 1). The application of WQI and HPI in conjunction with multivariate statistics can provide vibrant evidence relating to the sources of solutes and the geochemical and/or anthropogenic processes related to water composition. These methods perhaps present simple analytical tools for the evaluation and management of water quality in drylands. Remarkably, a large portion of global arid areas occurs in an underdeveloped part of the world (e.g. North Africa, Middle East, West Africa), where resources needed for large scale water quality evaluation is seldom available. Consequently, the significance of these tools lies with the fact that they are easy to apply, cheap and are able to provide the needed results on the hydrochemical composition of streams and aquifers both at local and regional scales. It is against this background that this review aimed at designing an integrated approach to water quality investigation in arid and semi-arid areas.

Water quality index

Water quality index (WQI), is measured as a formidable technique that can offer a wide-ranging delineation of sources of potable water. The WQI is the degree that mirrors the combined effect of multiple water quality parameters.^41–46,38 It is computed by assigning discrete weights (w_i) to each chemical parameter in a scale of 1 (smallest impact on water quality) to 5 (greatest impact on water quality) founded on their supposed impact on human health and based on its relative significance in the quality of drinking water.⁴⁷ Parameters that have grave health concerns and whose existence beyond the critical absorption limits could affect the usability of the water for domestic and drinking purposes (e.g. Cl, TDS, NO₃^-, Pb, Cd, As and SO₄^2-) were allotted highest weight of 5, whereas, parameters that have an inconsequential role in water quality evaluation like K were allotted the minimum weight of 1 (Table 2). The intermediate parameters, including pH, EC, TH, HCO₃, Ca, Mg, were assigned weights between 2 and 4 depending on their relative significance in the water quality evaluation. The relative weight (W_i) is calculated from Eq. 1:

$W_i=\frac{w_i}{{\displaystyle {\sum }_i^n{w}_i}}$ Eq.1

where the relative weight = $W_i$ , the weight of each parameter = $w_i$ , and n is the number of parameters. For instance, the calculated relative weight ($W_i$ ) values of individual parameters can be given as in Table 2.

The quality rating (qi) for individual parameters is allotted by dividing its concentration in each water sample by its reference values given by the World Health Organization (WHO), and the result is converted to a percentage (%) by multiplying 100:

$q_i=\left(\frac{C_i}{S_i}\right)x 100$ Eq.2

where the quality rating is $q_i$ , the concentration of each chemical parameter in individual water samples in mg/l is $C_i$ , and the drinking water standard for the individual chemical parameter in mg/l based on the guidelines of the WHO, is $S_i$ . The SI_i value is first computed using Eq. 3 before WQI is calculated. The equation is thus:

$S{I}_i= W_i x q_i$ Eq.3

$WQI= {\displaystyle \sum }_{i=1}^{n}SI$ Eq.4

where, $S{I}_i$ is the sub-index of the i^th parameter; $q_i$ is the quality rating based on the concentration of the i^th parameter. Accordingly, the calculated WQI values are normally grouped into five classes, viz: Excellent Water (<50); Good Water (50-100); Poor Water (100-200); Very Poor Water (200-300); and Unsuitable for Drinking (>300). Table 3 presents examples of literature reports on WQI in arid and semi-arid areas. Evaluation of WQI from 699 sampling sites (Table 3) showed that 235 (33.62%) of water sources in arid and semi-arid areas fall in Excellent Class, 178 (25.46%) fall in Good Class, 235 (33.62%) fall in Poor Class, 37 (5.29%) fall in Very Poor Class and 24 (3.43%) fall in Unsuitable Class (Figure 3).

Figure 3 Literature reports of WQI from arid and semi-arid areas.

Heavy metal pollution index

The heavy metal pollution index (HPI) is an outstanding tool for the evaluation of general pollution of water bodies with respect to heavy metals.⁴⁷ The HPI is built on weighted mathematical quality (Table 4). Weights ($W_i$ ) between 0 and 1 were allocated for individual metals and the hazardous contamination index is 100 in this indexing.^{48–51,40,47} The ranking is built on individual quality concerns, the relative importance of parameters and delineated as inversely proportional to the recommended standards ($S_i$ ) for the individual parameter. First of all, the HPI computation requires the calculation of weightage ($W_i$ ) of $i^{th}$  parameter employing the equation below:

$W_i=\frac{k}{S_i}$ Eq.5

where the proportionality constant is k and the standard reference value of $i^{th}$ parameter (based on WHO reference standard) is $S_i$ . Secondly, the computation of water quality is ($Q_i$ ) ranking for individual heavy metals:

$Q_i=\frac{100x{V}_i}{S_{i }}$  Eq.6

where the sub-index is of $i^{th}$  parameter is $Q_i$ , the supervised value of the $i^{th}$  parameter (µg/L) is $V_i$ and the permissible limit or standard value for the $i^{th}$  parameter is $S_i$ . The concentrations of individual pollutants after calculation of the results can be converted into HPI using Eq. 6. The computed results will be presented as outlined in Table 4.

$HPI=\frac{{{\displaystyle \sum }}_{i=1}^n{W}_i{Q}_i}{{{\displaystyle \sum }}_{i=1}^n{W}_i}$ Eq.7

Like WQI, HPI also aids understanding of water quality by measuring the range into which water pollution is likely to fall. Conversely, it is important to note that, computation of HPI is not a substitute for poor field sampling or laboratory analyses. Therefore, appropriate field sampling and laboratory analyses are essential for accurate reporting of HPI. Example of literature reports on HPI in arid and semi-arid areas is summarized in Table 5.

The computed HPI from the literature reports, showed that 180/425(42.35%) of sources of water supply in drylands fall in Excellent Class, 37/425(8.71%) fall in Good Class, 36/425(8.47%) fall in Poor Class, 33/425(7.76%) fall in Very Poor Class and 139/425(33.71%) fall in Unsuitable Class (Figure 4). Overall, 51.06% of sources of water supply fall in Excellent – Good Class, whereas, 48.94% fall Poor-Unsuitable Class.

Figure 4 Literature reports of HPI from arid and semi-arid areas.

Understanding controls on water quality

An integrated assessment of water quality using WQI and HPI, together with statistical techniques, notably Correlation (r), Principal Component Analysis (PCA), Factor Analysis (FA) and Hierarchical Cluster Analysis (HCA) in arid and semi-arid environments will aid understanding of the origin of solutes and processes controlling water composition in streams and aquifers. Assessment of water quality in drylands is essentially a multivariate problem owing to a wide range of physicochemical parameters (variables) related to several sampling locations (or observations).^{52–63,39,40} Consequently, Correlation (r), PCA/FA, and HCA are increasingly used to analyze hydrochemical data and have been recognized as suitable statistical techniques for the understanding hydrogeochemical composition of water bodies (Table 1).

Correlation analysis

Correlation analysis provides a basic tool for studying water/rock mineral interactions. Concentrations levels and relations between elements can expose the source of solutes and the processes that produced the detected water chemistry.⁶⁴ It could be assumed that a substantial amount of HCO₃ come from dissolution of carbonate minerals in streams and aquifers via the action of infiltering water (recharge) enhanced with CO₂ after being in interaction with the atmosphere. Therefore, the dissolution of carbonates minerals releases Ca into solution, producing Ca-HCO₃ water type.⁶⁴ Calculation of the slops of Ca, Mg and Na with HCO₃ give valuable evidence relating to the stoichiometry of the process. All these can be understood using correlation analysis. For instance, significant relationship (r = ≥0.50) between Ca and HCO₃, suggests that Ca is derived from calcite.⁶⁴

However, poor correlation between these elements (r= ≤0.40) may suggest that Ca ions originate from the dissolution of gypsum which can contribute SO₄ and Ca ions in streams and aquifers. Thus, significant correlations (r= ≥0.50) between Ca and SO₄ may suggest that Ca is derived from Gypsum.⁶⁴ If Ca and Mg correlates significantly (r= ≥0.50), it indicates that the two ions have the same origin. In the same vein, significant correlations (r= ≥0.50) between SO₄ and Mg, is an indicator that parts of SO₄ and Mg are derived from magnesium sulfate minerals.⁶⁴ Conversely, if HCO₃, SO₄, Mg and Ca originate from the simple dissolution of gypsum, dolomite and calcite rocks, then a charge balance must exist between the cations and anions. In addition, if there is a deficiency of (Ca + Ma) in comparison with (HCO₃ + SO₄) and (HCO₃ + SO₄) relative to (Ca +Mg), then the excess positive charge of Ca and Mg would be balanced by Cl, the only major anion. This may further suggest that HCO₃, SO₄, Mg and Ca are not derived from gypsum, dolomite and calcite minerals.⁶⁴

Though anthropogenic inputs can be measured through variations in TDS between sampling locations, ions including Na, SO₄, NO₃, and Cl in streams and aquifers can also be derived from anthropogenic sources -municipal wastes, fertilizer application, and organic wastes. Thus, a significant correlation (r= ≥0.50) between TDS and these ions is a strong indicator of water pollution from anthropogenic activities.⁶⁴ However, a significant correlation (r= ≥0.50) between ions derived from rock mineral and TDS, may suggest silicate weathering reaction. It is equally important to note that, some elements that are derived primarily from rock minerals such as Cd, Cr, and Pb can also be added into the environment through industrial sewage. For instance, Cd and Cr are added into surface waters from sewage ejections from dyeing plants, textile, paint, electroplating, and tanning industries. While Pb is primarily derived from ores, substantial amounts of Pb can enter surface and groundwater from effluent ejections.⁶⁵

Although correlations analysis can be used to establish the origin of ions in surface and groundwater, in-depth analyses of geology and land use is required. Otherwise, drawing conclusions relating to the origin of pollutants in streams and aquifer can be vague. In-depth knowledge of geochemistry of study area and land use types in addition to correlations analysis will aid understanding of the origin of heavy metals such as Cd, Cr, and Pb in streams and aquifers. A significant correlation (r= ≥0.50) between TDS with ions that can be derived from anthropogenic sources such as NO₃, Cl and Na can indicate water pollution from anthropogenic activities. Thus, significant correlation (r= ≥0.50) between NO₃ + Cl/Na⁺ molar ratio and NO₃ + Cl^-/HCO₃ molar ratio, can be used to further supports the anthropogenic inputs or impact of urbanization on water quality.⁶⁴

Principal component analysis

Among the leading multivariate statistical techniques applied in the interpretation of hydrochemical data is principal component analysis.^65–69,38 The PCA which is multivariate statistical method is applied to reduce the size of hydrochemical data, which tend to be intercorrelated to a less important set of ‘principal components’ (PCs) which can be interpreted.⁴⁴ Basically, PCA comprises of two steps, standardization of data and extraction of PCs.⁴⁴ The data contained in a correlation matrix is taken by the PCA and reordered in a way that better explains the fundamental processes that produced the observed concentration of ions. The PCA starts by generating a new collection of hydrochemical variables from the original dataset (i.e. PCs) which are a linear arrangement of original parameters. The eigenvectors and eigenvalues are first extracted by the PCA of the correlation matrix and then remove the less significant observations. Subsequently, PCs of the dataset are transformed from eigenvectors. Therefore, the first PC describes the larger part of the variance, while subsequent PCs describe recurrently reduced parts of the variance. How the PCs illustrate significant relationships (negative or positive) between hydrochemical variables and PC relating the variable is revealed by the PC loadings. For instance, PCs with high positive loadings (r= ≥0.65) of ions such as NO₃, Cl, PO_4, and Na can be related to anthropogenic inputs, in the absence of geologic sources in the study area.⁷⁰

In PCA, Kaiser Normalization Criterion,⁷¹ can be used to define the number of PCs to be extracted. This can best define the variance of analyzed hydrochemical data (i.e. eigenvalue >1), which can be used for additional analysis. How best the variance of a certain hydrochemical variable is explained by a specific set of factors is measured as ‘commonality’. Communalities retained in PCs or number of variables is derived by squaring the parameters in the PC matrix and adding the sum within each parameter. Preferably, if a PCA is effective, PCs will be easily interpretable in terms of specific processes influencing the hydrochemical composition of a stream or groundwater aquifer. Thus, commonalities will be high (~1) and number of PCs will be less. In water quality analysis, PCA is performed on a subset of selected variables (e.g. pH, EC, Temp., TDS, TSS, Ca, Mg, Na, K, HCO₃, Cl, SO₄, H₄SiO₄, Al, Ba, Be, Fe, Li, Mn, Pb, Se, and Sr), which may represent the overall water quality outline.

Though some related data on the variability between objects (parameters) or sampling locations (observation) may be lost via transformation, the explanation of the system is significantly abridged and it can be simply envisaged to derive suitable evidence on the relationship between parameters and observations.⁷² The PCA bilinear model can be rearranged following the matrix decomposition equation,⁷² thus;

$X=T{P}^T+E$  Eq.8

where X represents a matrix of data which is compressed into T which is the scores of matrices, PT is a matrix of loadings and E is matrix residual.⁷² The scores of matrices provide information relating to the patterns of loadings or pollution sources between observations. Information about the influence of the original variables to each one of these physicochemical patterns or sources will usually provide the matrix of loadings.

The principle of PCA

For a better understanding of why PCA is commonly applied in water quality studies, the following principles should be noted:⁷³

1. If the size or magnitude of the data is reduced devoid of any loss of info, i.e., lacking any loss of data variance, PCA can be of considerable advantage over other techniques;
2. After the above task has been achieved, it would be valuable to present this data diagrammatically if only because persons are so approachable to pictorial exhibitions;
3. At that point, it is necessary to have at least some pointers, which choose the likely central variables that influence the distribution of data in the diagram; and
4. Lastly, it is exceptionally useful to spot the relationship between the samples and the variables jointly on the same diagram.

The data structure of the matrix is often revealed, once the boundaries of the PCA technique and the scores-scores illustration are detected. Even though, a mathematical or statistical technique will process a collection of figures whether they are analytically expressive or not; it is the duty of the user to make sure the suitable quality of the data. Although there may not be anything worthy to realize after the application of statistical analysis, PCA is a technique of transforming data, which simplifies four points (a-d) outlined above. Subsequent to this procedure, the new axes, termed principal components (or PCs), are selected based on a linear model (Eq. 9) so that PC1 defines the greatest variance in the data set; which is trailed by PC2, which defines the second greatest expanse of variance within the data set, but which is built orthogonally to PC1, and accordingly, is autonomous to the PC1.

$P{C}_{jk}=a_{i1}{x}_{k2}+\mathrm{...}+a_{jn}{x}_{kn}$  Eq.9

where PC_jk is the value of the principal component, j for object k (the score value for object j on component k), aj1 is the loading of variable 1 on component j, xk1 is the measurement value for variable 1 on object k and n is the total number of variables studied. Such analysis can be repetitive until the number of PCs is equivalent to the number of the primary variables. The benefit of the PCA is that the variance in the data set is mostly confined in the first few PCs, hence the reduction in size or magnitude of the multivariate matrix.

Interpretation of PC loadings

The extraction of certain components (often 1-5) is normally built on the proportion of variance accrued, which included a percentage greater than 80%.^74,70 For instance, based on ‘scree test’, the certain defined PCs with typical PC loadings suggest different noticeable contributions were involved in controlling the hydrochemical composition of streams and aquifers. The PC 1 which explained the largest variance in the data matrix, may have high positive loadings on particular ions of either rock-mineral derivative or anthropogenic origin. If these ions are of rock mineral origin or anthropogenic sources, then the factor can be related to either of the two sources of solutes in streams and aquifers.

However, relating ions may require a thorough understanding of geochemistry and land use practice in the study area. For instance, if a particular factor is having high positive loadings (≥0.65) on physical parameters such as EC and Temperature, it could be deemed reasonable since Temperature level is closely associated with EC level in streams and groundwater aquifers. The later rises by 2% with an elevated temperature of 1^oC. Temperature range between 5 to10˚C in gravity flow water also affects TDS levels, which eventually disturbs solubility of gasses, ion exchange capacity, redox reaction, sorption processes, complexation, speciation, and pH level (EPA, 2001).

 For a better interpretation of factor loadings and relating them to either rock mineral or anthropogenic activities in drylands, a seasonal sampling approach must be employed. Because the behavior of certain ions tends to be correlated with seasonal rainfall and/or recharge. For instance, negative loadings on pH in a particular PC(s) can be deemed reasonable since pH usually attained a converse relationship with ions of carbonate origin.⁷⁴ The application of PCA can provide the needed information for the hydrochemical and geographical understanding of the data (Kokot and Stewart, 1995; Kokot et al., 1998; Olsen et al., 2012).^73,75 However, extracting this type of information may require submission of the PCA scores to another multivariate statistical tool for unverified classification analysis using hierarchical clustering analysis (HCA).

Hierarchical cluster analysis

The objective of applying HCA in water quality studies is too grouped sampling locations that have similar hydrochemical attributes into classes (i.e. clusters). Such a clustering technique would help in recognizing hydrochemical data sets of the locations base on the sources of solutes, i.e. anthropogenic or natural.^74,44 The HCA is an unverified outline identification method that exposes inherent assembly or pattern recognition of a dataset without a prior hypothesis with regards to the data so that the objects of the system can be classified into clusters based on their resemblances.^74,44

Basically, there are two major categories of HCA: (i) non-hierarchical; and (ii) hierarchical. The former is a widely used technique which can form clusters consecutively, beginning with the most identical pair of parameters and forming complex clusters after each step which is repeated until a single cluster comprising all the observations is attained.^74,44 The results are presented as a dendrogram, which offers a graphic summary presenting an image of the clusters and their closeness with a studied decrease in the dimensionality of original observations.^74,44 In clustering, observations with similar characteristics or else observations with dissimilarity would be collected into an identical group.^74,44 Often the Ward’s-algorithmic clustering technique subsequent to the squared Euclidean distance, is applied. This is measured as the most influential means of clustering.^74,44 Before the clustering analysis, the hydrochemical data, xji is standardized by Z-scale transformation, Eq. 10:

$Z=\frac{X_{Ji-X^{•}{}_j}}{Sj}$ Eq.10

where x_ji = value of the jth hydrochemical parameter measured at ith location, ẋ_j = mean (spatial) value of the j_th parameter and Sj = standard deviation (spatial) of the j_th parameter.

The clustering achieved with standardized data is anticipated to be influenced less by the large and/or small variance of the hydrochemical data. Also, the influence of diverse measurement units of the data can be removed by making the data dimensionless.⁴⁴ In water quality studies HCA is performed on a subset of selected variables (e.g. pH, EC, Temp., TDS, TSS, Ca, Mg, Na, K, HCO₃, Cl, SO₄, H₄SiO₄, Al, Ba, Be, Fe, Li, Mn, Pb, Se, and Sr), which represented the overall water chemistry outline. Depending on geology, land use and the studied ions, individual clusters can be related to the natural geogenic processes or anthropogenic activities.

The need for integrated approach to water quality analyses in drylands

Comparison of studies in Table 1 showed that 15.57% of studies have measurements on WQI and 12.29% have measured HPI. This suggests that most of water quality studies in arid and semi-arid areas, do not have adequate reporting on the WQI and HPI. Thus, water suitability for drinking, agriculture, and industrial uses remained poorly known in arid areas (Figure 5). In contrast, 37.70%, 67.21%, and 64.75% have applied correlation analysis, PCA and HCA in water quality investigations, indicative of the wider extent to which processes controlling water chemistry is understood in global drylands (Figure 6). However, the application of these statistical techniques alone is not enough, for the reason that the concentrations of ions in sources of water supply in relation to their suitability for drinking, agriculture, and industrial uses cannot be revealed by mere statistical applications; this calls for an integrated approach to water quality analysis.

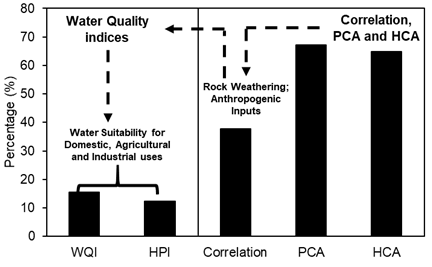
Figure 5 Example of studies on water quality using WQI, HPI, Correlation, PCA and HCA in arid and semi-arid environments.

Figure 6 Example of literature reports on major processes controlling water quality in arid and semi-arid environments.

Accordingly, it is imperative to note that, though the WQI, HPI, Correlation, PCA and HCA have provided simple tools for assessing water quality, especially in underdeveloped countries, where improved water supply is mostly lacking especially in remote areas, computation of WQI and HPI is not a substitute for poor field sampling or laboratory analyses. Therefore, appropriate field sampling and laboratory analyses are essential for accurate computation and reporting of WQI and HPI. One of the best ways for testing the internal consistency of water quality data is by Chemical Balance Error (CBE), where the hydrochemical data can be subjected to internal consistency tests.²⁴ Thus, it is beneficial to apply CBE (Eq. 11), in order to test the internal consistency of hydrochemical data (Eq. 11).

$CBE=\frac{{\displaystyle \sum Cations-{\displaystyle \sum Anions}}}{{\displaystyle \sum Cations+{\displaystyle \sum Anions}}}x100$ Eq.11.

where the entire absorptions of cations and anions are in meq/l.

Typically, the cations and anions must accurately balance, and under normal circumstances where the study recovers most of the elements, the cations and anions must not vary by more than 5%.²⁴ Further, apart from the CBE, the absorptions of certain ions in comparison with the total dissolved ion content, the consistency between physical parameters (pH, EC, TDS) measured in situ and those determined in the laboratory can be used to aid in measuring internal consistency of the water quality data. ²⁴ The TDS level for water in each sample, for example, can be checked by adding up the levels of the major ions. These concentration levels can then be related to the TDS levels determined in situ. These indices all imply that the data is essentially consistent internally and could be employed for further analyses. ²⁴

Though WQI, HPI, Correlation, PCA and HCA provide simple tools for assessment of water quality, yet an integrated model technique incorporating these tools is lacking. Thus, there is a dire need for joint application of water quality indices and multivariate statistics in future studies on water quality in drylands. In this review, we attempted a model design that can be used for water quality assessments in drylands (Figure 7). The need for the integrated conceptual model design is perhaps due to distinctive climatic conditions of arid and semi-arid environments, mainly high temperatures and low rainfall. The latter could affect the volume water received by streams and aquifers, whereas the former affects the solubility of gasses, ion exchange capacity, redox reaction, sorption processes, complexation, speciation and pH level in both streams and groundwater aquifers. However, several types of trace elements and heavy metals of rock origin are increasingly being added into streams and groundwater consequence of anthropogenic activities. Thus, defining the origin of these elements requires an integrated approach and in-depth analyses of the hydrogeochemical configurations the study area, as well as land use types. Overall, the natural geogenic processes, seasonality, environmental change (drought) appeared to exert more controls on water quality than human activities such as industry, agriculture, mining, and urbanization.

Figure 7 A conceptual model for water quality assessment in arid and semi-arid environments.

The literature is unanimous about the need for understanding the natural geogenic and anthropogenic processes controlling water quality in arid and semi-arid areas. Drylands constitute a distinctive ecological system which is mainly characterized by low rainfall, high rate evaporation, and poor vegetation cover. These coupled with human activities such as mining, irrigation, municipal and industrial water demand and improper sewage discharge from urban and industrial sources, have threatened water quality. Relating literature reports with the aforementioned drivers of water use results in the following remarks:

1. There is a need for incorporating computation of WQI and HPI by studies on water quality using multivariate statistical techniques in global drylands. This is essential because the measure of suitability or otherwise of sources of fresh water for various uses is central to any form of water quality investigation and this cannot be revealed exclusively via application of multivariate analysis.
2. Arid and semi-arid areas constitute a distinctive ecosystem, mainly characterized by fluctuations in annual rainfall and high temperatures. Thus, water quality investigations must incorporate seasonal sampling of water bodies, owing to the fact that concentrations of ions may vary with precipitation and temperature changes.
3. During drought periods, the volume of water in streams and aquifers may be reduced, with its resultant consequence of ionic drag force. This coupled with high temperatures which eventually disturbs solubility of gasses, ion exchange capacity, redox reaction, sorption processes, complexation, speciation and pH level in the water, will no doubt have a direct bearing on ions concentrations in stream and aquifers. Thus, water quality analyses in drylands must be climate-sensitive.
4. In-depth knowledge of geochemistry and land use types is required for proper identification of the origin of ions in water bodies. This is essential because, several ions of rock-mineral origin are increasingly being added into the environment through human activities, such as industry, urbanization, mining, and agriculture.
5. Also, consistent water quality records over wider spatial and temporal scales are necessary, for trend change detection analysis. This cannot be achieved by individual studies and/or syntheses of data from the literature. Observation boreholes must be provided, as this could enable the application of an integrated approach to water quality monitoring over a long period of time.
6. Consequently, annual and/or decadal data can be obtainable which can be employed for policy recommendations pertaining to water quality management in arid and semi-arid environments.

While there is significant reporting on water quality in arid and semi-arid areas around the world, water quality investigations are largely influenced by the prevailing environmental conditions as well as anthropogenic activities. These factors are also highly varied in arid and semi-arid environments. Thus, the rationality for establishing controls on water quality may be very difficult. Hence, water quality reports must be interpreted within the framework of the existing environmental conditions, time and regularly essential standard application for reporting water quality in the literature.

This study was supported by Universiti Teknologi Malaysia. Sincere thanks to all anonymous contributors.

The authors pronounce that there is no conflict of interest associated with this paper.

1. Anderson HR, Ogilbee W. Aquifers in the Sokoto Basin, Northwestern Nigeria, with a description of the general hydrogeology of the region: Contributions to the Hydrology of Africa and the Mediterranean Region. Geological Survey Water-Supply Paper. 1973;1757-L:1–88.
2. Hamidu H, Lawal M, Abdulganiyu Y, et al. Re-evaluation of Shallow Floodplain Aquifers Groundwater Potentials and Storage of Sokoto Basin, Northwestern Nigeria. American Journal of Water Resources. 2017;5(3):72–84.
3. Rizeei HM, Azeez OS, Pradhan B, et al. Assessment of groundwater nitrate contamination hazard in a semi-arid region by using integrated parametric IPNOA and data-driven logistic regression models. Environmental Monitoring Assessment. 2018;190(11):633.
4. Selck BJ, Carling GT, Kirby SM, et al. Investigating Anthropogenic and Geogenic Sources of Groundwater Contamination in a Semi-Arid Alluvial Basin, Goshen Valley, UT, USA. Water, Air, & Soil Pollution. 2018;229(6).
5. Wu J, Wang L, Wang S, et al. Spatiotemporal variation of groundwater quality in an arid area experiencing long-term paper wastewater irrigation, northwest China. Environmental Earth Sciences. 2017;76(13).
6. Vahabian M, Hassanzadeh Y, Marofi S. Assessment of landfill leachate in semi-arid climate and its impact on the groundwater quality case study: Hamedan, Iran. Environ Monit Assess. 2019;191(2):109.
7. Gutierrez M, Biagioni RN, Alarcon-Herrera MT, et al. An overview of nitrate sources and operating processes in arid and semiarid aquifer systems. Sci Total Environ. 2018;624:1513–1522.
8. FAO. The state of food and agriculture. Food and Agriculture Organization of the United Nations Viale delle Terme di Caracalla 00153 Rome, Italy. 2008. p. 138.
9. Acworth RI, Rau GC, Cuthbert MO, et al. Long-term spatio-temporal precipitation variability in arid-zone Australia and implications for groundwater recharge. Hydrogeology Journal. 2016;24(4):905–921.
10. Xue L, Zhu B, Yang C, et al. Study on the characteristics of future precipitation in response to external changes over arid and humid basins. Scientific Report. 2017;7(1):15148.
11. Adimalla N, Li P. Occurrence, health risks, and geochemical mechanisms of fluoride and nitrate in groundwater of the rock-dominant semi-arid region, Telangana State, India. Human and Ecological Risk Assessment: An International Journal. 2018;25(1-2):81–103.
12. Bretzler A, Stolze L, Nikiema J, et al. Hydrogeochemical and multi-tracer investigations of arsenic-affected aquifers in semi-arid West Africa. Geoscience Frontiers. 2019;10(5):1685–1699.
13. Abu Allaban M, El Naqa A, Jaber M, et al. Water scarcity impact of climate change in semi-arid regions: a case study in Mujib basin, Jordan. Arabian Journal of Geosciences. 2014;8(2):951–959.
14. Herrera-Pantoja M, Hiscock KM. Projected impacts of climate change on water availability indicators in a semi-arid region of central Mexico. Environmental Science & Policy. 2015;54:81–89.
15. Xia J, Ning L, Wang Q, et al. Vulnerability of and risk to water resources in arid and semi-arid regions of West China under a scenario of climate change. Climatic Change. 2016;144(3):549–563.
16. Chen H, Huo Z, Dai X, et al. Impact of agricultural water-saving practices on regional evapotranspiration: The role of groundwater in sustainable agriculture in arid and semi-arid areas. Agricultural and Forest Meteorology. 2018;263:156–168.
17. Yang Q, Li Z, Ma H, et al. Identification of the hydrogeochemical processes and assessment of groundwater quality using classic integrated geochemical methods in the Southeastern part of Ordos basin, China. Environmental Pollution. 2016;218:879–888.
18. El Alfy M, Lashin A, Abdalla F, et al. Assessing the hydrogeochemical processes affecting groundwater pollution in arid areas using an integration of geochemical equilibrium and multivariate statistical techniques. Environmental Pollution. 2017;229:760–770.
19. Kamtchueng BT, Fantong WY, Wirmvem MJ, et al. Hydrogeochemistry and quality of surface water and groundwater in the vicinity of Lake Monoun, West Cameroon: Approach from multivariate statistical analysis and stable isotopic characterization. Environmental Monitoring Assessment. 2015;188(9):524.
20. Sethy SN, Syed TH, Kumar A, et al. Hydrogeochemical characterization and quality assessment of groundwater in parts of Southern Gangetic Plain. Environmental Earth Sciences. 2016;75(3).
21. Andrade L, O'Dwyer J, O'Neill E, et al. Surface water flooding, groundwater contamination, and enteric disease in developed countries: A scoping review of connections and consequences. Environmental Pollution. 2018;236:540–549.
22. Blake S, Henry T, Murray J, et al. Compositional multivariate statistical analysis of thermal groundwater provenance: A hydrogeochemical case study from Ireland. Applied Geochemistry. 2016;75:171–188.
23. Jeevanandam M, Kannan R, Srinivasalu S, et al. Hydrogeochemistry and groundwater quality assessment of lower part of the Ponnaiyar River Basin, Cuddalore district, South India. Environmental Monitoring Assessment. 2017;132(1-3):263–274.
24. Yidana SM, Bawoyobie P, Sakyi P, et al. Evolutionary analysis of groundwater flow: Application of multivariate statistical analysis to hydrochemical data in the Densu Basin, Ghana. Journal of African Earth Sciences. 2018;138:167–176.
25. Cartwright I, Werner AD, Woods JA. Using geochemistry to discern the patterns and timescales of groundwater recharge and mixing on floodplains in semi-arid regions. Journal of Hydrology. 2019;570:612–622.
26. Kattan Z. Using hydrochemistry and environmental isotopes in the assessment of groundwater quality in the Euphrates alluvial aquifer, Syria. Environmental Earth Sciences. 2018;77(2).
27. Szczucińska A, Dłużewski M, Kozłowski R, et al. Hydrochemical Diversity of a Large Alluvial Aquifer in an Arid Zone (Draa River, S Morocco). Ecological Chemistry and Engineering S. 2019;26(1):81–100.
28. Alias N, Liu A, Egodawatta P, et al. Sectional analysis of the pollutant wash-off process based on runoff hydrograph. Journal Environmental Management. 2014;134:63–69.
29. Masoud AA, Koike K, Mashaly HA. Spatio-temporal trends and change factors of groundwater quality in an arid area with peat rich aquifers: Emergence of water environmental problems in Tanta District, Egypt. Journal of Arid Environments. 2016;124:360–376.
30. Stadler S, Osenbrück K, Knöller K, et al. Understanding the origin and fate of nitrate in groundwater of semi-arid environments. Journal of Arid Environments. 2008;72(10):1830–1842.
31. Shajib MTI, Hansen HCB, Liang T, et al. Metals in surface specific urban runoff in Beijing. Environmental Pollution. 2019;248:584–598.
32. St-Hilaire A, Duchesne S, Rousseau AN. Floods and water quality in Canada: A review of the interactions with urbanization, agriculture and forestry. Canadian Water Resources Journal. 2015;41(1-2):273–287.
33. Bonneau J, Fletcher TD, Costelloe JF, et al. Stormwater infiltration and the ‘urban karst’- A review. Journal of Hydrology. 2017;552:141–150.
34. Kløve B, Kvitsand HML, Pitkänen T, et al. Overview of groundwater sources and water-supply systems, and associated microbial pollution, in Finland, Norway and Iceland. Hydrogeology Journal. 2017;25(4):1033–1044.
35. Vrzel J, Solomon DK, Blažeka Ž, et al. The study of the interactions between groundwater and Sava River water in the Ljubljansko polje aquifer system (Slovenia). Journal of Hydrology. 2018;556:384–396.
36. Black W, Babin BJ. Multivariate data analysis: Its approach, evolution, and impact. The Great Facilitator. 2019;121–130.
37. Aminiyan MM, Aitkenhead Peterson J, Aminiyan FM. Evaluation of multiple water quality indices for drinking and irrigation purposes for the Karoon River, Iran. Environmental Geochemistry and Health. 2018;40(6):2707–2728.
38. Bouteraa O, Mebarki A, Bouaicha F, et al. Groundwater quality assessment using multivariate analysis, geostatistical modeling, and water quality index (WQI): a case of study in the Boumerzoug-El Khroub valley of Northeast Algeria. Acta Geochimica. 2019.
39. Abu Al Naeem MF, Yusoff I, Ng TF, et al. A study on the impact of anthropogenic and geogenic factors on groundwater salinization and seawater intrusion in Gaza coastal aquifer, Palestine: An integrated multi-techniques approach. Journal of African Earth Sciences, 2019;156:75–93.
40. Basahi JM, Masoud MHZ, Rajmohan N. Effect of flash flood on trace metal pollution in the groundwater - Wadi Baysh Basin, Western Saudi Arabia. Journal of African Earth Sciences. 2018;147:338–351.
41. Aminiyan MM, Aminiyan FM, Heydariyan A, et al. The assessment of groundwater geochemistry of some wells in Rafsanjan plain, Iran. Eurasian Journal of Soil Science (Ejss). 2016;5(3):221–230.
42. Eslami F, Yaghmaeian K, Mohammadi A. An integrated evaluation of groundwater quality using drinking water quality indices and hydrochemical characteristics: a case study in Jiroft, Iran. Environmental Earth Sciences. 2019;78(10).
43. Hamdi M, Zagrarni MF, Jerbi H, et al. Hydrogeochemical and isotopic investigation and water quality assessment of groundwater in the Sisseb El Alem Nadhour Saouaf aquifer (SANS), northeastern Tunisia. Journal of African Earth Sciences. 2018;141:148–163.
44. Machiwal D, Jha MK. Identifying sources of groundwater contamination in a hard-rock aquifer system using multivariate statistical analyses and GIS-based geostatistical modeling techniques. Journal of Hydrology: Regional Studies. 2015;4:80–110.
45. Mahfooz Y, Yasar A, Sohail MT, et al. Investigating the drinking and surface water quality and associated health risks in a semi-arid multi-industrial metropolis (Faisalabad), Pakistan. Environmental Science Pollution Research International. 2019;26(20):20853–20865.
46. Subba Rao N, Sunitha B, Adimalla N, et al. Quality criteria for groundwater use from a rural part of Wanaparthy District, Telangana State, India, through ionic spatial distribution (ISD), entropy water quality index (EWQI) and principal component analysis (PCA). Environmental Geochemistry and Health. 2020;42(2):579–599. 
47. Rakotondrabe F, Ndam Ngoupayou JR, Mfonka Z, et al. Water quality assessment in the Betare-Oya gold mining area (East-Cameroon): Multivariate Statistical Analysis approach. Science of the Total Environment. 2018;610-611:831–844.
48. El-Ameir YA. Evaluation of heavy metal pollution in Damietta Branch of Nile River, Egypt using metal indices and phyto-accumulators. Journal of Environmental Sciences. 2017;42(2):89–102.
49. Kwaya MY, Hamidu H, Kachalla M, et al. Preliminary Ground and Surface Water Resources Trace Elements Concentration, Toxicity and Statistical Evaluation in part of Yobe State, Northeastern Nigeria. Geosciences. 2017;7(4):117–128.
50. Maurya C, Srivastava JN. Current seasonal variations in physicochemical and heavy metals parameters of sewage treatment plant effluent and suitability for irrigation. Journal of Water Resource and Protection. 2019;11(07):852–865.
51. Rafiee M, Eslami A, Saeedi R, et al. Multivariate and geostatistical analysis of spatial distribution and potential sources of heavy metals in surface waters. Caspian Journal of Environmental Science. 2019;17(1):23–41.
52. Acikel S, Ekmekci, M. Assessment of groundwater quality using multivariate statistical techniques in the Azmak Spring Zone, Mugla, Turkey. Environmental Earth Sciences. 2018;77(22).
53. Agoubi B, Kharroubi A, Abida H. Geochemical Assessment of Environmental Impact on Groundwater Quality in Coastal Arid Area, South-Eastern Tunisia. Journal of Environmental Science and Engineering Technology. 2014;2(2):35-46.
54. Bencer S, Boudoukha A, Mouni L. Multivariate statistical analysis of the groundwater of Ain Djacer area (Eastern of Algeria). Arabian Journal of Geosciences. 2016;9(4).
55. Ehya F, Marbouti Z. Hydrochemistry and contamination of groundwater resources in the Behbahan plain, SW Iran. Environmental Earth Sciences. 2016;75(6).
56. Gubran M, Ghrefat H, Zaidi F, et al. Integration of hydrochemical, GIS, and remote-sensing data for assessment of shallow groundwater aquifers in Wadi Nisah, Central Saudi Arabia. Environmental Earth Sciences. 2019;78(5).
57. Jassas H, Merkel B. Assessment of hydrochemical evolution of groundwater and its suitability for drinking and irrigation purposes in Al-Khazir Gomal Basin, Northern Iraq. Environmental Earth Sciences. 2015;74(9):6647–6663.
58. Kolsi SJ, Bouri S, Hachicha W. Implementation and evaluation of multivariate analysis for groundwater hydrochemistry assessment in arid environments: a case study of Hajeb Elyoun–Jelma, Central Tunisia. Environmental Earth Sciences. 2013;1–10.
59. Kwami IA, Ishaku JM, Hamza YS, et al. Application of Multivariate Statistical Techniques for the Interpretation of Groundwater Quality in Gombe and Environs, North-East Nigeria. Journal of Geosciences and Geomatics. 2019;7(1):9–14.
60. Mountadar S, Younsi A, Hayani A, et al. Groundwater salinization process in the coastal aquifer Sidi Abed-Ouled Ghanem (Province of El Jadida, Morocco). Journal of African Earth Sciences. 2018;147:169–177.
61. Nadiri AA, Tsai FTC, Fijani E. Hydrogeochemical analysis for Tasuj plain aquifer, Iran. Journal of Earth System Science. 2013;122(4):1091–1105.
62. Sajil Kumar PJ. Hydrogeochemical and multivariate statistical appraisal of pollution sources in the groundwater of the lower Bhavani River basin in Tamil Nadu. Geology, Ecology, and Landscapes. 2019;4(1):1–12.
63. Zhu B, Wang X, Rioual P. Multivariate indications between environment and groundwater recharge in a sedimentary drainage basin in Northwestern China. Journal of Hydrology. 2017;549:92–113.
64. Marghade D, Malpe DB, Zade AB. Geochemical characterization of groundwater from northeastern part of Nagpur urban, Central India. Environmental Earth Sciences. 2011;62(7):1419–1430.
65. Amoo AO, Gambo YH, Adeleye AO, et al. Assessment of groundwater quality in Sharada Industrial Area of Kano, North-Western Nigeria. FUW Trends in Science & Technology Journal. 2018;3(2A):407-411.
66. Al Farraj AS, Al Wabel MI, El Saeid, MH, et al. Evaluation of Groundwater for Arsenic Contamination Using Hydrogeochemical Properties and Multivariate Statistical Methods in Saudi Arabia. Journal of Chemistry. 2013:1-9.
67. Barakat A, El Baghdadi M, Rais J, et al. Assessment of spatial and seasonal water quality variation of Oum Er Rbia River (Morocco) using multivariate statistical techniques. International Soil and Water Conservation Research. 2016;4(4):284–292.
68. Belkhiri L, Abdurrahman B, Lotfi M, et al. Multivariate statistical characterization of groundwater quality in Ain Azel plain Algeria. African Journal of Environmental Science and Technology. 2010;4(8):526–534.
69. Gasmi T, Khouni I, Ghrabi A. Assessment of heavy metals pollution using multivariate statistical analysis methods in Wadi El Bey (Tunisia). Desalination and Water Treatment. 2006;57(46):22152–22165.
70. Selvakumar S, Ramkumar K, Chandrasekar N, et al. Groundwater quality and its suitability for drinking and irrigational use in the Southern Tiruchirappalli district, Tamil Nadu, India. Applied Water Science. 2017;7(1):411–420.
71. Kaiser HFT. The varimax criterion for analytic rotation in factor analysis. Psychometrika. 1958;23:187–200.
72. Hildebrandt A, Guillamon M, Lacorte S, et al. Impact of pesticides used in agriculture and vineyards to surface and groundwater quality (North Spain). Water Research. 2008;42(13):3315–3326.
73. Kokot S, Grigg M, Panayiotou H. Data Interpretation by some Common Chemometrics Methods. Electroanalysis. 1988;10(16):1081–1088.
74. Lin CY, Abdullah MH, Praveena SM, et al. Delineation of temporal variability and governing factors influencing the spatial variability of shallow groundwater chemistry in a tropical sedimentary island. Journal of Hydrology. 2012;432-433:26–42.
75. Zhang X, Qian H, Chen J, et al. Assessment of groundwater chemistry and status in a heavily used Semi-Arid Region with multivariate statistical analysis. Water. 2014;6(8):2212–2232.
76. Kwaya MY, Hamidu H, Mohammed AI, et al. Heavy metals pollution indices and multivariate statistical evaluation of groundwater quality of Maru town and environs. Journal of Materials and Environmental Sciences. 2019;10(1);32–44.
77. Rasool A, Xiao T, Farooqi A, et al. Arsenic and heavy metal contaminations in the tube well water of Punjab, Pakistan and risk assessment: A case study. Ecological Engineering. 2015;95:90–100.
78. Abbasnia A, Alimohammadi M, Mahvi AH, et al. Assessment of groundwater quality and evaluation of scaling and corrosiveness potential of drinking water samples in villages of Chabahr city, Sistan and Baluchistan province in Iran. Data Brief. 2018;16:182–192.
79. Abu Khatita AM, Sabet HS, Shehata H, et al. Hydrogeochemical Characterization and Assessment of Sharm El-Sheikh Groundwater, South Eastern Sinai, Egypt. International Journal of Basic and Applied Sciences. 2014;3(4):196–209.
80. Alarcon Herrera MT,  Bundschuh J, Nath B, et al. Co-occurrence of arsenic and fluoride in groundwater of semi-arid regions in Latin America: Genesis, mobility and remediation. Journal of Hazard Material. 2013;262:960–969.
81. Amiri V, Nakhaei M, Lak R, et al. Investigating the salinization and freshening processes of coastal groundwater resources in Urmia aquifer, NW Iran. Environmental Monitoring and Assessment. 2016;188(4):233.
82. Ayadi Y, Mokadem N, Besser H, et al. Statistical and geochemical assessment of groundwater quality in Teboursouk area (Northwestern Tunisian Atlas). Environmental Earth Sciences. 2018;77(9).
83. Agoubi, B., and Gzam, M. (2016). Adverse Effects of Phosphate Industry on the Environment and Groundwater Geochemistry in the Ghannouch Field, Southeastern Tunisia. American Journal of Geophysics, Geochemistry and Geosystems. 2016;2(5):51–63.
84. Agoubi B, Kharroubi A, Abichou T, et al. Hydrochemical and geoelectrical investigation of Marine Jeffara Aquifer, Southeastern Tunisia. Applied Water Science. 2013;3(2):415–429.
85. Bahloul M, Baati H, Amdouni R, et al. Assessment of heavy metals contamination and their potential toxicity in the surface sediments of Sfax Solar Saltern, Tunisia. Environmental Earth Sciences. 2018;77(1).
86. Barzegar R, Asghari Moghaddam A, Soltani S. Heavy Metal(loid)s in the Groundwater of Shabestar Area (NW Iran): Source Identification and Health Risk Assessment. Exposure and Health. 2017.
87. Batayneh A, Zumlot T. Multivariate statistical approach to geochemical methods in water quality factor identification; Application to the shallow aquifer system of the Yarmouk Basin of North Jordan. Research Journal of Environmental and Earth Sciences. 2012;4(7):756–768.
88. Batsaikhan N, Lee J, Nemer B, Woo N. Water Resources Sustainability of Ulaanbaatar City, Mongolia. Water. 2018;10(6):750.
89. Belkhiri L, Mouni L. Application of Multivariate statistical methods so surface water and groundwater of the Soummam Basin, Algeria. 11th International Conference on Hydroinformatics HIC 2014, New York City, USA, 2014. p. 1–8.
90. Bhakar P, Singh AP. Groundwater quality assessment in a hyper-arid region of Rajasthan, India. Natural Resources Research. 2018;28(2):505–522.
91. Boughariou E, Bahloul M, Jmal I. Hydrochemical and statistical studies of the groundwater salinization combined with MODPATH numerical model: case of the Sfax coastal aquifer, Southeast Tunisia. Arabian Journal of Geosciences. 2018;11(4).
92. Singh CK, Kumar A, Shashtri S, et al. Multivariate statistical analysis and geochemical modeling for geochemical assessment of groundwater of Delhi, India. Journal of Geochemical Exploration. 2017;175:59–71.
93. Carlson MA, Lohse KA, McIntosh JC, et al. Impacts of urbanization on groundwater quality and recharge in a semi-arid alluvial basin. Journal of Hydrology. 2011;409(1-2):196–211.
94. Chaves LCG, Lopes FB, Maia ARS, et al. Water quality and anthropogenic impact in the watersheds of service reservoirs in the Brazilian semi-arid region. Revista CiÊncia Agron Ômica. 2019;50(2).
95. Dehghanzadeh R, Safavy Hir N, Shamsy Sis J. Integrated Assessment of Spatial and Temporal Variations of Groundwater Quality in the Eastern Area of Urmia Salt Lake Basin Using Multivariate Statistical Analysis. Water Resources Management. 2014;29(4):1351–1364.
96. El Yaouti F, El Mandour A, Khattach D, et al. Salinization processes in the unconfined aquifer of Bou-Areg (NE Morocco): A geostatistical, geochemical, and tomographic study. Applied Geochemistry. 2009;24(1):16–31.
97. Hamzaoui-Azaza F, Ketata M, Bouhlila R, et al. Hydrogeochemical characteristics and assessment of drinking water quality in Zeuss-Koutine aquifer, southeastern Tunisia. Environ Monit Assess. 2011;174(1-4):283–298.
98. Hamzaoui-Azaza F, Tlili-Zrelli B, Bouhlila R, et al. An integrated statistical methods and modelling mineral–water interaction to identifying hydrogeochemical processes in groundwater in Southern Tunisia. Chemical Speciation & Bioavailability. 2015;25(3):165–178.
99. Gomes P, Valente T, Pereir P. Addressing quality and usability of surface water bodies in semi-arid regions with mining influences. Environmental Processes. 2018;1–19.
100. Yu H, Song Y, Xi B, et al. Denitrification potential and its correlation to Physico-chemical and Biological characteristics of saline wetland soils in semi-arid regions. Chemosphere. 2012;89(11):1339–1346.
101. Jampani M, Huelsmann S, Liedl R, et al. Spatio-temporal distribution and chemical characterization of groundwater quality of a wastewater irrigated system: A case study. Science of the Total Environment. 2018;636:1089–1098.
102. Kaba M, Mesnage V, Laignel B, et al. Spatial and seasonal variability of groundwater hydrochemistry in the Senegal North Littoral aquifer using multivariate approach. Environmental Earth Sciences. 2016;75(9).
103. Karroum M, Elgettafi M, Elmandour A, et al. Geochemical processes controlling groundwater quality under semi-arid environment: A case study in central Morocco. Science of the Total Environment. 2017;609:1140–1151.
104. Ketata-Rokbani M, Gueddari M, Rachida B. Use of geographical information system and water quality index to assess groundwater quality in El Khairat deep aquifer (Enfidha, Tunisian Sahel). Iranica Journal of Energy & Environment. 2011;2(2):133–144.
105. Khazaala SH, Al-Azawia KF, Eassaa HA. Study the level of some metals in water of Lake Habbaniyyah in Al-Ambar-Iraq. Energy Procedia. 2019;157:68–74.
106. Kraiem Z, Zouari K, Chkir N, et al. Geochemical characteristics of arid shallow aquifers in Chott Djerid, south-western Tunisia. Journal of Hydro-environment Research. 2014;8(4):460–473.
107. Krishna AK, Mohan KR, Dasaram B. Assessment of groundwater quality, toxicity and health risk in an industrial area using multivariate statistical methods. Environmental Systems Research. 2019;8(1).
108. Kuisi MA, Abdel-Fattah A. Groundwater vulnerability to selenium in semi-arid environments: Amman Zarqa Basin, Jordan. Environmental Geochemistry Health. 2010;32(2):107–128.
109. Kumar M, Ramanathan A, Keshari AK. Understanding the extent of interactions between groundwater and surface water through major ion chemistry and multivariate statistical techniques. Hydrological Processes. 2010;23(2):297–310.
110. Kumssa A, Jones JF, Herbert Williams J. Conflict and human security in the North Rift and North Eastern Kenya. International Journal of Social Economics. 2009;36(10):1008–1020.
111. Belkhiri L, Boudoukha A, Mouni L, et al. Application of multivariate statistical methods and inverse geochemical modeling for characterization of groundwater- A case study: Ain Azel plain (Algeria). Geoderma. 2010;159(3-4):390–398.
112. Belkhiri L, Boudoukha A, Mouni L, et al. Multivariate statistical characterization of groundwater quality in Ain Azel plain, Algeria. African Journal of Environmental Science and Technology. 2010;4(8):526–534.
113. M’nassri S, Dridi L, Schäfer G, et al. Groundwater salinity in a semi-arid region of central-eastern Tunisia: insights from multivariate statistical techniques and geostatistical modelling. Environmental Earth Sciences. 2019;78(10).
114. Masoud AA, El-Horiny MM, Atwia MG, et al. Assessment of groundwater and soil quality degradation using multivariate and geostatistical analyses, Dakhla Oasis, Egypt. Journal of African Earth Sciences. 2018;142:64–81.
115. Mehrabi B, Mehrabani S, Rafiei B, et al. Assessment of metal contamination in groundwater and soils in the Ahangaran mining district, west of Iran. Environmental Monitoring Assessment. 2015;187(12):727.
116. Merzougui FZ, Makhloufi A, Merzougui T. Hydro-chemical and microbiological characterization of Lower Cretaceous waters in a semi-arid zone Beni-Ounif syncline, South-West of Algeria. Journal of Water and Land Development. 2019;40(1):67–80.
117. Modibo Sidibé A, Lin X, Koné S. Assessing Groundwater Mineralization Process, Quality, and Isotopic Recharge Origin in the Sahel Region in Africa. Water. 2019;11(4):789.
118. Monjerezi M, Ngongondo C. Quality of Groundwater Resources in Chikhwawa, Lower Shire Valley, Malawi. Water Quality, Exposure and Health. 2012;4(1):39–53.
119. Monjerezi M, Vogt RD, Aagaard P, et al. Hydro-geochemical processes in an area with saline groundwater in lower Shire River valley, Malawi: An integrated application of hierarchical cluster and principal component analyses. Applied Geochemistry. 2011;26(8):1399–1413.
120. Murgulet D, Trevino M, Douglas A, et al. Temporal and spatial fluctuations of groundwater-derived alkalinity fluxes to a semiarid coastal embayment. Science of the Total Environment. 2018;630:1343–1359.
121. Adimalla N, Wu J. Groundwater quality and associated health risks in a semi-arid region of south India: Implication to sustainable groundwater management. Human and Ecological Risk Assessment: An International Journal. 2019;7:1–6.
122. Adimalla N, Li P, Qian H. Evaluation of groundwater contamination for fluoride and nitrate in semi-arid region of Nirmal Province, South India: A special emphasis on human health risk assessment (HHRA). Human and Ecological Risk Assessment: An International Journal. 2018;1–18.
123. Noshadi M, Ghafourian A. Groundwater quality analysis using multivariate statistical techniques (case study: Fars province, Iran). Environmental Monitoring Assessment. 2016;188(7):419.
124. Ogwueleka TC. Use of multivariate statistical techniques for the evaluation of temporal and spatial variations in water quality of the Kaduna River, Nigeria. Environmental Monitoring Assessment. 2015;187(3):137.
125. Singh PK, Tiwari AK, Mahato MK. Qualitative Assessment of Surface Water of West Bokaro Coalfield, Jharkhand by Using Water Quality Index Method. International Journal of ChemTech Research. 2013;5(5):2351–2356.
126. Pei-yue L, Hui Q, Jian-Hua W. Groundwater quality assessment based on improved water quality index in Pengyang County, Ningxia, Northwest China. E-Journal of Chemistry. 2010;7(S1):209–216.
127. Qishlaqi A, Abdolahi M, Abbasnejad A. Hydrogeochemical Evolution of Groundwater Resource in an Arid Region of Southeast Iran (Ravar plain–Kerman province). Journal of Sciences, Islamic Republic of Iran. 2018;29(3):253–269.
128. Dehbandi R, Abbasnejad A, Karimi Z, et al. Hydrogeochemical controls on arsenic mobility in an arid inland basin, Southeast of Iran: The role of alkaline conditions and saltwater intrusion. Environmental Pollution. 2019;249:910–922.
129. Rachid E, Bahir M, Chamchati H, et al. Using Geochemical and Isotope Investigations for Groundwater Management Strategies Under Semi-Arid Area: Case of the Wadi Ouazzi Basin (Morocco). Journal of Environment and Earth Science. 2014;4(7):18–30.
130. Rocha FC, Andrade EM, Lopes FB. Water quality index calculated from biological, physical and chemical attributes. Environmental Monitoring Assessment. 2015;187(1):4163.
131. Sadat-Noori SM, Ebrahimi K, Liaghat AM. Groundwater quality assessment using the Water Quality Index and GIS in Saveh-Nobaran Aquifer, Iran. Environmental Earth Sciences. 2013;71(9):3827–3843.
132. Sahu P, Kisku GC, Singh PK, et al. Multivariate statistical interpretation on seasonal variations of fluoride-contaminated groundwater quality of Lalganj Tehsil, Raebareli District (UP), India. Environmental Earth Sciences. 2018;77(13).
133. Sakram G, Kuntamalla S, Machender G, et al. Multivariate statistical approach for the assessment of fluoride and nitrate concentration in groundwater from Zaheerabad area, Telangana State, India. Sustainable Water Resources Management. 2018;5(2):785–796.
134. Singh CK, Shashtri S, Mukherjee S. Integrating multivariate statistical analysis with GIS for geochemical assessment of groundwater quality in Shiwaliks of Punjab, India. Environmental Earth Sciences. 2010;62(7):1387–1405.
135. Soltani S, Asghari Moghaddam A, Barzegar R, et al. Hydrogeochemistry and water quality of the Kordkandi-Duzduzan plain, NW Iran: application of multivariate statistical analysis and PoS index. Environmental Monitoring Assessment. 2017;189(9):455.
136. Sudheer Kumar M, Dhakate R, Yadagiri G, et al. Principal component and multivariate statistical approach for evaluation of hydrochemical characterization of fluoride-rich groundwater of Shaslar Vagu watershed, Nalgonda District, India. Arabian Journal of Geosciences. 2017;10(4).
137. Tlili-Zrelli B, Hamzaoui-Azaza F, Gueddari M, et al. Geochemistry and quality assessment of groundwater using graphical and multivariate statistical methods. A case study: Grombalia phreatic aquifer (Northeastern Tunisia). Arabian Journal of Geosciences. 2013;6(9):3545–3561.
138. Trabelsi R, Zouari K. Coupled geochemical modeling and multivariate statistical analysis approach for the assessment of groundwater quality in irrigated areas: A study from North-Eastern of Tunisia. Groundwater for Sustainable Development. 2019;8:413–427.
139. Trabelsi R, Abid K, Zouari K. Geochemistry processes of the Djeffara Palaeogroundwater (Southeastern Tunisia). Quaternary International. 2012;257:43–55.
140. Vasanthavigar M, Srinivasamoorthy K, Vijayaragavan K, et al. Application of water quality index for groundwater quality assessment: Thirumanimuttar sub-basin, Tamilnadu, India. Environmental Monitoring Assessment. 2010;171(1-4):595–609.
141. Vasanthavigar M, Srinivasamoorthy K, Prasanna MV. Identification of groundwater contamination zones and its sources by using multivariate statistical approach in Thirumanimuthar sub-basin, Tamil Nadu, India. Environmental Earth Sciences. 2013;68(6):1783–1795.
142. Vesali Naseh MR, Noori R, Berndtsson R, et al. Groundwater Pollution Sources Apportionment in the Ghaen Plain, Iran. International Journal of Environmental Research and Public Health. 2018;15(1):172.
143. Wilson Y, Satake FH, Ayonghe SN, et al. Hydrogeochemical controls and usability of groundwater in the semi-arid Mayo Tsanaga River Basin: Far North Province, Cameroon. Environmental Geology. 2008;58:1281–1293.
144. Woocay A, Walton J. Multivariate analyses of water chemistry: surface and groundwater interactions. Ground Water. 2008;46(3):437–449.
145. Xiao J, Jin Z, Wang J. Assessment of the hydrogeochemistry and groundwater quality of the Tarim River Basin in an extreme arid region, NW China. Environment Management. 2014;53(1):135–146.
146. Yu Y, Song X, Zhang Y, et al. Identification of key factors governing chemistry in groundwater near the watercourse recharged by reclaimed water at Miyun County, Northern China. Journal of Environmental Sciences. 2013;25(9):1754–1763.
147. Yazidi A, Saidi S, Ben Mbarek N, et al. Contribution of GIS to evaluate surface water pollution by heavy metals: Case of Ichkeul Lake (Northern Tunisia). Journal of African Earth Sciences. 2017;134:166–173.
148. Yu ZQ, Amano H, Nakagawa K, et al. Hydrogeochemical evolution of groundwater in a quaternary sediment and cretaceous sandstone unconfined aquifer in Northwestern China. Environmental Earth Sciences. 2018;77(18).
149. Adimalla N. Controlling factors and mechanism of groundwater quality variation in semiarid region of South India: an approach of water quality index (WQI) and health risk assessment (HRA). Environmental Geochemistry and Health. 2020;42(6):1725–1752.
150. Ma X, Zuo H, Liu J, et al. Distribution, risk assessment, and statistical source identification of heavy metals in aqueous system from three adjacent regions of the Yellow River. Environmental Science Pollution Resources International. 2019;23(9):8963–8975.
151. Rasool A, Xiao T, Baig ZT, et al. Co-occurrence of arsenic and fluoride in the groundwater of Punjab, Pakistan: source discrimination and health risk assessment. Environmental Science Pollution Research International. 2017;22(24):19729–19746.
152. Wu Y, Liu T, Paredes P, et al. Water use by a groundwater dependent maize in a semi-arid region of Inner Mongolia: Evapotranspiration partitioning and capillary rise. Agricultural Water Management. 2015;152:222–232.