Essential oil (EO) production is the main objective of Damask rose cultivation but its stability at different environments has not been well documented. In order to this, 35 landraces of Damask rose were studied at 7 locations in Iran during 2007-8. The analysis of variance revealed significant differences (p≤0.01) in EO among landraces (G), locations (L), Years (Y/L) and for landrace×location (GL) interaction. A large portion of EO variation was attributed to environment (Location-year) and landrace×environment (GE) effects. The GL interaction was mainly crossover and mainly accounted for by non-linear (unpredictable) component. The total mean of EO was 286ppm and Kashan with 681 ppm and the landraces of SM2, SM1, AK1 and BA1 with 547, 442, 440 and 427 ppm respectively produced the highest oil among studied locations and landraces. According to the results, most of landraces that originated from warm temperate and arid regions produced higher EO than those from cool, semi-arid and humid regions. There was high consistency of stable genotypes with two stability models of Eberhart & Russell¹ and Shukla's² stability variance (σ_i²) and according to them the landraces of CM1, QM1, KZ1, KS1 and HO1 were general stable with dynamic stability concept. In addition, we recommend the landrace of CM1 as moderate essential oil with general stability and adaptability in different environments and locations, furthermore, SM1 and BA1 can be recommended as superior essential oil with specific adaptability for warm and arid of the southern part (Khuzestan, etc.) and SM2 and AK1 for temperate and cool areas of the northern half (Isfahan, Khorasan etc.) in Iran.

Key words: adaptability, aromatic - medicinal plants, damask rose (rosa damascena mill.), dynamic stability

Essential oil production is the main objective of Damask rose (Rosa damascena Mill.) cultivation in many areas of the world e.g. Bulgaria, Turkey, India etc.,³ thus, essential oil is the most important trait in this crop. Besides its application in aromatic industries, some valuable characteristics of rose oil such as anti-HIV, antibacterial and antioxidant activities have been demonstrated recently.^4,5 Essential oil is a complex trait, which is depended on yield components and is influenced by many genetic as well as environmental factors. Therefore evaluating of genotypes potential in different environments (location and years) is the important step in breeding programs of Damask rose before selecting desirable ones to commercial cultivation. A desirable landrace is one that does not only essential oil well in its area of initial selection but also maintains the high yielding ability over a wide range of environments. To identify such genotypes stability analysis is a good technique that measures the adaptability of different crop varieties to varying environments.⁶ Since, the literature on the effects of genotype - environment compatibility and stability are low in Rosa damascena, inevitably, should refer to the methods used in similar plants. Eberhart & Russell¹ model has widely used for evaluating of yield stability in both annual and perennial plants same as Campanula rapunculoides,⁷ Hevea brasiliensis^8,9 and Thea sp¹⁰ Eberhart & Russell¹ considered a stable genotype to have a slope (b value) equal to unity and deviation from regression (S²_d) equal to zero. Freeman¹¹ and Bernardo¹² described the Eberhart & Russell¹ model as the most widely used methods for evaluating of yield stability among main classical parametric methods that determine general and specific dynamic stability (adaptability) and measures linear and non-linear components of stability. Furthermore, multivariate methods of stability such as AMMI, while statistically more complex, despite of widely uses in annual plants, has no advantages over the conventional methods in perennial crops and forest trees and its application is limited.^13,14 We were also interested to know the contribution of each genotype in genotype×environmen (GE) interaction sum of squares. To do this, there are two stability parameters of Wricke's¹⁵ ecovalence (W_i) and Shukla's² stability variance (σ_i²) which give the same results for ranking genotypes.¹⁶ Shukla² the stablility variance of genotype as its variance across invironments after the main effects of environmental means have been removed. He used stability variance (σ_i²) to estimate a component of the GE interaction corresponding to each genotype. According to his model, genotypes with a low σ_i² have smaller deviations from the mean across environments and thus more stable. A significant departure of a genotype’s regression coefficient from zero will be indicated by a large stability variance. The existence of genetic variation in responses to environmental changes among genotypes or significant genotype×environment (GE) interaction is the primary basis for stability analysis. Considerable variation among Iranian Damask rose populations has been reported for many traits such as morphological, oil content and flower yield.^3,17,18 Results of some researches^19,20 showed environmental effects on the quality and quantity of flower and essence yield. Nirmal & Sushil Kumar²¹ also introduced Ranisahiba landrace of Damask rose with relative higher essential oil and stable for some morph-physiological traits. Despite the existence of relatively high essential oil landraces of Damask rose, stability and adaptability are important. This study was carried out with objective of evaluation of essential oil performance and stability of 35 landraces of Damask rose across various environments.

Material and field experiment. Thirty-five landraces of Damask rose from 13 different origin sites of Iran (Figure 1 & Table 1) evaluated for essential oil and stability at seven locations (Sanandaj, Arak, Kashan, Dezful, Stahban, Kerman and Mashhad) and two years (2007-8) in Iran (Figure 1 & Table 2). The safe and uniform annual saplings of the landraces were planted at each location in March 2004 using randomized complete block design with three replications. Plant spacing was 3^m×3^m (1111 plants per hectare) and each plot comprised of three plants. Normal cultural practices followed as and when necessary in each location.

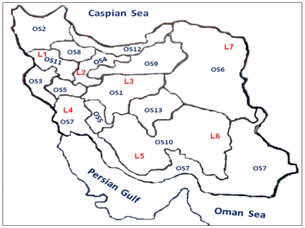
Figure 1 The origin sites of Damask rose landraces(OS1- Os13) and research locations (L1-L7) on the map of Iran.

Essential oil extraction process: The essential oils were extracted from 500g samples of fresh petals of each replication and landrace in each trial by hydro distillation for 1.5h using diethyl ether as solvent. The oils were dried over anhydrous sodium sulfate. The essential oil ratio (EO) of each sample was calculated as the essential oil weight relative to the fresh petal weight.

Statistical analysis: Initial ANOVA for essential oil of 35 Damask rose landraces (a perennial plant) in 7 locations and 2 years was performed based on the complete randomized block design with 3 replications as split-split plot in times (Location as main factor, landrace as sub factor and year as sub-sub factor) as following model:

$X_{íijk}=\mu +L_j+R{\left(L\right)}_{í(j)}+G_i+L{G}_{ij}+RG{\left(L\right)}_{íi(j)}+Y_{k(j)}+GY{\left(L\right)}_{ik(j)}+RY{\left(L\right)}_{ík(j)}+{Є}_{íik(j)}$ (1)

Where X_íijk is essential oil of íth replication of ith genotype at jth location and kth year, μ is population mean, L is effect of location, G is effect of genotype (landrace), Y is effect of year within location and Є is residual effects or error. After, determining of significance of landrace×location (GL) and landrace×year (location) (GY/L) interactions, stability parameters were estimated. The softwares of Minitab-14 and IRRISAT were used for statistical analyses.

Stability parameters estimation: The stability model proposed by Eberhart & Russell¹ and Shukla's² stability variance (σ_i²) was used to estimate stability parameters as follows.

Regression of essential oil on environmental index (bi): As described by Finlay & Wilkinson,²² Singh & Chaudhary:²³

$bi=\left(\sum Y_{ij}{I}_j\right)/\sum I_j$ (2)

Where Y_ij is yield of the ith landrace in the jth environment and I_j is environmental index and $I_j={\overline{Y}}_{oj}-{\overline{Y}}_{oo}$ where Ῡ1_oj is essential oil mean of the jth environment and Ῡ_oo is the total mean. The regression coefficients (b_i) were tested via t- test as $t=(b-\beta )/S_b$ where $S_b=\surd \left(Mse/\sum I_j{}^2\right)$ , Mse is pooled error and β=expected value of one.

Variance due to deviation from regression (Sd_i²): As described by Eberhart & Russell,¹ Singh & Chaudhary:²³ $S{d}_i{}^2=(\Sigma {\delta }_{ij}{}^2)/q-2$ where

$\Sigma {\delta }_{ij}{}^2=({\Sigma }_j{Y}_{ij}{}^2-Y_{io}{}^2/q)–{({\Sigma }_j{Y}_{ij}{I}_j)}^2/{\Sigma }_j{I}_j{}^2$ (3)

Where q is the number of environments, Σδ_ij² is sum of squares (SS) of deviations, Ῡ_io is mean yield of genotype i across environments, $({\Sigma }_j{Y}_{ij}{}^2-Y_{io}{}^2/q)$ is total sum of squares (SS) and ${({\Sigma }_j{Y}_{ij}{I}_j)}^2/{\Sigma }_j{I}_j{}^2$ is SS of regression. Sd_i² of genotypes were tested with pooled error (MSe).

Shukla's (1972) stability variance (σ_i²): is estimated as:

${\sigma }_i{}^2=p/[\left(p-2\right)\left(q-1\right)]W_i–SS\left(GE\right)/[\left(p-1\right)\left(p-2\right)\left(q-1\right)]$ where $W_i={\Sigma }_j{\left(Y_{ij}-{\overline{Y}}_{io}-{\overline{Y}}_{oj }+{\overline{Y}}_{oo}\right)}^2$ and ${\Sigma }_i{W}_i=SS\left(GE\right)$ (4)

There p is the number of genotypes, SS (GE) is the genotype×environment interaction sum of squares.

The result of combined analysis of variance for essential oil content (EO) of 35 Damask rose tested across 7 locations during 2007-8 revealed significant differences (p≤0.01) in EO among landraces (G), locations (L), Years (Y/L) and for landrace×location (GL) and Landrace×Year (Location) (GY/L) interactions. Analysis of variance also showed that about 44% of total sum of squares was attributed to environmental (Location-Year) effects, whereas genotypic and GE effects explained about 4% and 48% respectively. Also, only the non-linear component was significant in landrace×location (GL) interaction (Table 3). According to the means of environments and locations (Tables 2 and Table 4), the total mean of EO in this study was 286 ppm and the year of 2007, location of Kashan and the environment of Kashan - 2007 with 307, 681 and 713 ppm respectively produced the highest EO and the year of 2008, location of Arak and the environment of Arak - 2007 with 266, 37 and 35 ppm respectively produced the least oil yield among evaluated environments and locations. The correlation of EO mean of 2 years (2007-8) was r=0.48** with considerable variation (0.23 in Stahban to 0.94 in Kerman). Among origin sites of landraces, the origins of OS9 (provinces of Semnan and Qom) and OS4 (provinces of Tehran, Markazi) with 423 and 366 ppm respectively produced the highest and OS12 (Guilan) and OS6 (Khorasan) with 194 and 221 ppm respectively showed the least oil mean (Table 4). Also the landraces of SM2 (OS9), SM1 (OS9), AK1 (OS4) and BA1 (OS7) with 547, 442, 440 and 427 ppm respectively produced the highest while the landraces of GU1(OS12), IS6 (OS1), YZ2 (OS13) and AR1 (OS2) with 194, 201, 218 and 220 ppm respectively showed the least EO among studied landraces (Table 4). Arak and Kashan with 91.2 and 21169.5 respectively showed the least and the highest genetic (landrace) variance for EO between 2 years (Table 2). The stability model proposed by Eberhart & Russell¹ and Shukla's² stability variance (σ_i²) were used to estimate stability parameters in this study and their results are summarized in Table 4. As it is shown in it, in 2007, the landraces of KS1, IS5, KZ1, HO1, YZ1, IS8, IS3, CM1 and QM1 were stable based on the Eberhart & Russell¹ model conditions (regression of essential oil on environmental index - b_i equal to unity and variance due to deviation from regression - Sd_i² equal to zero). According to Shukla² model, in 2007, the landraces of IS4, CM1, KZ1, IS3, TH1, QM1, IS1, IS8, KS1 and IS10 showed the least stability variance (σ_i²) and thus were stable while In 2008, the landraces of KZ1, QM1, CM1 and ZA1 were stable based on the Eberhart & Russell¹ model and YZ1, IS2, CM1, HA1, HO1, IS3 and KZ1 were stable based on the Shukla² model. The correlation of regression of essential oil on environmental index (b) of genotypes between 2007 and 2008 (reproducibility of the regression) was r=0.31 and those that in locations were r=0.35 and r=0.55** respectively.

Finally, five landraces of CM1, QM1, KZ1, KS1 and HO1 with 277, 281, 238, 233 and 245 ppm respectively EO were stable GL interaction based on the Eberhart & Russell¹ model. All of these stable landraces for GL interaction, located among the first ten stable landraces for EO according Shukla² model with the least stability variance (σ_i²). The correlation of stability variance (σ_i²) of genotypes between 2007 and 2008 (reproducibility of the stability variance) was r=0.15 and those that in locations were r=0.81** and r=0.54** respectively.

The large environmental sum of squares (Nearly half of total sum of squares) indicated that environments were diverse and large differences among environmental means causing most of the variation in essential oil. Because of varying ecological conditions of studied locations in this research (seven areas involving almost all parts of Iran) (Figure 1), observed differences among locations and environments were expected. According to Table 2 and the obtained results, with the exception of two locations of Arak (L2) and Stahban (L5) the reproducibility between the years, measured by the correlation (Table 2), was generally acceptable. There were wide ecological variations both between and within two groups of high essential oil locations [Kashan (L3), Mashhad (L7) and Stahban (L5) with 476 ppm and low essential oil ones [Dezful (L4), Kerman (L6), Sanandaj (L1) and Arak (L2)] with 137 ppm mean of essential oil. The results suggest significant variation among landraces for essential oil. The existence of genetic variation is the primary base for breeding programs; therefore, selection for this trait could be possible. In accordance to this results, Tabaei Aghdaei et al.^3,17 and Babaei et al.,¹⁸ also found significant mean square among landraces for essential oil. Generally, because of asexual reproduction (through cuttings), there is a low genetic variation among Damask rose accessions and landraces, also, in Iran, unlike other countries such as Bulgaria and Turkey the main goal of rose cultivation isn’t essential oil, but is flower and rose water production. Thus, the Damask rose landraces haven't been subjected to genetic improvement for essential oil and there isn’t a considerable genetic diversity among Iranian landraces. This can be a description for low portion of genetic (landrace) variance in total variation for essential oil in present study (about 4%). Although there were varying origin sites, climates and ecological conditions in both high and low essential oil landraces groups, in addition, most of Damask rose landraces belonged to temperate, warm temperate and arid regions such as SM2 and SM1 (OS9), AK1 (OS4), some of Isfahan group of landraces such as IS9 and IS10 (OS1) and BA1 (OS7) produced higher essential oil than those originated from cool, cool temperate, semi-arid and humid regions such as GU1(OS12), HA1(OS11), KO2 (OS6) and AR1(OS2). Among the first ten superior landraces for essential oil, two of them were from origin site 1 (Isfahan) that wholly originated from Kashan area. Kashan is the main source of Damask rose landraces and Kashan farmers have longed experience in cultivation and production of Damask rose and rose water in Iran. Although the main objective of Kashan farmers is flower and rose water production, this result suggests of the effective role of selection (has been accomplished by traditional farmers either arbitrarily or randomized) for flower yield and essential oil improvement. The results showed high genetic (landrace) variance for essential oil between 2 years among studied locations (from 91.2 in Arak to 21169.5 in Kashan). In accordance to this, the non overlapping confidence intervals (Table 2) indicate highly significant differences in essential oil among the locations and could be important in practical implications. The significant landrace×location (GL) interaction indicating that essential oil is highly influenced by the changes in environments, thus leading to extension of analysis for estimating stability parameters. The magnitude of GE sum of squares was 12 times larger than of the genotypes (G), indicating that there were differences in genotypic response to environments. This variability was mainly due to the ecological characteristics across experimental locations and years. Based on the results, both landrace×environment (GE) and landrace×location (GL) interactions were mainly crossover or qualitative interaction that according to Gregorius & Namkoong²⁴ and Baker¹⁶ can be used in breeding practices. An interesting result of this study was the high relative consistency of type and order of the stable genotypes with two studied stability method of Eberhart & Russell¹ and Shukla² both in years (2007-8) individually and locations for GL interaction. This could be due to the fact that both of Eberhart & Russell¹ and Shukla² model measure dynamic stability of genotypes in environments, thus the high compliance of stable (adaptable) genotypes in them can be natural and expectable. As conclusion, according to Eberhart & Russell¹ considerations (b equal to unity, S²_d and equal to zero) and Shukla² (σ² or stability variance equal to zero), the landraces of CM1, QM1, KZ1, KS1 and HO1 were stable in locations. Kempton & Fox²⁵ described adaptation as yield stability in spatial dimension so we can announce the stable landraces in locations as adaptable and compatible ones. According to Ramagosa & Fox²⁶ adaptability or stability of a genotype often relates to physiological, morphological and phonological mechanisms and accumulation of tolerance to a number of stresses is the key to wide adaptation. The stable Damask rose landraces by Eberhart & Russell¹ method produced essential oil about average of landraces and also, absence of high essential oil landraces such as SM2, IS4, SM1, AK1 and BA1 among stable and adaptable ones, suggesting that this method measure general stability and adaptability.

The results of this study suggest that a large portion of essential oil variation was attributed to environment (Location-year) and landrace×environment (GE) effects. There were high variations in both essential oil and response to environmental changes among Damask rose landraces of Iran, which can be used in breeding programs. Both essential oil and stability of essential oil are influenced by genetic and environmental factors. Most of Damask rose landraces belonged to temperate, warm temperate and arid regions produced higher essential oil than those originated from cool, cool temperate, semi-arid and humid regions. The significant non-linear component of the landrace×location (GL) interaction was an indication of the importance of unpredictable genotype response to environmental changes and instability of performances of some landraces over locations. As conclusion, according to Eberhart & Russell¹ considerations (b equal to unity and S²_d equal to zero) and Shukla's² (σ² or stability variance equal to zero), the landraces of CM1, QM1, KZ1, KS1 and HO1 were stable in locations. Both models of Eberhart & Russell¹ and Shukla's² showed almost same results in determination of genotypes with dynamic stability in locations. The stable and adaptable Damask rose landraces by Eberhart & Russell¹ method produced essential oil about average of landraces. Absence of high essential oil landraces among stable ones, suggesting that selecting for essential oil stability and adaptability over environments and locations could result in lower oil. Finally, taking into consideration of essential oil, stability and adaptability potential, we recommend the landraces of CM1 as moderate essential oil landrace with general stability and adaptability in different environments and locations. According to Singh & Gupta²⁷ variety stability has genetic control thus the landrace of CM1 can be used as a parent-in-crosses to transfer genetic stability for essential oil to progenies. Finlay & Wilkinson²² pointed out that genotypes that have a slope (b value) greater than unity are specifically adapted to high yielding environments, so the landraces of SM1 and BA1 can be recommended as superior essential oil with specific adaptability for warm and arid southern part of Iran such as Khuzestan, Kerman, Sistan etc. and the landraces of SM2 and AK1 for temperate and cool areas such as the northern half (Isfahan, Markazi, Khorasan etc.) in Iran.

This research was supported by Research Institute of Forest and Rangelands (RIFR) of Iran. The authors are grateful to the co-executors and field staff of Agricultural and Natural Resources Research Centers of Kurdistan, Hamedan, Markazi, Isfahan, Khuzestan, Fars, Kerman and Khorasan for their assistance in data collection and maintaining the field trials.

Authors declare that there is no conflict of interest.

1. Eberhart SA, Russell WA. Stability parameters for comparing varieties. Crop Sci. 1966;6:36–40.
2. Shukla GK. Some statistical aspect of genotype–environment components of variability. Heredity. 1972;29:237–245.
3. Tabaei Aghdaei SR, Babaei A, Khosh Khui M, et al. Morphological and oil content variations amongst Damask rose (Rosa damascena Mill.) landraces from different regions of Iran. Scientia Horticulturae. 2007;113(1):44–48.
4. Mahmood NS, Piacente C, Pizza A, et al. The anti HIV activity and mechanisms of action of pure compounds isolated fromRosa damascena. Biochem Biophys Res Commun. 1996;229(1):73–79.
5. Ozkan G, Sagdic O, Baydar NG, et al. Antioxidant and anti bacterial activities of Rosa damascena flower extracts. Food Sci Technol Int. 2004;10:277–281.
6. Morales AC, Paragas AA, Carangal VR. Phenotypic stability for grain yield in mungbean (Vigna radiate (L), Wilczek). FLCG Newslett. 1991;16:12–15.
7. Vogler WD, Perets S, Stephenson AG. Floral plasticity in an iteroparous plant: the interactive effects of genotype, environment and ontogeny in Campanula rapunculoides. Am J Bot. 1999;86(4):482–494.
8. Paulo SG, Fujihara AF, Ortolant AA, et al. Phenotypic stability and genetic gains in six-year girth growth of Hevea clones. Pesquisa Agropecuária Brasileira. 1999;34(7):1223–1232.
9. Omokhafe KO. Interaction between flowering pattern and latex yield in Hevea brasiliensis Muell. Arg. Crop Breed Appl Biotechnol. 2004;4:280–284.
10. Wachira F, Ngetich W, Omolo J, et al. Genotype - environment interactions for tea yields. Euphytica. 2002;127(2):78–89.
11. Freeman GH. Statistical methods for the analysis of genotype-environment interactions. Heredity. 1973;31(3): 339–354.
12. Bernardo R. Quantitative traits in plants. Stemma Press. 2002. 369 p.
13. Falkenhagen ER. A comparison of the AMMI method with some classical statistical methods in provenance research: A case of the South African Pinus radiata trials. ForestGenetics.1996;3(2): 81–87.
14. Kanzler A. Genotype × Environment Interaction in Pinus patula and its Implications in South Africa. USA: Department of Forestry, North Carolina State University. 2002. 249 p.
15. Wricke G. On a method of understanding the biological diversity in field research. Z Pflanzenzuchtg. 1962;47:92–96.
16. Baker RJ. Tests for crossover genotype - environment interactions. Can J Plant Sci. 1988;68(2):405–410.
17. Tabaei Aghdaei SR, Rezaei MB, Jebeli M. Flower yield and morphological characteristics in some genotypes of Rosa damascena. Iran J Med Arom Plant. 2004;20(1):111–122.
18. Babaei A, Tabaei Aghdaei SR, Khosh khui M, et al. Microsatellite analysis of Damask rose (Rosa damascena Mill.) accessions from various regions in Iran reveals multiple genotypes. BMC Plant Biol. 2007;7:12–19.
19. Misra A, Sharma S, Singh A, et al. Influence of topographical and edaphic factors on Rose II. Flowering quality and quantity. Commun Soil Sci Plant Anal. 2002;33:15–18.
20. Baydar H, Baydar NG. The effects of harvest date, fermentation duration and Tween 20 treatment on essential oil content and composition of industrial oil rose (Rosa damascena Mill.). Industrial crops and products. 2004;21(2): 251–255.
21. Nirmal K, Sushil Kumar P. High yielding stable plant of Rosa damascena, called "Ranisahiba". India: Council of Scientific and Industrial Research; 2002.
22. Finlay KW, Wilkinson GN. The analysis of adaptation in plant breeding programs. Aust J Agri Res. 1963;14(6):742–754.
23. Singh RK, Chaudhary BD. Biometrical methods in quantitative genetic analysis. India: Kalyani Publishers; 1977. 288 p.
24. Gregorius HR, Namkoong G. Joint analysis of genotypic and environmental effects. Oetical Applied Genetics. 1986;72(3):413–422.
25. Kempton RA, Fox PN. Statistical Methods for Plant Variety Evaluation. London: Chapman & Hall; 1997;139–161.
26. Ramagosa I, Fox PN. Genotype × environment interaction and adaptation. In: Hayward MD, Bosemark NO, Romagosa I. Editors. Plant breeding: principles and prospects. London: Chapman & Hall; 1993;373–390.
27. Singh SV, Gupta PK. Phenotypic stability for tuber yield in Potato (Solanum tuberosum L.). Ind J Gen Plant Breed. 1988;48:9–12.