The radius of the universe can be determined by combining the Einstein formulas, which determine the degree of gravitational redshift and describe the angle of refraction of a beam of light running along celestial bodies. The relationship between the two equations is made by the ratio of the total angle to the angle of deflection of the beam of light passing by the Earth according to the rules of Euclidean geometry (2∙π/α). The so-called Darwinian evolutionary distances measured from the color changes of the respiratory pigments of biological creatures (in connection with the phase of their circulation) can be paralleled with this. It is possible to measure these to the radius of the universe determined in this way. During the nearly 4-billion-year uninterrupted process of Darwinian evolution, living organisms presumably adapted to surface gravity during mutations as well as to any other environmental factor. In this way, they can accelerate continuously along the imaginary straight line from the origin of life to the appearance of the human race, i.e., within the short evolutionary distance, due to the attractive effect of gravity. During the free fall from the past to the present, the curvature of space-time may gradually appear in their physiological processes and anatomical structure. Specifically in their circulatory system, the rate of evolution would correspond to the most qualitatively advanced level, i.e., the velocity of human blood circulation. In this way, the evolution accelerating to almost the speed of light is reduced to 5.23 cm/s due to an enormous time dilation (as a proportion of angles; α/2/π). With this average human blood flow velocity, together with data from cardiac and circulatory procedures, a toroidal, or even more refined, ‘interlocking figure 8 model’ can be constructed. It reflects the dimensions, flow and pressure conditions of the pulmonary and systemic circulation, as well as the work of the heart.

Keywords: high redshift galaxies, Earth's gravity, general relativity, Euclidean geometry, Newton's law of universal gravitation, free fall, Darwinian evolution, circulation-respiration, blood/lymph, respiratory pigments, color formation

The radius and age of the universe can be determined from information obtained from stellar evolution data (14.6±1.7 billion years),¹ as well as from the redshift of the light of galaxies (13.8±0.038 billion years).^2–5 The difference of a few billion years between the two methods can be eliminated if the gravitational refractive index of the cosmos is taken into account and the universe is considered to be three-dimensional.⁶

However, this latter method, based on the shift in the frequency of visible light, provides an opportunity to compare physical and biological systems. The time interval required for the development of an individual in the Darwinian evolutionary process^7,8 can be measured by comparing the red shift created in the gravitational and accelerating systems^9,10 with the shift of the reflection color band related to respiration and circulation appearing on the surface of biological creatures.¹¹

The distances to the radius of the universe can be estimated from the color change of the respiratory pigments based on the Einstein gravitation field equations.¹² The Darwinian evolutionary time intervals obtained by dividing the evolutionary distances comparable to the radius of the cosmos by the speed of light are the same as the geological time scale based on the radioisotope method.^13,14 The gradual development of the pulmonary and systemic circulation¹⁵ can occur in parallel with the passage of time. The blood vessel system that gradually returns to itself assumes a curved four-dimensional space-time structure,^16,17 which may result from the constantly present gravity of the earth's surface.

Such a complex, highly organized system that includes all branches of physics can only be imagined in biological individuals in the universe on habitable planets, mostly on Earth. This can only happen in living creatures, if those changes are constantly being recorded in the genetic information system.^18,19 The increasingly organized structure coded in this way is then inherited in a staggered form in proportion to time. This accumulation of gravitational effects may occur in the case of repeated mutations,^20,21 that occur during the adaptation of individuals to the environment. In this way, the curvature of the space-time structure can reach a maximum in the circulation at an increasingly advanced degree. From the origin of life, through the open and then closed blood circulation of mollusks, insects, fish, amphibians, reptiles, birds, mammals, to the appearance of human blood circulation and respiration, it can reach a high degree from which it can no longer develop.²² The pulmonary and cellular respiration, which develops in parallel with the development of the two, three, or four-cavity hearts, then reflects the color phenomena from which the evolutionary time intervals can be derived (blue-red).

However, the projection of the physical space-time curvature can also appear in living beings in a special form. Such can be the structure of the pulmonary vascular system taken from medical practice and revealed during radiological examinations with contrast material (computed tomography pulmonary angiogram /CTPA/)^23,24 the arterial system spreading in all directions in the chest and the venous vascular system converging from the sprawling periphery. This spatial arrangement is also typical of systemic circulation, but in a less conspicuous form.²⁵

Determination of the size and age of the universe

Based on the general relativity, it is known that behind the shift in the frequency of visible light in the direction of red light, there is also a time shift. In the presence of acceleration, or a gravitational field, or both, a change in the frequency of light occurs. Taking this information into account, even in a rapidly expanding universe, a specific, accurate time interval pointing in the direction of the past can be calculated based on the laws of modern physics. This shift to a smaller frequency of the spectrum line²⁶ is demonstrated by the original Einsteinian formula:

$\nu ={\nu }_0\left(1+\frac{\Phi }{c^2}\right)$   (1)

Where ν is the changed frequency, ν_o is the initial frequency, c is the speed of light and Φ is the gravitation potential difference.

The gravitation potential difference (Φ) is equal to the product of the acceleration of free fall (g) and the distance (h) between two points of different gravitational potential: Φ = g.h.²⁶ Therefore:

$\nu ={\nu }_0\left(1+\frac{g\cdot h}{c^2}\right)$   (2)

If we equate the redshift of the light measured in distant galaxies²⁷ with the acceleration of the Earth (as a component of our galaxy), then the above formula can be applied to this case as well. In this way, taking into account a redshift of 3.14 and knowing the Earth's surface gravity, a distance (h) can be calculated that points towards the origin of the universe. This distance can be called the “short evolving distance” (h_{past, present}), which is as follows:

$h_{past,present}=\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^2}{g_{Earth,s\tan d}}$   (3)

Where h_{past, present} is the unknown distance between two points of a gravitational field, (ν-ν_o)/ν_o = 3.141592653 is the redshift of the Earth as a component of high redshifted Milky Way Galaxy, c is the speed of light (2.99792458•10⁸ m•s^-1) and g is the standard gravity of the Earth (9.80665 m•s^-2). (See reference after Equation 6.)

Numerically:

$h_{past,present}=3.1416\cdot \frac{8.9875\cdot {10}^{16}{m}^2\cdot s^{-2}}{9.80665m\cdot s^{-2}}=2.879\cdot {10}^{16}m$   (4)

This distance depends both upon the ratio of the shift of the spectrum line, which matches to the motion of the Earth, and of the gravity of Earth (Figure 1). The “short evolving distance” (h_{past, present}) can be given by the ratio of the entire plane angle (2∙π) and the deviating angle (α) of a light beam passing near the Earth’s surface caused by the gravitational field: h/α=H/2∙π^-1.²⁸ With the ratio calculated from the known “short evolving distance” (h) and the known two angles (α, 2∙π), an enormous unknown distance can be calculated which might be termed ”long evolving distance” (H_{past, present} = H_universe) (Figure 2).

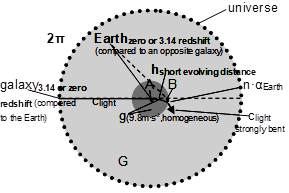
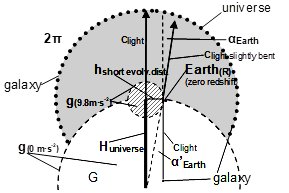
Figures 1&2. Relationship between the entire plane angle (2∙π) represented by the expanding universe (with the Earth in the center) and the deviating angle (α) of a light beam (c) passing through the gravitational field of the Earth’s surface (g). When the Earth is in motion (n•α) (as a component of our high redshifted galaxy) along h, from A to B (Figure 1), or is comparatively static (α) while in orbit (Figure 2).

The deviation angle (α) of a light beam, which passes near a celestial body’s surface, in this case the Earth, according to Einstein’s equation²⁶ is:

$\alpha =\frac{2\cdot G\cdot M}{c^2\cdot R}$   (5)

Therefore:

$H_{universe}=\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^2}{g_{Earth,s\tan d}}\cdot \frac{2\cdot \pi \cdot c^2\cdot R_{Earth,mean}}{2\cdot G\cdot M_{Earth}}$   (6)

Where Huniverse is the radius of the universe, (ν-ν_o)/ν_o = 3.141592653 is the redshift of the Earth (as a component of high redshifted Milky Way Galaxy), c is the speed of light (2.99792458•108 m•s^-1), π is the ratio of a circle’s circumference to its diameter (3.141592653). R is the volumetric mean radius of the Earth (6.371005•10⁶m), g is the standard gravity of the Earth (9.80665 m•s^-2). G is the gravitational constant (6.673848•10^-11m³•kg^-1•s^-2)²⁹ and M is the mass of the Earth (5.97219•10²⁴kg).³⁰

Numerically:

$\begin{array}{l}{H}_{universe}=3.141592\cdot \frac{80.77608713\cdot {10}^{32}{m}^4\cdot s^{-4}\cdot 3.141592653\cdot 6.371005\cdot {10}^{6}m}{9.80665m\cdot s^{-2}\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}\cdot 5.97219\cdot {10}^{24}kg}\\ =12.994509\cdot {10}^{25}m\end{array}$   (7)

The “long evolving distance” (H_{universe past, present}) can be transformed into “evolving time” (T_{universe past, present}) by dividing it by the speed of light (c). When considering the large redshift ((ν-ν_o)/ν_o = 3.141592), which may be measured from farther stars, the distance equals 12.994509•10²⁵ m, which in time (T_{universe past, present} = H_{universe past, present}/c) is 4.3345010∙10¹⁷s. Since one tropical year is 3.1556926∙10⁷s,³¹ this equates to 13.7355010 billion years the age of the universe according to our present knowledge.³²

Determining the evolutionary time periods of humans and advanced vertebrates based on their ‘biological redshifts’

To determine the age of biological individuals, the frequencies of the reflection colors appearing in connection with the phases of respiration and circulation must be substituted into the Einstein equation. This can be used to measure the shift within the spectrum of visible light behind the time-shift associated with the general relativity.

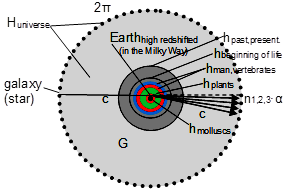
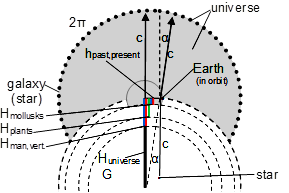
Figures 3&4. This representation shows the method developed for determining evolutionary distances and times. The first step is to determine the value of h_{past, present} corresponding to the radius of the universe based on the Einstein equation (Eq.3). The second step is to determine the degree of redshift based on the color change of the blood of biological beings (humans, vertebrates). At a lower level of development, the width of the reflected color band of their blood is used for calculations to substitute it also into the Einstein formulas. The third step is to match the decreasing distances in evolution (h_{short evolution distant}) with the corresponding radius of the cosmos (h_{past, present}). Then, by multiplying the value of hpast, present or the Darwinian evolutionary short distances hshort evolution distant (h_{man,vert, hplants, hmollusks}) by the ratio of the angles (2π/α), we can obtain the radius of the universe (Eq.6) or the Darwinian evolutionary time intervals characteristic of each species (H_man,vert, H_plants, H_mollusks; Eq.8 and Eq.10).

Hemoglobin is a component of the blood of humans and vertebrates. During pulmonary respiration, blood in the lungs becomes saturated with oxygen due to a carbon dioxide exchange. Along the visible light spectrum, this exchange results in the blue side of the spectrum being absorbed while the red is reflected, therefore the blood appears redder. This periodical colour change can be matched to a special range of the spectrum on the basis of their colour formation.³³ These are approximately in frequency: blue colour (ν): 705-620.10¹²s^-1 (mean frequency: 662.5.10¹² s^-1), red colour (ν_o): 430-390.10¹² s^-1 (mean frequency: 410.10¹² s^-1).

$H_{evolutio{n}_{}dis\tan t_{}man(blue-red)}=\frac{{\nu }_{blue}-{\nu }_{red}}{{\nu }_{red}}\cdot \frac{c^4}{g_{Earth,s\tan d}}\cdot \frac{\pi \cdot R_{Earth,mean}}{G\cdot M_{Earth}}$    (8)

The colour change that occurs periodically with the phase of breathing and circulation can also be called ‘biological redshift’.

Numerically:

$\begin{array}{l}{H}_{evolutio{n}_{}dist.man(blue-red)}=0.62\cdot \frac{80.77608713\cdot {10}^{32}{m}^4\cdot s^{-4}\cdot 3.141592653\cdot 6.371005\cdot {10}^{6}m}{9.80665m\cdot s^{-2}\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}\cdot 5.97219\cdot {10}^{24}kg}\\ =0.62\cdot 4.13628092\cdot {10}^{25}m=2.564494\cdot {10}^{25}m\end{array}$   (9)

Since one tropical year is 3.1556926∙10⁷s³¹ and c=2.99792458∙10⁸ m/s, this equates to 2.71073 billion years (T=H/c). Considering the inside and outside edge of each colour range in the blue-red, a minimum and a maximum (T_{past, present}) value can be given. These are (ν-ν_o)/ν_o= (620-430)/430=0.44 i.e., 1.94 billion years and (ν-ν_o)/ν_o = (705-390)/390=0.807 i.e., 3.54 billion years, respectively, resulting in a mean frequency of 2.71 billion years.

Determining the evolutionary time periods of immature species based on the color of their blood

Hemocyanin is the respiratory lymph pigment of decapod Crustacea, stomatopod Crustacea, cephalopod, gastropod Mollusca, as well as some arachnids.³³ It is blue when oxygen is attached to it and colourless when not attached. If the two ends of blue are: ν = 705•10¹² s^-1 and ν_o = 620•10¹² s^-1 respectively, then the ratio of their attached red shift is (ν-ν_o)/ν_o = 0.137; consequently, the evolution distance (H_{past, present}) from the past towards the present.

$\begin{array}{l}{H}_{Evolution.dist.mollus{k}_{}hemocyanin}=\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^4}{g_{Earth,s\tan d}}\cdot \frac{\pi \cdot R_{Earth,mean}}{G\cdot M_{Earth}}\\ =0.137\cdot 4.136281\cdot {10}^{25}m=0.56667\cdot {10}^{25}m\end{array}$   (10)

Since one tropical year is 3.1556926∙10⁷s and c=2.99792458∙10⁸ m/s, then the evolutionary time period (T_{past, present}) is equal to 598.98 million years.

Hemerythrin, which is found in very few animals including sipunculids and brachiopod Lingula, turns the lymph red when bonding with oxygen,³³ however, when it carries carbon dioxide it is essentially colourless. If the ratio of red shift of the two ends of red is (ν-ν_o)/ν_o= (440-390)/390 = 0.128, the evolution distance is 0.5369∙10²⁵m. Then the evolutionary time period (T_{past, present}) is 559.63 million years.

Chlorocruorin in annelids does not show any colour change within the phases of respiration and circulation, but instead only show dichroism dependent on concentration.³³ Despite this, a red shift can be matched to its colour in the green range of the spectrum (ν-ν_o)/ν_o= (605-535)/535 = 0.13084, so H_{past, present} is: 0.54119∙10²⁵m. Since one tropical year is 3.1556926∙10⁷s and c = 2.99792458∙10⁸ m/s, the evolutionary time period of it (T_{past, present}) is 572.05 million years.

The accelerating effect of Earth's gravity on Darwin's evolutionary process from the origin of life to the development of the human race

If the short and long evolutionary distances (h_{past, present} and H_{past, present}) from the past to the present defined above are considered continuous, then we can assume that the attractive effect of gravity prevails through this distance. Based on this consideration, along the uninterrupted line, biological individuals can theoretically accelerate continuously in the constant, earth-surface-valued homogeneous gravity field, like free-falling bodies. In this way, in the Darwinian evolutionary process, the members of each species, together with their circulatory structure, can show the characteristics of inanimate, very dense, high-gravity bodies.³⁴ By allowing biological creatures to fall freely in the Darwinian evolutionary process under constant earth’s surface gravity, vascular systems representing curved space-time evolve within them. Under the influence of gravity, along this long distance (almost one light year) the blood flowing in them accelerates almost to the speed of light. However, this extreme acceleration is reduced to the extent of the ratio of the angles (α/2∙π^-1) by the gradually increasing time dilatation (Figure 5, left side).

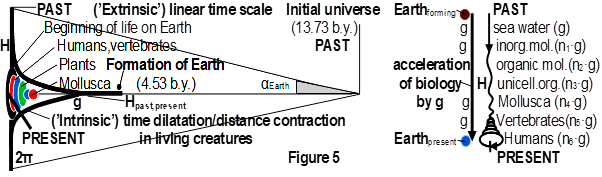
Figure 5. This figure depicts the position of the Earth and the Darwinian evolutionary process taking place on its surface in the universe. It shows some stages of life on the surface of the earth in close correlation with the value of g accumulating in them. The distance contraction and time dilatation associated with the space-time curvature that occurs during free fall are also illustrated. It also shows the non-curved parts of the entire cosmos other than livings where there is a linear time scale. (The early universe may be an exception to this, as extreme space-time curvature may exist here.)

According to the law of free-falling bodies, the velocity of a body falling vertically in the gravity of the earth's surface is uniformly accelerating. Due to the attractive effect of gravity, the body travels greater and greater distances in equal intervals, i.e., its speed increases gradually (v²=g∙h). However, this is only possible a small distance vertically from the surface of the earth, given the square descending gravity (a good example of which is the case of the stone dropped from the Leaning Tower of Pisa /by Galileo Galilei/). Furthermore, extending this case, with a sufficiently large distance in homogeneous gravity (in the absence of resistance), the velocity of a free-falling body can take on extremely high values, which can eventually even approach the speed of light. We hypothesize that this theoretical possibility can be found in biology. In the course of Darwin's evolutionary process, a horizontal straight line can be interpreted above the surface of the Earth, within which gravity prevails continuously. In this way, during the very slow process from the origin of life to the emergence of the human species, an extremely long distance can be defined in which biological individuals can accelerate with free fall from the past to the present (Figure 5, right side). This also means the development of an increasingly advanced structural state over nearly four billion years.

From the maximum value of the short evolutionary distance (h_{short evolution distance man (blue-red)}) specific to more advanced vertebrates or the human species (v-v₀/v₀ = 0.62),¹¹ the rate of the Darwinian evolution (_{vDarwinian evolution, man(blue-red)}) can be determined from the law of free fall (v² =2∙g∙h). Unlike before, the velocity (v) of free-falling bodies, including biological individuals, is used without the factor 2. In the case of movements close to the speed of light, this factor may lose its validity due to the changing space-time curvatures:

$v_{Darwin.evol.man(blue-red)}=\sqrt{h_{shor{t}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot g_{Earth}}$   (11)

Numerically:

$\begin{array}{l}{v}_{Darwinia{n}_{}evolution,man(blue-red)}=\sqrt{0.62\cdot \frac{8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}}{9.80665m\cdot s^{-2}}\cdot 9.80665m\cdot s^{-2}}\\ =\sqrt{5.572282\cdot {10}^{16}{m}^2\cdot s^{-2}}=2.360568\cdot {10}^8\frac{m}{s}\end{array}$   (12)

The surface gravity of the earth (g = 9.80665 m/s²) accelerates the organisms and their blood circulation to 78.6% of the speed of light at this distance h. By reducing this value in the ratio of the angles (2.2157∙10^-10), i.e., using time dilation, the velocity characteristic of the average flow rate of the human blood circulation is obtained: 5.2303 cm/s.

In higher vertebrates or in humans, cyanosis occurs in respiratory and circulatory insufficiency, or in its progression, complete blackening occurs. When breathing is permanently stopped, the speed of evolution paradoxically increases and approaches even more the speed of light. In the meantime, the individual loses its capacity to sustain life and biological death sets in.

$v_{Darwin.evol.man(black)}=\sqrt{h_{shor{t}_{}evol.dist.man(black)}\cdot g_{Earth}}$   (13)

Simplified by g, numerically after the square root subtraction:

$\begin{array}{l}{v}_{Darwin.evol.man(black)}=\sqrt{0.92\cdot \frac{8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}}{9.80665m\cdot s^{-2}}\cdot 9.80665m\cdot s^{-2}}\\ =\sqrt{8.26854763\cdot {10}^{16}{m}^2\cdot s^{-2}}=2.875508\cdot {10}^{8}m\cdot s^{-1}\end{array}$   (14)

The paradox that exists regarding the rate of evolution and the average blood circulation velocity of the biological individual is resolved by the infinitely increasing time dilation (as the redshift value reaches 1).

By reducing this value in the proportion of angles (α/2∙π^-1 =2.2157∙10^-10), i.e., using time dilation, the flow rate of the human blood circulation can be obtained in the case of cardio and respiratory failure: 6.371263 cm/s. This is 95.6% of the speed of light.

With the loss of life-sustaining capacity in the flow rate of the average human circulation (between 5.23 cm/s and 6.37 cm/s, or between 78.6% of the speed of light and 95.6% of the speed of light), a biological individual can die. In the animal world, this means, for example, whether a prey animal can escape from a predator chasing it or not. Does the capacity of the respiratory-circulatory system enable it to escape its pursuer under maximum physical exertion? In the case of the human race in prehistoric times, this capacity could also have a role in terms of survival. Nowadays, however, in strenuous work or in various sports, etc. it has significance. The other side of having the necessary capacity to sustain life is that, for example, in case of progression of respiratory-circulatory diseases, the individual has a certain reserve for survival (with the narrowing of range of motion).

Based on what has been said so far, more than one redshift is not possible according to the law of free fall, and there is no example of this in biology either. This limit can be clarified by the following equation. In the case of complete blackout observed at the cessation of human respiration and circulation,^35,36 when the full width of the visible light spectrum is affected by the shift, i.e., between 800∙10¹²Hz and 400∙10¹²Hz respectively,¹¹ the velocity of evolution is equal to the speed of light /(ν-ν_o)/ν_o = (800-400)/400=1/:

$v=\sqrt{1\cdot 8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}}=2.99792458\cdot {10}^8{}_{}\frac{m}{s}=c$   (15)

Multiplying the speed of light by the ratio of the angles, the maximum velocity of the Darwinian evolutionary process is: c∙α/2∙π^-1. This speed of light, reduced in proportion to the angles, corresponds to the speed of average human blood circulation, which is numerically as follows: 2.99792458∙10⁸ m/s ∙ 2.2157∙10^-10 = 6.6425cm/s.

The relationship between the mass of inanimate bodies and the mass of living creatures on the Earth's surface

The weight (W) of bodies and biological organisms located on the surface of the earth is equal to the force (F) with which they push the surface as a result of the Earth's attraction (W=F). The weight of bodies is the product of the body's mass (m) and the Earth's surface gravity (g). Newton's law of gravity states that the attractive force (F) between a body and the Earth is directly proportional to their mass (m, M) and inversely proportional to the square of the distance between them (r²). If we take the mass of the Earth at its center, this distance is equal to the radius of the Earth.³⁷ Since W = F, not only the mass of an individual at any level of Darwinian evolution, but also the mass of a body on the surface of the Earth is dropped from the formula (only the mass of the Earth remains in Eq. 16).

$\begin{array}{l}{W}_{weight}=F_{force},so,m_{bod{y}_{}o{r}_{}livin{g}_{}organism}\cdot g_{Earth\text{'}surface}=\\ G\cdot \frac{m_{bod{y}_{}o{r}_{}livin{g}_{}organism}\cdot M_{Earth}}{r_{Earth}{}^2},and:g_{Earth\text{'}surface}=\frac{G\cdot M_{Earth}}{r_{Earth}{}^2}\end{array}$   (16)

Where G is the gravitational constant (6.673848•10^-11m³•kg^-1•s^-2).

The reflection of Earth's parameters in the body structure of living creatures

Assuming that for some reason the value of the Earth's mass (M) in Eq.16 would gradually increase, the force of the gravitational field (g_maximum) on the Earth's surface would increase due to direct proportionality, while its radius (r) would remain unchanged. On the right side of the formula, a decrease in the value of the Earth's radius (r_minimum) in the denominator would result in an increase in the value of the Earth's surface gravity (g_submaximal). As a third possibility, if the Earth's mass increased and its radius decreased along with it, an even stronger gravitational field could be detected (g_maximum).

These theoretical possibilities would be realized under the following cardinal conditions:

1. The Earth's surface gravity field or gravitational waves emitted by the Earth are absorbed by biological individuals.
2. These absorptions are made possible by mutations occurring during the evolutionary process of living creatures.
3. During the development of living beings, through mutations, the effects of the gravitational field increase step by step, causing changes in the structure of their bodies.

If these conditions are fulfilled, from the point of view of biological individuals, this would mean that the mass of the Earth would appear multiplied after each gravitational absorption and behind them. In addition, the radius of the Earth could also decrease if the mass of the Earth remained unchanged. From the point of view of living beings, this would mean a fictitious increase in the mass of the earth, a decrease in the radius of the earth, or even a combination of both. In this way, the original formula (Eq.16) does not change, but is reevaluated. In the case of an uninterrupted evolutionary process, in an extreme case, this would lead to the point where the level of the gravitational field on the earth's surface (g_maximum) could approach the values around black holes.

The relationship between the law of free fall and the factors determining gravity

According to the law of freely falling bodies, the speed of a body falling vertically in the gravity of the earth's surface (ideally assumed to be homogeneous in the case of a small difference in level) accelerates uniformly. Due to the attractive effect of gravity, the body travels more and more distances at equal times.³⁷ Finally, theoretically, at a sufficient distance, in the case of homogeneous gravity, it could reach extremely high values (in the absence of resistance), even approaching the speed of light.

Applying this consideration to the Darwinian evolutionary process and extending it to the law of free fall (v²=g∙h) valid on the earth's surface, the definition of the horizontal section from the past to the present can form the basis of our studies. Accordingly, applying the law to the attraction in the direction of a horizontal line that can be drawn along the surface of the Earth, we can make the following statements.

The distance (h_{short evolution distance, man (blue-red)}) in homogenous gravity (g_Earth) can be related to the distance contraction associated with time dilatation known from general relativity. Then the speed of Darwinian evolution (v_{Darwinian evolution, man (blue-red)}) is the same as Equation 11.

The implementation of the combination of the law describing free fall,³⁷ and the general relativity,⁹ can be done through the involvement of biological systems, which can actually mean the merging of the two disciplines.

In the following, the applicability of the idea can be confirmed in the light of changes in the mass of the Earth. In this way, increasing the distance hshort evolution distance, man (blue-red) by the ratio of the angles (2∙π/α) to H:

$v_{Darwin.evol.man(blue-red)}=\sqrt{h_{shor{t}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot \frac{2\cdot \pi }{\alpha }\cdot g_{Earth}}$   (17)

And:

$v_{Darwin.evol.man(blue-red)}=\sqrt{H_{lon{g}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot g_{Earth}}$   (18)

After squaring both sides of the equation, the mass of the Earth (M_Earth) and radius of the Earth (r_Earth) values can be obtained from the Newtonian formula:

$v_{Darwinia{n}_{}evolution,man(blue-red)}{}^2=H_{lon{g}_{}evolutio{n}_{}dis\tan ce,man(blue-red)}\cdot \frac{G\cdot M_{\text{Earth}}}{r_{Earth}{}^2}$   (19)

Where H and r² are perpendicular to each other in this sense.

$So:past\cdot \cdot \cdot \cdot \cdot \to ••••000\updownarrow present$

Nevertheless, the extension pointing from the past to the present, i.e., perpendicular to the time axis, can be interpreted in 3 dimensions from all directions (obliquely and perpendicularly) around the biological individual. Regardless of the fact that this line (evolutionary distance) was originally defined in 2 dimensions parallel to the Earth's surface. This lateral, gradually increasing expansion is embodied in the blood circulation of biological individuals and applies to all its points, with which continuity is realized in their internal spatial structure. This is also manifested in a kind of increase in mass from less developed structures to more developed ones, starting from single-celled ones through multi-celled ones to mammals.

If the distance, which is increased in proportion to the angles (H_{long evolution distance, man (blue-red)}), is put into the free fall formula (Eq.20), the resulting mass (M_Earth) will be smaller.

$M_{\text{Earth}}=\frac{v_{Darwinia{n}_{}evolution,man(blue-red)}{}^2\cdot r_{Earth}{}^2}{H_{lon{g}_{}evolutio{n}_{}dis\tan ce,man(blue-red)}\cdot G}$   (20)

If the long evolutionary distance (H_{long evolution distance man (blue-red)}) calculated from Einstein's formula with a redshift of (ν-ν_o)/ν_o = 0.62 characteristic of humans is inserted into Newton's formula, a version of the Earth's mass that is 10 orders of magnitude smaller is obtained. In this case, a relativistic mass reduction occurs compared to the original mass. Numerically:

$M_{\text{Earth}}=\frac{{\left(2.360568\cdot {10}^{8}m\cdot s^{-1}\right)}^2\cdot {\left(6.371005\cdot {10}^{6}m\right)}^2}{2.564494\cdot {10}^{25}m\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}}=13.2151143\cdot {10}^{14}kg$   (21)

Magnified in the ratio of the angles, this mass will be equal to the original mass of the Earth (13.2151143∙10¹⁴kg ∙ 4.513249∙10⁹ = 5.96431∙10²⁴kg). The difference between the two masses can be understood as a relativistic mass increase, which results from the properties inherent in Newton's and Einstein's formulas. Therefore, the missing mass must be made up afterwards by increasing the ratio of the angles.

As a check, considering the opposite case, in which a short evolutionary distance (h_{short evolution distance, man(blue-red)}) calculated from Einstein's formula with a redshift of (ν-ν_o)/ν_o = 0.62 is inserted into Newton's formula, the mass of the Earth (M_Earth) can be obtained with high accuracy.

$M_{\text{Earth}}=\frac{v_{Darwinia{n}_{}evolution,man(blue-red)}{}^2\cdot r_{Earth}{}^2}{h_{shor{t}_{}evolutio{n}_{}dis\tan ce,man(blue-red)}\cdot G}$   (22)

Numerically:

$M_{\text{Earth}}=\frac{{\left(2.360568\cdot {10}^{8}m\cdot s^{-1}\right)}^2\cdot {\left(6.371005\cdot {10}^{6}m\right)}^2}{\text{0}\text{.56821464}\cdot {10}^{16}m\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}}=\text{59}\text{.6430978}\cdot {10}^{23}kg$   (23)

In this case, relativistic mass reduction does not occur compared to the original mass. When using the combined Einstein formula (before the combination with the law of free fall), however, it can be observed that a distance dilation is created between h and H, which is accompanied by a time contraction.

The relationship between the liquid flow laws describing the average human circulation and the equation containing a combination of general relativity and Newton's law of universal gravitation

Now let us consider the case of how much mass we get by substituting the radius of human blood circulation into the formula containing a combination of general relativity and Newtonian gravity (Eq.20) instead of the radius of the Earth. To do this, however, we must first consider some laws of fluid flow.

There are two fundamental laws regarding the flow of fluids. One expresses the flow intensity (Eq.24 left side) the other is the law of continuity (Eq.24 right side). Using them (separately but also together), the intensity (I), length (s), radius (r) and cross-sectional area (A) of the circulating fluid as well as the flow rate (v) can be determined theoretically with the knowledge of the appropriate members. Since:

$I=\frac{V_{2\pi }}{t_{2\pi }}=\frac{A\cdot s_{2\pi }}{t_{2\pi }}{}_{}an{d}_{}I=A\cdot v$   (24)

Equation 24 on the left has two unknowns, i.e., A and s are unknown. Thus, even if V and t are known, the cross section and path cannot be calculated. Equation 24 on the right also has two unknowns, since even if the intensity can be calculated based on the formula on the left of Eq.24, A and v cannot be determined separately. However, combining the two equations does not give us the opportunity to calculate A and s either. In fact, only intensity can be accurately determined. According to them, the following limited possibilities exist.

Equating the two formulas (Eq.24 left and right) based on the intensity (I) and the flow cross-sectional area (A):

$\begin{array}{l}\frac{A\cdot s_{2\pi }}{t_{2\pi }}=A\cdot v,so,\frac{s_{2\pi }}{t_{2\pi }}=v_{},and{s}_{2\pi }=v\cdot t_{2\pi },moreover:A=\frac{I\cdot t_{2\pi }}{s_{2\pi }},\\ and:A=\frac{I}{v},so:{}_{}\frac{I\cdot t_{2\pi }}{s_{2\pi }}=\frac{I}{v}{,}_{}and{:}_{}\frac{t_{2\pi }}{s_{2\pi }}=\frac{1}{v}{,}_{}and:{}_{}v\cdot t_{2\pi }=s_{2\pi }\end{array}$   (25)

Considering the previous case (Eq.24, left), which is better known from medical physiology, the data concerning the intensity of the flowing fluids (I) corresponds to the volume (V) per unit time (t). This value is the same as the concept of cardiac output (CO) determined on the basis of blood circulation tests.³⁸ Based on these, the intensity as a physical parameter corresponds to the value known from internal medicine as cardiac output (I = CO), also due to the same dimensions. According to these, in a 70 kg healthy person, the end-diastolic volume (EDV) of the heart is 120 mL and the end-systolic volume (ESV) is 50 mL. The difference between the two equals the stroke volume (sv), which is thus 70 mL. In this way, the circulating blood volume per minute, i.e., the minute volume, is 4.2 Liters/minute (60/minute x 70 mL=4200 mL/minute) with a heart rate of 60/minute. Because this value is the product of heart rate and stroke volume (CO=HR∙sv or CO=n∙sv). However, this value may change if the data is applied to half a minute or 25 s. The circulating blood volume (CO) is therefore the following for 25 or 30 seconds or 1 minute:

$\begin{array}{l}{I}_1=\frac{V_{2\pi }}{t_{2\pi (25s)}}=C{O}_{25s}=\frac{n_{25}\cdot sv}{t_{2\pi (25s)}}=\frac{25\cdot {70}_{}mL}{t_{2\pi (25s)}}=\frac{1750mL}{t_{2\pi (25s)}}=1750mL/25s=1.75L/25s_{},and:\\ I_2=\frac{V_{2\pi }}{t_{2\pi (30s)}}=C{O}_{30s(1/2\min )}=\frac{n_{30}\cdot sv}{t_{2\pi (30s)}}=\frac{30\cdot {70}_{}mL}{t_{2\pi (30s)}}=\frac{2100mL}{t_{2\pi (30s)}}=2.1L/0.5{\min }_{},moreover:\\ I=\frac{V_{2\pi }}{t_{2\pi (60s)}}=C{O}_{1\min }=\frac{n_{60}\cdot sv}{t_{2\pi (60s)}}=\frac{60\cdot {70}_{}mL}{t_{2\pi (1\min )}}=\frac{60\cdot 70mL}{\text{1}\min }=\frac{4200mL}{\text{1min}}=\text{4}.2L/1\min \end{array}$   (26)

During 25, 30, or 60 seconds (60 contractions in 60 seconds, i.e., with a heart rate of 60/1minute), the cardiac output is 1.75 L/min, 2.1 L/min, or 4.2 L/min, respectively. The first two CO values increase when projected at a heart rate of 60/min, the third remains unchanged. By dividing each CO by the ratio 25s/60s=0.41666 and 30s/60s=0.5 and 60s/60s=1, the result will be 4.2 L/min respectively (1.75 L/min/0.4166=4.2 L/min, 2.1 L/min/0.5=4.2 L/min, 4.2 L/min/1=4.2 L/min).

Projecting these CO values onto a heart rate of 72 contractions in 60 seconds, i.e., with a heart rate of 72/1minute, considering their ratios (25/72=0.3472, 30/72=0.4166, and 60/72=0.8333), the CO value will be higher than the previous ones. In this way, the output of the heart will be 1.75L/0.3472=5.04 L/min and 2.1L/0.4166=5.04 L/min, as well as 4.2L/0.833=5.4 L/min, which agrees with our knowledge of cardiology.³⁸

These are well-measurable but variable quantities, which can increase significantly under submaximal physical load (6-8 L/min).

In case of an extreme degree of load, which means an increase in static or dynamic work performed against the gravitational field, the work of the heart and the related performance increase. After reaching a limit value, CO reaches its highest value in case of maximum heart rate. For example, in the case of a relatively young adult male long-distance runner (from a starting value of 43/min), if the heart rate increases to a value of 170-175/min, the CO is as follows. As 25s/170=0.147, 30s/170=0.1764, 60s/170=0.3529, therefore 1.75L/min/0.147=11.9L/min, 2.1L/min/0.1764=11.9, 4.2L/min/0.353=11.9 L/min. An increase in heart rate increases the speed of blood circulation in direct proportion. The single turnaround time will therefore be smaller.

This maximum performance is a vital outcome in the animal world, a characteristic of selection in the Darwinian sense. Since the chosen prey can become a victim and die (the weaker one is selected), or the chasing animal obtains food, in this way, gaining energy to continue living (the stronger one survives).

However, cardiac output is only a special value that does not express the quantitative parameters and qualitative characteristics of the whole blood flow. Therefore, this should be supplemented, the following considerations are necessary.

The law of continuity of flowing fluids, which is another obligatory law, gives intensity (Eq.24 right side) as the product of the flow cross section area (A) and the flow rate (v). However, neither the cross-section area through which the blood would flow nor its flow rate is known. The situation is further complicated by the fact that, according to the law of continuity, A and v can change, while the intensity (in the sense of conservation of energy) remains unchanged. With a smaller cross-sectional area, the flow rate may increase, while with a larger cross-sectional area it may decrease (see also Bernoulli’s law). Therefore, since this flow formula is two unknowns, an average flow rate (v) would be needed to calculate an average cross-sectional area. One velocity determination approach is as follows. Given that the flow velocity in the capillaries is approximately 1 mm/s^39–41 and that the main artery (aorta) is 1m/s,^42,43 the average velocity should be somewhere in the middle, i.e., between cm and decimeter. This would mean an average of approximately 5 cm/s or 0.5 dm/s.⁴⁴

On the other hand, the other, much more accurate speed determination option is the value obtained from the degree of color change (blue-red)¹¹ of biological creatures. This would fit more organically into the flow conditions of the entire human blood circulation and would provide more accurate data than before for the interpretation of the processes. For this, we can use the velocity of Darwinian evolution, which was previously determined from the law of free fall (Eq.11 and Eq.12). From this rate determined by higher vertebrates or human blue-red color change, the average blood flow rate can then be calculated. To do this, account must be taken of the time delay that occurs during the free fall of bodies, in this case blood, traveling at high speed during free fall. The degree of time dilatation resulting from general relativity is known and specifically corresponds to the ratio of angles (α/2∙π^-1). With this ratio, the two velocity values (near the speed of light and the average human blood flow rate) can be matched and converted into each other.

In medicine, the one-time revolution of the human circulation can be determined by dye dilution,⁴⁵ thermo-dilution,⁴⁶ or radioisotope methods.⁴⁷ In healthy adults, the blood volume turnover time is on average 25-30 seconds at rest.^48,49 Based on this time interval (t_2π) and the reduced flow rate in relation to the angles (α/2∙π^-1) (v_{Darwinian evolution, man(blue-red) reduced by 2π/α}), the size of the average circulation can be determined.

The mean human circulation velocity (v) is the product of Darwinian evolution velocity /v_{Darwinian evolution, man(blue-red)}/ (2.360568•10⁸m/s, Eq.12) and the ratio of α/2∙π^-1(0.22156987•10^-9), which is 5.230307 cm/s. For a single turnaround time of 25 seconds, the tube length is as follows (see Eq.25):

$s_1=v\cdot t_{2\pi ,1}=5.2\cdot {10}^{-2}\frac{m}{s}\cdot 25s={1.3}_{}m$   (27)

For a single turnaround time of 30 s, the tube length (s₂) is:

$s_2=v\cdot t_{2\pi ,2}=5.2\cdot {10}^{-2}\frac{m}{s}\cdot 30s={1.56}_{}m$   (28)

For an average human blood circulation of round and circular cross-section (torus), the circumference (C) and radius (r) are as follows:

$C_{torus}=2\cdot r_{torus}\cdot {\pi }_{}{,}_{}s{o}_{}{,}_{}{r}_{torus}=\frac{C_{torus}}{2\cdot \pi }$   (29)

Since the perimeter (C₁) is equal to the length (s₁), the radius (r₁) of the torus is:

$r_{1torus}=\frac{s_1}{2\cdot \pi }=\frac{{1.3}_{}m}{6.2831853}=20.69cm$   (30)

Since the circumference (C₂) is equal to the length (s₂), the radius (r₂) of the circle is:

$r_{2torus}=\frac{s_2}{2\cdot \pi }=\frac{{1.56}_{}m}{6.2831853}=24.828cm$   (31)

The biological mass (M_{human circulation turnaround}) corresponding to the physical mass of the Earth (M_Earth) (Eq.22) when substituting the radius of the average human circulation (r_{average human blood circulation1}) in the formula of low of free fall (for a blue-red biological redshift) after rearranging will be:

$M_{\text{1 human blood circ}\text{.turnaround}}=\frac{v_{Darwin.evol.man(blue-red)}{}^2\cdot r_{Earth}{}^2}{H_{lon{g}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot G}$   (32)

Numerically:

$M_{\text{1 human blood circ}\text{.turnaround}}=\frac{{\left(2.360568\cdot {10}^{8}m\cdot s^{-1}\right)}^2\cdot {(0.207m)}^2}{2.564494\cdot {10}^{25}m\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}}=0.0139507\cdot {10}^{2}kg$   (33)

In the case of a larger radius of human circulation (r_{average human blood circulation2}), when the single circulation time increases to 30 s, the value of the mass also increases:

$M_{\text{2 human blood circ}\text{.turnaround}}=\frac{{\left(2.360568\cdot {10}^{8}m\cdot s^{-1}\right)}^2\cdot {(0.248m)}^2}{2.564494\cdot {10}^{25}m\cdot 6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}}=0.02002464\cdot {10}^{2}kg$   (34)

After determining the size of the average human blood circulation with the help of the laws of flow, the mass that falls on the time interval of the average human blood circulation once turning around can be determined by using Newton's law of gravity. Here, the role of the radius of the earth is taken over by the radius of the average human blood circulation. And the mass of the Earth will be correlated with the mass of the blood in one rotation, and will be reduced to its value. In this sense, a metamorphosis of the earth's parameters takes place and is thereby embodied in the parameters of human blood circulation. The reverse of this also seems to be true, that is, the parameters of human blood circulation can be transformed into those of Earth.

{In the absence of adequate data for mollusks, it is difficult to estimate their mean radius of circulation and the mass of blood volume per revolution. However, let us pick out a mollusk (gastropod Mollusca) whose tissue fluid (hemolymph) contains hemocyanin with a redshift of 0.137, for example (Eq.10). Then, based on Einstein's formulas, its short evolutionary distance (h_{short evol.dist.mollusks(blue)}) will be:

$h_{shor{t}_{}evolution.dist.mollusk(blue)}=0.137\cdot \frac{8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}}{9.80665m\cdot s^{-2}}=\text{0}\text{.125557}\cdot {10}^{16}m$   (35)

From this distance data, based on the law of free fall, the evolutionary rate (v_{Darwinian evolution, mollusks(blue)}) of this mollusk is:

$v_{Darwin.evol.mollusk(blue)}=\sqrt{0.137\cdot \frac{8.987551\cdot {10}^{16}{m}^2\cdot s^{-2}}{9.80665m\cdot s^{-2}}\cdot 9.80665m\cdot s^{-2}}$   (36)

$v_{Darwinia{n}_{}evolution,mollusk(blue)}=\text{1}\text{.109637}\cdot {10}^8\frac{m}{s}$   (37)

By reducing this speed in proportion to the angles (2∙π/α), we get the following value for the average circulation speed of mollusks: 1.109637∙10⁸m/s∙ 0.22156987∙10^-9 = 0.024586 m/s = 2.4586 cm/s.}

Mass calculated from the average radius of human circulation solely according to Newton's law of universal gravitation

Using Newton's law of gravitation alone to determine mass gives a much larger value than using the combined equation (GR and Newton) for the same (see Equation 32):

$m\cdot g_{Earth}=G\cdot {\frac{m\cdot M_{Earth}}{r_{Earth}{}^2}}_{}{,}_{}so{:}_{}{g}_{Earth}=\frac{G\cdot M_{Earth}}{r_{Earth}{}^2}$   (38)

Rearranging the equation to mass (M_Earth), and then using the radius of the average blood circulation (r_{average blood circulation}) instead of the radius of the Earth, the intermediate value of M is as follows:

$M_{Eart{h}_{}\mathrm{int}ermediate}={\frac{g_{Earth}\cdot r_{averagebloodcirculation}{}^2}{G}}_{},so,$   (39)

$M_{Eart{h}_{}\mathrm{int}ermediate}=\frac{9.80665m\cdot s^{-2}\cdot {\left(2.07\cdot {10}^{-1}m\right)}^2}{6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}}=6.2962948\cdot {10}^{9}kg$   (40)

This obtained mass (6.2963∙10⁹kg) will be 1.3987 kg (≈1.4 kg) multiplied by the ratio of the angles (2,2157∙10^-10). For a larger radius of 0.248 m, M = 9∙10⁹kg. From this mass, multiplied by the value of the widening of the time interval causing the flow rate to slow down, i.e., the ratio of α/2∙π^-1, the actual mass will be 2 kg. In essence, this can also be understood as a relativistic mass decrease. Viewed from the opposite direction, this may correspond to a relativistic mass increase resulting from the combination of Einstein's and Newton's formulas.

Further, by substituting the larger blood volume (mass) value determined in a single circulation of the human bloodstream, the square of the circulation radius (r_{average human blood circulation}²) can be determined:

Furthermore, the square of the circulation radius (r_{average human blood circulation}²) can be determined by:

$\begin{array}{l}{r}_{1_{}averagehumanbloodcirculation}{}^2=\\ H_{lon{g}_{}evol.dis\tan ce.man(blue-red)}\cdot \\ \frac{G\cdot M_{\text{human blood circulation turnaround}}}{v_{Darwinia{n}_{}evolution,man(blue-red)}{}^2}\end{array}$   (41)

substituting the larger blood volume (mass) determined on the basis of its single circulation in the human blood circulation into the combined Einstein and Newton formula.

The radius of the average human circulation (r_{average human blood circulation1}) after square root subtraction:

$\begin{array}{l}{r}_{1_{}averagehumanbloodcirculation}=\frac{1}{v_{Darwin.evol.man(blue-red)}}\\ \cdot \sqrt{H_{lon{g}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot G\cdot M_{\text{human blood circ}\text{.turnaround}}}\end{array}$   (42)

Numerically:

$\begin{array}{l}{r}_{1_{}humanbloodcirc.}=\frac{1}{2.360568\cdot {10}^{8}m\cdot s^{-1}}\cdot \\ \sqrt{2.564494\cdot {10}^{25}m\cdot 6.673848\cdot {10}^{-11}\frac{m^3}{kg\cdot s^2}\cdot 0.01395\cdot {10}^{2}kg}\\ =\frac{1}{2.360568\cdot {10}^8\frac{m}{s}}\cdot 0.488625472\frac{m^2}{s}={0.2069948}_{}m\end{array}$   (43)

Taking into account a single circulating time of 30 seconds, the radius of the average circulation (r_{average human blood circulation2}) will be larger:

$\begin{array}{l}{r}_{2_{}a.humanbloodcirc.}=\frac{1}{2.360568\cdot {10}^8\frac{m}{s}}\\ \cdot \sqrt{2.564494\cdot {10}^{25}m\cdot 6.673848\cdot {10}^{-11}\frac{m^3}{kg\cdot s^2}\cdot 0.02002464\cdot {10}^{2}kg}\\ =\frac{1}{2.360568\cdot {10}^8\frac{m}{s}}\cdot 0.585425125\frac{m^2}{s}={0.248001}_{}m\end{array}$   (44)

In summary, it can be concluded that by replacing the size of the blood circulation determined by cardiologic examination methods or the blood volume of a single circulation in the law of free fall combined with general relativity, one or the other value can be obtained. This also seems to prove the usefulness of physical formulas for human blood circulation. With this extension, the law can be generalized and the application of complex physical laws in biological organisms seems to be proven. It also supports the basic concept that gravity accumulates in living creatures. Based on these, it seems that gravity is one of the driving factors in the development of living organisms during the long process of Darwinian evolution.

Where h_{past, present in Darwinian evolution} and r_{average human circulation} are considered to be perpendicular to each other, like Newtonian orbits. That is, each point of h passing through the center of the plane of the toroidal average human circulation can be such a relationship between the center of mass and the blood circulating around it. However, since the average human circulation includes all directions of space, perpendicularity is not exclusive. One thing is certain, however, that h from the past to the present always points in the direction of a more curved space-time, i.e., more advanced structure. This is ensured by the increasing gravitational effect through the series of mutations.

So far, we have only dealt with the interpretation of h in the expression below the root, but there is also H, for which we have not made any findings. We have not explained how the law of free fall can work in the case of H. This can be done by correcting H for h. In this case, we have to multiply H by the ratio of the angles (α/2∙π^-1) which means a very significant distance reduction. This so-called distance contraction can be explained by time dilation derived from general relativity.

$v_{Darwin.evol.man(blue-red)}=\sqrt{H_{lon{g}_{}evol.dis\mathrm{t}.man(blue-red)}\cdot \frac{\alpha }{2\cdot \pi }\cdot g_{Earth}}$   (45)

Numerically:

$\begin{array}{l}{v}_{Darwin.evol.man(blue-red)}=\sqrt{\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^2}{g_{Earth}}\cdot \frac{2\cdot \pi \cdot c^2\cdot R_{Earth}}{2\cdot G\cdot M_{Earth}}\cdot \frac{2\cdot G\cdot M_{Earth}}{2\cdot \pi \cdot c{\cdot }^2{R}_{Earth}}\cdot g_{Earth}}\\ =\sqrt{\frac{\nu -{\nu }_0}{{\nu }_0}\cdot c^2}=\text{0}\text{.7874}\cdot c_{}{\text{=}}_{}\text{2}\text{.3622}\cdot {\text{10}}^8\frac{m}{s}\end{array}$   (46)

(The result is the same as in Eq.12.) In this case, for the short evolutionary distance, i.e., h, the formula works and can be used to determine the mass and size of the human bloodstream, including radius.

The decrease in the speed of light propagation near of a black hole is analogous and may correspond to the average flow rate in the human bloodstream:

$v_{c_{}i{n}_{}blac{k}_{}hole}=c\cdot \frac{\alpha }{2\cdot \pi }=c\cdot \frac{2\cdot G\cdot M}{2\cdot \pi \cdot c^2\cdot R}$   (47)

In this way, the speed of light (c) at this time dilation is as follows:

$\begin{array}{l}{v}_{c_{}a{t}_{}blac{k}_{}hole}=c\cdot \frac{6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}\cdot 5.97219\cdot {10}^{24}kg}{3.141592653\cdot 8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}\cdot 6.371005\cdot {10}^{6}m}\\ =c\cdot 0.22157\cdot {10}^{-9}\end{array}$   (48)

This velocity corresponds to a speed of light of 6.6425 cm/s (2.99792458∙10⁸m/s∙0.22157∙10^-9=0.66425∙10^-1m/s) and an average human circulation rate due to time dilation.

The time dilation and distance contraction behind the curved space-time structure

Our basic assumption that from the time of the formation of life, during the Darwinian evolutionary process on the surface of the Earth,⁷ the biological individual also adapts to the value of g. In this way, like adaptation to the environment, the value of surface gravity can multiply over billions of years. These effects accumulated by g can be stored in the genetic information system. In this way, stepping up, they would be fixed in deoxyribonucleic acid (DNA) at higher and higher values. One of the gravitational effects thus coded would be the curvature of space, which would correspond to the heart and circulatory system of biological creatures. These effects would therefore be hereditary, appearing in the offspring as an increasingly advanced anatomical structure. Extending the validity of Newton's law of gravity to the biology would make it possible to determine the parameters of human blood circulation. Without violating the basics of the law, the validity of data well known from the life sciences could be verified by applying it.

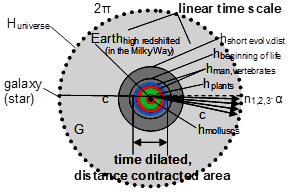
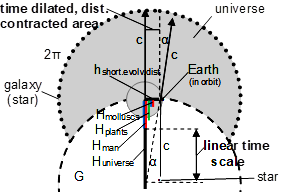
Figures 6&7. The representations show the parts of the universe where there are time-dilation and distance-contraction regions, and where there is a linear time scale. The part within h displays the former, and the range between h and H displays the latter. The colored circles or lines (spheres in 3 dimensions) show the evolutionary distance and time of the biological individual. Because they are located in the h range, they are also subject to space-time deflection and the associated change in time and distance.

The ratio of the angle of deflection of light passing through the Earth's surface to the total angle as a universal constant

The deviation angle (α) of a light beam, which passes near a celestial body’s surface, in this case the Earth, according to Einstein’s formula⁹ is:

$\alpha =\frac{2\cdot G\cdot M}{c^2\cdot R}$   (49)

The ratio of the alpha angle to the total angle can be considered as a universal constant that can be reciprocal to each other and can thus be called f_α/2π or f_2π/α. considering the first case:

$f_{\alpha /2\pi }=\frac{\alpha }{2\cdot \pi }=\frac{1}{2\cdot \pi }\cdot \frac{2\cdot G\cdot M}{c^2\cdot R}=\frac{G\cdot M}{\pi \cdot c^2\cdot R}$   (50)

Numerically:

$f_{\alpha /2\pi }=\frac{6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}\cdot 5.97219\cdot {10}^{24}kg\cdot }{3.14159265\cdot 8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}\cdot 6.371005\cdot {10}^{6}m}=\text{0}\text{.22156987}\cdot {10}^{-9}$   (51)

Inversely:

$f_{2\pi /\alpha }=2\cdot \pi \cdot \frac{1}{\alpha }=\frac{2\cdot \pi \cdot c^2\cdot R}{2\cdot G\cdot M}=\frac{\pi \cdot c^2\cdot R}{G\cdot M}$   (52)

Numerically:

$f_{2\pi /\alpha }=\frac{3.141592653\cdot 8.98755178\cdot {10}^{16}{m}^2\cdot s^{-2}\cdot 6.371005\cdot {10}^{6}m}{6.673848\cdot {10}^{-11}{m}^3\cdot k{g}^{-1}\cdot s^{-2}\cdot 5.97219\cdot {10}^{24}kg}=\text{4}\text{.513249}\cdot {10}^9$   (53)

The minuscule dimensionless value of f_α/2π may be followed by time dilation and distance contraction. On the other hand, behind an enormous value of f_2π/α, representing almost 10 orders of magnitude, there may be time contraction or distance dilatation, depending on the concept in which it is used.

The factor (f_α/2π) resulting from the ratio of the angles (α/2π) results in distance contraction through time dilation:

$\begin{array}{l}{H}_{lon{g}_{}evol.dis\mathrm{t}.man}\cdot f_{\alpha /2\pi }=h_{shor{t}_{}evol.dis\mathrm{t}.man}\cdot f_{2\pi /\alpha }\cdot f_{\alpha /2\pi }\\ =\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^2}{g_{Earth}}\cdot \frac{2\cdot \pi \cdot c^2\cdot R_{Earth}}{2\cdot G\cdot M_{Earth}}\cdot \frac{2\cdot G\cdot M_{Earth}}{2\cdot \pi \cdot c^2\cdot R_{Earth}}=h_{shor{t}_{}evol.dis\mathrm{t}.man}\end{array}$   (54)

The factor (f_2π/α) resulting from the inverse ratio of the angles (2π/α) results in distance dilation through time contraction:

$\begin{array}{l}{h}_{shor{t}_{}evol.dis\mathrm{t}.man}\cdot f_{2\pi /\alpha }=h_{shor{t}_{}evol.dis\mathrm{t}.man}\\ \cdot \frac{2\cdot \pi }{\alpha }=\frac{\nu -{\nu }_0}{{\nu }_0}\cdot \frac{c^2}{g_{Earth}}\cdot \frac{2\cdot \pi \cdot c^2\cdot R}{2\cdot G\cdot M}=H_{lon{g}_{}evol.dis\mathrm{t}.man}\end{array}$   (55)

Determining the cross-sectional area of the average human circulation based on a value derived from the Darwinian rate of evolution

When determining the cross-sectional area of an average human circulation with a circular shape and a circular cross-section (A), the following data (V, t and v) shall be taken into account.

Based on Equation 24, taking the single circulation time (t_2π(25)) as 25 s, the circular cross-sectional area (A₁) of the average circulation is as follows:

$\begin{array}{l}\mathrm{Sin}ce:\frac{V_{2\pi (25s)}}{t_{2\pi (25s)}}=A_1\cdot v_{Darninian}{}_{{}_{}evol.man(blue-red)},s{o}_{}{A}_1\\ =\frac{V_{2\pi (25s)}}{t_{2\pi (25s)}\cdot v_{Darninian}{}_{{}_{}evol.man(blue-red)}}=\frac{\frac{m}{\rho }}{t_{2\pi (25s)}\cdot v_{Darninian}{}_{{}_{}evol.man(blue-red)}}\\ =\frac{\frac{1.4kg}{1\cdot {10}^3\frac{kg}{m^3}}}{{25}_{}s\cdot 5.2\cdot {10}^{-2}\frac{m}{s}}=0.0107692\cdot {10}^{-1}{}_{}{m}^2=10.7692c{m}^2\end{array}$   (56)

Where V_2π(25) is the volume of single circulation of blood stream and v_{Darwinian evolution, man(blue-red)} is the rate of Darwinian process.

Taking the single turnaround time of the circulation (t_2π(30)) to be 30 s, the area of the circular cross-section (A₂) is:

$\begin{array}{l}{A}_2=\frac{V_{2\pi (30s)}}{t_{2\pi (30s)}\cdot v_{Darwin.evol.man(blue-red)}}\\ =\frac{2\cdot {10}^{-3}{m}^3}{30s\cdot 5.2\cdot {10}^{-2}\frac{m}{s}}=0.01282\cdot {10}^{-1}{m}^2=12.82c{m}^2\end{array}$   (57)

The radius of a circular tube (torus) (r) with a circular cross-sectional area (A) can be expressed from the relation A = r²∙π:

$A=r^2\cdot {\pi }_{}{,}_{}so{:}_{}r={\sqrt{\frac{A}{\pi }}}_{}{,}_{}and{:}_{}d=2\cdot r=2\cdot \sqrt{\frac{A}{\pi }}$   (58)

From this, the radius (r₁) of the circular cross-sectional surface of the torus is expressed numerically as follows:

$r_1=\sqrt{\frac{10.7693c{m}^2}{3.141592}}=1.8515cm{,}_{}and{:}_{}d=3.703cm$   (59)

And the radius (r₂) of the larger cross-section is:

$r_2=\sqrt{\frac{12.82c{m}^2}{3.141592}}=2.02cm{,}_{}and{:}_{}d=4.04cm$   (60)

For a blood flow rate derived from the Darwinian velocity of evolution (v_{Darwinian evolution, man(blue-red)}), the radius (r) of the average human circulation cross-section can be determined between 1.85 cm and 2 cm at rest (the diameter is between 3.7 cm and 4 cm).

The force of gravity affecting the average human blood circulation

If the mass (m₁), or in this case the volume of human blood (V₁) for a single revolution time (t₁) is accelerated by the force of gravity (g), the acceleration force (F₁):

$\begin{array}{l}F=m\cdot a=m_1\cdot g=V_1\cdot \rho \cdot g,so:\\ F_1={1.4}_{}kg\cdot {9.80665}_{}m\cdot s^{-2}={13.7293}_{}N\end{array}$   (61)

Where mass (m₁) is the product of volume (V₁) and density (ρ) of the human blood (m=V∙ρ; ρ≈1.060g/cm³). However, for the sake of simplicity, the density of blood is taken to be equal to that of water.

Moreover, for the larger volume (mass; m₂), the accelerating force (F₂):

$F_2=2_{}kg\cdot {9.80665}_{}m\cdot s^{-2}={19.6133}_{}N$   (62)

The gravitational attractive force, which according to our idea above accelerates the blood in biological evolution and which also maintains the average human blood circulation, can vary between 13.7 N and 19.6 N under physiological conditions at rest. In this setup, the driving force in the model corresponds to the pressure force of the heart. 

When determining the weight of a vertical column of blood (left and centre of Figure 8), the relationship between the mass of the blood and the gravity acting on it becomes evident. The compressive force (F) acting on the base of the column and the resulting pressure (P) are the same as the blood pressure prevailing in human blood circulation. Less obviously, but the same applies to a torus-shaped circulation (right side of Figure 8). Counting from any point of the circle (white dashed line), the length (s) of a single revolution is the same in all cases. The driving force (F) required to move this section (s) corresponds to the work (W) done by the heart against gravity (g) (W=m∙g∙s). If we place the torus symbolizing circulation in any plane in space, due to the pressure (P) spreading equally in all directions, it will behave similarly to the vertical column of blood. The compressive force will be the same regardless of whether the circulation is fractionated or not. The amount of blood ejected during a single contraction of the heart is 70 mL. In the model, the same corresponds to the blood volume of a 5 cm section. In this way, the continuously flowing blood within the entire circle is composed of fractionated elements.

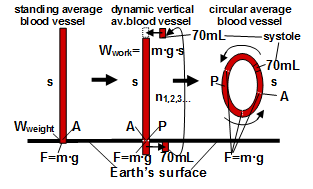
Figure 8 highlights the relationship between the Earth's gravitational (g) attractive force (F↓) acting on the mass (m) of a given column of blood and the driving force (Fͻ) required to turn the same volume of average human blood circulation (V≈m) around once. For further relationships (pressure /P/, work /W/, etc.), see the following chapters.

The pressure conditions established by the gravitational force in the average human blood circulation

The pressure (P) exerted by the acceleration force (F) per unit area (A), i.e., in this case the transverse cross-section of the average human circulation is as follows:

$P_1=\frac{F_1}{A_1}=\frac{13.7293N}{0.00107693m^2}={12748.55}_{}N/m^2$   (63)

In the case of the larger accelerating force (F₂) and the larger pipe cross-sectional area (A₂), the accelerating force (F₂) is as follows:

$P_2=\frac{F_2}{A_2}=\frac{19.6133N}{0.001282m^2}=15298.986\frac{N}{m^2}$   (64)

Since: 1 N/m² = 7.5∙10^-3 mmHg (torr), in the case of the smaller accelerating force (F₁), the value of the pressure (P₁) in the average human circulation is:

$P_{1(mmHg)}=12748.55\frac{N}{m^2}\cdot 7.5\cdot {10}^{-3}=\text{95}{\text{.614}}_{}\text{mmHg}$   (65)

Moreover, in the case of a greater acceleration force (F₂), the value of the pressure (P₂) in the circulation will increase:

$P_{2(mmHg)}=15300\frac{N}{m^2}\cdot 7.5\cdot {10}^{-3}={114.75}_{}\text{mmHg}$   (66)

The pressure (P) in the average human blood circulation can take values between 96 and 115 mmHg. Depending on the individual parameters (F, A), calculated with a simple mathematical average, in the previous case it corresponds to 115 mmHg systolic and 75 mmHg diastolic values (or in another version 120/70 mmHg blood pressure). The latter average blood pressure corresponds to a blood pressure value of 140/90 mmHg. These values are the same as the data determined by the invasive internal cardiac catheter method or by indirect external blood pressure measurement.⁵⁰

Gravitational work done during a single revolution of human blood circulation

The driving force behind the torus-shaped average human blood circulation is the pumping function of the heart. Metaphorically, it is the equivalent of the attractive force of gravity in the human body. The work required to maintain blood flow (W₁) is the product of force (F₁) and flow length (s₁):

$W_1=F_1\cdot s_1=13.7293N\cdot 1.3m={17.848}_{}Nm={17.848}_{}J$   (67)

In the other case, when the greater accelerating force prevails (F₂), the amount of work (W₂) increases:

$W_2=F_2\cdot s_2=19.6133N\cdot 1.56m=30.6Nm=30.6J$   (68)

The work of the heart muscle that maintains the average human blood circulation, which corresponds to the work of the gravitational force, can vary between 17.8 J and 30.6 J in a resting state under physiological conditions (Figure 8).

The output of the heart for a single cycle time of the average human blood circulation

The performance of the heart can be determined in two ways in relation to the time of one revolution (25-30s).^48,49 One method is to estimate it from the two extreme values of the maximum and minimum circulation flow rates (in the aorta and capillaries).⁴⁴ The other, as detailed above, is reduced from the speed of Darwinian evolution in proportion to the angles (Eq.46). However, since both flow rates are roughly the same (5cm and 5.2cm), the conclusions drawn from them and the result that can also be displayed visually are similar.

In this way, the performance (P_1(watt)) of the work (W₁) of the driving force (F₁) required maintaining the flow rate of the average human bloodstream (v_{Darwinian evolution, man(blue-red)reduced}) derived from the rate of Darwinian evolution (_{VDarwinian evolution, man(blue-red)}) is as follows:

$\begin{array}{l}{P}_{1(watt)}=\frac{m_1\cdot g\cdot s_1}{t_1}=\frac{F\cdot s_1}{t_1}=\frac{W_1}{t_1}\\ =\frac{13.7293kg\frac{m}{s^2}\cdot 1.3m}{25s}=\frac{17.848Nm}{25s}\\ =0.7139\frac{J}{s}=0.714W\end{array}$   (69)

(Since 1 J = 1 kg•1 m²•1 s^‒2, and 1 Joule per second [J/s] = 1 Watt [W].)

In the other case, when the greater work is performed (W₂) (even in the case of greater single flow time; t₂), the performance (P_2(watt)) also increases:

$P_{2(watt)}=\frac{W_2}{t_2}=\frac{{30.6}_{}J}{{30}_{}s}=\text{1}\text{.02}\frac{J}{s}=\text{1}{\text{.02}}_{}W$   (70)

The performance of the heart (P_watt) can also be determined directly from the value derived from the speed of the Darwinian evolutionary process (v_{Darwinian evolution, man(blue-red)}). This can be calculated from the product of the heart's work (W) and the average human blood circulation speed (v_{Darwinian evolution, man(blue-red)reduced}). Since the work involved in performance (P_Watt) can be broken down into the product of force and distance (s), the quotient of distance (s₂) and time (t_2π(25)) will be equal to velocity. Therefore, the value calculated from the velocity of the blood between the aorta and capillary (V_estimated) should be equal to _{vDarwinian evolution, man(blue-red)reduced}, and then the power determined in this way is the following:

$\begin{array}{l}{P}_{1(watt)}=\frac{W_1}{t_1}=\frac{F_{2\pi (25)}\cdot s_{2\pi (25)}}{t_{2\pi (25)}}=\\ F_{2\pi (25)}\cdot v,but,beequal:v=v_{Darwinian}{}_{}so:\\ F_{2\pi (25)}\cdot v_{Darwin}=m_{2\pi (25)}\cdot g_{Earth}\cdot v_{Darwin}=\\ {1.4}_{}kg\cdot 9.80665\frac{m}{s^2}\cdot 0.052\frac{m}{s}={0.714}_{}W\end{array}$   (71)

(Since 1 kg∙m/s² = 1 N, 1 kg∙m²/s³ =1 N∙m/s, 1 N∙m = 1 J, 1 N∙m/s = 1 J/s, 1J/s = 1 W.)

The power of the heart (P_2(watt)) for 30 s of average human blood circulation (t_2π(30)) and a mass of 2 kg (m_2π(30)) is slightly higher than the previous one, i.e., almost 1 watt.

Cardiac output (P_Watt) for a single cardiac contraction, that is, blood volume per systole (i.e., stroke volume /sv/ = 70 mL) individually, for average human circulatory velocity (v_{Darwinian evolution man(blue-red)}), aortic blood flow speed (v_aorta), and capillary blood flow rate (v_capillary) is:

$\begin{array}{l}{P}_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_1}=m_{sv}\cdot g\cdot v_{Darninian}{}_{{}_{}evol.man(blue-red)}\\ =0.07kg\cdot 9.8\frac{m}{s^2}\cdot 0.052\frac{m}{s}=0.0357{\frac{J}{s}}_{},but:\\ P_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_1}=m_{sv}\cdot g\cdot v_{aorta}=\\ 0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 1.5\frac{m}{s}=1.029\frac{J}{s}={1.03}_{}{W}_{},and:\\ P_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_1}=m_{sv}\cdot g\cdot v_{capillary}=\\ 0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 0.001\frac{m}{s}={0.000686}_{}W\end{array}$   (72)

These are therefore speed-dependent values and indicate how much the heart's performance is for a single contraction in each section of the vascular path.

The so-called average human blood circulation model derived from the above-mentioned physiological hemodynamic parameters according to the physical laws of flow can be presented as follows (Figure 9).

Figure 9. The representation shows a torus-shaped image of the average human blood circulation. The individual parameters, i.e., volume (V), radius (r), cross-sectional area (A), force (F), work (W), pressure (P_mmHg) and performance (P_watt) were derived from the speed of the Darwinian evolutionary process (v_{Darwinian evol.man)}. In addition, we created them from time (t_2π=25s-30s) and distance data (C=1.3m-1.56m) with the help of circulation test procedures (dye dilution, etc.). Using the estimated average human blood circulation speed (v_estimated=5cm/s), we can reach a similar conclusion. The hemodynamic parameters determined by the two methods essentially overlap (5.2cm/s and 5cm/s), supporting each other's results.

The above data refer to the average human blood circulation as a whole. The durations of the pulmonary and systemic circulation (t_{2π,pulmonary}=4s and t_2π,systemic=25s) can be precisely determined with different circulation testing procedures. These can be done with dye or heat dilution methods, as well as with radioisotope measurements, which lead to similar results.

Based on the two circulating blood volumes (V_2π,systemic and V_{2π,pulmonary}), as well as knowing the speed of the Darwinian evolutionary process (v_{Darwinian evolution, man(blue-red)}), a small and a large blood circulation can be distinguished, which ensures continuous one-way blood flow. With these data, the originally single circular blood flow (torus) can be divided into two separate parts (doubled torus), which represent human blood circulation in detail.⁵¹

Separation of toroidal average human blood circulation into average systemic and pulmonary circulation

The circulation size (s,C) resulting from the single circulation time of the human blood circulation (t_{2π,pulmonary}) and the average speed (v_{average,torus}) we arbitrarily determined includes the pulmonary circulation. Similarly, the circulation derived from the value of the Darwinian evolutionary rate also includes the pulmonary circulation. If in both cases the length of the pulmonary circulation (s_pulmonary) and the value of the volume of the blood in it are subtracted from the length (and volume) of the average human blood circulation, which is embodied in the form of the torus, the toroidal blood flow can be divided into two parts. With this method, a separate pulmonary and systemic circulation can be created (C_average - C_pulmonary = C_systemic and V_2π,average-V_{2π,pulmonary} = V_2π,systemic). In this way, the sophisticated system of human blood circulation is realized, which represents the highest degree of Darwinian evolution.

If a section is cut out of the torus-shaped average human blood circulation and reduced in proportion to the pulmonary circulation time, the intensity of the blood flow does not change with the same flow cross-sectional area (I=A∙v). Thus, the value of the s/t ratio, i.e., the flow rate, remains unchanged even with a smaller size, i.e., the blood flow rate does not change in the pulmonary circulation either.

The cross-sectional area and flow velocity of the pulmonary circulation should also be taken as equal to the toroidal average human circulation (v = 5.2 cm/s and A = 10.77-12.8 cm², see also (Figures 9&10). This is mandatory in order for the law of continuity to function, i.e., for equal volumes of blood to flow through a certain flow section during equal time intervals. If this law were not operated, disturbances would occur in the respiratory-circulatory system and various diseases and related symptoms would develop.

In this way, by separating the toroidal blood flow into two parts, a pulmonary and a systemic circulation, the highest degree of Darwinian evolution is realized, which culminates in the human circulatory system.

Given the pulmonary circulation time (t_{2π,pulmonary}=3.98 - 4.47s and 4.67s),^52,53 which means the time of blood flow from the right ventricle or the pulmonary artery to the left atrium (C_pulmonary), the average pulmonary circulation its radius (r), length (s) and cross-sectional area (A) can also be calculated.

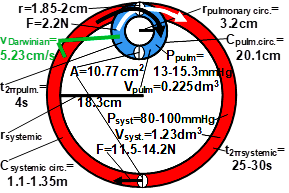
Figure 10. Representation of the average human blood circulation in the form of a "double torus", which approximately shows a ratio of minimum 1 to 5.5, or maximum 1 to 7.5. The figure shows the distribution of the blood volume per cycle (V_pulmonary = 0.225 dm³ and V_systemic = 1.23 dm³) in proportion to the circulation times (t_{2π,pulmonary} = 4 s and t_2π,systemic = 25-30 s). This blood flow model, which can also be called the "folded figure of eight", shows unique parameters /radius (r), circumference (C), volume (V), cross-sectional area (A), force (F), work (W), pressure (P_mmHg), power (P_Watt)/ for both blood circuits, i.e., the pulmonary and systemic blood circuits. These are consistent with data from medical circulation testing procedures and heart ultrasound examinations.          

The most important parameters of the pulmonary circulation

Similar to the above, the two obligatory flow laws apply to pulmonary circulation the path of circulating blood:

$\begin{array}{l}\mathrm{Sin}ce:\frac{A\cdot s}{t_{2\pi }}=A\cdot v,s{o}_{},\frac{s_{pulmonary}}{t_{2\pi (pulmonary)}}\\ =v_{Darwin.evol.man(blue-red)},and:\\ s_{pulmonary}=v_{Darwin.evol.man(blue-red)}\cdot t_{2\pi (pulmonary)}{}_{},{}_{}but:\\ s_{pulm.}=C_{pulm.circumf.}{,}_{}so:C_{pulm.circumf.}\\ =5.23\frac{cm}{s}\cdot 4s=20.9\text{2}cm\end{array}$   (73)

From the length of the circumference (C_{pulmonary circumference}), the radius of the average pulmonary circulation (r_{pulmonary circulation}) is as follows:

$C=2\cdot r\cdot {\pi }_{}{,}_{}so{:}_{}{r}_{pulmonar{y}_{}circulation}=\frac{C_{pulmonar{y}_{}circumf.}}{2\cdot \pi }=\text{3}\text{.33cm}.$   (74)

The magnitude of the average systemic circulation can be determined by subtracting the length of the average pulmonary circulation from the average toroidal circulation:

$\begin{array}{l}{s}_{averagehumancirculation1}-s_{averagehuma{n}_{}pulmonar{y}_{}circulation}=\\ s_{averagehumansystemi{c}_{}circulation1}=1.3m-0.2092m={1.09}_{}m\end{array}$   (75)

The length of the averege systemic circulation (Eq.75) in the Figure 8 circulation model based on the length of the larger averege toroidal circulation will be as follows:

$\begin{array}{l}{s}_{averagehumancirculation2}-s_{averagehumanpulmonar{y}_{}circulation}=\\ s_{averagehumansystemi{c}_{}circulation2}=1.56m-0.2092m=\text{1}\text{.3508}m\end{array}$   (76)

The volume (V_pulmonary ≈ m_pulmonary ) of blood (in the figure-8 circulation) passing through the smaller cross-sectional area in the average pulmonary circulation expressed in kilograms is as follows:

$\begin{array}{l}{V}_{pulmonary}=A_{systemic/pulmonary}\cdot s_{pulmonar{y}_{}circulation}=\\ =0.001077m^2\cdot 0.2092m=\text{0}{\text{.0002253}}_{}{m}^3\approx \text{0}{\text{.2253}}_{}kg\end{array}$   (77)

Since this mass is moved by gravity along the circumference, the force (F):

$F=m\cdot a=m\cdot g{,}_{}so{:}_{}{F}_1=0.2253kg\cdot 9.80665m\cdot s^{-2}=\text{2}\text{.20952}N$   (78)

The pressure (P_pulmonary) in the pipe is based on the force acting on the surface (A₁) as follows:

$P_{1pulmonary}=\frac{F_{1pulmonary}}{A_{1systemic/pulmonary}}=\frac{\text{2}{\text{.20952}}_{}N}{0.00107693m^2}=\text{2}051.6845\frac{N}{m^2}$   (79)

(A_1systemic= A_1pulmonary)

Since 1 N/m² = 7.5∙10^-3 mmHg, the pressure in the pulmonary circulation, expressed in millimeters of mercury:

$P_{1(mmHg)pulmonary}=\text{2}051.7\cdot 7.5\cdot {10}^{-3}mmHg=\text{15}.38\text{mmHg}$   (80)

However, with a larger cross-sectional area (A₂) (Eq.57), the pressure in the pulmonary circulation decreases:

$P_{2(mmHg)pulmonary}=\frac{F_1}{A_2}=\frac{\text{2}{\text{.20952}}_{}N}{0.001282m^2}=1723.5\frac{N}{m^2}$   (81)

Converted to mmHg:

$P_{2(mmHg)pulmonary}=1723.5\cdot 7.5\cdot {10}^{-3}mmHg={12.92}_{}\text{mmHg}$   (82)

According to them, the pulmonary pressure can vary between 12.9 mmHg and 15.3 mmHg under physiological conditions at rest, in accordance with our current knowledge.⁵⁰

Essential parameters of the systemic circulation

In contrast, the volume/mass (V₁ or V₂) values of the systemic circulation are numerically:

$\begin{array}{l}{V}_{1systemi{c}_{}circ.}=A_{1systemic/pulmonary}\cdot s_{1systemi{c}_{}circ.}\\ =0.001077m^2\cdot 1.0908m=\text{0}\text{.0011748}{m}^3\approx {1.1748}_{}k{g}_{},but:\\ V_{2systemi{c}_{}circ.}=A_{1systemic/pulmonary}\cdot s_{2systemi{c}_{}circ.}\\ =0.001077m^2\cdot 1.3508m=\text{0}\text{.00145481}{m}^3\approx 1.4548kg\end{array}$   (83)

The forces (F_1,2) acting on the systemic circulation are as follows:

$\begin{array}{l}{F}_{1systemi{c}_{}circ.}=m_{1systemi{c}_{}circ.}\cdot g{,}_{}so{:}_{}{F}_{1syst.c.}\\ =1.1748kg\cdot 9.80665\frac{m}{s^2}\text{=11}{\text{.52}}_{}N{,}_{}but:\\ F_{2systemi{c}_{}circ.}=m_{2systemi{c}_{}circ.}\cdot g{,}_{}so{:}_{}{F}_{1syst.c.}\\ =1.4548kg\cdot 9.80665\frac{m}{s^2}=\text{14}\text{.26}N\end{array}$   (84)

In the systemic circulation, the pressures (P_{systemic circulation1} and P_{systemic circulation2}) created as a result of the forces driving smaller and larger masses are the following:

$\begin{array}{l}{P}_{systemi{c}_{}circulation1}=\frac{F_{syst.circ.1}}{A_1}=\frac{\text{11}{\text{.52085}}_{}N}{0.00107693m^2}=10697.8656\frac{N}{m^2},and\\ P_{systemi{c}_{}circulation2}=\frac{F_{syst.circ.2}}{A_1}=\frac{\text{14}{\text{.2667}}_{}N}{0.00107693m^2}=\text{13}247.57822\frac{N}{m^2}\end{array}$   (85)

Since 1N/m² = 0.007501 mmHg, the pressure (P_{mmHg systemic circulation1}) is expressed in millimeters of mercury:

$\begin{array}{l}{P}_{systemi{c}_{}circulation1}=10697.86\cdot 7.5\cdot {10}^{-3}mmHg\text{ = 80}{\text{.234}}_{}mmHg,and\\ P_{systemi{c}_{}circulation2}=13247.57\cdot 7.5\cdot {10}^{-3}mmHg={99.356}_{}mmHg\end{array}$   (86)

These systemic average human blood pressure values, based on the two blood volumes (masses), are between 80 mm Hg and 100 mm Hg. This also means that they can take any value between the two values under physiological conditions at rest. This corresponds approximately to blood pressure values of 100/60 mm Hg and 120/80 mm Hg. Blood pressure values above and below these are essentially limit values. Values that differ from this, measured at rest, are already pathological in nature; in these cases, we can talk about diseases of various origins, high blood pressure or hypotensive states.⁵⁰ (Calculated with the A₂ value, the average pressure values are 83 and 90 millimeters of mercury.)

The relationship between pressure, cross-sectional area and flow intensity in the pulmonary circulation

Based on the formula P=F/A, and hence A=F/P (Eq.78 and Eq.81), the surface of the flow cross-sectional area (similar to the systemic blood circulation) in the pulmonary circulation is as follows:

$A_2=\frac{F_1}{P_{2(mmHg)}}=\frac{m_1\cdot g}{P_{2(mmHg)}}=\frac{\text{2}{\text{.21}}_{}N}{{1723.5}_{}\frac{N}{m^2}}=0.001282m^2=12.82c{m}^2$   (87)

Starting from the law of intensity and applying the A∙s/t ratio, the result of the cardiac output for the single revolution time of the pulmonary circulation (4s) and for the single contraction of the right heart (≈1s) is as follows:

$\begin{array}{l}I=\frac{V_{pulmonary}}{t_{pulmonary}}=A_{pulmonary}\cdot \frac{s}{t}=0.001282m^2\cdot \frac{0.2092m}{4s}\\ =\text{0}\text{.0000670486}\frac{m^3}{s}=\text{67}\text{.048}\frac{c{m}^3}{s}\end{array}$   (88)

Starting from the law of continuity and applying the product I=A∙v, the result is the same as the previous one, i.e., the stroke volume:

$\begin{array}{l}I=CO=A_{pulmonary}\cdot v=0.001282m^2\cdot 0.052\frac{m}{s}\\ =\text{0,0000670486}\frac{m^3}{s}=\text{67}\text{.05}\frac{mL}{s}\approx \text{67}\text{.05}\frac{g}{s}\end{array}$   (89)

(Using the product, I=A∙v, the stroke volume is also similar in the case of the systemic circulation, since the area and the speed are the same. Breaking down the speed into the quotient of the distance per time, the ratio is also the same: s/t=1.3m /25s=0.052m/s.)

Another condition for maintaining flow velocity (v=5.23 cm/s) and cross-sectional area constancy (A=12.82cm²) is that the pressure in the pulmonary circulation (P_{(mmHg)pulmonary}) is lower than in the systemic circulation:

$\begin{array}{l}{P}_{(mmHg)pulmonary}=\frac{W_{pulmonary}}{V_{pulmonary}}=\frac{F_{pulmonary}\cdot s_{pulmonary}}{A_2\cdot s_{pulmonary}}\\ =\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{V_{pulmonary}}=\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{\frac{m_{pulmonary}}{{\rho }_{blood(water)}}}\end{array}$   (90)

Numerically:

$\begin{array}{l}{P}_{(mmHg)pulmonary}=g\cdot s\cdot \rho =9.80665\frac{m}{s^2}\cdot 0.2092m\\ \cdot {10}^3\frac{kg}{m^3}=2051.55\frac{Nm}{m^3}=2051.55\frac{N}{m^2}\end{array}$   (91)

This is expressed in millimeters of mercury with the following conversion:

$P_{systemi{c}_{}circulation1}=2051.55\cdot 7.5\cdot {10}^{-3}mmHg\text{ =15}{\text{.386}}_{}mmHg$   (92)

The difference between the two blood flow circles can be illustrated by comparing them. The ratio of the two shows the relationship between the individual parameters according to the following equation in close connection with the statements of Bernoulli's law. According to this, the works (W) done by the contraction of both chambers of the heart is proportional to the product of the pressures (P) established in the two blood circuits and the systemic and pulmonary circulation volumes (V).

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{W_{systemic}}{V_{systemic}}}{\frac{W_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{F_{systemic}\cdot s_{systemic}}{A_2\cdot s_{systemic}}}{\frac{F_{pulmonary}\cdot s_{pulmonary}}{A_2\cdot s_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{V_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{V_{pulmonary}}}\\ =\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{m_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{m_{pulmonary}}}=\frac{s_{systemic}}{s_{pulmonary}}=\frac{1.3m}{0.2092m}=6.21\end{array}$   (93)

Moreover, the ratio of the pressures of the systemic and pulmonary circulation (P_{(mmHg)systemic} and P_{(mmHg)pulmonary}), as well as (by eliminating the flow cross-section; A₁ or A₂) the ratio of the forces (F_systemic and F_pulmonary) maintaining the circulation can also be determined in this model.

$\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{F_{systemic}}{A_2}}{\frac{F_{pulmonary}}{A_2}}=\frac{F_{systemic}}{F_{pulmonary}}=\frac{{13.73}_{}N}{{2.21}_{}N}=6.2$   (94)

But:

$\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{m_{systemic}\cdot g}{A_2}}{\frac{m_{pulmonary}\cdot g}{A_2}}=\frac{m_{systemic}}{m_{pulmonary}}=\frac{1.45kg}{0.22kg}=6.5$   (95)

The result of the change in the flow conditions in the model is the pressure difference between the two blood circuits, the ratio of which is the same as above. This explains the well-known physiological fact that the pulmonary circulation is a low-pressure system compared to the systemic circulation. This pressure ratio contains Bernoulli's law in hidden form. This states that, in addition to the flow intensity being unchanged, the differences in the flow cross-sections cause a change in the flow velocities, with parallel changes in the pressure conditions. In the model, however, the flow velocity (v) and cross-section of the flow (A) are both constant, but the dimensions and pressure change. The law of conservation of energy is also realized in this case through their reduction. In the case of a lack of this size and pressure compensation, disturbances appear in the normal human blood circulation, the physiological mechanisms become pathological and this leads to the development of various cardiovascular diseases.

The pressure established by the work of the heart in the small and large blood circulation can be broken down into its components in the following steps. Since the flow cross-sections and flow velocities are equal in both blood circuits, they drop out together with g. In this way, the formula is simplified and reduced to their blood volumes (masses), their dimensions, and their flow time.

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{W_{systemic}}{V_{systemic}}}{\frac{W_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{F_{systemic}\cdot s_{systemic}}{A_{systemic}\cdot v_{systemic}\cdot t_{systemic}}}{\frac{F_{pulmonary}\cdot s_{pulmonary}}{A_{pulmonary}\cdot v_{pulmonary}\cdot t_{pulmonary}}}\\ =\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{A_{systemic}\cdot v_{systemic}\cdot t_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{A_{pulmonary}\cdot v_{pulmonary}\cdot t_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot s_{systemic}}{t_{systemic}}}{\frac{m_{pulmonary}\cdot s_{pulmonary}}{t_{pulmonary}}}\\ =\frac{m_{systemic}\cdot s_{systemic}}{m_{pulmonary}\cdot s_{pulmonary}}\cdot \frac{t_{pulmonary}}{t_{systemic}}=\frac{1.45kg\cdot 1.3m\cdot 4s}{0.22kg\cdot 0.21m\cdot 25s}=6.5\end{array}$   (96)

Moreover, based on the relationship v=s/t, knowing the flow distance and flow time, these can be converted into flow speed. In this way, the ratio of the pressure of the systemic and pulmonary circulation (P_systemic and P_pulmonary) is proportional to the volume occupied in their circulation (m_systemic and m_pulmonary), the speed of the systemic circulation (v_sytemic), and the reciprocal of the speed of the pulmonary circulation (1/v_pulmonary).

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{m_{systemic}}{m_{pulmonary}}\cdot v_{systemic}\cdot \frac{t_{pulmonary}}{s_{pulmonary}}=\\ =\frac{1.4548kg}{0.2253kg}\cdot 0.052\frac{m}{s}\cdot \frac{4s}{0.2092m}=6.4571\cdot 0.052\cdot 19.12=6.4\end{array}$   (97)

Considering the velocities (v_systemic, v_pulmonary) since they are the same in the two blood circuits, they are eliminated and only the mass ratio (m_systemic/m_pulmonary) remains.

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{m_{systemic}}{m_{pulmonary}}\cdot v_{systemic}\cdot \frac{1}{v_{pulmonary}}\\ =\frac{m_{systemic}}{m_{pulmonary}}\cdot \frac{v_{systemic}}{v_{pulmonary}}=\frac{1.4548kg}{0.2253kg}=6.4571\end{array}$   (98)

Alternative definitions of the velocity of Darwinian evolution and the rate of average human circulation using the laws of classical and modern physics

Another option, different from the above, to determine the speed of the evolutionary process, is to insert the special case of Newton's law of general mass attraction, i.e., the formula of free fall, into the law of general relativity.

The following relation expresses the velocity (v) of freely falling bodies, including biological individuals (see also Eq.11):

$v^2=2\cdot g\cdot h{,}_{}and{:}_{}g\cdot h=\frac{v^2}{2}$   (99)

In the Einstein relation determining the redshift (Eq.1), the value of the gravitational potential difference (ΔΦ) is the following, broken down (Eq.2) into the product of g and h:

$\nu ={\nu }_0\left(1+\frac{\Delta \Phi }{c^2}\right)$   (100)

and:

$\nu ={\nu }_0\left(1+\frac{g_{Earth(mean)}\cdot h_{past,present}}{c^2}\right)$   (101)

According to the law of free fall, v squared is equal to the product of g and h multiplied by 2. In this way, the square of the velocity of the free-falling body can be substituted into the value of the product g∙h in the numerator of the Einstein formula. Then the formula changes as follows:

$\begin{array}{l}\frac{\nu -{\nu }_0}{{\nu }_0}=\frac{\frac{v_{Darwin.evol.man(blue-red)}{}^2}{2}}{c^2}and:\\ \frac{\nu -{\nu }_0}{{\nu }_0}\cdot 2\cdot c^2=v_{Darwin.evol.man(blue-red)}{}^2\end{array}$   (102)

Accordingly, if the degree of redshift (blue-red) is (ν-ν_o)/ν_o = 0.62 (Eq.8 and Eq.9) and taking the roots from both sides of the equation:

$\begin{array}{l}0.62\cdot 2\cdot c^2=v_{Darwin.evol.man(blue-red)}{}^{2}and:\\ \sqrt{0.62\cdot 2}\cdot c=v_{Darwin.evol.man(blue-red)}\end{array}$   (103)

Numerically:

$\begin{array}{l}{v}_{Darwin.evol.man(blue-red)}=0.7874\cdot 2.99792458\cdot {10}^8\frac{m}{s}\\ \cdot 1.4142=2.360568\cdot {10}^8\frac{m}{s}\cdot 1.4142\end{array}$   (104)

This value exceeds the speed of light. Multiplied by the ratio of the angles (α/2∙π^-1 = 2.2157∙10^-10), the speed of blood circulation would be equal to 5.2303 cm/s∙1.4142, i.e., 7.3967 cm/s.

$\begin{array}{l}\sqrt{1\cdot 2}\cdot c\cdot \frac{\alpha }{2\cdot \pi }=v_{Darwin.evol.man(black)},so:v_{Darwin.evol.man(black)reduce{d}_{}b{y}_{}\alpha /2\pi }=\\ 1\cdot 1.4142\cdot 3\cdot {10}^8\frac{m}{s}\cdot 0.22157\cdot {10}^{-9}=6.6425\cdot {10}^{-2}\frac{m}{s}\cdot 1.4142\end{array}$   (105)

This is the same as the result obtained by the above method for the average human blood circulation (6.6425 cm/s; see Chapter 3 and Eq.15). At complete blackout, when there is respiratory and circulatory insufficiency, the frequency shift will be (ν-ν_o)/ν_o =0.92 and 1, respectively. Then the blood flow speed in the human body would exceed the maximum value, i.e., 6.6425 cm/s ∙ 1.4142 = 9.3938 cm/s.

If we apply these two laws, the factor 2 must disappear from the classical formula (v²=2∙g∙h) due to the change in the curvature of space-time, otherwise the value obtained in this way exceeds the speed of light by a value of 1.41 (Eq.105).

However, instead of the redshift of 0.62, we take the shift of the two inner values of the red and blue reflection bands [(ν-ν_o)/ν_o=(630-420)/420=0.5] and calculate with a redshift of 0.5, then the product of the two terms under the square root (0.5 multiplied by 2) will be 1. In that case, it is not necessary to eliminate the factor 2 from the formula either, the end result will be the speed of light. Taking this into account, the speed of the Darwinian evolutionary process does not exceed the speed of light:

$\begin{array}{l}\frac{\nu -{\nu }_0}{{\nu }_0}=\frac{\frac{v_{Darwin.evol.man(blue-red)}{}^2}{2}}{c^2},and:0.5\cdot 2\cdot c^2=\\ v_{Darwin.evol.man(blue-red)}{}^2,so:c=v_{Darwin.evol.man(blue-red,medial)}\end{array}$   (106)

When substituting the formulas describing free fall and Newton's law of gravity, as well as the general relativity, an interaction of space-time curvatures is created. Since both equations separately contain a strong space-time curvature, when combined, they can add up or even reduce each other's curvature. When the two systems merges, taking into account a smaller redshift (0.5), factor 2 can be eliminated, so the unification of physical laws cannot violate the constancy of the speed of light. In the case of a larger redshift, i.e., complete blackening [(ν-ν_o)/ν_o=1], a phenomenon can cancel the excess value.

In general, it can be said from the aspect of the high redshifted Milky Way Galaxy (including the Earth) in correlation with the expanding universe, it may also describe the cosmos from various points of view.⁵⁴ Furthermore, by combining the laws and equations of Einstein and Newton, the physical laws of nature can be connected. Due to their joint effect, they can merge into one in the human blood circulation. In addition, they receive a supportive interpretation from the point of view of the living world, with particular regard to the evolution of biological organisms.