With the advancement of technology in the last century, the emergence of ever-higher resolution binoculars and the enhancement of astronomical spectroscopy have made it possible to observe distant galaxies.1 Before the creation of the General Relativity2 and even until the end of the twenties of the last century did not know that the universe expanded. After Edwin Hubble's milestone discovery (1926),3 it became apparent that the shift of the spectrum lines of the light from the galaxies to the Earths became proportional to the distance.4 In 1927, Georges Lemaitre, who was aware of the fact that retrogression in time, the distances of stars, leads to a certain well-defined point of the past,5 and the time calculated here, can be the interval of the emergence of the expanding universe.6 The mass of the point where the universe could have been born has not yet been precisely determined. The measure of this initial mass of the cosmos7 is cardinal, because then it is possible to find out what temperature the cosmos had at the moment of its creation in relation to the Planck mass.
To answer this question and to specify the mass quantity, the following approach is required. In the expanding universe, all galaxies are moving away from each other, so this view should be extended to the Milky Way Galaxy as well. If it goes away from each galaxy, then there is a Solar System in it, including the Earth.8 For this reason, the Earth can be treated as a separate entity, it moves on the one hand in the expanding universe at a very high speed,9 while circling around the Sun (Copernican system), it almost static. In this dual situation, when the Einstein equivalence principle exists together, using the Earth's parameters, it is possible to determine similar factors of the universe.10 In this way, the introduction of a special, repeatable angle ratio and a so-called thermos-relativistic factor can explain the evolution of the cosmos and present its scope holistically.
Determining the radius of the universe from the aspect of the high redshift Milky Way galaxy including the earth in the expanding cosmos
Since there is also time shift behind redshift, it is possible to calculate the exact point in time due to the rapid expansion of space in a manner to estimate the time interval involved by invoking the basic laws of physics. Alterations in either the acceleration or the gravitational fields (or both together) result in changes regarding the frequency of light. This shift of the spectrum line to a lower frequency is demonstrated by Einstein’s original formula11 (Eq.1):
(1)
Where ν is the altered frequency, νo is the initial frequency, c is the speed of light and Φ is the gravitation potential difference.
The gravitational potential difference (Φ) is equal to the product of free fall acceleration (g) and the distance (h) between two points of different gravitational potentials: Φ=g×h.11 Therefore (Eq.1.a):
(1a)
If the same extent of a light beam’s redshift measured at farther galaxies12 is equated to the acceleration of the Earth (as a component of our galaxy) the above formula may also be applied. In this manner, a distance (h) can be calculated pointing towards the origin of the universe. This ‘short evolving distance’ (hpast present) is (Eq.2):
(2)
Where hpast present is the unknown distance between two points of a gravitational field, (ν-νo)/νo= 3.141592653 is the redshift of the Earth as a component of the highly redshifted Milky Way Galaxy, c is the speed of light (2.99792458·108 m·s-1) and g is the standard gravity of the Earth (9.80665 m·s-2).
Numerically (Eq.2.a):
(2a)
This distance depends both on the spectrum line shift ratio, which matches the motion of the Earth, and on the gravity of Earth (Figure 1a). The ‘short evolving distance’ (hpast present) can be given by the ratio of the entire plane angle (2π) and the deviation angle (α) of a light beam passing near the Earth’s surface caused by the gravitational field: h/α=H/2π. With the ratio calculated from the known ‘short evolving distance’ (h) and the two known angles (α, 2π) an enormous unknown distance can be calculated which might be termed the ‘long evolving distance’ (Hpast present = Huniverse)13 (Figure 1b).

Figure 1 Earth by dualistic approach.
Relationship between the entire plane angle (2π) represented by the expanding universe (in a light gray circle with the Earth in the center as the black dot) and the deviation angle (α) of a light beam (c) coming from the left galaxy and grazing the Earth. If the same beam is passing through the gravitational field of the Earth (g=9.8m∙s-2) when the Earth is in motion (n·α) or is comparatively static (α) the degree of change in light properties (e.g. deflection) is different. In the left figure, compared to the opposite galaxy with (e.g.) 3.14 redshift, the Earth remotes with the same velocity from A to B together with the light beam in its g along their contact distance h. This relative one-dimensional movement of the galaxy and the Earth in three dimensions forms a sphere (dark gray circle) with the radius of h around the planet. All observable redshifts from every direction of the cosmos are transforming into this globular region by this principle. Due to the Earth's movement with various redshifts, this orb also contains a homogeneous gravitation field to a value of 9.8m∙s-2. Throughout the generation of the contact distance (h=n∙REarth) there will be a concentric relation to the radius of the universe upward and toward the Earth's size. From this data (h, 2∙π and α) based on Euclidean geometry the size of the universe (H) (right figure), in the case of the inverse ratio of angles (α/2∙π) the Earth's radius (REarth) can be determined symmetrically as well.
The deviation angle (α) of a light beam passing near a celestial body’s surface, in this case that of the Earth, according to Einstein’s formula11 is (Eq.3):
(3)
Numerically (Eq.3.a):
(3a)
Therefore, linking the two equations (Eq.2 and Eq.3) by 2∙π/α (Eq.4):
Where Huniverse is the radius of the universe, (ν-νo)/νo=3.141592653 is the redshift of the Earth (as a component of the highly redshifted Milky Way Galaxy), c is the speed of light (2.99792458·108 m·s-1), π is the ratio of a circle’s circumference to its diameter (3.141592653), R is the volumetric mean radius of the Earth (6.371005·106 m), g is the standard gravity of the Earth (9.80665 m·s-2), M is the mass of the Earth (5.97219·1024 kg)14 and G is the gravitational constant (6.673848·10-11 m3·kg-1·s-2).15
When considering the large redshift ((ν-νo)/νo= 3.141592) which may be measured from farther stars, the ‘long evolving distance’ (Hpast present) equals 12.994509·1025 m, the radius of the universe according to our present knowledge16,17 (Eq.4.a):
Which in time (Tuniverse=Huniverse/c) is 4.3345010∙1017s. Since one year is 3.1556926∙107s, this equates to 13.7355010 billion years.18 The usage of this redshift (3.14) value is important for symmetry regarding both mathematical and physical aspects.
Determination of the initial mass of the cosmos by the repetition of the ratio of angles
Solving the original Einstein equations (1 and 3) linked by 2π/α (4) for the mass (Eq.5):
Numerically (Eq.5.a):
This value is equal to the mass of the Earth, which mass is competent to determine the mass of the universe. In determining the size of the universe and of the Earth8 a symmetrical value in the ratio of the angles can detected in the direction of both the macro and microcosm. If we hypothesize that this symmetrical ratio is valid in nature and as the length and mass are also in correlation with each other (Eq.5 and Eq.6), we can apply it for the determination of mass and not just once but several times; it is possible to determine the initial and total mass of the universe as well.
Given that the re-application of the ratio of the angles (α/2∙π-1) can be repeated up to three times, since it fits three times between the Earth’s mass and the Planck mass, this is a limit. By utilizing this repetition, namely raising the ratio of angles to a cube value (α/2∙π)3, then multiplying the mass of the Earth (MEarth) by this value results in the following substance (Muniverse initial) (Eq.6):
Since (Eq.6.a):
Numerically (Eq.6.b):
This value may correspond to the mass of the initial universe (Muniverse initial) as it is closest to the Planck mass (MPlanck). (The next, the fourth step, would already go beyond the Planck mass, exceeding it in the direction of the smaller value.)
There is a difference between the calculated initial mass of the cosmos (Eq.6.b) and the Planck mass (CODATA: 2.17647051∙10-8kg) therefore divide it by 950.0863 and π and the result is the Planck mass (Eq.6.c):
This mass-difference factor, which refers to the derivation of the two main equations, the thermodynamic (Eq.7) and Einstein equations (Eq.9), can be called the thermo-relativistic factor (ftr). A comparison and analysis of the fundamental masses of physics is necessary (Equations 7 and 9). Although they are not numerically equal, exploring their relationships and evaluating their differences is mandatory for the development of a unifying approach. They can be connected under certain conditions, which can eliminate the inequality between the initial mass of the universe and the Planck mass. However, this will have consequences in terms of the physical laws that describe the universe.
Like all masses, the initial mass of the universe has extent (1.5334∙10-32 m = 950.0863∙ 1.61625518∙10−35m /Planck length/).7 In this way, normally, the volume cannot be separated from the material inside it. One cannot be defined without the other. In this way, a 3D representation must be used to convert the initial mass of the universe and the Planck mass into each other (Figure 2a&2b). To ensure continuity free of inequalities, a unique space-time-mass distribution system must be developed. In this, the masses and volumes must be placed in such a way that they are mosaic-like, fit exactly and do not overlap.
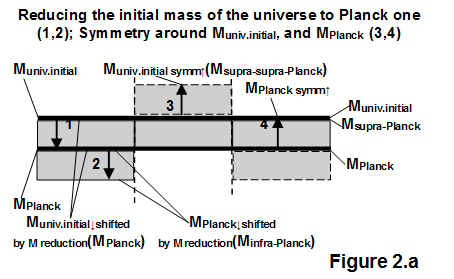
Figure 2a On the left side of the figure, the downward mass shift by the thermo-relativistic factor (ftr) is shown (1), which also implies a downward shift of the Planck mass by 1 unit (2, infra-Planck mass). The middle and right parts of the figure show the upward symmetrical shifts of the level of each mass value (3,4).
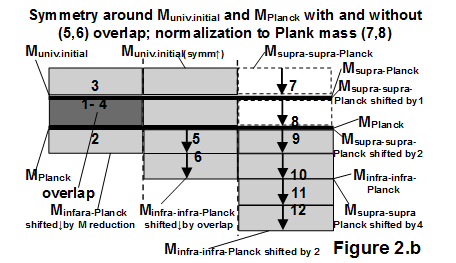
Figure 2b The left part shows the overlap (1-4) of the mass level caused by the increase in mass due to the formation of symmetry. The center column shows a unit downward shift (5 and 6) to eliminate the excess mass due to overlap congestion (3 and 4 /Fig.2.a/). The column on the right shows the reduction to Planck mass, which is now two steps (7, 8). This also results in a further two-step shift in the levels below them (9, 10 and 11, 12).
The left side of Figure 2a shows the decrease in the initial mass of the cosmos as it is shifted one unit down toward the Planck mass. Then the initial mass of the universe becomes equal to the mass of Planck. On this occasion, there will no longer be discontinuity between the two masses. This maneuver creates a direct link between macro and microphysics. With this solution, looking at the physical world from the other side, the current visible mass of the universe is obtained from its actual mass. After all, the value of the actual mass also shifts by one unit towards the smaller value. In view of continuity, the shift will necessarily be repetitive to lower values.
Since a value less than the Planck mass does not exist in nature by definition, the shift is transferred to the temperature values. This transition from mass to temperature is a compulsion arising from the peculiarity of physics. Yet this fiction of mass loss must be continued and interpreted in order to find an explanation for the existence of very low-energy material particles, or electromagnetic waves in the cosmos. In this sense, the Planck mass will also shift by one unit toward smaller values. However, due to the symmetries that exist in physical nature, the possibility of mass shifts in the opposite direction must also be considered. Therefore, both the initial mass of the universe and the Plank mass must be assigned an opposite, i.e., upward shift. In this way, the symmetry will be complete in both cases. However, it doesn't make sense to eliminate the overlap by pushing it up, because such a mass may no longer exist in the universe (950∙1053kg ≈ 1056kg, see Chapter 7).
The initial temperature of the universe determined by its original mass
There is no direct information regarding the universe’s temperature (Tuniverse initial temperature) in this model based on Einstein’s principles, only increasing mass density may indicate it.7 The following equation would prove competent in calculating the value of the initial Planck temperature of the universe (Tuniverse initial Planck temperature) in this model too. Therefore the classic formula for determining the Planck temperature is:
Where k is the Boltzmann constant (1.38064852·10-23J/K), c is the speed of light (2.99792458·108m·s-1) and MPlanck is the Planck mass (2.17647051∙10-8kg).15
Expressing the Planck mass from Equation 7:
The initial mass of the universe (M universe initial) is derived from the Einstein equations (Eq. 6 and 6.b):
Due to the different masses, the two formulas (Equations 8 and 9) can be described mathematically as follows according to the rules of inequality. Depending on which side we look at the two different degrees of mass, there are two ways to describe inequality. This symmetrical appearance is also in line with the symmetry generally perceived in relation to the laws of physical nature. The two possible true statements are:
There is a mirror symmetry between them (Eq.10.a and Eq10.b) as an inequality. In this way, they can be rotated 180 degrees in a horizontal direction along an imaginary vertical axis. With this reversibility to the right or left, their meaning remains the same, their truthfulness is not damaged.
It can be turned into equality mathematically by the solution of simple inequality. This means multiplying or dividing each mass by the dimensionless proportionality factor (thermo-relativistic factor /ftr ≈ 950/). By introducing the thermo-relativistic factor, inequality can be transformed into equality. In this way, the equations can be freely reversed in terms of bias without violating the content of truth and symmetry. Further, the inequality on the left (Eq.10.a) can be solved into equality in two ways:
The inequality on the right (Eq.10.b) can also be solved into equality in two ways:
Equations 11.a, 12.a, and formulas 11.b and 12.b are mirror images of each other (see Fig.2.a left).
None of the four equations is the same unless the side is reversed. According to the solutions of the equation, the mass of Planck changes twice and the initial mass of the universe also changes twice. In case of double mass decrease and double mass increase, continuity is formed symmetrically on both sides (Eq.11.a, 11.b, and Eq.12.a, 12.b). Otherwise, if there is only a single mass decrease unilaterally or only a mass increase, the continuity is partial (Eq.11.a, 11.b, or Eq.12.a and 12.b). When we lose mass in the macro universe on the other side, there is a lack of mass (from total mass to visible mass of the universe). While an increase in Planck's mass in microphysics at the other end would also result in a lack of mass. To avoid mass/energy congestion, the increase in Plank mass shifts the initial mass of the universe up one level, in this way assuming a supra-supra Planck value. Reducing the initial mass of the universe shifts the Plank mass down to the infra-Plank value to avoid mass/energy accumulation.
In the end, however, due to the mass and space-time shifts that occur at the opposite extreme (under extreme conditions) an equilibrium situation occurs in the universe. A symmetric balance that does not violate the laws of macro- and microphysics is created by the occasional separation of space-time and mass. In this way, the massless space-times are duplicated and combined. At other times, the unification and consolidation of space-timeless masses takes place. This space-time and mass separation would be perceptible at the two ends of the universe, in the intermediate case the space and the matter occupying it do not separate, but remain one. Consolidation of space-timeless masses can take place at the beginning of the universe. The joint appearance of the two space-times can occur simultaneously with the formation of the H atom and parallel to the expansion of the universe. According to them, in addition to the law of conservation of matter, the law of conservation of space-time also applies. If there is no space-time on one side, it must appear on the other side and vice versa.
Since, by definition, the value of the absolute temperature must not exceed the Planck temperature, a value exceeding this must be shifted to this level. In order not to step out of the framework defined by physics, the shift towards Planck temperature is possible by dividing by the square of the proportionality factor /ftr2 ≈ 9502/. However, this compulsion, which is not artificial but arising from natural laws, also results in a shift towards lower values at all unique temperature levels. This is done as follows for each of the critical temperature limits:
With this shift down 2 levels, 4 levels will appear below the Planck temperature. These four levels then move forward in time, under each step defined in proportion to the angles, from the beginning of the universe to the present day (see it later).
Using the classic formula for determining the Planck temperature it is possible to describe the thermal status of the cosmos numerically by substituting the initial mass of the universe (Muniverse initial supra-Planck) derived from the Einstein equation into this equation (Eq.13). This temperature value can be termed the initial supra-Planck temperature of the universe (Tuniverse initial supra-Planck temperature):
Considering the linear proportionality between mass and temperature in the formula, the mass surplus is converted to heat. It is numerically:
Variously, if the definitive Planck mass (1.416785·1032 K) can be recovered by the thermo-relativity factor (ftr = 950.863 and π) and dividing both sides of the combined formula with it:
(16)
There is a mass shortage between the Planck mass and the initial cosmic mass. The supra-Planck temperature of the initial universe will decrease to the Planck one (Tuniverse initial Planck temperature):
(17)
The result is as follows:
(18)
Considering the existing symmetry in nature and by extending this characteristic in the opposite direction and reducing the Planck mass into the infra-Planck one by re-dividing both sides of the equation with the factor /ftr ≈ 950/, it is possible to establish an infra-Planck temperature of the cosmos (Tuniverse initial infra-Planck temperature):
(19)
(20)
Or:
(21)
In this way, the temperature will be as follows numerically:
For such a modus to work a central symmetry has to form around the Planck mass and the Planck temperature. Besides symmetry, the other reason for its use is the law of energy conservation. In this case, the division of the thermo-relativity factor could eliminate the supra-Planck mass/energy /temperature surplus. The existing energy surplus would equalize the energy deficit created by introducing of the infra-Planck temperature.
In this manner, it is possible to reveal essential information at and around various stages of the universe's development (Figure 3).
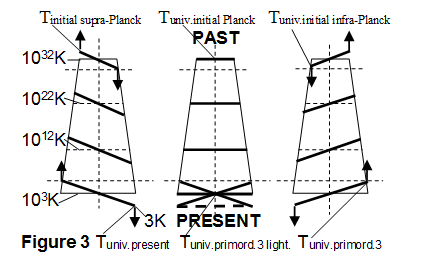
Figure 3 The decrease in the temperature of the universe from the beginning to the present (Tuniverse initial Planck, Tuniverse present (CMB)).
The two dimensional symmetrical figures show a decrease in the universe’s temperature in time by using the ratio of α/2∙π for one to three times (Tuniverse primord1, Tuniverse primord2, Tuniverse primord3). The trapezoid fixed on the middle axis creates a two dimensional surplus area downwards on the other side, if the left upper angle is displaced upwards. This trapezoid or truncated cone shape in three dimensions marks the range of motion of the system. There will be a connection between the initial supra-Planck temperature and the initial infra-Planck temperature around the Planck one. (The rate of temperature change associated with the thermo-relativistic factor at all levels /dashed line/ is also equal to the ratio of the initial cosmos radius and Planck length7).
Since the Einstein equation and the Planck formula are essentially equal, a common solution must be found that does not violate either one of them while each one retains its integrity. The problem has been solved and a uniform approach created by multiplying both sides of the equation (Eq.20) by the thermo-relativistic factor of 950.0863 and π.
The initial infra-Planck temperature of the universe (Tuniverse initial infra-Planck temperature) derived from the initial supra-Planck temperature (Tuniverse initial supra-Planck temperature) is as follows:
(22)
Ergo, the combined Einstein and Planck equation extended by multiplication of the thermo-relativistic factor is as follows:
(23)
However, by multiplying the supra-Planck temperature and the supra-Planck mass on both sides of the equation (Eq.23) by the factor could also establish a supra-supra-Planck temperature (Tuniverse initial supra-supra-Planck temperature) and a supra-supra-Planck mass (Muniverse initial supra-supra-Planck):
(24)
(By dividing the factor /and π/ square, the Planck units recovered without violating the Planck formula.)
Although the formulae (Eq.23 and Eq.24) can be simplified mathematically separately on the right and left or on both sides, physically this couldn’t be done. Due to the requirement of a secure Planck formula, symmetry and of the existing initial cosmos mass in the equation, simultaneous multiplication and division is obligatory on both sides.
The existence of the infra-infra-Planck energy level can be explained by two reasons. One is the symmetry of the supra-supra-Planck energy level mirror and the other is the displacement by two units due to the normalization of the supra-supra-Planck temperature down to the level of the Planck one. Along these lines, these equations also invariably include the original Planck temperature and the initial cosmos mass.
However, if the equation (Eq.23) is multiplied or divided separately more times (for example three or four) by the thermos-relativistic factor after the two unit shifts in the direction of the lower temperature values, there is no higher frequency and wavelength of electromagnetic radiation than gamma rays and the extremely low frequency (ELF).19
The initial energy of the universe and its decrease in time towards the present using the repetition of the ratio of angles and of the thermo-relativistic factor and π
According to mass-energy equivalence, by merging the individual components (m and c2) of the equation the combined formula (Eq.23) is modified as follows:
(25)
Transforming the equation to energy establishing the initial supra-Planck energy:
(26)
If the initial supra-Planck energy is multiplied by the factor in the equation, an initial supra-supra-Planck energy interpreted:
(27)
Divided by (950.0863∙π)2, it is 1.956114∙109J. The Planck energy is: EPlanck=mPlanck∙c2= 2.17647∙10-8kg∙ 8.987551787∙1016m2/s2 =1.956113∙109J.
The positive supra-Planck energy on the right side of the equation (Eq.13) originated from the initial mass of the cosmos is used to equalize the energy shortage generated by dividing by the factor one more time on both sides of the equation producing the infra-Planck energy (Eq.19). The potential difference between the energy surplus and of the energy deficit at the beginning of the universe would have shifted continuously parallel to the decrease in temperature of the cosmos expressed as a pressure wave. Especially at the end of the evolving process of the universe, energy shortage has also been created by dividing the factor of 950.0863 and π. Due to an expansion of space there is an energy deficit (3000K - 3K) in the aspect of the electromagnetic waves from the lighting of the cosmos towards the present /red light – microwave electromagnetic radiation (CMB).20
The energy decline of the cosmos from the initial supra-supra-Planck energy by the repetition of the angular ratio and of the thermo-relativistic factor and π
Regarding the development of the universe as a whole, the most important changes from the initial temperatures to the present day are the following:
(28)
Or:
(29)
The maximum initial supra-supra-Planck energy (Euniverse initial supra-supra-Planck energy) of the universe is the following:
(30)
Transforming this maximum initial supra-supra-Planck energy into temperature (Tuniverse initial supra-supra-Planck temperature):
(31)
The sub maximum initial supra-Planck (Euniverse initial supra-Planck energy) energy is as follows:
(32)
Transforming this sub maximum initial supra-Planck energy into temperature (Tuniverse initial supra-Planck temperature):
(33)
The initial Planck energy (Euniverse initial Planck energy) of the cosmos is in the center21
(34)
Transforming the initial Planck energy into temperature (Tuniverse initial Planck temperature) the result is the Planck temperature:
(35)
The initial infra-Planck energy (Euniverse initial infra-Planck energy) of the cosmos is:
(36)
Transforming the initial infra-Planck energy into temperature (Tuniverse initial infra-Planck temperature):
(37)
The minimum initial energy in the universe is the infra-infra-Planck energy (Euniverse initial infra-infra-Planck energy), which is as follows:
(38)
The lowest initial temperature value of the cosmos is the infra-infra-Planck one (Tuniverse initial infra-infra-Planck temperature):
(39)
The maximum primordial supra-supra-Planck energy1 (Euniverse primordial supra-supra-Planck energy1) of the cosmos is the following:
(40)
Transforming the maximum primordial supra-supra-Planck energy1 into temperature (Tuniverse initial infra-Planck temperature):
(41)
The maximum primordial supra-supra-Planck energy2 (Euniverse primordial supra-supra-Planck energy2) is:
(42)
Transforming the maximum primordial supra-supra-Planck energy2 into temperature (Tuniverse initial infra-Planck temperature):
(43)
The maximum primordial supra-supra-Planck frequency2 (νuniverse primordial supra-supra-Planck freq.2) is:
(44)
Finally, the maximum primordial supra-supra-Planck energy3 (Euniverse primordial supra-supra-Planck energy3) numerically is:
(45)
The maximum primordial supra-supra-Planck frequency3 (νuniverse primordial supra-supra-Planck freq.3) is:
Where h is the Planck constant (6.62607004·10-34 J·s), E is the energy (Euniverse primordial supra-supra-Planck energy3).
(46)
As c=ν∙λ and λ=c∙ν-1, this is in wavelength: 1.04791∙10-12m, which fits to the energy range of gamma electromagnetic wave radiation.22 (Since the energy of the electron is 8.187∙10-14 J, it is 2.3 electrons rest mass.) Multiply or divide it by π and 2∙π it is: 3.2921∙10-12m, 6.5842∙10-12m or 3.3356∙10-13m and 1.667∙10-13m respectively.
Transforming the maximum primordial supra-supra-Planck energy3 into temperature (Tuniverse primordial supra-supra-Planck temperature3):
(47)
The relevant temperature levels and temperature shifts of the developing cosmos performed by the usage of the angular ratio (α/2∙π) and of the factor (950.0863 and π) is shown in Figure 3.
Figure 4 shows a gradual decrease in the lowering temperature of the evolving universe based on the combined Einstein and Planck formulae from the very beginning to the present. In order to avoid violating the laws of physics, the extension of the temperature around the individual energy levels is required by introducing the so-called thermo-relativistic factor (π ∙ 950.0863). By definition, unchanged Planck temperatures, the initial supra-supra-Planck and infra-infra-Planck values can be obtained by multiplication and division by factors square. Because of the normalization of the supra-supra-Planck temperature resulting from the Einstein formula, the temperature values are shifted through two units to the lower values within each stair. Finally, in the fourth stage of the development of the cosmos, through the expansion of space, the entire spectrum of electromagnetic waves appears with two units shifted relative to each other. The light emitted by the universe is sparked from gamma rays, and HF is generated from the red light, from which ELF can be derived. At the intermediate energy levels, the CMB is generated from soft X-rays, the latter being the VLF equivalent.
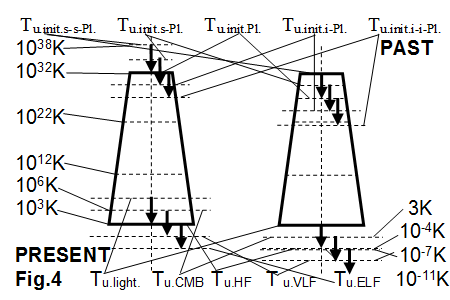
Figure 4 Gradual divisions and shifts in the universe's temperature.
Energy drop in the universe from the initial Planck level due to the repetition of the angular ratio and π
It is essential to know the four prominent energy levels that can be calculated from the central Planck temperature of the universe by repeatedly applying the ratio of angles.
The central initial Planck energy of the cosmos (Euniverse initial Planck energy)23 is:
(48)
At the first primordial stage of decreasing cosmos energy (Euniverse primordial Planck energy1) is as follows:
(49)
The second primordial energy grade of the universe (Euniverse primordial Planck energy2) is:
(50)
Since the energy of a photon is E=h∙ν, the frequency of the electromagnetic radiation created at the second primordial stage of the universe (νuniverse primordial Planck freq.2) is:
(51)
Where h is the Planck constant (6.62607004·10-34 J·s), ν is the frequency (νuniverse primordial Planck freq.2) and E is the energy (Euniverse primordial Planck energy2).
On the basis of the mass energy equivalence (E=m∙c2) and the energy of a photon (E=h∙ν) the mass of the particle created at the second primordial stage of the universe (muniverse primordial Planck2) is:
(52)
Where h is the Planck constant (6.62607004·10-34 J·s), ν is the frequency (νuniverse primordial Planck freq.2) and c is the speed of light (2.99792458·108 m·s-1).
Since the mass of a proton is 1.6726219∙10-27kg, this value corresponds to the mass of a quark-pair: 0.63881655∙10-27kg.24 Multiply it by π and 2∙π: 2.0069 u, the mass of a Deuteron nucleus, or 4.0138 u, the mass of Helium nucleus.25 This energy is close to the creation energy/mass of these elements in nuclear fusions (e.g. in the core of stars such as the Sun).
Finally, the third primordial energy stage of the cosmos (Euniverse primordial Planck energy3) is:
(53)
Converted to a frequency (νuniverse primordial Planck freq.3):
(54)
Since c=ν∙λ and λ=c∙ν-1, this is in wavelength =9.33578∙10-6m, the range of infrared electromagnetic waves.26 It is at a temperature (Tuniverse primordial Planck temperature3) occurring on the surface of the developing cosmos:
(55)
At this last stage of development, the surface of the universe glows a faint red color. However, multiplying this value by π and 2·π the temperatures are 4841.65 K and 9683.3 K respectively. In this situation, the temperature and color are approximately equal to light orange K-type stars or white A-type stars in terms of surface color and temperature.27 At this temperature, the universe suddenly begins to emit light and becomes transparent as space expands.
The energy decrease of the cosmos from the initial infra-infra-Planck energy considering the repetition of the angular ratio, thermo-relativistic factor and π
The minimal initial temperature of the universe is the infra-infra-Planck energy. From this point there is also a four stage gradual decrease in the temperature in the cosmos.
(56)
Or:
(57)
The minimum initial infra-infra-Planck energy (Euniverse initial infra-infra-Planck energy) numerically, is:
(58)
The first primordial energy stage of the universe at the primordial infra-Planck1 (Euniverse primordial infra-infra-Planck energy1) when the ratio of angles is used once:
(59)
Transforming it to a frequency (νuniverse primordial infra-infra-Planck freq.1):
(60)
Where h is the Planck constant (6.62607004·10-34 J·s), ν is the frequency (νuniverse primordial infra-infra-Planck freq.1) and E the energy (Euniverse primordial infra-infra-Planck energy1).
Which is in wavelength (as λ=c/ν): 4.086∙10-18m. Since E=h∙ν and E=m∙c2, the mass (muniverse primordial infra-infra-Planck1) is:
(61)
Where h is the Planck constant (6.62607004·10-34 J·s), ν is the frequency (νuniverse primordial infra-infra-Planck freq.1) and c is the speed of light (2.99792458·108 m·s-1).
Since the mass of a proton is 1.6726219∙10-27kg, it correlates with a mass of 323.6233 protons. This is the range of the interchanges of the bosons, or the field of the formation of their pairs. Divide this by 2 and 2∙π for a mass of 161.8 and 51.5 protons respectively, which is in the mass range of heavy bosons (e.g. top quark, Higgs, Z and W)28
However, multiply it by π and 2∙π the mass will be 1016.69 and 2033.38 protons mass respectively, which corresponds to the upper energy limit of Higgs field.
The temperature value of the universe at the first stage of the primordial infra-infra-Planck1 (Tuniverse primordial infra-infra-Planck temperature1) is as follows:
(62)
The energy of the primordial universe at the second stage of the primordial infra-infra-Planck2 (Euniverse primordial infra-infra-Planck energy2) when the ratio of angles is squared:
(63)
This is, as a frequency (νuniverse primordial infra-infra-Planck freq.2):
(64)
Where h is the Planck constant (6.62607004·10-34 J·s) and E is the energy (Euniverse primordial infra-infra-Planck energy2). 1 Joule= 1kg m2∙s-2
(65)
As c=λ∙ν and λ=c/ν =1.8428∙10-8m = 18.428 nm. Divide this by 2∙π and π and the wavelengths are 2.933 nm and 5.865 nm respectively, but multiply it by π and 2∙π and they are 57.893 nm and 115.786 nm respectively. These are the wavelengths of soft X-rays and extreme ultraviolet electromagnetic radiation29 respectively.
The temperature value of the universe at the second stage of the primordial infra-infra-Planck2 (Tuniverse primordial infra-infra-Planck temperature2) is as follows:
The energy of the cosmos at the third stage of the primordial infra-Planck3 (Tuniverse primordial infra-Planck energy3), when the angles ratio is cubed:
(66)
This as a frequency is (νuniverse primordial infra-infra-Planck freq.3):
(67)
Which corresponds to the initial high frequency radio electromagnetic wave (HF).30 Since c=λ∙ν and λ=c/ν it is 0.8317∙102 m, or 83.17 m as a wavelength. Multiply it by π and 2·π and it is 261.288 m and 522.576 m respectively. Divide it by π and 2∙π and the wavelengths are 26.473 m and 13.237 m respectively.
The temperature value (Tuniverse primordial infra-infra-Planck temperature3) by the ratio pair is as follows:
(68)
Since the initial supra-supra-Planck energy has shifted by the factor squared, recovering the original initial Planck one by two units the infra-infra-Planck primordial3 energy should also be pushed to the lower values.
(69)
Converted to frequency (νuniverse primordial infra-infra-Planck freq.3, shifted 2times) it is:
(70)
This is in the energy range of extremely low frequency electromagnetic waves (ELF).31 As λ=c/ν, the wavelength is: 7.411432∙108m or 741143.2 km (divide it by π and 2∙π: 235870 km and 117930 km respectively).
Given that electromagnetic waves with a lower frequency than this value are unknown in the macrocosm, this is a limit, which closes physics in this regard.
The conversion number between electron volt and temperature is:
(71)
The temperature of the primordial cosmos at the third stage of the infra-Planck primordial3 is (Tuniverse primordial infra-infra-Planck temperature3):
(72)
In summary, the three temperature values (supra-supra-Planck, Planck and infra-infra-Planck) thus shift to each other in the fourth stage of development of the cosmos when gamma, red and HF photons emerge. By restoring the Planck temperature with two units, the CMB is the VLF and the HF is the ELF.
Intermediate temperature levels in the gradual reduction of the initial Planck temperature of the universe according to the repetition of the angular ratio, thermo-relativistic factor and π
Utilizing the ratio of angles (α/2π) by one to three times, multiplying it by itself, or raising it to a square and cube, the initial Planck temperature of the cosmos gradually decreases to the present value. Since the initial Planck temperature (Tuniverse initial Planck temperature) is:
(73)
At the first stage of the primordial universe (Tuniverse primordial Planck temperature1), the temperature is higher than the energy of the quark-gluon plasma state of matter:
(74)
When using the ratio of angles once, the primordial cosmos temperature is as follows:
(75)
Transforming it into energy (3.139∙1022K /11604.522 = 2.7∙1018eV): 2.7 EeV.
Considering the temperature value of Eq.74 and multiplying it by 950.0863 and π, it is 9.36923∙1025 K (Tuniverse primordial supra-Planck temperature1), transformed into energy (9.36923∙1025K/11604.5): 8.0738∙ 1021eV, however multiply it by π and 2∙π: 2.536∙1026eV and 5.073∙1026eV respectively. Dividing this value (9.36923∙1025eV) by π and 2∙π, the results are as follows: 2.982∙1025eV and 1.491∙1025eV respectively.
By calculating from the initial Planck temperature of the universe one times derivative value (Eq.74) and dividing it by 950.0863 and π (Tuniverse primordial infra-Planck temperature1), it is 3.308∙1019 K, which in energy is (3.3∙1019K/11604.5=2.85 1015eV): 2.85 PeV, however, multiply it by 2∙π and π: 17.907 PeV and 8.9535 PeV respectively. Divide it by π and 2∙π: 0,907 PeV and 453.6 TeV respectively.
The twice-reduced initial Planck temperature of the cosmos (Tuniverse primordial Planck temperature2) by using the ratio of angles (α/2π) two times is at the second primordial infra-Planck2 temperature:
(76)
Numerically:
(77)
In energy, this is (6.955452∙1012K/11604.505=5.993751564∙108eV) 599.33 MeV (approximately the energy of a quark pair). Multiply it by π and 2∙π: 1.882992588 GeV and 3.765985176 GeV respectively. Since 1 u is 0.938272081 GeV, they are: 2.00687266 u (Deuteron nucleus) and 4.013745322 u (Helium nucleus). This energy level is close to the creation energy/mass of these elements in nuclear fusions. Divide it by π and 2∙π: 190.787 MeV and 95.393 MeV respectively, which is roughly the energy of a muon. At this temperature value (Eq.77) is created the cosmic rays.32
However, consider the initial Planck temperature of the universe derived twice (Eq.76) and multiplied by 950.0863 and π; this is 2.076∙1016 K (Tuniverse primordial supra-Planck temperature2), which in energy is (2.076∙1016 K/11604.5=1.7889 1012eV): 1.8 TeV, similar to high energy collisions in cyclotrons (lead-lead ion).33 However, multiply it by π and 2∙π: 5.654 TeV and 11.31 TeV respectively, similar to high energy collisions in cyclotrons (proton-proton).34 Divide it by π and 2∙π, it is: 0.5729 TeV and 286.47 GeV respectively.
On the other hand from the initial Planck temperature derived twice, divide it by 950.0863 and π and it is 2.33∙109K (Tuniverse primordial infra-Planck temperature2), which in energy is (2.33∙109K/11604.5 =2.0081∙105eV): 0.2 MeV (the energy level of gamma rays). Multiply it by π and 2∙π: 0.628 MeV and 1.256 MeV respectively, the energy level of 1-2 electrons. Divide it by π and 2∙π: 63.66 keV and 31.83 keV respectively, which is roughly the energy level of X-rays.
Ultimately, at the third primordial temperature stage (Tuniverse primordial Planck temperature3) of the cosmos and with the mass of the initial universe multiplied by the value of the angular ratio cubed (α/2π)3 the temperature will be as follows:
(78)
The combined equation detailed (Eq.6 and Eq.8):
(79)
The thrice derivative primordial temperature numerically:
(80)
Considering initial Planck temperature of the universe and its triple derivative value (Eq.78) and multiplying it by 950.0863 and π, the temperature is as follows: 4.5999∙106 K (Tuniverse primordial supra-Planck temperature3). Transform it into energy (4.6∙106K/11604.5): 3.9639∙102eV. This is roughly the same as that of soft X-ray radiation energy. Multiply it (4.6∙106 K) by π and 2π and it is 14.45∙106K and 2.89∙107K. This value is close to the temperature of the core of a star.35 However, divide it by π and 2π: 1.464∙106 K and 0.732∙106 K respectively. These are at the energy of 126.17eV and 63.85eV respectively, which is the energy of extreme ultraviolet radiation.
Since the initial supra-supra-Planck energy has shifted by the factor squared to the initial Planck one (under the fourth Chapter) the supra-Planck temperature should also be pushed to the lower values by two units to the level of the infra-Planck one. This is also the same in the case of the fourth temperature stage of the cosmos or its third primordial temperature stage (Tuniverse primordial infra-Planck temperature3) when soft X-ray radiation transforms into microwave electromagnetic radiation using the factor for two times or is squared:
(81)
Multiplied by π and 2π, it is 1.622 K and 3.244 K respectively. These values correspond to the maximum temperature value of cosmic microwave background electromagnetic radiation (CMB).36 However, if the formula is mathematically simplified (Eq.14), which means the formula, is extended once in the direction of lower temperatures:
(82)
In this way the same numbers eliminate each other in the equation, so the values are reduced and CMB is created from the red range of visible light throughout the inflation of space caused by dividing by the factor. In this sense, there is no difference between the individual energy levels since there is apparently only one unit of shift between them.
Alternatively, but with a similar result, shifting to normalize the initial supra-Planck temperature of the cosmos by the factor once, it will be the initial Planck one. The initial Planck temperature of the universe will be the initial infra-Planck temperature of the cosmos. Therefore, in the last stage of the universe the temperature (Tuniverse primordial infra-Planck temperature3, or what is equal to: Tuniverse primordial Planck temperature3. shifted 1 times) will be the following:
(83)
Numerically:
(84)
Finally, the validity of the angle ratio (α/2∙π, 2∙π/α) determined on the basis of the Einstein equation from the side of the Planck formula, can be elucidated. If the ratio of angles was not as much as calculated on the basis of equation 3, the most important physical parameters could not be determined. From the temperature or energy of the initial cosmos, the values in each step would be different in a positive or negative direction. Thus, the mass of quark-pair, proton and helium nucleus, the distribution of microwave background radiation or the energy range of the Higgs field would also be shifted. We would not get the well-known quantum mechanical energy ranges. On the contrary, if the ratio of angles was not equal to equation 3, neither the age of the universe nor the Earth's radius would correspond to the real one. Along these lines, it can be stated that the ratio of angles independently from each other in both cases can be applicable. The universal usability of the ratio on quantum mechanical and gravitational sides confirms the introduction of a general description of physical phenomena.
Reversibility of the cosmic temperature drop by utilizing the repetition of the angular ratio and of the thermo-relativistic factor
Consideration of the reversibility of the changes in the temperature of the cosmos, in the case of mirror symmetry, out of six units a total of four units of shortening occur back in time at every fourth stage of the universe. In the end, at the fourth stage is happened to the direction of the ELF towards the lightening of the cosmos.
Decreases in the initial temperature of the universe through the introduction of the thermo-relativistic factor and the shifts in the normalization of temperature in this model also points to the direction of entropy growth. However, by checking these results from the opposite direction by adding energy to the system, it is possible to return to the beginning of the universe (initial Planck temperature) (Eq.17). In this case however, a reverse offset should be used by the ratio of the angles (2π/α) and by the thermo-relativistic factor (π∙950.0863) towards higher temperatures.
(85)
Otherwise:
(86)
Considering the recurring property of processes occurring in the cosmos and utilizing the ratio of the angles (2π/α) up to three times, the initial Planck temperature of the universe is:
(87)
Dividing it by the factor and π we can obtain the initial infra-Planck temperature of the cosmos:
(88)
Numerically:
(89)
Since:
(90)
The temperature is:
(91)
Numerically detailed:
(92)
Moreover:
(93)
However, multiply it by the thermo-relativistic factor 950.0863 and π and we have back the definitive Planck temperature serving the thermal state of the initial universe:
(94)
Finally, according to energy levels and shifts the division of physics and the representation of this triple, tree-shaped division of it are shown in Figure 5.
Figure 5 Triple, tree-shaped physics structure.
Determination of the total mass of the present universe due to repetitive multiplication of the ratio of the angles
On the basis of the Einstein equation (see Chapter 2 and Formula 6.b) it is possible to determine the total mass of the universe by utilizing the ratio of the angles (2π/α) six times. Six times is obligatory, because symmetrically up and down from the Earth we use the ratio three to three times to determine the mass of the initial and present cosmos. In this way, the projected mass of the cosmos is:
(95)
Numerically:
(96)
Moreover:
(97)
This mass falls within the order of magnitude of the total mass of the cosmos and is almost identical to it.37
The modifying effect of the thermo-relativistic factor on the masses at higher levels in the cosmos
As in the case of determination of the initial mass of the cosmos, because of the symmetry the total mass of the cosmos could also be divided by the square of the thermos-relativistic factor. In this case the mass is:
(98)
However multiply it by the thermo-relativistic factor to obtain the actual, observable mass of the cosmos37:
(99)
If this mass is pushed down by two units, the result is approximately equal to the mass of a galaxy such as the Milky Way38:
(100)
Starting from the infra-infra Planck value and applying a double downward shift, the mass of the Milky Way Galaxy is:
(101)
(Multiplied it by π∙π, it is: 6.82∙1040 kg.)
After the smaller level shifts caused by the thermo-relativistic factor and due to the normalization to the Planck mass, applying the large temperature jump created in proportion to the angles (Eq.101 multiplied by 0.2215∙10-9), the amount of mass reduction is 1.5323∙1030 kg. Shifting this mass value down by another 2 (due to the square of the thermo-relativistic factor) level, the mass is 1.71943∙1023 kg.
In summary, by dividing the thermo-relativistic factor once there will be symmetry between today's total and actual mass of the universe as well as between the initial cosmos mass and the Planck mass. Both of the two mass surpluses fall out and the actual known mass of the cosmos and the Planck mass remain. In addition, a certain range can be determined, in which the mass of a galaxy (such as the Milky Way) fits, or the mass of an average-sized Sun or small planet can be obtained.





