
Technical Paper Volume 1 Issue 1
Stochastic thermo-elastic stability analysis of laminated composite plates resting on elastic foundation under non-uniform temperature distribution
Rajesh Kumar
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

School of Mechanical Engineering, Jimma University, Ethiopia
Correspondence: Rajesh Kumar, School of Mechanical Engineering, JIT, Jimma University, P.O. Box-378, Jimma, Ethiopia, Tel +251909462675
Received: May 11, 2017 | Published: June 2, 2017
Citation: Kumar R. Stochastic thermo-elastic stability analysis of laminated composite plates resting on elastic foundation under non-uniform temperature distribution. Aeron Aero Open Access J. 2017;1(1):10-29. DOI: 10.15406/aaoaj.2017.01.00003
Download PDF
Abstract
In this paper the stochastic thermo-elastic stability of laminated composite plates resting on elastic foundations under non-uniform temperature distribution is analyzed. The mathematical model is based on higher order shear deformation theory [HSDT] and von-Karman nonlinear kinematics is presented. A C0 nonlinear finite element method combined with direct iterative method in conjunction with mean centered first order Tailor series based perturbation technique is employed for the Eigen value problem in random environment to derive the second order statistics (mean and the standard deviation) of the thermal post buckling load under non-uniform temperature distribution. Typical numerical results for stacking sequence, no of plies, plate thickness ratios, amplitude ratios, aspect ratios, boundary conditions and temperature change are generated. Numerical results have been compared with available results in literatures and with independent Monte Carlo simulation [MCS].
Keywords: non uniform temperature distribution, thermal post buckling temperature, composite plates, system properties, elastic foundation, perturbation technique
Abbreviations
MCS, monte carlo simulation; HSDT, higher order shear deformation theory; FEM, finite element method; SFEM, stochastic finite element method
Introduction
Composite structures have inherent dispersion in system properties due to lack of strict quality control and the characteristics of the large parameters involved with the manufacturing and fabrication process. The transverse shear deformation effects are considerably pronounced in composite laminates and must be incorporated while studying the buckling and post-buckling behavior of laminates under in-plane thermally induced loading. Thermal buckling of geometrically nonlinear plate structures is one of the major design criteria for an efficient and optimal usage of materials and then buckling loads are of extremely inherent in the design and developments of high performance composite component for stability point of view. The variation in the system properties of the composite materials necessitates the inclusion of randomness of system properties in the analysis; otherwise predicted response may differ significantly rendering the structures unsafe. For reliable and safe design especially for sensitive engineering applications in thermal environments, accurate prediction of system behavior of composite structures in the present of uncertainties in the system properties fevers a probabilistic analysis approach by modeling their properties as basic random variables.
A considerable amount of literature exists on the thermal buckling and post-buckling of laminated composite plates supported with and without elastic foundation subjected to non-uniform temperature with deterministic system properties. Notably among them are Chen et al.1 Shen,2 Shen,3 Shen and Zhu,4 Shen and Lin,5 Shen6 and Shen.7 The research based on the assumption of complete determinacy of the structural parameters, the inherent randomness in the structures is neglected. To well define the original problem for better understanding and characterization of actual behavior of laminated composite materials for sensitive applications and reliable design, it is obviously of prime importance that inherent randomness in the system parameters to be incorporated in the analysis. However, the analysis of the structures with randomness in system properties is not developed to the some extent. The deterministic analysis is not sufficient to predict system behavior due to various system uncertainties as it gives only mean response and misses the deviation caused by the system parameters.
A considerable amount of literature exists on the initial thermal buckling and post buckling of laminated composite plates with temperature dependent and temperature independent thermo-elastic material properties.8-14
However, the analysis of the structures with randomness in system properties is not developed to the same extent.15-18 Nieuwenhof & Coyette19 investigated sensitivity analysis to the random parameters such as material and shape parameters using SFEM and independent MCS. Stefanou & Papadrakakis,20 Singh et al.21,22 & Onkar et al.25,26 have used a generalized layer wise stochastic finite element formulation for the buckling analysis of homogeneous and laminated plates with and without centrally loaded circular cutouts having random material properties using FOPT in conjunction with HSDT.25,27
The contribution of this paper is the investigation of HSDT based on C0 linear and nonlinear FEM in conjunction with mean centered FOPT, to compute the second order statistics of thermal post buckling temperature of laminated composite plates resting on elastic foundation involving randomness in system parameters such as material properties, thermal expansion coefficients, foundation parameters and lamina plate thickness are modeled as independent random variables (RVs) assuming non-uniform tent like temperature and uniform constant temperature and a linearly varying transverse temperature distribution across the thickness under uni-axial and biaxial edge compression over entire surface of the plate. This approach is valid for system properties with small random dispersion compared with the mean values. The condition satisfies by most of the engineering materials and fortunately composites fall in these categories.
Mathematical formulation
A rectangular laminated composite plate of length a, width b, and total thickness h, defined in (X, Y, Z) system with x- and -y axes located in the middle plane and its origin placed at the corner of the plate with consisting of N orthotropic layers with the fiber orientation of
. Let
be the displacement parallel to the (X, Y, Z) respectively as shown in Figure 1. The thickness coordinate Z of the top and bottom surfaces of any
layer are denoted by
and
respectively. The fiber of the
layer is oriented with angle
to the X- axes. The plate is resting on elastic foundation excluding any separation during the process of deformation as shown in Figure 1. The load displacement relationship between the plate and the supporting foundation can be described by two-parameter model of the Pasternak-type as
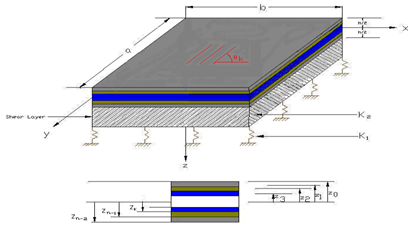
Figure 1 Geometry of laminated composite plate resting on elastic foundation.
with
. (1)
Where, P is the foundation reaction per unit area, and
is the Laplace differential operator, K1 and K2 are the Winkler and Pasternak Foundation stiffness [12], respectively, and “w” is the transverse displacement of the plate. This model is called Winkler type when
.
Displacement Field Model
In the present study the Reddy’s higher order shear deformation theory has been employed.16 The difficulty and complexity associated with making a choice of C1 continuity is inherent generality and has led to the development of nonconforming approaches. The displacement field model, after incorporating zero transverse shear stress conditions at the top and the bottom of the plate, is slightly modified, so that a C0 continuous element would be sufficient. The C0 continuity permits easy so parameters finite element formulation and consequently can be applied for non rectangular geometry is as well. In modified form, the derivatives of out-of-plane displacement are themselves considered as separate degree of freedom (DOFs). Thus five DOFs withC1 continuity are transformed into seven DOFs due to conformity with HSDT. In this change artificial constraints are imposed which can be enforced valiantly through the penalty approach, in ordered to satisfy the imposed.22,26
The displacement field along the x, y, and z directions for an arbitrary composite laminated plate is now written as
(2)
Where u, v, and w are corresponding displacements of a point on the mid plane.
and
are the rotations of normal to the mid plane about the y-axis and x-axis respectively. with
and
;
with
.
The displacement vector for the modified C0 continuous model can be written as
(3)
With
and
Where, comma (,) denotes partial differentiation.
Strain Displacement Relations
The strain-displacements relations are obtained by using the small deformation theory with linear elasticity based on HSDT are expressed.10
Stress–Strain Relation
The constitutive relationship between stress resultants and corresponding strains of laminated composite plate accounting for thermal effect can be written as10,22,27
or.
(4)
with
where,
,
and
are transformed stiffness matrix,, stress and strain vectors of the
lamina, respectively and
are the thermal expansion coefficients along x, y, z, direction, respectively which can be obtained from the thermal coefficients in the longitudinal
and transverse
directions of the fibers using transformation matrix.
is the uniform temperature [UT] and combined uniform temperature with linearly varying transverse temperature [TT] rise.
is the non-uniform tent-like temperature distribution. The non-uniform tent like temperature rise is assumed to be
(5)
where T0 is the uniform temperature rise, and T1 is the temperature gradient, as shown in Figure 2. The constitutive relationship between stress resultants per unit length and mid-plain strains and curvatures can be written in matrix form.
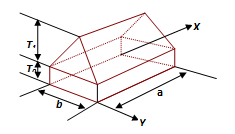
Figure 2 Geometry of non-uniform tent-like temperature distribution.
(i, j=1, 2, 6)
(6)
(j=4, 5)
(7)
Where
etc., are the plate stiffness’s defined in appendix . Thermal stress resultants
and
are calculated by
(8)
Strain Energy of the Plate
The potential energy of the laminated composite plates can be expressed as
(9)
Potential Energy due to Thermal Stresses
Due to uniform change in temperature, non-uniform tent like temperature distribution, pre-buckling stresses in the plate are generated. These stress resultants are the reason for the buckling. The potential energy due to the in plane thermal stress resultants is expressed as
(10)
Where,
are in plane applied thermal compressive stress resultants per unit length.
Strain energy due to foundation
The strain energy
due to elastic foundation having foundation layers can be written as:
(11)
Finite element model
Strain energy of the plate element
In the present study a C0 nine-noded is oparametric finite element with 7 DOFs per node is employed. For this type of element, the displacement vector and the element geometry are expressed as
and
(12)
Where
is the interpolation function for the
node,
is the vector of unknown displacements for the ith node, NN is the number of nodes per element and xi and yi are Cartesian Coordinate of the
node.
Total potential energy which can be expressed as
(13)
With
Where global bending stiffness matrix
shear stiffness matrix
foundation stiffness matrix
, global displacement vector {q} and thermal load vector [F] are defined in the appendix.
Thermal buckling analysis
Using finite element model Eq. (13), Eq. (11) after summing over the entire element can be written as
(14)
where,
and
are defined as the thermal buckling load parameters and the global geometric stiffness matrix, respectively.
Foundation analysis
Using finite element model
(15)
Where,
are the elemental linear foundation stiffness matrixes for the eth element.
Adopting Gauss quadrature integration numerical rule, the element linear and non-linear stiffness matrices, foundation stiffness matrix and geometric stiffness matrix respectively can be obtained by transforming expression in x, y coordinate system to natural coordinate system
.
Governing equations
The governing equation for thermal buckling of laminated composite plate can be derived using Variational principle, which is generalization of the principle of virtual displacement. For the prebuckling analysis, the first variation of total potential energy must be zero. By using Eq. 13 and Eq. 15
(16)
Eq.16. can be rewritten as
Where
For the critical buckling state corresponding to the neutral equilibrium condition, the second variation of total potential energy
must be zero. Following this conditions, ones obtains as standard eigenvalue problem
(17)
The stiffness matrix [K], foundation stiffness matrix [Kf] and geometric stiffness matrix [Kg] are random in nature, being dependent on the system geometric and thermo-elastic properties. Therefore the eigenvalues and eigenvectors also become random. The (Eq. 17) can be solved with the help probabilistic FEM in conjunction with perturbation technique or Monte Carlo simulation (MCS) to compute the mean and variance of the thermal post buckling load.
Solution technique: random thermal post buckling problem
Direct iterative method in conjunction with perturbation technique
Steps for the direct iterative technique
The nonlinear eigenvalue problem as given in (eq. 15), is solved by employing a direct iterative method in conjunction with the mean centered first order perturbation technique assuming that the random changes in eigenvector during iterations does not affect the nonlinear stiffness matrices with the following steps.
- By setting amplitude to zero, the random linear eigen value problem
is obtained from the (Eq. 15), by assuming that the system vibrates in its principal mode. Then the random linear eigenvalue problem is broken up into zeroth and first order equations using perturbation technique by neglecting higher order equations. The zeroth order linear eigenvalue problem is solved by normal Eigen solution procedure to obtain the linear critical load parameters
and the linear Eigen vector
. The first order perturbation equation is used to obtain the standard deviation of the thermal post buckling which is presented in next sub-section 6. 2. of perturbation technique.
- For a specified maximum deflection C at a center of the plate, the linear normalized eigenvector is scaled up by C times, so that resultant vector will have a displacement C at the maximum deflection point.
- Using the scale-up eigenvector, the nonlinear terms in the stiffness matrix [K] can be obtained. The problem may now be treated as linear eigenvalue problem with a new updated stiffness matrix. The random eigenvalue problem can again be broken up into zeroth and first order equation using perturbation technique. The deterministic zeroth order can be used to obtain nonlinear critical load
and eigenvector
and the random first order equations can be used to obtain the standard deviation (SD) of the Eigen solutions using the first order perturbation technique as presented in the next section.
- Steps (ii)-(iii) are repeated by replacing
by
in the step (ii) to obtain the converged mean and standard deviation of the nonlinear critical buckling load lnl to a prescribed accuracy (≈10-3)
- Steps (i) to (iv) are repeated for various value of C.
Solution technique: perturbation technique
In the present analysis, the lamina material properties, thermal expansion coefficients and the geometric properties are treated as independent random variables (RVs). In general, without any loss of generality any arbitrary random variable can be represented as the sum of its mean and zero mean random part, denoted by superscripts ‘d’ and ‘r’, respectively.21
(18)
Taylor’s series keeping the first order terms and neglecting the second and higher order terms, collecting same order of the magnitude term, one obtains as37
Zeroth order:
(19)
First order:
(20)
Eq. 19 is the deterministic equation relating to the mean eigenvalues and corresponding mean eigenvectors, which can be determined by conventional eigensolution procedures (eq. 20) is the random equation, defining the stochastic nature of the thermal buckling which cannot be solved using conventional method. For this a further analysis is required.
(21)
, (22)
Where
is the Kronecker delta.
The eigenvectors, which meet orthogonality, conditions after being properly, normalized form a complete orthonormal set and any vector in the space can be expressed as their linear combination of these eigenvectors. Hence, the ith random part of the eigenvectors can be expressed as
,
,
, i=1, 2, …. , p
(23)
Where
’s are small random coefficients to be determined.
Substituting eq. 23 in eq. 20, premultiplying, the first by
and second by
,
respectively and making use of orthogonality (eq. 22), one obtains as
(24)
,
(25)
Substituting eq. 25 into eq. 23, we obtain
,
(26)
For the present case
,
,
and
are random because of random geometric and material properties. Let
denote random variables (system properties).
The FEM in conjunction with FOPT has been found to be accurate and efficient [31-33]. According to this method, the random variables are expressed by Taylor’s series expansion. The expression only up to the first-order terms and neglecting the second- and higher-order terms are
(27)
Where (, j) denotes the partial differentiation with respect to
.
On substitution of eq. 27 into eq. 24, one obtain as
(28)
The variance of the eigenvalues can now be expressed as [21]
(29)
Where
is the covariance between
and
. The standard deviation (SD) is obtained by the square root of the variance.
Numerical examples and discussion
In present work a program in mat lab has been developed to find out Second-order statistics of the thermal buckling and thermal post buckling temperature for laminated composite plates subjected to uniform temperature (U.T.) distribution and combined uniform temperature with linearly varying temperature along transverse direction (T. T) and non-uniform tent like temperature distribution with random system properties. A nine noded Lagrange isoparamatric element with 63 DOFs per element for the present HSDT model has been used for discretizing the laminate and (5×5) mesh has been used throughout the study. The mean and standard deviation of the thermal buckling temperature are obtained considering the random material input variables, thermal expansion coefficients, foundation parameters and lamina plate thickness taking combined as well as separately as basic random variables (RVs) as stated earlier. However, the results are only presented taking SD/mean of the system property equal to 0.10 as the nature of the SD (Standard deviation) variation is linear and passing through the origin. However the obtained results revealed that the stochastic approach would be valid upto SD/mean=0.20 [32]. Moreover, the presented results would be sufficient to extrapolate the results for other SD/mean value keeping in mind the limitation of the FOPT. The basic random variables such as E1, E2, G12, G13, G23, υ12, α1, α2, k1, k2, and h are sequenced and defined as
The following dimensionless thermal buckling temperature, foundation parameters and post buckling temperature have been used in this study.
;
; and
where
,
, T, k1 and k2 are the dimensional mean thermal buckling load, the initial thermal expansion coefficient and the initial guessed temperature, Dimensionless Winkler and Pasternak foundation parameters, and
,
and T, are dimensionless mean thermal post buckling temperature, initial thermal expansion coefficient and the initial guessed dimensionless temperature (980) applied in x and y direction respectively. In the present study various combination of edge support conditions such as all edges simply support conditions (SSSS) (S1 and S2), Clamped conditions (CCCC) and simply support and clamped condition (CSCS) have been used for the analysis .
The following relative numerical values and relationship between the mean valves of the material properties and thermal expansion coefficients for graphite/epoxy composite have been used in the present investigation.
The plate geometry supported with elastic foundation used is characterized by various aspect ratios, side to thickness ratios, lamination scheme and number of layers.
The plate geometry used is characterized by aspect ratios (a/b) = 1 and 2, side to thickness ratios (a/h) = 20, 30, 40, 50, 60, 80 and 100. The only exception is the Poisson’s ratio, which can reasonably be assumed as constant deterministic due to weakly dependency on temperature change. The relation among elastic constants for the plate having all plies of equal thickness and temperature dependent material properties is given as [12,13]. For the temperature independent material properties (TID)
quantities are equal to zero. The material properties for non-uniform tent like and parabolic distribution are used as:
Validation study
Validation for mean buckling temperature for composite plate
The dimensionless mean thermal post buckling loads
of angle-ply
square laminated composite plate, temperature independent (TID) and temperature dependent (TD) material properties, without foundations (k1=0, k2=0), subjected to uniform constant temperature rise (U.T),
- linear solution , plate thickness ratio (a/h)=30, amplitude ratios
with simply supported (S2) boundary conditions are compared for validation in Figure 4 with the results of available literature given in Shen [8]. Clearly, it is seen that the present results are in good agreement. The difference of the two results is due to the HSDT employed in present result whereas semi analytical approach used by Shen [12].
The dimensionless mean thermal post buckling load of angle-ply
square laminated composite thin plate with temperature-dependent thermo material properties and subjected to uniform temperature rise. Amplitude ratio
, random input variables
where E111 is assumed to be function of temperature, plate thickness ratio (a/h) =100. Material properties are
with simple support SSSS (S1) boundary conditions are compared for validation in Figure 5. It is observed the present results are good in agreements and validated with semi analytical approach by Shen [12].
The present theoretical model is validated by comparing the mean dimensionless results with those available in literature [9] (Figure 3). Compares the results obtained from present FEM with existing results for a two layer and four layer anti-symmetric
square laminate, (a/h=20), for all edges CCCC supported boundary condition respectively. The results obtained HSDT are excellent agreement with FSDT results of literature [9].
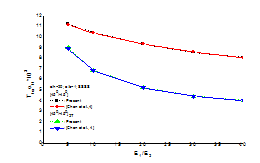
Figure 3 Validation study for analytical results.

Figure 4 Validation study for analytical results.
Thermal post buckling response of angle-ply
square laminated composite thin plates with amplitude ratios having temperature-dependent thermo-elastic properties and subjected to a uniform temperature rise with simple support SSSS (S1). Where E111 is assumed to be function of temperature and
respectively, b/h=100, material properties are
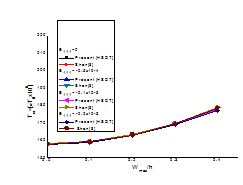
Figure 5 Validation study for analytical results.
The post buckling temperature results are compared in Figure 6 with9 of FSDT results and13 of HSDT results.
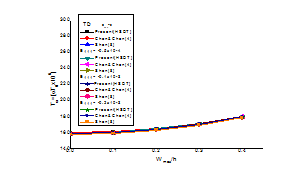
Figure 6 Validation study for analytical results.
Thermal post buckling response of angle-ply
square laminated composite thin plates with amplitude ratios having temperature-dependent thermo-elastic properties and subjected to a uniform temperature rise with simple support SSSS (S2). Where E111 is assumed to be function of temperature and
respectively, b/h=100, material properties are
The post buckling temperature results are compared in (Figure 7) with Shen [13] of HSDT results. To validate the present method, the results for thermal post buckling of a simply supported thin (b/h=20) square plate under non-uniform loading and resting on two parameters elastic foundation are listed in Figure 8 and compared with these given by Shen [3]. Clearly results obtained from present HSDT approach are in good agreement with the solution obtained from Riser midline plate theory approach.
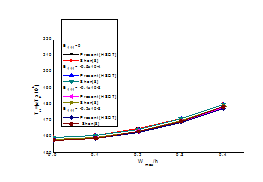
Figure 7 Validation study for analytical results.
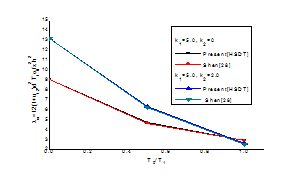
Figure 8 Validation study for analytical results.
Figure 9 examines the thermal post buckling load of 4-ply anti-symmetric angle-ply
laminated composite square plate under non-uniform temperature distribution, b/h=10 with simply supported S2 boundary conditions and are compared with those of Shen [4] and Shen & Lin [5]. Clearly, the results obtained from the present method accord quite well with the existing ones.
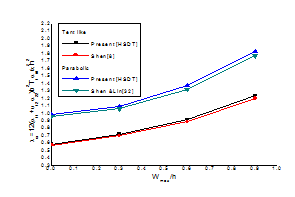
Figure 9 Validation study for analytical results.
Validation Study for random material and geometric properties
The present results of thermal buckling and post buckling load of laminated composite plates obtained from present FOPT approach have been compared and validated with an independent MCS approach.
Validation result for random material and geometric properties (TID)
Figure 10 & 11 plot the normalized standard deviation, SD/mean (i.e. the ratio of the standard deviation (SD) to the mean value), of the thermal buckling load versus the SD/mean of the random material constant and geometric parameter for an all simply supported cross-ply [00/900] and angle-ply [450/-450] square laminated composite plate subjected to non-uniform tent-like temperature distribution changing from 0 to 20% respectively. It is assumed that one of the material property (i.e., E22) and lamina plate thickness h changing at a time keeping other as a deterministic, with their mean values. The dashed line is the present [FOPT] result that is obtained by using FOPT and the solid line is independent MCS approach. For the MCS approach, the samples are generated using Mat Lab to fit the desired mean and SD. The number of samples used for MCS approach is 10,000 for material properties and 12,000 for lamina plate thickness based on satisfactory convergence of the results. The normal distribution has been assumed for random number generations in MCS.
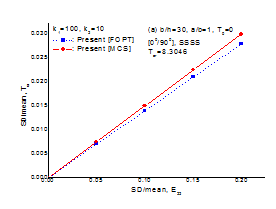
Figure 10 Validation of results the present FOPT approach from the independent MCS approach.
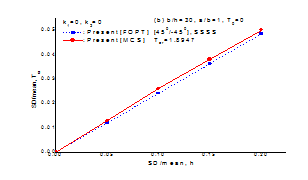
Figure 11 Validation of results the present FOPT approach from the independent MCS approach.
Validation result for random material and geometric properties (TD)
Figure 12,13 plots the normalized standard deviation, SD (i.e. the ratio of the standard deviation (SD) to the mean value), of thermal post buckling load versus the SD to the mean value of the random material property (E11) and geometric properties such as plate thickness (h) for an all simply supported (S2) angle-ply and cross-ply anti-symmetric [00/900] square laminated composite plate a/h=20 with amplitude ratio (Wmax/h=0.2) and uniform temperature distribution changing from 0 to 20% subjected to biaxial compression with TD thermo-material properties. It is assumed that one of the material property (i.e., E11) and geometric property (i.e., h) change at a time keeping others as deterministic, with their mean values of the material and geometric properties. From the Figure 12,13 it is clear that, close correlation is achieved between two results subjected to TD thermo-material properties.
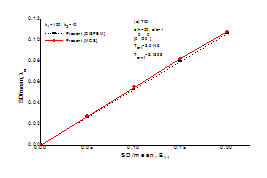
Figure 12 Validation of results the present DISFEM approach from the independent MCS approach.
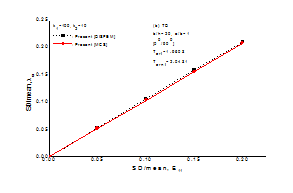
Figure 13 Validation of results the present DISFEM approach from the independent MCS approach.
Numerical results: second order statistics of thermal bucking and post buckling temperature
Parametric analysis of second order statistics (TD)
- Table 1: It is observed that increase in amplitude ratio
increases the mean thermal post buckling load and COV. Random input variable thickness (h) effects are significant where as shear modulus G(12) effects are least for uniform temperature (U.T) as well as combined uniform with transverse temperature (T.T) distribution. However for (T.T) temperature distribution, individual random input variables E11, E22,, G12 and h have fever effects whereas the other random input variables have no effects compared to uniform temperature distribution.
bi |
|
(TD), COV,
|
(T.T) |
(U.T) |
|
|
|
0.2 |
(0.8160) 0.0064 |
(0.8161) 0.0061 |
0.4 |
(0.8917) 0.0073 |
(0.8918) 0.0063 |
0.6 |
(0.9872) 0.0084 |
(0.9872) 0.0068 |
|
0.2 |
0.0135 |
0.0135 |
0.4 |
0.0115 |
0.0117 |
0.6 |
0.0086 |
0.0088 |
|
0.2 |
1.50e-04 |
1.32e-04 |
0.4 |
2.27e-04 |
1.73e-04 |
0.6 |
3.17e-04 |
2.30e-04 |
|
0.2 |
0.0059 |
0.0059 |
0.4 |
0.0057 |
0.0057 |
0.6 |
0.0057 |
0.0057 |
|
0.2 |
0.0024 |
0.0024 |
0.4 |
0.0023 |
0.0023 |
0.6 |
0.0023 |
0.0023 |
|
0.2 |
0.0815 |
0.0815 |
0.4 |
0.0749 |
0.0749 |
0.6 |
0.0682 |
0.0682 |
|
0.2 |
0.079 |
0.079 |
0.4 |
0.0723 |
0.0723 |
0.6 |
0.0653 |
0.0653 |
|
0.2 |
0.0017 |
0.0017 |
0.4 |
0.0016 |
0.0016 |
0.6 |
0.0014 |
0.0014 |
|
0.2 |
0.2183 |
0.2175 |
0.4 |
0.2102 |
0.2094 |
0.6 |
0.2031 |
0.2024 |
Table 1 Effects of Individual Random Variables [bi (i =1 to 9) = 0.10], Keeping Others as Deterministic with Amplitude Ratio
on the Dimensionless Mean
in Brackets and Coefficient of Variations
of Thermal Post Buckling Load of Angle Ply [±450]3T Square Laminated Composite Plates under Combination of Uniform and Transverse Temperature (T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h) =30 with Simple Support SSSS (S2) Boundary Conditions. Tcrl= Dimensionless Linear Mean Thermal Buckling Load
- Table 2: The thermal buckling temperature is most affected by random change in the E11 and h in the case of plate supported without foundation (k1=0, k2=0) while k1 and h for Winkler elastic foundation (k1=100, k2=0) and k2 and h for Pasternak elastic foundation (k1=100, k2=10) respectively, and the least affected by α2 in all the foundation cases. From the table it is clear that the dimensionless mean thermal buckling temperature increases when the plate supported with elastic foundation as the stiffness of the plate increases.
bi |
(k1=0, k2=0) |
(k1=100, k2=0) |
(k1=100, k2=10) |
|
|
|
|
|
|
|
0.0697 |
0.032 |
0.0155 |
|
0.051 |
0.0234 |
0.0113 |
|
3.29e-04 |
1.54e-04 |
7.42e-05 |
|
0.0056 |
0.0026 |
0.0012 |
|
0.0046 |
0.0021 |
0.001 |
|
0.0142 |
0.0065 |
0.0031 |
|
0.0011 |
5.20e-04 |
2.51e-04 |
|
1.35e-04 |
6.19e-05 |
2.99e-05 |
|
0 |
0.0541 |
0.0261 |
|
0 |
0 |
0.0517 |
|
0.0488 |
0.1332 |
0.213 |
Table 2 Effects of Individual Random Input Variables {bi, (i =1 to 11) = 0.10} Keeping Other as Deterministic at a Time with Various Foundation Stiffness Parameters on the Dimensionless Mean and Dispersion of Thermal Buckling Temperature of Anti-Symmetric, Angle-Ply [450/-450/450/-450] Square Laminates with SSSS Boundary Conditions Subjected Non-Uniform Tent Like Structures
- Table 3: It is expected that the thermal post buckling temperature increases as the amplitude ratio increases. It is observed that thermal post buckling strength is more pronounced when the plate becomes relatively thick. The COV of the thermal buckling temperature increases as the plate thickness ratio increases for all random system parameters bi, {i = (1,…,8), (7, 8) and (9)} varying simultaneously or individual.
- Table 4: For the fixed foundation parameters, the thermal buckling temperature increases as the plate thickness ratio decreases and vice versa for the case of dispersion. The thin plate (a/h=20) supported on Pasternak elastic foundation shows the highest dispersion with random change in all material properties and lamina plate thickness. However no definite trend is observed with random change in foundation parameters.
- Table 5: It is observed that increase of amplitude ratio increases the mean thermal post buckling temperature in both (U.T) and (T.T) temperature distribution. The effects of aspect ratios decreases the mean thermal post buckling temperature and dispersion significantly increases. If lay-up is changed then for square plate the mean thermal post buckling temperature decreases and for rectangular plate increases. The COV is significantly increased by increase of aspect ratio. The difference in results of (U.T) and (T.T) temperature distribution is insignificant.
a/h |
|
(TD), T.T |
(TD), U.T |
|
|
|
|
bi |
bi |
|
(i=1,...,8) |
i=7,8) |
(i=9) |
|
(i=1,...,8) |
i=7,8) |
(i=9) |
30 |
0.2 |
0.441 |
0.2153 |
0.1462 |
0.1855 |
0.441 |
0.2156 |
0.1462 |
0.1855 |
0.4 |
0.5399 |
0.1753 |
0.1194 |
0.1765 |
0.5399 |
0.176 |
0.1194 |
0.1765 |
0.6 |
0.6516 |
0.145 |
0.099 |
0.1706 |
0.6516 |
0.146 |
0.099 |
0.1706 |
Tcrl |
-0.4003 |
|
|
|
-0.4003 |
|
|
|
40 |
0.2 |
0.2536 |
0.3519 |
0.2542 |
0.1856 |
0.2536 |
0.3523 |
0.2542 |
0.1856 |
0.4 |
0.3121 |
0.2843 |
0.2066 |
0.1752 |
0.3121 |
0.2855 |
0.2066 |
0.1752 |
0.6 |
0.3886 |
0.2266 |
0.1659 |
0.1678 |
0.3886 |
0.2283 |
0.1659 |
0.1676 |
Tcrl |
-0.2303 |
|
|
|
-0.2303 |
|
|
|
Table 3 The Comparison of Variation of Plate Thickness Ratios (a/h) with Amplitude Ratios
= (0. 2, 0.4, 0.6) on the Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling load of 4-Layers Anti-Symmetric Cross-Ply [0/90]2s Square Plate with Simply Supported SSSS (S2) Condition for COV, {bi, i = (1,…,8), (7, 8) and (9) = 0.10} under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution, with Simple Support SSSS (S2) Boundary Conditions. Tcrl – Dimensionless Linear Mean Thermal Buckling Load
a/h |
Foundation parameters |
|
|
bi |
i=1,.., 8 |
i=7, 8 |
i=9, 10 |
i=11 |
5 |
|
49.5857 |
0.0996 |
4.1267e-004 |
0 |
0.0414 |
|
112.851 |
0.0763 |
1.7990e-004 |
0.0296 |
0.0494 |
|
278.6206 |
0.0308 |
7.2826e-005 |
0.0607 |
0.1837 |
10 |
|
15.4511 |
0.1022 |
0.0013 |
0 |
0.0318 |
|
36.4957 |
0.0442 |
5.6071e-004 |
0.0574 |
0.1514 |
|
78.2641 |
0.0206 |
2.6143e-004 |
0.0597 |
0.224 |
20 |
|
4.1756 |
0.1028 |
0.0049 |
0 |
0.0261 |
|
9.4379 |
0.0462 |
0.0022 |
0.0556 |
0.1517 |
|
19.8818 |
0.0219 |
0.0010 |
0.0588 |
0.2263 |
Table 4 Effects of Plate Thickness Ratios(a/h) with Foundation Parameters on the Dimensionless Mean and the Dispersion of Thermal Buckling Temperature for Angle-Ply Anti-Symmetric [450/-450] Laminated Composite Square Plate Resting on Elastic Foundation Subjected to Non-Uniform Tent-Like Temperature Distribution for COV, {bi, i =(1,...,8), (7,8), (9, 10) and (11) = 0.10 }with SSSS Boundary Conditions
No. of Layers |
a/b |
|
(TD), T.T |
(TD), U.T |
|
|
|
|
bi |
bi |
(i=1,...,8) |
(i=7,8) |
(i=9) |
(i=1,...,8) |
(i=7,8) |
(i=9) |
[00/900/00] |
1 |
0.2 |
0.0478 |
1.911 |
1.2972 |
0.1859 |
0.0478 |
1.9113 |
1.2972 |
0.1859 |
0.4 |
0.0531 |
1.6958 |
1.1077 |
0.234 |
0.0531 |
1.6965 |
1.1077 |
0.234 |
0.6 |
0.0551 |
1.6901 |
1.1684 |
0.1423 |
0.0551 |
1.6912 |
1.1684 |
0.1423 |
Tcrl |
0.0446 |
|
|
|
-0.0446 |
|
|
|
2 |
0.2 |
0.0136 |
6.4749 |
4.1785 |
0.2436 |
0.0136 |
6.476 |
4.1785 |
0.2436 |
0.4 |
0.0196 |
4.485 |
2.8901 |
0.2313 |
0.0196 |
4.4872 |
2.8901 |
0.2313 |
0.6 |
0.0199 |
4.4345 |
2.8642 |
0.2116 |
0.0199 |
4.4372 |
2.8642 |
0.2116 |
Tcrl |
-0.0111 |
|
|
|
-0.0111 |
|
|
|
[00/900]2T |
1 |
0.2 |
0.0423 |
2.2174 |
1.5254 |
0.1852 |
0.0423 |
2.218 |
1.5254 |
0.1852 |
0.4 |
0.0516 |
1.8138 |
1.2495 |
0.1731 |
0.0516 |
1.8154 |
1.2495 |
0.1731 |
0.6 |
0.0636 |
1.4682 |
1.0133 |
0.1629 |
0.0636 |
1.4706 |
1.0133 |
0.1629 |
Tcrl |
-0.0383 |
|
|
|
-0.0383 |
|
|
|
2 |
0.2 |
0.0333 |
2.7309 |
1.8726 |
0.2318 |
0.0344 |
2.7315 |
1.8726 |
0.2318 |
0.4 |
0.0408 |
2.2275 |
1.5597 |
0.2124 |
0.0413 |
2.2731 |
1.5597 |
0.2124 |
0.6 |
0.0465 |
1.9735 |
1.3575 |
0.1922 |
0.0475 |
1.9743 |
1.3585 |
0.1926 |
Tcrl |
-0.03 |
|
|
|
-0.0311 |
|
|
|
Table 5 Effects of Number of Layers, Aspect Ratios (a/b) , Amplitude Ratios
and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of Symmetric Cross-ply [00/900/00] and Ant-Symmetric [00/900]2T Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=100), with Simple Support SSSS (S2) Boundary Conditions
- Table 6: For the fixed foundation parameters and number of layers, rectangular plate shows higher dispersion to random change in material properties plus thermal expansion coefficients and vice versa for random change in thermal expansion coefficients, foundation parameters and lamina plate thickness. For the same aspect ratio and foundation parameters, as the number of layer increases the dimensionless mean and dispersion increases for random change in all system properties.
- Table 7: It is observed the increase of amplitude ratio increases the mean thermal post buckling temperature and decreases the dispersion for both (U.T) and (T.T) temperature distribution. Clamp support (CCCC) conditions significantly affect the thermal post buckling temperature and lowers the dispersions where as simple support conditions have least effects. It shows that for CCCC boundary conditions can withstand higher thermal post buckling temperature. On comparing uniform temperature and combined uniform with transverse temperature distribution the difference in parameters is very less.
- Table 8: For the three cases of support conditions, the plate with CCCC boundary condition shows the highest thermal buckling temperature and its scattering, while the SSSS plate shows the least for the fixed foundation parameters considered. For the fixed support conditions, the thermal buckling temperature is greatest for plate resting on Pasternak elastic foundation, while least for plate without elastic foundation. From the table it can be seen that the scattering in the thermal buckling temperature is strongest to random change in all eight system parameters in the case of plates resting on Winkler elastic foundation with SSSS and CCCC support conditions, while strongest for plate without elastic foundation in case of CSCS support condition. The dispersion in the plates resting on Pasternak elastic foundation is highest with random change in foundation parameters and lamina plate thickness, while plate without foundation shows highest dispersion with the random change in thermal expansion coefficients.
- Table 9: It is noticed that on rise in temperature the mean thermal post buckling temperature decreases for TID material properties, however the coefficient of variations for combination of input random variables and considering only thermal coefficients or geometric property plate thickness also decreases. For the TD material properties there is further decrease of expected mean thermal post buckling temperature while the COV for all input random variables increases which is an important parameter when the rise of temperature is taken into consideration.
- Table 10: For the TD material properties there is further decrease of expected mean thermal post buckling temperature while the COV for all input random variables increases which is an important parameter when the rise of temperature is taken into consideration.
- Table 11: For the fixed foundation parameters, an anti-symmetric plate shows higher dispersion to random change in all system properties. However the mean thermal buckling temperature of symmetric cross-ply plate is higher than anti-symmetric cross-ply plate.
- Table 12 & 13: The effects of amplitude ratios increases the mean thermal post buckling temperature and decreases the COV in both uniaxial and biaxial compression with TD and TID thermo-material properties, however the effects are more dominant in uniaxial TID for mean thermal post buckling load and dispersion in biaxial TD compression respectively. Among invidual random variation in material properties, thermal expansion coefficients and plate thickness the COV is significant decreases for plate thickness in uniaxial as well as in biaxial for TD and TID material properties. As a matter of facts the COV for temperature dependent thermo material properties is of significant nature.
- Table 14: It can be sheen that the laminated plate under non-uniform tent-like temperature distribution has higher initial buckling load and post buckling load than non-uniform parabolic temperature distribution for the same thermal load ratio. It can also be seen that thermal post buckling strength under non-uniform tent like temperature distribution is more pronounced when the plate becomes heavily loaded thermal load as compared to parabolic temperature distribution. The dispersion of thermal post buckling temperature are same for both of the non-uniform tent-like and parabolic temperature distribution are almost same for all random system parameters bi, {i = (1,…,8) and (7, 8)} varying simultaneously. However, dispersion of thermal post buckling temperature of the plate subjected to non-uniform tent-like distribution is higher than parabolic temperature distribution having random lamina propertiesbi, {i = (9)}.
a/b |
Lamination scheme |
Foundation parameters |
|
|
bi |
i=1,.., 8 |
i=7, 8 |
i=9, 10 |
i=11 |
1 |
|
|
0.1739 |
0.1554 |
0.1177 |
0 |
0.0213 |
|
0.3843 |
0.0707 |
0.0533 |
0.0547 |
0.1534 |
|
0.8021 |
0.0339 |
0.0255 |
0.0583 |
0.2291 |
|
|
0.1847 |
0.1446 |
0.1081 |
0 |
0.0369 |
|
0.3935 |
0.0689 |
0.0504 |
0.0527 |
0.1389 |
|
0.8213 |
0.0325 |
0.0243 |
0.0579 |
0.2234 |
2 |
|
|
0.2052 |
0.1358 |
0.0992 |
0 |
0.0193 |
|
0.2472 |
0.1128 |
0.0823 |
0.017 |
0.0348 |
|
0.4561 |
0.0612 |
0.0446 |
0.0467 |
0.156 |
|
|
0.2197 |
0.1256 |
0.091 |
0 |
0.0317 |
|
0.2616 |
0.1055 |
0.0764 |
0.016 |
0.0212 |
|
0.4736 |
0.0582 |
0.0423 |
0.0456 |
0.1459 |
Table 6 Effects of Aspect Ratios (a/b) , Number of Layers with Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=100), with Simple Support SSSS (S2) Boundary Conditions
BCs |
|
(TD), T.T |
(TD), U.T |
|
|
|
|
bi |
bi |
(i=1,...,8) |
(i=7,8) |
(i= 9) |
(i=1,...,8) |
(i=7,8) |
(i= 9) |
SSSS (S1) |
0.2 |
0.2989 |
0.2813 |
0.2156 |
0.1801 |
0.299 |
0.2815 |
0.2157 |
0.1791 |
0.4 |
0.3277 |
0.2557 |
0.1967 |
0.1736 |
0.3277 |
0.2563 |
0.1967 |
0.1726 |
0.6 |
0.3706 |
0.2249 |
0.1739 |
0.1658 |
0.3707 |
0.2259 |
0.174 |
0.1648 |
Tcrl |
-0.2883 |
|
|
|
-0.2884 |
|
|
|
SSSS |
0.2 |
0.2956 |
0.2861 |
0.218 |
0.1821 |
0.2957 |
0.2863 |
0.2181 |
0.1809 |
0.4 |
0.324 |
0.2602 |
0.1989 |
0.1752 |
0.324 |
0.2608 |
0.199 |
0.1741 |
0.6 |
0.3665 |
0.2291 |
0.1759 |
0.1668 |
0.3665 |
0.23 |
0.1759 |
0.1657 |
Tcrl |
-0.2851 |
|
|
|
-0.2851 |
|
|
|
CCCC(1) |
0.2 |
0.5721 |
0.1741 |
0.1126 |
0.1919 |
0.5724 |
0.1742 |
0.1127 |
0.1906 |
0.4 |
0.6249 |
0.159 |
0.1031 |
0.1879 |
0.625 |
0.1593 |
0.1032 |
0.1866 |
0.6 |
0.7023 |
0.1409 |
0.0917 |
0.1834 |
0.7023 |
0.1414 |
0.0918 |
0.1822 |
Tcrl |
-0.5531 |
|
|
|
-0.5533 |
|
|
|
CSCS(2) |
0.2 |
0.408 |
0.2165 |
0.158 |
0.1976 |
0.4079 |
0.2167 |
0.1581 |
0.1962 |
0.4 |
0.4594 |
0.1921 |
0.1404 |
0.1885 |
0.4594 |
0.1925 |
0.1404 |
0.1871 |
0.6 |
0.5329 |
0.165 |
0.121 |
0.1796 |
0.5328 |
0.1658 |
0.121 |
0.1783 |
Tcrl |
0.3896) |
|
|
|
-0.3895 |
|
|
|
Table 7 Effects of Boundary Conditions(BCs) , Amplitude Ratios
and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of Angle-Ply Antisymmetric [450/-450]2T Square Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=50)
BCs |
Foundation Parameters |
|
|
bi |
i=1,.., 8 |
i=7, 8 |
i=9, 10 |
i=11 |
SSSS |
|
14.1382 |
0.0719 |
0.0014 |
0 |
0.0461 |
|
33.0055 |
0.0935 |
6.1642e-004 |
0.0255 |
0.021 |
|
74.7823 |
0.0413 |
2.7206e-004 |
0.057 |
0.17 |
CCCC |
|
37.3257 |
0.0794 |
5.4764e-004 |
0 |
0.0475 |
|
51.7059 |
0.1284 |
3.9341e-004 |
0.0124 |
0.0227 |
|
93.4827 |
0.071 |
2.1760e-004 |
0.0452 |
0.1161 |
CSCS |
|
23.1902 |
0.0742 |
8.8186e-004 |
0 |
0.0464 |
|
38.1211 |
0.0721 |
5.3461e-004 |
0.0296 |
0.0429 |
|
79.8979 |
0.0344 |
2.5507e-004 |
0.0542 |
0.171 |
Table 8 Effects of Three Different Support Conditions, SSSS, CCCC and CSCS with Various Foundation Parameters) and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9, 10) and (11) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of Cross-Ply Symmetric [00/900/900/00] Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=10)
(ΔT) |
|
(TID) |
|
|
bi |
(i=1,...,8) |
(i=7,8) |
(i= 9) |
50 |
0.2 |
0.0459 |
0.0733 |
0.0016 |
0.0755 |
0.4 |
0.051 |
0.0677 |
0.0015 |
0.0718 |
0.6 |
0.0524 |
0.0662 |
0.0014 |
0.0679 |
Tcrl |
-0.0439 |
|
|
|
100 |
0.2 |
0.0229 |
0.0717 |
0.0033 |
0.0755 |
0.4 |
0.0255 |
0.0663 |
0.0029 |
0.0718 |
0.6 |
0.0287 |
0.0615 |
0.0026 |
0.0679 |
Tcrl |
-0.0219 |
|
|
|
150 |
0.2 |
0.0153 |
0.0702 |
0.0049 |
0.0755 |
0.4 |
0.017 |
0.0649 |
0.0044 |
0.0718 |
0.6 |
0.0191 |
0.0602 |
0.0039 |
0.0679 |
Tcrl |
-0.0146 |
|
|
|
200 |
0.2 |
0.0115 |
0.0687 |
0.0065 |
0.0755 |
0.4 |
0.0127 |
0.0636 |
0.0059 |
0.0718 |
0.6 |
0.0143 |
0.0591 |
0.0052 |
0.0679 |
Tcrl |
-0.011 |
|
|
|
Table 9 Effects of Temperature Change (ΔT), Amplitude Ratios and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of angle-ply [±45]2T square Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=20)
(ΔT) |
|
(TD) |
|
|
bi |
(i=1,...,8) |
(i=7,8) |
(i= 9) |
50 |
0.2 |
0.0306 |
0.0884 |
0.0022 |
0.077 |
0.4 |
0.034 |
0.0823 |
0.002 |
0.072 |
0.6 |
0.0386 |
0.0785 |
0.0017 |
0.067 |
Tcrl |
-0.0294 |
|
|
|
100 |
0.2 |
0.0153 |
0.0861 |
0.0044 |
0.077 |
0.4 |
0.017 |
0.0802 |
0.004 |
0.072 |
0.6 |
0.0193 |
0.0767 |
0.0035 |
0.067 |
Tcrl |
-0.0147 |
|
|
|
150 |
0.2 |
0.0102 |
0.0838 |
0.0066 |
0.077 |
0.4 |
0.0113 |
0.0782 |
0.0059 |
0.072 |
0.6 |
0.0129 |
0.0749 |
0.0052 |
0.067 |
Tcrl |
-0.0098 |
|
|
|
200 |
0.2 |
0.0077 |
0.0817 |
0.0088 |
0.077 |
0.4 |
0.0085 |
0.0763 |
0.0079 |
0.072 |
0.6 |
0.0097 |
0.0731 |
0.007 |
0.067 |
Tcrl |
-0.0073 |
|
|
|
Table 10 Effects of Temperature Change (ΔT), Amplitude Ratios and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of angle-ply [±45]2T square Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=20)
Lamination Scheme |
Foundation Parameters |
|
|
bi |
i=1,.., 8 |
i=7, 8 |
i=9, 10 |
i=11 |
[0/90]2T |
|
0.3265 |
0.1026 |
0.0689 |
0 |
0.0419 |
|
0.7915 |
0.0423 |
0.0284 |
0.0587 |
0.1574 |
|
1.7098 |
0.0196 |
0.1457 |
0.0602 |
0.2325 |
[0/90]2s |
|
0.3473 |
0.0978 |
0.0648 |
0 |
0.0379 |
|
0.8123 |
0.0418 |
0.0277 |
0.0572 |
0.154 |
|
1.7306 |
0.0196 |
0.013 |
0.0595 |
0.23 |
Table 11 Effects of Lamination Scheme with Foundation Parameters and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=50)
Material Properties |
|
Uni-Axial Compression |
|
|
bi |
(i=1,..,8) |
(i=7, 8) |
(i=9) |
TD |
0.2 |
0.1316 |
1.4007 |
0.9774 |
0.3417 |
0.4 |
0.1487 |
1.2385 |
0.8655 |
0.3226 |
0.6 |
0.1676 |
0.9928 |
0.6984 |
0.2833 |
Tcrl |
(0.1254) |
|
|
|
TID |
0.2 |
0.2024 |
0.9505 |
0.6977 |
0.351 |
0.4 |
0.2293 |
0.8378 |
0.6161 |
0.3307 |
0.6 |
0.2533 |
0.6754 |
0.5027 |
0.2909 |
Tcrl |
(0.1925) |
|
|
|
Table 12 Effects of Material Properties, Amplitude Ratios
and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of of angle-ply symmetric [45/-45]2T square Laminated Composite Plates under Combination of Uniform and Transverse Temperature (T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=100)
Material Properties |
|
Bi-Axial Compression |
|
|
bi |
(i=1,..,8) |
(i=7, 8) |
(i=9) |
TD |
0.2 |
0.0659 |
1.4024 |
0.9786 |
0.2422 |
0.4 |
0.0745 |
1.2386 |
0.8656 |
0.2228 |
0.6 |
0.0871 |
1.0565 |
0.74 |
0.2023 |
Tcrl |
(0.0628) |
|
|
|
TID |
0.2 |
0.1014 |
0.952 |
0.6987 |
0.2515 |
0.4 |
0.1149 |
0.8379 |
0.6161 |
0.2307 |
0.6 |
0.1347 |
0.7129 |
0.5258 |
0.2092 |
Tcrl |
(0.0964) |
|
|
|
Table 13 Effects of Material Properties, Amplitude Ratios
and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on Dimensionless Mean
and Coefficient of Variations
of Thermal Post Buckling Load of of angle-ply symmetric [45/-45]2T square Laminated Composite Plates under Combination of Uniform and Transverse Temperature(T.T), Uniform Temperature (U.T) Distribution., Plate Thickness Ratio (a/h=100)
|
|
Tent-Like |
Parabolic |
|
|
|
|
bi |
bi |
i=1,.., 8 |
i=7, 8 |
i=9 |
i=1,.., 8 |
i=7, 8 |
i=9 |
0 |
0.2 |
3.8831 |
0.0796 |
0.0059 |
0.0438 |
2.0885 |
0.0795 |
0.00588 |
0.041 |
0.4 |
4.2161 |
0.0747 |
0.0054 |
0.0429 |
2.266 |
0.0746 |
0.00538 |
0.0402 |
0.6 |
4.5643 |
0.0705 |
0.005 |
0.0424 |
2.4533 |
0.0704 |
0.005 |
0.0398 |
Tcrl |
(3.7319) |
|
|
|
(2.0076) |
|
|
|
0.5 |
0.2 |
1.9411 |
0.0802 |
0.0118 |
0.0438 |
1.114 |
0.0802 |
0.0118 |
0.0412 |
0.4 |
2.1061 |
0.0754 |
0.0109 |
0.0429 |
1.2116 |
0.0752 |
0.0108 |
0.0402 |
0.6 |
2.2802 |
0.0711 |
0.01 |
0.0425 |
1.3147 |
0.071 |
0.01 |
0.0394 |
Tcrl |
(1.8659) |
|
|
|
(1.0708) |
|
|
|
1 |
0.2 |
1.294 |
0.0813 |
0.0177 |
0.0438 |
1.006 |
0.0813 |
0.0177 |
0.0424 |
0.4 |
1.4041 |
0.0763 |
0.0163 |
0.0429 |
1.0942 |
0.0763 |
0.0163 |
0.0415 |
0.6 |
1.519 |
0.072 |
0.0151 |
0.0426 |
1.1873 |
0.072 |
0.0151 |
0.0406 |
Tcrl |
(1.244) |
|
|
|
(0.9671) |
|
|
|
Table 14 The Effect of Thermal Load Ratio T0/T1 ( = 0.0, 0.5, 1.0) with Amplitude Ratios Wmax/h ( = 0. 2, 0.4, 0.6) and Random Input Variables [bi, (i =1 to 8), (7, 8) and (9) = 0.10] on the Dimensionless Mean (
and Dispersion(lcrnl ) of Thermal Post Buckling Load of 4-Layers Anti-Symmetric Angle-ply [450/-450]2T Square Plate with Simply Supported SSSS (S2) Condition and a/h=20 under Non-Uniform Tent Like and Parabolic Temperature Distribution
|
Laminate stiffnesses |
a, b |
Plate length and breadth |
h |
Thickness of the plate |
|
Elastic moduli of fiber and matrix, respectively. |
|
Shear moduli of fiber and matrix, respectively. |
|
Poisson’s ratio of fiber and matrix, respectively. |
|
Volume fraction of fiber and matrix, respectively. |
|
Coefficient of thermal expansion of fiber and matrix, respectively. |
bi |
Basic random material properties |
E11, E22 |
Longitudinal and Transverse elastic moduli |
G12, G13, G23 |
Shear moduli |
Kl, |
Linear bending stiffness matrix |
Kg |
Thermal geometric stiffness matrix |
D |
Elastic stiffness matrices |
|
Mass and inertia matrices |
ne, n |
Number of elements, number of layers in the laminated plate |
Nx, Ny, Nxy |
In-plane thermal buckling loads |
nn |
Number of nodes per element |
Ni |
Shape function of ith node |
|
Reduced elastic material constants |
|
Vector of unknown displacements, displacement vector of eth element |
u, v, w |
Displacements of a point on the mid plane of plate |
|
Displacement of a point (x, y, z) |
|
Stress vector, Strain vector |
|
Rotations of normal to mid plane about the x and y axis respectively |
θx, θy, θk |
Two slopes and angle of fiber orientation wrt x-axis for kth layer |
x, y, z |
Cartesian coordinates |
|
Mass density, eigenvalue, variance |
 |
Fundamental frequency and its dimensionless form |
RVs |
|
DT, DC, |
Difference in temperatures and moistures |
|
Thermal expansion and hygroscopic coefficients along x and y direction, respectively. |
Conclusion
A C0 FEM and direct iterative method in conjunction with FOPT is employed to compute the mean and standard deviation of the thermal post buckling load of the laminated composite plate with thermo-mechanical properties, random change in all input variables, aspect ratios, amplitude ratios and plate thickness. The following conclusion can be drawn from this limited study:
- The characteristics of the thermal buckling load of plates are significantly influenced by various support conditions, plate thickness ratios, aspect ratios, number of layers, lamination scheme and foundation parameters. The first order perturbation technique gives acceptable results for the range of dispersion (SD/mean) taken in the study. The characteristics of the thermal post buckling temperature of plates are significantly influenced by various support conditions, plate thickness ratios, aspect ratios and temperature changes. The mean and dispersion of thermal post buckling temperature of laminated composite plates is higher when the plates are subjected to temperature dependent (TD) thermo-material properties.
- The thermal buckling load strongly depends on the foundation parameters and increases with increase the foundation parameters. The clamp supported plates buckle at slightly higher temperature compared to other supports as mean thermal post buckling temperature is higher and COV is lower for clamped support when compared with other types of support conditions. Post buckling is more dominant in plates of (TD) thermo-material properties. The random change in input variables thickness (h) has more impact on thermal post buckling temperature scattering compared to individual random changes in material properties and thermal expansion coefficients.
- The dispersion in thermal buckling is the greatest with scatter in E11and h in the case of the plate supported without foundation, k1 and h for Winkler elastic foundation and k2 and h for Pasternak elastic foundation respectively. This means that the care should be taken during fabrication process so as to allow less variation in these system properties with various foundation parameters. The sensitivity of thermal post buckling temperature and COV due to variation in temperature dependent thermo-material properties is dependent mainly on thickness ratio, and boundary conditions besides other parameters of the laminate. The COV in the thermal post buckling temperature is most affected with random change in lamina thickness h and least affected with scatter in G12. In general the plate is more sensitive to individual random change in
. The strict control of these random parameters is therefore required for reliable design if high reliability of laminated composite plate is required
- In general, the square plate is more sensitive as compared to rectangular plate. The thermal post buckling temperature for square plate is more compared to rectangular plate. The thermal post buckling temperature is more prone to SSSS (S2) boundary conditions while it is least for clamped support CCCC boundary conditions.
- The plate with all edges clamed support condition is less desirable in comparison with other support conditions from scattering point of view. The impact of randomness in all random system variables is more for thin plate as compared to thick and moderately thick plate.
Acknowledgement
Conflicts of Interest
Author declares that there is no conflict of interest.
References
- Chen WS, Lin PD, Chen LW. Thermal buckling behavior of thick composite laminated plates under non-uniform temperature distribution. Comput Struct. 1991;41(4):637‒645.
- Shen HS. Thermal post-buckling analysis of imperfect shear-deformable plates on two-parameter elastic foundations. Computers & Structures. 1997;63(6):1187‒1193.
- Shen HS. Thermal post-buckling analysis of imperfect laminated plates using higher order shear deformation theory. Int J Non-Linear mechanics. 1997;32(6):1035‒1050.
- Shen HS, Zhu XG. Thermal post-buckling analysis of moderately thick plates. Applied Mathematics and Mechanics. 1995;16(5):475‒484.
- Shen HS, Lin Zhong-Qin. Thermal post-buckling analysis of imperfect laminated plates. Computer & Structures. 1995;57(3):533‒540.
- Shen HS. Nonlinear analysis of composite laminated thin plates subjected to lateral loading and resting on elastic foundation. Composite Structures. 2000;49(2):115‒128.
- Shen HS. Thermal post-buckling analysis of imperfect Reissne-Mindlin plates on softening nonlinear foundation. J Engineering Mathematics. 1998;33(3):259‒270.
- Chen LW, Chen LY. Thermal buckling behavior of laminated composite plates with temperature-dependent properties. Composite Structures. 1989;13(4):275‒287.
- Chen LW, Chen LY. Thermal post buckling behaviors of laminated composite plates with temperature-dependent properties. Composite Structures. 1991;19:267‒283.
- Huang A, Tauchert TR. Post buckling response of antisymmetric angle-ply laminates to uniform temperature loading. Acta Mechanica. 1988;72(1):173‒183.
- Pandey Ramesh, Shukla KK, Jain Anuj. Thermoelastic stability analysis of laminated composite plates, An analytical approach. Communications in Nonlinear Science and Numerical Simulation. 2009;14(4):1679‒1699.
- Shariyat M. Thermal buckling analysis of rectangular composite plates with temperature-dependent properties based on a layer wise theory. Thin-Walled Structures. 2007;45(4):439‒452.
- Shen HS. Thermal post buckling behaviors of imperfect shear deformable laminated composite plates with temperature-dependent properties. Comput Methods Appl Mech Engg. 2001;190:5377‒5390.
- Thankam Sita V, Singh G, Venkateswara Rao G, et al. Thermal Post buckling Behaviors of Laminated Composite Plates using shear flexible element based on coupled-displacement field. Composite Structures. 2003;59(3):351‒359.
- Nigam NC, Narayan S. Application of Random vibrations. Narosa Publishing House, New Delhi; 1994. p. 557.
- Zang Z, Chen S. The standard deviations of the eigensolutions for random MDOF systems. Comp Struct. 1991;39(6):603‒607.
- Zhang J, Ellingwood B. Effects of uncertain material properties on structural stability. J Struct Engrg. 1995;121(4):705‒716.
- Graham LL, Deodatis G. Response and eigenvalue analysis of stochastic finite element systems with multiple correlated material and geometric properties. Probt Engrg Mech. 2001;16(1):11‒29.
- Van den, Nieuwenhof B, Coyette JP. Modal approaches for the stochastic finite element analysis of structures with material and geometric uncertainties. Comput Methods Appl Mech Engrg. 2003;192(33‒34):3705‒3729.
- Stefanou G, Papadrakakis M. Stochastic finite element analysis of shell with combined random material and geometric properties. Comput Methods Appl Mech Engrg. 2004;193:139‒160.
- Singh BN, Iyengar NGR, Yadav D. Effects of random material properties on buckling of composite plates. J Engrg Mech. 2001;127(9):873‒879.
- Singh BN, Iyengar NGR. Yadav D. A C0 finite element investigation for buckling analysis of composite plates with random material properties. Struct Engrg and Mech. 2002;13(1):53‒74.
- Onkar AK, Upadhyay CS, Yadav D. Generalized buckling analysis of laminated plates with random material properties using stochastic finite elements. Int J Mech Sci. 2006;48(7):780‒798.
- Onkar AK, Upadhyay CS, Yadav D. Stochastic finite element buckling analysis of laminated plates with circular cutout under uniaxial compression. J Appld Mech. 2007;74(4):789‒809.
- Shakhar A, Abedelrahman WG, Tawfik Mohammad, et al. Stochastic finite element analysis of the free vibration of laminated composite plates. Comput Mech. 2008;41(4):493‒503.
- Shankara CA, Iyenger NGR. A C0 element for the free vibration analysis of laminated composite plates. J Sound and Vibration. 1996;191(5):721‒738.
- Lal A, Singh BN, Kumar R. Effect of random system properties on the initial buckling of laminated composite plate resting on an elastic foundation. Int J Struct stability Dyn. 2008;8(1):1‒28.
- Jones RM. Mechanics of Composite Materials. MC Graw-Hill Book Company, MC Graw Hill, New York USA; 1975.
- Franklin JN. Matrix theory. Englewood Cliff, Prentice Hall, USA; 1968. p. 292.
- Reddy JN. Mechanics of Laminated Composite Plate. CRC Press, Florida, USA; 1996.
- Graham LL, Siragy EF. Stochastic finite element analysis for elastic buckling of stiffend panels. J Engg Mech. 2001;127(1):91‒97.
- Liu WK, Belytschko T, Mani A. Random field finite elements. Int J Numer Meth Engrg. 1986;23:1831‒1845.
- Klieber M, Hien TD. The Stochastic Finite Element Method. Wiley, Chichester, UK; 1992.
- Reddy JN. A simple higher order theory for laminated composite plates. J Appld Mech. 1984;51(4):745‒752.
- Chia CY. Nonlinear analysis of plates. McGraw-Hill, New York USA; 1980.
- Reddy JN. Energy and variational methods in applied mechanics. Wiley, New York, USA; 1981. p. 560.
- Yamin Z, Chen S, Lue Q. Stochastic perturbation finite elements. Comp and Struct. 1996;59(3):425‒429.

©2017 Kumar. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


