In this article, simultaneous impacts of surface elasticity, initial stress, residual surface tension and nonlocality on the nonlinear vibration of single-walled carbon conveying nanotube resting on linear and nonlinear elastic foundation and operating in a thermo-magnetic environment are studied. The developed equation of motion is solved using Galerkin’s decomposition and Temini and Ansari method. The studies of the impacts of various parameters on the vibration problems revealed that the ratio of the nonlinear to linear frequencies increases with the negative value of the surface stress while it decreases with the positive value of the surface stress. The surface effect reduces for increasing in the length of the nanotube. Ratio of the frequencies decreases with increase in the strength of the magnetic field, nonlocal parameter and the length of the nanotube. Increase in temperature change at high temperature causes decrease in the frequency ratio. However, at room or low temperature, the frequency ratio of the hybrid nanostructure increases as the temperature change increases. The natural frequency of the nanotube gradually approaches the nonlinear Euler–Bernoulli beam limit at high values of nonlocal parameter and nanotube length. Nonlocal parameter reduces the surface effects on the ratio of the frequencies. Also, the ratio of the frequencies at low temperatures is lower than at high temperatures. It is hoped that the present work will enhance the control and design of carbon nanotubes operating in thermo-magnetic environment and resting on elastic foundations.

Keywords: surface effects, carbon nanotubes, nonlocal elasticity theory, Temini and Ansari method

A, area of the nanotube; E, modulus of elasticity; EI, bending rigidity; Hs, residual surface stress; Hx, magnetic field strength; I moment of area; L, length of the nanotube; mc mass of tube per unit length; N, axial/Longitudinal force; T, change in temperature; t, time coordinate; w, transverse displacement/deflection of the nanotube; W, time-dependent parameter; x, axial coordinate; $\varphi (x)$ , trial/comparison function; ${\alpha }_x$ , coefficient of thermal expansion; η, permeability

Carbon nanotubes have shown to be nanostructures with remarkable physical, mechanical, electrical and chemical properties. Such excellent properties have aided their various medical, industrial, electrical, thermal, electronic and mechanical applications.^1–5 Due to their importance for the practical applications, their dynamic behaviours have been studied.^6–13 However, the effects of the surface energy and initial stress are neglected in the studies. Indisputably, the properties of the region of the solid surface are different properties from the bulk material. Also, for classical structures, surface energy-to-bulk energy ratio is small. However, nanostructures have large surface energy-to-bulk energy ratio and high ratio of surface energies to volume, elastic modulus and mechanical strength. Consequently, the mechanical behaviours, bending deformation and elastic waves of the nanostructures are greatly influenced. Therefore, the surface energy effects cannot be neglected in the dynamic behaviour analysis of nanostructures.  Such surface energy of nanostructures is composed of the surface tension and surface modulus exerted on the surface layer of nanostructures.^13–21 Consequently, different works have been presented in literature to analyze the impacts of surface energy on the dynamic response and instability of nanostructures.^22–28

Due to residual stress, thermal effects, surface effects, mismatches between the material properties of CNTs and surrounding mediums, initial external loads and other physical issues, carbon nanotubes often suffer from initial stresses The effects of initial stress on the dynamic behaviour of nanotubes have been studied.^29–37 However, because of their significant in practically nano-apparatus applications, there is a need for a combined on the effects of surface behaviours, initial stress and nonlocality on the physical characteristics and mechanical behaviours of carbon nanotubes.

In the above past studies, different mathematical methods have been used to analyze the problem.  However, most of these methods require high skill in mathematical analysis for their applications. As a means of overcoming the drawbacks in the other approximation analytical methods, recently, Temimi and Ansari³⁸ introduced the semi-analytical iterative technique in 2011 for solving nonlinear problems. The new iterative method has been used to solve many differential equations, such as nonlinear differential equations.^39–55 The results obtained in these studies indicate that the Temimi and Ansari method (TAM) provides excellent approximations to the solution of nonlinear equation with low computational time, high accuracy, and high order of convergence. The previous studies^39–55 have shown that the TAM can solve nonlinear differential and integral equations without linearization, discretization, restrictive assumptions, closure, perturbation, approximations, discretization and round-off error that could result in massive numerical computations. This method has not been applied to solve vibration problems in nanostructures. Also, scanning through the past works and to the best of the authors’ knowledge, a study on simultaneous effects of surface energy and initial stress on the vibration characteristics of nanotubes resting of Winkler and Pasternak foundations in a thermo-magnetic environment has not been carried out. Therefore, in this work, Temini and Ansari method is applied with Galerkin’s decomposition method to study the coupled impacts of surface effects, initial stress and nonlocality on the nonlinear dynamic behaviour of single-walled carbon nanotubes resting on Winkler (Spring) and Pasternak (Shear layer) foundations in a thermal-magnetic environment. Erigen’s nonlocal elasticity, Maxwell’s relations, Hamilton’s principle, surface effect and Euler-Bernoulli beam theories are adopted to develop the systems of nonlinear equations of the dynamics behaviour of the carbon nanotube. The studies of the impacts of various parameters on the vibration problems are also carried out.

Figure 1 shows a single-walled CNT of length L and inner and outer diameters Di and Do resting on Winkler (Spring) and Pasternak (Shear layer) foundations.  The SWCNTs conveying a hot fluid and resting on elastic foundation under external applied tension, initial stress, magnetic and temperature fields as shown in the figure.

Based on Erigen’s theory, Euler-Bernoulli’s theory and Hamilton’s principle.^56–58 The partial differential equation governing the dynamic behaviour is derived as

$\begin{array}{l}\left(EI+E_s{I}_s\right)\frac{{\partial }^{4}w}{\partial x^4}+(m_{cn}+m_f)\frac{{\partial }^{2}w}{\partial t^2}+2u{m}_f\frac{{\partial }^{2}w}{\partial x\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{2}w}{\partial x^2}\\ +\left(m_f{u}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{2}w}{\partial x^2}+k_{1}w+k_3{w}^3\\ -{\left(e_{o}a\right)}^2\left[\begin{array}{l}(m_{cn}+m_f)\frac{{\partial }^{4}w}{\partial x^2\partial t^2}+2u{m}_f\frac{{\partial }^{4}w}{\partial x^3\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{4}w}{\partial x^4}\\ +\left(m_f{u}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{4}w}{\partial x^4}\\ +k_1\frac{{\partial }^{2}w}{\partial x^2}+3k_3{w}^2\frac{{\partial }^{2}w}{\partial x^2}+6k_{3}w{\left(\frac{\partial w}{\partial x}\right)}^2\end{array}\right]=0\end{array}$   (1)

Figure 2 shows the effect of flow in a channel. In the fluid-conveying carbon nanotube, the condition of slip is satisfied since in such flow, the ratio of the mean free path of the fluid molecules relative to a characteristic length of the flow geometry which is the Knudsen number is larger than 10^-2. Consequently, the velocity correction factor for the slip flow velocity is proposed as⁵⁹:

$VCF=\frac{u_{avg,slip}}{u_{avg,no-slip}}=\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]$   (2)

Where Kn is the Knudsen number, σ_v is tangential moment accommodation coefficient which is considered to be 0.7 for most practical purposes^41,42

$a_k=a_o\frac{2}{\pi }\left[ta{n}^{-1}\left(a_{1}K{n}^B\right)\right]$   (3)

$a_o=\frac{64}{3\pi \left(1-\frac{4}{b}\right)}$   (4)

$a_1=4$   and B = 0.04 and b is the general slip coefficient (b = −1).

From Eq. (2),

$u_{avg,slip}=\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]u_{avg,no-slip}$   (5)

Therefore, Eq. (1) can be written as

$\begin{array}{l}\left(EI+E_s{I}_s\right)\frac{{\partial }^{4}w}{\partial x^4}+(m_{cn}+m_f)\frac{{\partial }^{2}w}{\partial t^2}+2m_f\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\frac{{\partial }^{2}w}{\partial x\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{2}w}{\partial x^2}\\ +\left(m_f{\left[\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{2}w}{\partial x^2}+k_{1}w+k_3{w}^3\\ -{\left(e_{o}a\right)}^2\left[\begin{array}{l}(m_{cn}+m_f)\frac{{\partial }^{4}w}{\partial x^2\partial t^2}+2m_f\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\frac{{\partial }^{4}w}{\partial x^3\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{4}w}{\partial x^4}\\ +\left(m_f{\left[\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{4}w}{\partial x^4}\\ +k_1\frac{{\partial }^{2}w}{\partial x^2}+3k_3{w}^2\frac{{\partial }^{2}w}{\partial x^2}+6k_{3}w{\left(\frac{\partial w}{\partial x}\right)}^2\end{array}\right]=0\end{array}$   (6)

where the transverse area and the bending rigidity are given as

$A=\pi dh$

$EI=\frac{\pi d^{3}h}{8}$

and

$E_s{I}_s=\frac{\pi E_{s}h(d_o^3+d_i^3)}{8}$

$H_s=2{\tau }_s\left(d_o+d_i\right)$

The symbol H_s is the parameter induced by the residual surface stress. τ is the residual surface tension, d and h are the nanotube internal diameter and thickness, respectively. It should be noted that the diameter of the nanotube can be derived from chirality indices (n, m)

$d_i=\frac{a\sqrt{3}}{\pi }\sqrt{n^2+mn+m^2}$   (7)

where $a\sqrt{3}=0.246nm$ . ”a” represents the length of the carbon-carbon bond. d is the inner diameter of the nanotube.

It is difficult to solve Eq. (6) exactly because of the nonlinear term. Therefore, an approximate analytical method is used to solve the nonlinear model. In order to develop analytical solutions for the developed nonlinear model, the partial differential equation is converted to ordinary differential equation using the Galerkin’s decomposition procedure to decompose the spatial and temporal parts of the lateral displacement functions as

$w(x,t)=\varphi (x)u(t)$   (8)

Where $u(t)$ the generalized coordinate of the system and $\varphi (x)$ is a trial/comparison function that will satisfy both the geometric and natural boundary conditions.

Applying one-parameter Galerkin’s solution given in Eq. (8) to Eq. (6)

${\displaystyle {\int }_0^{L}R\left(x,t\right)\varphi \left(x\right)dx}$   (9)

where

$\begin{array}{l}R\left(x,t\right)=\left(EI+E_s{I}_s\right)\frac{{\partial }^{4}w}{\partial x^4}+(m_{cn}+m_f)\frac{{\partial }^{2}w}{\partial t^2}+2m_f\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\frac{{\partial }^{2}w}{\partial x\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{2}w}{\partial x^2}\\ +\left(m_f{\left[\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{2}w}{\partial x^2}+k_{1}w+k_3{w}^3\\ -{\left(e_{o}a\right)}^2\left[\begin{array}{l}(m_{cn}+m_f)\frac{{\partial }^{4}w}{\partial x^2\partial t^2}+2m_f\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\frac{{\partial }^{4}w}{\partial x^3\partial t}+\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{\partial w}{\partial x}\right)}^{2}dx}\right]\frac{{\partial }^{4}w}{\partial x^4}\\ +\left(m_f{\left[\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]}^2+\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\right)\frac{{\partial }^{4}w}{\partial x^4}\\ +k_1\frac{{\partial }^{2}w}{\partial x^2}+3k_3{w}^2\frac{{\partial }^{2}w}{\partial x^2}+6k_{3}w{\left(\frac{\partial w}{\partial x}\right)}^2\end{array}\right]=0\end{array}$

We have the nonlinear vibration equation of the pipe as

$M\ddot{u}(t)+G\dot{u}(t)+(K+C)u(t)+V{u}^3(t)=0$   (10)

where

$M=(m_p+m_f)\left[{\displaystyle {\int }_0^L{\varphi }^2(x)}dx-{\left(e_{o}a\right)}^2{\displaystyle {\int }_0^L{\varphi }^2(x)}\frac{d^2\varphi }{d{x}^2}dx\right]$

$G=\left[2m_f\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]{\displaystyle {\int }_0^L\left[\varphi (x)\left(\frac{d\varphi }{dx}\right)dx-{\left(e_{o}a\right)}^2{\displaystyle {\int }_0^L\varphi (x)}\frac{d^3\varphi }{d{x}^3}dx\right]}$

$K={\displaystyle {\int }_0^L\left(EI+E_s{I}_s\right)\varphi (x)\frac{d^4\varphi }{d{x}^4}dx+k_1}\left[{\displaystyle {\int }_0^L{\varphi }^2(x)dx}-{\left(e_{o}a\right)}^2{\displaystyle {\int }_0^L\varphi (x)}\frac{d^2\varphi }{d{x}^2}dx\right]$

$C=\left(\begin{array}{l}{m}_f{\left[\left(1+a_{k}Kn\right)\left[4\left(\frac{2-{\sigma }_v}{{\sigma }_v}\right)\left(\frac{Kn}{1+Kn}\right)+1\right]\right]}^2\\ +\delta A{\sigma }_x^o-H_s-\eta H_x^{2}A-k_p+\frac{EA\alpha \Delta T}{1-2\nu }\end{array}\right)\left[{\displaystyle {\int }_0^L\varphi (x)\frac{d^2\varphi }{d{x}^2}dx-{\left(e_{o}a\right)}^2{\displaystyle {\int }_0^L\varphi (x)}\frac{d^4\varphi }{d{x}^4}dx}\right]$

$\begin{array}{l}V=k_3\left[{\displaystyle {\int }_0^L{\varphi }^4(x)}dx-{\left(e_{o}a\right)}^2\left(3{\displaystyle {\int }_0^L{\varphi }^3(x)}\frac{d^2\varphi }{d{x}^2}dx+6{\displaystyle {\int }_0^L{\varphi }^2(x)}{\left(\frac{d\varphi }{dx}\right)}^{2}dx\right)\right]\\ +{\displaystyle {\int }_0^L\varphi (x)}\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{d\varphi }{dx}\right)}^{2}dx}\right]\frac{d^2\varphi }{d{x}^2}dx-{\left(e_{o}a\right)}^2{\displaystyle {\int }_0^L\varphi (x)}\left[\frac{EA}{2L}{\displaystyle {\int }_0^L{\left(\frac{d\varphi }{dx}\right)}^{2}dx}\right]\frac{d^4\varphi }{d{x}^4}dx\end{array}$

The circular fundamental natural frequency gives

${\omega }_n=\sqrt{\frac{K+C}{M}}$   (11)

For the simply supported pipe,

$\varphi (x)=sin{\beta }_{n}x$   (12a)

where

$sin\beta L=0\Rightarrow {\beta }_n=\frac{n\pi }{L}$

Therefore,

$\varphi (x)=sin\frac{n\pi x}{L}$   (12b)

Eq. (12) can be written as

$\ddot{u}(t)+\gamma \dot{u}(t)+\alpha u(t)+\beta u^3(t)=0$   (13)

where

$\alpha =\frac{(K+C)}{M},\beta =\frac{V}{M},\gamma =\frac{G}{M},$

For an undamped simple-simple supported structures, where G = 0, we have

$\ddot{u}(t)+\alpha u(t)+\beta u^3(t)=0$   (14)

In order to determine the natural frequency of the vibration, we make use of the transformation, $\tau =\omega t$ , Eq. (14) becomes

${\omega }^2\ddot{u}(\tau )+\alpha u(\tau )+\beta u^3(\tau )=0$   (15)

The symbolic solution of Eq. (15) can be provided by assuming an initial approximation for zero-order deformation to be

$u_o(\tau )=Acos\tau$   (16)

Substitution of Eq. (16) into Eq. (15) provides

$-{\omega }_o^{2}Acos\tau +\alpha Acos\tau +\beta A^{3}cos{}^3\tau =0$   (17)

Through trigonometry identity, we have

$-{\omega }^{2}Acos\tau +\alpha Acos\tau +\beta A^3\left(\frac{3cos\tau +cos3\tau }{4}\right)=0$   (18)

Collection of like terms gives

$\left(\alpha A+\frac{3\beta A^3}{4}-{\omega }^{2}A\right)cos\tau +\frac{1}{4}\beta A^{3}cos3\tau =0$   (19)

The elimination of secular term is produced by making

$\left(\alpha A+\frac{3\beta A^3}{4}-{\omega }_o^{2}A\right)=0$   (20)

Therefore, the zero-order nonlinear natural frequency becomes

${\omega }_o\approx \sqrt{\alpha +\frac{3\beta A^2}{4}}$   (21)

The ratio of the zero-order nonlinear natural frequency to the linear frequency

$\frac{{\omega }_o}{{\omega }_b}\approx \sqrt{\alpha +\frac{3\beta A^2}{4}}$   (22)

Similarly, the first-order nonlinear natural frequency is given as

${\omega }_1\approx \sqrt{\frac{1}{2}\left\{\left[\alpha +\frac{3\beta A^2}{4}\right]+\sqrt{{\left[\alpha +\frac{3\beta A^2}{4}\right]}^2-\left(\frac{3{\beta }^2{A}^4}{32}\right)}\right\}}$   (23)

The ratio of the first-order nonlinear natural frequency to the linear frequency

$\frac{{\omega }_1}{{\omega }_b}\approx \sqrt{\frac{1}{2}\left\{\left[1+\frac{3\beta A^2}{4\alpha }\right]+\sqrt{{\left[1+\frac{3\beta A^2}{4\alpha }\right]}^2-\left(\frac{3{\beta }^2{A}^4}{32{\alpha }^2}\right)}\right\}}$   (24)

The nonlinearity in the above Eq. (15) makes it very difficult to generate closed form solutions to the equations. Therefore; in this work, recourse is made Temini and Ansari method to provide approximate analytical solution to the problem.

Principle of Temini and Ansari method

The principle of the method is described as follows. The general system of nonlinear equation is in the form

$L\left(u(x)\right)+N\left(u(x)\right)+g(x)=0$   (25)

with the boundary conditions

$B\left(u,\frac{du}{dx}\right)=0$   (26)

where x denotes the independent variable, u(x) represents an unknown function, g(x) is a known function, L is a linear operator, N is a nonlinear operator and B is a boundary operator. Since L is taken as the linear (highest order derivative) part of the DE, it is possible to take some or the remaining linear parts of the DE and add them to N as needed. The procedure of the proposed TAM is as follows.

Assuming that u(x) is an initial guess of the solution to the problem u(x) and is the solution of the equation

$L\left(u_0(x)\right)+g(x)=0,B\left(u,\frac{d{u}_0}{dx}\right)=0$   (27)

In order to generate the next improvement to the solution, Eq. (28) is solved

$L\left(u_1(x)\right)+g(x)+N\left(u_0(x)\right)=0,B\left(u_1,\frac{d{u}_1}{dx}\right)=0$   (28)

Following the above procedure, the Temini and Ansari method gives the possibility to write the solution of the general nonlinear equation in the iterative formula

$L\left(u_{n+1}(x)\right)+g(x)+N\left(u_n(x)\right)=0,B\left(u_{n+1},\frac{d{u}_{n+1}}{dx}\right)=0$   (29)

Application of Temini and Ansari method to the nonlinear problem

From Eq. (15), it is clear that

$\ddot{u}(\tau )+\frac{\alpha }{{\omega }^2}u(\tau )+\frac{\beta }{{\omega }^2}{u}^3(\tau )=0$   (30)

Assuming that u(t) is an initial guess of the solution to the problem and is the solution of the equation

The initial problem is

$L\left(u_0(\tau )\right)=0\Rightarrow {\ddot{u}}_0(\tau )=0$   (31)

with initial conditions

$u_o(0)=Acos\tau ,{\dot{u}}_o(0)=0$   (32)

On solving Eq. (32), one arrives at

$u_o(\tau )=Acos\tau$   (33)

In order to generate the next improvement to the solution, Eq. (34) is solved

$L\left(u_1(\tau )\right)+g(\tau )+N\left(u_0(\tau )\right)=0$   (34)

with initial conditions

$u_1(0)=Acos\tau ,{\dot{u}}_1(0)=0$   (35)

Where

$L\left(u_1(\tau )\right)={\ddot{u}}_1(\tau ),N\left(u_0(\tau )\right)=\frac{\alpha }{{\omega }^2}{u}_0(\tau )+\frac{\beta }{{\omega }^2}{u}_0^3(\tau ),g(\tau )=0$

The above equations implies that

${\ddot{u}}_1(\tau )+\frac{\alpha }{{\omega }^2}{u}_0(\tau )+\frac{\beta }{{\omega }^2}{u}_0^3(\tau )=0$   (36)

Which can be written as

${\ddot{u}}_1(\tau )=-\frac{1}{{\omega }^2}\left[\alpha u_0(\tau )+\beta u_0^3(\tau )\right]$   (37)

Substitute Eq. (33) into Eq. (37), we have

${\ddot{u}}_1(\tau )=-\frac{1}{{\omega }^2}\left[\alpha Acos\tau +\beta A^{3}co{s}^3\tau \right]$   (38)

Integrating both sides twice, we have

$u_1(\tau )=-\frac{1}{{\omega }^2}{\displaystyle \underset{0}{\overset{\tau }{\int }}{\displaystyle \underset{0}{\overset{\tau }{\int }}\left(\alpha Acos\tau +\beta A^{3}co{s}^3\tau \right)d\tau d\tau }}$   (39)

Using trigonometric identity in Eq, (39), one arrives at

${\ddot{u}}_1(\tau )=-\frac{1}{{\omega }^2}{\displaystyle \underset{0}{\overset{\tau }{\int }}{\displaystyle \underset{0}{\overset{\tau }{\int }}\left[\alpha Acos\tau +\beta A^3\left(\frac{3cos\tau +cos3\tau }{4}\right)\right]d\tau d\tau }}$   (40)

After the integration, we arrived at

$u_1(\tau )=Acos\tau +\frac{1}{{\omega }^2}\left[\alpha A\left(cos\tau -1\right)+\beta A^3\left(\frac{27\left(cos\tau -1\right)+\left(cos3\tau -1\right)}{36}\right)\right]$   (41)

and subsequent problems can be obtained from the iterative problem generating relation by we build a correcting practical as

$L\left(u_{n+1}(\tau )\right)+g(\tau )+N\left(u_n(\tau )\right)=0$   (42)

with initial conditions

$u_{n+1}(0)=Acos\tau ,{\dot{u}}_{n+1}(\tau )=0$   (43)

where

$L\left(u_{n+1}(\tau )\right)=\ddot{u}(\tau ),N\left(u_{n+1}(\tau )\right)=\frac{\alpha }{{\omega }^2}u(\tau )+\frac{\beta }{{\omega }^2}{u}^3(\tau ),g(\tau )=0$

The solutions of $u_n(\tau )$ form the approximate analytical solutions of $u(\tau )$ . The analytical solutions are simulated and the results are shown below

Recall that $\tau =\omega t$

$u(t)=Acos\omega t+\frac{1}{{\omega }^2}\left[\alpha A\left(cos\omega t-1\right)+\beta A^3\left(\frac{27\left(cos\omega t-1\right)+\left(cos3\omega t-1\right)}{36}\right)+\mathrm{...}\right]$   (45)

where

$\omega \approx \sqrt{\frac{1}{2}\left\{\left[\alpha +\frac{3\beta A^2}{4}\right]+\sqrt{{\left[\alpha +\frac{3\beta A^2}{4}\right]}^2-\left(\frac{3{\beta }^2{A}^4}{32}\right)}\right\}}$

Substitute Eq. (12) and (45) into Eq. (8), we have

$w(x,t)=\left[Acos\omega t+\frac{1}{{\omega }^2}\left[\alpha A\left(cos\omega t-1\right)+\beta A^3\left(\frac{27\left(cos\omega t-1\right)+\left(cos3\omega t-1\right)}{36}\right)\right]+\mathrm{...}\right]\left\{sin\frac{n\pi x}{L}\right\}$   (46)

Figure 1 shows the comparison between the results of Temimi and Ansari method (TAM) and numerical method (NM) using Fourth-order Runge-Kutta method. The obtained results of using TAM as compared with the numerical procedure are in good agreements. The high accuracy of TAM gives high confidence about validity of the method in providing solutions to the problem. Also, the effects of various parameters of the model on the dynamic response of the single-walled carbon nanotube are also presented in the figures under various subsections in the section in Figure 3.

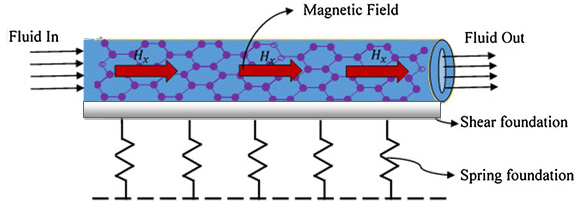
Figure 1 Carbon nanotube conveying hot fluid resting on elastic foundation.

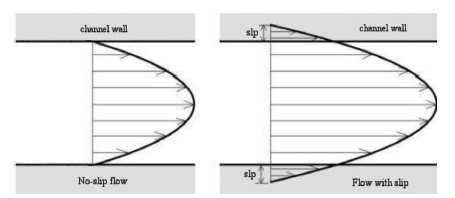
Figure 2 Effect of slip boundary condition on velocity profile.⁵⁹

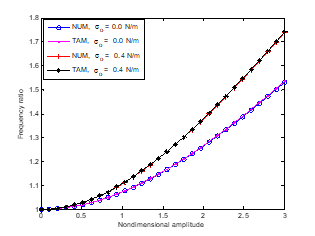
Figure 3 Comparison between the obtained results and the numerical solution for the nonlinear vibration.

The importance of surface residual stress on the vibration behaviour of the nanotube is shown in Figure 4. It is shown that the dynamic response of the nanotube different for negative and positive values of surface residual stress. This establishes that the dynamic behaviour of the fluid-conveying nanotube depends on the sign of the residual surface stress. Indisputably, as it is shown in the figure, at any given dimensional amplitude, there is an increase in the frequency ratio when the negative value of the surface stress increases while the frequency ratio decreases when the positive value of the surface stress increases. This is because, the negative values of surface stress decrease the linear stiffness of the nanostructure while the positive values of surface stress increase the linear stiffness of the carbon nanotube.

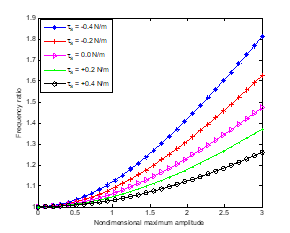
Figure 4 Effect of surface residual stress per unit length on the frequency ratio of the nanotube.

Additionally, the positive surface elasticity produces softening effect in the nanotube, while negative surface elasticity gives stiffening influence in the nanotube. Therefore, it can be stated that when the surface stress is zero, the effect of surface elasticity is not so important. Consequently, one can infer that the surface stress alone is important and effective even without consideration of the surface elasticity. However, when the surface stress is nonzero, the surface elasticity plays a significant role in the dynamic behaviour of the nanostructure.

The importance of surface stress, nonlocality and nanobeam length on the frequency ratio of the fluid-conveying nanostructure is displayed in Figure 5. The figures show that the frequency ratio decreases with increase in the length and thickness ratio of the of the nanotube. It could also be stated that nonlocal parameter reduces the influence of the surface energy and stress on the frequency ratio. The results also presented that the vibration frequency of the nanotube under the consideration of the effects of surface energy and stress is larger than vibration frequency of the nanobeam given by the classical beam theory which does not consider the surface effect. Also, the figures present a clear statement that when the nanotube length increase, the natural frequency of the nanotube gradually approaches the nonlinear Euler–Bernoulli beam limit. This is as a result of decrease in the surface effect. Therefore, high thickness ratios and long nanotube length make the impacts of surface energy and stresses on the on the frequency ratio to vanish. The impact of the initial stress on the dynamic behaviour of the nanotube is shown in Figure 6. It is depicted at any adimensional amplitude increases, there is an increase in the frequency ratio as the initial stress increases.

Figure 5 Effects of the nanotube nonlocal parameter and length on the frequency ratio.

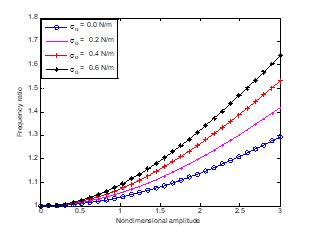
Figure 6 Effect of initial stress on the frequency ratio of the nanotube.

The nonlocal parameter is a scaling parameter which makes the small-scale effect to be accounted in the analysis of microstructures and nanostructures. The effect of the nonlocality on the frequency ratio decrease for varying adimensional amplitude is illustrated in Figure 7. The fundamental frequency ratio of the fluid-conveying structure decreases as the nonlocal parameter increases. Also, the effect of the nonlocality on the frequency ratio decreases by increasing the amplitude ratio of the structure. The variations in the ratio of the frequencies with adimensional nonlocal parameter for different change in temperature are presented in Figure 8&9. In Figure 8, it is shown that increase in temperature change at high temperature causes decrease in the frequency ratio. However, at room or low temperature, the frequency ratio of the hybrid nanostructure increases as the temperature change increases as shown in Fig. 8. Also, the ratio of the frequencies at low temperatures is lower than at high temperatures.

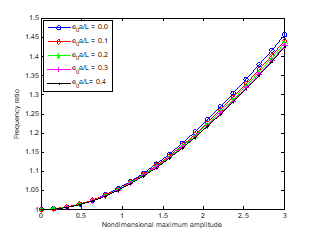
Figure 7 Effects of maximum amplitude and nonlocal parameter on ratio of the frequency ratio.

Figure 8 Effects of change in temperature on the frequency at high temperature.

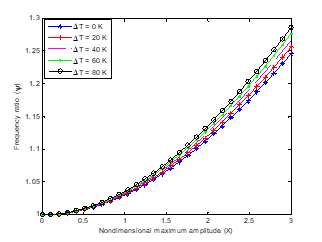
Figure 9 Effects of change in temperature on the frequency ratio at low temperature.

Figure 10 shows the significance of the magnetic field strength on the frequency ratio of the nanotube. It is shown that the frequency ratio decreases when the strength of the magnetic field increases. Also, at high values of magnetic fields and amplitude of vibration, the discrepancy between the nonlinear and the linear frequencies increases. A further investigation shows that the vibration of the nanotube approaches linear vibration when the magnetic force strength increases to a certain high value. Such very high value of magnetic force strength which causes great attenuation in the beam can be adopted as a control and instability strategy for the nonlinear vibration system. 

Figure 10 Effects of magnetic field strength on the frequency ratio.

Comparison of the midpoint deflection of linear and nonlinear vibrations of the nanostructure is analyzed in Figure 11. The nonlinear term causes stretching effect in the nonlinear in the nonlinear vibration. As stretching effect increases, the stiffness of the system increases which consequently increases in the natural frequency and the critical fluid velocity.

Figure 11 Linear and nonlinear dynamic behaviour of the nanostructure.

Figure 12 presents the effect of nonlocal parameter on the vibration of the nanotube. It is depicted that increase in the nonlocal parameter leads to decrease in the frequency of vibration and decrease in the critical velocity. The significance of slip parameter on the dynamic response of the carbon nanotube is shown in Figure 13. From the figure, it is established that increase in the slip parameter causes decrease in the frequency of vibration and the critical velocity. Also, the Figures depict the critical speeds corresponding to the divergence condition for different values of the system’s parameters for the varying nonlocal and slip parameters.

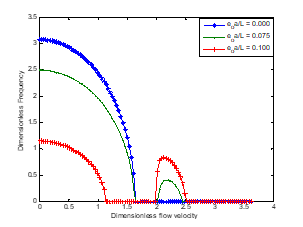
Figure 12 Effects of nonlocal parameter and fluid flow velocity on the natural frequency of the nonlinear vibration.

Figure 13 Effects Slip parameter (Knudsen number) on the natural frequency of the nonlinear vibration.

In the current paper, Galerkin decomposition and Temini and Ansari methods have been applied to explore the simultaneous impacts of surface elasticity, initial stress, residual surface tension and nonlocality on the nonlinear vibration of single-walled carbon conveying nanotube resting on linear and nonlinear elastic foundation and operating in a thermo-magnetic environment have been analyzed. Through the parametric studies, it was revealed that the

1. Ratio of the nonlinear to linear frequencies increases with the negative value of the surface stress while it decreases with the positive value of the surface stress  At any given value of nonlocal parameters, the surface effect reduces for increasing in the length of the nanotube.
2. Ratio of the frequencies decreases with increase in the strength of the magnetic field, nonlocal parameter and the length of the nanotube. The natural frequency of the nanotube gradually approaches the nonlinear Euler–Bernoulli beam limit at high values of nonlocal parameter and nanotube length.
3. Nonlocal parameter reduces the surface effects on the ratio of the frequencies.
4. Increase in temperature change at high temperature causes decrease in the frequency ratio. However, at room or low temperature, the frequency ratio of the hybrid nanostructure increases as the temperature change increases. Also, the ratio of the frequencies at low temperatures is lower than at high temperatures.
5. Increase in the nonlocal and slip parameters leads to decrease in the frequency of vibration and decrease in the critical velocity.

It is hoped that through this study, the control and design of carbon nanotubes operating in thermo-magnetic environment and resting on elastic foundations will be greatly enhanced.

None.

The author declares that there is no conflict of interest.

None.

1. Iijima S. Helical microtubules of graphitic carbon. Nature. 1991;354:56–58.
2. Abgrall, Nguyen NT. Nanofluidic devices and their applications. Anal Chem. 2008;80:2326–234.
3. Zhao D, Liu Y, Tang YG. Effects of magnetic field on size sensitivity of nonlinear vibration of embedded nanobeams. Mech Adv Mater Struct. 2018;1–9.
4. Azrar A, Ben Said M, Azrar L, et al. Dynamic analysis of Carbon Nanotubes conveying fluid with uncertain parameters and random excitation. Mech Adv Mater Struct. 2018;1–16.
5. Rashidi V, Mirdamadi HR, Shirani E. A novel model for vibrations of nanotubes conveying nanoflow. Comput Mater Sci. 2012;51:347–352.
6. Reddy JN, Pang S. Nonlocal continuum theories of beams for the analysis of carbon nanotubes. J Appl Phys. 2008;103:023511.
7. Wang L. A modified nonlocal beam model for vibration and stability of nanotubes conveying fluid. Physica E. 2011;44:25–28.
8. Lim CW. On the truth of nanoscale for nanobeams based on nonlocal elastic stress field theory: equilibrium, governing equation and static deflection. Appl Math Mech. 2010;31:37–54.
9. Lim CW, Yang Y. New predictions of size-dependent nanoscale based on nonlocal elasticity for wave propagation in carbon nanotubes. J Comput Theor Nanoscience. 2010;7:988–995.
10. Bahaadini R, Hosseini M. Nonlocal divergence and flutter instability analysis of embedded fluid-conveying carbon nanotube under magnetic field. Microfluid Nanofluid. 2016;20:108.
11. Mahinzare M, Mohammadi K, Ghadiri M, et al. Size-dependent effects on critical flow velocity of a SWCNT conveying viscous fluid based on nonlocal strain gradient cylindrical shell model. Microfluid Nanofluid. 2017;21:123.
12. Bahaadini R, Hosseini M. Flow-induced and mechanical stability of cantilever carbon nanotubes subjected to an axial compressive load. Appl Math Modell. 2018;59:597–613.
13. L Wang. Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Physica E. 2010;43:437–439.
14. Zhang J, Meguid SA. Effect of surface energy on the dynamic response and instability of fluid-conveying nanobeams. Eur J Mech A/Solids. 2016;58:1–9.
15. Hosseini M, Bahaadini R, Jamali B. Nonlocal instability of cantilever piezoelectric carbon nanotubes by considering surface effects subjected to axial flow. J Vib Control. 2016.
16. Bahaadini R, Hosseini M, Jamalpoor A. Nonlocal and surface effects on the flutter instability of cantilevered nanotubes conveying fluid subjected to follower forces. Physica B. 2017;509:55–61.
17. Wang GF, Feng XQ. Effects of surface elasticity and residual surface tension on the natural frequency of micro-beams. J App Phys. 2007;101:013510.
18. GF Wang, Feng XQ. Surface effects on buckling of nanowires under uniaxial compression. Appl Phys Lett. 2009;94:1419133.
19. Farshi B, Assadi A, Alinia ziazi A. Frequency analysis of nanotubes with consideration of surface effects. Appl Phys Lett. 2010;96:093103.
20. Lee HL, Chang WJ. Surface effects on axial buckling of non-uniform nanowires using non-local elasticity theory. Micro & Nano Letters. 2011;6(1):19–21.
21. Lee HL, Chang WJ. Surface effects on frequency analysis of nanotubes using nonlocal Timoshenko beam theory. J Appl Phys. 2010;108:093503.
22. Guo JG, Zhao YP. The size dependent bending elastic properties of nanobeams with surface effects. Nanotechnology. 2007;18:295701.
23. Feng XQ, Xia R, Li XD, et al. Surface effects on the elastic modulus of nanoporous materials. Appl Phys Lett. 2009;94:011913.
24. He J, Lilley CM. Surface stress effect on bending resonance of nanowires with different boundary conditions. Appl Phys Lett. 2008;93:263103–8.
25. He J, Lilley CM. Surface effect on the elastic behavior of static bending nanowires. Nano Lett. 2008;8:1798–1802.
26. Jing GY, Duan HL, Sun XN, et al. Surface effects on elastic properties of silver nanowires: contact atomic-force microscopy. Phys Rev B. 2010;73:235406.
27. Sharm P, Ganti S, Bhate N. Effect of surfaces on the size-dependent elastic state of nano-inhomogeneities. Appl Phys Lett. 2003;82:535–537.
28. ZQ Wang, Zhao YP, Huang ZP. The effects of surface tension on the elastic properties of nano structures. Int J Eng Sci. 2010;48:140–150.
29. Selim MM.Vibrational analysis of carbon nanotubes under initial compression stresses. NANO Conference. King Saud University; KSA; 2009.
30. Zhang H, Wang X. Effects of initial stress on transverse wave propagation in carbon nanotubes based on Timoshenko laminated beam models. Nanotechnoology. 2006;17:45–53.
31. Wang X, Cai H. Effects of initial stress on non-coaxial resonance of multi-wall carbon nanotubes. Acta Mater. 2006;54:2067–2074.
32. Liu K, Sun C. Vibration of multi-walled carbon nanotubes with initial axial loading. Solid State Communications. 2007;143:202–207.
33. Chen X, Wang X. Effects of initial stress on wave propagation in multi-walled carbon nanotubes. Phys Scr. 2008;78:015601.
34. Selim MM. Torsional vibration of carbon nanotubes under initial compression stress. Brazilian J Phys. 40(3):283.
35. Selim MM. Vibrational Analysis of Initially Stressed Carbon. Acta Physica. 2011;119.
36. Selim MM. Vibrational analysis of initially stressed carbon nanotubes. Acta Phys Pol A. 2011;119(6):778–782.
37. Selim MM, El Safty SA. Vibrational analysis of an irregular single-walled carbon nanotube incorporating initial stress effects. Nanotechnology Reviews. 2020;9:1481–1490.
38. Temimi H, Ansari AR. A semi analytical iterative technique for solving nonlinear problems. Comput Math Appl. 2011;61:203–210.
39. Temimi H, Ansari AR. A new iterative technique for solving nonlinear second order multi point boundary value problems. Appl Math Comput. 2011;218:1457–1466.
40. Temimi H, Ansari AR. A computational iterative method for solving nonlinear ordinary differential equations. LMS J Comput Math. 2015;18:730–753.
41. Al Jawary MA, Al Razaq SG. A semi analytical iterative technique for solving duffing equations. Int J pure app Math. 2016;108(4):871–885.
42. Ehsani F, Hadi A, Ehsani F, et al. An iterative method for solving partial differential equations and solution of Kortewegde Vries equations for showing the capability of the iterative method. World App Program. 2013;3(8):320–327.
43. Al Jawary MA, Raham RK. A semi-analytical iterative technique for solving chemistry problems. J King Saud Univer Sci. 2017;29(3):320–332.
44. Al-Jawary MA. A semi-analytical iterative method for solving nonlinear thin film flow problems. Chaos, Solitons & Fractals. 2017;99:52–56.
45. Al-Jawary MA, Radhi GH, Ravnik J. Semi-analytical method for solving Fokker-Planck’s equations. J Assoc Arab Univer Basic App Sci. 2017;24:254–262.
46. Al-Jawary MA, Hatif S. A semi-analytical iterative method for solving differential algebraic equations. Ain Shams Eng J. 2018;9(4):2581–2586.
47. Al-Jawary MA, Al-Qaissy HR. A reliable iterative method for solving Volterra integro-differential equations and some applications for the Lane–Emden equations of the first kind. Monthly Notices of the Royal Astronomical Society. 2015;448(4):3093–3104.
48. Al-Jawary MA, Adwan MI, Radhi H. Three iterative methods for solving second order nonlinear ODEs arising in physics. J King Saud Univer Sci. 2020;32(1):312–323.
49. Al-Jawary MA, Mohammed AS. A Semi-Analytical Iterative Method for Solving Linear and Nonlinear Partial Differential Equations. Int J Sci Res. 2015;6(5):978–982.
50. Al-Jawary MA, Nabi AZA. Reliable iterative methods for solving convective straight and radial fins with temperature-dependent thermal conductivity problems. Gazi Univer J Sci. 2019;32(3):967–989.
51. Yassein SM. Application of Iterative Method for Solving Higher Order Integro-Differential Equations. Ibn AL Haitham J Pure App Sci. 2019;32(2):51–61.
52. Agheli B. Solving fractional Bratu’s equations using a semi analytical technique. Punjab Univer J Math. 20220;51(9).
53. Sobamowo MG, Adeleye OA. Application of a New Iterative Method to Analysis of Kinetics of Thermal Inactivation of Enzyme. UPB Sci Bull Series B. 2019;81(1).
54. Ehsani F, Hadi F, Ehsani R. An iterative method for solving partial differential equations and solution of Kortewegde Vries equations for showing the capability of the iterative method. World Appl Program. 2013;3(8):320–327.
55. Eringen AC. Nonlocal polar elastic continua. Int J Eng Sci. 1972;10(1):1–16.
56. Eringen AC. Linear theory of nonlocal elasticity and dispersion of plane waves. Int J Eng Sci. 1972;10(5):425–435.
57. Eringen AC. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys. 1983;54(9):4703–4710.
58. Arania GA, Roudbaria MA, Amir S. Longitudinal magnetic field effect on wave propagation of fluid conveyed SWCNT using Knudsen number and surface considerations. Applied Mathematical Modelling. 2016;40:2025–2038.
59. Bahaadini R, Hosseini M. Effects of nonlocal elasticity and slip condition on vibration and stability analysis of viscoelastic cantilever carbon nanotubes conveying fluid. Comput Mater Sci. 2016;114:151–159.