hyperstatic mechanism, geometric tolerancing, thermo-mechanics, polytope

The development of new manufacturing methods and the revolution in the production system enable the design of innovative systems with high-performance and most of time complex geometries and architectures (i.e. high-efficiency engines, lightweight aircraft structures, etc.). This is also the case in the aeronautic field for which the overall performance of aeronef requires rigorous optimization of both the engines and the structure. At the mechanical system level (i.e. turboshaft engine), methods and tools take into account variations in component parts and movement restrictions imposed in contact to simulate system compliance with functional requirements (stator rotor clearance, flush, etc.). The tolerance optimization is a critical point to address since the mechanisms most of time corresponds to hyperstatic architectures. In such cases, the contact between surfaces of parts induced by these architectures considerably increases the complexity of the problems to be solved. More to this, the parts are generally assumed to have an infinitely rigid behaviour. This limitation should be overcome in case of flexible parts of the mechanisms subject to thermal expansion and external mechanical loads.

Studies introduced by Fleming in 1988 provided the foundation for a variational approach to tolerance analysis, based on operations by sets of geometric constraints.¹ A set of geometric constraints defines all the possible positions of a surface within a tolerance zone² which can be generated by offsets of the nominal model of the part.³ In this way the geometric variations of a part that are compliant with ISO specifications for orientation or position tolerances can be characterised.^4‒7 In the same way, a set of geometric constraints can also be used to characterise all relative positions between two distinct surfaces that are potentially in contact.⁸ Fleming established the correlation between cumulative defect limits on parts in contact and the Minkowski sum of finite sets of geometric constraints.¹ A detailed synthesis of this is given in.⁹ Algorithms of Minkowski sums applied to the problem of tolerance analysis have also been developed.^10,11 Giordano showed that modelling the relative positions of two parts resulting from several potential contacts can be formalised by an operation involving the intersection of sets of geometric constraints.¹² More generally, the variational approach to tolerancing consists of characterising the relative position of two surfaces from any two parts of a system by intersections and Minkowski sums of sets of geometric constraints derived from ISO specifications for the parts and specifications formulated specifically for two parts potentially in contact.¹³

The variational approach to geometric tolerancing differs from parametric approaches.¹⁴ Parametric approaches, especially those used in the various commercial tools, formalise the relative position of any two surfaces of a mechanism at a specific point by a simple relation (linear or non-linear) between parameters of position (translation and/or rotation). This relation is obtained using either an analytical method^15‒18 or a Monte Carlo method.¹⁹ This type of approach does not support the redundancy of suppressing degrees of freedom between two parts. In addition, it is generally necessary to generate several equations to simulate the relative position of two surfaces. Historically the procedures for tolerance analysis using a variational or parametric approach are based on the following physical hypotheses: no defect in the shape of the real surfaces, no local strain on surfaces in contact, and no flexible parts. Many studies have been developed using a parametric approach where distortion in the parts is taken into account. Some models can simulate the geometric variations of an aeronautical structure^20,21 or an automobile structure^22,23 by seeking to minimise strains caused in the parts by the assembly process. Maciej et al. have proposed a tolerance analysis platform incorporating the strain caused in parts by the assembly process and the dynamic behaviour of a mechanical system.²⁴

In a variational approach using domains, Giordano et al. have incorporated local strains in surfaces in contact in a ball bearing and in a cylindrical gear transmission.²⁵ The aim of this study is to propose a multiphysical approach, able to take into account variability’s due to the processes involved in obtaining and assembling the parts, as well as variations due the thermo-mechanical behaviour of the parts. This multiphysical approach uses a variational method based on operations on polytopes. This means that each geometric constraint is a halfspace of which the boundary is a hyperplane of the affine space of dimension n, which we will call n-hyperplane. The domains developed by Giordano et al.,¹² and T-Maps developed by Davidson et al.,⁷ manipulate halfspaces of which the boundaries are generally not linear. In the first part, we describe modelling the topological structure of a mechanical system by means of a contact graph with one connected component. Next we present the method for determining geometric variations in a mechanical system within reference behaviour. In the context of the reference behaviour all the parts are at 20°C and are considered as being infinitely rigid: the geometric variations considered are only those resulting from processes for obtaining the parts and the assembly processes.

The second part of the article sets out the physical hypotheses that define thermo-mechanical behaviour when a mechanical system is subjected to a thermal field. The method we propose incorporates thermo-mechanical strains into the geometric variations of the parts and contacts. Thermo-mechanical strains are determined using a finite element model. An example of analysis of a functional requirement is also described in parts one and two.

In the third part, we examine a global procedure which can be used to simulate geometric variations in a system for an operating cycle discretized into several specific behaviours, and finally we discuss future developments and prospects for this work.

Here we define a mechanical system in reference behaviour where the following physical hypotheses are put forward: there is no defect in the shape of the real surfaces, no local strain on surfaces in contact, and no flexible parts.

Defining and setting the parameters of geometric deviations

Characterisation of the geometric deviations of a part:

Real surfaces, those resulting from the manufacturing process, are modelled by substituted surfaces.²⁶ A substituted surface is an ideal surface (i.e. geometrically perfect) of the same type as the nominal surface of which it characterises particular physical features, i.e. a surface that is nominally cylindrical will be modelled by a cylindrical substituted surface. Figure 1 shows the nominal model and the model of the substituted surfaces of a part. In particular, we can see the cylindrical substituted surfaces 1,1 and 1,2 which correspond to nominal cylindrical surfaces 1,1n and 1,2n respectively. The nominal model is by definition the geometrically perfect model used in the CAD/CAM system. The geometric defects of a real surface can be simulated on the substituted surface model, using situation deviations and dimension deviations.

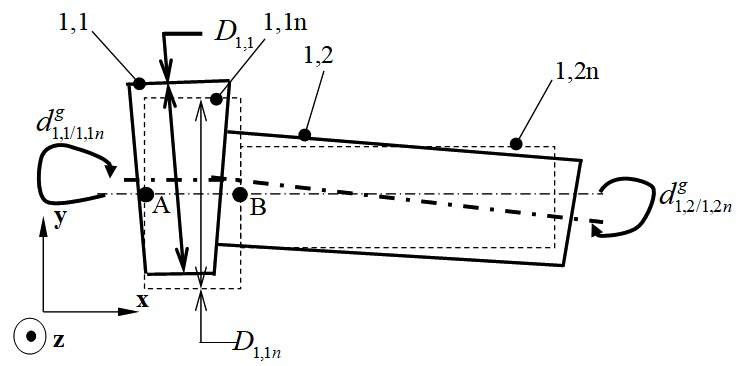
Figure 1 Geometric deviations (situation deviations and dimension deviations).

Situation deviations define the positioning of situation elements of the substituted surface in relation to those of the corresponding nominal surface being used as a reference.²⁰ In Figure 1, $d_{1,1/1,1n}^g$ and $d_{1,2/1,2n}^g$ illustrate situation deviations between surfaces 1,1 and 1,1n and between surfaces 1,2 and 1,2n respectively. The difference between the diameter of the substituted surface, denoted $D_{1,1}$ , and the diameter of the nominal surface, denoted $D_{1,1n}$ , is the dimension deviation of a cylindrical surface denoted $d_{1,1}$ (see Figure 1):

$D_{1,1}-D_{1,1n}=d_{1,1}$ (1)

The situation and dimension deviations define the geometric deviations of a part. Situation deviations can be formalised mathematically by a small displacement torsor²⁷ to characterise the situation deviations between two surfaces.

The following equation expresses the small displacement torsor of substituted surface 1,1 in relation to the nominal surface 1,1n denoted $\left[d_{1,1/1,1n}^g\right]$ at point B:

$\left[d_{1,1/1,1n}^g\right]={}_{\text{B}}\left[\begin{array}{c}{\rho }_{1,1/1,1n}\\ {\epsilon }_{\mathrm{B}-1,1/1,1n}\end{array}\right]$ (2)

Vector ${\rho }_{1,1/1,1n}$ characterises the rotation deviations, while vector ${\epsilon }_{B\text{-}1,1/1,1n}$ characterises the translation deviations at point B (see Figure 1).

According to the property of the small displacements field, we than have:²⁷

${\epsilon }_{N\text{-}1,1/1,2}={\epsilon }_{M\text{-}1,1/1,2}+NM\times {\rho }_{1,1/1,2}\forall N,\forall M\in \text{euclidean}\text{space}$ (3)

Thus, the relative position between surfaces 1,1 and 1,2 can be deduced from the equation:

$\left[d_{1,1/1,2}^g\right]=\left[d_{1,1/1,1n}^g\right]+\left[d_{1,1n/1,2n}^g\right]+\left[d_{1,2n/1,2}^g\right]=\left[d_{1,1/1,1n}^g\right]+\left[d_{1,2n/1,2}^g\right]$ (4)

The geometric deviations between the two nominal surfaces 1,1n and 1,2n are by definition null. Let us consider the coaxiality specification shown in Figure 2a. According to,⁴ the axis of the cylindrical substituted surface 1,1 is contained within a tolerance zone ZT. ZT is a cylinder of diameter $\varnothing t_{1,1}$ and its axis coincides with axis A (axis of cylinder 1,2), see Figure 2b. To ensure that the axis of surface 1,1 is located within the tolerance zone ZT, the following equation should be written at the two extremities A and B, where $n_{\theta i}$ is a unitary vector orthogonal to axis A and $n$ is the angular discretization step around axis A:

$\left\{\begin{array}{l}-\frac{t_{1,1}}{2}\le {\epsilon }_{A\text{-}1,1/1,2}.n_{\theta i}\le \frac{t_{1,1}}{2}\\ -\frac{t_{1,1}}{2}\le {\epsilon }_{B\text{-}1,1/1,2}.n_{\theta i}\le \frac{t_{1,1}}{2}\end{array}\right\}\text{with}\{\begin{array}{l}{n}_{\theta i}=\cos {\theta }_i.y+\sin {\theta }_i.z\hfill \\ {\theta }_i=i\frac{\pi }{n}\text{,}0\le i<n\text{and}\left(i,n\right)\in \mathbb{N}\hfill \end{array}$ (5)

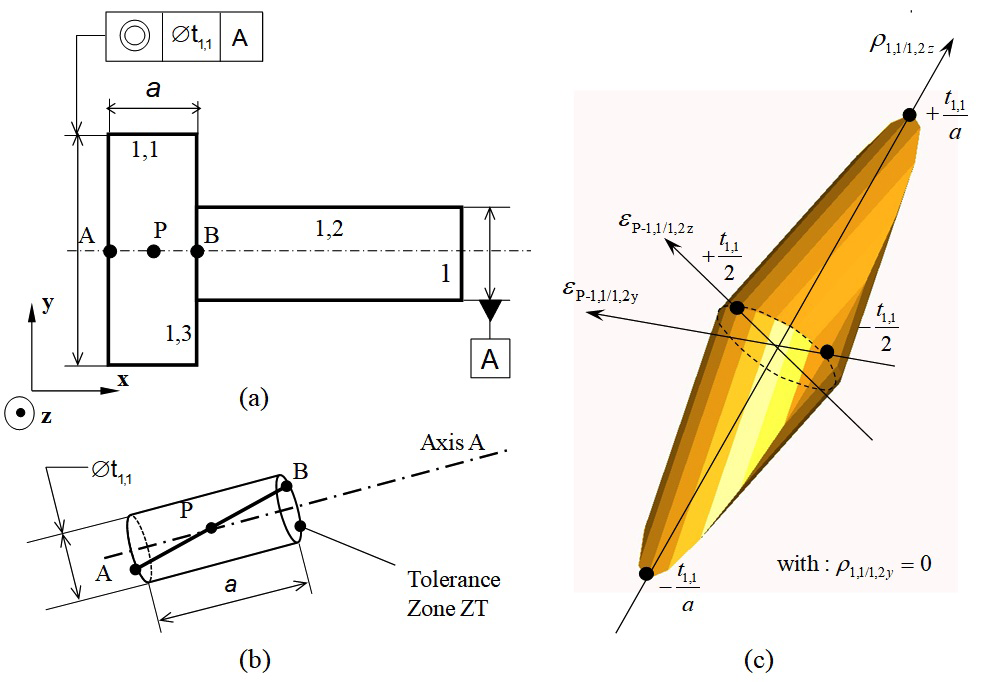
Figure 2 Coaxiality modelled by a geometric polytope.

By expressing equation (5) in terms of  (3) as a function of translation deviations at point P in the middle of the line segment limited by A and B, in the base (x,y,z)if we postulate AB=a we have:

$\begin{array}{l}\left\{\begin{array}{l}-\frac{t_{1,1}}{2}\le \cos {\theta }_i.\left({\epsilon }_{\text{P-}1,1/1,2y}-\frac{a}{2}.{\rho }_{1,1/1,2z}\right)+\sin {\theta }_i.\left({\epsilon }_{\text{P-}1,1/1,2z}+\frac{a}{2}.{\rho }_{1,1/1,2y}\right)\le \frac{t_{1,1}}{2}\\ -\frac{t_{1,1}}{2}\le \cos {\theta }_i.\left({\epsilon }_{\text{P-}1,1/1,2y}+\frac{a}{2}.{\rho }_{1,1/1,2z}\right)+\sin {\theta }_i.\left({\epsilon }_{\text{P-}1,1/1,2z}-\frac{a}{2}.{\rho }_{1,1/1,2y}\right)\le \frac{t_{1,1}}{2}\end{array}\right\}\\ \text{with : }{\theta }_i=i\frac{\pi }{n}\text{,}0\le i<n\text{and}\left(i,n\right)\in \mathbb{N}\end{array}$ (6)

The equations in (6) form a finite set of closed halfspaces of ${ℝ}^4$ . Respecting these equations (6) can be formalised by an intersection limited to a finite number of closed halfspaces of which the boundaries are hyperplanes of ${ℝ}^4$ .¹³ Generally, the H-representation of a polytope of ${ℝ}^n$ can then be formalised.^28,29 Thus the equations in (6) characterise a polytope which we will call a geometric polytope, denoted ${\mathfrak{D}}_{1,1/1,2}^{\text{g}}$ , of the coaxiality specification of 1,1 in relation to 1,2. This is a 4-polytope which can be represented graphically in ${ℝ}^3$ for ${\rho }_{1,1/1,2y}=0$ for example, see Figure 2c. In the same way, it is possible to define a geometric polytope that represents the boundaries of the situation deviations of all orientation or position specifications.¹³

Characterisation of the geometric deviations between two surfaces potentially in contact:

The definition of contact between two surfaces, i.e. a joint, can be expressed using a set of parameters. There have been several studies on this subject.^30-32 Hereafter we will use the definition proposed in,³³ which is a direct application of that proposed in.³² A joint is defined by its type (planar pair, cylindrical pair, ball and cylinder pair, etc.),³⁴ its situation element(s) (plane, line, point), its nature (fixed, sliding or floating) and by its clearance (minimal clearance, maximal clearance).³³

Consider Figure 3: two parts 1 and 2 are in contact via their respective surfaces 1,2 and 2,2 and also via surfaces 1,3 and 2,3.The joint between surfaces 1,2 and 2,2 is a cylindrical pair type and the situation element is a line (B,x). Contact is of a floating nature, with clearance J being the difference between the diameter of surface 2,2 (bore) and the diameter of surface 1,2 (shaft):

$J=D_{2,2}-D_{1,2}$ (7)

Figure 3 Contact specifications.

The joint between surfaces 1,3 and 2,3 is a planar pair type and the situation element is a plane (B,x). Contact is of a sliding nature and hence clearance is null.³³ Situation deviations between two surfaces that are potentially in contact can be formalised mathematically by a small displacement torsor. The torsor $d_{1,2/2,2}$ defines deviations in the joint between surfaces 1,2 and 2,2 at point B:

$\left[d_{1,2/2,2}^{}\right]={}_{\text{B}}\left[\begin{array}{c}{\rho }_{1,2/2,2}\\ {\epsilon }_{B\text{-}1,2/2,2}\end{array}\right]$ (8)

Equation (9) defines the different positions between surfaces potentially in contact for any point N on the contact surface $E_c$ according to $n_N$ , with a vector normal to $E_c$ at point N:

$\forall N\in E_c{\epsilon }_{N\text{-}1,2/2,2}.n_N\le J$ (9)

The contact surface $E_c$ is the intersection of the surfaces in contact in the specific configuration where:

1. Situation deviations between the two surfaces are null (the situation elements of the surfaces are the same),
2. Intrinsic dimensions (diameter of a cylinder, angle at the top of a cone, etc.) of the two surfaces are the same.

Distance d_N is the local distance in N between the two surfaces in contact according to n_N specifically in the position where situation deviations between the two surfaces are null. In the example of contact between surfaces 1,2 and 2,2, $E_c$ is a cylinder and its axis is the line segment [B,C] and $d_N=\frac{J}{2}$ .

As when characterising the geometric deviations of a part, equation (9) should be written at the two extremities B and C of the axis of the cylindrical contact surface where n is the angular discretization step around axis (B,x) of the contact surface cylinder:

$\begin{array}{l}\left\{\begin{array}{l}{\epsilon }_{\text{B-}1,2/2,2}.n_{\theta i}\le \frac{J}{2}\\ {\epsilon }_{\text{C-}1,2/2,2}.n_{\theta i}\le \frac{J}{2}\end{array}\right\}\text{with}\{\begin{array}{l}{n}_{\theta i}=\cos {\theta }_i.y+\sin {\theta }_i.z\hfill \\ {\theta }_i=i\frac{2\pi }{n}\text{,}0\le i<n\text{et}\left(i,n\right)\in \mathbb{N}\hfill \end{array}\Rightarrow \\ \left\{\begin{array}{l}-\frac{J}{2}\le {\epsilon }_{\text{B-}1,2/2,2}.n_{\theta i}\le \frac{J}{2}\\ -\frac{J}{2}\le {\epsilon }_{\text{C-}1,2/2,2}.n_{\theta i}\le \frac{J}{2}\end{array}\right\}\text{with}\{\begin{array}{l}{n}_{\theta i}=\cos {\theta }_i.y+\sin {\theta }_i.z\hfill \\ {\theta }_i=i\frac{\pi }{n}\text{,}0\le i<n\text{et}\left(i,n\right)\in \mathbb{N}\hfill \end{array}\end{array}$ (10)

Equations (10) are called non-interference constraints.³² Equations (10) written as a function of the translation deviations of the midpoint of the line segment limited by B and C, characterise the contact polytope ${\mathfrak{D}}_{1,2/2,2}^{\text{c}}$ defined in the base (x,y,z) by:                                                           

This is a 4-polytope defined by its graphic representation in  for  which is similar to polytope ${\mathfrak{D}}_{1,1/1,2}^{\text{g}}$ shown in Figure 2.

If $d_N=\frac{J}{2}\le 0$ (in the case of clamping), the contact polytope is a vertex centred on the origin according to the physical hypotheses formulated at the beginning of section 2. In this case, the joint is defined as one of fixed contact.³³ In the same way, a contact polytope can be defined which characterises the limits of the situation deviations of surfaces potentially in contact for all types of joints (spherical pair, ball and cylinder pair, ball and plane pair, etc.) defined in.^34,13

Topological structure of a mechanical system, condition for cycle closure

Formalising the topological structure of a mechanism may be based on a contact graph with one connected component on which the dimension chains³⁵ can be visualised. Figure 4, based on Figure 3, is a graphic representation of the mechanism consisting of a shaft labelled 1 and housing labelled 2. The shaft is represented by a large circle and the three surfaces 1,1, 1,2 and 1,3 are small circles. All the nominal surfaces of the shaft are represented in a single small circle, called 1,0, representing a marker associated to the nominal model of part 1.² The edge linking surface 1,1 to vertex 1,0 represents situation deviations for surface 1,1 in relation to its nominal surface. The edges that link together two surfaces belonging to two different parts represent the joints. For example, the edge that links surface 1,2 to surface 2,2 represents the cylindrical pair joint (label CP) between surfaces 1,2 and 2,2 while the edge linking surface 1,3 to 2,3 represents the planar pair joint (label PP). The features of these two joints are described in paragraph 2.1.2 and are shown in Figure 3.

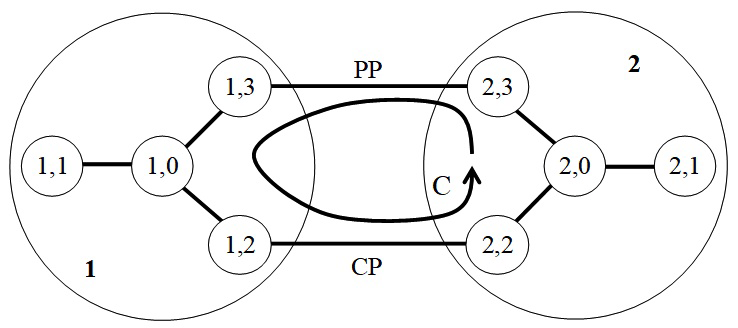
Figure 4 Graph representation.

We searched for independent cycles in order to determine which equations guaranteed that a mechanism can exist, i.e. that it can be assembled. The number of independent cycles is the cyclomatic number $\mu$ of the graph. In a graph with one connected component,$\mu$ is defined as follows:

$\begin{array}{l}\mu =e-v+1\\ \text{with:}\\ e\text{: number of edges of the graph}\\ v\text{: number of vertices of the graph}\end{array}$ (12)

In our example:

$\mu =8-8+1=1$ (13)

For each cycle closure,³⁶ considers that the condition of interchange ability can be verified if the sum of the deviation hulls, written $\left[{\text{E}}_{i,j/i,k}^{}\right]$ , is included in the sum of the clearance hulls, written $\left[{\text{J}}_{i,j/u,v}^{}\right]$ . This condition guarantees assembly in the worst case, thus in our example:

$\left(\left[{\text{E}}_{2,2/2,3}\right]+\left[{\text{E}}_{1,3/1,2}\right]\right)\subseteq \left(\left[{\text{J}}_{1,2/2,2}^{\min }\right]+\left[{\text{J}}_{2,3/1,3}\right]\right)$ (14)

In our case, condition (14) which is formalised by the hulls can be transposed by operations on polytopes. ${\mathfrak{D}}_{i,j/u,v}^{\text{c,min}}$ represents the contact polytope in the minimum clearance configuration that corresponds to the most unfavourable case for an assembly condition.

$\left({\mathfrak{D}}_{2,2/2,3}^{\text{g}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g}}\right)\subseteq \left({\mathfrak{D}}_{1,2/2,2}^{\text{c,min}}+{\mathfrak{D}}_{2,3/1,3}^{\text{c}}\right)$ (15)

Figure 5 shows how the Minkowski sum of the two contact polytopes is determined, where polytope ${\mathfrak{D}}_{1,2/2,2}^{\text{c,min}}$ characterises the CP joint in the minimum clearance configuration. The two geometric polytopes ${\mathfrak{D}}_{1,2/1,3}^{\text{g}}$ and ${\mathfrak{D}}_{2,2/2,3}^{\text{g}}$ correspond to two perpendicularity specifications on parts 1 and 2 respectively (see Figure 6).

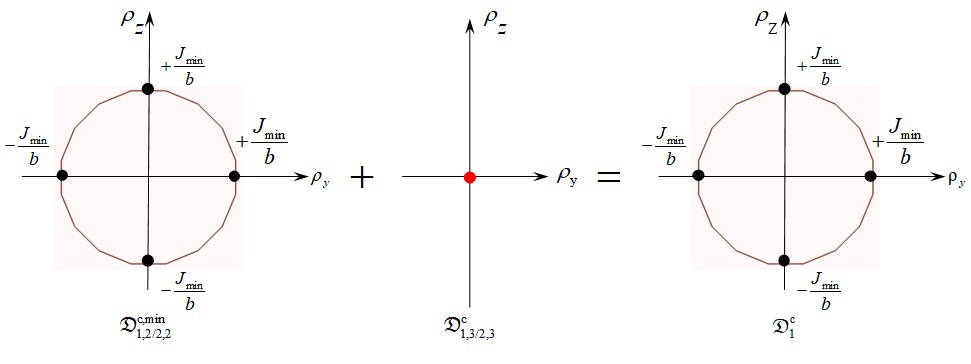
Figure 5 Minkowski sum of contact polytopes.

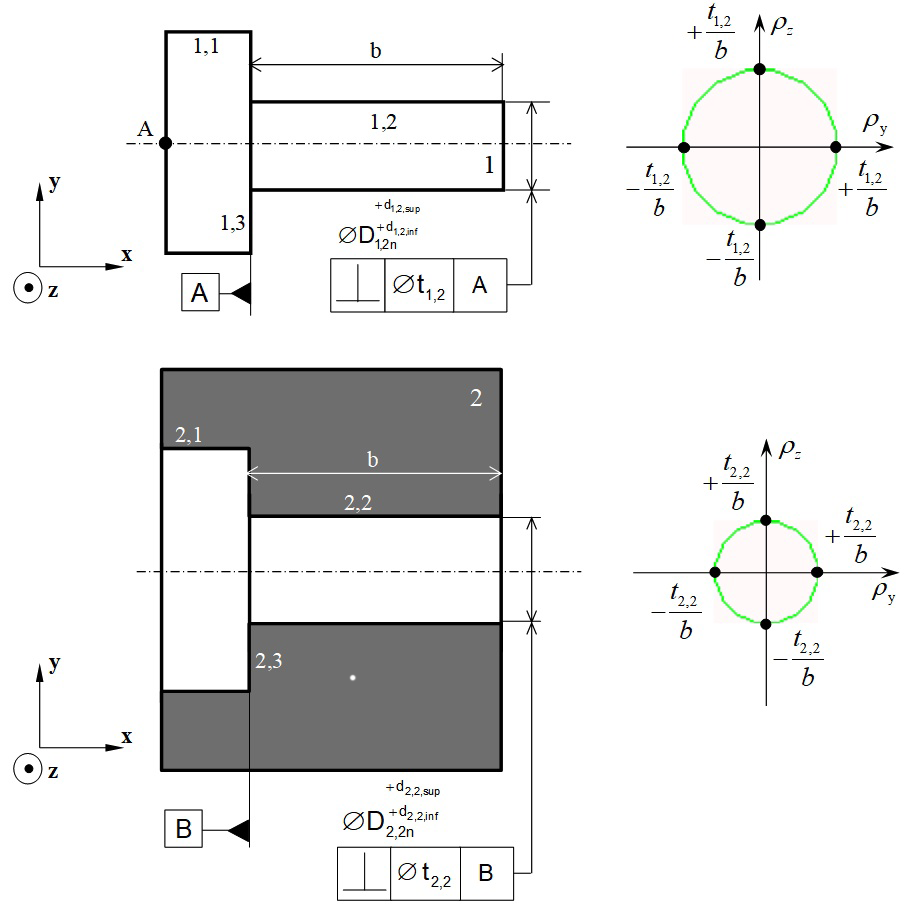
Figure 6 Perpendicularity specifications modelled by geometric polytopes.

Finally, Figure 7 illustrates equation (15) where the sum of geometric polytopes must be inside the sum of contact polytopes in a cycle. From this, we deduce the condition for assembling the system in the worst case scenario, as defined in the following equation:

$\frac{t_{1,2}}{b}+\frac{t_{2,2}}{b}\le \frac{J_{\min }}{b}$ (16)

Figure 7 Inclusion of a sum of geometric polytopes inside a sum of contact polytopes in a cycle.

Simulation of respecting a functional condition

A functional condition (or requirement) is a condition placed on a functional characteristic of position or orientation between two surfaces, which are usually on different parts, and which are not potentially in contact. Figure 8 illustrates the example presented above. Let us suppose that a functional condition FC has to be respected which limits the relative position of surfaces 1,1 and 2,1. In the diagram this is represented in a rectangle labelled FC on an edge linking surfaces 1,1 and 2,1. This example shows a condition of coaxiality being modelled in a unidirectional functional condition. The functional condition FC limits the displacement of point A on the axis of surface 1,1 in relation to the axis of surface 2,1 along axis y:

${\mathrm{e}}_{\min }\le e\le {\mathrm{e}}_{\max }\text{ with }e={\epsilon }_{\text{A-}1,3/2,3}.y$ (17)

Equation (17) represents two halfspaces of dimension 1, whose intersection defines the functional polytope ${\mathfrak{D}}_{1,1/\text{2,1}}^{\text{f}}$ characterising the functional condition FC. The functional condition FC depends on two cycles C₁and C₂: see Figure 8. For the FC to be respected, the intersection of the two geometric polytopes representing the deviations between surfaces 1,1 and 2,1 by C₁ and C₂ respectively must be included in the functional polytope ${\mathfrak{D}}_{1,1/\text{2,1}}^{\text{f}}$ :¹³

$\begin{array}{l}\left({\mathfrak{D}}_{1,1/\text{2,1}}^{\text{1}}\cap {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{2}}\right)\subseteq {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{f}}\\ \text{with :}\\ {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{1}}\text{ polytope corresponding to }{C}_1\\ {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{2}}\text{ polytope corresponding to }{C}_2\end{array}$ (18)

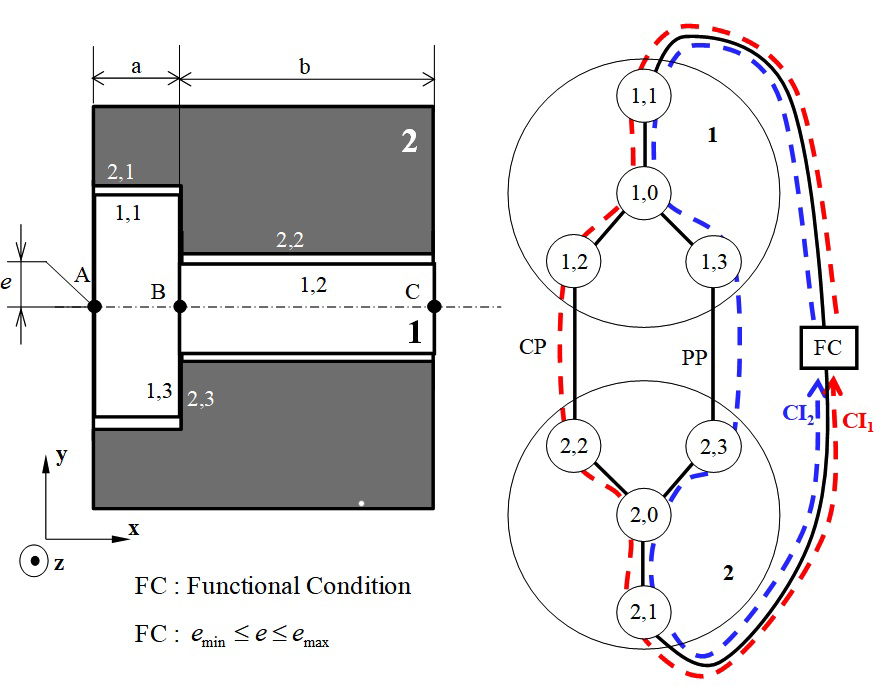
Figure 8 Cycles influent on the Functional Condition FC.

The position of surface 1,1 (cylinder) can be controlled in relation to surfaces 1,3 (primary plane) and 1,2 (secondary cylinder) by defining a location specification using ISO standards:⁴ see Figure 9 and Figure 10. The position of surface 2,1 in relation to 2,3 and 2,2 can be defined in the same way by a location specification: see Figure 9 and Figure 10. Finally, the geometric polytope characterising the deviations of surface 1,1 in relation to surface 2,1 is given in:

$\begin{array}{l}{\mathfrak{D}}_{1,1/\text{2,1}}^{\text{1}}\cap {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{2}}={\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g}}+\left({\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c}}\cap {\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c}}\right)+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g}}\\ \text{with:}\\ {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{1}}={\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g}}+{\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c}}+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g}}\\ {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{2}}={\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g}}+{\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c}}+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g}}\end{array}$ (19)

Figure 9 Graph representation of geometric specifications ensuring respect of the Functional Condition FC.

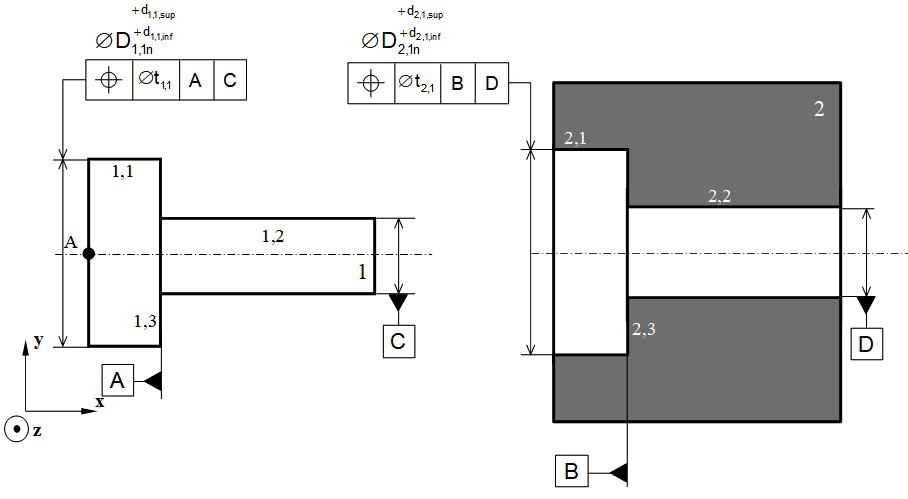
Figure 10 ISO representation of geometric specifications ensuring respect of the Functional Condition FC.

From this we deduce that respecting the functional condition FC can be written:

${\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g}}+\left({\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c}}\cap {\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c}}\right)+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g}}\subseteq {\mathfrak{D}}_{1,1/\text{2,1}}^{\text{f}}$ (20)

Let us suppose:

${\mathfrak{D}}_{1,1/\text{2,1}}^{}={\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g}}+\left({\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c}}\cap {\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c}}\right)+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g}}$ (21)

Figure 11a shows determining polytope ${\mathfrak{D}}_{1,1/\text{2,1}}^{}$ using Minkwoski sums and an intersection. Figure 11b shows respecting the functional condition where the geometric polytope ${\mathfrak{D}}_{1,1/\text{2,1}}^{}$ (of dimension 2) must be included inside polytope ${\mathfrak{D}}_{1,1/\text{2,1}}^{\text{f}}$ (of dimension 1). Consequently, respect for the functional condition FC can be defined by the following equations in the worst of cases:

$\begin{array}{l}-\frac{J_2^{\max }}{2}-\frac{t_{1,1}}{2}-\frac{t_{2,1}}{2}\ge e_{\min }\\ +\frac{J_2^{\max }}{2}+\frac{t_{1,1}}{2}+\frac{t_{2,1}}{2}\le e_{\max }\end{array}$ (22)

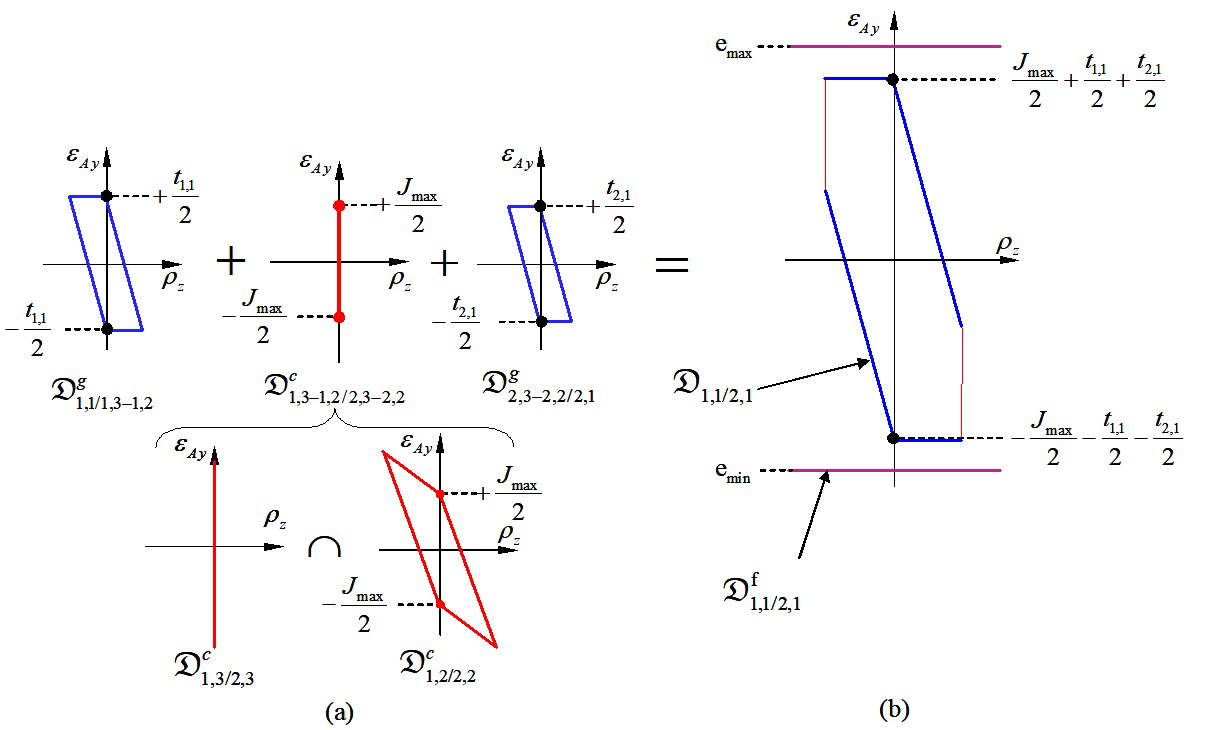
Figure 11 Respect of the Functional Condition FC by operations on polytopes.

Description of the thermo-mechanical operating cycle of a system:

So that thermo-mechanical strains can be included in the geometric variations of the reference behaviour, several different behaviours are considered for each system studied:

1. One reference behaviour,
2. One or several thermo-mechanical behaviours.

A reference model is defined from the reference behaviour, where all the parts are at 20°C. This reference model is based on the hypotheses traditionally put forward in geometric tolerancing, and set out at the beginning of section 2. Thermo-mechanical behaviour corresponds to a particular operating point in the system where certain parts are subjected to thermo-mechanical constraints. Thermo-mechanical constraints on the parts cause strains, leading to situation, dimension and form deviations which must be considered when modelling geometric variations. The functioning of the system studied here over time is discretized into several different thermo-mechanical behaviours. No transitional state is considered. Next in section 3 we show how modelling particular thermo-mechanical behaviour with polytopes can be deduced from the model already defined for the reference behaviour.³⁷

The following hypotheses are postulated:

1. Invariance of the topological structure of the contact graph,
2. Consideration of variations in the form and dimensions of the parts,
3. No local strain on surfaces in contact.

Invariance of the topological structure of the contact graph means that there is no additional contact or any suppression of contact between two behaviours. In addition, each contact type remains the same: a cylindrical pair remains a cylindrical pair; a planar pair remains a planar pair, etc. However, the different parameters that characterise contact (minimal clearance, maximal clearance, nature of contact, etc.) may change. The thermo-mechanical behaviour of the system is presumed to be elastic; it is modelled in small strains and in small displacements.

Integration of thermo-mechanical strains on the parts in a free state

For each part, a thermo-mechanical simulation is carried out with finite elements in a free state. The purpose of a simulation is to determine geometric variations of thermo-mechanical origin in a part, while considering no contact stress with the surrounding parts. A method commonly used in tridimensional metrology²⁶ assesses geometric variations in a part in a free state that are thermo-mechanical in origin. A deformed part is modelled by a finite number of points, each of which corresponds to a node in the mesh of the deformed part. An ideal surface (plane, cylinder, cone, etc.) is associated to the mesh nodes using the least squares criterion. Thus a plane surface is associated to the nodes of the deformation of a nominal plane surface; a cylindrical surface is associated to the nodes of the deformation of a nominal cylindrical surface, etc. It is thus possible to characterise the geometric deviations caused by thermo-mechanical strain between two associated surfaces, using a small displacement torsor from which a reduced polytope with a vertex of ${ℝ}^n$ can be deduced.

Let us consider part 1 shown in Figure 12: Figure 12a shows the nominal model of the part from which the deformation of the part subjected to thermo-mechanical strains is determined. Figure 12b shows the associations of two cylindrical surfaces 1,1th and 2,2th with deformations deduced from the nominal cylindrical surfaces 1,1n and 2,2n respectively. In the same way, the plane surface 1,3th is associated with the deformation deduced from the nominal plane surface 1,3n. The relative position of surfaces 1,3th and 1,2th can be expressed by the following equation, based on (3):

$\left[d_{1,2th/1,3th}\right]=\left[d_{1,2th/1,2n}\right]+\left[d_{1,3n/1,3th}\right]$ (23)

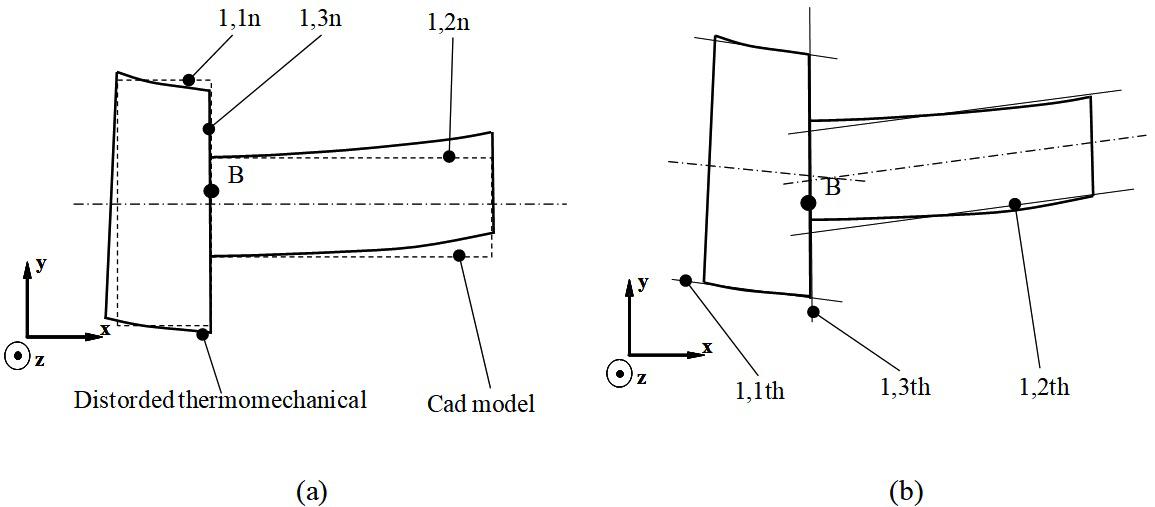
Figure 12 Characterisation of thermo-mechanical strains by geometric deviations defined by substituted surfaces.

In the base (x,y,z), we have:

$\left[d_{1,2th/1,3th}\right]=\begin{array}{c}\\ {}_B\end{array}\left[\begin{array}{c}{\rho }_{1,2th/1,3th}\\ {\epsilon }_{B-1,2th/1,3th}\end{array}\right]\text{with}{\rho }_{1,3th/1,2th}\left[\begin{array}{c}0\\ {\rho }_{1,2th/1,3th-y}\\ {\rho }_{1,2th/1,3th}{}_{-z}\end{array}\right]\text{and}{\epsilon }_{B-1,2th/1,3th}=0$ (24)

We can characterise the geometric deviations defined by $\left[d_{1,2th/1,3th}\right]$ by the polytope ${\mathfrak{D}}_{1,2/1,3}^{\text{g,th}}$ . This polytope is a vertex of ${ℝ}^2$ the components of which are given by ${\rho }_{1,2th/1,3th-y}$ and ${\rho }_{1,2th/1,3th-z}$ . We can hypothesise that in any thermo-mechanical behaviour:

${\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}={\mathfrak{D}}_{1,3/1,2}^{\text{g}}\text{defined in the reference behaviour}$ (25)

The geometric polytope characterising geometric variations between surfaces 1,3 and 1,2, brought about by manufacturing processes and cumulated with variations caused by thermo-mechanical strains, is then defined by the following Minkowski sum:

${\mathfrak{D}}_{1,3/1,2}^{\text{g}}={\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g,th}}$ (26)

Determination of polytope ${\mathfrak{D}}_{1,3/1,2}^{\text{g}}$ is shown in Figure 13.

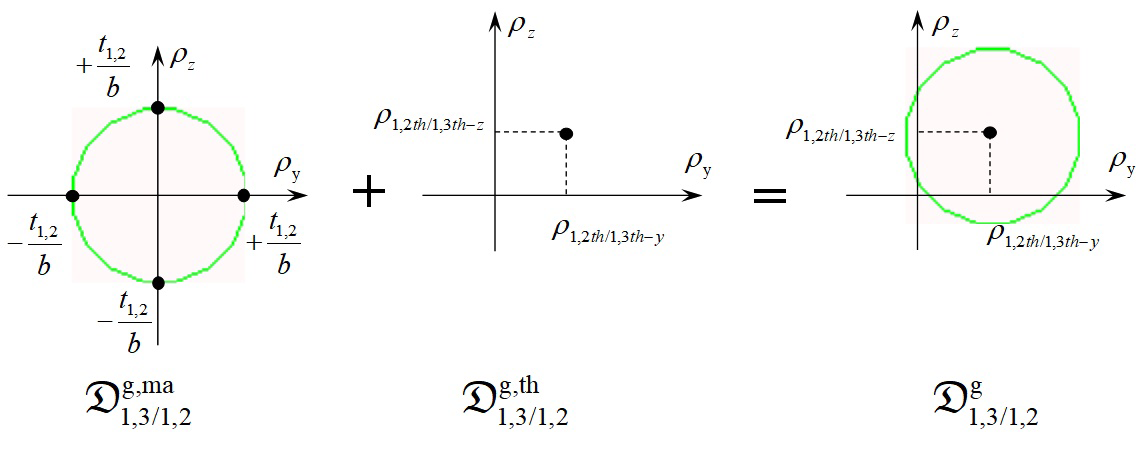
Figure 13 Characterisation of geometric deviations induced by manufacturing process and thermo-mechanical behaviour.

Integrating thermo-mechanical strains into the contacts

Simulation of a joint between two parts potentially in contact consists of determining the contact polytope in the event that the surfaces in contact are thermo-mechanically deformed. The condition of non-interference defined in (9) no longer depends only on clearance between the two surfaces due to manufacturing deviations but also on local clearance due to dimension and form deviations of thermo-mechanical origin. In this case, the non-interference constraints between surfaces i, j and u, v formalised in equation (27) generalise equation (9) where d_N represents local clearance at point N:

$\forall N\in E_c{\epsilon }_{N,i,j/u,v}.n_{\text{N}}\le d_{\text{N}}$ (27)

Local clearance d_N at point N is defined as a function of clearance J between the two substituted surfaces and as a function of form deviations of thermo-mechanical origin $de{v}_{\text{N-}i,j-th}$ and $de{v}_{\text{N-}u,v-th}$ in surfaces i, j and u, v respectively:

$d_{\text{N}}=\frac{J}{2}+\left(de{v}_{\text{N-}i,j-th}-de{v}_{\text{N-}u,v-th}\right)$ (28)

Figure 14 shows the case of the CP joint between surfaces 1,2 and 2,2 studied in paragraph 2.1.2 under thermo-mechanical behaviour. Here, clearance J between the two substituted surfaces is defined by the following equation:

$\begin{array}{l}J={\mathrm{D}}_{2,2}-{\mathrm{D}}_{1,2}=\left({\mathrm{D}}_{2,2n}+d_{\text{2,2\_ma}}+d_{\text{2,2\_th}}\right)-\left({\mathrm{D}}_{1,2n}+d_{\text{1,2\_ma}}+d_{\text{1,2\_th}}\right)\\ \text{with:}\\ {\mathrm{D}}_{1,2n},{\mathrm{D}}_{2,2n}:\text{ nominal diameters}\\ d_{\text{1,2\_ma}},d_{\text{2,2\_ma}}:\text{diameter deviation du to manufacturing process}\\ d_{\text{1,2\_th}},d_{\text{2,2\_th}}:\text{diameter deviation du to thermomechanical strains}\end{array}$ (29)

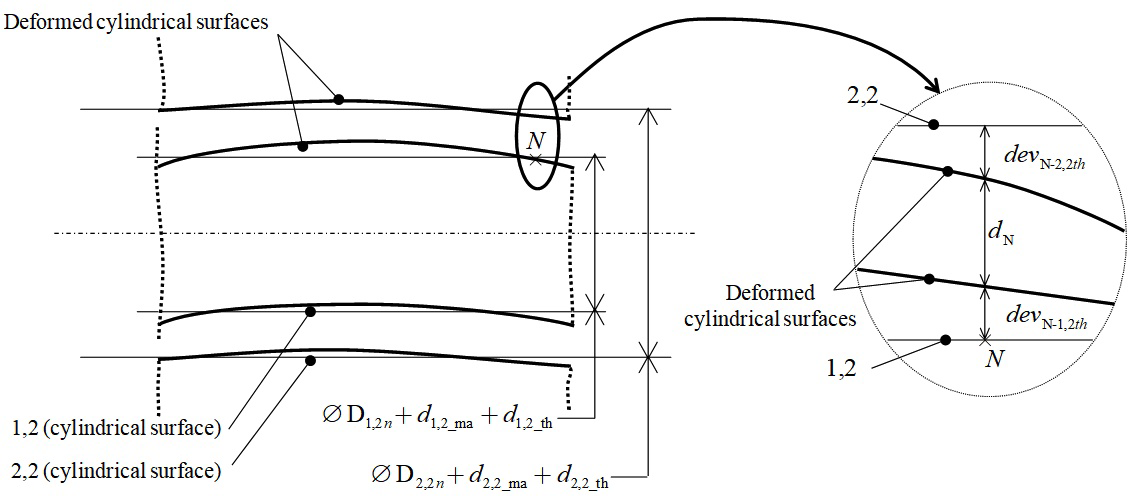
Figure 14 Geometric deviations between two disturbed surfaces potentially in contact.

The least favourable configuration for assembly in terms of manufacturing deviations is that which corresponds to:

$J_{\min }=\left({\mathrm{D}}_{2,2n}+{\left(d_{\text{2,2\_ma}}\right)}_{\text{mini}}+d_{\text{2,2\_th}}\right)-\left({\mathrm{D}}_{1,2n}+{\left(d_{\text{1,2\_ma}}\right)}_{\text{maxi}}+d_{\text{1,2\_th}}\right)$ (30)

Finally, equations are written as follows for the CP joint:

$\begin{array}{l}\forall N\in E_c\\ \left\{-\frac{J}{2}-\left(de{v}_{\text{N-}2,2-th}-de{v}_{\text{N-1,2}-th}\right)\le \left({\epsilon }_{N-1,2/2,2}+AN\times {\rho }_{1,2/2,2}\right).n_N\le \frac{J}{2}+\left(de{v}_{\text{N-}2,2-th}-de{v}_{\text{N-1,2}-th}\right)\right\}\end{array}$ (31)

The upper and lower boundaries of the halfspaces are no longer constants as they were in equation (9). It is not possible to express this polytope simply, in a similar way to (11). The polytope characterised by (31) is generally written ${\mathfrak{D}}_{1,2/2,2}^{\text{c,th}}$ or ${\mathfrak{D}}_{1,2/2,2}^{\text{c,th,min}}$ giving consideration to (30). There are two possibilities:

1. The intersection between the halfspaces defined by (25) generates a polytope,
2. The intersection between the halfspaces defined by (26) generates an empty set.

Case (a) is illustrated in Figure 15 where the polytope ${\mathfrak{D}}_{1,2/2,2}^{\text{c,th,min}}$ , represented in two specific projection planes, characterises the relative positions of surfaces 1,2 and 2,2 at point A. Contact between 1,2 and 2,2 gives rise to no additional strain in the mechanical system. It is specified that the joint has floating contact.

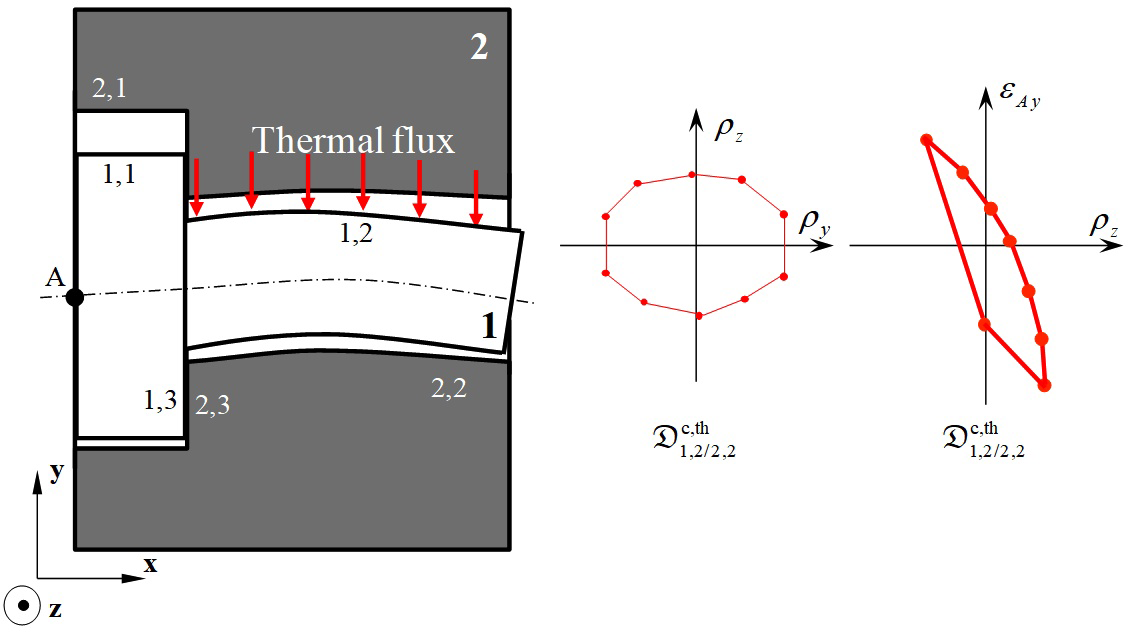
Figure 15 Contact polytope between two disturbed surfaces: case of no clamping.

Case (b) corresponds to a local clamping phenomenon, also called local tightening, between the two parts. No movement between the two surfaces relative to one another is possible: it is specified that the joint has fixed contact. The contact polytope ${\mathfrak{D}}_{i,j/u,v}^{\text{c,th,min}}$ is a vertex that coincides with the origin: see Figure 16. Clamping will cause additional strains locally in the two parts in contact which will have to be determined in a thermo-mechanical simulation of the complete system.

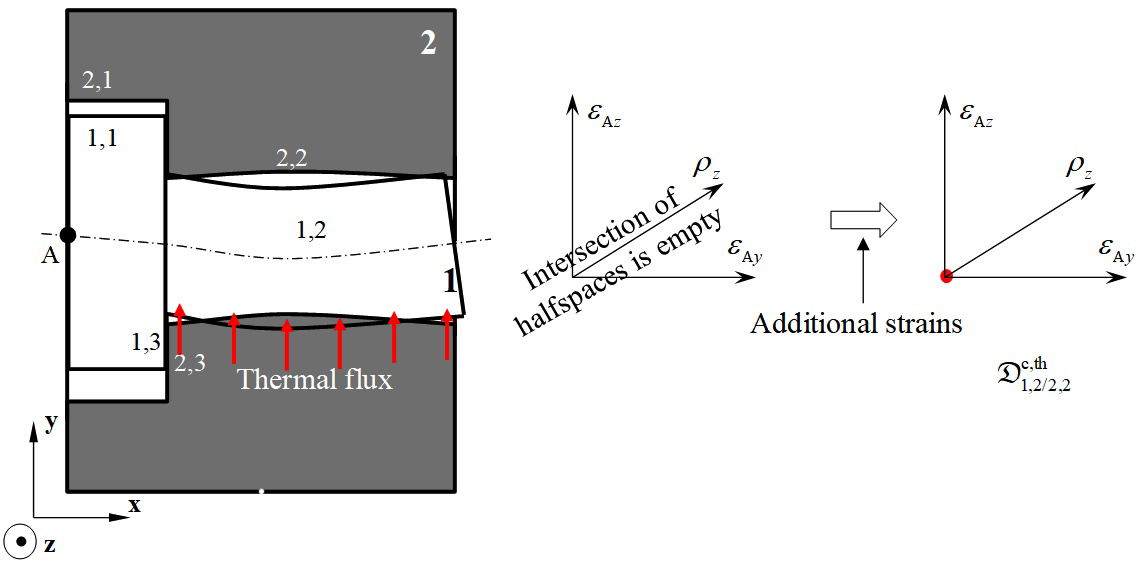
Figure 16 Contact polytope between two disturbed surfaces: case of clamping.

Condition for cycle closure

In paragraph 2.2, we saw that the topological structure of a mechanism is made up of a number of independent cycles and it must be ensured that these are closed. Closing a cycle requires the inclusion of ${\displaystyle \sum {\mathfrak{D}}_{i,j/i,k}^{\text{g}}}$ , the Minkowski sum of the geometric polytopes of the cycle, in ${\displaystyle \sum {\mathfrak{D}}_{i,j/u,v}^{\text{c}}}$ , the Minkowski sum of the contact polytopes of the cycle:

$\left({\displaystyle \sum {\mathfrak{D}}_{i,j/i,k}^{\text{g}}}\right)\subseteq {\displaystyle \sum {\mathfrak{D}}_{i,j/u,v}^{\text{c}}}$ (32)

In thermo-mechanical behaviour, equation (32) becomes:

${\displaystyle \sum \left({\mathfrak{D}}_{i,j/i,k}^{\text{g,ma}}+{\mathfrak{D}}_{i,j/i,k}^{\text{g,th}}\right)}\subseteq {\displaystyle \sum {\mathfrak{D}}_{i,j/u,v}^{\text{c,th}}}$ (33)

with:

1. ${\mathfrak{D}}_{i,j/i,k}^{\text{g,ma}}$ +${\mathfrak{D}}_{i,j/i,k}^{\text{g,th}}$ : geometric polytope defining geometric variations between surfaces i, j and i, k of part i caused by manufacturing processes, cumulated with variations caused by thermo-mechanical strains in i in the free state,
2. ${\mathfrak{D}}_{i,j/u,v}^{\text{c,th}}$ : contact polytope which takes into account thermo-mechanical strains between surfaces i, j and u, v which are potentially in contact.

Determining polytope $\left({\mathfrak{D}}_{i,j/i,k}^{\text{g,ma}}+{\mathfrak{D}}_{i,j/i,k}^{\text{g,th}}\right)$ is described in paragraph 3.2. Determining polytope ${\mathfrak{D}}_{i,j/u,v}^{\text{c,th}}$ is described in paragraph 3.3.

Figure 17 shows the three possible cases representing verification that the sum of the geometric polytopes is included in the sum of the contact polytopes, based on the example described in paragraph 2 in the most unfavourable configuration for the assembly. Figure 17a illustrates the following configuration:

$\left({\mathfrak{D}}_{2,2/2,3}^{\text{g,ma}}+{\mathfrak{D}}_{2,2/2,3}^{\text{g,th}}\right)+\left({\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g,th}}\right)\subseteq \left({\mathfrak{D}}_{1,2/2,2}^{\text{c,min,th}}+{\mathfrak{D}}_{2,3/1,3}^{\text{c,th}}\right)$ (34)

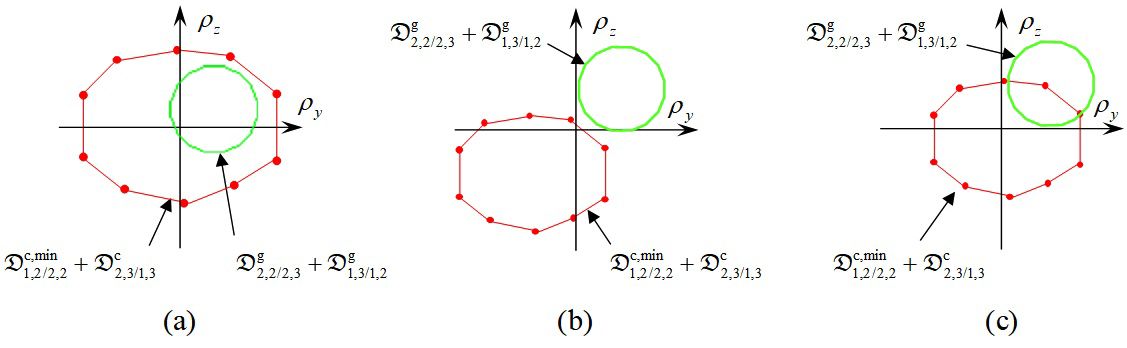
Figure 17 Inclusion of a sum of geometric polytopes inside a sum of contact polytopes taking into account the thermo-mechanical behaviour of the system.

This means that it is possible to assemble the system without any further strain in the parts. Thermo-mechanical strains in the parts in the Free State leave sufficient clearance in the joints to produce the assembly. Figure 17b illustrates the following configuration:

$\left(\left({\mathfrak{D}}_{2,2/2,3}^{\text{g,ma}}+{\mathfrak{D}}_{2,2/2,3}^{\text{g,th}}\right)+\left({\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g,th}}\right)\right)\cap \left({\mathfrak{D}}_{1,2/2,2}^{\text{c,min,th}}+{\mathfrak{D}}_{2,3/1,3}^{\text{c,th}}\right)=\varnothing$ (35)

This means that it is not possible to assemble the system without adding further strain in the parts. Equation (35) represents clamping of the cycle. Thermo-mechanical deformations in the free state have suppressed clearance in the joints enabling the assembly to be produced. A finite element thermo-mechanical simulation of the complete system must be carried out, taking into account the contact conditions between the parts under thermo-mechanical behaviour. Figure 17c illustrates the following configuration:

$\left\{\begin{array}{l}\left({\mathfrak{D}}_{2,2/2,3}^{\text{g,ma}}+{\mathfrak{D}}_{2,2/2,3}^{\text{g,th}}\right)+\left({\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g,th}}\right)\not\subset \left({\mathfrak{D}}_{1,2/2,2}^{\text{c,min,th}}+{\mathfrak{D}}_{2,3/1,3}^{\text{c,th}}\right)\hfill \\ \left(\left({\mathfrak{D}}_{2,2/2,3}^{\text{g,ma}}+{\mathfrak{D}}_{2,2/2,3}^{\text{g,th}}\right)+\left({\mathfrak{D}}_{1,3/1,2}^{\text{g,ma}}+{\mathfrak{D}}_{1,3/1,2}^{\text{g,th}}\right)\right)\cap \left({\mathfrak{D}}_{1,2/2,2}^{\text{c,min,th}}+{\mathfrak{D}}_{2,3/1,3}^{\text{c,th}}\right)\ne \varnothing \hfill \end{array}\right\}$ (36)

The inclusion condition is generally not verified. However, with certain configurations it is possible for the two parts to be assembled without further strain: the intersection of the two polytopes is not empty. This represents an uncertain clamping of the cycle.

Simulating respect of a functional requirement

Let us consider the functional condition defined by equation (17) characterised by the functional polytope ${\mathfrak{D}}_{1,1/2,1}^{\text{f}}$ . Equation (20), which defines respect of the functional condition, remains the same, given that the topological structure of the system between the reference behaviour and thermo-mechanical behaviour remains the same by virtue of the hypotheses set out at the beginning of paragraph 3.1. In the first configuration, we assume that no local clamping is detected in the CP joint between 1,2 and 2,2 (see Figure 15) and that no clamping is detected in the cycle (see Figure 17a).

According to equation (22), it follows that:

${\mathfrak{D}}_{1,1/2,1}^{\text{g}}={\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,ma}}+{\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,th}}+\left({\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c,th,max}}\cap {\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c,th}}\right)+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,ma}}+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,th}}$ (37)

with:

1. ${\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,th}}$ and ${\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,th}}$ : geometric polytopes representing deviations of thermo-mechanical origin in the free state in parts 1 and 2 respectively,
2. ${\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,ma}}$ and ${\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,ma}}$ : geometric polytope representing manufacturing deviations in parts 1 and 2 respectively,
3. ${\mathfrak{D}}_{1,2/2,2}^{c,th,\max }$ ,${\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c,th}}$ : contact polytope incorporating thermo-mechanical strains between parts 1 and 2 of the CP joint with J_max clearance and of the PP joint with null clearance respectively.

Respecting the functional condition FC in this first configuration is illustrated in Figure 18 and defined by(38):

$\begin{array}{l}-\frac{t_{1,1}^{}}{2}-\frac{t_{2,1}^{}}{2}-J_{\max }^{th}+{\epsilon }_{A-1,1th/1,3th-1,2th-y}+{\epsilon }_{A-2,3th-2,2th/2,1th-y}\ge {{\displaystyle e}}_{\min }\\ +\frac{t_{1,1}^{}}{2}+\frac{t_{2,1}^{}}{2}+J_{\max }^{th}+{\epsilon }_{A-1,1th/1,3th-1,2th-y}+{\epsilon }_{A-2,3th-2,2th/2,1th-y}\le {{\displaystyle e}}_{\max }\end{array}$ (38)

Figure 18 Respect of the Functional Condition FC by operations on polytopes: case of no clamping.

Let us consider the mechanism in a second configuration where local clamping in the CP joint between 1,2 and 2,2 (see Figure 16) and clamping of the cycle (see Figure 17b) have been detected. The appearance of one or several clamps requires a further thermo-mechanical study of the complete system to be carried out which takes into account these added strains over and above the strain on the parts in their free state. Clamping phenomena are modelled with marginal contact conditions between the parts in finite element modelling. When defining marginal contact conditions the characteristics of the joints defined in the thermo-mechanical behaviour must be respected:

1. Cylindrical pair type contact of a fixed nature between 1,2 and 2,2,
2. Planar pair type contact of a sliding nature (null clearance) between 1,3 and 2,3.

Figure 19 shows the result from a thermo-mechanical calculation on the complete system. The purpose of the thermo-mechanical simulation is to define the geometric polytope ${\mathfrak{D}}_{1,1/2,1}^{\text{g,th}}$ which will determine deviations of thermo-mechanical origin between surfaces 1,1 and 2,1. The method used is the same as in paragraph 3.2 to determine deviations of thermo-mechanical origin on a distorted part in the free state: see Figure 19.

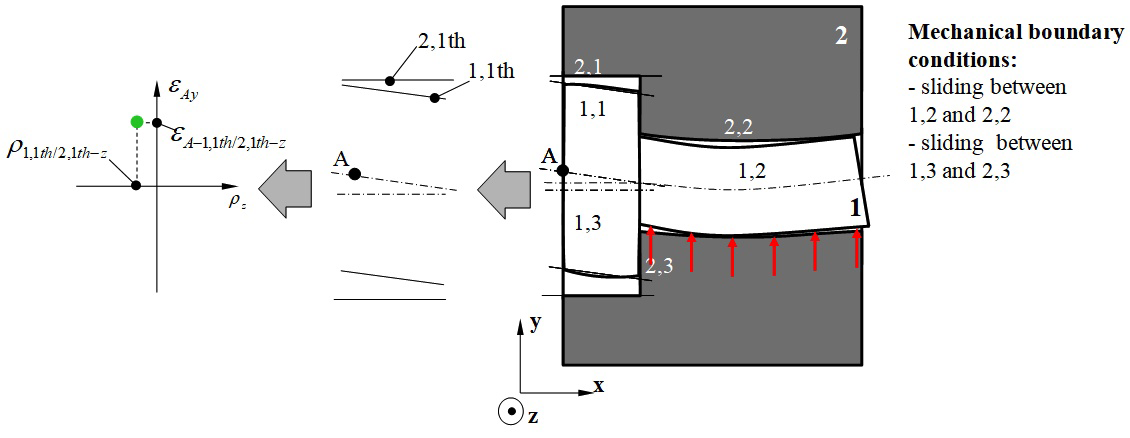
Figure 19 Characterisation of the thermo-mechanical behaviour of the complete system: case of clamping.

According to (21), this polytope is determined as follows:

${\mathfrak{D}}_{1,1/2,1}^{\text{g}}={\mathfrak{D}}_{1,1/2,1}^{\text{g,th}}+{\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,ma}}+\left({\mathfrak{D}}_{1,2/\text{2,2}}^{\text{c,th,max}}\cap {\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c,th}}\right)+{\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,ma}}$ (39)

with:

1. ${\mathfrak{D}}_{1,1/2,1}^{\text{g,th}}$ : geometric polytope characterising deviations of thermo-mechanical origin between surfaces 1,1 and 2,1 from the thermo-mechanical simulation of the complete system,
2. ${\mathfrak{D}}_{1,1/\text{1,3-1,2}}^{\text{g,ma}}$ and ${\mathfrak{D}}_{2,3-2,2/\text{2,1}}^{\text{g,ma}}$ : geometric polytope characterising manufacturing deviations in parts 1 and 2 respectively,
3. ${\mathfrak{D}}_{1,2/2,2}^{c,th,\max }$ ,${\mathfrak{D}}_{1,3/\text{2,3}}^{\text{c,th}}$ : contact polytope between parts 1 and 2 of the cylindrical pair joint with J_max and the planar pair joint respectively including thermo-mechanical strains.

Respect of functional condition FC in this second configuration is illustrated in Figure 20 and defined by equation (40):

$\begin{array}{l}-\frac{t_{1,1}^{}}{2}-\frac{t_{2,1}^{}}{2}+{\epsilon }_{A-1,1th/2,1th-y}\ge {{\displaystyle e}}_{\min }\\ +\frac{t_{1,1}^{}}{2}+\frac{t_{2,1}^{}}{2}+{\epsilon }_{A-1,1th/2,1th-y}\le {{\displaystyle e}}_{\max }\end{array}$ (40)

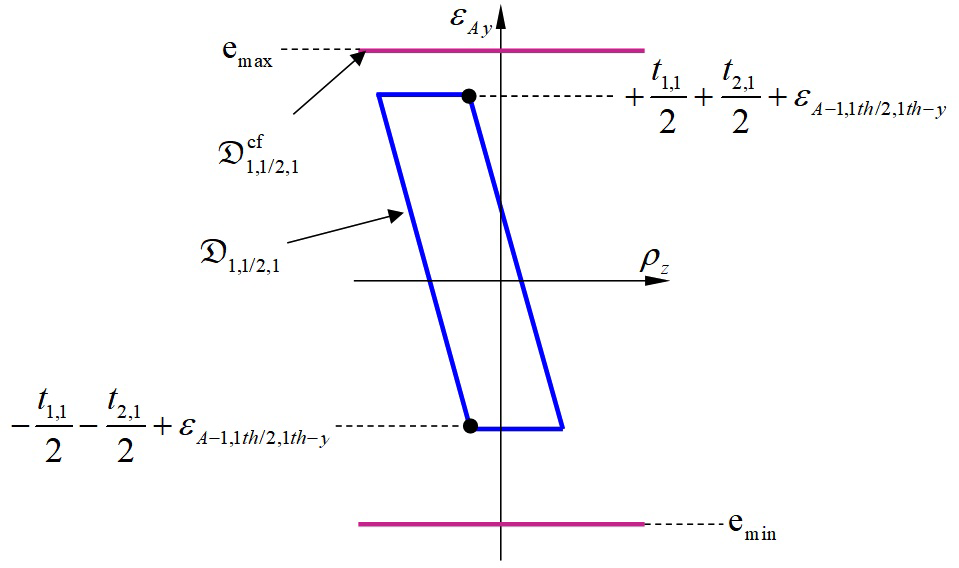
Figure 20 Respect of the Functional Condition FC by operations on polytopes: case of clamping.

Global tolerance analysis procedure

The organisational chart in Figure 21 breaks down the procedure proposed in this article into two distinct parts. The first corresponds to the preparation of the reference tolerance analysis model representing the reference behaviour. The start data consists of:

1. A functional requirement,
2. CAD model of the complete system,
3. Specifications for contact between the parts,
4. ISO geometric specifications for the parts.

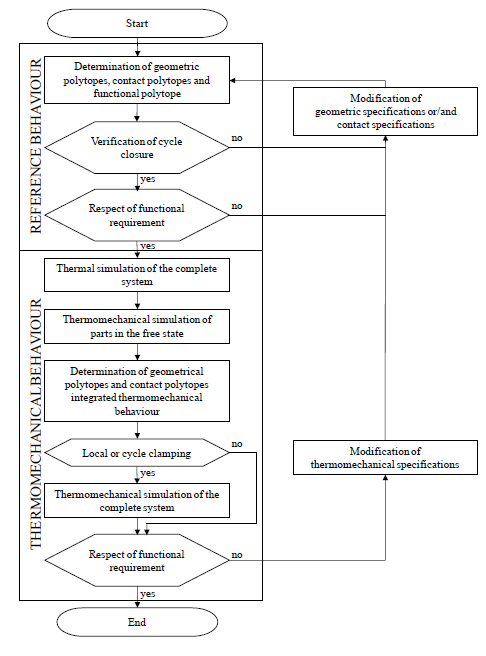
Figure 21 Global method of tolerancing analysis taking into account thermo-mechanical behaviour.

If the system cannot be assembled without distorting the parts (i.e. if cycle closure independent of the system graph is not possible) or if the functional requirement is not respected, then the global method has provisions for suggesting to the designer that the geometric specifications of the parts should be modified. This may simply involve reducing the dimensions of the tolerance zones and increasing minimum clearance, for example. If this is not sufficient, perhaps in terms of manufacturing criticality criteria, then it is suggested that the designer modifies the contact specifications. This may involve removing or adding joints and hence potentially modifying the number of parts. In general, this modifies the system architecture considerably. Implementation of the tolerance analysis process in this first part of the global method is described in paragraph 2. All thermo-mechanical behaviours are based on the reference model in accordance with the hypotheses set out in paragraph 3.

Next, the tolerance analysis model of specific thermo-mechanical behaviour is produced. The thermo-mechanical specifications of the system are added to the start data needed to produce the reference model. These are temperature and material specifications. In the first phase, temperature specifications are taken into account in a thermal simulation of the complete system. In the second phase, the thermo-mechanical strains of all the parts in the free state are determined. For these two phases we used a commercial thermo-mechanical finite element calculation tool. In the third phase, all the joints are characterised by a thermo-mechanical contact polytope incorporating the variations in dimension and form of surfaces potentially in contact. In this way, any possible local clamping (or tightening) between two parts can be detected. Finally, by simulating closure of the independent cycles any clamping of the cycles can be identified. If clamping is detected, a thermo-mechanical study of the complete system is carried out to determine the thermo-mechanical variations in the surfaces specified by the functional requirement in terms of situation, dimension and form deviations. If no clamping is detected, the thermo-mechanical behaviour of the system depends only on strains in the parts in the free state: no further thermo-mechanical simulation is required. Finally, if the functional requirement is not respected, then this suggests that the designer should modify the thermo-mechanical specifications as well as the geometric specifications of the parts and the contact specifications of the system. In general, modifying the temperature, materials or contact specifications can change the system architecture considerably. Implementation of the tolerance analysis processes in this second part of the global method is described in section 3.

Discussion of the proposed procedure

The operational cycle of the system studied is discretized into several behaviours: one reference behaviour and several thermo-mechanical behaviours. The reference behaviour is based on modelling infinitely rigid solids and does not take into account any strain that may be caused by residual stresses during manufacture or assembly. Each thermo-mechanical behaviour is defined by constant temperature specifications. The functioning of a high pressure turbine is thus defined by a finite set of behaviours where the turbine combustion chamber is at 20°C. This set of behaviours characterises the turboshaft engine's thermo-mechanical operating cycle.³⁸ The thermo-mechanical behaviour of the system is assumed to be elastic. In addition, the invariance of the topological structure of contacts between behaviours means that geometrical variations in the system can be determined from closure of the same cycles in all behaviours. These cycles characterise the 3D dimension chains and determine the operations (Minkowski sum and intersection) to be put in place. These operations are characterised in the reference behaviour. Only the polytope operands are liable to change from one behaviour to another. The global method outlined in Figure 21 uses a finite element thermo-mechanical simulation tool.

This tolerance analysis method is based solely on a worst case analysis.

We have shown how to use operations on polytopes to characterise geometric variations limited by ISO geometric specifications for the parts and by contact specifications between the parts. After setting up a method adapted to modelling a system of infinitely rigid solids, we described the principles of integrating thermo-mechanical strain in the parts and the contacts. Statistical formulations are planned in future studies, but these may prove ineffective in behaviours where the original determinist thermo-mechanical deviations are very great in comparison with deviations due to manufacturing processes. Finally, future developments are planned which will take into account strains arising from residual stresses in manufacturing processes (e.g. Resin Transfer Moulding) or in assembly processes where rivets or bolts are used. This will enhance the multiphysical nature of this approach.

None.

Authors declare that there is no conflict of interest.

1. Fleming A. Geometric relationships between toleranced features. Artificial Intelligence. 1988;37(1-3):403‒412.
2. Teissandier D, Couétard Y, Gérard A. A Computer Aided Tolerancing Model : Proportioned Assemblies Clearance Volume. Computer-Aided Design. 1999;31(13):805‒817.
3. Requichaa AAG. Toward a theory of geometric tolerancing. The International Journal of Robotics Research. 1993;2(4):45‒60.
4. Geometrical Product Specifications (GPS), Geometrical tolerancing, Tolerances of form, orientation, location and run-out. ISO. 1101:2004.
5. Giordano M, Pairel E, Samper S. Mathematical representation of tolerance zones. In Netherlands: Proc. of 6th CIRP Seminar on Computer Aided Tolerancing Enschede; 1999. 177‒186 p.
6. Roy U, Li B. Representation and interpretation of geometric tolerances for polyhedral objects. II.: Size, orientation and position tolerances. Computer-Aided Design. 1999;31(4):273‒285.
7. Davidson JK, Mujezinovic A, Shah JJ. A new mathematical model for geometric tolerances as applied to round faces. ASME Transactions on Journal of Mechanical Design. 2002;124(4):609‒622.
8. Fleming AD. Analysis of Uncertainties and Geometric Tolerances in Assemblies of Parts. PhD thesis, Scotland: University of Edinburgh; 1987.
9. Srinivasan V. Role of Sweeps in Tolerancing Semantics. CRTD. 1993;27:69‒78.
10. Wu Y, Shah JJ, Davidson JK. Improvements to algorithms for computing the Minkowski sum of 3-polytopes. Computer-Aided Design. 2003;35(13):1181‒1192.
11. Teissandier D, Delos V. Algorithm to calculate the Minkowski sums of 3-polytopes based on normal fans. Computer-Aided Design. 2011;43(12):1567‒1576.
12. Giordano M, Duret D. Clearance Space and Deviation Space. In: Proc. of 3rd CIRP seminar on Computer Aided Tolerancing, Cachan (France); 1993. 179‒196 p.
13. Teissandier D, Delos V. Operations on polytopes: application to tolerance analysis. In: Proc. of 6th CIRP Seminar on Computer Aided Tolerancing, Enschede (Netherlands); 1999. 425‒433 p.
14. Shah JJ, Ameta G, Shen Z, et al. Navigating the tolerance analysis maze. Computer-Aided Design and Applications. 2007;4(5):705‒718.
15. Anselmetti B. Generation of functional tolerancing based on positioning features. Computer-Aided Design. 2006;38(8):902‒919.
16. Clozel P, Rance PA. MECAmaster: a Tool for Assembly Simulation from Early Design, Industrial Approach. In: Geometric tolerancing of products. ISTE-WILEY; 2010. 241‒273 p.
17. Ballot E, Bourdet P. Geometrical behavior laws for computer aided tolerancing. In: Proc. of 4th CIRP Seminar on Computer Aided Tolerancing, Tokyo (Japan); 1995. 143‒153 p.
18. Johannesson H, Soderberg R. Structure and matrix models for tolerance analysis from configuration to detail design. Research in Engineering Design. 2000;12(2):112‒125.
19. Tolerance Analysis, GD&T, and Quality Solutions. DCS; 2011.
20. Bourdet P, Thiébaut F, Cid G. Writing the 3D Chain of Dimensions (Tolerance Stack-Up) in Symbolic Expressions. In: Geometric tolerancing of products. ISTE-WILEY; 2010. 125‒149 p.
21. Stewart ML, Chase KW. Variation simulation of fixtured assembly for compliant structures using piecewise-linear analysis. Orlando (USA): Proc. of ASME IMECE2005-82371; 2005. 591‒600 p.
22. Hu JS, Camelio J. Modeling and control compliant assembly systems. CIRP Annals. 2006;55(1):19‒22.
23. Söderberg R, Lindkvist L, Dahlström S. Computer-aided robustness analysis for compliant assemblies. Journal of Engineering Design. 2006;17(5):411‒428.
24. Maciej M, Leary M, Subic A. Computer Aided Tolerancing (CAT) platform for the design of assemblies under external and internal forces. Computer-Aided Design. 2011;43(6):707‒719.
25. Samper S, Petit J, Giordano M. Elastic clearance domain and use rate concept applications to ball bearing and gears. In: Proc. of 9th CIRP Seminar on Computer Aided Tolerancing; 2005. 331–340 p.
26. Bourdet P, Mathieu L, Lartigue C, et al. The concept of the small displacement torsor in metrology. Advanced Mathematical Tools in Metrology II. 1996;40:110‒122.
27. Clément A, Bourdet P. A study of optimal-criteria identification based on the small-displacement screw model. CIRP Annals. 1988;37(1):503‒506.
28. Boissonnat JD, Yvinec M, Algorithmic Geometry. Cambridge University Press; 1998.
29. Ziegler G. Lectures on polytopes. Springer Verlag; 1995.
30. Defazio TL, Edsall AC, Gustavson RE, et al. A prototype of feature based design for assembly. Journal of Mechanical Design. 1993;115(4):723‒734.
31. Whitney DE, Adams JD. Application of screw theory to analysis of mobility and constraint of mechanisms. Journal of Mechanical Design. 2001;123:26‒32.
32. Dantan JY, Mathieu L, Ballu A, et al. Tolerance synthesis: quantifier notion and virtual boundary. Computer-Aided Design. 2005;37(2):231‒240.
33. Dufaure J, Teissandier D. A tolerancing framework to support geometric specifications traceability. International Journal of Advanced Manufacturing Technology. 2008;36(9-10):894‒907.
34. Kinematic diagrams-Graphical symbols-Part 1. ISO; 1981.
35. Ballu A, Mathieu L, Legoff O. Representation of Mechanical Assemblies and Specifications by Graphs. In: Geometric tolerancing of products. ISTE-WILEY; 2010. 87‒110 p.
36. Giordano M, Samper S, Pairel E. Tolerance Analysis and Synthesis, Method of Domains. In: Geometric tolerancing of products. ISTE-Wiley; 2010. 152‒181 p.
37. Pierre L, Teissandier D, Nadeau JP. Integration of thermomechanical strains into tolerancing analysis. International Journal on Interactive Design and Manufacturing. 2009;3:247‒263.
38. Pierre L, Teissandier D, Nadeau JP. Integration of multiple physical behaviours into a geometric tolerancing approach. In: Proc. of 11th CIRP Seminar on Computer Aided Tolerancing in CDRom, Annecy (France); 2009. 9 p.