An analytical computation of aircraft’s longitudinal trimmed conditions considering its fuel mass flow rate

doi:10.15406/aaoaj.2021.05.00121

eISSN: 2576-4500

Aeronautics and Aerospace Open Access Journal

Research Article Volume 5 Issue 1

An analytical computation of aircraft’s longitudinal trimmed conditions considering its fuel mass flow rate

Laurent Bovet

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

ELISA-Aerospace, France

Correspondence: Laurent Bovet, MINES ParisTech, Center for Materials Forming (CEMEF), UMR CNRS 7635, BP 207, 06904 Sophia-Antipolis, France

Received: November 25, 2020 | Published: January 28, 2021

Citation: Bovet L. An analytical computation of aircraft’s longitudinal trimmed conditions considering its fuel mass flow rate. Aeron Aero Open Access J. 2021;5(1):1-7. DOI: 10.15406/aaoaj.2021.05.00121

Download PDF

Abstract

The aim of this article is to give simple expressions of aircraft’s longitudinal trimmed conditions taking into account the instantaneous fuel mass flow rate, i.e. the variation of total mass. The computation of aircraft trim points is not a new problem. Nevertheless, current analytical computations are classically performed with a constant total weight of the aircraft, hence assuming that the rate of decrease of the weight due to the fuel mass flow rate has insignificant effects on the results. Thus, the goal of this study has been to assess the effect of weight variation on aircraft trimmed condition and to compute correctly “extended trimmed conditions” defined as the equilibrated conditions in flight considering the weight decrease of the aircraft. It has been demonstrated that the weight variation must have an ad-hoc form to lead to extended trimmed conditions. Moreover, extended trimmed conditions do not correspond to a perfect level flight as it is the case at constant weight, but must present a slightly positive flight path angle leading to a regular increase in altitude. And the corrected longitudinal commands including throttle and elevator positions at a given airspeed and altitude have been computed for extended trimmed conditions and compared to the basic case at constant weight. Finally, all the analytical expressions given in this article have been verified through a numerical simulation performed in the case of a twin-engine aircraft representative of the Airbus wide-body family.

Keywords: longitudinal flight, trimmed conditions, fuel mass flow rate, flight dynamics

Introduction

The computation of the aircraft steady-state or trimmed conditions is of importance in many flight dynamics problems. Indeed, trimmed conditions are the starting points to flight simulations¹ and are used for further operations performed by pilots or engineers.² Furthermore, linear models used for handling qualities analysis are derived from trim points,³ and performance analysis requires flight conditions to be as close as possible to the equilibrium.⁴ Finally, finding the general solution of trim states corresponding to given flight conditions can become non-trivial⁵ and lead to complex algorithms which aim at minimizing ad-hoc cost functions.⁶

Nevertheless, these analyses are always performed considering that the aircraft has a constant weight, assuming that the fuel mass flow rate–which is the airplane mass loss–has insignificant effects on trim. If this makes sense for short to medium term analyses, for long term, the weight decrease turns out in conflict with the initial trim assumptions. One of these concerns the well-known cruise at constant airspeed and angle of attack. In that case, the equilibrated states are computed assuming a constant altitude, but a simple analysis shows that the weight decrease automatically implies a gain of altitude and a residual flight path angle during the cruise.⁷

Indeed, a simple numerical computation of the longitudinal aircraft dynamics shows that the introduction of a weight decrease leads the aircraft to reach a slightly different equilibrated condition from the case computed at constant weight. Moreover, the well-known Bréguet equation predicting the range of an aircraft flying at constant airspeed and angle of attack has to be corrected by a small factor to take into account the mass variation in flight.⁸ Here this study makes a focus on the trimmed conditions taking into account the mass variation in flight and a simple way to compute these analytically by correcting the current flight dynamics expressions.

Definition of the equilibrium

Condition on the state parameters

The equilibrium of a mechanical system is reached when the sum of the forces and moments are equal to zero. This leads to write that the acceleration of the body and the rate of change of angular momentum are null. Thus, considering a body with 6 Degree of Freedom (DoF) described by the 12 state parameters including:

The velocity (3 coordinates);
The angular rate (3 coordinates);
The position (3 coordinates);
The orientation or attitude (3 coordinates).

The equilibrium is reached when the time derivative of each parameter is equal to zero, except for the 3 position coordinates for which the second time derivative is equal to zero. Thus, the 12 state parameters have been divided into two complementary vectors:

The first vector, noted $\to Y$ $\vec{Y}$ , gathers the 3 position coordinates;
The second vector, noted $\to X$ $\vec{X}$ , gathers the 9 other state parameters.

With this notation, the equilibrium is defined by:

$E q u i l i b r i u m \Rightarrow ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} ˙ \to X = \to 0 ¨ \to Y = \to 0 \end{matrix}$ $E q u i l i b r i u m \Rightarrow {\begin{matrix} \dot{\vec{X}} = \vec{0} \\ \ddot{\vec{Y}} = \vec{0} \end{matrix}$ (1)

Case of a variable mass system

Let us assume that each coordinate x_i of the vector $\to X$ $\vec{X}$ is described by a first order differential equation g_ifunction of the state variables and mass of the system. In addition, each position coordinate y_i of the vector $\to Y$ $\vec{Y}$ is described by a first order differential equation h_i coming from the kinematics equations and function of the state variables only but not mass:

${\begin{matrix} {˙ x}_{i} = g_{i} (x_{1}, ..., x_{n}, y_{1}, ..., y_{k}, m) {˙ y}_{i} = h_{i} (x_{1}, ..., x_{n}, y_{1}, ..., y_{k}) \end{matrix}$ ${\begin{matrix} {\dot{x}}_{i} = g_{i} (x_{1}, ..., x_{n}, y_{1}, ..., y_{k}, m) \\ {\dot{y}}_{i} = h_{i} (x_{1}, ..., x_{n}, y_{1}, ..., y_{k}) \end{matrix}$ (2)

The equations g_i and h_i are gathered in the vectors $\to G$ $\vec{G}$ and $\to H$ $\vec{H}$ resp., which leads to write:

$⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} ˙ \to X = \to G ˙ \to Y = \to H \end{matrix}$ ${\begin{matrix} \dot{\vec{X}} = \vec{G} \\ \dot{\vec{Y}} = \vec{H} \end{matrix}$ (3)

Considering that a variation of mass affects the equations g_i only, a variation dm during dt leads to a variation $d {˙ x}_{i}$ $d {\dot{x}}_{i}$ and dx_i given by:

$d {˙ x}_{i} = \frac{\partial g_{i}}{\partial x_{1}} d x_{1} + ... + \frac{\partial g_{i}}{\partial x_{n}} d x_{n} + \frac{\partial g_{i}}{\partial y_{1}} d y_{1} + ... + \frac{\partial g_{i}}{\partial y_{k}} d y_{k} + \frac{\partial g_{i}}{\partial m} d m$ $d {\dot{x}}_{i} = \frac{\partial g_{i}}{\partial x_{1}} d x_{1} + ... + \frac{\partial g_{i}}{\partial x_{n}} d x_{n} + \frac{\partial g_{i}}{\partial y_{1}} d y_{1} + ... + \frac{\partial g_{i}}{\partial y_{k}} d y_{k} + \frac{\partial g_{i}}{\partial m} d m$

i.e.:

${¨ x}_{i} = \frac{\partial g_{i}}{\partial x_{1}} {˙ x}_{1} + ... + \frac{\partial g_{i}}{\partial x_{n}} {˙ x}_{n} + \frac{\partial g_{i}}{\partial y_{1}} {˙ y}_{1} + ... + \frac{\partial g_{i}}{\partial y_{k}} {˙ y}_{k} + \frac{\partial g_{i}}{\partial m} ˙ m$ ${\ddot{x}}_{i} = \frac{\partial g_{i}}{\partial x_{1}} {\dot{x}}_{1} + ... + \frac{\partial g_{i}}{\partial x_{n}} {\dot{x}}_{n} + \frac{\partial g_{i}}{\partial y_{1}} {\dot{y}}_{1} + ... + \frac{\partial g_{i}}{\partial y_{k}} {\dot{y}}_{k} + \frac{\partial g_{i}}{\partial m} \dot{m}$

which can also be written in the matrix form:

$¨ \to X = G_{x} ˙ \to X + G_{y} ˙ \to Y + \frac{\partial \to G}{\partial m} ˙ m$ $\ddot{\vec{X}} = G_{x} \dot{\vec{X}} + G_{y} \dot{\vec{Y}} + \frac{\partial \vec{G}}{\partial m} \dot{m}$

with:

$G_{x} = [\frac{\partial \to G}{\partial x_{1}}; ... \frac{\partial \to G}{\partial x_{n}}]$ $G_{x} = [\frac{\partial \vec{G}}{\partial x_{1}}; ... \frac{\partial \vec{G}}{\partial x_{n}}]$

and:

$G_{y} = [\frac{\partial \to G}{\partial y_{1}}; ... \frac{\partial \to G}{\partial y_{k}}]$ $G_{y} = [\frac{\partial \vec{G}}{\partial y_{1}}; ... \frac{\partial \vec{G}}{\partial y_{k}}]$

The traditional equilibrium condition (EQ. (1)) gives in this case:

$¨ \to X = G_{y} ˙ \to Y + \frac{\partial \to G}{\partial m} ˙ m$ $\ddot{\vec{X}} = G_{y} \dot{\vec{Y}} + \frac{\partial \vec{G}}{\partial m} \dot{m}$

This expression means that the equilibrated condition $˙ \to X = \to 0$ $\dot{\vec{X}} = \vec{0}$ is generally not kept in time with a mass variation. Thus, another condition must be introduced to keep the equilibrium conditions (EQ. (1)) when the mass varies. This leads to the definition of an “extended trimmed conditions” given by:

$E x t e n d e d t r i m m e d c o n d i t i o n s \Rightarrow ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} ˙ \to X = \to 0 ¨ \to Y = \to 0 ¨ \to X = \to 0 \end{matrix}$ $E x t e n d e d t r i m m e d c o n d i t i o n s \Rightarrow {\begin{matrix} \dot{\vec{X}} = \vec{0} \\ \ddot{\vec{Y}} = \vec{0} \\ \ddot{\vec{X}} = \vec{0} \end{matrix}$ (4)

Considering that $¨ \to Y = \to 0$ $\ddot{\vec{Y}} = \vec{0}$ , the vectoris a constant noted $\to C$ $\vec{C}$ . Then, (EQ. (4)) can also be written as:

$E x t e n d e d t r i m m e d c o n d i t i o n s \Rightarrow ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} ˙ \to X = \to G = \to 0 ¨ \to Y = \to H = \to C G_{y} ˙ \to Y + \frac{\partial \to G}{\partial m} ˙ m = \to 0 \end{matrix}$ $E x t e n d e d t r i m m e d c o n d i t i o n s \Rightarrow {\begin{matrix} \dot{\vec{X}} = \vec{G} = \vec{0} \\ \ddot{\vec{Y}} = \vec{H} = \vec{C} \\ G_{y} \dot{\vec{Y}} + \frac{\partial \vec{G}}{\partial m} \dot{m} = \vec{0} \end{matrix}$ (5)

Application to the longitudinal flight

The theoretical framework of the definition of the extended equilibrium is now applied to the case of a pure longitudinal flight, i.e. a flight in the vertical plane only. In this case, the airplane has 3 DoF, i.e. 1 in rotation (pitch) and 2 in the vertical plane (horizontal and vertical movement), and 6 state variables describe the motion of the aircraft in this case.

Assumptions and models

In this application, the atmosphere state parameters are given by the International Standard Atmosphere (ISA) model.⁹ For analytical computations, an exponential model of air density is defined:¹⁰

$ρ = ρ_{r e f} e_{h}^{a_{h} (z - z_{r e f})}$ $ρ = ρ_{r e f} e^{a_{h} (z - z_{r e f})}$ (6)

where ρ_ref and z_ref denote reference air density and altitude depending on the atmosphere layer.

In the troposphere, i.e. from sea level to 11km of altitude where the temperature decreases linearly, a_h is approximated by a least-squares curve fit of the actual evolution of the air density vs. altitude, i.e.:

$a_{h} = - 1 / 9042 m^{- 1}$ $a_{h} = - 1 / 9042 m^{- 1}$

In the lower stratosphere, i.e. from 11 km to 25 km of altitude where the temperature is constant, a_h is directly

computed with the ideal gas law, i.e.:

$a_{h} = - {1.577710}^{- 4} m^{- 1}$ $a_{h} = - {1.577710}^{- 4} m^{- 1}$

Drag and lift are the result of the projection of the aerodynamic force acting on the aircraft on the longitudinal

aerodynamic axes:¹¹

${\begin{matrix} D = \frac{1}{2} ρ S V^{2} C_{D} L = \frac{1}{2} ρ S V^{2} C_{L} \end{matrix}$ ${\begin{matrix} D = \frac{1}{2} ρ S V^{2} C_{D} \\ L = \frac{1}{2} ρ S V^{2} C_{L} \end{matrix}$ (7)

In these expressions, V denotes the True Air Speed (TAS), S corresponds to the aircraft’s reference area and the coefficients C_D and C_L are the drag and lift coefficient resp. The drag coefficient C_D is modeled as:¹⁵

$C_{D} = C_{D_{o}} + K C_{L}^{2}$ $C_{D} = C_{D_{o}} + K C_{L}^{2}$ (8)

where K corresponds the induced drag factor and C_Do denotes the parasite drag coefficient.

Considering simple static models, the lift coefficient C_L is a function of the angle of attack α only:

$C_{L} = C_{L α} (α - α_{o})$

Concerning the aerodynamic pitching moment M, we have:

$M = \frac{1}{2} ρ S V^{2} c C_{m}$ (9)

The pitching moment coefficient Cm is expressed in terms of angle of attack α, pitch rate q and elevator deflection δe:¹³

$C m = C m_{o} + C m_{α} (α - α_{o}) + C m_{q} \frac{q c}{V} + C m_{δ e} δ e$ (10)

The thrust is assumed to be proportional to the air density and throttle lever δx:¹⁴

$T = T_{S L} \frac{ρ}{ρ_{S L}} δ x$ (11)

In this expression, T_SL denotes the total thrust of the aircraft at sea level.

Longitudinal equations of motion

As said above, it’s necessary to take into account 6 state variables to describe the motion of a pure longitudinal flight. The first 2 state variables concern the position of the aircraft in the vertical plane, i.e. the horizontal distance x and altitude z.

Each variable is given by a first order differential equation coming from the kinematics:

${\begin{matrix} \dot{x} = V \cos γ \\ \dot{z} = V \sin γ \end{matrix}$ (12)

where γ denotes the Flight Path Angle (FPA) of the aircraft.

With these equations, it is possible to define the vectors $\vec{Y}$ and, i.e.:

$\vec{Y} = (\begin{matrix} x \\ z \end{matrix}) a n d \vec{H} = (\begin{matrix} V \cos γ \\ V \sin γ \end{matrix})$

Considering a symmetric aircraft with the thrust aligned with the fuselage reference line, the longitudinal equations of motion are the projections of the Newton’s second law on the aerodynamic axes:¹⁵

${\begin{matrix} \dot{V} = \frac{1}{m} (T \cos α - D - m g \sin γ) \\ \dot{γ} = \frac{1}{m V} (T \sin α + L - m g \cos γ) \end{matrix}$ (13)

Assuming that the thrust is located at the aircraft center of gravity, the pitch rate comes from the aerodynamic pitching moment only¹⁶ and we have:

$\dot{q} = \frac{M}{I_{Y Y}}$ (14)

This set is completed by the kinematic equations in pitch:

$\dot{α} = q - \frac{1}{m V} (T \sin α + L - m g \cos γ)$ (15)

With these equations, it’s possible to define the vectors $\vec{X}$ and $\vec{G}$ :

$\vec{X} = (\begin{matrix} V \\ γ \\ α \\ q \end{matrix}) a n d \vec{G} = (\begin{matrix} \frac{1}{m} (F \cos α - \frac{1}{2} ρ S V^{2} C_{D} - m g \sin γ) \\ \frac{1}{m V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α - m g \cos γ) \\ q - \frac{1}{m V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α - m g \cos γ) \\ \frac{1}{I_{Y Y}} \frac{1}{2} ρ S V^{2} c C_{m} \end{matrix})$

Definition of the extended trimmed conditions

The first condition coming from the definition of the extended equilibrium (EQ. (5)), i.e. $\vec{G} = \vec{0}$ , leads to:

${\begin{matrix} F \cos α - \frac{1}{2} ρ S V^{2} C_{D} = m g \sin γ \\ \frac{1}{2} ρ S V^{2} C_{L} + F \sin α = m g \cos γ \\ q = 0 \\ C m = 0 \end{matrix}$ (16)

The second condition from (EQ. (5)), i.e. $\dot{\vec{Y}} = \vec{C}$ , gives:

${\begin{matrix} \dot{x} = C_{1} \\ \dot{z} = C_{2} \end{matrix}$

where C₁ and C₂ denote the 2 coordinates of $\vec{C}$ .

For the third condition from (EQ. (5)), it’s necessary to compute the matrix G_y:

$G_{y} = [\frac{\partial \vec{G}}{\partial x}; \frac{\partial \vec{G}}{\partial z}]$

i.e.:

$G_{y} = [\begin{matrix} 0 & \frac{a_{h}}{m} (F \cos α - \frac{1}{2} ρ S V^{2} C_{D}) \\ 0 & \frac{a_{h}}{m V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α) \\ 0 & - \frac{a_{h}}{m V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α) \\ 0 & \frac{a_{h}}{I_{Y Y}} \frac{1}{2} ρ S V^{2} c C_{m} \end{matrix}]$

With (EQ. (16)), this leads to:

$G_{y} = [\begin{matrix} 0 & a_{h} g \sin γ \\ 0 & \frac{a_{h}}{V} g \cos γ \\ 0 & - \frac{a_{h}}{V} g \cos γ \\ 0 & 0 \end{matrix}]$

We also have:

$\frac{\partial \vec{G}}{\partial m} = (\begin{matrix} - \frac{1}{m^{2}} (F \cos α - \frac{1}{2} ρ S V^{2} C_{D} - m g \sin γ) - \frac{g \sin γ}{m} \\ - \frac{1}{m^{2} V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α - m g \cos γ) - \frac{g \cos γ}{m V} \\ \frac{1}{m^{2} V} (\frac{1}{2} ρ S V^{2} C_{L} + F \sin α - m g \cos γ) + \frac{g \cos γ}{m V} \\ 0 \end{matrix})$

With (EQ. (16)), this leads to:

$\frac{\partial \vec{G}}{\partial m} = \frac{1}{m V} (\begin{matrix} - g V \sin γ \\ - g \cos γ \\ g \cos γ \\ 0 \end{matrix})$

Finally, the third condition from (EQ. (5)) gives the following vector equation:

$(\begin{matrix} a_{h} g \sin γ \\ \frac{a_{h}}{V} g \cos γ \\ - \frac{a_{h}}{V} g \cos γ \\ 0 \end{matrix}) \dot{z} + \frac{1}{m V} (\begin{matrix} - g V \sin γ \\ - g \cos γ \\ g \cos γ \\ 0 \end{matrix}) \dot{m} = \vec{0}$

This leads to a single condition on the evolution of the altitude in trimmed condition when the mass varies:

$\dot{z} = \frac{\dot{m}}{a_{h} \dot{m}}$ (17)

Finally, the longitudinal trimmed condition of the aircraft taking into account the case $\dot{m} \neq 0$ is defined as follows:

$E x t e n d e d t r i m m e d c o n d i t i o n s \Rightarrow {\begin{matrix} \dot{V} = 0 \\ \dot{γ} = 0 \\ \dot{α} = 0 \\ \dot{q} = 0 \\ \ddot{x} = 0 \\ \dot{z} = \frac{\dot{m}}{a_{h} \dot{m}} \end{matrix}$ (18)

Discussion of the results

In extended trimmed conditions when the mass varies, the equations (EQ. (18)) show that the altitude must increase $(\dot{z} > 0)$ when the mass decreases $(\dot{m} < 0)$ to keep the equilibrium.

These equations also show that the condition on altitude $\dot{z} = 0$ only apply to the case $\dot{m} = 0$ , i.e. at constant mass. Moreover, as no equation in $\vec{G}$ depends on the horizontal distance x, i.e. $\frac{\partial \vec{G}}{\partial x} = \vec{0}$ , it’s not possible to compute the constant C₁ corresponding to $\dot{x}$ , and the only condition in this case is $\ddot{x} = 0$ .

In addition, as we also have $\dot{z} = C_{2}$ , this gives the following expression of $\dot{m}$ :

$\dot{m} = C_{2} a_{h} m$ (19)

which means that the mass variationmust be proportional to the total mass m to get a trimmed condition in longitudinal flight. For an aircraft equipped with jet engines, this condition can be achieved through a very simple model with a fuel flow rate proportional to the thrust:

$\dot{m} = - C_{T} T$ (20)

where c_T denotes the thrust-specific fuel consumption (TSFC).

Indeed, considering the thrust given by the trimmed conditions, this leads to the following expression of the equilibrated thrust:

$T = m g (\frac{\sin γ + \cos γ \frac{C_{D}}{C_{L}}}{c o s α + \sin α \frac{C_{D}}{C_{L}}})$

which gives:

$\dot{m} = - C_{T} g (\frac{\sin γ + \cos γ \frac{C_{D}}{C_{L}}}{c o s α + \sin α \frac{C_{D}}{C_{L}}}) m$

Assuming that the TSFC c_T remains constant and as every parameter in this equation are constant in trimmed condition, including α and γ which are small, this leads to:

$\dot{m} = - C_{T} g \frac{C_{D}}{C_{L}} m$ (21)

Thus, this expression is equivalent to (EQ. (19)), which also gives the value of C₂:

$C_{2} = \dot{z} = - C_{T} \frac{g}{a_{h}} \frac{C_{D}}{C_{L}}$ (22)

Analytical computation of the extended trimmed conditions

In this paragraph, the trimmed conditions in longitudinal flight at constant mass will be corrected to get the exact trimmed conditions when the mass varies.

To get this correction, the mass variation is assumed to be equivalent to the form given by (EQ. (19)), i.e.:

$\dot{m} = k_{\dot{m}} m$ (23)

with $k_{\dot{m}}$ constant.

To clarify the notations, the subscript e denotes an equilibrated parameter computed with $\dot{m} = 0$ , whereas the subscriptdenotes an equilibrated parameter computed with $\dot{m} \neq 0$ .

In addition, the comparison between both cases will be performed at a given weight for the same case of altitude and True Airspeed, i.e.:

${\begin{matrix} V_{e} = V_{\dot{m}} \\ z_{e} = z_{\dot{m}} \end{matrix}$

As $\dot{z} = \frac{\dot{m}}{a_{h} m}$ when the mass varies (EQ. (18)), by introducing both the kinematic equation in altitude (EQ. (12)) and the expression of m˙ (EQ. (23)), this leads to:

$V_{e} γ_{\dot{m}} = \frac{k_{\dot{m}}}{a_{h}}$

i.e.:

$γ_{\dot{m}} = \frac{k_{\dot{m}}}{a_{h} V_{e}}$ (24)

Moreover, the pitch rate is equal to zero in both cases, i.e.:

$q_{e} = q_{\dot{m}} = 0$ (25)

The longitudinal trimmed equations are written at constant weight (lift and drag equations):

${\begin{matrix} T_{e} \cos α_{e} - \frac{1}{2} ρ_{e} S V_{e}^{2} C_{D_{e}} = 0 \\ T_{e} \sin α_{e} + \frac{1}{2} ρ_{e} S V_{e}^{2} C_{L_{e}} = m g \end{matrix}$ (26)

and with varying mass:

${\begin{matrix} T_{\dot{m}} \cos α_{\dot{m}} - \frac{1}{2} ρ_{\dot{m}} S V_{\dot{m}}^{2} C_{D_{\dot{m}}} = m g \sin γ_{\dot{m}} \\ T_{\dot{m}} \sin α_{\dot{m}} + \frac{1}{2} ρ_{\dot{m}} S V_{\dot{m}}^{2} C_{L_{\dot{m}}} = m g \cos γ_{\dot{m}} \end{matrix}$ (27)

Assuming that the equilibrated FPA $γ_{\dot{m}}$ is very small and considering that $ρ_{\dot{m}} = ρ_{e}, {\dot{V}}_{\dot{m}} = V_{e}$ and $T_{\dot{m}} = T_{e} \frac{δ x_{\dot{m}}}{δ x_{e}}$ , this

leads to:

${\begin{matrix} T_{e} \frac{δ x_{\dot{m}}}{δ x_{e}} \cos α_{\dot{m}} - \frac{1}{2} ρ_{\dot{m}} S V_{\dot{m}}^{2} C_{D_{\dot{m}}} = m g γ_{\dot{m}} \\ T_{e} \frac{δ x_{\dot{m}}}{δ x_{e}} \sin α_{\dot{m}} + \frac{1}{2} ρ_{\dot{m}} S V_{\dot{m}}^{2} C_{L_{\dot{m}}} = m g \end{matrix}$

Assuming that α_e and $α_{\dot{m}}$ are small, the difference between each drag equation gives:

$T_{e} (\frac{δ x_{\dot{m}}}{δ x_{e}} - 1) = m g γ_{\dot{m}}$

which leads to:

$ε_{δ x} = \frac{C_{L_{e}}}{C_{D_{e}}} γ_{\dot{m}}$ (28)

where ɛ_δx denotes the relative correction on the throttle lever δx to consider the mass variation, i.e.:

$δ x_{\dot{m}} = δ x_{e} (1 + ε_{δ x})$

Moreover, the difference between each lift equation gives:

$T_{e} (α_{e} - \frac{δ x_{\dot{m}}}{δ x_{e}} α_{\dot{m}}) + \frac{1}{2} ρ_{e} S V_{e}^{2} (C_{L e} - C_{L \dot{m}}) = 0$

which finally leads to:

$ε_{α} = - \frac{ε_{δ x}}{1 + \frac{C_{L_{α}}}{C_{D_{e}}}}$ (29)

where ɛ_α is the relative correction on α to consider the mass variation, i.e.:

$α_{\dot{m}} = α_{e} (1 + ε_{α})$

Considering that the longitudinal trimmed condition is also given by the condition Cm = 0 in both cases, we have:

${\begin{matrix} C m_{o} + C m_{α} (α_{e} - α_{o}) + C m_{δ e} δ e_{e} = 0 \\ C m_{o} + C m_{α} (α_{\dot{m}} - α_{o}) + C m_{δ e} δ e_{\dot{m}} = 0 \end{matrix}$

The difference between both equations gives:

$C m_{α} (α_{\dot{m}} - α_{o}) + C m_{δ e} (δ e_{\dot{m}} - δ e_{e}) = 0$

which leads to:

$ε_{δ e} = - \frac{C m_{α} α_{e}}{C m_{δ e} δ e_{e}} ε_{α}$ (30)

where ɛ_δe denotes the relative correction on the elevator deflection δe to consider the mass variation, i.e.:

$δ e_{\dot{m}} = δ e_{e} (1 + ε_{δ e})$

Numerical verification

These results have been verified through a numerical simulation performed in the case of a twin-engine aircraft representative of the Airbus wide-body family:¹⁷

Total mass: m=130 10³ kg
Reference area: S_ref=260m²
Lift-slope derivative: C_Lα=5 rad⁻¹
Induced drag factor: K=0.055
Parasite drag coefficient: C_Do=0.02
Pitch stiffness: Cm_α=−1 rad⁻¹
Pitch control effectiveness: Cm_δe=−1.46 rad⁻¹
Total thrust at sea level: T_SL=470 10³N

The aircraft is assumed to fly in cruise at z_e=30 000 ft and M=0.82, i.e. V_e=248.58 m/s, with=−10⁻⁵ kg/s which corresponds to a typical fuel consumption during the cruising phase. From initial conditions computed at z_e and V_e, the mass variation $\dot{m} = k_{\dot{m}} m$ has been applied abruptly, leading to the evolution of the longitudinal state vector computed with a numerical solver based on the Runge-Kutta algorithm.

Firstly, the computation is initialized with the trimmed condition with, i.e. γ₀ = 0, α₀ = α_e, q₀ = 0, δ_e = δe_e, δ_x = δx_e. The figures (Figure 1) and (EQ. (2)) show that, after a transient including a classical “phugoïd mode” and a slow aperiodic mode, the TAS reaches a final state slightly different from the initial value. Moreover, the figure (Figure 2) shows that the FPA reaches a stabilized value $γ_{\dot{m}}$ equal to its analytical expression, i.e..

$γ_{\dot{m}} = \frac{k_{\dot{m}}}{a_{h} V_{e}}$

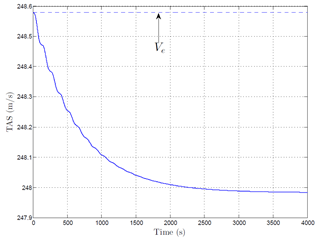
Figure 1 Evolution of the TAS vs. time with $\dot{m} = k_{\dot{m}} m$ initiated with the traditional equilibrium.

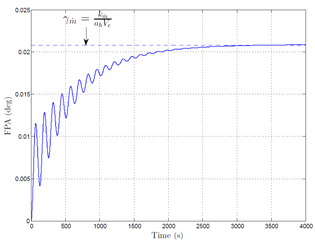
Figure 2 Evolution of the FPA vs. time with $\dot{m} = k_{\dot{m}} m$ initiated with the traditional equilibrium.

The second step is to compute the evolution of the system with the simulation initiated with the corrected trimmed conditions with $\dot{m} \neq 0$ , i.e. $γ_{0} = \frac{k_{\dot{m}}}{a_{h} V_{e}}, α_{0} = α_{\dot{m}}$ , q₀=0, $δ e = δ e_{\dot{m}}, δ x = δ x_{\dot{m}}$ . The figure (Figure 3) shows that the TAS (red curve) is well stabilized in time and almost equal to V_e in these conditions (relative difference equal to 4 10⁻⁶). Concerning the FPA, the figure (Figure 4) shows the transient in this case is very small and $γ = γ_{\dot{m}}$ during the whole simulation.

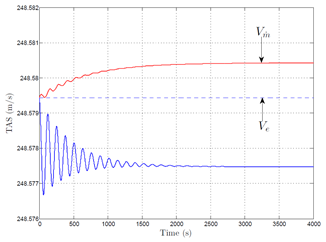
Figure 3 Evolution of the TAS vs. time with $\dot{m} = k_{\dot{m}} m$ initiated with the extended equilibrium.

Figure 4 Evolution of the FPA vs. time with $\dot{m} = k_{\dot{m}} m$ initiated with the extended equilibrium.

This computation also shows that the correction ɛ_α and ɛ_δe can be considered as second order terms. Indeed, considering the simulation initiated with $γ_{0} = \frac{k_{\dot{m}}}{a_{h} V_{e}}$ , α₀ = α_e, q₀ = 0, δe = δe_e, $δ x = δ x_{\dot{m}}$ , i.e. without correcting the terms α_e and δe_e, the evolution of the system (blue curve) is very close to the complete correction. In this case, the main difference lies in the transient which is slightly more pronounced.

Finally, the comparison between the trimmed conditions computed at a given altitude and airspeed considering a constant mass, i.e., vs. the trimmed conditions taking into account a mass variation given by $\dot{m} = k_{\dot{m}} m$ , are gathered in the following tabular with the “first order” and “second order” corrections:

Correction		First order	Second order
Flight Path Angle	γ_e = 0	$γ_{\dot{m}} = \frac{k_{\dot{m}}}{a_{h} V_{e}}$	$γ_{\dot{m}} = \frac{k_{\dot{m}}}{a_{h} V_{e}}$
AoA	α_e	$α_{\dot{m}} = α_{e}$	$α_{\dot{m}} = α_{e} (1 + ε_{α})$
Pitching rate	q_e = 0	$q_{\dot{m}} = 0$	$q_{\dot{m}} = 0$
Elevator deflection	δe_e	$δ e_{\dot{m}} = δ e_{e}$	$δ e_{\dot{m}} = δ e_{e} (1 + ε_{δ e})$
Throttle position	δx_e	$δ x_{\dot{m}} = (1 + ε_{δ x}) δ x_{e}$	$δ x_{\dot{m}} = (1 + ε_{δ x}) δ x_{e}$

Concluding remarks

In this article, it has been demonstrated that the fuel flow rate of the aircraft affects the trimmed conditions. This has led to the definition of extended trimmed conditions, which are the equilibrated conditions in flight considering the weight decrease of the aircraft. When considering these extended trimmed conditions, correcting factors have to be applied on the control commands computed at constant weight to get the exact equilibrated flight taking into account the fuel mass flow rate of the aircraft. Moreover, it has been demonstrated that the mass derivative vs. time itself must be proportional to the total mass of the aircraft to get correct trimmed conditions. As a conclusion, the correcting factors given in this article give a sharper computation of trim points to be used as the starting points of numerical simulation and erase undue transients due to the sudden application of in-flight fuel burn. Moreover, these corrections should be taken into account to compute analytically the performance of the aircraft (endurance, climb, . . . ) as it has been already done for the range given by the Bréguet range formula.