
Research Article Volume 6 Issue 4
Optimization of intersecting straight lines methods for the evaluation of acidity constants of single equilibria from spectrophotometric data
Julia Martin,1
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Agustin G Asuero,2 M Angeles Herrador,2 Gustavo Gonzalez3
1Department of Analytical Chemistry, Escuela Politecnica Superior, University of Seville, Spain
2Department of Analytical Chemistry, Faculty of Pharmacy, University of Seville, Spain
3Department of Analytical Chemistry, Faculty of Chemistry, University of Seville, Spain
Correspondence: Julia Martin, Department of Analytical Chemistry, Escuela Politecnica Superior, University of Seville, C/ Virgen de Africa, 7, E-41011 Seville, Spain, Tel 34-9-5455-6250
Received: July 12, 2018 | Published: August 30, 2018
Citation: Martín J, Asuero AG, Herrador MA, et al. Optimization of intersecting straight lines methods for the evaluation of acidity constants of single equilibria from spectrophotometric data. Pharm Pharmacol Int J. 2018;6(4):333-338. DOI: 10.15406/ppij.2018.06.00197
Download PDF
Abstract
The acid dissociation constant (Ka) is among the most frequently used physicochemical parameters, and its determination is of interest to many research fields. A number of graphical methods has been proposed for the spectrophotometric evaluation of acidity constants of single equilibrium HR=H+R (charges omitted for the sake of generality), in those cases in which the limit absorbance’s of the pure species HR or R, A1 and A0, respectively, are unknowns. The raw values of absorbance’s versus pH data are transformed in linear functions, which allow to evaluate the unknown parameter Ka and A0/or A1 by a graphical approach or by the application of the least squares method. Among the various methods proposed the double reciprocal, Agren-Sommer and Nash methods yield to a family of intersecting straight lines when experimental measurements of absorbance and pH are made at different wavelengths. The purpose of this paper is to critically examine these methods on the basis of the requirements of single linear regression.
Keywords: intersecting straight lines methods, acidity constants, spectrophotometric data
Introduction
Among the physico-chemical properties of molecules, the acidity constants are of vital importance both in the analysis of drugs as well as in the interpretation of their mechanism of action.1–4 The solution of many galenical problems requires the knowledge of the acidity constants of compounds4 of pharmaceutical interest. Many compounds of biological interest have acidity constants, which lie close to each other. Their absorption, further transport and effect in the living organism are affected by the ratio of concentration of protonated and non-protonated forms in various media. Thus, the knowledge of acidity constants is worthy. The evaluation of acidity constants of organic reagents is also of great value to plan analytical experiments,5 e.g., the acidity constants can be employed in the design of titration procedures6 and to examine the likelihood of separation of mixtures of compounds by extraction.
Although black-box computer software’s are easily available nowadays, the spectrophotometric determination of equilibrium constants7 of single equilibria, such as acidity constants (Ka) of monoprotic acids by graphical plots seems to be valuable, due to the transparency of the linearized methods applied. Spectrophotometry is the choosen method when pKa values are either enough high or low and/or solubility problems8 appear. The correct evaluation of pKa of substances of therapeutic interest has vital importance in drug analysis and for the interpretation of their mechanisms of action. A number of graphical methods has been proposed9 for the spectrophotometric evaluation of acidity constants, HR=H+R (charges omitted for the sake of generality) in those cases in which the limit absorbance of the pure species HR, A1, or R, A0, are unknown. Among them, the double reciprocal or Maroni-Calmon,10 Agren-Sommer11–12 and Nash13 methods, lead to a family of intersecting straight lines when experimental measurements of absorbance and pH are made at varying wavelengths.
In these classical spectrophotometric methods the experimental absorbance pH curves are linearized. For the straight lines (Y=a0+a1 X) obtained in each case by the least squares method, we may easily evaluate the unknown parameters, that is, the acidity constant Ka, and the unknown absorbance, A0 or A1, from the slope, a1, and the intercept, a0, of the corresponding lines. The expressions applied in the available methods as well as the calculations of Ka values are shown in Table 1. If the A-pH measurements are made at different wavelengths a set of intersecting straight lines is obtained, given the coordinates of the cut-off points included (summarized) in Table 2. The purpose of this paper is to shown which of the three methods is more appropriate for linear regression analysis.
Method |
Known absorbance limit |
Expression |
X |
Y |
Ka |
Agren-Sommer |
A0 |
|
|
|
|
A1 |
|
|
|
|
Maroni-Calmon |
A0 |
|
|
|
|
A1 |
|
|
|
|
Nash |
A0 |
|
|
|
|
A1 |
|
|
|
-
|
Table 1 Expressions used according to various methods and other parameters of interest
|
Method
|
Limit absorbance
|
Intersecting point
|
|
Agren-Sommer and Maroni-Calmon
|
A0 known
|
(-1/Ka, 0)
|
|
A1 known
|
(-Ka, 0)
|
|
Nash
|
A0 known
|
(0, -1/Ka)
|
|
A1 known
|
(0, -Ka)
|
Table 2 Coordinates of intersecting points in when measurements are made at varying wavelengths
Theory
The correct use of the least squares method requires14–15 several assumptions when it is applied to linear regression analyses:
- The measurement of the variable X is assumed error-free.
- The Y values obtained (replicates) for the same X value must show a Gaussian distribution.
- The standard deviation of the Y values should not change in the range of values covered by the X values (homocedasticity).
If the various expressions proposed in Table 1 are examined in this regard, it can be accepted in the first instance that conditions b) and c) are met, but not a). Given the different nature of the mathematical function that relates the variables of regression X and Y with the experimental values of A and pH in each method, condition a) should be checked through the propagation of errors made in the mean values of A and pH over the various pairs of data X, Y object of the regression.
Error analysis
Let z be a function of the variables A and pH, z=f(A, pH). The errors involved in the measurement of A and pH will be propagated through Z according16 to the random error propagation law
(1)
where sA2 and spH2 are the variances (squared standard deviations) of the absorbance and pH, respectively. Measurements of A and pH are independent, and then cov(A, pH)=0. The application of the Eqn. (1) to the expression of the three methods tested is compiled in Table 3.
Method |
Known absorbance limit |
Variance of variables |
Agren-Sommer |
A0 |
|
A1 |
|
Maroni-Calmon |
A0 |
|
A1 |
|
Nash |
A0 |
|
A1 |
|
Table 3 Propagation of errors in the different variables
If it is assumed that sA and spH have the values of 0.001 and 0.01, respectively, given the precision of common spectrophotometers and pH-meters, we may evaluate the standard deviation of the variables X and Y, sX and sY, respectively, by using five series of synthetic absorbance versus pH data, with 21 points uniformly distributed in the pH range pKa±1, applying the Monte Carlo method, detailed e.g. in reference.17 The results obtained from this study, expressed as relative standard deviations sX/X and sY/Y are shown in Table 4.
Method |
Known absorbance limit
|
|
|
Agren-Sommer |
A0 |
|
|
A1 |
|
|
Maroni-Calmon |
A0 |
|
|
A1 |
|
|
Nash |
A0 |
|
|
A1 |
|
|
Table 4 Relative precision of the different regression variables
Transformation of Expressions
It can be seen from results included in Table 4 that the method of Nash led to a greater precision in the measurement of the variable X compare to the other two methods. If we are interesting in applying both Agren-Sommer and Maroni-Calmon method in a more rigorous way, the role of the variables X and Y must be interchanged leading to the expressions found in Table 5. An additional advantage of the transformed expressions is that allow a simple calculation of the standard deviation of Ka values
(2)
because the acidity constant coincides with the intercept (A0 known) or the reciprocal intercept (A1 known) of the corresponding straight line obtained.
By using the classical expressions we obtain instead more complex relationships for the standard deviation of Ka
(3)
However, by using the new expressions proposed with the synthetic data generated, smaller standard deviations values are obtained (approximately half) than by applying the classical equations. To illustrate the above, a practical application has been developed.
Method |
Known absorbance limit |
Expression |
X |
Y |
Ka |
Agren-Sommer |
A0 |
|
|
|
|
A1 |
|
|
|
|
Maroni-Calmon |
A0 |
|
|
|
|
A1 |
|
|
|
|
Table 5 Transformed expressions for the Agren-Sommer and Maroni-Calmon methods
Materials and methods
In this paper a pH meter CRISON model 501pH meter with combined glass-Ag/AgCl electrodes (In gold) with a range of use of 0 to 14pH units, has been used in pH measurements. A Spectrophotometer SPECTRONIC 2000 (Bausch & Lomb) provided with a graphic XY recorder and equipped with quartz cells of 1-cm path-length has been used for absorbance measurements.
The two classical methods as well as the new expressions have been applied to the pKa evaluation of the methylglyoxal bis (4-phenyl-3thiosemicarbazone) (MGBPT).18–19 Although this reagent has two close pKa corresponding to the equilibria of the type expressed in the following scheme20
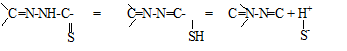
applying the Coleman or Polster methods1,21–23 it can be shown that in the range of about 10-12pH, the two species corresponding to the first ionization equilibrium are found from a practical point of view.
To obtain the A-pH curves of the reagent, solutions of MGBPT concentration equal to 1.08 10-5M are prepared in 25-mL volumetric flasks. The appropriate pH is achieved by adding different volumes of KOH or HCl of various concentrations. To ensure the homogeneity of the solutions, N-N'-dimethylformamide (DMF) is added (the optimum solvent for this reagent is a mixture of DMF and water) so that the samples have 60% V/V of DMF. To fix the ionic strength of the medium in 0.1, 2.5ml of solution of KCl 1M were added. Finally, it is poured with distilled water in 25mL volumetric flasks, and the pH values measured by passing the solutions to 25ml beakers. Absorption spectra are recorded against blanks prepared in the same manner, without reagent. The temperature was about 20±1°C.
10-5M are prepared in 25-mL volumetric flasks. The appropriate pH is achieved by adding different volumes of KOH or HCl of various concentrations. To ensure the homogeneity of the solutions, N-N'-dimethylformamide (DMF) is added (the optimum solvent for this reagent is a mixture of DMF and water) so that the samples have 60% V/V of DMF. To fix the ionic strength of the medium in 0.1, 2.5ml of solution of KCl 1M were added. Finally, it is poured with distilled water in 25mL volumetric flasks, and the pH values measured by passing the solutions to 25ml beakers. Absorption spectra are recorded against blanks prepared in the same manner, without reagent. The temperature was about 20±1°C.
Results and discussion
Though somewhat unpopular in the computer era, graphical analysis is a very appropriate method to study the acid-base behaviour of single equilibria from a spectrophotometric point of view. Since we may assume that in the pH range of choice there are only two species in solution, it is justifiable2 to apply the methods already seen. The results obtained are shown in Table 6. Applying to these results the appropriate statistical criteria24 we can admit that the average values of pKa obtained from the classical expressions did not differ from those obtained with the new expressions. Moreover, there are also no significant differences as regards their precisions.
|
Agren-Sommer Method |
|
Maroni-Calmon Method |
|
Nash Method |
Classic |
Transformed |
Classic |
Transformed |
340 |
10.903 |
10.926 |
0.023 |
10.961 |
10.965 |
0.004 |
10.951 |
345 |
10.909 |
10.931 |
0.022 |
10.963 |
10.967 |
0.004 |
10.939 |
* |
10.906±0.004 |
10.928±0.003 |
|
10.962±0.001 |
10.966±0.001 |
|
10.945±0.008 |
Table 6 pKa1 values at different wavelengths
(*) average value ±standard deviation
(**)
However, some limitations are inherent to this study:
- The calculations were only made for values of sA=0.001 and spH=0.01.
- It was assumed that absolute values of A are independent of the actual values for the whole range of absorbance found.
- If the Gauss law holds for A and pH measurements, this is not necessary so for X and Y of the type used for the calculations in the manuscript; a serious objection, however, the authors does not know whether this is.
- The variance analysis did not include the uncertainty of the instruments readings.
Transmittance and concentration are related by means of a logarithmic relationship, in such a way that small errors in transmittance measurement causing large relative absorbance errors. However, the main source of indeterminate error in modern spectrophotometers lies in the measure of the absorbance. However, the procedure devised in this paper has the inherent advantage of its simplicity, which makes it attractive. Bisthiosemicarbazones are clinically relevant for a variety of diseases, e.g. tuberculosis, viral infections, malaria and cancer.25 Copper (II) uncharged lipophilic complexes of bisthiosemicarbazones posses fascinating biological activity26–28 including applications in nuclear medicine.28 Recent reviews show the biological importance of thiosemicarbazones as anticancer agents.25,29–33
Conclusion
Among the physico-chemical properties of molecules, the acidity constants are of vital importance both in the analysis of drugs as well as in the interpretation of their mechanism of action. The solution of many galenical problems requires the knowledge of the acidity constants of compounds having pharmaceutical interest. As it has previously indicated, calculation of acidity constants of monoprotic acids by graphical methods may be advantageously used in spite of the existence of modern black-box computer software’s. The exchange of the role of the variables X and Y of the classical Agren-Sommer and Maroni-Calmon methods resulted in new expressions that fulfil the mathematical conditions required for the regression analysis, and led to more simplified equations for the calculation of the pKa and its individual standard deviation. As far as the results are concerned, there are no significant differences and, therefore, this reformulation may be considered valid. Note that bisthiosemicarbazones are biological relevant as shown at the end of the previous section.
Acknowledgement
Conflict of interest
Authors declare that there is no conflict of interest.
References
- Martin J, Soria AH, Asuero AG. A slope-intercept method for the spectrophotometric evaluation of overlapping acidity constants of diprotic acids when limiting absorbances are known. J Lab Chem Educ. 2018;6(4):107–117.
- Martin J, Suarez IA, Asuero AG. An annotation of normalized diagrams for the existence of two species of a diprotic acid in solution. Open Access J Chem. 2018;2(1):23–25.
- Avdeef A, Testa B. Physicochemical profiling in drug research; a brief survey of the state-of-the-art of experimental techniques. Cell Mol Life Sci. 2002;59(10):1681–1689.
- Asuero AG. A bilogarithmic method for the evaluation of acidity constants of amphoteric substances from solubility measurements. Int J Pharm. 1989;52(2):129–137.
- Papanastasiou G, Kokkinidis G. Development of iterative methods for the exact determination of acid dissociation constants and specific reaction rates in various ionic or electrochemical systems: A review. Collect Czechoslovak Chem Commun. 2003;68(8):1345–1378.
- Asuero AG, Michalowski T. Comprehensive formulation of titration curves for complex acid-base systems and its analytical implications. Crit Rev Anal Chem. 2011;41(2):151–187.
- Fuchs H, Gessner R. The result of equilibrium-constant calculations strongly depends on the evaluation method used and on the type of experimental errors. Biochem J. 2001;359(Pt 2):411–418.
- Avdeef A. Solubility of sparingly-soluble ionizable drugs. Adv Drug Deliv Rev. 2007;59(7):568–590.
- Meloun M, Havel J, Högfeldt E. Computation of Solution Equilibria, a guide to methods in potentiometry, extraction, and spectrophotometry. Chichester: Ellis Horwood; 1988.
- Maroni C, Calmon JP. Détermination spectrophotométrique des pK de dissociation des b–dicé 1. Technique expérimentale et mise au point de méthodes graphiques. Bull Soc Chim France. 1964;1:519–524.
- Agren A. The complex formation between iron(III) ion and some phenols. II. Salicylic acid and p-amino salicylic acid. Acta Chem Scand. 1954;8(6):1059–1072.
- Sommer L, Langova M. Spectrophotometric methods for the investigation of metal complex formation. Crit Rev Anal Chem. 1988;19(3):225–269.
- Nash CP. The calculation of equilibrium constant from spectrophotometric data. J Phys Chem. 1960;64(7):950–953.
- Asuero AG, Gonzalez AG. Some observations on fitting a straight line to data. Microchem J. 1989;40(2):216–225.
- Sayago A, Boccio M, Asuero AG. Fitting straight lines with replicated observations by linear regression: the least squares postulates. Crit Rev Anal Chem. 2004;34(1):39–50.
- Asuero AG, Gonzalez G, de Pablos F, et al. Determination of the optimum working range in spectrophotometric procedures. 1988;35(7):531–537.
- Martin J, Mairena JP, Asuero AG. On the evaluation of autoprotolysis constants of amphiprotic and inert solvents obtained from electrochemical measurements: consideration of liquid junction potentials when necessary. Curr Top Anal Chem. 2016;10:49–71.
- Herrador MA, Jimenez AM, Asuero AG. Spectrophotometric determination of zinc in potable waters and insulin with methylglyoxal bis(4-phenyl-3-thiosemicarbazone). 1987;112(9):1237–1246.
- Herrador MA. Analytical Applications of Metylglyoxal Bis(4-Phenyl-3-Thiosemicarbazone). Seville: PhD Thesis, University of Seville, Department of Analytical Chemistry; 1986.
- Asuero AG, González-Balairon M. Analytical applications of biacetyl bis(4-phenyl-3-thiosemicarbazone) and bipyridylglyoxal bis(4-phenyl-3-thiosemicarbazone). Microchem J. 1980;25(1):14–45.
- Coleman JS, Varga LP, Mastin H. Graphical methods for determining the number of species in solution. Inorg Chem. 1970;9(5):1015–1020.
- Polster J, Lachmann H. Spectrometric Titrations: Analysis of Chemical Equilibria. Weinheim: VCH; 1989. 433 p.
- Boccio M, Sayago A, Asuero AG. A bilogarithmic method for the spectrophotometric evaluation of stability constants of 1:1 weak compleses from mole ratio data. Int J Pharm. 2006;318(1-2):70–77.
- Miller JN, Miller JC. Statistics and Chemometrics for Analytical Chemistry. 6th Essex: Pearson; 2010.
- Heffeter P, Pape VFS, Enyedy EA, et al. Anticancer thiosemicarbazones: chemical properties, interaction with iron metabolism, and resistance development. Antioxid Redox Signal; 2018.
- Mckenzie-Nickson S, Bush AI, Bamham KJ. Bis(thiosemicarbazone)metal complexes as therapeutics for neurodegenerative diseases. Curr Top Med Chem. 2016;16(27):3058–3068.
- Djoko KY, Goytia MM, Donnelly PS, et al. Copper(II)-bis(thiosemicarbazonato) complexes as antibacterial agents: insights into their mode of action and potential as therapeutics. Antimicrob Agents Chemother. 2015;59(10):6444–6453.
- Paterson BM, Donnelly PS. Copper complexes of bis (thiosemicarbazones): from chemotherapeutics to diagnostic and therapeutic radiopharmaceuticals. Chem Soc Rev. 2011;40(5):3005–3018.
- Suvarapu LN, Somala AR, Kodoru JR, et al. A critical review on analytical and biological applications of thio- and phenylthiosemicarbaonones. Asian J Chem. 2012;24(5):1889–1898.
- Kaur H, Gupta M. Recent advances in thiosemicarbazones as anticancer agents. Int J Pharm Chem Biol Sci. 2018;8(2):259–265.
- Khan T, Ahmad R, Joshi S, et al. Anticancer potential of metal thiosemicarbaone complexes: a review. Der Chem Sinica 2015;6(12):1–11.
- Pape VFS, Tóth S, Fürdi A, et al. Design, synthesis and biological evaluation of thiosemicarbazones, hydrazinobenzothiazoles and arylhydrazones as anticancer agents with a potential to overcome multidrug resistance. Eur J Med Chem. 2016;117:335–354.
- Sharma N, Pathak DP. Combatting challenging aspects of cancer with thiosemicarbazones. Int J Pharm Pharm Sci. 2016;8(8):27–34.

©2018 Martín, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


![]() 10-5M are prepared in 25-mL volumetric flasks. The appropriate pH is achieved by adding different volumes of KOH or HCl of various concentrations. To ensure the homogeneity of the solutions, N-N'-dimethylformamide (DMF) is added (the optimum solvent for this reagent is a mixture of DMF and water) so that the samples have 60% V/V of DMF. To fix the ionic strength of the medium in 0.1, 2.5ml of solution of KCl 1M were added. Finally, it is poured with distilled water in 25mL volumetric flasks, and the pH values measured by passing the solutions to 25ml beakers. Absorption spectra are recorded against blanks prepared in the same manner, without reagent. The temperature was about 20±1°C.
10-5M are prepared in 25-mL volumetric flasks. The appropriate pH is achieved by adding different volumes of KOH or HCl of various concentrations. To ensure the homogeneity of the solutions, N-N'-dimethylformamide (DMF) is added (the optimum solvent for this reagent is a mixture of DMF and water) so that the samples have 60% V/V of DMF. To fix the ionic strength of the medium in 0.1, 2.5ml of solution of KCl 1M were added. Finally, it is poured with distilled water in 25mL volumetric flasks, and the pH values measured by passing the solutions to 25ml beakers. Absorption spectra are recorded against blanks prepared in the same manner, without reagent. The temperature was about 20±1°C.