Consequences of the diffeomorphisms induced by $K-$ invariant connections of the space of 1-forms of certain endomorphisms defined over a Lie algebra that is isomorphic to the tangent space seated in the identity element, of homogeneous spaces $G\mathrm{<mo>/</mo>}K\subset G\mathrm{<mo>/</mo>}H$ , are analized. The images of these diffeomorphisms in $G\mathrm{<mo>/</mo>}H$ , are 2-form of curvatures that can be induced to each class of the $G\mathrm{<mo>/</mo>}K$ . Then using the $K-$ invariant connection of this homogeneous space, the curvature can be determined as a regular representation that admits a finite discomposing of irreducible sub-representations of finite type, accord with the generalizing in dimensions of the Gauss-Bonnet theorem and the generalized Radon transform to obtain curvature through of co-cycles of the image of the corresponding space. Such irreducible sub-representations will be isotopic components of the certain smoothly embedded image in a manifold modelled this last, by a generalized function space. Likewise, through these realizations we have the curvature integrals as dual case of their field equations. Finally, using the complex Riemannian structure of our model of the space-time, and the $K-$ invariant $G-$ structure of the orbits used to obtain curvature, are obtained as consequences of the diffeomorphisms the field equations to the energy-matter tensor density in each case of the gravitational field. Of this manner, is determined their energy-mass tensor density as an integral which represents the energy spectra of the curvature when this is obtained in duality to the homogeneous field equations to the Riemann tensor R${}^{\mu \nu }-\frac{1}{2}{g}^{\mu \nu }$ R.

Keywords: action integrals to gravity, curvature on homogeneous spaces, hessian curvatures, integral curvature, integration on orbits, integration invariants, local diffeomorphisms, regular representation, symmetric hermitian spaces, smooth embedding

Through consider the unification the curvature from a point of view of two-study frame,¹ and after with the generalizing of curvature as an integration invariant is suggested the curvature as regular representation that admits a finite decomposing of irreducible sub-representations of finite type.^1,2

This representation, from several points of view of the field theory are considered in this paper to obtain applications of the “integral curvature” in cosmic curvature that includes the curvatures of the solution of the Einstein equations and the curvatures of the quantum model of the Universe (model of superstrings, particle physics and gravitational waves).

Likewise, diffeomorphisms of the form $Diff\mathrm{<mo\; stretchy="false">(</mo>}{G}^0\mathrm{<mo>/</mo>}K\mathrm{<mo\; stretchy="false">)</mo>}$ , $\cong$  exp(${\mathfrak{m}}_0$ ), are developed around of establish the field equations to start of action integrals model to particles and microscopic structure of the flag manifolds, the modelling of the gravitational field in the complex Riemannian model used to relativity description and other theories that complement the Einstein theory.

The connections used involve ant $K-$ invariant $G-$ structure of the manifold. Likewise, if M, is a reductive homogeneous space $G\mathrm{<mo>/</mo>}{G}_0$ , then the $G-$ structure $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , admits an $K-$  invariant ${\tilde{\nabla }}_K$ :-conection. This connection $K-$ invariant in $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , defined by the equation ${\tilde{\nabla }}_K\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ , is the canonical connection of $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , respect to the decomposing $\mathfrak{t}=\mathfrak{h}\oplus \mathfrak{m}$ . Of this way, we have that all $K-$ invariant connection of the reductive space $G\mathrm{<mo>/</mo>}{G}_0$ , is equal to the canonical connection of the space $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , respect to the decomposing $\oplus {\mathfrak{m}}_j$ . This establish the fact of that both connections have equal geodesics set. Thus the integrations that are realized on the orbits of the spaces $G\mathrm{<mo>/</mo>}{G}_0$ , and $S_G{\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}}_K$ , meet, additionally the fact of the preservation of the inner product’, in M, under the actions of the semi-simple group subjacent to the isometric complete differentiable manifold M.

We are interested in the cosmological study, and in particular, in the determination of their curvature from the microscopic aspects considering the particles as little deformations of the microscopic structure of the space-time.

Let M, be a Riemannian manifold at least complex of dimension 2n¹. Then given that an at least differentiable structure is an at least complex holomorphic structure and this is an at least Hermitian structure then their connection is constructed through their at least Hermitian structure of their corresponding at least complex Riemannian bundle.

Let $\pi \mathrm{<mo>:</mo>}J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}\to M$ , the bundle of at least Hermitian structure of M. Thus a fiber in $\chi \in M$ , is the space

$J_{\chi }\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo>\{</mo>}j\in End\mathrm{<mo\; stretchy="false">(</mo>}{T}_{\chi }\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}|j^2\mathrm{<mo>=</mo>}-\mathrm{1,}conj\mathrm{,}symmetric\mathrm{<mo>\}</mo>}$   (1)

Then the bundle is associated to the orthonormal frame bundle of M, with typical fiber $J\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo>}$ =O (2n)/U(n), which is a symmetric Hermitian space² These typical fibres have an invariant complex O(2n)-structure.³ Then the following diagram of the at least complex Riemannian bundle $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , establishes the bijective correspondence with $J\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo>}$ , and their horizontal and vertical spaces of the corresponding induced distributions for the Levi-Civita connection, having the diagram:

$J\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}O\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{,}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}\leftarrow O\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{,}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo>}\to O\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{,}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}\tilde{O}\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}O\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$

$O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}\downarrow \pi \text{'}O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}\times O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}\downarrow \pi O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}\downarrow \pi \text{'}\text{'}$   (2)

$M\leftrightarrow M\leftrightarrow M$

With orbits or horo-spheres in the irreducible symmetric compact Hermitian space S O(2n)/U(n).⁴

Then the tangent bundle of the fibres in $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , satisfies the equation (sum of diffeomorphisms as mapping of the tangent spaces):

$TJ\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{E}_V\oplus E_H\mathrm{,}$   (3)

With the vertical distribution given for

$E_V\mathrm{<mo>=</mo>}Kerd\pi \mathrm{,}$   (4)

And $E_H$ , the corresponding horizontal distribution identified isomorphically by the space $\mathrm{<mo\; stretchy="false">(</mo>}{\pi }^{-1}T\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$ .

Of this way, we can characterize an at least complex tautological holomorphic structure $J^H$ , on $E_H$ , given For the endomorphisms $J_j^H\mathrm{<mo>=</mo>}j\in End\mathrm{<mo\; stretchy="false">(</mo>}{T}_{\chi }\mathrm{<mo\; stretchy="false">(</mo>}{\pi }^{-1}T\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}$  

Adding this to $J^V$ , is established an at least complex structure $\mathcal{I}$ , given for $TJ\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , as in the equation (3). This help us to induce the at least complex structure on holomorphic submanifolds of the manifold $JM$  and thus of the manifold M.

Due to that we want calculate geometrical properties of the space through the submanifolds such as their curvature, torsion, etc., is wanted to have an integrability criteria on $JM$ , through their differentiable projections (that are fibres of sections of the bundle⁵ $TJ\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}$  This criteria based in their differentiable projections takes said condition resolving the homogeneous equation to the integrability condition, given this by the corresponding integral equation, staying the field differential equation to the space given in (3). This will be applied in the next section to the corresponding study on gravitational field theory to quantum level and which has macroscopic effects in the behaviour of the matter-energy tensor, as is mentioned in the Einstein field equations.

The $O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}$ - structure permits the validation of the invariance of the equations, but also the appearing of the conformal transformation as an exact symmetry property of the space-time to the symmetry of the Riemann tensor to the spherical case.

An adequate criteria is given by the integrability obstruction of the distribution of the spaces $E_H\mathrm{<mo\; stretchy="false">(</mo>}J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}$  But this is obtained, if the corresponding curvature tensor to the structure $\mathcal{I}$ , is annulled.³⁶

Thus $\mathcal{I}$ , is integrable if $R\mathrm{<mo\; stretchy="false">(</mo>}{T}^{+}\mathrm{,}{T}^{+}\mathrm{<mo\; stretchy="false">)</mo>}{T}^{+}$ , is satisfied to all isotropic maximal subspaces $T^{+}$ , of TM. This is equivalent to consider that to the mass-energy tensor the energy integral takes the form:

$W\mathrm{<mo\; stretchy="false">(</mo>}{T}^{+}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\wedge {\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}dx\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}d{x}^{\prime }\mathrm{<mo\; stretchy="false">)</mo><mo>\{</mo>}{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\prime }\mathrm{<mo\; stretchy="false">)</mo>}{T}_{\mu \nu }-\frac{1}{2}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\prime }\mathrm{<mo\; stretchy="false">)</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\prime }\mathrm{<mo\; stretchy="false">)</mo><mo>\}</mo>,}$   (5)

This re-fall as a condition to the curvature tensor R in their $O\mathrm{<mo\; stretchy="false">(</mo>2}n\mathrm{<mo\; stretchy="false">)</mo>}$ - invariant anti-symmetric part, that is to say, in their Weyl tensor.⁷

Then $\mathcal{I}$ , is integrable if and only if the Weyl tensor $W_{\mu \nu }$ , of $R_{\mu \nu }$ , is such that

$W_{\mu \nu }\mathrm{<mo>=</mo>0}$   (6)

That is to say, that M is local and conformally flat.

Likewise, considering an $K-$ invariant connection of the reductive homogeneous space $G\mathrm{<mo>/</mo>}{G}_0$ , corresponding to a Stein manifold $M_D$ ,⁸ subjacent to the complex Riemmanian manifold M (that is to say, we consider a closed and compact orbit of M), then $G_0\mathrm{<mo>=</mo>}K$ .

Indeed, we consider the De Rham cohomology of the exterior algebras $ℂ\wedge \mathrm{<mo\; stretchy="false">(</mo>}V\mathrm{<mo\; stretchy="false">)</mo>}$ , and $ℂ{\wedge }^{\ast }\mathrm{<mo\; stretchy="false">(</mo>}V\mathrm{<mo\; stretchy="false">)</mo>}$ , of the vector bundle $E\to M$ , and we construct the K- invariant connection on the vector bundle $P\to M$ , (the vector $G-$  bundle) that is an affine connection in M⁹. By orbitalizing¹⁰

$G\mathrm{<mo>/</mo>}D\circlearrowleft G\mathrm{<mo>/</mo>}P\circlearrowleft G\mathrm{<mo>/</mo>}{G}_0\mathrm{,}{G}_0\mathrm{<mo>=</mo>}K\mathrm{,}$   (7)

We have that can be constructed a smooth embedding in $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , of flag submanifolds $\mathbb{F}$ , such that the images of said embedding on $\mathbb{F}$ , are $G_0-$ orbits(that is to say, $K-$ orbtis) in $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ .

But this always is possible for the reduction of the holonomy group of M, and that M, is a complex locally symmetric and connect inner Riemannian manifold, that is to say, that the Nijenhuis tensor satisfies on the corresponding sub-bundle $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , of M, that

$R_{\mathcal{I}}^M\mathrm{<mo\; stretchy="false">(</mo>}j\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}$   (8)

Thus our sub-bundle has integrable structure and as the considered space is an at least complex manifold, one can find complex submanifolds of $J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , to which the $K-$ orbits are flag manifolds of the $G-$ structure of M. This brings in our study of integral curvature (study of curvature through the integral geometry) on $K-$ orbits of a Riemannian manifold, the curvature on symmetric spaces (null Weyl tensor and non-null Ricci tensor), since the unique complex integrable submanifolds that can be realized as $K-$ orbits in a simply connect, inner, symmetric and of compact type manifold M, are the flag $G-$ manifolds.

Theorem

The $K-$ invariance given by the $G-$ structure $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , of M, complex and holomorphic, is induced to each closed submanifold given for the flag manifolds of the corresponding vector holomorphic $G-$ bundle. Furthermore, the integral cohomology given of such complex submanifolds is equivalent to the integral cohomology on submanifolds of a maximum complex torus.

In the superstring theory the space-time has 10 dimensions separated in two parts, 4 dimensions of the ordinary Minkowski space-time and 6 extra dimensions to microscopic level. This conform the microscopic space $G\mathrm{<mo>/</mo>}{G}_0$ , with $G_0\mathrm{<mo>=</mo>}K$ . The form of the extra six dimensions must correspond to a solution to the Einstein equations in the vacuum of the gravity. If the 6-dimensional manifold is extended in real variable, the unique solution is a flat space-time. However, if is considered the 6-dimensional manifold as a complex manifold of three dimensions, exist solutions of the field theory to the vacuum called Calabi-Yau manifolds.⁵

This result is fundamental to the consistency of the theory that we propose since will establish the geometrical elements necessary to create a Cosmos theory unifying the quantum mechanics with special and general relativity, using a method in⁶ which we have baptized with the name “orbitalization”. Then we can to pass of the integral calculation on geodesics of the space-time to Feynman integrals or string integrals considering the orbit of the corresponding filtration to the reductive homogeneous space of M.

The reduction process of the holonomy group of the structure $S_G\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , help us to obtain reductive homogeneous spaces of $G\mathrm{<mo>/</mo>}H$ , whose orbits inherit of the $G-$  structure of the widest space, for example the model of the space-time $\mathbb{M}$ , (Figures 1 (A & B)). Finally we can tell the curvature spectra as the energy of the energy-matter tensor, which can be determined by the action integrals to a particle level. This we will do in the following section.

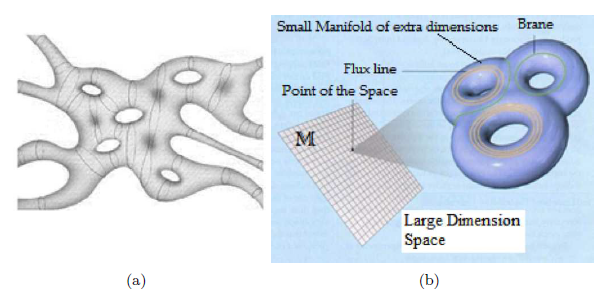
Figure 1 A) 2-dimensional superstring model of the microscopic space-time. The spaces are tacking themselves, from the fundamental strings in each point of the complex Riemannian model of the space-time $\mathbb{M}$ B) Small manifold, which represents a superposing of maximum complex torus.

¹An at least complex structure of a differentiable manifold M, is a complex structure whose Hermitian form is defined on the tangent space of M.³

²Of fact, are two disjoint components of the compact subgroup S O(2n)/U(n), of $J\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{2n}\mathrm{<mo\; stretchy="false">)</mo>}$ .

³ M, has as structural group the Lie group O(2n).

⁴Of fact, the orbits that will be used to the generalization of the curvature of the space-time will be the submanifolds belonging to said irreducible Hermitian symmetric space S O(2n)/U(n), to the case n=4.

⁵ Theorem. Let $j\in J\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ , with i-eigen-space $T^{+}\subset T_{\chi }M\mathrm{.}$  Let $R\in {\wedge }^{2}T\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}{\otimes }_{ℝ}E$  (with E, a complex vector space belonging to a holomorphic bundle). Then the Nijenhuis tensor $R_{\mathcal{I}}^M\mathrm{<mo>=</mo>0}$ , if and only if $R\mathrm{<mo\; stretchy="false">(</mo>}{T}^{+}\mathrm{,}{T}^{+}\mathrm{<mo\; stretchy="false">)</mo>}{T}^{+}\subset T^{+}$ .

⁶Riemann Tensor = Ricci Tensor + Weyl Tensor. The Weyl tensor represents the anti-symmetrical part of the curvature tensor.

⁷Defination: A Stein manifold is an open orbit of a semi-simple Lie group in a generalized flag manifold.

⁸Procedure to generate orbits in reductive Lie groups.

⁹Flag $G-$ manifolds of M. G, acts transitively on such complex submanifolds.

¹⁰Ricci Curvature Tensor.

We consider the density of matter given for the scalar , which appears when is varied the integral of the energy-matter of the tensor ,

$W\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{k}{2}{\displaystyle \int }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}d\chi \mathrm{,}$   (9)

From a point of view of field theory in the microscopic field theory, results more natural understand the affecting of the space-time due to the matter-energy, which does arise the gravitational field whose action is measurable through their curvature tensor. Then the integral (9) consider the density h, to start from $R^{\mu \nu }$ , or $S^{\mu \nu }$ ¹¹.

Using the massless particles frame of helicity $\pm 2$ , we consider the energy integral of the energy-mass tensor to these particles as:

$W\mathrm{<mo\; stretchy="false">(</mo>}{T}^{+}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{k}{2}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>\{</mo>}{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{T}_{\mu \nu }-\frac{1}{2}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>\}</mo>,}$   (10)

With the condition

${\partial }_{\mu }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}$   (11)

Then the symmetric tensor field $h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , is defined for the variation to said integral (10) as:

$\delta W\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo>}\delta T^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{h}_{\mu \nu }\mathrm{,}$   (12)

Subject to the condition:

${\partial }_{\mu }\delta T^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}$   (13)

Which is had that

$h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}k{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">[</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}-\frac{1}{2}{g}_{\mu \nu }T\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}+{\partial }_{\mu }{\xi }_{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\nu }{\xi }_{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (14)

But the indices contraction of the tensor, deduces that

$h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{g}_{\mu \nu }{h}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-k{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}+2{\partial }_{\mu }{\xi }^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (15)

This is the density of the displacement field, determined to each particle that is displaced from $\chi$ , to ${\chi }^{\text{'}}$ . In this point, the density $h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , arises of a variation of the energy-mass tensor density, which gives legitimacy to the field tensor which can characterize the curvature tensor through of the spectra.

Then the difference of densities, to know, produce:

$h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\frac{1}{2}{g}_{\mu \nu }h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}k{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{D}_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\xi }_{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\nu }{\xi }_{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-g_{\mu \nu }{\partial }_{\lambda }{\xi }^{\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (16)

But the appearing of the “source” condition through of the divergence of the equation (16) in their left side, establishes:

${\partial }_{\mu }\mathrm{<mo\; stretchy="false">(</mo>}{h}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2<mo\; stretchy="false">)</mo>}{g}^{\mu \nu }h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{\partial }^2{\xi }^{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (17)

But by the expression (14) is deduced of (17) that:

$-{\partial }^2{h}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\partial }^{\lambda }{h}_{\lambda \lambda }+{\partial }_{\nu }{\partial }^{\lambda }{h}_{\mu \lambda }-{\partial }_{\mu }{\partial }_{\nu }h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}k\mathrm{<mo\; stretchy="false">(</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2<mo\; stretchy="false">)</mo>}{g}_{\mu \nu }T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}$   (18)

Contracting the indices in (18) or becoming the integral (15) to a differential equation we have:

$-{\partial }^{2}h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\partial }_{\nu }{h}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}kT\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (19)

Here we establish a diffeomorphism such that we can to obtain from (19) other version of the differential equation given in (18), to know:

$-{\partial }^2{h}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\partial }^{\lambda }{h}_{\lambda \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\nu }{\partial }^{\lambda }{h}_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-{\partial }_{\mu }{\partial }_{\nu }h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-g_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}-{\partial }^{2}h\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_n{\partial }_{\lambda }{h}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}k{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (20)

As we know, the left side of (20) is such that their divergence is null. The null divergence of the source tensor now appears as an algebraic consequence of the field equations. Then for the arbitrary of ${\xi }_{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , the field equations are not affected and the no affectation is due to the re-definition of $h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , which is maintained. Likewise, we have to points of the plane in local theory that:

$h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\mapsto h_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\xi }_{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\nu }{\xi }_{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (21)

Which is a gauge gravitational transformation. Then the massive particle (that we call “graviton” or particle of spin 2) is described for

$W\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>\{</mo>}{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}+\frac{2}{m^2}{\partial }_{\nu }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\partial }^{\lambda }{T}_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>\}</mo>}+$

$\left(\frac{1}{m^4}\right){\partial }_{\mu }{\partial }_{\nu }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\partial }_n^{\text{'}}{\partial }_{\lambda }^{\text{'}}{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\frac{1}{3}\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-m^{-2}{\partial }_{\mu }{\partial }_{\nu }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-m^{-2}{\partial }_n^{\text{'}}{\partial }_{\lambda }^{\text{'}}{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}$   (22)

In which,

$T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{g}_{\mu \nu }{T}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (23)

However, the symmetric tensor field that is introduced through:

$\delta W\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo>}\delta T^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{\varphi }_{\mu \nu }\mathrm{,}$   (24)

Which is obtained as:

${\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}-\left(\frac{1}{m^2}\right){\partial }_{\mu }{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\partial }^{\lambda \text{'}}{T}_{\lambda \nu }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}$

$-\left(\frac{1}{m^2}\right){\partial }_{\nu }{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\partial }^{\lambda \text{'}}{T}_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}+\left(\frac{1}{m^4}\right){\partial }_{\mu }{\partial }_{\nu }{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\partial }_n^{\text{'}}{\partial }_{\lambda }^{\text{'}}{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}$

$-\frac{1}{3}\mathrm{<mo\; stretchy="false">(</mo>}{g}_{\mu \nu }-\left(\frac{1}{m^2}\right){\partial }_{\mu }{\partial }_{\nu }\mathrm{<mo\; stretchy="false">)</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{\Delta }_{+}\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\left(\frac{1}{m^2}\right){\partial }_n^{\text{'}}{\partial }_{\lambda }^{\text{'}}{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$   (25)

Has as divergence the vector

${\partial }^{\mu }{\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\left(\frac{1}{m^2}\right)\partial \mu T_{\mu \nu }{\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}}^{\text{'}}-\left(\frac{1}{3m^2}\right){\partial }_{\nu }\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+\left(\frac{2}{m^4}\right){\partial }_n{\partial }_{\lambda }Tn\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}$   (26)

Which is annulled in free regions of sources. Then the equations described of the before integral expression (25) are:

$\begin{array}{l}\mathrm{<mo\; stretchy="false">(</mo>}-{\partial }^2+m^2\mathrm{<mo\; stretchy="false">)</mo>}{\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{T}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\left(\frac{1}{m^2}\right)\mathrm{<mo\; stretchy="false">(</mo>}{\partial }_{\mu }{\partial }^{\lambda }{T}_{\lambda \nu }+{\partial }_{\nu }{\partial }^{\lambda }{T}_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}+g_{\mu \nu }\left(\frac{1}{m^2}\right){\partial }_n{\partial }_{\lambda }\mathrm{,}{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\\ \left(\frac{1}{3}\right)\mathrm{<mo\; stretchy="false">(</mo>}{g}_{\mu \nu }-\left(\frac{1}{m^2}\right){\partial }_{\mu }{\partial }_{\nu }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+\left(\frac{2}{m^2}\right){\partial }_n{\partial }_{\lambda }{T}^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\end{array}$   (27)

The combining of scalar and vector sources are re-placed by an equivalent field. Then the differential equations (27) taken the form:

$\mathrm{<mo\; stretchy="false">(</mo>}-{\partial }^2+m^2\mathrm{<mo\; stretchy="false">)</mo>}{\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\mu }{\partial }^{\lambda }{\varphi }_{\lambda \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_{\nu }{\partial }^{\lambda }{\varphi }_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-{\partial }_{\mu }{\partial }_{\nu }\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-g_{\mu \nu }\mathrm{<mo\; stretchy="false">[</mo><mo\; stretchy="false">(</mo>}-{\partial }^2+m^2\mathrm{<mo\; stretchy="false">)</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_n{\partial }_{\lambda }{\varphi }^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}{T}_{\mu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (28)

Where using the trace information we have:

$\mathrm{<mo\; stretchy="false">(</mo>}-{\partial }^2+m^2\mathrm{<mo\; stretchy="false">)</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\partial }_n{\partial }_{\lambda }{\varphi }^{n\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}\mathrm{<mo\; stretchy="false">(</mo>}T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+m^2\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}$   (29)

Which can be presented as:

${\partial }^{\lambda }{G}_{\mu \nu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-{\partial }_{\nu }{G}_{\mu \lambda }^{\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+m^2\mathrm{<mo\; stretchy="false">(</mo>}{\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+\frac{1}{2}{g}_{\mu \nu }\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{T}_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (30)

Here appears the expression of the energy-matter tensor difference to the field equation $R^{\mu \nu }-\frac{1}{2}{g}^{\mu \nu }R\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\chi T^{\mu \nu }$ .

Of (20), and using a functional distribution that permits smoothly to embed a space region with tensor $T_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , in a space of the integral (15) (that is to say, belonging to a spectral distribution $D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$ , we have that, if the matter distribution produced by the tensor field $T_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , has a spherical symmetry then the field equations have the diffeomorphism of the curvature tensor of the spherical mapping. Then in a local region of the space affected by this tensor, $\sigma \mathrm{<mo\; stretchy="false">(</mo>}T-T^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}\subset D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^n\mathrm{<mo\; stretchy="false">)</mo>}$ ,¹² we have:

$dimE{E}_{O\mathrm{<mo\; stretchy="false">(</mo>}N+\mathrm{1<mo\; stretchy="false">)</mo>,}{T}_{\chi }\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}\Re \mathrm{<mo\; stretchy="false">(</mo>}T-T^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>,}{D}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}dim{S}^{n}dim\sigma \mathrm{<mo\; stretchy="false">(</mo>}T-T^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\kappa n\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>,}$   (31)

The space region is diffeomorfically embedded in $D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^n\mathrm{<mo\; stretchy="false">)</mo>}$ . In particular to our Ricci tensor $R\equiv R_{\alpha \beta }^{\alpha \beta }\mathrm{<mo>=</mo>}{g}^{\alpha \beta }{R}_{\alpha \beta }$ , in a 2-dimensional region we have that (31) takes the value 2(2-1)P,P=1.

Likewise, a functional $\mathcal{L}$ , in the distribution space $D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}H\mathrm{<mo\; stretchy="false">)</mo>}$ , with H, energy states space

$H\mathrm{<mo>=</mo><mo>\{</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}H\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">(</mo>1<mo>/</mo>2}m\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo>}\varphi {\mathrm{<mo>|</mo><mo>|</mo>}}^2+\begin{array}{c}•\\ V\end{array}\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>\}</mo>}$   (32)

Is the Lagrangian to gravitational field:

$\mathcal{L}\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{,}g\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}\frac{1}{2}\mathrm{<mo\; stretchy="false">[</mo>}{\partial }_{\mu }\varphi g^{\mu \nu }{\partial }_{\nu }\varphi +\mathrm{<mo\; stretchy="false">(</mo>}{m}^2+\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>6<mo\; stretchy="false">)</mo>}R\mathrm{<mo\; stretchy="false">)</mo>}{\varphi }^2\mathrm{<mo\; stretchy="false">]</mo>,}$   (33)

Likewise, this described energy system to curvature tensor from their corresponding matter-energy tensor (in their duality) has a spherical symmetry (Figures 2 (A & B)). Then with $m\mathrm{<mo>=</mo>0}$  this system is conformal and invariant, thus one can see that:

$\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\mapsto {\mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{-\mathrm{1<mo>/</mo>2}}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (34)

Figure 2 A) 3-dimensional region with Ricci curvature and conformal transformation with plane action in XY-plane. Their curvature obeys the dimension 2(2-1)P,P=1. B) Spherical symmetry of the quasi-static gravitational field, that is to say, with curvature $R_{\mu \nu }\mathrm{<mo>=</mo>0}$ .

$\forall \varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\in H$ , and ${\mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{-\mathrm{1<mo>/</mo>2}}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\in D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}H\mathrm{<mo\; stretchy="false">)</mo>}$ . If $\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , is constant this space has a curvature with a static field with spherical symmetry on XY-plane (Figure 2B).

Then we can extended this conformally to other scalar fields that response to conformal transformations,⁷ for example, let $\psi$ , be a new scalar field or energy state such that:

$\psi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\mapsto {\mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}\psi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (35)

We consider additionally that the conformal response of the gravitational Lagrange function given in $2\kappa \mathcal{L}\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">(</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}\chi {\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}{g}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{R}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ ,⁸ could be compensated by the multiplication with $\psi {\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}}^2$ , at least for constant $\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , which leaves $R_{\mu \nu }$ , unchanged. Then part of the Lagrangian that is symmetric of the conformal part is ${\mathrm{<mo\; stretchy="false">(</mo>}-g\mathrm{<mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}R{\psi }^2$ , (case when $m\mathrm{<mo>=</mo>0}$ , and $\varphi \mapsto \psi$ ) thus the generalization to an arbitrary $\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$  is obtained immediately, leading to the complete conformal invariant

$\mathcal{L}\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{,}\psi \mathrm{,}\varphi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}\frac{1}{2\kappa }\mathrm{<mo\; stretchy="false">[</mo>}R{\psi }^2+6{\partial }_{\mu }\psi g^{\mu \nu }{\partial }_{\nu }\psi \mathrm{<mo\; stretchy="false">]</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}-g\mathrm{<mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}\frac{1}{2}\mathrm{<mo\; stretchy="false">[</mo>}{\partial }_{\mu }\varphi g^{\mu \nu }{\partial }_{\nu }\varphi +\mathrm{<mo\; stretchy="false">(</mo>}{m}^2{\psi }^2+\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>6<mo\; stretchy="false">)</mo>}R\mathrm{<mo\; stretchy="false">)</mo>}{\varphi }^2\mathrm{<mo\; stretchy="false">]</mo>,}$   (36)

With associated field equation

$R\mathrm{<mo>=</mo>}{g}^{\mu \nu }{R}_{\mu \nu }\mathrm{<mo>=</mo>0,}$   (37)

Which can be a spherical symmetry in a general sense. Likewise, considering these symmetric parts of the conformal component of the space-time, we can establish spectral models on sources which in the beginning can be considered along the space-time as spherical.

Likewise, is known that in high energy particle physics not happens always that the harmonious and symmetrical possibility is present in the deep space-time. Perhaps, the formal invariance under conformal transformation is broken when a massless field or zero spin particles does exist or appears. However, this symmetry can be broken from measure frame used to explore this conformal action using a gauge field of electromagnetic type (Figure 3).

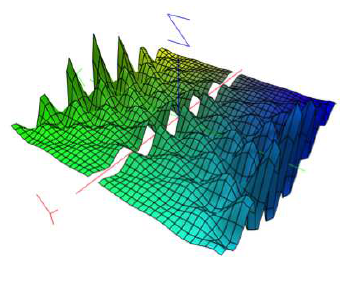
Figure 3 2-dimensional flat model of a space-time region where is broken the formal invariance (and symmetry) due to the no existence of a source. The zero spin particle appears on the Y, axis. The increase waves due the inflation factor and the annihilation of the combination $R+\kappa \tau$ , due the deviation of $\lambda \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , which provokes the annulation of the stress tensor component $t^{\mu \nu }$ . The two components represented are due to spin $\pm \mathrm{1<mo>/</mo>2}$ , (fermions), which interact with the gravitational background broken the invariance of the field $\psi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>.}$

For example, the fermions act with the gravitational background producing two components of interacting that go increasing by the expansion of the Universe. This could shape the inflation factor, yet when the level matter of the Universe is insufficient. However, for the field $\psi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , would still have source, which could be necessary to annihilate the combination $R+\kappa t$ ¹³, with t¹⁴, the corresponding stress tensor due the matter presence, which is affected

Likewise, the annihilation of the combination $R+\kappa t$ , can be done arbitrary, although in theoretical physics are presented two possibilities on the removing the factor ${\sigma }^2$ , that multiplies $m^2$ , or that multiples R, in the Lagrangian term of (36). The first procedure gives the B-D theory¹⁵. The goals of this research are not study the consequences of these procedures. But, one conclusion of this respect is the appearing of spectra of curvature that can be constructed via the gravitational waves determined to start the stress tensor of matter presence and the gauge fields that can be designed to conserve the conformal properties to a first curvature. The second curvature also could be obtained but under considerations on the studies in B-D theory.⁹

¹¹The process more simple is introduce a tensor density $g^{\mu \nu }$ , covariant of weight establishing $h\mathrm{,<mo>=</mo>}{g}^{\mu \nu }{R}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo><mo>=</mo>}{g}^{\mu \nu }{S}_{\mu \nu }\mathrm{<mo\; stretchy="false">)</mo>,}$
The law of transforming to $g^{\mu \nu }$ , must be:$g^{\mu \nu }{}^{\ast }\mathrm{<mo>=</mo>}\frac{\partial {\chi }^{{\mu }^{\ast }}}{\partial {\chi }^{\mu }}\frac{\partial {\chi }^{{\nu }^{\ast }}}{\partial {\chi }^{\nu }}{g}^{\mu \nu }\mathrm{<mo>|</mo>}\frac{\partial {\chi }^n}{\partial {\chi }^{\mu }}\mathrm{<mo>|</mo>,}$
where the indices are referred to different coordinates systems, yet when have been used these same letters, are considered as independent ones of others. Then we have:${\displaystyle \int }{h}^{\ast }d\tau \mathrm{<mo>=</mo>}{\displaystyle \int }\frac{\partial {\chi }^{i^{\ast }}}{\partial {\chi }^i}\frac{\partial {\chi }^{k^{\ast }}}{\partial {\chi }^k}{g}^{ik}\mathrm{<mo>|</mo>}\frac{\partial {\chi }^i}{\partial {\chi }^{i^{\ast }}}\mathrm{<mo>|</mo>}•\frac{\partial {\chi }^S}{\partial {\chi }^{S^{\ast }}}{S}_{st}\mathrm{<mo>|</mo>}\frac{\partial {\chi }^S}{\partial {\chi }^{S^{\ast }}}\mathrm{<mo>|</mo>}d\tau \mathrm{<mo>=</mo>}{\displaystyle \int }hd\tau \mathrm{,}$
which is an integral of an invariant transformation.

¹²Here σ is a smooth embedding, which smoothly embeds the submanifold created by the affected region by the energy-mass tensor.

¹³ $R{\mathrm{,}}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\kappa \mathrm{<mo\; stretchy="false">(</mo>}{t}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2<mo\; stretchy="false">)</mo>}{g}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}t\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$ , which is equivalent to the Einstein gravitational field equation $G_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\kappa t_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ .

¹⁴ $t\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{g}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}{t}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ .

¹⁵Inside the theoretical physics, the B-D theory is the Brans–Dicke theory of gravitation, which consists a theoretical framework to explain gravitation phenomena. This is an alternative theory to the general relativity theory due Einstein in which the gravitational interacting is mediated by a scalar field as $\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , as well as the tensor field in general relativity given by $R_{\mu {\nu }^{•}}$ . The gravitational constant G is not considered to be constant but their reciprocal 1/G is replaced by a scalar field $\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , which can vary from place to place and with time.

Which is the aspect of curvature of the quantum perturbing space on the space

$H\mathrm{<mo>=</mo><mo>\{</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}H\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">(</mo>1<mo>/</mo>2}m\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo>}\varphi {\mathrm{<mo>|</mo><mo>|</mo>}}^2+\begin{array}{c}•\\ V\end{array}\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>\}</mo>}$

Here is the space of the energy states that determine the Hamiltonian densities of the energy spectra due curvature. Likewise, these densities can be superposed to integrate a curvature spectrum as has been established in Figure 4.^10,11

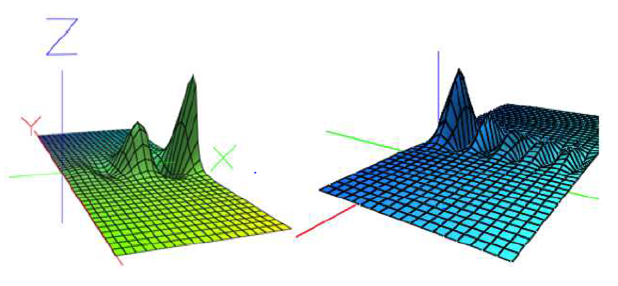
Figure 4 Superposing of the Hamiltonian state densities measuring curvature.¹¹

Newly, using the formal invariance under conformal transformation, the H-states can determine not only first curvature, also second curvature, since these energy states arise in natural way of the study of fermion states interacting of the gravitational background designing a gauge field as “dilaton” of magnetic nature, which could to evade the strong radiation that arises of this interacting. The study of strong gravitational sources realized from a point of view of the kinematic tensor , to stress-matter tensor is a method to determine the existence of space-time singularities (Figures 5 (A & B)).

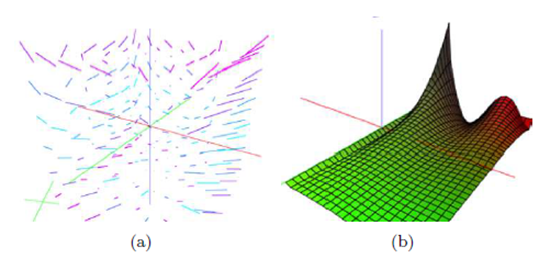
Figure 5 A) Gravitational field of perturbed spherical symmetry. B) Cylindrical gravitational waves determining a gravitational source in the space-time.

But far of these considerations arise the question on how can be recognized the spin 2 particles or gravitons, which can determine the gravitational energy scenario useful in field theory to generate a curvature spectra of spectral curvature directly of the actions of the gravitational field on space. The generalized stress tensor conservation law given by the equation

${\nabla }_{\mu }{t}^{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}$   (38)

Will fail inside particle sources (such and as was showed in the Figure 3) unless one recognizes the pre-existence of the energy and momentum that is transferred to the emitted particle. However, there is not an electromagnetic analogue to the graviton source problem. The photons are electrical neutral, whereas gravitons carry energy-momentum, which also must be transferred rather than created within the source.

Then is introduced to provide the correct gauge transformation behaviour of charged particle sources. But these source problems can be viewed as the search the explicit $g_{\mu \nu }-$ dependence that will give the various sources the correct response to general coordinate transformations. Then considering all before, the simplest example is a scalar source $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ , appearing in the action integral though the term:

${\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}\chi {\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{\mathrm{1<mo>/</mo>2}}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$   (39)

But these terms are useful to establish the graviton emission through certain special function such as impulse functions, whereas have us that the terms as (39) take the form in the frame of the stress tensors $t_{\mu \nu }$ , to high radiation emission:

${\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}+h\mathrm{<mo\; stretchy="false">)</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\chi }^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}h\mathrm{<mo\; stretchy="false">)</mo>}{\partial }_{\mu }\Omega \mathrm{<mo\; stretchy="false">)</mo>,}$   (40)

Where are the densities defined in (15). Then assuming that the graviton detection sources do not overlap the $\Omega$ support region, one can use the source-free weak gravitational field equations deriving to:

${\partial }_{\lambda }{\chi }^{\lambda }\mathrm{<mo>=</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}d{\chi }^{\text{'}\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{f}^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}{f}^{\nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}\text{'}}\mathrm{<mo\; stretchy="false">)</mo>,}{\partial }_{\mu }^{\text{'}\text{'}}{\partial }_{\nu }^{\text{'}\text{'}}h\mathrm{<mo\; stretchy="false">(</mo>}{\chi }^{\text{'}\text{'}}\mathrm{<mo\; stretchy="false">)</mo>,}$   (41)

Where $f^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>}$ , is one of familiar class of functions such that

${\partial }_{\mu }{f}^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\delta \mathrm{<mo\; stretchy="false">(</mo>}\chi -{\chi }^{\text{'}}\mathrm{<mo\; stretchy="false">)</mo>,}$   (42)

Mentioned before.

An additional work in the term inside the integral (40) $\varphi \mathrm{<mo\; stretchy="false">(</mo>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+{\chi }^{\mu }\mathrm{<mo\; stretchy="false">(</mo>}h\mathrm{<mo\; stretchy="false">)</mo>}{\partial }_{\mu }$  produced of the local diffeomerphism that create the field equations in this context, can be transformed in a Hill equation of the form, which can under certain conditions to come of the equation (29):

${\nabla }^2\varphi +\Phi \varphi \mathrm{<mo>=</mo>0,}$   (43)

Which under the integral geometry study and the $G-$ structure of the complex Riemannian manifold, furthermore of the $K-$ invariance of their submanifolds or cycles under integral transforms takes the form of the Bulnes s equation¹⁶:^1,12

$R_{\sigma }\mathrm{<mo\; stretchy="false">(</mo>}{R}_{\sigma }\otimes Ad\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}$   (44)

Both equations are generalizations of the Ricatti equation whose solutions can to represent generalized harmonic oscillators. Then their solutions to curvature will be a spectrum of curvature, whose oscillations will be produced when energy-matter affects the space-time. In the case of the equation (44) results the incorporation of the intrinsic image of curvature of a submanifold, which is embedded smoothly in the space $D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ .

For example, the intrinsic image of curvature of a curved surface as submanifold, which is embedded smoothly in the distribution space, $D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}$ is their curvature energy.

¹⁶This equation arises of the property of the generalized X-Ray transform which says that $R_{\gamma }\mathrm{<mo\; stretchy="false">(</mo>}Ad\mathrm{<mo\; stretchy="false">(</mo>}{G}^0\mathrm{<mo\; stretchy="false">)</mo>}\otimes D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{R}_{\gamma }\mathrm{<mo\; stretchy="false">(</mo>}{C}^{\infty }\mathrm{<mo\; stretchy="false">(</mo>}\Sigma \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$ , is solution of the endomorphic equation: $R_{\gamma }^2-R_{\gamma }\mathrm{<mo\; stretchy="false">(</mo>}Ad\mathrm{<mo\; stretchy="false">(</mo>}{G}^0\mathrm{<mo\; stretchy="false">)</mo>}\otimes D^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>0.}$  

Theorem

The Hill equation is equivalent to Bulnes equation considering the cohomology class of 1-forms spaces of lines of the lines bundles $O\mathrm{<mo\; stretchy="false">(</mo>2<mo\; stretchy="false">)</mo>}$ , on ${\mathbb{P}}^3$ .

Proof. To prove this is necessary use the relation between Radon transform with the Laplacian on curved spaces (because the Hill equation has a curved differential operator) and their relation with the Penrose transform. Likewise, if we consider the Einstein bundle $E\to M$ ¹⁷, then the Penrose transform is: 

$\mathcal{P}\mathrm{<mo>:</mo>}\Gamma \mathrm{<mo\; stretchy="false">(</mo>}{\mathbb{P}}^3\mathrm{<mo\; stretchy="false">(</mo>}ℂ\mathrm{<mo\; stretchy="false">)</mo>,}E\mathrm{<mo\; stretchy="false">)</mo>}\cong \mathrm{<mo>\{</mo>}\varphi ofconformalweight1onMsatisfaying{\nabla }_{\mathrm{<mo\; stretchy="false">(</mo>}A}^{\mathrm{<mo\; stretchy="false">(</mo>}{A}^{\text{'}}}{\nabla }_{B\mathrm{<mo\; stretchy="false">)</mo>}}^{B{\mathrm{<mo\; stretchy="false">)</mo>}}^{\text{'}}}\varphi +{\Phi }_{AB}^{A^{\text{'}}{B}^{\text{'}}}\varphi \mathrm{<mo>=</mo>0<mo>\}</mo>,}$   (45)

And are satisfied the Einstein equation to tensor $T_{ab}\mathrm{<mo>=</mo>0}$ . Also using the fact that $\mathcal{P}\Delta {\mathrm{<mo>|</mo>}}_{O\mathrm{<mo\; stretchy="false">(</mo>}k\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>=</mo>}\Delta {\mathrm{<mo>|</mo>}}_{O\mathrm{<mo\; stretchy="false">(</mo>}k\mathrm{<mo\; stretchy="false">)</mo>}}$ ,¹³ and the conformally given for (34) in the space-time M. 

Theorem (F Bulnes, S Fominko)

The action integral (39) generate spatial diffeomorphisms along orbits defined by $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ .

The result establish that the orbits of the group SO (4, R), are spaces isomorphic to spheres.

Proof. We consider the action integral (39). Then their orbits $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}$ can have measure as spatial regions whose curvature is a Ricci curvature.

Lemma (F Bulnes, S Fominko)

A diffeomorphism of gravitational field is:

$R_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\kappa \mathrm{<mo\; stretchy="false">(</mo>}{t}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2<mo\; stretchy="false">)</mo>}{g}_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}t\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}$   (46)

Then for the formula (31), the gravitational field can be given as (Figure 6):

$G^{\mu \nu }\mathrm{<mo>=</mo>}\frac{\alpha \kappa }{n\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}\kappa }{t}^{\mu \nu }\mathrm{,}$   (47)

Figure 6 The gravitational field to n=2, in the equation.⁴⁷

Remark: The corresponding equation (47) comes from an analysis using generalized curvature on the distribution spaces in integral geometry. The theorem can be found in.¹

The considerations realized in this paper have as objective establishes the spectrum of curvature when there is symmetry or when can to have breaking of this. This last result or lemma, as the result obtained of incorporate the general relativity to the quantum field theory to obtain spectra of the curvature tensor $R_{\mu \nu }$ , through of other tensors (that directly or indirectly are related with this curvature tensor, and which are product of diffeomorphism applied to the microscopic structure of the homogeneous space of form $G\mathrm{<mo>/</mo>}{G}_0$ ) considers the possibility of discrete the energy spectra of the gravitational field to computational applications¹⁰ where $\kappa$ , can be a constant sectional curvature. Of fact, this is the re-interpretation that gives us.

Also, the conformally in the Spectrum of Curvature on the space was established as a condition to measure in duality the curvature, which appear as a pseudo-symmetry condition that generalize the spherical mapping given to Gaussian curvature, but to this case in the energy Hamiltonian space to the gravitational field source (Figure 7).

Figure 7 Appearing of Gravitational field source reproducing more nodes of gravitational waves due the orbital actions when the dilaton is interacting with the background. These are model of the spectrum of the Hill equations.

Also were obtained images of curvature energy of the Hamiltonian manifold in the complex Riemannian manifold obtaining a formula of gravitational field depending of the dimension of the space on which acts the tensor . The interesting is that is used the empirical constant $\alpha \mathrm{<mo>></mo>0}$ .

¹⁷Homogeneous vector bundle with constant Ricci curvature.

Some astrophysics and astronomy observational facts are:

A). Gravitational waves arise as deformation of the space-time when dilaton acts on the background. For example, perturbed black holes in Einstein-dilaton-Gauss-Bonnet gravity, can produce stability, ring-down, and gravitational-wave emission that are propagated as part of the space-time (Figure 8).¹⁴

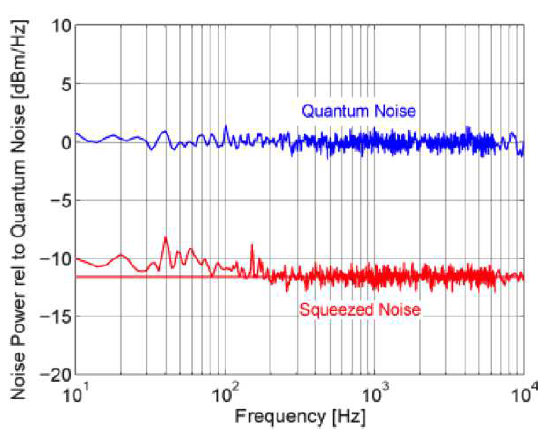
Figure 8 First measurement of greater than 10dB squeezing across the audio gravitational-wave detection band, with 11.6dB from 200Hz and above. The degradation of squeezing level below 100Hz is due to remaining residual classical noise entering the squeezing detector. Adapted from,¹⁶ and includes resolution bandwidth and window information.¹⁵

B). At least must to have a conformal constant action along the gravity action or sufficiently large. This can to be broken if the dilaton action is prolonged beyond of this conformal constant action. This could to be seemed to the Brans-Dicke argumentation,¹⁸ from a point of view of the variation of the gravitational constant, which varies from the place in time. But assuming the gravitational field with invariant due the gravitational diffeomorphism (30) whose action is constant then the gravitational waves are evidenced from the remote source (Figure 9). But if is affected by the dilaton action, the corresponding scalar field action due the electromagnetic action of the dilaton could “dilute the gravity” action trying vacumm in the space-time. Likewise, if we consider one of the Brans-Dicke equations, for example,

$\square \varphi \mathrm{<mo>=</mo>}\frac{8\pi }{3+2\omega }T\mathrm{,}$   (48)

Figure 9 Variation of the gravitational constant.

The equation says that the trace of the stress-energy acts as the source for the scalar field $\varphi$ . But electromagnetic fields contribute only a traceless term to the stress-energy tensor, which implies that in a region of space-time containing only electromagnetic field the right side of (48) vanishes and the curved space-time obeys the wave equation. But, this electromagnetic wave is propagated infinitely (Figure 10). In such case, we can say that the field is a long-range field.^15,16

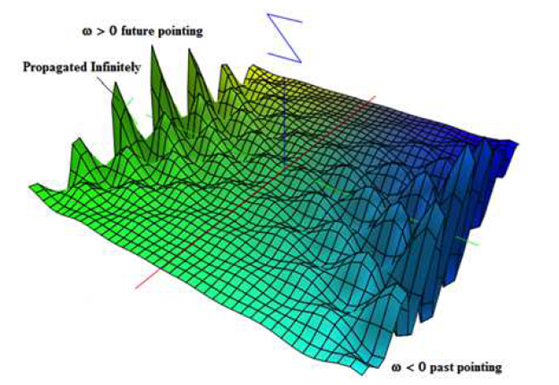
Figure 10 2-Dimensional model of electromagnetic wave solutions on space-time without matter-energy (long-range field).¹⁶

In other case, when the conformal action is constant then the gravitational fields are created with spherical symmetry. Then the tensor of gravity $G_{\mu \nu }$ , is proportional to the production of energy-matter determined in the matter-energy tensor $T_{\mu \nu }$ , which can to create a source of matter-energy accord to the diffeomorphism

${\partial }^{\lambda }{G}_{\mu \nu \lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}-{\partial }_{\nu }{G}_{\mu \lambda }^{\lambda }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+m^2\mathrm{<mo\; stretchy="false">(</mo>}{\varphi }_{\mu \nu }\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}+\frac{1}{2}{g}_{\mu \nu }\varphi \mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{T}_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }T\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>,}$

Established before, which is related with the diffeomorphic formula (31).

¹⁸As mentioned before, the Brans Dicke theory of gravitation is a theoretical framework to explain gravitation from a point of view of electromagnetic wave to explain the variation of the gravitational constant that is assumed in this theory as function of a time, possibly is an inverse time. The gravitational interaction is mediated by a scalar field and also the corresponding tensor field of general relativity. Then the scalar field can vary from place to place and in time.

None.

Authors declare there is no conflict of interest.

1. Bulnes F. Research on Curvature of Homogeneous Spaces. 1st ed. TESCHA: State of Mexico, Mexico, 2010. p. 44–66.
2. Bulnes F. Curvature Spectrum to 2-Dimensional Flat and Hyperbolic Spaces through Integral Transforms. Journal of Mathematics. 2015;1(1):1–8.
3. Kobayashi K, Nomizu K. Foundations of Differential Geometry. Wiley and Sons, New York, USA. 1969.
4. Burstall FE. Riemannian Twistor Spaces and Holonomy Groups. In: Bailey TN, Baston RT, editors. Twistor in Mathematics and Physics, Cambridge Press, UK; 1990. p. 1–15.
5. Hitchin N. Generalized Calabi–Yau manifolds. The Quarterly Journal of Mathematics. 2003;54(3):281–308.
6. Bulnes F. Orbital Integrals on Reductive Lie Groups and Their Algebras, Orbital Integrals on Reductive Lie Groups and Their Algebras. In: Bulnes F, editor, InTech, Croatia, 2013. p. 1–194.
7. Kozameh CN, Newman ET, Tod KP. Conformal Einstein Spaces. General Relativity and Gravitation. 1985;17(4):343–352.
8. Schwinger J. Particles, Sources and Fields. Advanced Book Program, Perseus Books, New York, USA. 1998.
9. Brans CH, Dicke RH . Mach’s Principle and a Relativistic Theory of Gravitation. Physical Review. 1961;124(3):925–935.
10. Bulnes F. Quantum Gravity Sensor by Curvature Energy: their Encoding and Computational Models. Proceedings of the IEEE, London, UK, 2014. p. 855–861.
11. Bulnes F. Integral Methods in the Geometrical Langlands Program. SCIRP, USA. 2016.
12. Bulnes F. Electromagnetic Gauges and Maxwell Lagrangians Applied to the Determination of Curvature in the Space-Time and their Applications. Journal of Electromagnetic Analysis and Applications. 2012;4(6):252–266.
13. Eastwood M, Wolf J, Zirau R. The Penrose Transform and Analytic Cohomology. AMS-IMS-SIAM Summer Research Conference, USA. 1992.
14. Blázquez-Salcedo JL, Macedo CFB, Cardoso V, et al. Perturbed black holes in Einstein-dilaton-Gauss-Bonnet gravity: Stability, ringdown, and gravitational-wave emission. Physical Review D. 2016;94:1–15.
15. Stefszky MS, Mow-Lowry CM, Chua SSY, et al. Balanced Homodyne Detection of Optical Quantum States at Audio-Band Frequencies and Below. Classical and Quantum Gravity. 2012;29(14).
16. Bulnes F. Electromagnetic waves in conformal actions of the group SU (2,2), on a dimensional flat model of the space-time. Sicth International Conference “Geometry, Dynamics, Integrable Systems”-GDIS, Izhevsk, Russia. 2016.