As the resistive instabilities with their serious difficulty at the thermonuclear fusion programs have concentrated much interest of the researchers, the present study has the ambition to provide an applicable and useful criterion for examining and identifying if a observed plasma wave is resistive or not. A dispersion relation is obtained, by using the two fluids equation and considering that a resistive force exists, and then the growth rate can be solved. Subsequently, the resistance factor is calculated using the experimental values and data obtained. Finally, a comparison of the calculated resistance factor with the ones published in bibliography will be performed, which gives the expected answer about the type of the examined wave.

Keywords: Thermonuclear fusion; Fluids equation; Plasma physics; Astrophysics; Energy; Plasma waves; Electric field

The resistive instabilities are between the most investigated phenomena of the plasma physics and the astrophysics, as well,^1–5 and the dripping on these are passed-printed in the relevant bibliography.^6–10 Early 60’s the topic has been investigated very enough as it is accused for energy losses in the plasma,¹¹ but and presently the interest on them is very strong.^12–14 As the all instabilities resulted into every kind plasma waves and their organized energy is absents from the plasmas' chaotic (thermal) energy, so, early they faced as obstacles in the thermonuclear fusion process.^15–17 Instabilities in fusion plasmas appear at all times and by many types of them, therefore it will not try to catalog them here. Only instabilities and plasma waves which investigated and studied in our plasma laboratory of ‘Demokritos’ are mentioned in the present and this briefly. So, early 70's, ion-acoustic waves have been fund into non magnetized argon plasma,¹⁸ and after this the energy losses of the plasma due to these waves have been published as well.¹⁹ Furthermore, drift waves have been fund into magnetized argon plasma (in Q-machine), whish identified as caused on the if electric field gradient.²⁰ With newer publications the influence of these drift waves on the Hall conductivity of the plasma have be given.^21,22 Recently, another kind low frequency waves observed into our semi Q-machine; these waves identified as collisional one and caused on the electron-neutral collisions as well.²³ As the experience with the plasma wave’s study have be increased, it was appears the need to finding a criterion suitable for the identification of the appeared waves into our plasma. With the present theoretical work a criterion is proposed, suitable to distinguish if a plasma wave is resistive or not.

As our experience on the plasma waves' study have be increase, it was appears the need to finding a criterion for the identification of the appeared waves into our plasma. By the present work a criterion is proposed, suitable to distinguish if a wave is resistive or not.

For this way, the kinetic equation for both, ions and electrons have be taken, with the inclusion of the resistance term, and after mathematical elaboration and the necessary approaches we resulted with the dispersion relation (D.R.),from which the growth rate have be calculated; so, the derived resistance’s factor  may be the indicator for a resistive wave or not.

The paper is written as following: the apparatus's description and the experimental data are presented in Section 2. Afterwards, the D.R. is elaborated in the Section 3, and its complete study has been made in the next Section 4. Finally, in the Section 5 the Conclusion-discussion has been given. The paper is ended with the Appendix A and Appendix B, which contain more mathematical details for alleviation of the text.

Although many improvised experimental devices are produced and used in the plasma laboratory of 'Demokritos', only two of them are mentions here: the first was the device into which by a non-magnetized argon plasma, the ion-acoustic instabilities appeared, and decently the semi-Q machine where the drift waves caused on the rf electrical field gradient, and the collisional instabilities are appear and studied, as well.

In the Figure 1 the first apparatus is shown, when in the Figure 2 (A) the spectrum of the ion-acoustic wave is presented and the Figure 2 (B) is a photo of oscillator screen.

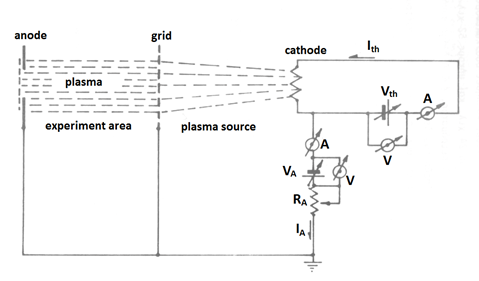
Figure 1 The arrangement of the plasma production and the experiment’s space are presented.

Figure 2A The spectrum one typical ion-acoustic wave and its harmonic are presented.

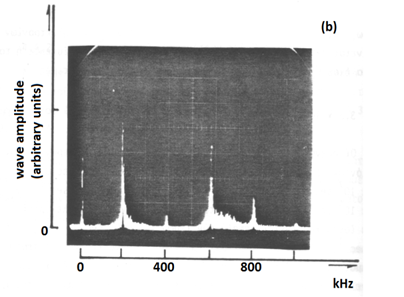
Figure 2B ThreeA photo of the oscillator’s screen is given.

In the Figure 3 the drawing of the Q machine is shown and in the Figure 4 (A&B) the spectrum of the drifts waves and the collisional are given, as well.

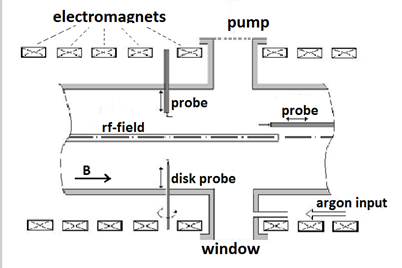
Figure 3 A drawing of the ‘Demokritos’ Q-machine is shown.

Figure 4 (a) The spectrum one typical drift wave and (b) the spectrum one typical collisional wave have been given too.

Furthermore, on the Table 1 the typical values of the plasma parameters for the ion-acoustic wave are presented.

Likewise, on the Table 2 the analogous plasma parameters in the Q-machine are given.

The kinetic equation for the ions is written as following:

$\frac{d{\overrightarrow{V}}_i}{dt}=\frac{e\overrightarrow{E}}{m_i}+{\omega }_{ci}.{\overrightarrow{V}}_{i}x{\overrightarrow{e}}_z-\frac{\eta e^2{n}_0}{m_i}({\overrightarrow{V}}_i-{\overrightarrow{V}}_e)-{\nu }_{in}{\overrightarrow{V}}_i$   (1)

It is valid that

${(\nabla P)}_i\cong 0$  (Because the ions have low temperature $T_i\cong 0$ )

It is valid the Ampere’s law,

$\overrightarrow{J}+{\epsilon }_0\frac{\partial \overrightarrow{E}}{\partial t}=\nabla x\overrightarrow{{\rm H}}=0$  and the relation $\overrightarrow{J}=n_{0}e({\overrightarrow{V}}_i-{\overrightarrow{V}}_e)$

Then, it is results the equation,

$n_{0}e({\overrightarrow{V}}_i-{\overrightarrow{V}}_e)=j\varpi {\epsilon }_0\overrightarrow{E}$   (2)

It is valid the relation

$\overrightarrow{E}=-\frac{\nabla \Phi }{R.\partial \vartheta }$

And the equation (2) is written as following;

$n_{0}e(V_{i\vartheta }-V_{e\vartheta })=\frac{{\epsilon }_{0}l\omega }{R}\Phi$   (3)

The equation (1) due to equation (2) becomes,

$\frac{d{\overrightarrow{V}}_i}{dt}=\frac{e}{m_i}(1-j{\epsilon }_0\omega \eta )\overrightarrow{E}+{\overrightarrow{V}}_{i}x{\overrightarrow{\omega }}_{ci}-{\nu }_{in}{\overrightarrow{V}}_i$   (4)

By taking the following relations,

$\Phi ={\Phi }_o.e^{jl\vartheta -j\omega t}$ , $\overrightarrow{V}\approx e^{jl\vartheta -j\omega t}$ , $n\approx e^{jl\vartheta -j\omega t}$

And separating in the two components, it is written as,

$-j\omega V_{i\vartheta }=-\frac{e}{m_i}j\frac{l}{R}(1-j{\epsilon }_0\omega \eta ).\Phi -V_{ir}{\omega }_{ci}-{\nu }_{in}{V}_{i\vartheta }$   (5)

$-j\omega V_{ir}=V_{i\vartheta }.{\omega }_{ci}-{\nu }_{in}{V}_{ir}\Rightarrow V_{ir}=\frac{{\omega }_{ci}}{{\nu }_{in}-j\omega }.V_{i\vartheta }$

By putting the $V_{ir}$ from the last relation into equation (5) it is taken:

$\frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }{V}_{i\vartheta }=-\frac{e}{m_i}.\frac{jl}{R}.(1-j{\epsilon }_0\eta \omega )\Phi$   (6)

From the Ampere’s Law we have the equation (3)

For electrons, The continuity equation for electrons, keeping the first order terms only may be written as following,

$\frac{D{n}_e}{Dt}+n_0.\frac{1}{R}.\frac{\partial V_{e\vartheta }}{\partial \vartheta }=0$

Fitting the suitable tensor in the above continuity equation we have,

$V_{e\vartheta }=\frac{\omega -l\Omega }{\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$R$}\right.}.\frac{n_e}{n_0}$   (7)

(Where is $\Omega =\raisebox{1ex}{$u$}\!\left/ \!\raisebox{-1ex}{$R$}\right.$ )

The equation of motion for electrons is,

$\frac{D{\overrightarrow{V}}_e}{Dt}=-\frac{e}{m_e}(1-j{\epsilon }_0\eta \omega )\overrightarrow{E}-{\overrightarrow{V}}_{e}x{\overrightarrow{\omega }}_{ce}-{\stackrel{⌢}{e}}_{\vartheta }.j\frac{l{\upsilon }_t^2}{R}\frac{n_e}{n_0}.-{\nu }_{en}{\overrightarrow{V}}_e$

By using the equation (2), the last term of the above equation is formed as following,

$-\eta \frac{n_0{e}^2}{m_e}({\overrightarrow{V}}_e-{\overrightarrow{V}}_i)=\frac{\eta e}{m_e}j{\epsilon }_0\overrightarrow{E}$

And by putting it into the last equation it becomes,

$\frac{D{\overrightarrow{V}}_e}{Dt}=-\frac{e}{m_e}(1-j{\epsilon }_0\eta \omega )\overrightarrow{E}-{\overrightarrow{V}}_{e}x{\overrightarrow{\omega }}_{c{e}_e}-{\stackrel{⌢}{e}}_{\vartheta }.j\frac{l{\upsilon }_t^2}{R}\frac{n_e}{n_0}.-{\nu }_{en}{\overrightarrow{V}}_e$

Where it is valid ${\upsilon }_t^2\equiv \raisebox{1ex}{$K_B{T}_e$}\!\left/ \!\raisebox{-1ex}{$m_e$}\right..$  the thermal velocity.

From equation (7) we have

$\frac{n_e}{n_0}=\frac{\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$R$}\right.}{\omega -l\Omega }{V}_{e\vartheta }$

And the above equation becomes,

$j(l\Omega -\omega ){\overrightarrow{V}}_e=\frac{e}{m_e}j\frac{l}{R}(1-j{\epsilon }_0\eta \omega )\Phi .{\stackrel{⌢}{e}}_{\vartheta }-{\overrightarrow{V}}_{e}x{\overrightarrow{\omega }}_{c{e}_e}-{\stackrel{⌢}{e}}_{\vartheta }.j\frac{\raisebox{1ex}{$l^2{\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }{V}_{e\vartheta }.{\stackrel{⌢}{e}}_{\vartheta }.-{\nu }_{en}{\overrightarrow{V}}_e$   (8)

Now, the equation (8) is separated in two components from which the first equation becomes,

$j(l\Omega -\omega )V_{e\vartheta }=\frac{e}{m_e}j\frac{l}{R}(1-j{\epsilon }_0\eta \omega )\Phi .-\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}{V}_{e\vartheta }-.j\frac{\raisebox{1ex}{$l^2{\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }{V}_{e\vartheta }.-{\nu }_{en}{V}_{e\vartheta }.$

$\Rightarrow V_{e\vartheta }=\frac{j\frac{l}{R}(1-j{\epsilon }_0\eta \omega )\frac{e\Phi }{m_e}}{j(l\Omega -\omega )+\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\varpi -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }+{\nu }_{en}}$

The above value of the $V_{e\vartheta }$ is enter into equation (3) and the value of the component $V_{e\vartheta }$ will be find, so

$V_{i\vartheta }=\frac{{\epsilon }_{0}l\Phi \omega }{R{n}_{0}e}+\frac{j\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$R$}\right.(1-j{\epsilon }_0\eta \omega )\frac{e\Phi }{m_e}}{-j(\omega -l\Omega )+\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }+{\nu }_{en}}$

With the substitution of the into the eq.(6) we resulted with the complete dispersion relation,

$\begin{array}{l}\frac{{\epsilon }_{0}l\Phi \omega }{R{n}_{0}e}.\frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }+\frac{j\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$R$}\right.(1-j{\epsilon }_0\eta \omega )\frac{e\Phi }{m_e}}{-j(\omega -l\Omega )+\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }+{\nu }_{en}}.\\ \frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }=-\frac{e}{m_i}(1-j{\epsilon }_0\eta \omega ).j\frac{l}{R}.\Phi \end{array}$   (9)

The fund dispersion relation may be written as following:

$\begin{array}{l}\frac{{\epsilon }_0\omega }{n_0{e}^2}.\frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }+\frac{\raisebox{1ex}{$j$}\!\left/ \!\raisebox{-1ex}{$m_e$}\right.(1-j{\epsilon }_0\eta \omega )}{-j(\omega -l\Omega )+\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }+{\nu }_{en}}.\\ \frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }=-\frac{j}{m_i}(1-j{\epsilon }_0\eta \omega )\end{array}$

It is valid that ${\lambda }_D^2=\frac{{\epsilon }_0{K}_B{T}_e}{n_0{e}^2}$  (the Debay length) and  $C_s^2=\frac{K_B{T}_e}{m_i}$ , the ion-acoustic velocity then, we have,

$\frac{{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2}{{\nu }_{in}-j\omega }\left[{\lambda }_D^2\omega +\frac{j(1-j{\epsilon }_0\eta \omega ).{\upsilon }_t^2}{-j(\omega -l\Omega )+\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }+{\nu }_{en}}\right]=-j(1-j{\epsilon }_0\eta \omega ).C_s^2$   (10)

By taking the approaches ${\nu }_{in}\prec \prec \omega$  and ${\nu }_{en}$ , $-j(\omega -l\Omega )\prec \prec \frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}$

The last relation may be written in the simple form,

$\frac{{\omega }_{ci}^2-{\omega }^2}{-j\omega }\left[{\lambda }_D^2\omega +\frac{j(1-j{\epsilon }_0\eta \omega ).{\upsilon }_t^2}{\frac{{\omega }_{ce}^2}{{\nu }_{en}-j(\omega -l\Omega )}+j\frac{l^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}{\omega -l\Omega }}\right]=-j(1-j{\epsilon }_0\eta \omega ).C_s^2$

The dispersion relation additional elaboration

Now, the equation (10) with mathematical elaboration (Appendix A) gives the following equation (11),

$\begin{array}{l}j{\upsilon }_t^2{\nu }_{en}(1-j{\epsilon }_0\eta \omega ).(\omega -l\Omega ).\left[{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2\right]=\\ =-C_s^2(1-j{\epsilon }_0\eta \omega ).(\omega +j{\nu }_{in}).\left[(\omega -l\Omega )({\omega }_{ce}^2+{\nu }_{en}^2)+j{l}^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.{\nu }_{en}\right]-\\ -{\lambda }_D^2\omega \left[{({\nu }_{in}-j\omega )}^2+{\omega }_{ci}^2\right].\left[(\omega -l\Omega )({\omega }_{ce}^2+{\nu }_{en}^2)+j{l}^2\raisebox{1ex}{${\upsilon }_t^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.{\nu }_{en}\right]\end{array}$   (11)

Which may becomes,

$\begin{array}{l}j{\upsilon }_t^2{\nu }_{en}\left[j{\epsilon }_0\eta {\omega }^2-(1+j{\epsilon }_0\eta l\Omega )\omega +l\Omega \right].\left[{\omega }^2+2{\nu }_{in}j\omega -{\omega }_{ci}^2-{\nu }_{in}^2\right]\\ =\left[\omega ({\omega }_{ce}^2+{\nu }_{en}^2)-l\Omega ({\omega }_{ce}^2+{\nu }_{en}^2)+j\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\right].\\ \left[{\lambda }_D^2{\omega }^3+(j{\epsilon }_o\eta C_s^2+2{\lambda }_D^2{\nu }_{in}j){\omega }^2-(C_s^2+C_s^2{\epsilon }_o\eta {\nu }_{in}+{\lambda }_D^2{\nu }_{in}^2+{\lambda }_D^2{\omega }_{ci}^2)\omega -C_s^2{\nu }_{in}j\right]\end{array}$   (12)

Order -arrangement according to  forces

The last equation (12) may be written,

$\begin{array}{l}-\left[{\upsilon }_t^2{\nu }_{en}.{\epsilon }_0\eta +({\omega }_{ce}^2+{\nu }_{en}^2).{\lambda }_D^2\right].{\omega }^4+\\ +\left[\begin{array}{l}-j2{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta .{\nu }_{in}-j{\upsilon }_t^2{\nu }_{en}(1+j{\epsilon }_0\eta l\Omega )-j({\omega }_{ce}^2+{\nu }_{en}^2).({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\\ +l\Omega ({\omega }_{ce}^2+{\nu }_{en}^2){\lambda }_D^2-j\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\end{array}\right].{\omega }^3+\\ +\left[\begin{array}{l}{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta ({\omega }_{ci}^2+{\nu }_{in}^2)+2{\upsilon }_t^2\nu (1+j{\epsilon }_0\eta l\Omega ).{\nu }_{in}+j{\upsilon }_t^2{\nu }_{en}.l\Omega +\\ ({\omega }_{ce}^2+{\nu }_{en}^2)(C_s^2+C_s^2{\epsilon }_0\eta {\nu }_{in}+{\lambda }_D^2{\nu }_{in}^2+{\lambda }_D^2{\omega }_{ci}^2)+\\ +jl\Omega ({\omega }_{ce}^2+{\nu }_{en}^2)({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}.{\nu }_{en}({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\end{array}\right].{\omega }^2+\\ +\left[\begin{array}{l}j{\upsilon }_t^2{\nu }_{en}(1+j{\epsilon }_0\eta l\Omega ).({\omega }_{ci}^2+{\nu }_{in}^2)-2{\upsilon }_t^2.{\nu }_{en}l\Omega .{\nu }_{in}+j({\omega }_{ce}^2+{\nu }_{en}^2)C_s^2{\nu }_{in}\\ -l\Omega ({\omega }_{ce}^2+{\nu }_{en}^2)(C_s^2+C_s^2{\epsilon }_0\eta {\nu }_{in}+{\lambda }_D^2{\nu }_{in}^2+{\lambda }_D^2{\omega }_{ci}^2)+\\ j\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}(C_s^2+C_s^2{\epsilon }_0\eta {\nu }_{in}+{\lambda }_D^2{\nu }_{in}^2+{\lambda }_D^2{\omega }_{ci}^2)\end{array}\right].\omega +\\ +\left[-j{\upsilon }_t^2{\nu }_{en}.l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)-jl\Omega ({\omega }_{ce}^2+{\nu }_{en}^2).C_s^2{\nu }_{in}-\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}.C_s^2{\nu }_{in}\right]=0\end{array}$

A separation of real and imaginaries parts is making in the next,

$\begin{array}{l}-\left[{\upsilon }_t^2{\nu }_{en}.{\epsilon }_0\eta +{\omega }_{ce}^2.{\lambda }_D^2\right].{\omega }^4+\\ +\left[\begin{array}{l}l\Omega \left\{{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2{\lambda }_D^2\right\}-\\ -\left\{{\upsilon }_t^2{\nu }_{en}(2{\epsilon }_0\eta {\nu }_{in}+1)+{\omega }_{ce}^2({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\right\}.j\end{array}\right].{\omega }^3+\\ +\left[\begin{array}{l}\left\{\begin{array}{l}{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta ({\omega }_{ci}^2+{\nu }_{in}^2)+2{\upsilon }_t^2{\nu }_{en}{\nu }_{in}+{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\omega }_{ci}^2+{\nu }_{in}^2)\right]+\\ +\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\end{array}\right\}+\\ +\left\{2{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega {\nu }_{in}+{\upsilon }_t^2{\nu }_{en}l\Omega +l\Omega {\omega }_{ce}^2.({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\right\}j\end{array}\right].{\omega }^2+\\ +\left[\begin{array}{l}\left\{-{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)-2{\upsilon }_t^2.{\nu }_{en}l\Omega .{\nu }_{in}-l\Omega .{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right\}+\\ +\left\{{\upsilon }_t^2{\nu }_{en}({\omega }_{ci}^2+{\nu }_{in}^2)+{\omega }_{ce}^2.C_s^2{\nu }_{in}+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right\}j\end{array}\right].\omega +\\ +\left[-\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}.C_s^2{\nu }_{in}-\left\{{\upsilon }_t^2{\nu }_{en}l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)+l\Omega {\omega }_{ce}^2{C}_s^2{\nu }_{in}\right\}j\right]=0\end{array}$   (13)

The growth rate calculation

By taking the approaches below,

$\omega ={\omega }_r+{\omega }_{i}j$ ,${\omega }^2\approx {\omega }_r^2+2{\omega }_r{\omega }_{i}j$ ,${\omega }^3\approx {\omega }_r^3+3{\omega }_r^2{\omega }_{i}j$ ,${\omega }^4\approx {\omega }_r^4+4{\omega }_r^3{\omega }_{i}j$

And putting them into the last equation (13), we may be to define the real part and the imaginary part of its. So, we have the following.

Real Part

The real part is,

$\begin{array}{l}-\left[{\upsilon }_t^2{\nu }_{en}.{\epsilon }_0\eta +{\omega }_{ce}^2.{\lambda }_D^2\right].{\omega }_r^4+l\Omega \left[{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2{\lambda }_D^2\right]{\omega }_r^3\\ +3{\omega }_r^2{\omega }_i\left[{\upsilon }_t^2{\nu }_{en}(2{\epsilon }_0\eta {\nu }_{in}+1)+{\omega }_{ce}^2({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\right]\\ +\left[{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta ({\omega }_{ci}^2+{\nu }_{in}^2)+2{\upsilon }_t^2{\nu }_{en}{\nu }_{in}+{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\omega }_{ci}^2+{\nu }_{in}^2)\right]+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\right].{\omega }_r^2\\ -\left[2{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega {\nu }_{in}+{\upsilon }_t^2{\nu }_{en}l\Omega +l\Omega {\omega }_{ce}^2.({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\right].2{\omega }_r{\omega }_i\\ +\left[-{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)-2{\upsilon }_t^2.{\nu }_{en}l\Omega .{\nu }_{in}-l\Omega .{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right]{\omega }_r\\ -\left[{\upsilon }_t^2{\nu }_{en}({\omega }_{ci}^2+{\nu }_{in}^2)+{\omega }_{ce}^2.C_s^2{\nu }_{in}+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right].{\omega }_i-\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}.C_s^2{\nu }_{in}=0\end{array}$

 Imaginary Part

The imaginary part is as well,

$\begin{array}{l}-4{\omega }_r^3{\omega }_i\left[{\upsilon }_t^2{\nu }_{en}.{\epsilon }_0\eta +{\omega }_{ce}^2.{\lambda }_D^2\right]+l\Omega ({\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta +{\lambda }_D^2{\omega }_{ce}^2).3{\omega }_r^2{\omega }_i\\ -\left[{\upsilon }_t^2{\nu }_{en}(2{\epsilon }_0\eta {\nu }_{in}+1)+{\omega }_{ce}^2({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\lambda \right]{\omega }_r^3\\ +\left[\begin{array}{l}{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta ({\omega }_{ci}^2+{\nu }_{in}^2)+2{\upsilon }_t^2{\nu }_{en}{\nu }_{in}+\\ +{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\omega }_{ci}^2+{\nu }_{in}^2)\right]+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\end{array}\right].2{\omega }_r{\omega }_i\\ +\left[2{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega {\nu }_{in}+{\upsilon }_t^2{\nu }_{en}l\Omega +l\Omega {\omega }_{ce}^2.({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in}\right].{\omega }_r^2\\ +\left[-{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)-2{\upsilon }_t^2.{\nu }_{en}l\Omega .{\nu }_{in}-l\Omega .{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right]{\omega }_i\\ +\left[{\upsilon }_t^2{\nu }_{en}({\omega }_{ci}^2+{\nu }_{in}^2)+{\omega }_{ce}^2.C_s^2{\nu }_{in}+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right]{\omega }_r\\ -\left[{\upsilon }_t^2{\nu }_{en}l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)+l\Omega {\omega }_{ce}^2{C}_s^2{\nu }_{in}\right]=0\end{array}$

Considering that the below approach ${\omega }_r\cong \omega$ is valid, then the imaginary part is written,

$\begin{array}{l}-4{\omega }^3{\omega }_i\left[{\upsilon }_t^2{\nu }_{en}.{\epsilon }_0\eta +{\omega }_{ce}^2.{\lambda }_D^2\right]+l\Omega ({\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta +{\lambda }_D^2{\omega }_{ce}^2).3{\omega }^2{\omega }_i\\ +\left[\begin{array}{l}{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta ({\omega }_{ci}^2+{\nu }_{in}^2)+2{\upsilon }_t^2{\nu }_{en}{\nu }_{in}+\\ +{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\omega }_{ci}^2+{\nu }_{in}^2)\right]+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})\end{array}\right].2\omega {\omega }_i\\ +\left[-{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)-2{\upsilon }_t^2.{\nu }_{en}l\Omega .{\nu }_{in}-l\Omega .{\omega }_{ce}^2\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right].{\omega }_i=\\ =\left[{\upsilon }_t^2{\nu }_{en}(2{\epsilon }_0\eta {\nu }_{in}+1)+{\omega }_{ce}^2({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\right]{\omega }^3\\ -\left[2{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta l\Omega {\nu }_{in}+{\upsilon }_t^2{\nu }_{en}l\Omega +l\Omega {\omega }_{ce}^2.({\epsilon }_0\eta C_s^2+2{\lambda }_D^2{\nu }_{in}\right].{\omega }^2\\ -\left[{\upsilon }_t^2{\nu }_{en}({\omega }_{ci}^2+{\nu }_{in}^2)+{\omega }_{ce}^2.C_s^2{\nu }_{in}+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}\left[C_s^2(1+{\epsilon }_0\eta {\nu }_{in})+{\lambda }_D^2({\nu }_{in}^2+{\omega }_{ci}^2)\right]\right]\omega \\ +\left[{\upsilon }_t^2{\nu }_{en}l\Omega ({\omega }_{ci}^2+{\nu }_{in}^2)+l\Omega {\omega }_{ce}^2{C}_s^2{\nu }_{in}\right]\end{array}$

 By putting,

${\omega }^2{\omega }_i\left[{\upsilon }_t^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2{\lambda }_D^2\right](3l\Omega -4\omega )\cong {\omega }^2{\omega }_i{\lambda }_D^2({\omega }_{pe}^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2)(3l\Omega -4\omega )$ ,

the last relation becomes,

$\begin{array}{l}{\omega }^2{\omega }_i{\lambda }_D^2({\omega }_{pe}^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2)(3l\Omega -4\omega )\\ +\left[{\upsilon }_t^2{\nu }_{en}({\epsilon }_0\eta {\omega }_{ci}^2+2{\nu }_{in})+{\omega }_{ce}^2{\lambda }_D^2\left[{\omega }_{pi}^2(1+{\epsilon }_0\eta {\nu }_{in})+{\omega }_{ci}^2\right]+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2({\omega }_{pi}^2{\epsilon }_0\eta +2{\nu }_{in})\right].2\omega {\omega }_i\\ +\left[-{\upsilon }_t^2{\nu }_{en}l\Omega ({\epsilon }_0\eta {\omega }_{ci}^2+2{\nu }_{in})-l\Omega {\omega }_{ce}^2.{\lambda }_D^2\left[{\omega }_{pi}^2(1+{\epsilon }_0\eta {\nu }_{in})+{\omega }_{ci}^2\right]\right].{\omega }_i=\\ =\left[{\upsilon }_t^2{\nu }_{en}(2{\epsilon }_0\eta {\nu }_{in}+1)+{\omega }_{ce}^2{\lambda }_D^2({\epsilon }_0\eta {\omega }_{pi}^2+2{\nu }_{in})+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\right].{\omega }^3\\ -\left[{\upsilon }_t^2{\nu }_{en}l\Omega (2{\epsilon }_0\eta {\nu }_{in}+1)+l\Omega {\omega }_{ce}^2.{\lambda }_D^2({\epsilon }_0\eta {\omega }_{pi}^2+2{\nu }_{in})\right].{\omega }^2\\ -\left[{\upsilon }_t^2{\nu }_{en}{\omega }_{ci}^2+{\omega }_{ce}^2{C}_s^2{\nu }_{in}+\frac{l^2{\upsilon }_t^2}{R^2}{\nu }_{en}{\lambda }_D^2\left[{\omega }_{pi}^2(1+{\epsilon }_0\eta {\nu }_{in})+{\omega }_{ci}^2\right]\right].\omega +l\Omega \left[{\upsilon }_t^2{\nu }_{en}{\omega }_{ci}^2+{\omega }_{ce}^2{C}_s^2{\nu }_{in}\right]\end{array}$

Which by using suitable mathematical elaboration (Appendix B), we results with,

$\begin{array}{l}{\omega }^2{\omega }_i({\omega }_{pe}^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2)(3l\Omega -4\omega )\\ +\left[{\nu }_{en}{\epsilon }_0\eta {\omega }_{pe}^2({\omega }_{ci}^2+\frac{l^2{\upsilon }_t^2}{R^2}\frac{{\omega }_{pi}^2}{{\omega }_{pe}^2})+{\omega }_{ce}^2({\omega }_{pi}^2+{\omega }_{ci}^2)\right].2\omega {\omega }_i\\ -\left[{\omega }_{pe}^2{\omega }_{ci}^2{\nu }_{en}{\epsilon }_0\eta +{\omega }_{ce}^2.({\omega }_{pi}^2+\omega )\right].l\Omega {\omega }_i=\\ =\left[{\nu }_{en}{\omega }_{pe}^2(1+\frac{l^2{\lambda }_D^2}{R^2})+{\omega }_{ce}^2{\omega }_{pi}^2{\epsilon }_0\eta \right].{\omega }^3-l\Omega .({\omega }_{pe}^2{\nu }_{en}+{\omega }_{ce}^2.{\omega }_{pi}^2{\epsilon }_0\eta ).{\omega }^2\\ -{\nu }_{en}{\omega }_{pe}^2\left[{\omega }_{ci}^2+\frac{l^2{\lambda }_D^2}{R^2}({\omega }_{pi}^2+{\omega }_{ci}^2)\right].\omega +l\Omega .{\omega }_{pe}^2{\omega }_{ci}^2{\nu }_{en}\end{array}$

By using the approach ${\lambda }_D^2\prec \prec R^2$ , and then, $\raisebox{1ex}{${\lambda }_D^2$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.\to 0$ . The last becomes,