The mechanism the regioselectivity of prop–2–yn–1–ol 4 with Azido–benzene, 4–Azido–benzonitrile and 1–Azido–4–nitro–benzene in [3+2] cycloaddition, have been theoretically studied using DFT methods at the B3LYP/6–311 G (d,p) computational level. The possible ortho/meta regioselective channels were explored and characterized. Analysis of the free energies associated with the different reaction pathways indicates that the 32CA reactions of the between prop–2–yn–1–ol 4 and azides 1, 2 and 3 are highly meta regioselectivities, in agreement with the experimental results.

Keywords: molecular electron–density theory, regioselectivities, dft, pes, parr functions

1,2,3–Triazoles are N–Heterocyclic compounds which have found a range of important applications in the pharmaceutical such as may display biological activities and there are numerous examples in the literature including anti–HIV activity,^1,2 antimicrobial activity against Gram positive bacteria,³ 1,2,3–Triazoles have also found wide use in industrial applications such as dyes, corrosion inhibition, photographic materials, and agricultural industries.⁴ The most widely used method for synthesis of 1,2,3–Triazoles has involved the thermal 1,3–dipolar cycloaddition of organic azides with alkynes pioneered by Huisgen.⁵ However, there are major problems commonly associated with this methodology, including the need for long reaction times and high temperatures. It was recently reported that is possible to impart some regioselectivity into these thermal cycloadditions by utilizing sterically or catalyze or electronically biased alkynes.^6,7 Herein, we used new theory recently proposed by Domingo named a Molecular Electron Density Theory (MEDT) to study the cycloaddition reaction of the Prop–2–yn–1–ol with azides 1, 2 and 3 experimentally studied by Jesus et al.⁸ (Scheme 1). Our aim is to explain the regioselectivity experimentally found.

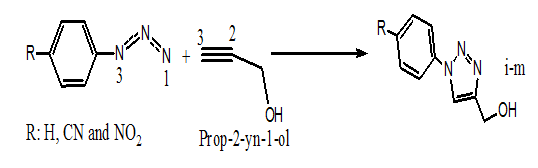
Scheme 1: The 32CA reaction between the Prop-2-yn-1-ol (4) and azides 1,2 and 3.

DFT computations were carried out using the B3LYP functional together with the standard 6–311(d,p) basis set. The optimizations have been realized using the Berny analytical gradient optimization method.⁹ All computations have been shown with the Gaussian 09 suite of programs.¹⁰ The global electrophilicity index11 $\omega$ , was given by the following expression, $\omega =({\mu }^2/2\eta )$ , in terms of the electronic chemical potential $\mu$ and the chemical hardness $\eta$ . Both quantities could be approached in terms of the one–electron energies of the frontier molecular orbital HOMO and LUMO, ${\epsilon }_H$ and ${\epsilon }_L$ , as $\mu =\left({\epsilon }_H–{\epsilon }_L\right)/2$ and $\eta =\left({\epsilon }_{L–}{\epsilon }_H\right)$ , respectively.¹²

The empirical (relative) nucleophilicity index N,¹³ based on the HOMO energies obtained within the Kohn–Sham,¹⁴ and defined as N = EHOMO (Nu)–EHOMO (TCE). The nucleophilicity was referred to tetracyanoethylene (TCE). This choice allowed us to handle conveniently a nucleophilicity scale of positive values. Electrophylic $P^{+}{}_k$ and nucleophilic $P^{-}{}_k$ Parr functions,^15–19 were obtained through the analysis of the Mulliken atomic spin density (ASD) of the radical anion and radial cation of the reagents. The local electrophilicity indices were evaluated using the following expressions: $N_k=N.P^{-}{}_k$ .²⁰ The stationary points were characterised by frequency computations in order to verify that TSs have one and only one imaginary frequency. Intrinsic reaction coordinates (IRC)21 pathways were traced to verify the connectivity between minima and associated TSs.

The present theoretical study has been divided in three parts:

1. An analysis of the conceptual DFT indices of the reagents involved in cycloaddition reaction of the Prop–2–yn–1–ol with azides 1, 2 and 3.
2. Next the potential energy surface (PES) associated with the cycloaddition reaction of the Prop–2–yn–1–ol with azides 1, 2 and 3 are explored and characterized,
3. Finally a transition states geometries are analyzed.

Comparative analysis of the conceptual DFT indices of the reagents

The global DFT indices, namely the electronic chemical potential $\mu$ , chemical hardness $\eta$ , electrophilicity $w$ and nucleophilicity $N$ , are given in Table 1.

The electronic chemical potential of Prop–2–yn–1–ol 4, −3.27 $eV$ , is higher than that of azides 1, 2 and 3, −3.79, –4.42 and –4.97 $eV$ respectively, indicating that along a polar reaction the global electron density transfer22 (GEDT) will flux from the Prop–2–yn–1–ol (4) framework towards the azides. The electrophilicity $\omega$ and nucleophilicity $N$ indices of the simplest Prop–2–yn–1–ol 4 are 0.69 and 2.39 $eV$ , being classified on the borderline of marginal electrophiles and as a strong nucleophile within the electrophilicity²³ and nucleophilicity¹³ scales. Inclusion of one phenyl group at each of the carbon atoms of azides notably increases both the electrophilicity $\omega$ and nucleophilicity $N$ index of azides 1, 2 and 3 to 1.24 and 2.91 $eV$ , being classified as a moderate electrophile and a strong nucleophile. Due to the high nucleophilic character of the azides, in 32CA reactions are favored with the participation of good electrophilic through polar reactions. Consequently, it is expected that azides 1, 2 and 3 participates as a good electrophile towards the strong nucleophilic Prop–2–yn–1–ol 4.

In polar cycloaddition reactions involving the participation of non–symmetric reagents, the most favorable reactive channel is that involving the initial two–centre interaction between the most electrophilic centre of the electrophile and the most nucleophilic centre of the nucleophile. The electrophilic ${\text{P}}_{\text{k}}^{+}$ and nucleophilic ${\text{P}}_{\text{k}}^{+}$ Parr functions, derived from the changes of spin electron density reached via the GEDT process from the nucleophile to the electrophile, as powerful tools in the study of the local reactivity in polar processes. Accordingly, the nucleophilic and electrophilic Parr functions of the Prop–2–yn–1–ol with azides 1, 2 and 3 were analyzed in order to characterize the most electrophilic and nucleophilic centers of the species involved in this 32CA reaction and, thus, to explain the regioselectivity experimentally observed (Figure 1).

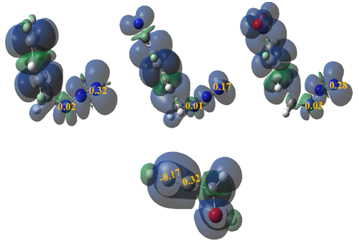
Figure 1 3D representations of the ASD of the radical anion and the radical cations as well as the electrophilic Parr functions of the azides 1, 2 and 3 and nucleophilic Parr functions of prop-2-yn-1-ol 4.

Analysis of the electrophilic ${\text{P}}_{\text{k }}^{+}$ Parr functions of the azides 1, 2 and 3 indicates that the N1 nitrogen is the most electrophilic centre of these species presenting the maximum value, ${\text{P}}_{\text{k }}^{+}=0.32,0.17\text{ and }0.28$ respectively. Note that the N3 nitrogen is very law as electrophilically activated as the N1 nitrogen. On the other hand, the nucleophilic ${\text{P}}_{\text{k}}^{+}$ Parr functions of prop–2–yn–1–ol 4 indicate that the C₂ carbon is the most nucleophilic centre of this molecule ${\text{P}}_{\text{k }}^{-}=0.32$ (Figure 1). Consequently, in the 32CA reactions of azides 1, 2 and 3 with prop–2–yn–1–ol 4, the most favorable electrophile–nucleophile interaction along the nucleophilic attack of the prop–2–yn–1–ol 4 on the azides 1, 2 and 3 will take place between the most nucleophilic centre of prop–2–yn–1–ol 4, the C₂ carbon, and the most electrophilic centre of azides 1, 2 and 3, the N₁ nitrogen, in clear agreement with the total meta selectivity experimentally observed.

Kinetic study of the 1,3–dipolar cycloaddition reaction of the prop–2–yn–1–ol 4with 2 azides 1, 2 and 3

Due to the non–symmetry of both reagents, the 32CA reaction between Prop–2–yn–1–ol with azides 1, 2 and 3 can take place through two competitive reactive channels, related to the two regioisomeric approach modes of Prop–2–yn–1–ol to azides 1, 2 and 3, namely meta and ortho (Scheme 2).

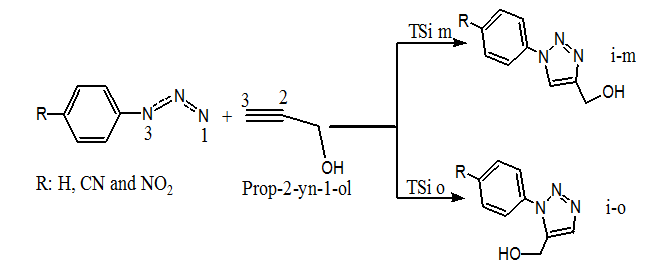
Scheme 2: Regioisomeric reactive pathways associated with the 32CA reaction between the prop-2-yn-1-ol and azides 1, 2 and 3.

The values of the Gibbs free energy G and the relative Gibbs free energy (ΔG), of the stationary points involved in the Diels–Alder 1,3–dipolar cycloaddition reaction of the prop–2–yn–1–ol and azides 1, 2 and 3 are given in Table 2.

The activation energies of 1,3–dipolar cycloaddition reaction of the prop–2–yn–1–ol and azides 1 associated with the two competitive reactive channels are found in the narrow range of 3.82–4.16 kcal mol⁻¹. These 32CA reactions are strongly exothermic, by between 71 and 74 kcal mol⁻¹. Analysis of these relative energies leads to some appealing conclusions:

1. This 32CA reaction presents very low activation energy, evidencing the high reactivity of the phenyl substituted azide 1 towards prop–2–yn–1–ol 4.
2. This 32CA reaction is presents a very low regioselectivity, as TS–m1 is only 0.34 kcal mol⁻¹ lower in energy than $T{S}^{-o1}$ .
3. The strong exothermic character of this 32CA reaction makes the formation of 1m and 1o irreversible. Consequently, formation of these products $1^m$ and $1^o$ is under kinetic control.

The activation energies associated to $T{S}^{2-m}$ and $T{S}^{2-o}$ of the 1,3–dipolar cycloaddition reaction of the prop–2–yn–1–ol and azides 2 presents are 3.61 and 11.57 kcal mol⁻¹ respectively these energies indicate that the formation of the products $2^{-m}$ is kinetically favored than $2^{-o}$ and the formation of the products $2^{-m}$ is slightly exothermic by 1.73 kcal mol⁻¹. Consequently the formation of $2^{-m}$ is kinetically and thermodynamically favored.

The activation energies of the 1,3–dipolar cycloaddition reaction between prop–2–yn–1–ol and azides 3 indicated that the meta approach modes are slightly more favorable than the ortho ones by 7.40 kcal•mol⁻¹. In addition, the low difference between the activation energy of both $T{S}^{‐on}$ and $T{S}^{‐mn}$ reveals that this 32CA reaction should lead to the formation of the product $1^{-m}$ as the kinetic favored. Formation of all CAs is exothermic in the range between 45 and 74 kcal•mol−1, indicating that this 32CA reaction is only under kinetic control. These results are in disagreement with the meta regioselectivity observed experimentally.⁸

The new Molecular Electron Density Theory (MEDT) recently proposed by Domingo Consists that the partition of the TS geometry into two separated structures does not have any physical sense within density functional theory (DFT) since in this quantum chemical model the energy of a system is a functional of the electron density and the external potential, i.e. the nucleus positions. Consequently, the energy of the two separated fragments cannot be correlated with the energy of the TS because each of them losses the external potential created by the other fragment.²⁴ The optimized density map ad geometries of the TSs at B3LYP/6‐311G (d, p) computational method involved in this 32CA reaction are given in Figure 2.

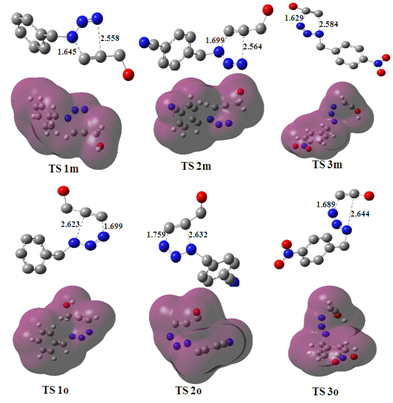
Figure 2 DFT/6-311G (d,p) optimized density map and structures of the TSs of the 32CA reaction between the mesitonitrile oxides and 2-Fluoren-9-ylidene-malononitrile. Lengths are given in Angstroms.

The lengths of the N³–C³ and N¹–C² newly formed bonds at the TSs associated with the meta channels are 1.645 and 2.558 Å at $T{S}^{‐1m}$ and 1.699, 2.564 Å at $T{S}^{‐2m}$ and 1.629, 2.584 Å at $T{S}^{‐3m}$ , respectively, while the lengths of the N³–C² and N¹–C³ newly formed bonds at the ortho channels are 2.623 and 1.699 Å at $T{S}^{‐1o}$ , 2.632 and 1.759 Å at $T{S}^{‐2o}$ and 2.644 and 1.689 Å at $T{S}^{‐3o}$ , respectively. These values suggest that the bond formation process at the meta TSs is slightly more asynchronous than that at the ortho ones, in which the formation of the C¹–C³ bond is the more advanced one.

The 1,3–dipolar cycloaddition reaction of prop–2–yn–1–ol 4 with Azido–benzene, 4–Azido–benzonitrile and 1–Azido–4–nitro–benzene has been studied within the MEDT through DFT calculations at the 6–311(d, p) computational level. The obtained results are supported by the combination of the analysis of the reactivity indices at the ground state of the reagents, derived from the conceptual DFT, the exploration of the values of the Gibbs free energy G and the relative Gibbs free energy (ΔG) of these 32CA reactions.

The analysis of the electrophilic ${\text{P}}_{\text{k }}^{+}$ Parr functions allows characterising the N¹ nitrogen atom as the most electrophilic centre of the azides 1–3 indicate, in clear agreement with the regioselectivity found in the 32CA reaction. An exploration of the of the values of the Gibbs free energy G and the relative Gibbs free energy ΔG of these 32CA reactions indicates that it takes place through a one–step mechanism. The exothermic character of these 32CA reactions makes the formation of the four products 1m, 2m, and 3m irreversible, and finally meta position is thermodynamically and kinetically favored in good agreement with experimental observations.

None.

The author declares no conflict of interest.

1. Alvarez R, Velazquez S, San F, et al. J Med Chem. 1994;37:4185–4194.
2. Velazquez S, Alvarez R, Perez C, et al. Regiospecific synthesis and anti–human immuno–deficiency virus activity of novel 5–substituted N–alkylcarbamoyl and N,N–dialkyl carbamoyl 1,2,3–triazole–TSAO analogues. Antiviral Chemistry & Chemotherapy. 1998;9:481–489.
3. Genin MJ, Allwine DA, Anderson DJ, et al. Substituent effects on the antibacterial activity of nitrogen–carbon–linked (azolylphenyl) oxazolidinones with expanded activity against the fastidious gram–negative organisms Haemophilus influenzae and Moraxella catarrhalis. J Med Chem. 2000;43(5):953–970.
4. Fan WQ, Katritzky AR. Comprehensive heterocyclic chemistry II. In: Katritzky AR, editor. USA: Elsevier Science, Oxford; 1996. p. 1–126.
5.  Rolf Huisgen. 1,3–Dipolar Cycloadditions. Past and Future. Angewandte Chemie International Edition. 1963;2(10):565–598.
6. Laura Rinaldi, Katia Martina, Francesca Baricco, et al. Solvent–Free Copper–Catalyzed Azide–Alkyne Cycloaddition under Mechanochemical Activation. Molecules. 2015;20:2837–2849.
7. Maya Shankar Singh, Sushobhan Chowdhury, Suvajit Koley. Advances of azide–alkyne cycloaddition–click chemistry over the recent decade. Tetrahedron. 2016;72(35):5257–5283.
8. Aizpurua JM1, Azcune I, Fratila RM, et al. Click Synthesis of Nonsymmetrical Bis(1,2,3–triazoles). Org Lett. 2010;12(7):1584–1587.
9. Schlegel HB. Optimization of Equilibrium Geometries and Transition Structures. Journal of Computational Chemistry. 1982;3(2):214–218.
10. Frisch MJ. Gaussian 09, Revision A 02, GW Trucks, HB Schlegel. 2009.
11. Parr RG, Szentpaly LV, Liu S. Electrophilicity Index. J Am Chem Soc. 1999;12(9):1922–1924.
12. Parr RG, Pearson RG. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J Am Chem Soc. 1983;105:7512–7516.
13. Jaramillo P, Domingo LR, Chamorro E, et al. A further exploration of a nucleophilicity index based on the gas–phase ionization potentials. Journal of Molecular Structure: THEOCHEM. 2008;865:68–72.
14. Kohn W, Sham L. Self–Consistent Equations Including Exchange and Correlation Effects. Phys Rev. 1965;140(4A):1133–1138.
15. Zeroual A, Benharref A, El Hajbi A. Theoretical study of stereoselectivity of the [1+2] cycloaddition reaction between (1S,3R,8S)–2,2–dichloro–3,7,7,10–tetramethyltricyclo[6,4,0,01.3]dodec–9–ene and dibromocarbene using density functional theory (DFT) B3LYP/6–31G*(d). Journal of Molecular Modeling. 2015;21(44):2594–2599.
16. Zeroual A, El Haib A, Benharref A, et al. A combined experimental and theoretical study of highly chemioselectivity acetylation of diterpene. JCMMDA. 2015;5(3):58–62.
17. Zeroual A, Zoubir M, Hammal R, et al. Understanding the regioselectivity and reactivity of Friedel–Crafts benzoylation Using Parr functions. Moroccan Journal of Chemistry. 2015;3(2):356–360.
18. Zoubir M, Zeroual A, El Idrissi M, et al. Understanding the Chemoselectivity and Stereo selectivity in Michael Addition Reactions of β–Hydroxyparthenolides and Amines such as Pyrrolidine, Morpholine, Piperidine and 1–Methylpiperazine: a DFT Study. Journal of Materials and Environmental Sciences. 2017;8(3):990–996.
19. Zeroual A, Hammal R, Benharref A, et al. A theoretical investigation of the reactivity and regioselectivity of triterpene derivatives using difference local index, Parr functions. Moroccan Journal of Chemistry. 2016;4(4):938–944.
20. El Idrissi M, Zoubir M, Zeroual A, et al. A Theoretical Study of the Mechanism and Regioselectivity of the 1,3–Dipolar Cycloaddition Reaction of Azides with Alkynes. J Mar Chim Heterocycl. 2016;15(1):145–151.
21. Fukui K. Formulation of the reaction coordinate. J Phys Chem. 1970;74(23):4161–4163.
22. Domingo LR. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014;4:32415–32428.
23. Domingo LR, Aurell M J, Pérez P, et al. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron. 2002;58(22):4417–4423.
24.  Domingo LR. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules. 2016;2:1319.