A theoretical approach to the possibility of an upper limit to temperature

doi:10.15406/oajmtp.2018.01.00038

Open Access Journal of

eISSN: 2641-9335

Mathematical and Theoretical Physics

Research Article Volume 1 Issue 5

A theoretical approach to the possibility of an upper limit to temperature

Marvel Bate Eno Aiyuk

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Engineering, Ecole National Superieure des Travaux Publics, Cameroon

Correspondence: Marvel Bate Eno Aiyuk, Department of Engineering, Ecole National Supérieure des Travaux Publics,Yaoundé, Cameroon

Received: September 18, 2018 | Published: October 23, 2018

Citation: Aiyuk MBE. A theoretical approach to the possibility of an upper limit to temperature. Open Acc J Math Theor Phy. 2018;1(5):219-223. DOI: 10.15406/oajmtp.2018.01.00038

Download PDF

Abstract

Temperature is known to have a lower limit, absolute zero corresponding to a temperature of 0K. Is there also an upper limit above which matter as we know it cannot exist? This paper is aimed at obtaining a theory for the establishment of a possible upper limit to temperature, with the use of concepts from thermodynamics and special relativity. This is done by using the kinetic theory and ideal gas equation to obtain an expression of temperature as a function of velocity of the particles, then using special relativity to establish the speed of light as a velocity barrier, thus providing a corresponding upper limit to temperature. Such a temperature should be unreachable, or the particles would be moving at the speed of light, which is against the second postulate of special relativity. This approach leads to results indicating the existence of not one but several temperature limits, characteristic to each element.

Keywords: maximum temperature, ideal gas equation, kinetic theory of gases, special relativity

Introduction

This paper aims at presenting a theory postulating an upper limit to temperature. An upper limit to temperature is not a completely new concept in physics. Examples of temperatures considered as upper limits include the Plank temperature (~10³²K) and the Hagedorn temperature (~10³⁰K).¹

In this paper, a different approach, using concepts from special relativity is used. This leads to an interesting observation, that this temperature is characteristic to each element. This work is done using the same assumptions used in the kinetic theory and in the ideal gas equation, coupled with some additional ones. The entire system is also considered at rest. Only the particles are considered to be moving; the container is in a state of rest. This is done to avoid complications such as the Lorentz invariance of thermodynamic quantities. For example, some papers suggest that temperature is invariant,^2‒6 while others suggest it is not.^2,3,6 Such questions will be avoided entirely. The relativistic kinetic theory⁷ will not be considered either.

Also, the theory is formulated assuming the system is composed only of atoms. As such, the temperatures are considered to be high enough for bond energies of all compounds to be reached and that atomic processes such as fusion and fission do not occur. This temperature limit differs with respect to the different elements, since it depends on the molar mass. Thus an element with a higher molar mass will have a higher temperature limit.

In this paper the temperature as a function of velocity is analyzed to answer the following: if there is a velocity limit, can there be a corresponding temperature limit?

Concepts and theory

We will begin by looking at some concepts which will be necessary for the establishment of the theory.

The ideal gas equation

The ideal gas equation is the result of a macroscopic analysis of the behavior of gases. It gives the relationship between the macroscopic properties of volume, pressure and temperature and the mass of a gas expressed as number of moles. An ideal gas is defined as a gas whose behavior (pressure, volume and temperature) can be completely described using the ideal gas equation. The equation is gotten from the three gas laws:⁸

Boyle's law: pressure is inversely proportional to volume at constant temperature.

Charles' law: volume is directly proportional to temperature at constant volume.

Gay-Lussac's law: pressure is directly proportional to temperature at constant volume.

These laws are combined to give the ideal gas equation:

PV= nRT^9,10

P is the pressure of the gas

V is volume

n is the number of molecules; n = m/M, where m is the mass and M is the molar mass

R is the gas constant, and it is equal to 8.31J/mol.K

T is the temperature

The kinetic theory of gases

The kinetic theory of gases aims at explaining the behavior of gases by considering the motion of their molecules. Here, the pressure of a gas is considered to be generated due to the bombardment of the walls of a container by the molecules of gas within the container. The following assumptions are made to simplify the calculations:¹⁰

The volume of the molecules is negligible compared with the volume of the container
The motion is considered to be random and isotropic
Intermolecular forces between the molecules are negligible
Collisions between molecules considered to be perfectly elastic

The kinetic theory, in accordance with the above assumptions, provides a relationship between the pressure generated by a gas and the speed with which the gas molecules move through the following equation:

$p = (1 / 3) p < v^{2} >$ ¹⁰

P is the pressure

p is the density of the gas

<v²> is called the mean square speed

$< v^{2} > = (v_{1}^{2} + v_{2}^{2} + v_{3}^{2} + .............. + v_{N}^{2}) / N$

The kinetic theory also provides a relationship between the kinetic energy and the temperature of the gas:

$K E = (3 / 2) K_{B} T$ ^10,11

KE is kinetic energy

is the Boltzmann's constant:

$K_{B} = R / N_{A}$ ⁹

Where R is the gas constant and is the Avogadro's constant (6.02x10²³)

T is the temperature

Einstein's special theory of relativity

Einstein's special theory of relativity provides us with some interesting concepts in the realm of physics. It is based on two postulates:¹¹

The laws of physics are the same for every observer who is not accelerating. This implies that an experiment performed in a lab at rest should give the same results when performed in a lab moving at constant velocity with respect to the one at rest.

The speed of light is constant for every observer; c=3x10⁸m/s. (This value has been rounded up). This means the speed of light, contrary to the common notion of relative speed, remains unchanged whether the observer is moving or not.

The speed of light thus represents an upper limit to velocity with positive rest mass; no massive object can move faster than light or even quite reach the speed of light.¹²

Some important consequences of special relativity are time dilation and length contraction. These lead to the introduction of the Lorentz factor:

$γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$ ^13,14

The theory of maximum temperature

First, some extra assumptions will be added to those already presented in the kinetic theory:

The temperatures are high enough for all matter to be present in the gaseous phase; thus the theory is extended beyond gases at room temperature.

All the gases behave like ideal gases. The gas container system is isolated and all the energy entering is used solely to increase the speed of the gas molecules.

Based on these assumptions, we can begin the mathematical analysis:

$P V = n R T$ thus, $p = \frac{n}{V} R T$

$P = ρ < v^{2} >$

This implies that $\frac{n}{V} R T = \frac{1}{3} ρ < v^{2} >$

$R T = (\frac{1}{3}) (\frac{V}{n}) ρ < v^{2} >$ (1)

But $ρ = m / V$

$\begin{array}{l} (1) = (\frac{1}{3}) (\frac{V}{n} \times \frac{m}{V}) v^{2} > \\ \begin{matrix} = \end{matrix} (\frac{m V}{3 n V}) < v^{2} > \\ \begin{matrix} = \end{matrix} (\frac{m}{3 n}) < v^{2} > \end{array}$ (2)

But $n = m / M$

$\begin{array}{l} (2) = (\frac{m M}{3 m}) < v^{2} > \\ \begin{matrix} \end{matrix} = (\frac{M}{3}) < v^{2} > \\ R T = (\frac{M}{3}) < v^{2} > \end{array}$

$T h u s T = (\frac{M}{3 R}) < v^{2} >$ (3)

Now $v = v_{x} + v_{y} + v_{z}$ and $v_{x} = v_{y} = v_{z}$

This implies that $v = 3 v_{x}$

Let's establish that $v_{x} < c, v_{y} < c, v_{z} < c$ where c is the speed of light.

From special relativity, $v_{m a x} = c$

Thus $v_{x, m a x} = v_{y, m a x} = v_{z, m a x} = c / 3 = 1 X 10^{8}$

This enables us to write $V_{m a x} = 3 V_{x} = c$

The system is isolated and all the energy input goes in increasing the speed of the molecules, so this will go on until all the molecules are at their maximum speed, c.

Thus, $< v^{2} > = (Σ v_{i}^{2}) / N = (Σ c^{2}) / N = N c^{2} / N = c^{2}$

Thus, $(3) = (M / 3 R) c^{2}$

Since c is the maximum speed, this temperature represents the maximum temperature.

$T_{m a x} = (M / 3 R) c^{2}$

Now, about the molar mass:

We are left to wonder: Is the molar mass Lorentz invariant? At first glance it appears not to be, considering the concept of relativistic mass. Being fully aware of the disagreements on whether or not it’s correct,^15‒18 let’s consider it here for the purpose of this analysis. Relativistic mass tells us that the mass of a point particle is not constant, but depends on the particle’s velocity. We have the following formula:

$m = γ m_{0}$ ¹⁹

Where $m_{0}$ is the particle’s rest mass.

The molar mass is defined as the atomic mass expressed in grams per mole. For an element, the molar mass is the same as the atomic mass.⁸The molar mass is the mass of an atom exactly equal to one-twelfth the mass of one carbon-12atom. Thus it is a mass dependent on a reference mass, one-twelfth the mass of one carbon-12atom. The mass of the particle will increase as its velocity increases. Now consider a setup for the determination of the molar mass of an element. If the entire frame is considered to be moving at a constant velocity with respect to a stationary one, the mass of both an atom belonging to the element and the reference C-12atom will increase by the same factor. Let the molar mass of the element be x and the mass of the C-12atom be y.

$X = (1 / 12) y$ at rest. At v different from 0, we have:

$γ x = (1 / 12) (γ y)$ which implies $x = (1 / 12) y$ . Thus the molar mass is considered invariant.

Thus we have our equation:

$T = \frac{1}{3} q_{A} c^{2}$

Where $q_{A}$ is the constant M/R. This result can also be obtained from the kinetic energy of gases:

The total translational kinetic energy of the molecules is given by the following formula:

$K E_{T o t} = (3 / 2) n R T$ ¹¹

Solving for T, and placing v = c, we obtain the same result:

$T = (M / 3 R) c^{2}$

Now let's take a look at the kinetic energy.

Special relativity tells us that the kinetic energy of a body goes to infinity as v approaches c. Thus if the temperature has an upper limit, then something else must be changing. Consider the following approach:

Relativistic mass of an object corresponds to its energy.²⁰ The number of moles is given by

$n = m / M$

As v approaches c, m goes to infinity and M doesn’t change. Thus, the number of moles equals infinity at c. But n can also be defined as N/N_A, where N is the number of molecules, N_A is Avogadro’s number. This means at c, either N goes to infinity or N_A goes to zero. Due to the law of conservation of mass,⁸ N must remain constant so N_A must go to zero. This can be interpreted as each molecule occupying more ‘space’ in the mole as its mass increases, so a lesser amount of particles are sufficient for one mole.

The kinetic energy of one particle is given by

$K E = (3 / 2) K_{B} T$

Where K_B the Boltzmann is constant. We can consider the kinetic energy as going to infinity not due to the temperature, but due to a change in K_B.

$K_{B} = R / N_{A}$

Where, N_A is Avogadro’s number. Thus KE goes to infinity even though the temperature reaches a limit because K_B goes to infinity due to N_A going to zero.

Results

The equation for the calculation of the maximum temperature indicates the dependence on the molar mass of the substance. This implies that the maximum attainable temperature will be different for each element, progressively getting higher as the molar mass increases. Below is a curve showing the progression of maximum temperature with molar mass (for the first 20 elements of the periodic table) (Figure 1).

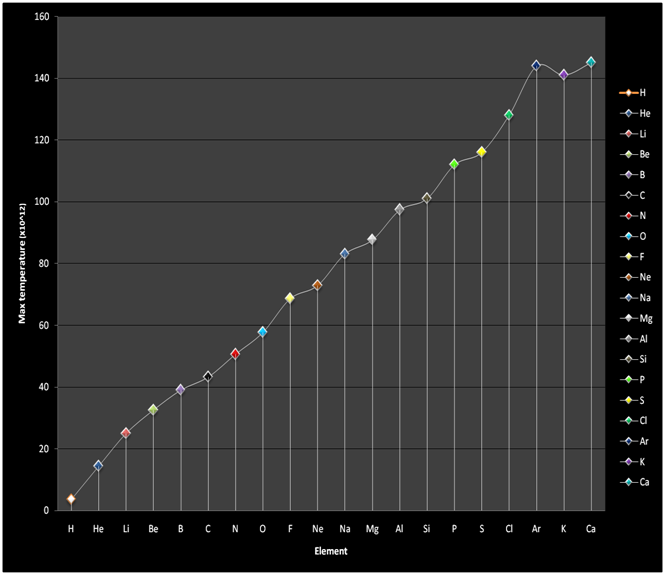
Figure 1 Graph showing variation in temperature limit for the first 20 elements. The temperature limit increases with molar mass. The value of R used is 8.31J/mol.K and M is in Kg/mol. The values are x10¹².

Table 1 shows the variation of this temperature with respect to element for the first 20 elements of the periodic table. The temperatures are rounded up and are times 10 to the power 12 (x10¹²). The temperatures are measured in Kelvin.

Na	Mg	Al	Si	P	S	Cl	Ar	K	Ca
H	He	Li	Be	B	a	N	O	F	Ne
3.64	14.4	25	33	39	43	51	58	69	73
83	88	97	101	112	116	128	144	141	145

Table 1 Maximum temperature values for the first 20 elements (x10¹²)

Discussion

This study suggests that there is an upper limit to temperature which is characteristic to each element. Thus there are several upper temperature limits for each element. Reaching or going above this temperature would require the particles to be moving at or above c, which is in contradiction with the second postulate of special relativity.
This differs from other suggested upper temperature limits in that it is based on special relativity and there is not a unique temperature limit.

This approach has some limitations:

Lack of experimental backup, rendering the work purely theoretical.
Oversimplification of the model by neglecting concepts and using many assumptions. This helps in the mathematical analysis and all assumptions are kept reasonable.
The dependence of temperature on molar mass indicates that the theory works only for atomic systems. Atomic systems here mean systems composed of atoms and molecules, such as a gas in a container. The theory breaks down if considering for example a subatomic or elementary particle system.
An upper temperature limit based on thermodynamics and special relativity is possible. Although these temperatures may be unrealistically high for real gas systems, the approach is aimed at shedding some light on the issue.

Conclusion

An upper limit to temperature dependent on molar mass implies a variation of this temperature with respect to the various elements. Thus contrary to the lower limit absolute zero, there are not one but several upper limits. Based on this, a more absolute upper limit might be that of the element with the highest molar mass.