Frictional interaction of tool and part during composite manufacturing is critical as it can affect a range of processing outcomes such as residual stress during the shrinkage of resin, formation of wrinkles at the tool side, possibility of surface cracks during de-moulding, among others. This article, through a systematic design of experiments (DOE) methodology, investigates how different processing configurations can affect the static and dynamic coefficients of friction at the mould-fiber interface. The study factors chosen are the type of mould material, mould surface roughness, mould surface preparation (use of release agent), temperature, and the applied pressure. The mould materials employed include a a Glass Fiber Reinforced Polymer (GFRP) as well as a steel, interacting with a set of unidirectional fibreglass tows. Results indicate to what extent each of the above design and processing factors can have a statistical effect on the level of dry friction between the tool and fiber tow, both at static and dynamic states.

Keywords: GFRP composites, processing, tool-part friction

DOE, design of experiments; CTE, coefficient of thermal expansion; UD, unidirectional

Friction is an important parameter considered during composite forming processes^1-8 as the limitations imposed by friction at tool-part interaction can play a role in the development of certain processing outcomes such as residual stresses and subsequent spring-in and warpage of the part, as well as surface cracks. These outcomes in turn can have a direct effect on the mechanical performance of manufactured components, or their ability to be assembled due to residual strains.

Residual stresses are generated within composite materials during manufacturing from a range of mechanisms.¹ many of which are inherently unavoidable due to the anisotropic nature of composite materials, yet may be minimised. There are two sources of residual stresses; intrinsic and extrinsic. Intrinsic type refers to materials, lay-up and part shape factors, and extrinsic refers to processing and tooling conditions. An extrinsic source of stress largely affects structural length scales, while intrinsic source affects fibre-matrix interactions and bonding. As an example of residual stress outcome, spring-in is a phenomenon in which there is a reduction of geometric angle in the part from the original mould specification.⁴ Resin shrinkage during cure of thermosetting polymer matrices and the coefficient of thermal expansion (CTE) mismatches between fibres and matrix, as well as the composite and tooling materials are among known factors that contribute to spring-in.⁴ As another example, in the context of tool and part CTE mismatch and resin shrinkage, the frictional contact and adhesion between tool and part can create shear stress gradients through the thickness of the part, which in turn can contribute to the development of warpage in flat samples,⁶ also spring-in in curved geometries ¹. To investigate the influence of tool-part interaction on such processing outcomes, the experiments conducted by Albert et al.² on a series of geometries (Figure 1) showed the presence of release agent and FEP sheeting, as a suggested method to lesson tool-part interactions, could reduce spring-in of 90-degree angled composite parts.

Figure 1 Images of manufactured composite samples by Albert et al. ²
(A) C-shaped parts,
(B) L-shaped parts.

To date, there has been little investigation into contributing factors of tool-part interactions; instead most research has been focused on the effects of this interaction upon the process outcomes such as residual stresses and deformations. The present article intends to broaden understanding of factors affecting the tool-part frictional interaction.

In many stages of composite manufacturing, such as autoclave curing of prepreg laminates, or open moulding processes, tool part interaction is a wet procedure, implying that the presence of polymer resin affects various mechanisms of the interaction. As a result, fibre-dominated tool-part interaction is typically smaller than what is in a resin-dominated interaction (where regions of Boundary Lubrication, Mixed Lubrication, and (Elasto) Hydrodynamic Lubrication can form.³) However, for other stages of manufacturing, such as dry fiber lay-up/draping on to the mould, the primary mechanism of mechanical interaction is between the fiber reinforcement and the mould face. Focusing on such fiber-dominated interaction cases, in this study a set of parameters have been selected to understand their effects statistically on static and dynamic coefficients of fiction. The study parameters included the type of mould material, mould surface roughness (mean average roughness, Ra), mould surface preparation (use of release agent), moulding temperature, as well as applied pressure on the system. Roughness was selected as a parameter, as it is known surface morphological parameters can have a direct correlation to friction⁸ understandably, the rougher a mould surface, the higher the resistance to displace an object on it. As surface roughness contributes to friction, surface preparation also plays a role hand in hand in reducing or increasing frictional forces. The use of release agents defines how the “stickiness” contributes to friction. It is important to note that the primary purpose of release agent is to prevent adhesion between the part and tool, and hence to allow for ease of de-moulding after consolidation and cure. However, it inherently influences the tool-part interaction during cure, hence the development of residual stresses. Moulding temperature is another parameter analysed, as it has been anticipated that heat changes the physical properties of some release agents. When wax-based release agents are heated, they become less viscous and as such produce a different surface for tool-part interaction. During moulding of composite materials, an external pressure is often applied to help with consolidation. Given the multi-scale nature of composite materials, the application of pressure may alter the orientation and compaction of fibres, in turn affecting the tool-part interaction once more. The statistical evaluations of these intuitive effects are presented in the sections to follow.

Materials and Design of Experiments

The materials applied in the experiments included representative samples of a GFRP composite mould and a 304 steel mould (both flat and 3” by 3” in size), interacting with a set of fiberglass roving (by Jushi inc) from a spool laid out in unidirectional (UD) arrangement. The moulds were made in-house and waterjet cut.

Each treatment factor (mould material, mould surface roughness, mould surface preparation, moulding temperature, and applied pressure) in the experimental design was chosen to have two levels of “high” and “low”. For example, a “high” for mould surface preparation was the application of release agent versus the “low” for no release agent. For cases using release agent, TR-102 Mold Release (supplied by TR Industries) was applied three times in a circular motion, using a wax on, wax off method to ensure full coverage on the mould surface. Each time prior to the application of the release agent in a new experiment, the mould was completely cleaned with acetone and lint-free clean cloth. The surface roughness was altered using 400 and 100 grit sand paper for low and high roughness levels, respectively. A “high” level of applied temperature factor was attributed to 40 OC, achieved using an industrial oven to heat the system before testing, as opposed to “low” of 21OC (room temperature). An average mean “high” roughness (Ra) was 0.586 µm, and an average “low” roughness was 0.072 µm for the mould surfaces (it is to note that the composite tool surface was inherently rougher than the steel tool, but for the sake of statistical analysis with fixed effects, low and high levels were defined as average). A high pressure was approximately 1.5 kPa (using extra weight on the friction tester carriage-expanded on in Section 2.2) and low pressure was approximately 0.5 kPa (self-weight of the load carriage). To have a cost-effective experimental plan, the test matrix was designed as a partial factorial of nine sets of experiments (Table 1), with three repeats of each set-up.⁹

Friction Testing

A Qualitest FPT F-1 Friction/Peel Tester and its data acquisition software was used to perform the friction tests on each of the factor combination in Table 1, both with composite mould and steel mould, each repeated three times (i.e., total of 9×2×3 tests). The friction tester (Figure 2) has three major components; the belt (1), the load carriage (2), and the load cell (3). Of the two components interacting in the test (i.e., part and tool), one is placed down and affixed to the belt (here UD fiberglass), while the load carriage holds the other component (mould). The load carriage and load cell are connected to each other via a wire. The load cell measures the friction force induced by the carriage unit. As a result, when the experiment is set up and run, the belt moves to the left and the load carriage unit remains in a constant state allowing the load cell to record the data.

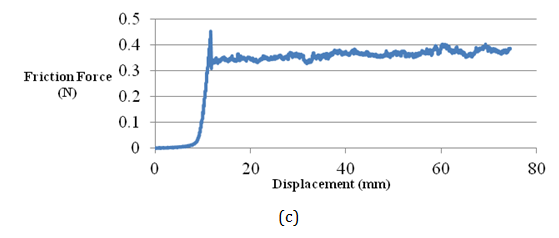
Figure 2 (A) FPT-F1 experimental set-up (1: belt, 2: the load carriage, 3: load cell), with UD fibers laid on the belt and the flat mould attached to the load carriage;
(B) Close-up image of composite mould attachment to the carriage;
(C) Sample of obtained force-displacement response.

All tests were performed at a quasi-static carriage speed of u=5 mm/s. The normal force, N, based on the total mass, m, of the carriage (including mould) was used to estimate the corresponding friction coefficient, $\mu$ , based on the force, $F$ , measured from the device:

$N=mg$     (1)

$\mu =\frac{F}{N}$   (2)

A sample measured dataset by the FPT-F1 is shown in Figure 2. The coefficient of static friction is found by using the peak value of the force. The dynamic coefficient of friction is approximated by taking an average line in the secondary portion of the force-displacement response (after the static force drop), where the system dynamics is stabilised.

After running all 54 friction tests (Appendices A and B), a series of fractional-factorial ANOVA analysis were run to find the significance of each input parameter on the static and dynamic coefficients of friction. Throughout the subsequent analyses the interaction factor %contributions were generally low and ignored during P-value calculations/de-aliasing of individual factors.

Metal Mould-Fiberglass Interaction (Static)

Table 2 shows the ANOVA results of the steel mould-UD fibreglass system, for the static coefficient of friction with the significance level of α=0.05. The results indicate that roughness, surface preparation, and pressure have high contributions to the coefficient of static friction, under this manufacturing set-up. The applied pressure on the fibers shows a significant effect (p-value<5%), but relatively moderate compared to the highest effect that is coming from the use of release agent (stickiness at the tool-part interface). Note that statistically, the order of significant effects may be judged from the percentage contributions. Similarly, it is quite reasonable that roughness has a very high significance, as the more coarse and unsteady the tool-part surface becomes, the more resistance to relative mobility, hence causing a higher coefficient of friction. The temperature, in the tested range (21 OC - 40 OC), has had no significance.

Metal Mould-Fiberglass Interaction (Dynamic)

Similar to the previous section, the test data were analysed to evaluate the variation of coefficient of dynamic friction in the steel mould-UD fibreglass system. Table 3 indicates that the pressure is the only significant factor in this case, while the other factors’ effect is lower than the random error/noise in the tests at α=0.05. Although Eq. (2) suggests that theoretically normal force (N) alone should not have any effect on a constant-µ state, a hypothesis can be made on why the present set of results proves otherwise. That is, although effort was made to use non-crimped fibre strands to limit the waviness, they are not perfectly straightened/aligned and the samples tested with low pressure allow air gaps to be formed between the fibers and friction tester belt. In that case the applied force, F, would be partially associated with the local bending of fibers under the load carriage. Increasing the normal pressure, readily de-crimps/straightens the fiber tow and closes the air gaps, and hence creating a lower resistance to the horizontal shear mobility. It has been also reported that at very high pressures the transverse compaction of tows can increase the effective transverse Young’s modulus.¹⁰ It is worth noting that in the static case (Table 2), the pressure also had a significant effect, but to a much lesser degree when compared to the dynamic case.

 Composite Mould-Fiberglass Interaction (Static)

The summary of the analysis for this tool-part interaction system is shown in Table 4, where surface preparation, temperature, and applied pressure have in order the highest impact on the coefficient of static friction. Similar to the steel mould case (Table 1), the release agent played the greatest role as it is a waxy material that creates a “sticky” surface on the mould,¹¹ while acting as a de-couplant to prevent the curing resin from providing a stronger bond to the mould material. Also as in the metal mould case, pressure has had a fairly high percentage contribution in the composite mould case, hypothetically by means of compressing the air gaps and straightening the fiber tows under high pressure. The effect of temperature on the coefficient of friction in the composite case has been significant; in general it is known that temperature can change (decrease or increase) the surface coefficient of friction, depending on a given material type, its thermal properties and the applied temperature range.¹² Roughness shows no influence in this case, perhaps since the noise in the average roughness of composite moulds is inherently very high in both low and high levels.

Figure 3 shows a comparison of the metal and composite moulds at low (room) temperature, with no release agent use, and at low pressure (e.g., mimicking a manual lay-up process). As can be seen, on average the metallic mould release force is lower than that associated with the GFRP mould, suggesting a lower frictional interface between the part and steel mould and subsequently less potential surface defects during de-moulding of the part. 

Figure 3 Sample comparison of friction force for the composite tool versus steel tool (at low temperature and low pressure, with no release agent).

Composite Mould-Fiberglass Interaction (Dynamic)

The ANOVA analysis of the dynamic coefficient of friction was not possible for this manufacturing set-up, due to very fluctuating/inconsistent force-displacement measurements in the dynamic response region. An individual study of different factor combinations showed that the use of ‘release agent’ was what led to the aforementioned unstable data readings. Figure 4 shows sample force-displacement curve of such a case, where the load carriage had repetitions of sticking and releasing cycles. This jerking motion is likely caused by excessive sticking of the fibres to the mould through the use of release agent, hence highlighting the critical effect of sufficient resin curing before a part can be de-moulded (i.e., allowing a smooth sliding motion of part on mould surface). The peak forces at release for these cases were at least 150% greater than those of other mould type.

Figure 4 Sample data of jerking slipping-then-sticking motion of fibres on a composite tool with release agent.

What can be defined as tool-part interaction during composite manufacturing is broad and complex in nature, given that many different physical and mechanical mechanisms occur at this interface. For example, the thermal resistance across the tool-part interface can affect the thermal history of the part dung curing, and at the same time the change in coefficient of friction between mould and part can affect various properties of the manufactured composite part such as wrinkling near the tool.¹⁰ Focusing on the dry contact friction state between mould and fibers, the summary Tables 5-7 from this study may be useful to show how significant each process parameter can be in defining the coefficient of friction, under different tool materials. Arrows denote the direction of each significant factor effect on average. For example, in Table 5 a higher pressure lowers the friction coefficient on average, and it is statistically a significant (repeatable/robust) observation. Further research is worthwhile to correlate these characterization results to actual forming processes with complex geometrical shapes.

The authors would like to acknowledge financial support from the Natural Sciences and Engineering Research Council of Canada, as well as the UBC-Okanagan Work-Study Program. The work was also presented at the Canadian-International Conference on Composites (CANCOM15), August 18-20, Edmonton, Canada.

The author declares no conflict of interest.

1. Fernlund G, Poursartip A, Twigg G, et al. Residual stress, spring-in and warpage in autoclaved composite parts. Proceedings for the 4th international conference on composite materials, San Diego, USA: Society of manufacturing engineers; 2003.
2. Albert C, Fernlund G. Spring-in and warpage of angled composite laminates. Composites Science and Technology. 2002;62(14):1895–1912.
3. R Akkerman, R Thije, L van der Meer, et al. Tool-ply friction in composite forming. AIP Conference Proceedings. 2007;907(1):10.1063.
4. Fernlund G, Floyd A, McKay S. Process analysis and tool compensation for curved composite L-angles. Proceedings. 2007.
5. Fernlund G, Floyd A, Shewfelt M, et al. Process analysis and tool compensation for a complex composite panel. Proceedings for the 6th international conference on composite materials, Winnipeg, Canada; 2007.
6. Twigg G. Tool-Part Interaction in Composites Processing. Dissertation, Department of Metals and Materials Engineering. Vancouver, Canada: University of British Columbia; 2001.
7. Harrison P, Thije R, Akkerman R, et al. Characterisation and modelling friction at the tool-ply interface for thermoplastic Woven composites. Proceedings of NATO workshop “Textile Composites”, May 18th -22nd, Kiev, Ukraine, Europe: University of Twente; 2009.
8. Sedlacek M, Vilhena LMS, Podgornik B, et al. Surface topography modeling for reduced friction. Journal of Mechanical Engineering. 2010;57(9):674–680.
9. Gotardo MA, Pezza L, Pezza HR. Determination of hydrochlorothiazide in pharmaceutical formulations by diffuse reflectance spectroscopy. Eclética Química. 2005;30(2):17–24.
10. Lightfoot JS, Wisnom MR, Potter K. A new mechanism for the formation of ply wrinkles due to shear between plies. Composites: Part A. 2013;49:139–147.
11. Long C, Lin H, Sherburn M, et al. Finite element modelling of compaction for textile reinforcements using automatically generated unit cell models. The 9th International conference on flow processes in composite materials, Montréal, Canada: 2008. p. 1–8.
12. Labthink International, Inc. Influence of temperature on coefficient of friction; 2013.