MOJ
eISSN: 2574-8130


Research Article Volume 1 Issue 6
Department of Electronics and Communication, Manipal Institute of Technology, India
Correspondence: Ex-Professor, Department of Electronics and Communication, Manipal Institute of Technology, India
Received: March 27, 2017 | Published: August 3, 2017
Citation: Kamath C. Influence of neurodegenerative disorders on gait dynamics using poincaré symbolic measures. MOJ Gerontol Ger. 2017;1(6):164-173. DOI: 10.15406/mojgg.2017.01.00033
The aim of this study is to evaluate the stride-to-stride fluctuations in walking, to investigate dynamic changes in gait variability, to quantify effects of locomotor neuromuscular system complexity and its manifestation in healthy control and pathological subjects using Poincaré plot (PP) symbolic complexity measures. It is found in the literature that the standard descriptors used with PP, although intuitive, can measure only linear gross variability of the time series, but cannot capture nonlinear changes in the plot. Moreover, these descriptors exhibit limitations where the occurrence of nonlinear behavior may be responsible to distinguish the PP patterns. Hence, in this study, the changes in PP patterns of gait dynamics resulting from nonlinear processes in healthy controls and subjects suffering from neurodegenerative diseases are captured employing two complexity measures, symbolic dynamics entropy (SDEn) and forbidden words (FW). It is found that the values of SDEn and FW are significantly different in healthy and pathological subjects and are suitable to discriminate them.
Keywords: Forbidden words; Human gait; Poincaré plot; Stride interval time series; Symbolic complexity measures; Symbolic dynamic entropy
Human gait refers to the walking style of an individual. Gait is both a voluntary and an automated process and its rhythmic motor behavior is mostly controlled by subcortical locomotor regions of the brain. Recent research evidences show that the dynamical perspective of human gait can be investigated using stride interval time series. The stride interval is a measure of the gait rhythm and is defined as the time interval between the heel strikes of the same foot. Gait analysis is concerned with the measurements and analysis of the chronological vacillations in the stride-to-stride interval. One of the major aims of studying gait patterns is to identify features from the stride time series, which show manifestation of gait disturbances/degeneration due to aging, pathologies, trauma, or neurodegenerative disease. This can help in better understanding of the mechanisms of movement disorders, and also in monitoring the progression of a particular neurodegenerative disease under therapeutic interventions.1,2 The lack of simple and economically viable quantitative gait analysis systems has hindered the clinical use of gait analysis in many areas and hence, there is a greater need for such systems.
The underlying dynamics involved in the locomotion control has been found to be complex and nonlinear.3-5 Analysis of linear statistics does not directly provide any information about complexity and thus may potentially miss useful inherent information. Hence, various tools in the field of nonlinear dynamical systems have been applied to human gait data analysis.6-13 In specific, regularity or complexity measures like, approximate entropy and sample entropy have been tried to study the complexity of gait signal.8,13 While these tools demand the signal to be stationary, threshold dependent symbolic entropy and control entropy, which do not require the signal to be stationary, have also been used to differentiate between trained and untrained runners.14-16 Khandokar et al.17 quantified gait dynamics in the elderly subjects using approximate entropy and Poincare plot (PP) indices of minimum foot clearance variability and found that by monitoring these measures it is possible to improve the gait performance.17 Golinska used PP standard descriptors to distinguish healthy subjects from patients with Parkinson and Huntington diseases.18 Lyapunov exponents, Hurst exponent and Poincare short-term descriptor have been used to evaluate nonlinear and chaotic dynamics of normal, slow, and fast gait signals.19 Poincare indices have also been used from a different perspective where short range correlations of gait variability reflected in these indices have been used to separate healthy and neurodegenerative patients.20 Symbolic entropy has been tried on binary partitioned stride interval series in capturing human gait dynamics and it was found that symbolic entropy can discriminate human gait (1) at normal, slow and fast metronomically paced stressed conditions, and (2) in healthy and pathological states.21,22 However, since underlying dynamics involved in the gait series has been found to be complex and nonlinear, we showed that mere binary partition may not be sufficient in all discriminative applications.23,24 Although a few nonlinear methods have been used earlier to investigate the complexity of human locomotion process, further quantitative studies call for simpler and economically viable clinical computational tools suitable for gait analysis. Poincaré plot (PP) has been extensively used for nonlinear analysis of biomedical signals. This is because the PP can serve as a geometrical visual representation of the time series to demonstrate patterns of the dynamics resulting from nonlinear processes.25-27 However, it has been found in the literature that the standard descriptors used with PP can measure only linear gross variability of the time series, but cannot capture patterns in the plot resulting from underlying nonlinear processes.28,29 As an implication it is also important to understand the limitations of these descriptors where the occurrence of nonlinear behavior may be responsible to distinguish the patterns. This is the first study, where the changes in PP patterns of the gait dynamics resulting from nonlinear processes in healthy and different physiological/pathological states are captured employing two complexity measures, symbolic dynamics entropy (SDEn) and forbidden words (FW), which we call, Poincaré plot symbolic measures or simply, Poincaré symbolic measures. The healthy dynamic stability of the human locomotion system arises from the combination of spontaneous properties interconnected networks and specific feedback mechanisms. The weak connection between the systems or within the system during aging or disease/disorder gets manifested as a decreased complexity in the gait time series. Since SDEn and FW serve as measures of complexity of gait time series, we hypothesize that they provide a direct evaluation of the feedback and connection in the locomotor system. Lower (higher) values of SDEn (FW) measures indicate lower complexity, which is indicative of a less adaptive system and higher (lower) values indicate higher complexity of the gait system, which implies a more adaptive system. In aging and pathological conditions system adaptation diminishes and in turn, complexity of the time series is decreased. In this study, we use left-foot and right-foot gait databases from three major neurodegenerative diseases (Amyotrophic lateral sclerosis (ALS), Huntington disease (HD), and Parkinson disease (PD)). ALS is basically pathology of the motor neurons while HD and PD are due to pathologies of the basal ganglia. The Poincaré symbolic measures are applied to stride interval series of healthy (young and elderly) and pathological subjects suffering from ALS, HD, and PD to characterize their respective gait dynamics. The results have implication for quantifying gait dynamics in these subjects and thus, could be useful for a better understanding of the mechanisms of movement disorders, and also in monitoring the progression of a particular neurodegenerative disease. The prime advantages of SDEn and FW quantifiers are: (1) they can be used to characterize a signal irrespective of the nature of the underlying dynamics, i.e. whether the signal is chaotic, deterministic, or stochastic.30-32 (2) SDEn and FW are found to reflect complexity of the time series. The values of SDEn and FW are significantly different in healthy and pathological subjects and hence, are suitable to discriminate them. (3) SDEn or FW has the advantage of easy implementation and fast computation.
Gait interval records
The stride interval database used in this study is downloaded from the public domain database.33 These databases are contributed by Hausdorff et al.34,35 Goldberger et al.36 which can be downloaded from the physionet.org.37 This database includes stride time series from 13 ALS patients (10 males and 3 females, age mean ± standard deviation: 55.6 ± 12.8 years), 15 PD patients (10 males and 5 females, age mean ± standard deviation: 66.80 ± 10.85 years), 20 HD patients (6 males and 14 females, age mean ± standard deviation: 46.65 ± 12.60 years), and 16 healthy control subjects (2 males and 14 females, age mean ± standard deviation: 39.3 ± 18.5 years). Heights and weights in the four groups were not significantly different. It was confirmed that the patients free from other pathologies which might lead to lower extremity weakness only participated. Over the duration of treatment the medication usage was not changed. It was also confirmed that the healthy subjects were free from visual, respiratory, cardiovascular, or other neurological diseases.
A population based study has shown that 85% of the 60-year-olds still walk normally, 35% of the persons above 70 years exhibit gait disturbances while 80% of the persons above 80 years show prevalent gait disorders.38,39 of course, it is to be well understood that gait disturbances are not an inevitable accompaniment of old age.
The subjects from all the groups were asked to walk at their normal pace up and down a 77 m long hallway for 5 min. To measure the gait rhythm and the timing of the gait cycle, force sensitive insoles were place inside or under subject’s shoes. These sensors produce a measure proportional to the force applied to the ground during movement. The output from the footswitches which corresponds to force signal is sampled at 300 Hz and digitized using an analog-to-digital converter and then stored in a recorder. The recorded data is then analyzed using a validated software that determined initial and end contact times (and also, stride and swing times) of each stride.
Pre-processing the gait data
Before the application of the method of analysis it is necessary to pre-process the gait data. To minimize the start-up effects the samples in the first 20 seconds of the recordings are removed.35 Over the monitoring interval of 5 minutes, each time the subject reached the end of the hall-way the subject had to turn around and continue walking. The strides associated with these turning events are to be treated as outliers and should be removed from the rest of the time series. To remove the outliers we employed the three-sigma-rule,40 which states that 99.7% of the normally distributed probability values lie within the range of (mean ± 3.SD), where SD is the standard deviation. This implies that those samples which lie outside the range (median ± 3.SD) are outliers and hence, can be removed. In the removal process, median value and not mean value of the time series has been used because some outliers possessed large values and will affect the computation of the mean.
Poincaré plot symbolic measures
Poincaré phase plane is a geometrical representation of a time series into a cartesian plane, where the values of each pair of successive elements of the time series define a point in the scatter plot.41,42 In the case of time series analysis each element is plotted against its predecessor in the scatter plot. This procedure provides an indication of the probability of occurrence of one element from its predecessor and allows assessment of short-term dynamic properties of time series variation. Each plots shows (1) element-to-element variability (variation in xn for a given value of xn-1), which is reflected in the scatter of values on the y-axis for a given value on the x-axis and (2) overall variation, which is reflected in absolute extent of dispersion of points along the axes. A conventional Poincaré plot is analyzed quantitatively by evaluating SD2 and SD1, the dispersions of points along the line y = x and the line y = -x+2*Xm, respectively, where Xm represents the mean of the time series. The intersection of these two lines is given by (Xm, Xm). The scatter plot width (SD1) is closely related to short-term variability of the time series; scatter plot length (SD2) is correlated with long-term variability of the time series. The dispersion of the points (variability) in the Poincaré plot is related to complex dynamics of the time series. An increased temporal dispersion indicates an increased variability of the time series.
It has been proved in the literature that the standard descriptors used with Poincaré plot can measure only linear gross variability of the time series, but cannot capture nonlinear changes.28,29 Thus, it is also important to understand the limitations of these descriptors where the occurrence of nonlinear behavior may be a distinguishing feature between the patterns. With this in mind, instead of using SD1 and SD2, in this study, we employ Poincaré plot symbolic measures, namely symbolic dynamics entropy (SDEn) and forbidden words (FW), to capture patterns of the gait dynamics in the PP resulting from nonlinear processes during different physiological/pathological states.
Symbolic dynamics entropy (SDEn)
Symbolic dynamic analysis (SDA) involves transformation of raw time series into a series of discretized symbols, usually employing a coarse-graining technique, which are processed to extract information about the evolving process. Although some microscopic detailed information is lost during transformation, the robust coarse information is preserved, which is sufficient to analyze the dynamics of the time series. The chief advantages of SDA are: (1) It does not make any assumptions about the structure of the underlying dynamical system and can be applied to deterministic or stochastic, linear or nonlinear systems; (2) The efficiency, in terms of computer time and storage, is greatly increased over what it would be for the original data; (3) The method is often less sensitive to measurement noise. SDA is primarily used to characterize and identify temporal patterns in processes that are primarily nonlinear and possibly, chaotic. Important areas of applications of SDA include topological dynamics, complex dynamics, astronomy, geophysics, fluid flow, biology and medicine, chemistry, mechanical systems, data mining, artificial intelligence, information theory, and communication. SDA, though popular, has been tested rarely in gait analysis.
As mentioned above, SDA is based on the concept of coarse-graining the dynamics of a complex system.41-44 In our approach, we adopt a new procedure to recreate the system dynamics in phase space using the time series and its delayed version (τ = 1). In this context, the phase space is divided into eight, six or four sections or partitions as defined by the straight lines ± 3*k SDNN ± 2*k SDNN, and ± 1*k SDNN or ± 2*k SDNN and ± 1*k SDNN, or ± 1*k SDNN, where SDNN corresponds to standard deviation of all the stride intervals and ‘k’ is a real number in the range 0.1 ≤ k ≤ 1.0, which we call resolution constant of the phase plane. This range of ‘k’ is decided on the hypothesis that under pathological conditions the distribution of points in the phase plane is comparatively decreased from those of healthy controls and hence can capture the dynamics better. It is also to be noted that it strongly depends upon the time series under investigation. Each region is then assigned a symbol, creating either eight (0 to 7) symbols or six (0 to 5) symbols or four (0 to 3) symbols depending upon number of partitions. An example of this plot for the case of eight partitions or symbols, with k = 1, is shown in Figure 1. The order in which the regions are visited by the evolving dynamics generates a sequence of symbols. This symbol sequence is then divided into word sequences with a length of two, three, or four symbols. The frequency of occurrence for each word is counted, and a histogram is constructed. The Shannon entropy of this histogram is computed, which we designate as SDEn. The above partition based on SDNN allows SDEn to reflect system complexity rather than variability. As a consequence a decrease in SDEn reflects a decrease in complexity of the spontaneous output of the human locomotion system and vice versa.

Figure 1 An example of Poincaré phase space plot partitioning, with symbols defining the sections, to generate symbolic sequences. SD represents the standard deviation of the time series.
Forbidden word (FW)
Forbidden words (FWs) derived from symbolic word histogram provide a separate measure of system complexity. Those words which seldom or never occur within the distribution of specific length words constitute FWs. This method has been tried for the evaluation of heart rate and blood pressure variability in patients with dilated cardiomyopathy.42 In practice, the words with a probability of occurrence less than 0.001 are treated as FWs. An increased number of FWs reflects a reduced dynamics or increased regularity of the time series and vice versa.
Surrogate data test
If the dynamics that generated the time series is not known or if the time series is noisy, in that case it is essential to investigate whether the amount of nonlinear deterministic dependencies is worth analyzing further or to treat the time series as stochastic. Hence, one of the first steps while applying the nonlinear technique to the data is to investigate if the application of such technique is justified. The main reason behind this rationale is that linear stochastic processes can generate very complicated looking signals and that not all the structures that we observe in the data are likely to be due to nonlinear dynamics of the system. The method of surrogate data test, introduced by Theiler et al.45 has been a popular validating test to address this issue. This test facilitates to find out if the irregularity of the data is most likely due to nonlinear deterministic structure or due to variations in system parameters or due to random inputs to the system.
This section presents a brief sketch of the idea in that connection. The starting point is to create an ensemble of random nondeterministic surrogate data sets that have the same mean, variance, and power spectrum as the original time series, but has no further determinism built in. The measured topological properties of the surrogate data sets are compared with those of the original time series. If, in case, the surrogate data sets and original data yield the same values for the topological properties (within the standard deviation of the surrogate data sets) then the null hypothesis that the original data is random noise cannot be ruled out. On the other hand, if the data under test is generated by a nonlinear process, the value for the topological property would be different from that of the surrogate data, and the null hypothesis that a linear method characterizes the data can be rejected.
The method of computing surrogate data sets with the same mean, variance, and power spectrum as the original time series, but otherwise random is as follows: First find the Fourier transform of the original time series, then randomize the phases, and find the inverse Fourier transform. The resulting time series is that of the surrogate data. More details can be found in.33 However Rapp et al.33 have shown that inappropriately constructed random phase surrogates can lead to false-positive rejections of the surrogate null hypothesis.46 They found that numerical errors in the computation of Fourier transform was the cause for this problem and that Welch windowing the data can eliminate false-positive rejections of the surrogate null hypothesis. Hence, in this study, we made sure that Welch window was introduced before the computation of the Fourier transform of the stride interval segment whose surrogate needs to be found.
Statistical and receiver operating characteristic (ROC) analyses
Kruskal-Wallis tests are used to evaluate the statistical significances among Poincare symbolic measures of the stride time series of the control and neurodegenerative disorder groups. If statistical significances are found then the statistical difference of symbolic measures between different groups can be evaluated using Mann-Whitney or Wilcoxon rank sum tests. These non-parametric tests are used because they make no assumption about the underlying distribution of the data. A p-value ≤ 0.05 is considered statistically significant. In our case, if significant differences between groups are found, then the ability of the nonlinear analysis method to discriminate gait of healthy control and neurodegenerative disorder group is evaluated using receiver operating characteristic (ROC) plots in terms of area under ROC curve (AUC), instead of Wilcoxon rank sum test.47 In general, ROC analysis is useful in evaluating the performance of medical diagnostic tests that classify subjects into one of the two categories, diseased (category-1) or non-diseased (category-2). ROC curves are obtained by plotting sensitivity values (which represent that proportion of the patients identified as category-1) along the y axis against the corresponding (1-specificity) values (which represent the proportion of the controls correctly identified as category-2) for all the available cutoff points along the x axis. Accuracy is a related parameter that quantifies the total number of subjects (both category-1 and category-2) precisely classified. The AUC measures this discrimination, that is, the ability of the test to correctly classify stride of category-2 and category-1 subjects and is regarded as an index of diagnostic accuracy. The optimum threshold is the cut-off point in which the highest accuracy (minimal false negative and false positive results) is obtained. This can be determined from the ROC curve as the closet value to the left top point (corresponding to 100% sensitivity and 100% specificity). An AUC value of 0.5 indicates that the test results are better than those obtained by chance, where as a value of 1.0 indicates a perfectly sensitive and specific test. Through this analysis we measure AUC, sensitivity, specificity, precision, and accuracy of the evaluation.
For the purpose of analysis, all the stride interval records are passed through a preprocessing procedure to eliminate start-up effects and outliers.35 From each gait record the samples recorded in the first 20 seconds were removed to eliminate start-up effects. During the monitoring period of 5 minutes, every time a subject reached the end of hallway, the subject had to turn around and then continue walking. The stride effects associated with these turning events are to be treated as outliers and removed from statistical analysis, because they are different from those recordings made during walking in a straight line along the hallway. The well known ‘three-sigma rule’ is employed to remove such outliers. This rule says that about 99.7% of the normally distributed probability values lie within ± 3*SD distance from the mean. From each stride record, those samples (outliers) whose amplitude is either in excess of 3*SD or falls below 3*SD from the median of the entire stride series are removed. Median value, instead of mean value, is used because some samples (outliers) have large values and can affect the computation of the mean. The preprocessed stride interval data are divided into segments of 400 samples. For each segment, the system dynamics of the time series is recreated in phase space using stride interval series and its lagged version (τ = 1). In our study the recreated phase space is then divided into six partitions defined by ± 1*k SDNN and ± 2*k SDNN, where k is chosen to be 0.26 for the analysis of left-foot stride time series and 0.3 for right-foot stride time series. Each partition is then assigned a symbol, creating six (0 to 5) symbols. The symbol sequence generated by the system dynamics is then divided into word sequences with a length of four symbols. This leads to a possible 1295 word combinations. The frequency of occurrence for each word is counted, and a histogram is constructed. The Shannon entropy of this histogram, SDEn, is computed. FWs are also computed from each histogram. The respective results of the healthy controls, ALS, Huntington, and Parkinson groups are averaged. In this section, we compare the results of Poincaré phase plane, probability distribution of symbolic words (6-symbol, length 4 words), SDEn, and FW for the four groups and for both the left and right stride time series. In order to compare qualitatively or visually the gait patterns of the healthy controls, ALS, Huntington, and Parkinson stride interval series, representative Poincaré phase planes from each group (only for left-foot stride series) are shown in Figures 2(a), 2(b), 3(a), 3(b), respectively. The following observations are made. The shapes of the Poincaré phase planes for the four cases are distinctly different. In the healthy controls, the stride series has its dynamics extended to each of the defined regions of the phase plane, with the dispersion of points along the major axis increased. Under pathological conditions, however, the distribution of points is comparatively increased, particularly in the case of ALS and Huntington diseases. An increased temporal dispersion during pathology implies an increased variability or it can also imply a decreased complex dynamics compared to that of healthy control, as is shown below. The decreased dynamics during pathology gets clearly reflected in their respective probability distributions as (1) an increased probability of some symbolic words (at the cost of others) and (2) an increased number of FWs. A closer inspection of the probability distributions of symbolic words (6-symbol, length 4 words) for healthy controls, ALS, Huntington, and Parkinson groups portrayed (only for left-foot stride series) in Figures 4(a), 4(b), 5(a), 5(b), respectively, reveal these remarks. From these probability distributions we search for significant patterns like most frequently occurring words (as shown by larger peaks) and number of those words which do not or seldom occur (as shown by amplitude smaller than 0.001). It is found that the peaks corresponding to symbolic words (184, 834, 1261, 1102, 1112, 618, 1099) are characteristic words of healthy controls, the peak corresponding to symbolic word (555) is the characteristic word of ALS group, (211, 1086, 1116, 181) are peak characteristic words of Huntington group, and (525, 345) are peak characteristic words of Parkinson group. Each peak characteristic word represents a dominant pattern for that group and corresponds to high dynamics in that time series. The listing of these characteristic words is in the decreasing order of prominence (or dynamics) from left to right. For example, the Huntington group has four significant patterns, which a typical of this group, while the Parkinson group shows two significant patterns and ALS group displays only one significant pattern which are representative of these groups. Another interesting fact is that the peaks corresponding to four symbolic words (556, 741, 561, 736) appear as common peak dominant patterns in all the neurodegenerative disorder groups, whereas they remain suppressed in healthy controls. In other words, they correspond to significant patterns of neurodegenerative disorders. Similarly, the peak significant patterns (184, 834, 1261, 1102, 1112, 618, 1099) in the healthy controls remain suppressed in disease groups. The healthy control group shows least number of FWs = 328 and ALS group shows maximum number of FWs = 795. Huntington and Parkinson groups show intermittent count of FWs 371 and 430, respectively. Since an increased number of FWs reflects a reduced dynamics of the time series, healthy control group exhibits more complex dynamics than the disordered groups, with ALS group affected maximum. The implications of these findings can be quantitatively ascertained by comparing the value of SDEn and FW for the four groups for both the left and right stride time series. Figures 6(a) and 6(b) show respectively, the distribution of SDEn and FW for healthy controls, ALS, Huntington, and Parkinson groups (only for left-foot stride series) using box-whisker plots. The corresponding results of Poincaré phase plane analysis, for both the left and right feet stride time series in each group, are shown in Table 1. All the values are expressed as mean ± SD. Healthy controls show comparatively higher entropy values and neurodegenerative groups indicate lower entropy values. Similarly, healthy controls show comparatively smaller number of forbidden words and neurodegenerative groups indicate larger number of forbidden words. In other words, the SDEn values are decreased, while FW values are increased during pathology compared to healthy control. The least SDEn and maximum FW is found in the case of ALS. This implies that there is loss of complexity in diseased subjects with ALS group affected the maximum and Parkinson the least as seen from Table 1. These inferences imply that the complexity of the stride time series is certainly reduced during pathology. These results are consistent with the previous findings in the literature.48-51
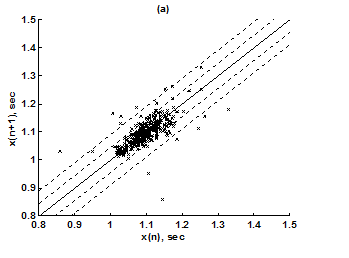
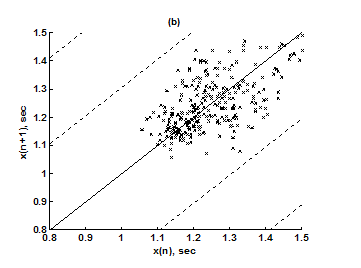
Figure 2 Poincaré phase plane plots for left-foot stride interval series (a) healthy control group and (b) ALS group.

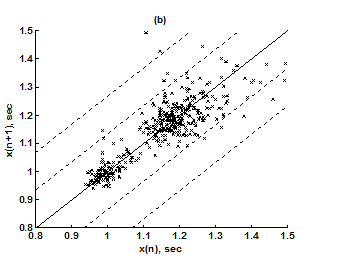
Figure 3 Poincaré phase plane plots for left-foot stride interval series (a) Huntington group and (b) Parkinson group.
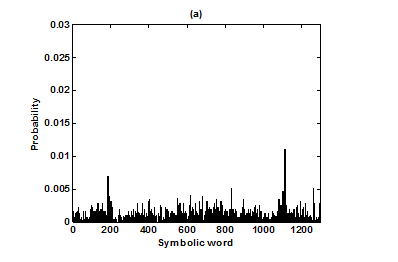
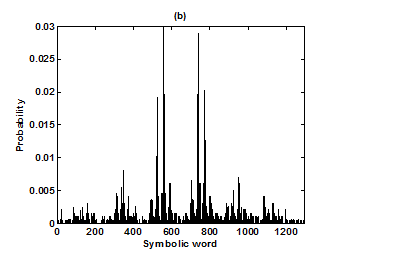
Figure 4 Probability distributions of symbolic words (6-symbol, length 4 words) (a) healthy control group and (b) ALS group.
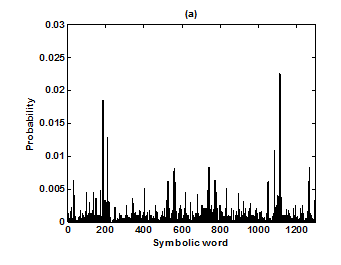
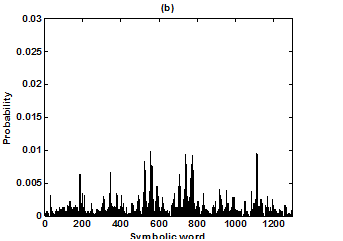
Figure 5 Probability distributions of symbolic words (6-symbol, length 4 words) (a) Huntington group and (b) Parkinson group.
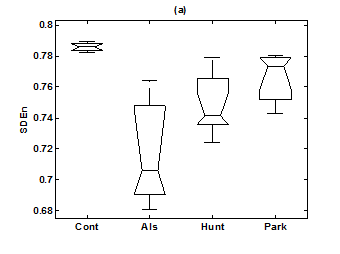

Figure 6 Box-whisker plots of (a) SDEn (6-symbol, length 4 words) in healthy control group, ALS group, Huntington group, and Parkinson group. (b) FW (6-symbol, length 4 words) in healthy control group, ALS group, Huntington group, and Parkinson group.
To test the presence of deterministic structures in the stride time series and thereby ascertain appropriateness of the application of our nonlinear approach, we carried out surrogate data analysis. Fifteen surrogate series for each of the original series are constructed as explained in the above section. The mean of surrogate SDEn and FW values for the fifteen surrogate series are computed and compared with that of the original series. Table 2 shows results of surrogate data analysis of symbolic measures derived from both the left and right stride interval series of healthy controls, ALS, Huntington, and Parkinson groups. The values are expressed as mean ± SD. In the control group, SDEn and FW of the original left stride interval series are 0.785±0.002 and 989.5±3.75, respectively, and those of the surrogate series are 0.386±0.006 and 1276±4.761, respectively, while in the ALS group, SDEn and FW of the original left gait series are 0.719±0.023 and 1060±22.80, respectively and those of the surrogate series are 0.585±0.076 and 1172±43.38, respectively. In the Huntington group, SDEn and FW of the original left gait interval series are 0.745±0.010 and 1039±8.12, respectively, and those of the surrogate series are 0.699±0.068 and 1090±65.07, respectively, while in the Parkinson group, SDEn and FW of the original left stride time series are 0.770±0.011 and 1011±15.69, respectively and those of the surrogate series are 0.620±0.051 and 1158±38.81, respectively. The results for the right stride series are similar to those of the left side, not only in the control group but also in other groups, though not necessary. This is because in pathology both the sides are usually not affected equally. The statistical significance of the differences between symbolic measures of the original and surrogate series of healthy controls, ALS, Huntington, and Parkinson groups investigated using Mann-Whitney rank sum tests is also specified in the table. Interestingly, comparison between the respective SDEn and FW of the stride original and surrogate series, reveals highly significant differences (p-value < 0.005) implying that the relevant patterns in the original time series cannot be considered present by chance. This indicates that the fluctuations observed in the original time series are not randomly derived, instead may reflect deterministic processes due to neuromuscular system. This also establishes an intrinsic relationship of the neuromuscular control of the locomotor system with symbolic measures of the stride interval series. In other words, this also substantiates the appropriateness of the application of the Poincaré symbolic measures to the analysis of stride interval series.
Group |
Poincaré symbolic measure |
|
||
|
Left SDEN |
Left FW |
Right SDEN |
Right FW |
Control |
0.785±0.002 |
989.5±3.75 |
0.781±0.006 |
996.5±9.88 |
ALS |
0.719±0.023 |
1060±22.80 |
0.674±0.038 |
1087±11.46 |
Huntington |
0.745±0.010 |
1039±8.12 |
0.750±0.011 |
1035±12.36 |
Parkinson |
0.770±0.011 |
1011±15.69 |
0.772±0.009 |
1007±10.06 |
Table 1 Results of Poincaré symbolic analysis (6-symbol, length 4 words) of control and neurodegenerative disorders for left and right gait time series. All values are expressed as mean ± SD
Group |
Symbolic measure |
Original |
Surrogate |
Mann-Whitney rank sum test p-value |
Control |
Left SDEn |
0.785±0.002 |
0.386±0.006 |
1.5540x10-004 |
Left FW |
989.5±3.75 |
1276±4.761 |
0.0025 |
|
Right SDEn |
0.781±0.006 |
0.389±0.007 |
1.5540x10-004 |
|
Right FW |
996.5±9.88 |
1274±5.94 |
0.0025 |
|
ALS |
Left SDEn |
0.719±0.023 |
0.585±0.076 |
0.0015 |
Left FW |
1060±22.80 |
1172±43.38 |
3.1080x10-04 |
|
Right SDEn |
0.674±0.038 |
0.602±0.063 |
0.0015 |
|
Right FW |
1087±11.46 |
1166±48.05 |
1.5540x 10-04 |
|
Huntington |
Left SDEn |
0.745±0.010 |
0.699±0.068 |
1.5540x10-04 |
Left FW |
1039±8.12 |
1090±65.07 |
0.0031 |
|
Right SDEn |
0.750±0.011 |
0.708±0.061 |
1.5540x10-04 |
|
Right FW |
1035±12.36 |
1083±61.55 |
0.0031 |
|
Parkinson |
Left SDEn |
0.770±0.011 |
0.620±0.051 |
0.0028 |
Left FW |
1011±15.69 |
1158±38.81 |
3.1080x10-04 |
|
Right SDEn |
0.772±0.009 |
0.595±0.044 |
0.0028 |
|
|
Right FW |
1007±10.06 |
1176±25.03 |
1.5540x10-04 |
Table 2 Results of surrogate data analysis of Poincaré symbolic measures (6-symbol, length 4 words) derived from control and neurodegenerative disorder left and right gait time series. All symbolic measures are expressed as mean ± SD
Kruskal-Wallis tests are performed to evaluate the statistical differences among the symbolic measures of four groups. The test detected significant group differences (in the case of SDEn: p = 0.0003 and chi-square > 18.68 for left-foot stride analysis while p = 0.0003 and chi-square > 18.59 for right-foot stride analysis and in the case of FW: p = 0.0003 and chi-square > 17.84 for left-foot stride analysis while p = 0.0002 and chi-square > 19.27 for right-foot stride analysis). The tests show highly significant statistical differences (p < 0.0005) among the symbolic measures of four groups. Now, to show the importance of the symbolic measures we evaluate the diagnostic capacity of SDEn and FW in different discriminations using ROC analysis. The group results of evaluation of diagnostic parameters of the SDEn and FW in separating neurodegenerative disorder and control groups for the left-foot and right-foot stride time series are summarized in Tables 3 & 4, respectively. It is found that both the symbolic measures perform very well in their diagnostic ability i.e., in separating healthy control subjects from those suffering from ALS, Parkinson, and Huntington diseases. ALS patients can be readily separated from HD and PD patients. However, HD and PD patients cannot be easily separated. This is because both HD and PD disorders occur due to impairment of basal ganglia and the gait patterns of HD and PD patients are similar.51
Comparison between |
Symbolic measure |
AUC |
Average sensitivity% |
Average specificity% |
Average precision% |
Average accuracy% |
Control and ALS |
SDEn |
1 |
100 |
100 |
100 |
100 |
FW |
1 |
100 |
100 |
100 |
100 |
|
Control and |
SDEn |
0.975 |
100 |
87.5 |
90.9 |
94.4 |
Huntington |
FW |
0.975 |
100 |
87.5 |
90.9 |
94.4 |
Control and |
SDEn |
0.9375 |
100 |
87.5 |
88.9 |
93.8 |
Parkinson |
FW |
0.9375 |
100 |
87.5 |
100 |
93.8 |
Huntington and ALS |
SDEn |
0.76 |
60 |
100 |
83.3 |
86.7 |
FW |
0.76 |
60 |
100 |
100 |
86.7 |
|
Parkinson and |
SDEn |
0.7125 |
70 |
75 |
77.8 |
72.2 |
Huntington |
FW |
0.6563 |
68 |
72 |
75.2 |
71.5 |
ALS and |
SDEn |
0.85 |
87.5 |
80 |
87.5 |
84.6 |
Parkinson |
FW |
0.8 |
75 |
80 |
66.7 |
76.9 |
Table 3 Descriptive results of ROC analysis using Poincaré symbolic measures (6-symbol, length 4 words) derived from control and neurodegenerative disorder left-foot gait time series
Comparison between |
Symbolic measure |
AUC |
Average sensitivity% |
Average specificity% |
Average precision% |
Average accuracy% |
Control and ALS |
SDEN |
1 |
100 |
100 |
100 |
100 |
FW |
1 |
100 |
100 |
100 |
100 |
|
Control and |
SDEN |
0.9375 |
90 |
87.5 |
90 |
88.9 |
Huntington |
FW |
0.9375 |
100 |
87.5 |
90.9 |
94.4 |
Control and |
SDEN |
0.8438 |
75 |
75 |
75 |
75 |
Parkinson |
FW |
0.8906 |
87.5 |
87.5 |
87.5 |
87.5 |
Huntington and ALS |
SDEN |
0.9 |
100 |
90 |
83.3 |
93.3 |
FW |
0.9 |
100 |
90 |
83.3 |
93.3 |
|
Parkinson and |
SDEN |
0.675 |
68 |
72 |
75.2 |
71.5 |
Huntington |
FW |
0.681 |
71 |
74 |
76.5 |
72.5 |
ALS and |
SDEN |
0.975 |
87.5 |
100 |
83.3 |
92.3 |
Parkinson |
FW |
0.975 |
87.5 |
100 |
83.3 |
92.3 |
Table 4 Descriptive results of ROC analysis using Poincaré symbolic measures (6-symbol, length 4 words) derived from control and neurodegenerative disorder right-foot gait time series
One limitation of the current study is the relatively small sample size, which did not permit best statistical comparisons. Factors like high variance, age differences, and differing male-to-female ratios between groups will have an impact on the results when statistical analyses are carried out on small sample sizes. It has been shown in the literature that the age of the healthy subject does affect the gait.52 In our case, the data size of the control group (two males and fourteen females) being small, it is not possible to arrive at a suitable correlation between age and SDEn or FW. This is because with the smaller sample sizes our estimates of the correlation are going to become extremely noisy. With increasing sample size the correlation coefficient will collect more information about the linear correlation provided by the data. Further, the p-value is a bad guidance because in small samples the confidence intervals turn out to be very huge. Furthermore, correlation coefficient is rather susceptible to outliers, which is even more serious in small samples. To circumvent all these problems we employ Fisher's exact test which is more reliable for small sample sizes. Fisher's exact test has no formal test statistic and no critical value. Also, Fisher's exact test does not produce a confidence interval. This test only provides a p-value. Fisher's exact test is a statistical test used to resolve non-random associations between two categorical variables, and like other tests of independence, assumes that the individual observations are independent. The null hypothesis is that the relative proportions of one variable are independent of the second variable; in other words, the proportions at one variable are the same for different values of the second variable. The hypogeometric distribution is used to calculate the probability of getting the observed data and this is an exact calculation of the probability; unlike most statistical tests, there is no intermediate step of calculating a test statistic whose probability is approximately known. Fisher's exact test is more accurate than the chi-squared test or G-test of independence when the expected numbers are small (when the total sample size is less than 100). To explore the effect of age on the gait, we perform experiments where SDEn or FW for both male and female subjects (all the 16 subjects from the healthy control group) of different/increasing age are compared using Fisher's exact test. The results show a statistically significant association through p=3.330x10-06 for the case of SDEn and a significant association through p=6.660x10-06 for the case of FW. This shows that age effect does exist. This is also in agreement with the earlier study.52 However, it has been shown in the literature that the effect of gender on usual gait patterns is considerably small.52 To investigate the influence of gender on the gait, we perform experiments where SDEn or FW is compared for both male and female control subjects of almost the same age. First, we apply Fisher’s exact test to six subjects (one male and five females) of almost the same age (around 22 years), from the healthy control group. The test statistics show a weak association for the case of SDEn through p=0.0167 and also a weak association for the case of FW through p=0.0167. Next, we apply Fisher’s exact test to four subjects (one male and three females) of almost the same age (around 74 years). The results again show a weak association for the case of SDEn through p=0.0417 and also a weak association for the case of FW through p=0.0417. This means that one can readily ignore gender effect on gait in comparison with age effect on gait. This outcome is in concurrence with the previous study [52]. Thus, in general, the gender does not severely influence the gait results unlike the age of the subject which does influence the results to some extent. Though the effect of age on gait is complex, the effect of neurodegenerative disorders considerably predominates over the aging effects as is evident from Table 1. Nevertheless, the results of this study provide sufficient evidence to warrant the execution of larger studies that can provide more statistically robust confirmation of the application of these methods as reliable measures of different types of locomotion.
The following are the key findings of this research: Under pathological conditions the dispersion of points in the Poincaré phase plane is comparatively increased compared to that of healthy controls. This implies an increased variability under pathological conditions. Surrogate analysis of the stride interval series indicates that the fluctuations observed in the original gait time series are not randomly derived, instead may reflect deterministic processes due to neuromuscular control of the locomotor system. This also establishes an intrinsic relationship of the neuromuscular control of the locomotor system with symbolic measures, SDEn and FW, of the stride interval series. Both the complexity measures, SDEn and FW, showed that spontaneous output of human locomotion system in healthy controls is more complex. The SDEn values are decreased, while FW values are increased during pathology compared to those in healthy control. These inferences imply that the neuromuscular system complexity of the stride time series is reduced during pathology.
In this paper, we presented two computationally simple, but efficient measures to evaluate dynamic changes of stride time intervals reflected in the PP. Both the complexity measures, SDEn and FW, showed that spontaneous output of human locomotion system in healthy controls is more complex than those in neurodegenerative disordered subjects. Compared to normal, subjects with Parkinson disease showed a little lowering of complex dynamics in the stride interval series, those with Huntington disorder showed a further decrease in complexity, while patients with ALS exhibited maximum decrease in complex dynamics of the gait series. These results are notable because the proposed technique probes a dynamic property not identified by other statistics and have strong implications for quantifying and modeling gait control in normal and pathological conditions, thus could be useful for a better understanding of the mechanisms of movement disorders, and also has high potential to measure responses to therapeutic interventions in monitoring of the progression of a particular neurodegenerative disease.
The author, who is also the corresponding author, is the sole contributor to this work.
'The author(s) declare that they have no competing interests'.

©2017 Kamath. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.