Lateral earth pressure for smooth retaining wall with inclined backfill has been obtained by Rankine¹ and is used for many years without being questioned. Some interesting problems associated with the classical Rankine’s earth pressure with sloping ground which should be noted for engineering design is investigated in the present work. The Rankine’s active and passive pressure coefficients can give unreasonable behavior with different ground sloping angle. From the results of analysis, it can be concluded that the Rankine’s equations are unnecessarily conservative for sloping ground condition. Based on the rigorous solution of this problem by the slip line method (method of characteristic), it is also demonstrated that the assumption used in the original Rankine’s equation is not appropriate.

Keywords: lateral earth pressure, rankine, coulomb, slip line

Lateral earth pressure has been a very important civil engineering problem, both in terms of theoretical and practical significance. There are several methods of analysis of this problem: lower bound approach, upper bound approach, limit analysis and plasticity based approach. It is generally accepted that the plasticity based approach yields the most accurate results at the expense of complicated numerical computation. The method of characteristic (plasticity based approach) considers the yield and equilibrium of a soil mass controlled by the Mohr-Coulomb’s criteria, and the occurrence of slip plane under ultimate limit state of soil mass has supported the use of this method in many geotechnical problems. A typical slip line system is shown in Figure 1, and the equations are governed by the α & β characteristic equations as given by Sokolovskii.²

$\begin{array}{l}\alpha characteristic:-\frac{\partial p}{\partial S_{\alpha }}\sin 2\mu +2R\frac{\partial \theta }{\partial S_{\alpha }}+\gamma [\sin (\alpha +2\mu )\frac{\partial y}{\partial S_{\alpha }}+\cos (\alpha +2\mu )\frac{\partial x}{\partial S_{\alpha }}]=0\text{ (1)}\\ \beta characteristic:\frac{\partial p}{\partial S_{\beta }}\sin 2\mu +2R\frac{\partial \theta }{\partial S_{\beta }}+\gamma [\sin (\alpha -2\mu )\frac{\partial y}{\partial S_{\beta }}+\cos (\alpha -2\mu )\frac{\partial x}{\partial S_{\beta }}]=0\text{ (2)}\end{array}$

Figure 1 α and β lines in slip line solution.

γ = unit weight of soil, $\mu =\left(\pi /4-\varphi /2\right),\varphi$ is the angle of shearing resistance of soil, θ is the angle between the direction of principal stress and y-axis, Sα and Sβ are the arc length along the α & β lines, α is the angle between the direction of the body force and the vertical direction (y-axis), p and R are the mean stress and radius of Mohr circle at state of failure defined by

By solving the slip line equations as given by equation (1) & (2), solutions too many geotechnical problems have been developed and used. Detailed treatment about the solutions of equation (1) & (2) are given by Sokolovskii & Russell,^2-10 and others. A detailed and updated treatment of this problem has also been provided by Cheng et al.¹¹

Lateral earth pressure is a classical soil mechanics problem, and the lateral earth pressure coefficients by Rankine¹ are well known to engineers Bowles &Terzaghi et al.^12-14 For a retaining wall with a backfill inclined at angle β as shown in Figure 2,¹¹ assumed that (1) the retaining wall is a vertical wall with a wall friction equal toβ, (2) the stress acting on the vertical face CD is parallel to the backfill ground angle or θ=β, (3) the total force acting on the bottom face DE which is parallel to the ground line AG is vertical in direction, (4) the backfill soil cohesion c is 0. Based on the above four assumptions, Rankine obtained the active and passive earth pressure coefficients (Ka and Kp) as Clayton.¹⁵

$K_a=\frac{\cos \beta -\sqrt{{\cos }^2\beta -{\cos }^2\phi }}{\cos \beta +\sqrt{{\cos }^2\beta -{\cos }^2\phi }}$ (4)

$K_p=\frac{\cos \beta +\sqrt{{\cos }^2\beta -{\cos }^2\phi }}{\cos \beta -\sqrt{{\cos }^2\beta -{\cos }^2\phi }}$ (5)

Figure 2 Rankine active or passive pressure with inclined backfill.

Since backfill soil cohesion is not considered in the original Rankine’s equations, equation (4) & (5) cannot be applied for soil with cohesion strength. The equations for lateral earth pressure are further extended by Gnanapragasam¹⁶ using Rankine’s assumptions (1) ~ (3). The original Rankine’s equations will be the special case of the equations by¹⁶ by setting c=0. The use of equation (4) & (5) have also been adopted in the retaining wall design code (Geoguide 1 in Hong Kong), the famous textbook by Clayton et al.¹⁷ and others. In view of that, the accuracy of these two equations becomes important and critical towards a realistic and economical design of retaining structures.

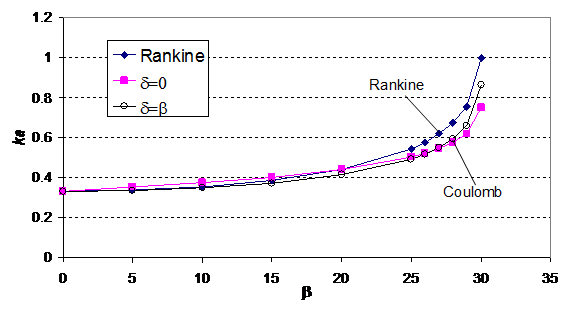
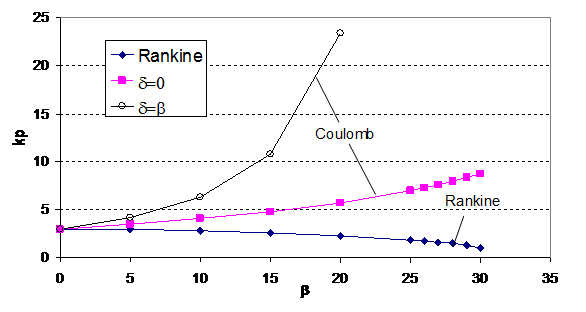
For a retaining wall with a backfill inclined at angle β as shown in Figure 2, the values of Ka and Kp from equations (4) & (5) are independent of $\varphi$ and are equal to 1.0 when β= $\varphi$ . These two coefficients are equal and are independent of the friction angle. These results are obviously not acceptable, in particular for equation (5) which decreases with increasing β and is physically unacceptable. The values of Ka and Kp are independent of the strength of soil as predicted from equation (4) & (5) for the case of β= $\varphi$ and this will contradict the physical observation soil with a high friction angle is physically stable while soil with a low friction angle is not. In the present paper, the basic assumptions in Rankine’s equations will be examined by comparisons with the slip line method. Besides the slip line method, Coulomb’s method which is well known to be not good for passive pressure but acceptable for active pressure determination will also be compared with the Rankine’s equations. Even though the values of Coulomb’s passive coefficient is not correct, the general trend of Kp with increasing β is more reasonable than the original Rankine’s passive pressure coefficient.

Studies for Rankines active earth pressure equation

¹¹Assumed that the direction of active earth pressure is parallel to the backfill ground AG but has not clearly specified the wall friction angle δ. This is based on the assumption that the ground pine AG extends to infinity and every section (CD) is similar to the other section (EF). For the stress state along AG and far away from the wall, the assumption by Rankine is correct. For any section close to the retaining wall, it is actually different from a section far away from the retaining wall as the stress state is largely controlled by the condition of the retaining wall. In this respect, the basic assumption of “same internal stress at every section” by Rankine will not be correct for the section close to the retaining wall, which is equivalent to that the Rankine’s lateral pressure may not be correct under this case. For the case where AG is horizontal and the wall friction is zero, the stress along AB will be equal to that along CD or EF, so the Rankine’s coefficient will be correct under this case.

Clayton & Gnanapragasam^16,17 have suggested that Rankine’s assumption has implicitly implied that is equal to which is however not clearly mentioned in Rankine’s original study. In fact, the wall friction angle is controlled by the roughness of the retaining wall as well as the soil type but is not necessarily controlled by β which is a major limitation of equation (4) & (5). More importantly, it will be demonstrated that even if the wall friction angle is β, the Rankine’s coefficients are still not correct. The active earth pressure values as determined from Rankine’s equation, Coulomb’s equation¹⁸ and method of characteristic are given in Table 1. The lateral earth pressure coefficients are determined by the method by³ and the values have been checked to be similar to those by Kerisel & Absi.¹⁹ When β is close to, $\phi$ there are great differences between the three results. Rankine’s Ka value tends to 1.0 and is independent of the internal friction angle! On the other hand, the values by Coulomb’s equation or slip line solution are close. Coulomb’s active pressure is hence a good solution and it has been used frequently for engineering design. The slip line solutions by Cheng³ are practically equal to the values as given by.¹⁹ As active pressure coefficient is less sensitive to wall friction δ but is more sensitive to ground slope angle β, it appears that equation (4) can be applied without major problem if β is less than 2/3 $\phi$ . Beyond that, equation (4) appears to be unnecessary conservative and is not suggested to be used for design purpose.

Theoretically, the direction of active earth pressure close to the retaining wall should be determined by the wall fiction instead of the backfill slope angle. Consider the case of wall fiction angle δ=0°, φ=30° and β=10° (unit weight of soil assumed as 20 kN/m3), the direction of the active earth pressure with different D/H ratio see Figure 2 from slip line analysis is shown in Figure 3. The active earth pressure at the back of the wall is horizontal as the wall friction is 0 and is not parallel to ground surface as assumed by Rankine.¹ If the point under interest moves away from the wall along AG, the direction of active earth pressure varies with distance D in the neighborhood of the retaining wall at a small D/H value. When distance D is far enough, the direction of active earth pressure will be constant and is parallel to backfill ground line which is equal to the original Rankine’s assumption.²⁰ The direction of active earth pressure as obtained is clearly different from Rankine’s assumption at $\delta =0^{\circ }$ . In Figure 4, the direction of the minimum principal stress along ground line AG is constant and varies with β. Figure 4 demonstrates that the angle between the minimum principal stress and backfill ground line AG is not equal to the inclined angle, and this has proved that the direction of the minimum principal stress is not parallel to the ground line AG.

Figure 3 Direction of active earth pressure with horizontal for different D/H along AG ( $\phi ={30}^{\circ }$ , $\beta ={10}^{\circ }$ , $\delta =0^{\circ }$ and β).

Figure 4 Direction of the minimum principal with respect to horizontal for different inclined angle β along AG.( $\phi ={30}^{\circ }$ $\delta =0^{\circ }$ )

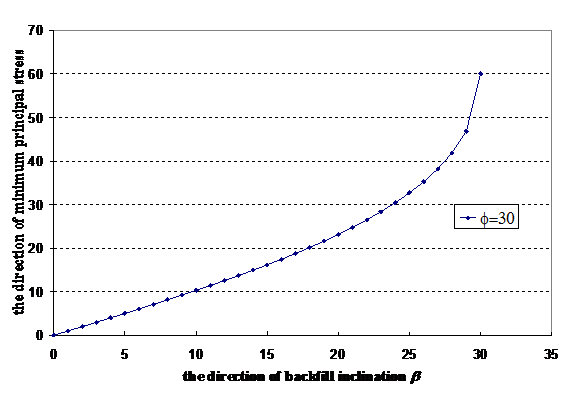
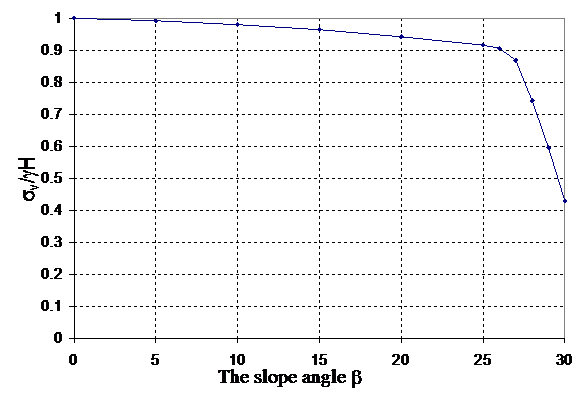
If δ=β, Rankine’s assumption on the direction of the lateral earth pressure is correct which is shown by θ=β at all locations in Figure 3. Equation (4) is however still not acceptable as Ka=1.0 and is independent ofφ, though the horizontal component of the active pressure is still dependent on $\varphi /\beta$ . Besides the assumption on the direction of active earth pressure, the vertical stress σv acting on face DE along line AB (see Figure 2) is assumed to be equal to γH by¹¹ or.²¹ For any section which is very close to the retaining wall, from slip line solution or even simple reasoning, σv will not be equal to γH if δ is not 0 (should not mix up with normal stresses acting along DE which isγHcos2β . For example, when $\phi ={30}^{\circ }$ , $\delta =0^{\circ }$ and $\delta ={\beta }^{\circ }$ , the active pressure by Rankine, Coulomb and slip line method are shown in Figure 5 & 6. Coulomb’s method has implicitly (not explicitly) implied that σv acting on face DE is different from γH by the force equilibrium relation even though stress is not directly considered in Coulomb’s equation. From Figure 7, we can see that σv from slip line method is less than γH because of the effect of wall friction. Since the vertical stress σv is smaller than γH, it is not surprising that Rankine’s equation will be different from slip line solution even when δ=β, and its values are largest among the three methods as discussed in the present study.²² It is interesting to note that σv is slightly smaller than γH when δ is less than 2/3 However, σv drops significantly with δ when δ > 2/3 $\phi$ which is a major limitation of the Rankine’s assumption. The effect of σv appears to be a very critical factor for the problem of Rankine’s equation, and the original Rankine’s equation has neglected the effect of the wall friction in equation (4). In conclusion, equation (4) has different fundamental problems for the cases of =0 and =β, and it is not correct in the basic assumptions. In conclusion, both Coulomb’ method and slip line solution are applicable for general active pressure determination while Rankine’s active pressure is acceptable only for the case δ < 2/3 $\phi$ .

Figure 5 Coefficient of active earth pressure with different backfill inclined angle (Rankine’s results with Coulomb results).

Figure 6 Coefficient of active earth pressure with different backfill inclined angle (Rankine’s results with slip line results).

Figure 7 ${\sigma }_v/\gamma H$ for different slope angle $\beta$ for active pressure slip line solution when δ=β (adjacent to the retaining wall).

Studies for Rankine’s passive earth pressure equation

The passive earth pressure values calculated from the Rankine’s equation, Coulomb’s equation and the slip line method are given in Table 2. The passive earth pressure coefficients from Coulomb’s equation and slip line method are much larger than the Rankine’s values, particularly when δ is large. When δ is large, Coulomb’s coefficients are particularly high which is well known to be incorrect because of the assumption of straight line failure surface. Rankine’s passive pressure coefficient as given by equation (5) decreases with β and tends to 1.0 (independent of $\phi$ ) is also an unreasonable prediction. In Table 2, Rankine’s passive pressure coefficients decrease with increasing β and this is obviously wrong. The reason for such major discrepancy is that Rankine assumed the direction of the passive earth pressure to be parallel to the backfill ground line and this is equal to δ=-β. In fact, the direction of passive earth pressure cannot be negative as the sign of friction angle is controlled by the failure mechanism. Consider the case of φ=30° and β=10° as shown in Figure 8, it can be seen that the direction of the passive earth pressure at the back of wall is 0 (δ=0) or –β (δ=β) and tends to the Rankine’s original assumption at a distance far behind the wall which is similar to the Rankine’s active condition. For region close to the retaining wall, Rankine’s assumption is not applicable. It is shown from Figure 8 that the angle between the maximum principal stress and backfill ground line varied with distance D away from the retaining wall. From Figure 9, the angle between the maximum principal stress and the backfill ground line AG is not equal to the slope angle of the ground line, and this has proved that the direction of the maximum principal stress is not parallel to the ground line.

Figure 8 Direction of passive earth pressure with horizontal with different D/H ( $\phi ={30}^{\circ }$ , $\beta ={10}^{\circ }$ $\delta =0^{\circ }$ and β.).

Figure 9 Direction of passive earth pressure with horizontal line for different β along AG ( $\phi ={30}^{\circ }$ , $\delta =0^{\circ }$ )

For the vertical stress σv as shown in Figure 10, it increases significantly with δ and this is the main reason why passive pressure is large (σv = γH by Rankine and is true for δ=0 only). Coulomb’s passive pressure tends to a very big number when δ is high and is well known to be incorrect as a straight line failure surface has been used in the formulation. Based on the results in Figure 11 and 12, it can be concluded that Coulomb’s method is suitable only δ and β are small while slip line solution is a more reasonable solution. Rankine’s passive pressure is acceptable only for the case of δ=β=0.

Figure 10 Coefficient of passive earth pressure with different backfill inclined angle (Rankine’s results with Coulomb results).

Figure 11 Coefficient of active earth pressure with different backfill inclined angle (Rankine’s results with slip line results).

Figure 12 ${\sigma }_v/\gamma H$ with different slope angle $\beta$ for passive pressure slip line solution when δ=β.

In this paper, the slip line method has been used to study the Rankine’s earth pressure coefficients with inclined backfill. The use of this plasticity based method can overcome the basic limitations in the Rankine’s original assumptions on lateral earth pressure. From the above analysis, it can be concluded as follow:

The differences between the Rankine’s active earth pressure, Coulomb’s earth pressure and the slip line solutions are small for β < 2/3 $\varphi$ . When β > 2/3 $\varphi$ , the differences between the three values are relatively major and the Rankine’s active earth pressure is conservative for design. The two major problems of the Rankine’s active pressure is that the direction of active pressure is not parallel to backfill ground line for δ=0 and the base vertical stress is not equal to γH when δ=β (close to the wall). In fact, the direction of the active earth pressure should be determined by the wall friction which in controlled by the soil and the retaining wall and is practically independent of the slope angle of backfill. Active earth pressure is generally not sensitive to wall friction and it is found that Rankine’s active earth pressure equation should not adopted for δ>2/3 $\varphi$ .

Rankine’s passive earth pressure value is good only for horizontal backfill. Other than this condition, equation (5) is a very poor solution to the passive pressure. Rankine’s passive pressure decreases with slope angle of backfill ground which is obviously wrong. Furthermore, Rankine’s passive earth pressure value is much smaller than Coulomb’s passive earth pressure value and slip line passive earth pressure. The two major problems of the Rankine’s active pressure is that the direction of active pressure is not parallel to backfill ground line for δ=0 and the base stress is not equal to γH when δ=β. In fact, Rankine’s passive pressure is equivalent to δ=-β and this is physically unacceptable. The direction of passive earth pressure is parallel to the ground line only at distance far away from the retaining wall for δ=0 or δ=β. The problem with Rankine’s passive pressure is major and is not recommended for use except for level backfill.

The present project is funded from Research Grants Council through the project PolyU 513808 and research project “Evaluation of Different Types of Soil Nails for Slopes with Poor Access Mechanism” with account YBBY by PolyU.

The author declares no conflict of interest.

1. Sokolovskii VV. Statics of Granular Media. USA: Pergamon Press; 1965.
2. Booker JR, Zheng X. Modeling in Geomechanics. USA: John Wiley; 2000.
3. Cheng YM. Seismic lateral earth pressure coefficients for c–φ by slip line method. Computers and Geotechnics. 2003;30(8):661–670.
4. Cheng YM, Au SK. Slip line solution of bearing capsacity problems with inclined ground. Canadian Geotechnical Journal. 2005;42:1232–1241.
5. Liu FQ, Wang JH, Zhang LL. Axis–symmetric active earth pressure obtained by the slip line method with a general tangential stress coefficient. Computer and Geotechnics. 2009;36(1–2):352–358.
6. Liu FQ. Lateral earth pressures acting on circular retaining walls. Int J Geomech. 2014;14(3):04014002.
7. Peng MX, Chen J. Slip–line solution to active earth pressure on retaining walls. Geotechnique. 2013;63(12):1008–1019.
8. Thanh Vo, Russell R. Slip line theory applied to a retaining wall–unsaturated soil interaction problem. Computers and Geotechnics. 2014;55(1):416–428.
9. Thanh Vo, Russell R. Bearing capacity of strip footings on unsaturated soils by the slip line theory. Computers and Geotechnics. 2016;74(1):122–131.
10. Cheng YM, Wong H, Chin L, et al. Frontiers in Civil Engineering. Stability analysis of geotechnical structures. USA: Benjamin Press; 2016.
11. Macquorn Rankine WJ. On the stability of loose earth. Philosophical Transations. 1857;147:9–27
12. Bowles Joseph E. Foundation Analysis and Design. 4th ed. USA: McGraw Hill; 1996.
13. Das BM. Principle of Foundation Engineering. Boston: PWS Publishing; 1999.
14. Karl Terzaghi Ralph B Peck, Golamreza Mesri. Soil Mechanics in Engineering Practice. 3rd ed. USA: Wiley; 1996.
15. GEO. Guide to retaining wall design. Hong Kong: GEO Guide 1 Hong Kong Government; 1993.
16. Gnanapragasam N. Active earth pressure in cohesive soils with an inclined ground surface. Canadian Geotechnical Journal. 2000;37(1):171–177.
17. Chris RI Clayton, Rick I Woods, Andrew J Bond, et al. Earth pressure and earth retaining structure. 3rd ed. CRC press; 2013. 608 p.
18. Coulomb CA. Su rune application des regles de maximis et minimis a quelques problemes de statique relatifs a l’ architecture. CRC press; 1776. 7:343–382.
19. Absi E, Kerisel J. Active and Passive Earth Pressure tables. CRC press; 1990. 234 p.
20. Graham J, Andrew M, Shields DH. Stress Characteristics for Shallow Footing in Cohesion less Slopes. Canadian Geotechnical Journal. 1988;25(2):238–249.
21. Shukla S, Gupta S, Sivakugan N. Active earth pressure on retaining wall for c–φ soil backfill under seismic loading condition. J Geotech Geoenviron Eng. 2009;135(5):690–696.
22. Chen WF, Liu XL. Limit Analysis and Soil Plasticity. Elsevier; 1975. 52 p.