A person's intelligence is shaped by genes and later by environmental conditions. This paper explores the question: Is there an influence of the fluctuations of the planetary gravitational field on the development of the human brain?

The oscillations of the planetary gravitational field lead to higher oscillations, to higher harmonics, in material structures. A correlation function, which can describe nonlinear correlations and which has already been used with success in triggering earthquakes, is applied in this investigation to the development of the highly complex human brain.

At the time of birth, it is not only the genes that determine a person's intelligence. The research also suggests that fluctuations in the planetary gravitational field also have an influence. The results suggest that there is something like a "quality of time" in the temporal environment of birth that has a stimulating effect on the development of the brain.

Galaxies in space, planetary systems, clouds, geological formations, plants and animals, human societies, our nervous system, quantum physical systems form simple and also complex structures on scales of different sizes. Possibly describe the formation of such structures from a model of more or less strongly coupled, oscillating subsystems.

One such oscillating subsystem is the planetary system. Sun and moon are weakly coupled with the system of oceans and make them oscillate even in ebb and flow. Cause and effect are related in a relatively simple and proportional way. But are there also non-linear relationships in which cause and effect are not directly proportional to each other?

One hypothesis underlying such investigations is the assumption that nature, but also society, can be modeled by nonlinear coupled oscillators on many scales. Starting with quantum fluctuations and ending with the "great cosmic rhythms of our solar system"¹ the complex human organism is influenced in its evolution but also in its individual development. The mathematical model for the influence of the fluctuations of the gravitational field on complex systems in nature (e.g. triggering of earthquakes) and the human organism has developed more or less accidentally from different, originally separate investigations.

A correlation function that indicates stabilizing and destabilizing states with a certain probability is suitable for describing these processes. The underlying hypothesis is the oscillation between stable and unstable states throughout evolution.

The planetary system of the sun is on the one hand a research object of astronomy, on the other hand also an influence factor on the evolution of the earth and its inhabitants. Thus, the Earth's moon acts not only in the formation of romantic and mystical ideas in human consciousness, but also through its stabilizing effect on the Earth's axis. Thus he guarantees the relative stability of the climatic conditions necessary in the biological evolution.

Nonlinear interactions

The fundamental Newtonian equation of motion of N mass points has the form:

$\ddot{r}i=G{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{N}Mj}\frac{rj-ri}{|rj-ri{|}^3}$   (1)

ri, rj = position vectors of planets i, j with masses Mi and Mj;

G = gravitational constant

This equation is the starting point for the derivation of the "Cosmic Fluctuations", however, it is not yet in the form favorable for the present problem of the fluctuations. For this purpose it becomes necessary to consider first ordering points of view, which result from the structure and dynamics of the planetary system.

These are:

1. The stability of the solar
2. Cosmic rhythms are considered over very long periods of
3. The planets of the solar system all move around the sun on circular orbits lying almost in one

They represent natural oscillators whose couplings generate the superposition frequencies of the cosmic fluctuations.

A cosmic cycle begins with the conjunction (seen from the earth) of two planets i, j and ends after the opposition with the next conjunction.

From the ordering aspects A, B and C a model of the cosmic fluctuation can be set up.

From a heliocentric point of view, the cosmic cycles can be described in terms of angular frequencies i,j can be given for the cosmic cycles, which are relatively stable and change only little with time.

$\omega i,j=\frac{2\pi }{Ti,j}$   (2)

Ti,j = time duration from conjunction to conjunction of planets i, j.

Without considering the direction of the resulting planetary forces (only direction-invariant processes are studied), one can apply for the changes of the planetary forces (in first approximation).

Fi,j        fi,j(t) + ki,j(t) cos (wi,j) (3)* t = time

*The relation (3) follows from the vectorial addition of the forces Fi and Fj. 

Fi,j = Fi + Fj

F ² = F ² + F ² + 2 |Fi||Fj|cos(w i,j) (4)

The quantities fi,j(t) and ki,j(t) contain the slowly and not very regularly changing components resulting from distance changes of the planets.

From a geocentric point of view, cosmic cycles are not quite so stable, so instead of i,j(t) it is easier to substitute the angle i, j at which planets i, j appear from Earth into (3).

Fi,j             fi,j(t) + ki,j(t) cos (wi,j)               (5)

For the further investigations only the faster and more "regular" changing cosine part in (4) is considered for the cosmic fluctuations. For a conjunction ( a_i,j = 0°) Fi,j is maximal and for the opposition (a_i,j = 180°) minimal.

The weak gravitational field changes, in particular their cosine component, can be considered as a kind of excitation field strength on matter.

The quantities fi,j(t) and ki,j(t) are set approximately constant since they change weakly and less regularly with time.

Fi,j  =  fi,j(t) + ki,j(t) cos (ai,j)                     (6)

The interactions of these "waves" (6) with matter and its different structures will be non-linear. It must be noted that these are not the gravitational waves derived from a linearization of Einstein's General Relativity. In analogy to other nonlinear interactions with matter (e.g. nonlinear optics), with

$\gamma 1=\frac{k1}{k0};\gamma 2={\left(\frac{k1}{k0}\right)}^2;\mathrm{.........}$   (7)

a general correlation function Hi,j for the influence of two planets i, j can be established.

Hi,j(a) = g1Fi,j +  g2Fi,j2 +  g3Fi,j3 + …                     (8)

Better suited is the transformation of (8) into a Fourier series.

H_i,j(a) = a₀ + a₁cos(a) + a₂cos(2a) + a₃cos(3a) +................................................ (9)

with a = a_i,j

The correlation function

The problem of the correlation function is the determination of the coefficients ak in (9) and the definition of the meaning of H.

It is not intended to measure a force or a "deflection" with H. This would certainly cause insurmountable difficulties experimentally.

This would certainly cause insurmountable difficulties experimentally, if one wanted to determine the influence of the fluctuations on test specimens with rotating lead balls. Moreover, evolution, which has extended over millions of years, is unlikely to be simulated experimentally.

Since the fluctuations of the planetary gravitational field are very weak in their effect, only the following areas come into question for correlations:

1. spatial structure-forming processes that are not or only very slightly determined by other
2. Formation of not fully determined biological
3. Critical states in high-dimensional dissipative
4. Highly complex systems, far from thermal equilibrium and on the edge of

The coefficients a_k will thus be determined from the study of interactions with regions a) to d).

It is obvious to construct a correlation function H interacting with stable (harmonic) and unstable (disharmonic) states in regions a) to d).

Determining the coefficients a_k

from statistical studies of unstable or chaotic processes, where small perturbations can have an effect, is very costly. Therefore, it seems reasonable to first obtain an approximation for the coefficients ak from theoretical considerations, which can then be adjusted by optimization procedures if necessary (Figure 1).

Since we are dealing with cosmic cycles from conjunction to conjunction, one can take structural considerations about these oscillations as a starting point. If one takes the circle division as a basis (Figure 2), then the following structural points can be found:

1. Point: "starting point" (conjunction)
2. Points: polar structure; opposites that need balancing. Due to their tension and, if necessary, the impossibility of balancing them, they can nevertheless form a unity over a longer period of time. Score: strongly disharmonic
3. Points: very stable structure; especially in engineering it is a prerequisite for stability in mechanical Score: very harmonious
4. Points: unstable, dynamic structure; in engineering, this structure is often the basis for lever gears. Score: disharmonious
5. Points: quasi-stable pentagram - structure; borderline between stability and instability. Complicated patterns and structures can be formed that do not repeat. Score: indifferent
6. Points: Honeycomb - structure; close to the circle, relatively stable structure in the compound with good use of space. Rating: harmonious

The addition of further points is possible, but the changes in the qualities become smaller as the structure becomes more similar to the circle. These qualitative statements are quantified step by step and plotted in a diagram (Figure 3).

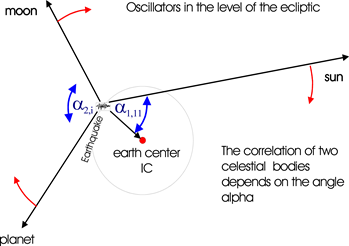
Figure 1 Angle α2,i is the distance between the moon and planet i. Angle α1,11 gives the angular difference between the sun and the center of the earth IC.

Figure 2 Structures of the circle division. The starting point is the conjunction, followed by the opposition, and so on.

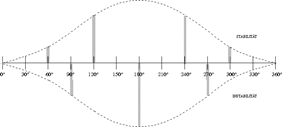
Figure 3 Quantification of the division of the circle subdivided according to structural aspects.
A symmetrical oscillation and decay process is assumed. The image is the basis for a Fourier transform for the 1st approximation of the coefficients ak.

Since it is a periodic cycle, a Fourier transform can be performed. The obtained coefficients are the first Fibonacci numbers, alternately mirrored, see (11). The correlation function takes the following form:

$Hi,j={\displaystyle \sum _{s=1}^{N.12-1}ak}\cos (s.\alpha );mit(k=s\mathrm{mod}12)$   (10)

$a\text{k ={0,1,-2,3,-5,0,3,0,-5,3,-2,1}}$   (11)

The angles a are calculated according to the astronomical algorithms of Jean Meeus.⁴ The 1st order correlation function is shown in Fig 4. It represents a first approximation for the study of the influence of cosmic fluctuations on the stable and unstable states of complex systems.

Consideration of higher orders may need to be made dependent on the problem under investigation. In general, it can be said that the higher orders will be more suitable for resonance and triggering.

It must be said at this point that the hypothesis: "Stable and unstable processes of complex systems are reflected in the structures of the circle division" seems daring at first. Only practical investigations can bring the confirmation that these assumptions are sufficient for a first approximation.

For this purpose, it must be ensured that the correlation function (10) is not only suitable for describing one process, but also provides useful results for different processes and states.

Expected values, at least in tendency, must occur and there must be no negative correlations, in that, for example, the correlation function (10) indicates a higher probability for stability, but in reality there is a higher probability for an unstable state. Initial studies conducted with this correlation function confirm these trends for stability and instability.⁵

Complex nonlinear processes are widespread in nature and society. High-dimensional, complex systems are the rule. Far from thermodynamic equilibrium, these processes show a diverse spatiotemporal behavior. The fluctuations of the planetary gravitational field are, absolutely seen, certainly very weak. However, they have a stable effect on a very large scale for billions of years and on all material structures of the earth. Decisive for the proof of the influence of these fluctuations is the emergence of the "higher harmonics" in the complex structures of the matter.

The human brain is a highly complex system of nerve cells whose organization and interconnection via synapses is neither genetically nor otherwise completely determined.

Thoughts, feelings and strategies of the human intellect are not predetermined in all details. In the course of the evolution of the human brain, the ability to learn has emerged as an important element of human development. Learning due to synaptic plasticity is a lifelong process.

The extent to which planetary fluctuations could possibly gain influence on the structural formation of the brain during evolution will be investigated in the following calculations.

Here, the intelligence of the brain is assumed to be a complex system performance characterized by stability and instability of the neuronal structures for survival strategy. A generally accepted definition of intelligence does not yet exist today.

The development of intelligence of a human individual depends on many influencing factors. Very important is the genetic constellation, which is given by the parents. In addition, many environmental factors also have an effect on this development. Last but not least is also the psychological personality concept significantly involved in the further formation of intelligence. The observation of children whose intelligence quotient was measured at about 10 years of age and whose further school career was followed clearly indicate the great influence of such personality factors as ambition, diligence, motivation and others on the formation of intelligence. Thus, it is not expected that planetary fluctuations will have a dominant influence on structural formation processes of the brain. In fact, it is doubtful that such influences can be detected at all and are not simply an artifact. If planetary fluctuations do have an effect on structure-forming processes of the brain, it will certainly be for a lifetime.

For a proof of this influence, the following hypothesis is assumed.

Hypothesis:

1. Planetary fluctuations affect structure formation and stabilization processes of the brain throughout life.
2. Especially in times of great synaptic plasticity, the impact will be
3. The short period of the individual's becoming autonomous - his birth period - will be particularly formative for the structural formation of the
4. A harmonious correlation function at the time of birth will have a positive stabilizing effect on intelligence
5. A positive 1st derivative of the correlation function will also have a positive effect on intelligence development.
6. It is expected that especially the higher frequencies in smaller spatial areas (the human individual) exert an

The 5th point of the hypothesis highlights the importance of the period immediately before and after birth.

Since there is no generally accepted definition of intelligence, there are the most different methods and procedures to measure the intelligence of a person with an intelligence quotient (IQ). This problem cannot be dealt with here, although it would certainly lead to new insights, if, for example, the connection between personality type and intelligence form were also examined. That there can be such a connection is also shown by the following investigations.

Baseline data:

1. A group of children160 for whom IQ was determined with the PSP (according to Horn).
2. A group of low-intelligent14 people who have "special school level". The IQ is not
3. A group of higher12 intelligent people, mainly academically active. The IQ is not known. The group of children was tested in the Pedagogical Center Groups 2 and 3 are a compilation of the teacher Walter Böhr.³

The group of 160 children is not representative in terms of the cross-section of the population. They are all children who were tested with learning problems in a therapeutic institution for dyslexia and dyscalculia for diagnostic reasons. At the same time, not all children are dyslexic. Among the children tested, there were also no "special needs" students and certainly very few will later pursue an academic career.

From group 1 the hour of birth is not known, therefore the correlation were calculated for 12 o'clock. For groups 2 and 3, the hours of birth and places of birth are known.

Regarding group 1, group 2 is beyond the lower intelligence level and group 3 is above the upper intelligence level.

Comments on the study method:

The group of children was sorted into 20 subgroups ( 8 children each ) by ascending IQ score.

For each child, the correlation matrices Hi,j, Ii,j, Di,j and DAi,j were calculated at the time of birth and superposed within the subgroup. Table 1 shows the sums over i and j as H, D, I, and DA in columns 5, 7, 9, and 11, respectively. All values in the table were calculated for the 3rd order correlation function.

For each subgroup, 10000 control groups were calculated, each with 8 randomly selected birth times. It was tested how many groups have a smaller value than the group of 8 children.

These values, calculated with the control groups, are listed in percentages under H[%], D[%], I[%] and DA[%] in columns 5, 6, 7 and 8. They indicate how rare this group is and are the probability of error for the corresponding hypothesis. The control groups were selected from the same period in which the 8 children were born.

The third column contains the mean IQ of the IQ scores of the group, and the fourth column contains the range of the IQ score.

The row 1 contains the values for the group of 2less14 intelligent persons. Line contains 23the less intelligent 12 persons of group 3.

If the individuals from Table 1 are divided into 4 equally strong groups, then the strong fluctuations are balanced and the trend becomes more visible.

Of course, it must always be emphasized that these are statistical statements that cannot say anything about individual cases.

If we form two marginal groups, one group consisting of the 16 lowest IQ scores of the children and one group consisting of the 14 individuals with special education level of group 2, the probability of error is 1.05% for the statement. "Individuals with low IQ scores have a greater probability of a discordant correlation function at birth" .

If we proceed in the same way with the marginal groups of higher IQ scores and form a new group from the 16 children with the highest IQ scores and group 3 of academics, then the probability of error is 1.51% for the hypothesis: "Individuals with a higher IQ score have a greater probability of a harmonic correlation function at the time of birth".

A summary of these results is given in the table 3.

Which oscillators are essential for the differences between the two groups of IQ? (Figure 4-Figure 6).

Figure 4 1st order correlation function Hi,j according to equation (10) with N=1. It was obtained via a Fourier transform from the structural aspects of Figure 2.

Figure 5 7th order correlation function Hi,j according to equation (10) with N=7. The higher orders of the correlation function are suitable for resonance problems.

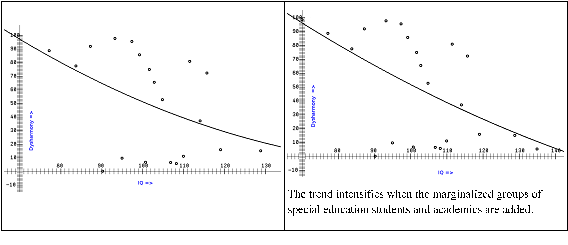
Figure 6 Trend of harmony with the increase of IQ of the 160 tested children. Despite the variations due to the small groups, a trend can be identified: The higher the IQ, the more harmonious the correlation function H becomes.

The sums of the matrices do not give any information about this. The following pictures give exemplarily the error probabilities for the row sum for comparison (Table 4,5).

Matrix H

In Figure 7, 8 out of 10 oscillators (planets) are above 61%. The probability of error that 8 and more are above 61% is 0.01.

Figure 7 Matrix and row sums for H with low IQ.

In Figure 8, 9 of oscillators 10 are below 46%. The probability of error, that 9 and more are below 46%, is even 0.005.

Figure 8 Matrix and row sums for H with high IQ.

Matrix I

Figure 9 and Figure 10 show a similar picture for the energy. Striking is the low energy of Mars, Saturn and Uranus for both groups of events. Moon and Pluto have a lot of energy for the low IQ group.

Figure 9 Matrix and row sums for I with low IQ.

Figure 10 Matrix and row sums for I with high IQ.

Matrix D

The high dynamics for Moon and Uranus in Figure 11,12 are striking. The dynamics indicate the speed of the changes, compared to the control groups.

Figure 11 Matrix and row sums for D with low IQ.

Figure 12 Matrix and row sums for D with high IQ.

Matrix DA

Mars Saturn and Uranus have little energy in the dynamics for the low IQ group Figure 13,14. Similar is the case for the higher IQ group. Here it is Jupiter, Saturn and Uranus that bring little energy to the dynamic.

Figure 13 Matrix and row sums for DA with low IQ.

Figure 14 Matrix and row sums for DA with high IQ.

It is still interesting to examine the different orders of the correlation function on the marginal groups for high and low IQ scores. Not only will the correlation function at the time of birth exert an influence, but the period immediately before and after the birth will also be of influence. These ratios are described by the derivative of1 the correlation function (Figure 15,16).

Figure 15 Example of an IQ test. Factor is 12 very weak in these children.

Figure 16 Differentiated influence of the oscillators (planets).

However, it must be noted at this point that a harmonic correlation function, around birth, also affects the environment, e.g. the mother. Thus, harmonizing influences from the environment can also have additional significance. These results are hardly understandable and were not expected at all, if one allows only the micro fluctuations of the gravity as explanation. Is the evolution of the brain stimulated by these fluctuations? These results allow the conclusion. Nevertheless, there is still the probability for an artifact.

These investigations have shown that also for the very complex process of the development of the intelligence of a human being the planetary oscillations of the gravitational field are of importance with high probability. Here, first of all, an optimization of the calculation was renounced. Thus, it is not considered that the individual correlations certainly do not enter into the correlation function H with the same weighting. All planets were always included in the calculations with equal weighting. This optimization is reserved for further, more profound investigations. Also not examined was the relevance of individual correlations and frequencies. This is also left to further investigations, which then directly calculate probabilities for the correlation function. Such statements are then e.g. : "A person with a higher IQ score will have a harmonic correlation quality above the statistical mean with probability p."

Detailed examination of individual subgroups of the 160 children, sorted by individual factors of the IQ test, also show indications of further correlations. The following example illustrates this.

Investigation into a factor in an IQ test

One factor (no. 12) of the intelligence test used measures the fast guessing of garbled words. It has a high correlation (0.88) with the overall IQ test score. Observations of children for whom this factor was lowest revealed that these children were usually somewhat shy, insecure, and unwilling to take risks.

Therefore, it could be suspected that this very "risk factor" might have a correlation with a function describing stable and unstable states of structure formation. It is not clear at first whether the correlation exists for harmonic or disharmonic states.

To investigate this question, 25 children were selected from the 160 tested for whom the factor (No. 12) had the relatively lowest values.

The results for the different orders of the correlation function are shown in Table 6.

From Table 6, first important conclusions can be drawn for the interpretation of the correlation function [10] regarding the structuring of personality factors. If we assume that the children are less willing to take risks than the statistical mean, then the positive correlation with the "harmonious" values of the correlation function (10) indicates that these children have a predisposition for harmony and they avoid processes that can lead to disharmony, which can always be the case with a higher risk.

These are only first hypotheses, further investigations have to follow. It is interesting that the significant results are obtained for the small orders of the correlation function. This suggests a larger period around birth, which could be of influence in this particular case. Which oscillators contribute significantly to this harmony?

It can be seen from table 6 that the correlation function H has a maximum for the 2nd order. This shows that certain frequencies have a dominant significance. On the other hand, if we look at the first derivative D, the correlation is greatest for the 5th order.

This means that the change in the correlation function in a small period around birth is also not negligible.

Since in Table 6 all 10 celestial bodies with relevant gravitational influence have been considered, the question naturally arises whether all these celestial bodies are also of influence in this case. The correlation matrix shows, and this is quite to be expected, that not all 10 celestial bodies have the same significance. Especially of influence are the moon, Venus, Mars, Jupiter and Saturn. If only these planets are allowed to correlate, then the following result is obtained in Table 7.

9                   *            *             *             *             *             *            *             *             *             *

10                 *            *             *             *             *             *            *             *             *             *

Matrix H of the probability of error:

1                                    2             3             4            5             6             7             8             9           10

1                   *            *             *             *             *             *            *             *             *             *       PR    0.00

8                   *            *             *             *             *             *            *             *             *             *       PR    0.00

9                   *            *             *             *             *             *            *             *             *             *       PR    0.00

10                 *            *             *             *             *             *            *             *             *             *       PR    0.00 bigger are:      0.00 %

1, SUN; 2, MOON; 3, MERKUR; 4, VENUS; 5, MARS; 6, JUPITER; 7, SATURN; 8, URANUS; 9, NEPTUN; 10, PLUTO; 11, IC;

BEGIN: year: 1979 month: 1 day: 1 hour: 0 END: year: 1989 month: 1 day: 1 hour: 0

According to the table 7 the probability of error for the statement is:

"Children with relatively low performance of the IQ factor "guessing garbled words (risk factor)" have particularly harmonious correlations of Moon, Venus, Mars, Jupiter and Saturn at birth" < 0.005% !

Of course, further optimizations of the correlation of the 10 celestial bodies can be done. But that would go beyond the scope of this publication. It should be shown here only that optimizations, which do not change the correlation function, already bring clearly better correlations, which can be used then also practically.

The above example shows how and in which direction further investigations are to be carried out. The correlations contain a multitude of the most different frequencies, which can all be examined for their special effect and meaning. The rough selection of frequencies can be done by the correlating celestial bodies and by the order of the correlation function. At the same time as the multitude of correlation frequencies, the great complexity of planetary fluctuations becomes visible. A further factor for the optimization of the correlation function is the weighting of the individual celestial bodies, which has only been shown here by way of suggestion through the selection of the planets.

Persons with a high level of giftedness

A list of 62 children tested for giftedness forms the birth data for the study. The children were tested at the University of Munich or the Munich Children's Center. The results are listed in Table 8 for different orders of the correlation function.

Assuming that highly gifted individuals have an IQ >130, this group can be classified in the same way as the previously studied group. Does the trend remain?

Also this trend for the harmonic H remains, in addition the calculations show a significantly higher energy. The calculations were made without consideration of the IC (center of the earth) (Table 9).

If we add the IC as the oscillator with the highest frequency and shift the time before and after the birth, we get the following table 10.

The special nature of the gifted group can be seen if the IC is omitted. The time around birth is relatively stable for a larger period of time (Table 11).

This clearly shows that it cannot be a triggering. There is a larger window of stability. This means that in individual cases it can be important that it is still harmonious days after the birth. Since the harmonious quality of time affects not only the baby, but also all the people who are present at the birth, it seems more likely that the starting conditions for a good development of the child's brain are laid here. This is very surprising, but it coincides with the experience from birth psychology.

The high energy indicates that relatively many oscillators (planets) are in a harmonic state.

However, it is important to note that these are only statistical results, which do not have to be true in individual cases. Correlations are not causalities!

What do specific individual cases look like?

From the list of 62 high gifted, the correlation function around birth (1966-8-12- 1h:45m) looks very harmonious this month. This is very rare.

The harmonic correlation function in Figure 17 does not apply to all birth times of the gifted. In the picture 19 the birth 1966 times are marked for the year.

Figure 17 Significance range before and after birth for the gifted group.

List are marked by vertical lines. In this year there are harmonic times (marked red) and disharmonic times (marked blue) (Figure 18).

Figure 18 Correlation function 1966-8. Only the moon is slightly disharmonious at the time of birth (1966- 8-12-1h-45m). The time of birth is marked by the vertical line.

Of course, the birth is not freely selectable and bound to a natural time frame. The following pictures (30 and 31) show the environment of the 2 birth times more clearly. The third birth time is to be seen in the picture 28 (Figure 19-Figure 21).

Figure 19 Correlation function for the year 1966. The birth times of the 3 highly gifted persons from the list are marked by vertical lines. In this year there are harmonic times (marked red) and disharmonic times (marked blue).

Figure 20 Environment of birth 1966-2-3-11h-57m. Zoom from image 29.

Figure 21 Environment of birth 1966-9-1-10h-58m. Zoom from image 18.

The matrix of probabilities shows which oscillators (planets) are important for the group of 62 highly gifted people:

Statistics 4: Probability of events: correlation matrix H Order of the correlation: 1; time shift d: 0 h: 0; GROUP-MEMBERS: 62 ; NUMBER OF THE GROUPS: 10000

Julian-date-start: 2434012.458333 Julian-date-end: 2451910.458345 Accidental selection; TEST: Number of accidental selection >= correlation

CORRELATION-MATRIX H AS INPUT

1                                    2             3             4            5             6             7             8             9           10

1                   *           -0.63      -0.27       0.14       0.22       0.03     -0.09       0.20       0.24     -0.26

2                 -0.63       *           -0.28       0.21       0.90     -0.08       0.05     -0.36       0.63       0.03

3                 -0.27      -0.28       *             0.15     -0.77        1.18       0.42       0.11       0.14     -0.68

4                   0.14       0.21       0.15       *             0.28     -0.47       0.59       0.07     -0.26        0.63

5                   0.22       0.90     -0.77       0.28       *             1.10       0.32       0.46       0.35       0.34

6                   0.03     -0.08       1.18     -0.47        1.10       *            0.77       0.41       0.36     -0.06

7                 -0.09       0.05       0.42       0.59       0.32       0.77       *           -0.70       0.50       0.39

8                   0.20     -0.36       0.11       0.07       0.46       0.41     -0.70       *           -0.44        0.39

9                   0.24       0.63       0.14     -0.26        0.35       0.36       0.50     -0.44       *             2.34

10               -0.26       0.03     -0.68       0.63       0.34     -0.06       0.39       0.39       2.34       *

Matrix H of the probability of error:

1                                    2             3             4            5             6             7             8             9           10

1                   *           92.73     93.16    14.73     40.68     51.35     59.99     33.48    29.10     73.51 PR 70.38

2                 92.73      *           74.28    32.67       2.02     56.16     44.80     79.59      7.81     48.09 PR 36.47

3                 93.16     74.28      *           98.17     99.45       0.27     17.14     40.30    36.82     94.54 PR 67.88

4                 14.73     32.67     98.17      *           40.81     87.86      7.18     44.09    70.80       8.21 PR 27.08

5                 40.68      2.02     99.45    40.81       *             0.20     10.35     16.72    16.84     24.88 PR    0.46

6                 51.35     56.16      0.27     87.86       0.20       *            4.04     20.33    25.75     52.70 PR    0.53

7                 59.99     44.80     17.14      7.18     10.35       4.04       *           91.36      9.89     28.40 PR    2.45

8                 33.48     79.59     40.30    44.09     16.72     20.33     91.36      *           51.74     82.02 PR 48.84

9                 29.10      7.81     36.82    70.80     16.84     25.75      9.89     51.74      *           90.59 PR    6.17

10               73.51     48.09     94.54      8.21     24.88     52.70     28.40     82.02    90.59       *       PR 51.76

bigger are:                1.80 %

1, SUN; 2, MOON; 3, MERKUR; 4, VENUS; 5, MARS; 6, JUPITER; 7, SATURN; 8, URANUS; 9, NEPTUN; 10, PLUTO; 11, IC;

BEGIN: year: 1952 month: 1 day: 1 hour: 0 END: year: 2001 month: 1 day: 1 hour: 0

Statistics 4: Probability of events: energy I

Order of the correlation: 1; GROUP-MEMBERS: 62; NUMBER OF THE GROUPS: 10000 Accidental selection; TEST: Number of accidental selection >= correlation

MATRIX I energy AS INPUT (absolut)

1                                    2             3             4            5             6             7             8             9           10

1                   *            2.96       0.82       0.57       1.98       2.36       2.28       2.97       2.69       2.15

2                   2.96       *             2.87       2.78       2.58       2.77       2.95       2.94       2.53       2.65

3                   0.82       2.87       *             0.89       2.19       2.34       2.48       2.99       2.68       2.53

4                   0.57       2.78       0.89       *             1.85       2.31       2.69       2.44       2.98       2.66

5                   1.98       2.58       2.19       1.85       *             2.46       3.02       2.65       2.73       2.08

6                   2.36       2.77       2.34       2.31       2.46       *            2.55       2.16       2.91       2.16

7                   2.28       2.95       2.48       2.69       3.02       2.55       *             2.58       2.03       2.77

8                   2.97       2.94       2.99       2.44       2.65       2.16       2.58       *             1.96       1.26

9                   2.69       2.53       2.68       2.98       2.73       2.91       2.03       1.96       *             2.34

10                 2.15       2.65       2.53       2.66       2.08       2.16       2.77       1.26       2.34       *

Matrix I of the probability of error:

1                                    2             3             4            5             6             7             8             9           10

1                   *            8.88     45.27    28.56     41.35     51.25     73.97      6.72     31.30     89.39 PR 27.88

2                   8.88       *           14.01    21.34     43.45     24.17      9.47       9.77     49.74     35.97 PR    2.85

3                 45.27     14.01      *           72.85     10.06     54.84     49.53      3.96     21.65     42.40 PR    6.99

4                 28.56     21.34     72.85      *           82.61     63.01     28.96     62.56      7.33     30.39 PR 27.55

5                 41.35     43.45     10.06    82.61       *           61.06      5.26     36.36    30.41     85.18 PR 30.14

6                 51.25     24.17     54.84    63.01     61.06       *           43.26     66.54      7.73     72.69 PR 45.50

7                 73.97      9.47     49.53    28.96       5.26     43.26      *           44.02    78.74     26.49 PR 19.98

8                   6.72       9.77       3.96     62.56     36.36     66.54     44.02      *             0.32       0.76 PR    1.34

9                 31.30     49.74     21.65      7.33     30.41       7.73     78.74      0.32       *           90.59 PR    4.76

10               89.39     35.97     42.40    30.39     85.18     72.69     26.49      0.76     90.59       *       PR 58.62

bigger are:                3.80 %

1, SUN; 2, MOON; 3, MERKUR; 4, VENUS; 5, MARS; 6, JUPITER; 7, SATURN; 8, URANUS; 9, NEPTUN; 10, PLUTO; 11, IC;

BEGIN: year: 1952 month: 1 day: 1 hour: 0 END: year: 2001 month: 1 day: 1 hour: 0

A comparison of the matrix for harmony (group of 62 gifted) with the matrix for harmony of group 4 in table 9 shows that it is not always the same oscillators that produce harmony. If it were so, then only at certain times children with a high giftedness could be born (with a higher probability).

Matrix of correlation function for the group (high IQ) for comparison:

Statistics 4: Probability of events: correlation matrix H Order of the correlation: 1; time shift d: 0 h: 0; GROUP-MEMBERS: 28 ; NUMBER OF THE GROUPS: 10000

Julian-date-start: 2419037.458333 Julian-date-end: 2447527.458345 Accidental selection; TEST: Number of accidental selection >= correlation

CORRELATION-MATRIX H AS INPUT

1                                    2             3             4            5             6             7             8             9           10

1                   *            0.41     -0.27       0.17       0.97     -0.35       0.94       0.18       0.42     -0.98

2                   0.41       *             0.27     -0.39        0.77     -0.67       0.83     -0.94     -0.79      -0.78

3                 -0.27       0.27       *             0.57       0.87     -0.47       0.91       0.95       0.44       0.25

4                   0.17     -0.39       0.57       *           -0.21      -0.04      -0.26      -0.15       0.74     -1.48

5                   0.97       0.77       0.87     -0.21        *             0.21     -0.03       0.09       0.10     -0.43

6                 -0.35      -0.67      -0.47     -0.04        0.21       *            0.56       0.76       1.53       0.65

7                   0.94       0.83       0.91     -0.26      -0.03        0.56       *             0.31       0.15       0.75

8                   0.18     -0.94       0.95     -0.15        0.09       0.76       0.31       *             0.54       0.07

9                   0.42     -0.79       0.44       0.74       0.10       1.53       0.15       0.54       *             1.90

10               -0.98      -0.78       0.25     -1.48      -0.43        0.65       0.75       0.07       1.90       *

Matrix H of the probability of error:

1                                    2             3             4            5             6             7             8             9           10

1                   *           26.71     83.98    19.20       5.62     73.50      7.57     40.02    25.69     93.92 PR 20.72

2                 26.71      *           33.98    72.26     12.18     85.46     10.50     92.22    88.30     88.84 PR 74.98

3                 83.98     33.98      *           28.20       6.60     80.25      8.85       7.26     25.58     34.26 PR    3.29

4                 19.20     72.26     28.20      *           77.64     56.01     64.10     61.10    13.82     99.00 PR 87.19

5                   5.62     12.18      6.60     77.64       *           33.75     47.48     47.59    48.67     80.72 PR 15.38

6                 73.50     85.46     80.25    56.01     33.75       *           20.02     12.96      1.08     15.06 PR 15.41

7                   7.57     10.50      8.85     64.10     47.48     20.02      *           34.02    46.08     11.03 PR    1.50

8                 40.02     92.22      7.26     61.10     47.59     12.96     34.02      *           38.13     71.18 PR 30.92

9                 25.69     88.30     25.58    13.82     48.67       1.08     46.08     38.13      *           20.69 PR    7.92

10               93.92     88.84     34.26    99.00     80.72     15.06     11.03     71.18    20.69       *       PR 88.74

bigger are:                9.14 %

1, SUN; 2, MOON; 3, MERKUR; 4, VENUS; 5, MARS; 6, JUPITER; 7, SATURN; 8, URANUS; 9, NEPTUN; 10, PLUTO; 11, IC;

BEGIN: year: 1911 month: 1 day: 1 hour: 0 END: year: 1989 month: 1 day: 1 hour: 0

For this group, the order of 6. correlation for H indicates higher significances at the time of birth.

Statistics 4: Probability of events: correlation matrix H Order of the correlation: 6; time shift d: 0 h: 0; GROUP-MEMBERS: 28 ; NUMBER OF THE GROUPS: 10000

Julian-date-start: 2419037.458333 Julian-date-end: 2447527.458345 Accidental selection; TEST: Number of accidental selection >= correlation

CORRELATION-MATRIX H AS INPUT

1                                    2             3             4            5             6             7             8             9           10

1                   *            0.13     -0.14     -0.01        0.18     -0.34       0.08     -0.04       0.22     -0.07

2                   0.13       *             0.09       0.44       0.09     -0.10       0.56       0.19       0.29     -0.50

3                 -0.14       0.09       *             0.03       0.26       0.12       0.06       0.12       0.34       0.47

4                 -0.01       0.44       0.03       *           -0.05        0.21       0.09     -0.23     -0.05        0.46

5                   0.18       0.09       0.26     -0.05        *           -0.06      -0.20       0.08     -0.19        0.10

6                 -0.34      -0.10       0.12       0.21     -0.06        *            0.62       0.05       0.54       0.17

7                   0.08       0.56       0.06       0.09     -0.20        0.62       *           -0.03       0.08       0.25

8                 -0.04       0.19       0.12     -0.23        0.08       0.05     -0.03       *             0.26     -0.08

9                   0.22       0.29       0.34     -0.05      -0.19        0.54       0.08       0.26       *             0.82

10               -0.07      -0.50       0.47       0.46       0.10       0.17       0.25     -0.08       0.82       *

Matrix H of the probability of error:

1                                    2             3             4            5             6             7             8             9           10

1                   *           28.80     90.12    61.35     21.41     91.41     36.46     57.89    19.15     63.07 PR 48.43

2                 28.80      *           35.40      5.13     35.17     65.75      2.00     22.79    12.75     96.56 PR    6.83

3                 90.12     35.40      *           65.23     11.54     32.58     41.40     32.49      9.74       3.98 PR    3.14

4                 61.35      5.13     65.23      *           68.06     20.43     35.87     82.28    60.04       4.12 PR 13.98

5                 21.41     35.17     11.54    68.06       *           60.03     79.92     37.71    80.19     33.07 PR 43.98

6                 91.41     65.75     32.58    20.43     60.03       *            1.16     39.18      3.98     27.71 PR    7.59

7                 36.46      2.00     41.40    35.87     79.92       1.16       *           52.52    41.63     16.42 PR    3.48

8                 57.89     22.79     32.49    82.28     37.71     39.18     52.52      *           20.37     76.11 PR 40.75

9                 19.15     12.75      9.74     60.04     80.19       3.98     41.63     20.37      *             4.07 PR    1.64

10               63.07     96.56      3.98       4.12     33.07     27.71     16.42     76.11      4.07       *       PR    8.35

bigger are:                0.36 %

1, SUN; 2, MOON; 3, MERKUR; 4, VENUS; 5, MARS; 6, JUPITER; 7, SATURN; 8, URANUS; 9, NEPTUN; 10, PLUTO; 11, IC;

BEGIN: year: 1911 month: 1 day: 1 hour: 0 END: year: 1989 month: 1 day: 1 hour: 0

Pluto is always considered here, although its gravitational effect, physically seen, is negligible. Obviously, however, an oscillator with this frequency is not negligible.

The only question is, can the small planet Pluto be considered as a pointer of this oscillator? Here further investigations must follow.

The addition of further IQ-relevant data to the original studies⁴ have strengthened the conviction that it is highly unlikely to be an artifact. This has led me to publish the results now.

It is a fact, as also other researches show,⁵ that the dynamic planetary gravitational field has an influence on many areas of evolution on Earth, although the gravitational forces exerted are very weak. To find an explanation for this, this research should also stimulate.

The aim of the publication is to draw attention to this oscillating subsystem (the solar system) and to stimulate further research. The computer program developed for this purpose is accessible for research projects and available for download.^6,7

List of the highly gifted people

None.

None.

1. Kurths J, Seehafer N, Spahn F. Nichtlineare Dynamik in der Physik: Forschungsbeispiele und Forschungstrend. In: Mainzer K. Komplexe Systeme und Nichtlineare Dynamik in Natur und Gesellschaft. Springer, Heidelberg New York Barcelona Budapest Hong Kong, London Milan Paris Santa Clara Singapore Tokyo. 1999.
2. Nitsche M E, The non-linear interaction of the planetray gravitational field on earthquakes; Lecture on the International Association for Mathematical Geology IAMG 2003 Portsmouth, UK; 2003. EGS - AGU - EUG Joint Assembly, Abstracts from the meeting held in Nice, France, 6 - 11 April 2003, abstract id.1319; 2003.
3. Michael Nitsche. Microgravity - Fluctuations of the planetary gravitational field and nonlinear interactions with matter.
4. Jean Meeus. “Astronomische Algorithmen; publisher Johann Ambrosius Barth; ISBN-13 978-33350031824.
5. Lecture – script. “Are the stabilizing and destabilizing influences of the planetary gravitational field on the structural formation of biological patterns real?“ Lecture on the 10th conference on synergetics and complexity research: "Self. Organization in Psychology, Psychiatry and Social Sciences” 6th - 8th June 2002 conference centre Bildungszentrum Kloster Seeon (Bavaria, Germany).
6. Sean CL Deoni, Jennifer Beauchemin, Alexandra Volpe, et al. “The COVID-19 Pandemic and Child Cognitive Development“.
7. Nitsche M. computer program.