Several chemometric models were used for the determination of cefoperazone sodium in presence of its alkaline degradation product. The methods are either traditional (Partial Least Squares) or advanced (Artificial Neural Network). Partial Least Squares method was used with and without variable selection (Genetic Algorithm GA). Artificial Neural Network (ANN) was used with and without variable selection procedure (Genetic Algorithm GA) and data compression procedure (principal component analysis PCA). The chemometric methods used are PLS-1, GA-PLS-1, ANN, GA-ANN and PCA-ANN. The methods were used for the determination of cefoperazone sodium in bulk powder and pharmaceutical preparation. A 2-factor 5-level experimental design was built leading to 25 mixtures containing different ratios of cefoperazone sodium and its alkaline degradation product. Thirteen mixtures were used as a training set and the other twelve were used as a validation set.

Keywords:cefoperazone, PLS-1, GA-PLS-1, ANN, GA-ANN, PCA-ANN

Cefoperazone is sodium (7R)-7-((R)-2-(4-ethyl-2,3-dioxopiperazin-1 ylcarboxamido)-2-(4-hydroxyphenyl) acetamido)-3-((1-methyl-1H-tetrazol-5-yl) thiomethyl)-3-cephem-4-carboxylate. Its molecular weight is 667.6 and its molecular formula is C₂₅H₂₆N₉NaO₈S₂. Cefoperazone is a third generation cephalosporin antibiotic, beta-lactam and inhibitor of cell wall synthesis. Cefoperazone (CPZ) is commonly used for infections caused by Gram-negative bacteria.^1,2 Literature survey reveals that CPZ was determined in pure form, pharmaceuticals and biological fluids using spectrophotometric,^3-12 voltammetric,^13-16 chromatographic^17-21 and fluorimetric²² methods (Figure 1).

Figure 1 Structure of Cefoperazone Sodium. Mwt 667.6

The rationales of this work were to:

1. Develop simple and accurate methods for determination of CPZ in presence of its alkaline degradation product.
2. Show the effect of variable selection (GA) and data compression (PCA) methods on enhancing the prediction power of different chemometric models.

ANN is a kind of information processing chemometrical technique. It simulates some properties of human brain i.e. the way the input data are treated by the artificial (computer simulated) neuron is similar in action to a biological neuron exposed to incoming signals from neighboring neurons. In the computer the neurons are represented as weight vectors. Artificial Neural Network (ANN) applied in the field of regression or classification. In this manuscript ANN has been applied to establish a correlation between relationship between inputs and outputs. ANNs are composed of some units (input, hidden and output) and connection weights between the units. The neural networks where information flows from the input to the output layer are frequently termed ‘feed-forward’ ANNs (i.e. the type of ANN used in this manuscript is feed-forward network trained with the back propagation of errors learning algorithm). It is called feed-forward ANN as information passes one way through the network from the input layer, through the hidden layer and finally to the output layer. The outputs (predicted concentrations), are compared with targets (actual concentrations), and the difference between them is called error.²³

The transfer functions

There are two transfer functions used in ANN; one between input and output of a node in the hidden layer and the other is applied in output layer. The use of these functions depends on relationship between the inputs and the outputs. Tansig-purelin transfer functions are commonly used for non-linear systems,²⁴ while purelin-purelin functions are used for linear ones.²⁵

Hidden neurons number (HNN)

It is related to the converging performance of the output error function during the learning process.

Number of neurons

Unfortunately, there are no fixed rules as to how many neurons should be included in the hidden layer. If there are too few nodes in the hidden layer the network may have difficulty generalizing to problems it has never encountered before. On the other hand, if there are too many nodes in the hidden layer, the network may take an unacceptably long time to learn anything of any value.

Lc, Lcd and Lci

The learning coefficient (Lc) controls the degree at which connection weights are modified during the learning process. The learning coefficient decrease (Lcd) and learning coefficient increase (Lci) control the variation of Lc value. It varies as a function of performance of the ANN.

Materials and reagents

1. Cefoperazone sodium was kindly supplied by Egyptian International Pharmaceutical Industries Company (EIPICO), 10^th of Ramadan City, Egypt; its purity was certified to be 99.9 ± 0.5.
2. Pharmaceutical Preparations: “Cefozon” vial: (batch number1408881A) containing 1000 mg of cefoperazone sodium per vial.
3. Solvent: distilled water.

Instruments

SHIMADZU dual beam UV-visible spectrophotometer (Kyoto/ Japan), model UV-1650 PC connected to IBM compatible and aHP1020 laser jet printer. The bundled software, UV-Probe personal spectroscopy software version 2.1 (SHIMADZU) was used. The spectral band was 2 nm and scanning speed is 2800 nm/min and 1 nm data interval.

Software

All chemometrics methods were implemented in Mat lab 8.2.0.701 (R2013b). PLS, GA-PLS, ANN, GA-ANN and PCA-ANN were carried out using PLS toolbox software version 2.1 in conjunction with Neural Network toolbox. The t-test and F-test were performed using Microsoft Excel.

Standard solutions

1. Standard stock solution of CPZ 1100 µg/mL in distilled water.
2. Standard working solutions of CPZ were prepared from stock solutions by appropriate dilutions with distilled water.
3. Preparation of the degradation product (DCPZ): 1M NaOH solution (50mL) was added to pure cefoperazone sodium (100mg) in a flask for 20 minutes at room temperature. 1M HCL solution was added to the degraded solution till pH about 7. Then the solution was evaporated slowly in rotavapor just to dryness. The residue was dissolved in methanol, filtered into 100-mL measuring flask and completed to volume with the distilled water.¹² Complete degradation was confirmed by using TLC. Working solution of degradate (100 μg/mL) was obtained by dilution of the stock solution with water. These solutions were scanned over a range of 200-400 nm and stored in the computer.

Spectral characteristics of CPZ and its degradate

The zero order (D₀) absorption spectra were recorded against distilled water as a blank over a range of 200-400nm.

Experimental design for chemometric methods

A 5-level, 2-factor design was performed using 5 concentration levels for the drug and its alkaline degradate to be analyzed. The design spans the mixture space fairly well; where there are 5 mixtures for each compound at each concentration level, resulting in 25 mixtures.²⁶ The central level of the design is 10µg/mL for both. Table 1 represents the concentration design matrix. The regions from 200 to 210nm and from 300 to 400nm were rejected. Thirteen mixtures of this design were used as a calibration set and the other 12 mixtures were used as a validation set to test the predictive ability of the developed multivariate models.

Analysis of Cefozon^® by the proposed methods

Contents of 5 Cefozon^® vials (1000mg/vial) were mixed well. An accurately weighed amount equivalent to 10mg of cefoperazone sodium was transferred into 100-mL volumetric flask. Cefoperazone sodium is dissolved in about 50mL distilled water, sonicated for 15min, diluted to the mark with distilled water mixed well and filtered; the first portion of the filtrate was rejected. The solution labeled to contain 100 μg/mL of cefoperazone sodium. Repeat the general procedure using aliquots covering the working concentration range. Determine the content of the vials from the corresponding regression equation. The spectra of these solutions were scanned from 200 to 400nm, stored in the computer and analyzed by the proposed methods.

Figure 2 shows the zero order UV absorption spectra of cefoperazone and its alkaline degradation product. The spectral overlapping of the drug and its degradation product prevents resolution of the mixture by the direct spectrophotometric measurements.

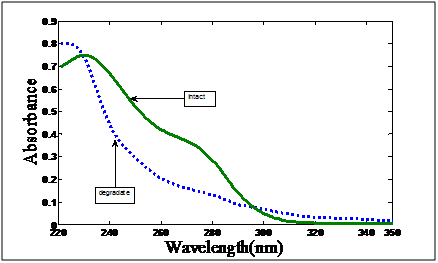
Figure 2 Zero order absorption spectrum of 24μg/mL cefoperazone and 24μg/mL its alkaline degradation product using distilled water as blank.

The aim of this study was to develop accurate and simple chemometric methods for determination of CPZ in presence of its degradate and to show the effect of data compression and variable selection on improving the predictive power of PLS and ANN models.

The first step in model building, involves constructing the calibration matrix for intact and its degradate. In this study the model was optimized with the aid of the 5-level 2-factor design²⁶ resulting in 25 sample mixture. Table 1 shows the composition of the 25 sample mixtures. These 25 sample mixtures were divided to 13 training mixtures (for building the models) (odd numbers) and 12 validation mixtures (for measuring predictive power of the models) (even numbers).

The quality of multi component determination depends on the wavelength range and spectral mode used.²⁷ The wavelengths used were in the range 221-350nm. Wavelengths less than 221 nm were rejected due to the noisy content. Wavelengths more than 350nm were not used because they were uninformative (no absorption is mentioned in these regions).

Variable selection: genetic algorithm (GA)

GA is used for optimization and for other applications such as wavelength selection in spectroscopy. Molecular spectroscopy has been greatly improved by the use of variety of multivariate statistical methods.^28,29 Methods such as Partial Least Squares (PLS) or Principal Component Regression (PCR), allow taking into account the whole spectrum without performing variable selection.³⁰ It has been recognized that an efficient variable selection can be beneficial to improve the predictive ability of the model and to reduce its complexity.³¹ Several techniques devoted to variable selection in PLS models applied to spectral data have been presented.^32,33 It has already been shown that genetic Algorithms (GAs) can be successfully used as a variable selection technique.^34,35 The architecture of a GA can be divided into five components: Initiation, Evaluation, Exploitation, Exploration and Mutation. An important issue of successful GA performance is the adjustment of GA parameters.³⁶

Variable selection can be seen as an optimization problem. Among the different variable selection algorithms available, Genetic Algorithms (GA) are the most commonly employed. The main idea behind the use of GA in numerical optimization is the mathematical translation of the biological concept of the ‘survival of the fittest’. The fitness values were used as response variables. Mutation rate was 0.005 in all cases as when it increased above this value, no convergence occurred between average fitness and best fitness values and model stop. The adjustment of the GA parameters is shown in Table 2.

Each solution (chromosome) is evaluated using the PRESS value reached in the calibration. The genetic algorithm searches for the minimum PRESS in the space of all the possible chromosomes without establishing, a priori, the latent structure of the calibration.

Where and are predicted and true concentrations in µg/mL, respectively. The GA was run for 129 variables (in the range 221- 350) for cefoperazone. The selected variables (86) were used for running of PLS model and ANN. GA reduced absorbance matrix to about 34-36 % of the original matrix.

Partial least squares (PLS-1)

The purpose of PLS method is to build a calibration model between the concentration of the components under study (CPZ and DCPZ) and the latent variables of the data matrix.^37,38 Two different aspects can be used in Partial Least Squares called PLS-1 and PLS-2. PLS-2 uses the whole information about the concentration of all components to form latent variables (LVs), while PLS-1 uses only the information about the concentration of one component to create the LVs used by the model.³⁸

Including extra LVs in the model increases the possibility of the known problem of over fitting. On the other hand, if the number of LVs was too small meaningful data that could be necessary for the calibration might be discarded. Therefore, optimization of number of the LVs is a critical issue in PLS method. Leave one out (LOO) cross validation and the bootstrap³⁹ can be applied to predict the optimum number of PLS components. PLS-1 calibration on 12 calibration spectra was performed and, using this calibration, the concentration of the sample left out during the calibration process was predicted. This process was repeated 13 times until each training sample had been left out once.⁴⁰ The predicted concentrations of the components in each sample were compared with the actual concentrations in this calibration samples and the root mean squares error of cross-validation (RMSECV) was calculated as follows:

Where I is the number of objects in the calibration set, Y_t is the known concentration for sample, and Y_predt is the prediction concentration of sample.

The RMSECV was used as a diagnostic test for examining the error in the predicted concentrations. It indicates both of the precision and accuracy of predictions.

Appropriate selection of the number of factors to be used to construct the model is a key to achieve correct quantitation in PLS-1 calibration. The most usual procedure for this purpose involves choosing the number of factors that result in the minimum RMSECV. However, this criterion is subjected to some constraints since, occasionally; the RMSECV does not reach a sharp minimum, but decreases gradually above a given number of factors. For this reason, the method developed by Haal et al.²⁸ was used for selecting the optimum number of factors, which involves selecting that model including the smallest number of factors that results in an insignificant difference between the corresponding RMSECV and the minimum RMSECV (Figure 3a & 3b).

Figure 3a The optimum number of LV for cefoperazone sodium and it’s degradate concentration prediction from raw data.

Figure 3b The optimum number of LV for cefoperazone sodium and it’s degradate concentration prediction from GA model.

ANN

An ANN is a set of interconnected neurons (also termed nodes, cells, units or process elements) distributed in a specific arrangement, usually termed architecture. In general, neurons are organized in layers. The most common neural nets, the feed-forward nets, are fully connected, i.e. each node is connected to all the nodes in the next layer. The information we want to enter in the ANN (e.g. the spectra) is given to the ‘input layer’, which is the set of neurons that receive directly the information from the external world of the net. In inverse calibration, the inputs could be the absorbances at various wavelengths and the output could be the concentrations of one or more analyte. The ANN consists of three layers; two layers with connections to the outside world (an input layer where data are presented to the network and an output layer which holds the network response to given inputs ) and one hidden layer (optimized afterwards). Reduce the number of input variables without losing relevant information leads to time saving. A powerful tool to carry out such a reduction in the dimensionality of the original data was principal components analysis (PCA). We can consider that the scores of (PCs) alone represent the calibration standards. So, instead of using the full original absorbance variables to train the ANN, only a reduced number of PC scores can be used. Also, genetic algorithm was used to select the best wavelengths to represent each compound. This means that, the absorbance matrix was reduced either by Genetic Algorithm (variable selection procedure) to about 34% of the original matrix or Principal Component Analysis (PCA) (variable compression procedure) to three principal components. Thus, three ANNs (ANN, GA-ANN and PC-ANN) were applied in our work. The output layer is the concentration matrix of one component. The hidden layer consists of just single layer which has been considered sufficient to solve similar or more complex problems. Moreover, more hidden layers may cause over fitting.²⁵

Optimization of ANN parameters is of a great importance for a proper modeling. These parameters are HNN, Lc, Lci. Placket- Burman design was used for Optimization as shown in Table 3. The choice of the proper transfer function depends on the nature of data.

After optimization of parameters and architectures of the ANNs the training step is preceded. In other words, learning is the process by which an ANN modifies its weights and bias terms in response to the input information (spectra and concentration values). The error correction learning is known as back-propagation. This learning mode compares the outputs of the ANN with the true concentration values. The error derived from such a comparison will control the ANN training. The errors can be used to adjust the top weights directly by means of a predefined algorithm. Error-correction learning algorithms attempt to minimize error on each iteration. TRAINLM³² was thus preferred as it is time saving.

Since relationship between absorbance and concentration is linear, purelin-purelin (as a transfer function between input and hidden layer; and between hidden layer and outer layer) was found to give best results in our work.

The network is trained using the training set: in the calibration example the ANN would calculate concentrations for each member of the training set, and any discrepancies between the network’s output and the known concentrations would be used to adjust internal parameters in the network. These prediction and adjustment steps are repeated until the required degree of accuracy, evaluated with a test set, is achieved. Since the training and test sets are bound to differ to some extent, it is important not to over-fit the training set, otherwise the network may perform less well with the test set, and subsequently with ‘unknown’ samples.

ANNs are useful when the mathematical model is unknown or uncertain because they do not assume any mathematical relationship between the input and output variables. The proposed chemometric methods were run on the calibration data using optimal parameters. The concentrations of the drug and it’s degradate in the calibration set (13 mixtures) were calculated. In order to validate the proposed methods, the validation set (12 mixtures) was analyzed with the proposed methods (Table 4).

The proposed PLS-1, GA-PLS, ANN, GA-ANN and PCA-ANN methods were successfully used for the determination of CPZ in Cefozon vial, Table 5.

The results obtained for the analysis of CPZ in Cefozon vial by the suggested methods were statistically compared with those obtained by applying the reported second derivative method¹² and no significant difference between the results was obtained as shown in (Table 5). Using one-way ANOVA test, the obtained results by applying these methods showed no significant differences among all of them as shown in Table 6.

GA reduced the optimal number of latent variables of PLS-1 model for CPZ from three into two factors. Also, recoveries and RMSEP (Root Mean Square Error of Prediction) were decreased indicating a better resolution power of GA-PLS model than PLS-1 model (Table 4).

The comparison shows that GA-ANN is more suitable for the determination of cefoperazone because GA allows the use of less number of neurons (so shorter training time) for cefoperazone than those used in the networks utilized raw. While PCA-ANN did not show any improvement than ANN, even the results were worse (Table 4). These results indicate that variable selection models (GA) are more suitable than data compression procedure (PCA), when preceding ANN, for the analysis of this binary mixture. This result may be attributed to the fact that GA introduces the most relevant wavelengths to the drug concentration.

ANN is better than PLS-1 (Table 4), which may be due to the fact that ANN is a type of artificial intelligence and that in ANN there is no chance for over fitting that may occur in PLS calibrations.

In conclusion, the described chemometric methods gave accurate and precise results for determination of cefoperazone in presence of its alkaline degradation product without prior separation and can be applied for routine analysis.

None.

Authors declare that there is no conflict of interest.

1. O'Neil MJ, Maryadele J. The merck index an encyclopedia of chemicals, drugs, and biologicals. 15th ed. Cambridge, UK; 2006.
2. Sean C, Martindale S. The complete drug reference. 38th ed. Pharmacutical Press: London, UK; 2002.
3. Saleh GA, Askal HF, Darwish IA, et al. Spectroscopic analytical study for the charge-transfer complexation of certain cephalosporins with chloranilic acid. Anal Sci. 2003;19(2):281‒287.
4. Saleh GA, Askal HF, Radwan MF, et al. Use of charge-transfer complexation in the spectrophotometric analysis of certain cephalosporins. Talanta. 2001;54(6):1205‒1215.
5. Salem H, Askal H. Colourimetric and AAS determination of cephalosporins using Reineck's salt. J Pharm Biomed Anal. 2002;29(1):347‒354.
6. Salem H, Saleh GA. Selective spectrophotometric determination of phenolic β-lactam antibiotics. J Pharm Biomed Anal. 2002;28(6):1205‒1213.
7. Salem H. Selective spectrophotometric determination of phenolic β-lactam antibiotics in pure forms and in their pharmaceutical formulations. Analytica chimica acta. 2004;515(2):333‒341.
8. Elazazy MS, Shalaby A, Elbolkiny MN, et al. Spectrophotometric determination of cefepime hydrochloride, cefoperazone sodium, ceftazidime pentahydrate, cefuroxime sodium and etamsylate using ammonium molybdate. Scientia pharmaceutica. 2003;71(3):211‒228.
9. Saleh GA, El-Shaboury SR, Mohamed FA, et al. Kinetic spectrophotometric determination of certain cephalosporins using oxidized quercetin reagent. Spectrochim Acta A Mol Biomol Spectrosc. 2009;73(5):946‒954.
10. El Walily AFM, Gazy AAK, Belal SF, et al. Use of cerium (IV) in the spectrophotometric and spectrofluorimetric determinations of penicillins and cephalosporins in their pharmaceutical preparations. Spectroscopy Letters: An International Journal for Rapid Communication. 2000;33(6):931‒948.
11. Hoang VD, Loan NT, Tho VT, et al. UV spectrophotometric simultaneous determination of cefoperazone and sulbactam in pharmaceutical formulations by derivative, Fourier and wavelet transforms. Spectrochim Acta A Mol Biomol Spectrosc. 2014;121:704‒714.
12. Korany MA, El-Sayed MAH, Galal SM. Utility of derivative spectrophotometry for the determination of certain cephalosporins and their alkali-induced degradation products in combination. Analytical letters. 1989;22(1):141‒157.
13. El‐Maali NA, Ali AM, Ghandour MA. Electrochemical reduction and oxidation of two cephalosporin antibiotics: Ceftriaxone (Rocephin) and cefoperazone (Cefobid). Electroanalysis. 1993;5(7):599‒604.
14. Hammam E, El-Attar MA, Beltagi AM. Voltammetric studies on the antibiotic drug cefoperazone: Quantification and pharmacokinetic studies. J Pharm Biomed Anal. 2006;42(4):523‒527.
15. Ali AM, El‐Maali NA, Ghandour MA. Determination of cefobid using adsorptive stripping voltammetric technique in different media. Electroanalysis. 1993;5(1):85‒89.
16. Billová S, Kizek R, Jelen F, et al. Square-wave voltammetric determination of cefoperazone in a bacterial culture, pharmaceutical drug, milk, and urine. Anal Bioanal Chem. 2003;377(2):362‒369.
17. Gáspár A, Andrási M, Kardos S. Application of capillary zone electrophoresis to the analysis and to a stability study of cephalosporins. Journal of Chromatography B. 2002;775(2):239‒246.
18. Tsou TL, Huang YC, Lee CW, et al. Simultaneous determination of ampicillin, cefoperazone, and sulbactam in pharmaceutical formulations by HPLC with β‐cyclodextrin stationary phase. J Sep Sci. 2007;30(15):2407‒2413.
19. Sørensen LK, Snor LK. Determination of cephalosporins in raw bovine milk by high-performance liquid chromatography. J Chromatogr A. 2000;882(1):145‒151.
20. Becker M, Zittlau E, Petz M. Residue analysis of 15 penicillins and cephalosporins in bovine muscle, kidney and milk by liquid chromatography-tandem mass spectrometry. Analytica Chimica Acta. 2004;520(1):19‒32.
21. Mohamed FA, Saleh GA, El-Shaboury SR, et al. Selective densitometric analysis of cephalosporins using dragendorff’s reagent. Chromatographia. 2008;68(5-6):365‒374.
22. Bebawy LI, El Kelani K, Fattah LA. Fluorimetric determination of some antibiotics in raw material and dosage forms through ternary complex formation with terbium (Tb (3+)). J Pharm Biomed Anal. 2003;32(6):1219‒1225.
23. Dawson CW, Wilby R. An artificial neural network approach to rainfall-runoff modelling. Hydrological Sciences Journal. 1998;43(1):47‒66.
24. Abbaspour A, Baramakeh L. Application of principle component analysis-artificial neural network for simultaneous determination of zirconium and hafnium in real samples. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. 2006;64(2):477‒482.
25. Khanchi AR, Mahani MK, Hajihosseini M, et al. Simultaneous spectrophotometric determination of caffeine and theobromine in Iranian tea by artificial neural networks and its comparison with PLS. Food chemistry. 2007;103(3):1062‒1068.
26. Brereton RG. Multilevel multifactor designs for multivariatecalibration. Analyst. 1997;122(12):1521‒1529.
27. Blanco M, Coello J, Gonzalez F, et al. Spectrophotometric analysis of a pharmaceutical preparation by principal component regression. J Pharm Sci. 1993;82(8):834‒837.
28. Haaland DM, Thomas EV. Partial least-squares methods for spectral analyses. 2. Application to simulated and glass spectral data. Analytical Chemistry. 1988;60(11):1202‒1208.
29. Lindberg W, Persson JA, Wold S. Partial least-squares method for spectrofluorimetric analysis of mixtures of humic acid and lignin sulfonate. Analytical Chemistry. 1983;55(4):643‒648.
30. Thomas EV, Haaland DM. Comparison of multivariate calibration methods for quantitative spectral analysis. Analytical Chemistry. 1990;62(10):1091‒1099.
31. Thomas EV. A primer on multivariate calibration. Analytical Chemistry. 1994;66(15):795A‒804A.
32. Darwish HW, Hassan SA, Salem MY, et al. Different approaches in Partial Least Squares and Artificial Neural Network models applied for the analysis of a ternary mixture of Amlodipine, Valsartan and Hydrochlorothiazide. Spectrochim Acta A Mol Biomol Spectrosc. 2014;122:744‒750.
33. Forina M, Casolino C, Millan CP. Iterative predictor weighting (IPW) PLS: a technique for the elimination of useless predictors in regression problems. Journal of Chemometrics. 1999;13(2):165‒184.
34. Davis L. The handbook of genetic algorithms Van Nostrand Reingold. 3rd ed. New York, USA; 1991.
35. Michalewicz Z. Genetic algorithms + data structures = evolution programs. Springer-Verlag Berlin Heidelberg: New York, USA; 2013.
36. Tong HL, Lucasius CB, Kateman G. Optimization of calibration data with the dynamic genetic algorithm. Analytica Chimica Acta. 1992;268(1):123‒134.
37. Kramer R. Chemometric techniques for quantitative analysis. CRC Press: USA; 1998.
38. Massart D, Vandeginste B, Buydens L, et al. Handbook of chemometrics and qualimetrics: part A. Applied Spectroscopy. 1998;52:302.
39. Efron B, Tibshirani RJ. An introduction to the bootstrap. CRC press: USA; 1994.
40. Espinosa MA, Salinas F, Paya IDO. Simultaneous determination of sulfadiazine, doxycycline, furaltadone and trimethoprim by partial least squares multivariate calibration. Analytica chimica acta. 1995;313(1):103‒112.