The research article looks for providing information about some aspects of stock assessment of Otolithoides pama in Thanlwin River mouth for strategic management and sustainability. A total of 4,620 specimens were collected from 2017 January to 2017 December. The length frequency data was analyzed using FiSAT II software. The asymptotic length, growth co-efficient and the theoretical age at birth were estimated as: L∞=40.9cm SL, K=0.98yr^-1 and t₀=-0.78yr^-1 respectively, with the maximum age (tmax) at 3.06 years. The instantaneous rate of total mortality (Z), natural mortality (M) and fishing mortality (F) were found to be 2.24yr^-1, 1.52yr^-1 and 0.72yr^-1 respectively. The estimated exploitation rate (E) was 0.32 and the maximum exploitation rate (Emax) and the fishing exploitation rate (Fmax) were found to be 0.37 and 1.06, respectively. Length at first capture (L50 or Lc) is 26.13 cm which is lower than length at first maturity (Lm=100cm). As regards the life span of O. pama, it was found in 4years old according to the otolith and scales results. Based on the present study, it was well known that O. pama is not overexploited during the study period.

Keywords: thanlwin, otolithoides pama, growth, mortality, exploitation rate

The croakers which are included in family Sciaenidae are widely distributed in many different parts of the world, especially in the tropical and sub-tropical waters of Indian Ocean.¹ These species are recorded in small to moderately large size range, even more than a meter in length. They are primarily found in coastal areas, though some are distributed in the estuarine waters, even upto a depth of 350 m.¹ Around 20 species of sciaenids, which are known as Nga-poke-thin in local, have been reported in Myanmar coastal waters.² Among them, Otolithoides pama (Hamilton, 1822) was one of the most abundant in Thanlwin River mouth and they are also the fishes which command very good price and their swim bladder is also much in demand because they are mainly exported to the China and they are useful for soups and traditional medicines.

Based on the interview information, the local fisher men said that there was a declining problem for fish population in Thanlwin River Mouth. Therefore the present study was aimed to analyze the O. pama population and fishery in Thanlwin River Mouth theorectically to give indications on the level of exploitation and to propose indicators of declining stocks, suggesting a strategy for better management. As there has not been any study about the stock assessment of O. pama in Myanmar, this study is proposed as a basic informational providing data for further observing on stock assessment.

From 2017 January to 2017 December, the length frequency data of Otolithoides pama were monthly collected from the gill net fishing boats and trawl net fishing boats along the Thanlwin River mouth, including Mawlamyine, Kyaikkhami and Ahlet (Figure 1).

Figure 1(A) 4 growth rings on scale and (B) on otolith.

Growth parameters

For the preliminary estimations of asymptotic length (Lα) and growth constant (K) the length frequency distribution data was used in ELEFAN-I. The growth coefficient of Otolithoides pama was estimated by fitting the von Bertalanffy growth function (VBGF). The van Bertalanffy growth equation was defined by Haddon as: L_t=L_∞(1−exp(−K[t−t₀])), where, Lt is the length at the predicted time t, L∞ is the asymptotic length, K was the growth coefficient and the hypothetical age (t₀) is estimated by the empirical formula by Pauly as:

log10(‐t₀) =‐0.3922‐0.275 log10 L∞‐1.038 log10 K

The longevity was estimated as tmax=3/K³.

Natural and fishing mortality, and exploitation rate

The length of the converted catch curve was used to estimate instantaneous total mortality (Z), natural mortality (M) and fishing mortality (F) by using FiSAT package. The merged monthly data of length frequency distribution was arranged to obtain catch curve and natural logarithm (ln) of the number of individuals with respect to the age group (N) were designed against the results of their relative age (t).⁴ In order to obtain independent estimates of M, the subsequent formula of Pauly was used: Log10M=0.0066‐0.279 log10L∞+ 0.654log10 K+0.4634log10T. The annual average water surface temperature (SST) was taken as 28°C, because it was the average monthly water temperature. F was derived by subtracting Z from M. The ratio F/Z can also be used to obtain the exploitation ratio (E).

Virtual population analysis (VPA)

The inputs for VPA included ‘a’ and ‘b’ constants from length weight relationship, F, M, terminal fishing mortality (Ft) and growth parameters – asymptotic length (L∞) and growth rate (K). The required file for VPA was Length-frequency data file, while the required inputs were L∞ and K. However, it is noteworthy that L∞ must be at least 10% larger than the largest fish in the length frequency distribution. The actual procedure for VPA in FiSAT II was as follows: The initial step is to estimate the terminal population (Nt) given the inputs, from:

Nt=Ct· (M+Ft)/Ft, where Ct is the terminal catch (i.e. the catch taken from the largest length class). Then, starting from Nt, successive values of F are estimated by iteratively solving: Ci=Ni+t ·(Fi/Zi)· (EXP (Zi·ti)-1), where ti=(ti+1-ti), and ti=to-(1/K)· ln(1-(Li/L)), where population sizes (Ni) are computed from: Ni=Ni+t · EXP (Zi).

 Relative yield per recruit and biomass per recruit

Relative yield-per-recruit (Y′/R) was computed using the formula,

$Y^{\text{'}}/R=E{U}^m\left(1-\frac{3U}{(1+m)}+\frac{3U^2}{(1+2m)}-\frac{U^3}{(1+3m)}\right)$

$m=\frac{(1-E)}{(M/K)}=K/Z$ and $U=1-(L_C/L_{\infty })$

Relative biomass-per-recruit (B′/R) was estimated from the relationship

$B^{\text{'}}/R=\frac{(\frac{Y^{\text{'}}}{R})}{F}$

The value of Emax, E0.1 and E0.⁵ were estimated using the first 120 derivative of this function. Here, Emax is maximum sustainable exploitation rate, E0.1 is the exploitation rate which is the marginal increase of relative yield per recruit is 1/10th and E0.5 is value of E under which the stock has been reduced to 50% of its unexploited biomass.

Probability of capture

The probabilities of capture were estimated through the logistic transformation of the probabilities from the left hand-side of the length-converted curve fitted in FiSAT II Tool. Additionally, the length at which 25% and 75% of the stock captured were taken as corresponding to the cumulative probability at 25% and 75% respectively. The length at first capture (Lc 50) was taken as corresponding to the cumulative probability at 50%.

Recruitment pattern

Recruitment pattern was obtained by the backward projection of the frequencies into the time axis of a time-series defined by Von Bertalanffy growth equation. This routine reconstructs the recruitment pulses from the time series data of given length-frequency data to determine the number of pulses per year and the relative strength of each pulse.⁶

Age determination with otoliths and scales

To estimate the age of a fish the annual banding of otoliths and scales could read under the binocular microscope. Each pair of rings represents a year in the fish’s life (Figure 2). The growth rings were counted and the length at age data was input in FiSAT II Tool.

Figure 2 The map showing the stations conducted the present study.

A total of 4620 length frequency distribution data was used to estimate the growth parameters by ELEFAN method. The von Bertalanffy growth parameters for Otolithoides pama was estimated as L∞=40.9cm (SL) and K=0.98 per year (Figure 3). The t0 value was calculated by equation of Pauly as t₀=-0.78 per year.

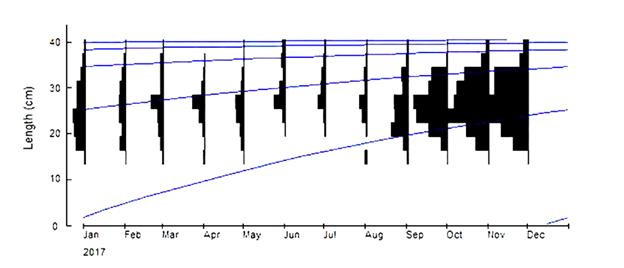
Figure 3 The total length, von Bertalanffy growth curve in this study during 2017 estimated (L∞=40.9 cm and K=0.98 year-1, t0=-0.78)

Mortality and exploitation rate

Applying the length converted catch curve analysis VBGF, the total mortality parameters of Z=2.24 per year was estimated at confidence interval (CI=-1.49-5.96). The value of M was calculated 1.52 per year, and F resulted 0.71, using annual average water surface temperature (SST) 28⁰C. E was found to be 0.32(Figure 4).

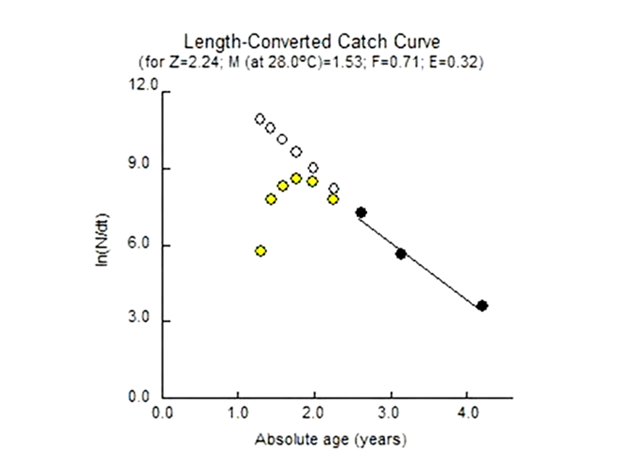
Figure 4 A Length converted catch curve analyzed for O. pama using input value of VBGF growth parameters (the von Bertalanffy growth).

Probability of capture and recruitment pattern

From the probability of capture analysis, L25, L50 and L75 values of Otolithoides pama were found to be 21.95 cm, 26.13 cm and 29.90cm, respectively (Figure 6A). The estimated L50 or Lc value indicates that the fish become susceptible to the fishing gear when it reach at 26.13 cm standard length, and at this length the fish has 50 % chance of being retained by the gear used to capture it14. A continuous recruitment of Otolithoides pama was done all along the year. It shows that there is one peak from March to October with 86.85% and the highest recruitment is in April with 16.11% (Figure 6B).

Figure 6 (A) Probability of Capture (showing the L25, L50 and L75)and (B) Recruitment pattern.

Virtual population analysis

Otolithoides pama began to experience natural losses due to natural mortality at the length interval of 15cm to 33cm, with the highest loss due to natural mortality observed at 15cm to 27cm and natural losses were decreasing with the increasing length. Catches by fishing gears occurred from size 15 cm and peaked at 27cm. The highest catches were at the length range of 24cm to 27cm. The maximum fishing mortality rate of 1.06 yr-¹ corresponded to length interval 33cm (Figure 5A).

Relative yield per recruit and biomass per recruit

The Relative yield-per-recruit (Y’/R) and biomass-per-recruit (B’/R) curve for different exploitation rates produced an Emax value from which Fmax was calculated. The value of Emax and corresponding Fmax were calculated to be 0.37 and 1.06, respectively. The E0.50 and E0.10 was found 0.247 and 0.308, respectively (Figure 5B).

Figure 5 (A) Virtual population analysis and (B) Relative Yield per Recruit and Biomass per Recruit

Age determination with otolith and scales

The relative growth of Otolithoides pama was shown in Figure 7. The potential longevity (tmax) as estimated by Pauly’s equation³ (3/K) was estimated as 3.06. Of the 54 otoliths, some otoliths were discarded because they were unreadable and some were broken. When the otoliths could not read, the growth rings of scales were used. A total of 54 otoliths and scales had three readings that 2 year fish was 16.6 % and three years had 55.7% and four years had 25.92% (Figure 8). The maximum age was four years.

Figure 7 Von Bertalanffy growth function fitted to age- length data from length frequency distribution data.

Figure 8 Von Bertalanffy growth function fitted to age- length data from growth band counting in otoliths and scales.

The present study was the first record about the stock assessment of Otolithoides pama in Myanmar although Ohnmar Min² & Kyaw Phone Maung¹² have studied the biology and age determination of O. pama. The fishing mortality (F=0.72) of O. pama was found to be lower than the natural mortality (M=1.52), which indicates the species is relatively underexploited in this region⁷ (Figure 4). However, Gulland⁸ noted that the exploitation rate should be lower than 0.5, while Patterson⁹ stated that the exploitation rate should be kept at 0.4 and if the exploitation values exceeds 0.4, it should be assumed that stock is overexploited state. As a result of the present study, the stock of O. pama is not overexploited on account of the exploitation rate obtained (E= 0.32). On the other hand, it is likely to be overexploited state in the future if the fishes would be more exploited than the present rate since the value of E was found to be 0.32, which is nearly equal to the maximum sustainable yield (Emax=0.37). Furthermore, it can be considered that this can be perhaps because the species O. pama is commercially being exploited in the study area and there is slightly high pressure on this species.

The value of Emax and corresponding Fmax were found to be 0.37 and 1.06, respectively. The result suggested that the fishing mortality (Fmax) should be increased to 1.06 per year to obtain the maximum sustainable exploitation rate (Emax=0.37) for this species. The result of YPR analysis indicated that, although the current fishing mortality (0.72) was not very high, most of the croakers were caught by fishermen before reaching standard size, without economic advantages.

According to the results from VPA, small sized fish species experience low fishing mortality rate, whereas large-sized fish species encounter high fishing mortality rate, depicting that fishing mortality rate is size specific. Considering harvesting rate, fish species within the large mid-length groups experienced relatively higher harvesting rate (catches) than fish species contained by small mid-length groups (Figure 5A). It can be possible for the consumer satisfaction by economic reasons.

Recruitment is demonstrated with a graph that displays variation in intensity of recruitment with time. In this population there was one major recruitment peak in a year to give a continuous year-round pattern (Figure 6B). As a general rule, if Z/K ratio <1, the population is growth-dominated, if it is >1, then it is mortality-dominated; if it is equal to 1, then the population is in equilibrium state where mortality balances growth.¹⁰ In this study, Z/K was 2.48 indicating that O. pama was being lost by both normal mortality and fishing mortality.

Estimates of the probability of capture indicate that 25%(L25) of the fish would be retained in the meshes of the gears if fish of 21.95cm is targeted and the remaining 75% escaped capture. Also if 26.13cm and 29.90cm were targeted 50% and 75% (L50 and L75) would be retained respectively in the meshes of the gears used for fishing on the estuary (Figure 6A). The L50 was referred to as length-at-first capture (Lc). Mess and Rousseau¹¹ also described L50 or Lc is greater than Lm (length-at-first maturity), effort controls are less important and overfishing is unlikely to occur. In this study, L50 or Lc = 26.13cm is too much less than Lm=100 cm estimated by Fishbase¹³ in Myanmar. Therefore overfishing has a potential to occur in the future.

In reference with length based approach, the life span of O. pama was estimated as 3.06years. Accordingly to the growth rings on sagitta otoliths and scales, the maximum year of this fish was found 4years. However Kyaw Phone Maung¹² reported that the maximum year of this fish was 3 years in his otolith study. Therefore it can be infered that O. pama is medium to high longevity and slow to moderate growth.

The stock of Otolithoides pama is not overexploited and the fish might be one of the commercial fishes in the study area in relation with their mortality and exploitation rate. In addition it is shown that larger fishes were being harvested higher than smaller fishes on account of the consumer demands. Although the local fisher men said that there was a declining problem for fish population in Thanlwin River Mouth, the declining reasons for O. pama were not definitely found in the results based on the present study. Unfortunately, there were not any previous records about the stock assessment of O. pama in Myanmar to consider the variations of fish population.

I would like to express my gratitude to Dr. Aung Myat Kyaw Sein, Rector of Mawlamyine University, Dr Mie Mie Sein and Dr San San Aye, Pro-rectors of Mawlamyine University for their permission to undertake this research work. I would like to express my sincere thanks to Dr. San Tha Tun, Professor and Head of Department of Marine Science in Mawlamyine University and Dr. Naung Naung Oo, Assistant Lecturer, Department of Marine Science in Mawlamyine University for their advices and their needful assistances.

Authors declare that there is no conflict of interest.

1. Druzhinin AD. Distribution of Lutjanidae and Sciaenidae (Pisces) of the Indian Ocean. Indian J. Fish. 1971;18(1&2):52– 66.
2. Ohnmar Min. Fishery biology of Sciaenid fishes in Mon Coastal Waters. Unpublished PhD. Dissertation. Department of Marine Science. Mawlamyine University. Myanmar. 2013. 305 p.
3. Pauly D. Fish population dynamics in tropical waters: A manual for use with programmable calculators, studies and review. Manila, Philippines: International Center for Living Aquatic Resources Management. 1984;(8):325 p.
4. Pauly D. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J du Con. 1980; 392(2):175–192.
5. BOBP (Bay of Bengal Program). Marine small scale fisheries of Bangladesh: A general description, BOBP/INF/08, Madras, India. 1885; 35 p.
6. Gayanilo FC, Sparre P, Pauly D. FAO–  ICLARMStock Assessment Tools II (FiSAT II), user’s guide, computerized information series (Fisheries) No. 8, (Revised Version), Food and Agriculture Organization of the United Nations, Rome, Italy. 2005; 168 p.
7. King M. Fisheries biology assessment and management. Fishing News Books, Oxford. 1995; 341 p.
8. Gulland JA. The concept of the maximum sustainable yield and fishery management. FAO Fisheries Technical Paper. 1968; 70, 265 p.
9. Patterson K. Fisheries for small pelagic species: an empirical approach to management targets. Rev Fish Biol Fisheries. 1992; 2(4):321–338.
10. Barry JP, Tegner MJ. Inferring demographic processes from size– frequency distribution: simple models indicate specific patterns of growth and mortality. US Fish Bull. 1989;88:13–19.
11. Mess CC, Rausea JA. The potential yield of the Lutjanid fish Pristipomoides filamentous from the Malie Plateau, Seychelles: managing with uncertainty. Fisheries Research. 1997;33:73–87.
12. Kyaw Phone Maung. Estimation of Age– Determination in Croaker Fish. Unpublished MSc. Thesis. Department of Marine Science. Mawlamyine University. Myanmar. 2011. 53 p.
13. Frose R, Pauly D. Fishbase. World Wide Web electronis publication.
14. King M. Fisheries biology assessment and management. Fishing News Books, Oxfords. 1995; 341 p.