The limits of the six biomes of the Brazilian territory (i.g. Amazon, Atlantic Forest, Cerrado, Caatinga, Pampa and Pantanal) were recently revised,¹ and a new territorial section of the ocean-continent interface, called Marine Coastal System (CMS) was presented. However, despite being a central theme for conservation planning, the spatial relationship between federal conservation units of Brazil (FCU) and CMS remained without integration. In this work we investigate ecological and territorial representativeness of FCU on Brazil's four geopolitical regions with biomes and ocean interface by developing spatial modeling (five models) encompassing a broad biogeographic context. The objective was to determine the spatial relationship between CMS and FCU, through the application of a set of topological and algebraic rules. Maps of spatial distribution of the FCU in the 5 biomes and in the 4 geopolitical regions shows overlapping CMS. The results indicate that among the 63 FCU found by the M_5 model, 51 FCU present a territorial sharing area with 5 biomes: Amazon, Pampa, Atlantic Forest, Caatinga and Cerrado. In the Amazon and Pampa biomes occur the largest area of overlap with the CMS, but the highest concentration of FCU occurs in the Atlantic Forest biome. The CMS area in the Northeastern region presented the highest environmental heterogeneity, and overlaps four biomes, encompassed most of the FCU of the ocean-continent interface, and also evidenced that the lack of integration of both legal concepts and government databases might cause differences on ecological and territorial representativeness of FCU on Brazil's four geopolitical regions with biomes-ocean interface.

Keywords: algebraic topology; geospatial analysis; conservation unit; biodiversity; conservation laws and policies

1. New Brazil’s Coastal-Marine System have 63 Federal Conservation Units
2. Lack integration of governmental database negatively affect the conservation
3. Interface of the Coastal-Maritime System with Caatinga and Pampa needs protected areas
4. Ecological and geographical representativeness highlighted by geospatial analysis

At the end of 2019, the Brazilian Institute of Geography and Statistics (IBGE) published an interdisciplinary report entitled Biomes and Marine Coastal System.¹ In this work, geospatial analyses supported the revision of the limits of the six biomes of the Brazilian territory (i.g. Amazon, Atlantic Forest, Cerrado, Caatinga, Pampa and Pantanal) and allowed the mapping of biomes with a 1:250,000 reference scales. In addition, a new territorial section was presented, from the biomes-ocean interface, called Coastal-Marine System (CMS). IBGE is Brazil's main provider of both spatial data and geostatistical information, which are used for legal purposes and to define governmental policies of country.

IBGE¹ highlighted 4 important points related to the geometry and geobiodiversity of the CMS. First, the total area of the CMS (194,837 km²) includes a continental part, and three structuring factors were considered for this domain: geology, geomorphology and vegetation; second, the limit of the oceanic part of the CMS is related to the outer edge of to the 3 Large Marine ecosystems (LMEs) of the Brazilian continental margin (North, East and South Brazil Platforms); third, the CMS continental part was mapped at 1:250,000 scale ; and fourth, the continental part of the CMS should be interpreted as a "territorial sharing area with the biomes".

According to the IBGE,¹ the definition of Brazilian biomes states: “biome represents the biotic unit with the largest geographic extension, encompassing various communities in different stages of evolution, however it is determined accordingly with the dominant vegetation cover". Thus, the biome bears a singular biodiversity, fauna and flora, associated with a vegetation cover identifiable on a regional scale, besides physical predominant aspects related to climate, geology, geomorphology, and pedology.

The CMS predominantly represents marine domains (93.7%), which do not correspond to the concept of biomes from the same IBGE. The terrestrial part of the CMS (6.3%) corresponds to the geographic areas of terrestrial biomes along the eight thousand km of Brazilian coastal domains. The CMS’ terrestrial part is under direct influence of climatic and physical-chemical forces determined by the vicinity of the sea.^2–6 The interaction between these forces, at various levels, plays a key role in explaining the disjunctions of vegetation and geomorphology at the ocean-continent interface. In this territorial range, there is the delimitation of specific coastal ecosystems, such as mangroves, sandbanks and dunes.^7,8

On national scale a critical question arises regarding the creation of the CMS¹ to treat the conservation planning in the ocean-continent interface zone: what is the ecological and territorial representativeness of the Federal Conservation Units (FCU) in the CMS? The administration, protection, enforcement and monitoring of FCU are performed by another government agency, the Chico Mendes Institute for Biodiversity Conservation (ICMBio). The databases of these two governmental institutions are managed independently and are not integrated.

Conservation units are protected areas, created by the ICMBio to protect biological diversity, genetic resources and threatened species, with the main goal to conserve and restore diversity in natural ecosystems.⁹ Brazil’s FCU represents 171 million hectares,¹⁰ which protects a representative part of global biodiversity.¹¹ In general, protected areas support several types of ecosystem services and are essential for the success of conservationist policies,¹² both for threatened species (e.g. IUCN Red list of threatened species), and maintenance of the structural elements of ecosystems.¹³

Conservation planning in the CMS depends on the biogeographic representativeness of the FCU in the ocean-continent interface region.^14,15 Geometry is necessary to determine the topological relationship between the pairs of territorial clippings FCU - CMS, through the selection and delimitation of geographical spaces.¹⁶

To address the problems that could arise in the spatial representation of FCU over the CMS we have used an algebraic topological method processed on a Geographic Information System (GIS) environment to test the different spatial arrangements and discuss its implications to the public policies and conservation planning on large spatial scale, such as biome and geographic regions.

In GIS environment, geospatial analyses make it possible to identify multidimensional relationships, which characterize geographic spaces and their various structural elements.^17,18 The recognition of the topological relationship between the geometries of geographical spaces precedes other multidimensional analyses of interest and it is the tool used by government institutions to manage the use of space in cities, and for monitoring and conservation planning of natural biodiversity.^19,20 Analyses of multidiscipline data is critical to enforce protection of accelerated species loss preservation of natural habitats or restoration of ecosystems.^21–23

Possible spatial relationships between geographic spaces (e.g. FCU - CMS), can be described based on algebraic concepts. These concepts usually apply to a two or three-dimensional Euclidean space^24,25 and present definitions based on the theory of sets and Boolean algebra and matrices. However, the conservation management of natural resources in extensive areas (>100,000 km²), such as the CMS, also requires the integration of biotic and abiotic data, which better describe the environment and its conditionings on a regional scale.^26,27 If these requisites are observed for analyses in a regional scale (1:250,000), environmental heterogeneity can be spatially qualified and quantified by attributes related to geology, geomorphology and plant typologies.^2,28,29

Because of the recent integration of the CMS to the official division of maritime limits of Brazil and the continuous need to advance the activities for conservation of national coastal-marine protected areas,^14,30–32 it is necessary to verify what kind of integrated information can be extracted from the government national databases regarding the location and spatial relationship of these units and the biomes along the geographic regions.

The work aimed to test how the manipulation of government databases, with commonly used GIS tools, represents the spatial relationship between the FCU and the CMS, in relation to the 5 biomes and in the 4 geopolitical regions of Brazil. The consideration of geopolitical regions is important because the present system of FCU management is executed by 5 national management offices of ICMBio.

Here we show that the lack of integration of both legal concepts and government databases might result on different ecological and territorial representativeness of FCU on Brazil's four geopolitical regions with biomes-ocean interface.

Database

The set of vector and geostatistical data applied in this study are freely accessible and were obtained from the database of two government agencies, ICMBio and IBGE. The limits of the FCU and associated geostatistical data, was acquired from ICMBio in shapefile format (.shp).³³ The limits of the CMS were acquired from IBGE in shapefile format.³⁴

The GIS was referenced to the geographic coordinate system: GCS_SIRGAS_2000, Angular Unit: Degree, Prime Meridian: Greenwich (0.0), Datum: D_SIRGAS_2000, Spheroid: GRS_1980. The original file in shapefile format (polygon feature), is available in the ICMBio database, and constitutes an asymmetric matrix with 17 columns (attributes) and 334 rows (elements). The shapefile file corresponding to the CMS, is available in the IBGE database, constitutes a matrix with 5 columns (spatial attributes) and only one row (element). Finally, the database now houses a large amount of vector and geostatistical data stored in the form of interrelated matrices.

Base layer and target layer

The two feature classes, FCU and CMS, have been added to the software content table towards recognition of the area of study and initial exploratory analyses (Figure 1).

In Figure 1, the CMS feature class is indicated as the base layer, while the target layer is the feature class, which represents the geometry of 334 conservation units (FCU). In the target layer there is a subset of FCU which is overlapping to the CMS, and can be selected separately, based on algebraic topology models.

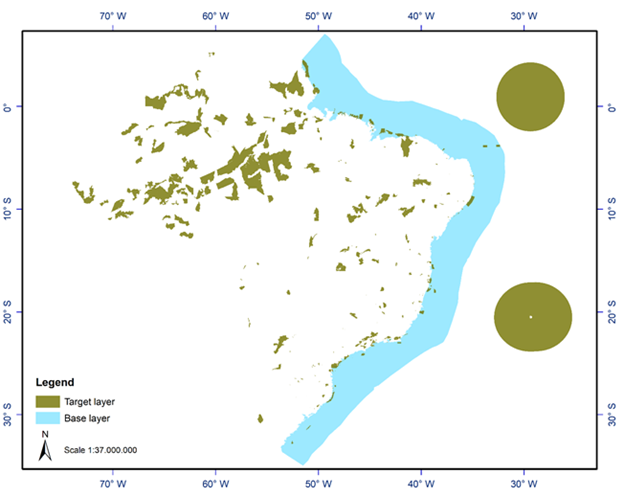
Figure 1 Feature class of base and target layers. The base layer represents the geometry of the new territorial division called Coastal-Marine System – CMS (Source: IBGE). The target layer represents the geometry of 334 federal conservation units – FCU.³³

Algebraic topology

Algebraic conceptual model

The spatial and geostatistical data allowed us to apply the concept of spatial object to represent the real condition.³⁵

These spatial objects (e.g. geometry of conservation units), as a basic element of the mathematical universe, has an algebraic solution in a real coordinated space, in the ordered pair ${ℝ}^2$  ( $ℝ$  = set of real numbers), according to algebraic model suggested by Camara et al.³⁵

so = [S, A, ƒ]   where:

so   is the spatial object (i.e. geographic space)

$\text{S}$ $\subset$ ${ℝ}^2$ is a subset of the Euclidean 2D plane (${ℝ}^2$ ) (geometric support)

A is a domain set of attributes A₁, A_{2 ,} ...... , A_n

$ƒ:\text{ S}\to {\text{A}}_{\text{1}}\text{x} {\text{A}}_{\text{2}}\text{x} \mathrm{......} {\text{xA}}_{\text{n}}$ is the attribute function of the spatial object. For each location of the geometric support there is an associated value of the attribute domain.

In the algebraic model applied in the present study, the spatial object (e.g. conservation unit, CMS) is a subset of the two-dimensional Euclidean plane $\text{S}$ $\subset$ ${ℝ}^2$ , which has a set of attributes A (e.g. geology, geomorphology, vegetation), which are associated as a function of location $ƒ:\text{ S}\to {\text{A}}_{\text{1}}\text{x} {\text{A}}_{\text{2}}\text{x} \mathrm{......} {\text{xA}}_{\text{n}}$  (e.g. geographical regions, biomes).

Using a formal definition, the modeling was based on a spatial predicate, here denoted by $\text{ξ}$  where the spatial relationship of FCU and CMS pairs – so_i and so_j – had topological restriction. So, the FCU set of the target layer are space objects $\text{SO = {} {\text{so}}_{\text{1} }\text{, }\mathrm{...}{\text{, so}}_{\text{n}} \text{}}$ which has as spatial reference the object of the base layer {so*}. The spatial selection operation had topological restriction $\text{φ: SO}\to \text{SO}$  and spatial predicate $\text{ξ}$ , which related the spatial objects so $\in$  SO to the so* object. Thus, the mathematical expression of the spatial relationship between the target layer and the base layer (Figure 1) is defined by the Equation 1:

${\text{φ}}_{ \text{ξ}}\left(\text{S} \text{O}\right)=\{\text{so}\in \text{S} \text{O }| \text{ξ} \left( \left(\text{s} \text{o},\text{ s} \text{o}*\right) \right)\}$    Eq. 1

Topologic rules

Four topological rules were applied to extract subsets of spatial objects (e.g. FCU) from the spatial relationship between the base and target layers (Figure 1), according to topological structure models. The definition of each topological rule and its graphic models, in addition to the respective mathematical representations of matrix calculus are indicated in the diagrams in Figure 2.

Figure 2 Topological rule diagrams used in the spatial analyses. Polygon A represents the base layer. Polygons B - F and centroids B - D represent spatial objects of the target layer. Right to each diagram; show a general model of the matrix scheme of topological relationships between pairs of features. The spatial relationships are binary, where each intersection pair can be empty (⦰) or occupied (⌐⦰), considering the spatial relationship of the objects, regarding their boundary (∂), interior (i) and complement (e).

The topology spatial relationships between the base and target layers is based on the principles of disjunction, adjacency and coincidence between pairs of features,^36,37 as polygon - polygon and polygon - point (Figure 2). The interactive computational processing bases on the geometric model and the topological rules aimed to identify in the target layer different types of spatial arrangements of the conservation units in relation to the geometry of the base layer (CMS).

The flow of spatial analyses in this study applied the concept of the Jordan's Theorem^38,39 and interpreted the polygon feature class as a list of arches that represents its border and defines its perimeter. Point, by definition, is a zero-dimensional object.⁴⁰

The first three diagrams of Figure 2 are graphical representations based on the interpretation of the binary topological relations model developed by Egenhofer et al.,⁴¹ to compare the boundary ( $\partial A,\partial B$  and interior (A, B) of objects embedded in a space ${ℝ}^2$ . Thus, the first three diagrams of Figure 2 were algebraically represented by a $\text{2X2}$  matrix, called 4-intersection⁴² as show in Equation 2:

${\Im }_4\left(\text{A,} \text{B}\right)= \left[\begin{array}{cc}A\cap B& A\cap \partial B\\ \partial A\cap B& \partial A\cap \partial B\end{array}\right]$    Eq. 2

In the case of diagram four of Figure 2, the topological relationship is between polygon – point features, which are objects embedded in different dimensions, since points are zero-dimensional objects and are incorporated into the ${ℝ}^0$  dimensional space.⁴⁰ Then, diagram four was based on the mathematical model of spatial relations proposed by Egenhofer et al.,⁴³ and computed by the winding number method,^44,45 accordingly to Equation 3:

$wn={\displaystyle \sum }_{ i=0}^{ n-1} co{s}^{-1}$    Eq. 3

Where $v_{i = v1, v2, v3, \mathrm{.....} vn}$  are the vertices of the polygon, unit vector of the point of each vertex. Thus, if:$wn=0$ ⇒ indicates that the point is outside the polygon, otherwise the point will be within or at the polygon boundary.

Thus, the topological relationship polygon – point (diagram four) established that the space in ${ℝ}^2$ , defined by the interior A and the border, has a binary topological relationship with a finite subset of coordinate points ${\text{(Xn}}_{\text{i}}{\text{, Yn}}_{\text{i}}\text{)}$ . The topological relation has returned the appropriate value empty ⌐$\bcancel{{\rm O}}$ or non-empty (⌐ $\bcancel{{\rm O}}$ ), by comparing the geometry of the polygon with the point feature. The model has returned non-empty (⌐ $\bcancel{{\rm O}}$ )if the dot matches with A or $\partial A$ . Alternatively, the model has returned empty $\bcancel{{\rm O}}$ ) if any of these conditions are not met, indicating that the point is located in the complement (exterior).

For example: let A⁰ be the set of points that returned non-empty (⌐$\bcancel{{\rm O}}$ ). If A⁰ is within A or on boundary $\partial A$ , then the topological setting of rule 4 is true. In the spatial model developed in this study, the feature of points is represented by the centroids of the polygons of 334 federal conservation units.

Centroid calculation

The feature of points corresponds to the centroids calculated for the geometry of each of the 334 FCU, contextualized in the biomes and geographical regions (Figure 3). The objective was to identify the geographic center of the conservation unit area and use it as a spatial reference in the geometric model. Once the polygons of the FCU areas are predominantly associated with irregular geometries, the general case of centroid calculus was applied by differential and integral calculus. Thus, the coordinate pairs X_Centroid and Y_Centroid were obtained, using the Calculate_Geometry of ArcMap^TM. The complete FCU's centroids list is given in Appendix A.

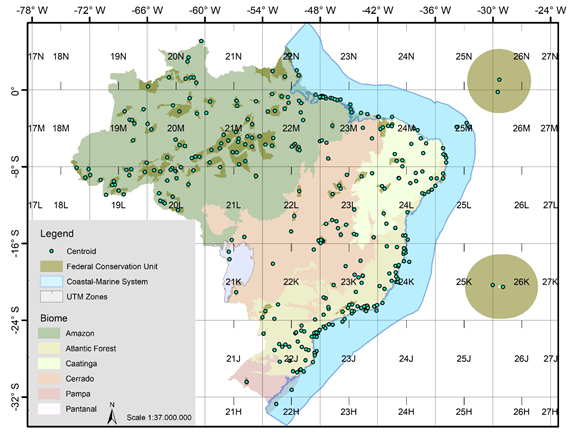
Figure 3 Location of centroids of 334 federal conservation units of Brazil. The perimeters of some FCU are not visible due to map scale. The position of the central meridian of each UTM zone is indicated by a vertical line perpendicular to the latitudinal line. Base map layers source: CMS and Biomes layers (IBGE); Federal Conservation Units layer (ICMBio).

Algebraic-topological models with independent spatial structures

The mathematical method used to compare the base and target layers (Figure 1), does not depend on the extent, type or geometric shape of the objects. The types of spatial relationships resulting from geometric modeling were highlighted in 4 subsets of elements of the target layer (FCU), according to the respective topological rules (Figure 2).

In addition to these 4 subsets, a fifth subset was obtained by consulting directly to the ICMBio database, using Boolean operators in SQL (Structure Query Language). In this way, the 5 subsets of elements correspond to spatial structures independent of each other, but all subsets are contained in the database of the target layer (334 elements).

In the ICMBio database, each element corresponds to a row in the table and each row corresponds to only one unit of conservation, which is described by 17 attribute domains. At the end of each round of analysis, the elements selected in the database and their attributes have been exported as a new feature class, which were named Model_1, Model_2, Model_3, Model_4, and Model_5. The results are shown in the form of maps.

Model_1 (M_1): the cartographic representation of the FCU relationship with the CMS zone obtained in this model corresponds to what is currently in use for government policies in Brazil. The shapefile file obtained from the ICMBio database, has no metadata. However, the examination of the structure of the database revealed the existence of a string type attribute domain named 'biomaIBGE,' which contains a value named 'MARINE COASTAL'. Thus, the query to the database and the selection of matrix elements was executed using expressions in SQL language and Boolean logic. The selected subset of the data matrix was exported to feature datasets as M_1 in the file and personal geodatabase feature class format.

Models 2 to 5 (M_2 to M_5): These models correspond to the new classes of features obtained after computational processing of topological rules. The cartographic representation and the relationship of FCU shown in each model correspond to the application of only one topological rule. Thus, the classes of features named M_2, M_3, M_4 and M_5 correspond, respectively, to the ordered sequence of the 4 topological rules presented in the diagrams shown in Figure 2. In order, the four selected subsets of the data matrix, in each round of analyses, were exported to the GIS feature datasets.

Model_1: the 'coastal marine' system according to ICMBio data

In the M_1 model, 26 FCU have been found in the attribute field of the ICMBio database, by using the 'coastal marine' value. Among the selected FCU, 10 are located in the coastal zone and 16 are islands. Some national parks such as “Lagoa do Peixe, Lençóis Maranhenses and Jericoacoara, RESEX Marinha do Delta do Parnaíba and ARIE Ilha Do Ameixal” were not shown by this selection. The acronyms refer to the category of conservation unit according to National System of Conservation Units (SNUC) of Brazil, and the acronyms meaning is give in Appendix A.

The cartographic representation of the model M_1 (Figures 4C1, 5C1, 6C1 and 7C1), shows that the southern, northeast, and southeast geographical regions have a low density of conservation units, although several FCU contained in the borders of terrestrial biomes are visibly overlapping with the CMS. The map of the northern region (Figure 7C1) does not present any FCU, which means that there is no 'coastal marine' FCU in this region of Brazil, according to the current ICMBio database. The ID numbers indicated on the maps correspond to the federal conservation units given in Appendix B.

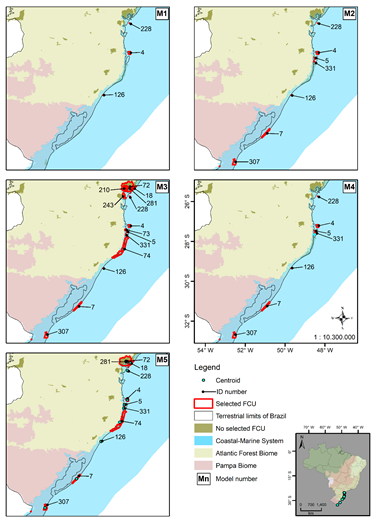
Figure 4 Brazil's southern region. The panels show the simplified cartographic representation of models M_1 to M_5, regarding topological relationship between FCU and CMS. The ID numbers indicated on the maps correspond to the federal conservation units given in Appendix D.

Figure 5 Brazil's northeast region. The panels show the simplified cartographic representation of models M_1 to M_5, regarding topological relationship between FCU and CMS. The ID numbers indicated on the maps correspond to the federal conservation units given in Appendix D.

Figure 6 Brazil's southeast Region. The panels show the simplified cartographic representation of models M_1 to M_5, regarding topological relationship between FCU and CMS. The ID numbers indicated on the maps correspond to the federal conservation units given in Appendix D.

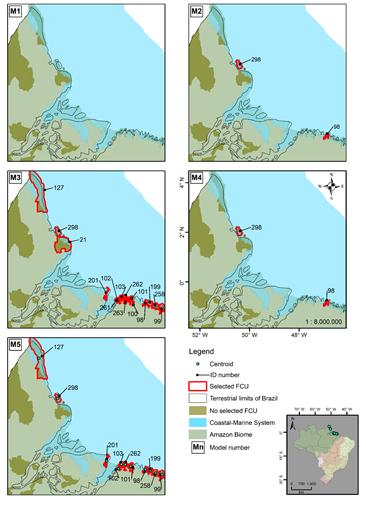
Figure 7 Brazil's north region. The panels show the simplified cartographic representation of models M_1 to M_5, regarding topological relationship between FCU and CMS. The ID numbers indicated on the maps correspond to the federal conservation units given in Appendix D.

Most of the 26 FCUs found by the M_1 model is apparently overlapping with the CMS, with the exception of 4 large FCU, which are indicated by 2 circles in Figure 3. The circle to the north encompasses the geometry of the Preservation Environmental Area (APA) and Natural Monument (MONA) of the Archipelago of São Pedro and São Paulo. The circle to the south encompasses the geometry of the APA and MONA of the Trindade and Martim Vaz Archipelago and Mount Columbia. These latter two FCU are located in Areas beyond National Jurisdiction (ABNJ), because they are FCU located beyond the Exclusive Economic Zone of Brazil (EEZ).

Applying algebraic topology in spatial relationship modeling

The APA and MONA of the Archipelago of São Pedro and São Paulo and the APA and MONA of the Trindade and Martim Vaz archipelago and Monte Columbia, were not selected in the M_2 to M_5 models, because there is no topological relationship of adjacency or coincidence between the base and target layers, which means that their geometry is disjointed relative to the geometry of the base layer (CMS). The five models created (from M_1 to M_5), found a total of 86 FCU, which represents about 25% of all FCU in Brazil (Appendix B- sorted by ID).

Models from M_2 to M_5 was obtained through the integration of 4-intersection⁴² and winding number methods.^44,45 Appendix C presents the result of the matrix model of binary topological relationships of order , according to the application of the binary topological rules indicated in the diagrams of Figure 2.

The models M_2 and M_4 found a total of 12 insular FCU of both Marine Island and fluvial island types, in addition to another 14 FCU located at the continent - ocean interface. The models M_2 and M_4 presented identical distribution of FCU, which indicates that by the rules used the 26 FCU geometries are represented within the CMS geometry.

The M_3 and M_5 models found an expressive number of FCU, 25% of the total FCU, which indicates the existence of different types of topological relationships between the base layer (CMS) and the target layer (FCU), when considering the topological relationship between polygon - polygon and polygon - point.

The M_3 model, with less restrictive topological rules (Figure 2), revealed that 82 FCU have a topological relationship with CMS by considering the polygon – polygon relation. The model M_5 found that 63 FCU present the centroid coordinates located within or on the boundary of the CMS.

Algebraic topology and the indication of CFUs overlap with the CMS

The CMS has a wide longitudinal variation overlapping with 4 UTM zones (Universal Transverse Mercator) and is completely inserted in the EEZ over areas which the country has sovereignty. Outside the limits of the EEZ the creation of Brazilian protected areas depends on international agreement.⁴⁶

The M_1 model found 4 large federal conservation units located beyond the external limits of the CMS: two located on the limits of the EEZ and two located in international waters zone (Figure 3). Thus, in future reviews of the current limits of the CMS, it is necessary to include the geometry of these FCU, because their obvious relevance, both in area and in terms of their ecological representativeness.^47,48 Protected areas located in international waters (ABNJ) are important for the conservation of global biodiversity.⁴⁹

However, the definition of strategies for the conservation of biological diversity of the two CFUs located outside the Exclusive Zone of Brazil is a complex task, because it represents a theme still poorly known by scientists and little addressed by policy makers.^48,50 The model M_1 revealed a situation in which the FCU found does not agree with reality. Thus, this model shows that the use of government database will provide a completely inadequate answer to the basic applications for legal purposes, such the real number of FCU located within the CMS and their relationship with other legal limits (states, cities, biomes).

The M_2 and M_4 models produced maps with 12 FCU related to eleven oceanic islands, and one fluvial island, in addition to 14 other FCU located at the biome – ocean interface. However, some coastal FCU were not found, such as the Coral Coast APA, Parnaíba Delta APA, Algas Coast APA and Tamoios ESEC. The exclusion of FCU located on coastal areas and islands of remarkable importance indicates that the way the information is placed on the database cannot result in adequate reports, regarding the simple consultation about the real number of FCU related to the new CMS limits.

The inadequacy of the topologic processing for models M_2 and M_4, based on the interaction between pairs of irregular polygons, may be associated with two factors: a) in some parts, along the shoreline, the overlap range between the continent and the CMS is narrow, which prevents the limits of the FCU from being completely within the CMS; b) topological rules 1 and 3 (Figure 2) require that "the geometry of the target layer element must be completely within the geometry of the base layer", while the spatial model proposed by IBGE (2019) admits a partial overlap between features of irregular polygons, represented by the irregular geometry of the CMS and biomes. Thus, to improve the M_2 and M_4 models, it would be necessary to determine, in the topological rule, what is the degree of partial overlap of the CMS - FCU pair for the FCU to be selected. This presents itself as a quantitative challenge, both for the theoretical bases of the structuring vectors proposed by IBGE (2019), and to select alternatives among the various types of non-empty topological interactions, considering irregular polygons pairs in ${ℝ}^2$ .⁴¹

The higher number of FCU found in the M_3 model is explained by the application of rule 2 (Figure 2), which offered less topological restriction than any other topological rule tested. Thus, the matrix model returned non-empty ${(}^{}\bcancel{{\rm O}})$  in all possibilities of topological relation between two polygons.^36,41,42 However, in the topological processing of M_3 a ‘geometric mismatch’ was also observed. In this model, the topological relationship between polygon-type features – polygon enabled the selection of FCU whose border only touched the border of the CMS. According to Jordan's Theorem,³⁸ the boundaries of polygons are "a list of arches" and arches are objects embedded in ${ℝ}^1$ which means a one-dimensional object.^39,40,42 Thus, geometric principles indicate that there is no territorial sharing area between polygons, as is required in the IBGE spatial model,¹ because the area is a property of objects incorporated in the two-dimensional Euclidean space ${ℝ}^2$ .

The model M_5 (63 FCU) represents a subset of the number of FCU found in M_3 (82 FCU), although they derive from very distinct algebraic-topological models. While the topological rule applied to process the M_3 model establishes spatial relationships between polygons,⁴² the topological rule applied to the M_5 model, imposed topological restrictions based on a binary state of presence or absence of an infinitesimal point,^44,45 indicated by the centroid, i.e., by the geographic center of the FCU. In the M_5 model, the selected FCU has its geographical center within the SMC or is on its border.^40,42 Therefore, when complying with topological rule 4 (Figure 2), it is expected that the total or partial territorial sharing of the FCU with the CMS should be a valid condition, because the point is in the geographic center of the conservation unit. Thus, the model M_5 represented the most robust approach to represent the real distribution of FCU which overlaps with the CMS. The rule of M_5 model showed the most coherent topological analysis and meets the spatial condition proposed by IBGE,¹ regarding the sharing of information between the biomes (terrestrial) and the CMS. Output data obtained after the processing of the M_5 model, in the shapefile format, was made available in the Mendeley Data repository.⁵¹

The spatial component shared between the biomes and the CMS is related to the continental FCU. In the case of the 12 oceanic islands (e.g. Parna and Fernando de Noronha's APA, among others), the concept of biome does not apply. Thus, the inclusion of oceanic islands in the M_5 model occurred because they all have their centroid coincident with a pair of geographic coordinates within the CMS limits. The inclusion of oceanic islands occurred only because the applied topological criteria.

However, the selection of CFU overlapping the CMS in its continental part must go beyond the definition of geographic space based on the metric of mathematical models, or topological rules or concepts related to the distance, proximity and vicinity of spatial objects.²⁵ The representation of FCU in these databases need careful treatment, in this context for model, and it should have included environmental descriptors convergent with the geomorphology, geology and vegetation of the biomes.

Spatial relation of biomes and geographical regions with the FCU

Biomes

The Amazon and Atlantic Forest biomes are home to the largest number of FCU found within the overlapping zones between biomes and the CMS. These biomes also contain the largest number of FCU.¹⁰ Considering the number of FCU in the overlapping zones between the Pampa, Cerrado and Caatinga biomes with CMS in the M_5 model we have found the smallest number (Figure 8), despite the relevant continental area that these biomes have overlapped with the CMS.¹ The Pampa biome shares 25% of its total area with the CMS.¹ In this extensive territorial domain, the M_5 model found only two FCU, PARNA da Lagoa do Peixe and ESEC do Taim (Figure 4 and Appendix B), both of which are located near the coastline. The responsibility over the CFU is carried out by the five regional offices of ICMBio (legal jurisdiction), and in Figure 8 we also showed the number of FCU found in the overlapping zone between biomes and CMS by the four geopolitical regional divisions (Figure 8E and 8F). The Northeastern regions present the largest number of FCU on this condition.

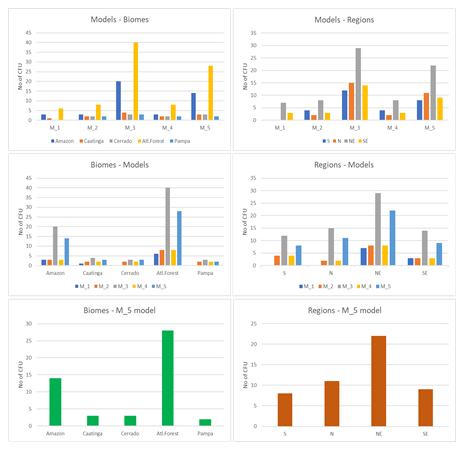
Figure 8 Spatial relationships between FCU and CMS regarding their origin from Brazilian biomes and distributed by the geographic regions. M_5 model is the most representative of the FCU overlapping to CMS, when compared to all other models.

The area of conservation between the CMS and the Cerrado biome, which represents 8.9% of the total amount of area shared by all biomes, has a relatively short coastline,¹ and the model found 3 FCU in the CMS overlapping with this biome.

The Caatinga biome occurs exclusively in Brazil,⁵² and it occupy mostly the northeastern region, and three FCU from this biome share location with the CMS, with possible phytogeographic disjunction related to the island environment of Fernando de Noronha.⁵³ The coastline which marks the oceanic limits of the biome is relatively long, but the overlapping of the Caatinga biome with the CMS is the smallest among the five biomes.¹

Despite the long coastline of the Atlantic Forest biome is with the Amazon biome that the CMS presents the largest territorial overlap.¹ In the Amazon domain, the M_5 model found 11 FCU, but this number should increase in the future with the acquiring of more information about geology, geomorphology and vegetation. For model, the centroids of REBIO Lago Piratuba (ID 21) and of the RESEX Chocoaré-Mato Grosso (ID 100) are close to the present limit of the CMS.¹ However, these FCU do not have an approved official management plan, which should contain the environmental descriptors of the FCU, within the reserve itself and in the surrounding area, and that could change the spatial definition of both FCU and CMS limits. Management plans are technical-scientific documents that establish the zoning, land use, and management of natural resources of FCU.⁵⁴ In general, the Amazonian units have difficulty in implementing the management plan due possibly the scarcity of information at the regional level.⁵⁵ The improvement of technical-scientific information would certainly bring better representation of FCU in the CMS.

The Amazon biome is mostly represented by Dense Ombrophile Forest, which occurs in about 20% of the CMS area.¹ In addition to this phytophysiognomy, the biome houses other types of vegetation typical of the CMS, such as sandbanks and mangroves, which occur in a large sector near the coastal zone, mainly in the State of Pará,^55–57 where are most of the FCU found through the M_5 model. Recent evaluations of the coastal regions of the Amazon³² indicated that most of its coastal ecosystems remained relatively intact (40-60% intact), but with increasing anthropogenic pressure, which bring urgency to the context pointed herein.

In the area of territorial sharing between the CMS and the Amazon biome, geology and geomorphology are characterized by sedimentary deposits related to marine transgressions of the Oligo-Miocene/Miocene period.⁵⁸

Later, during the Neogene and Quaternary, these deposits were covered by reworked siliciclastic sediments and were accommodated by neotectonic activity.⁵⁹ From this process resulted in modern alluvial and Holocene sediments where CMS ecosystems such as mangroves, sandbanks, and dunes are present and characterize the FCU of the M_5 model in the Amazon.⁵⁴

Geographical regions

The FCU showed in the M_5 model represents 4.25 Mi hectares (42,500 km²) overlapping with the CMS, which represents 21.8% of the CMS total area, and it is distributed along more than 11.2 thousand kilometers of land and sea borders which need to be monitored, over 4 geopolitical regions of Brazil. The enforcement of efficient public policies for the protection of the biodiversity of the FCU still represents a constant challenge for the Brazilian government.⁶⁰ In general, the FCU showed wide variability in the size of the areas to be legally protected and monitored, between 65 and 664,548 hectares (Figure 9 and Appendix D) and distributed in a vast biogeographic context (> 30° variation in latitude). The M_5 model dataset relative to FCU perimeters and areas in the geopolitical regions is available in excel format, in the Appendix D. Once the costs of government policies to protect FCU depends on its location in the territory and its territorial extension,^12,61,62 the quantity and size of FCU per geopolitical region is also of critical importance and asymmetries, as observed in Figure 9, can help define the right strategies for the creation of new protected areas.⁶³

Figure 9 Variability of FCU areas in the geographical regions. High and low outliers are indicated by circles and stars, respectively. The asymmetries in area can represent challenges to keep present FCU or create new units.

The northeastern region presented the largest number of FCU related to the CMS (Figure 8). This region has a biogeographic scope scale, and it presents a high environmental heterogeneity because it is characterized by environmental descriptors related to four different biomes.^1,52 This is an important aspect for establishment of public policies, because it presents the potential of good ecological representativeness,⁶⁴ in a region of high geobiodiversity.¹

The subset of FCU in the northeastern region allows the continuity of several ecological processes and ecosystem services.^65,66 However, little improvement is expected in the Ocean Health Index (OHI) in the future, due to the low regional performance of economic and social indicators.⁵⁵

Considering the ideal condition for a system of protected, ecologically representative, and functional areas,⁶⁷ the FCU of the southeastern region can be considered of relatively small dimensions, if compared to the other FCU sets located in other Brazilian geopolitical regions.¹⁰ This finding is relevant for the conservationist public policies on a regional scale, since the extent of habitat protection is an important indicator for biodiversity conservation,^55,68 because some species may require an area larger than others for the maintenance of stochastic processes related to demography and genetic structure of populations.⁶⁹

In the southeastern region, the FCU are relatively well distributed along the latitudinal gradient of the CMS, which shares territory exclusively with the Atlantic Forest biome. This biome is considered a hotspot of global biodiversity⁷⁰ and occupies most of the country's coastal zone.¹ However, a recent geospatial analysis of satellite high-resolution images revealed a residual native vegetation of the Atlantic Forest that covers 28%, or 32 million hectares. Of these, only 30% represents native forest located within protected areas.⁷¹

In the northern region, two FCU are located completely within the CMS and 11 FCU present its geographical centers at the limits or within the CMS, as indicated in the M_5 model. However, it is important to highlight that the M_1 model, the present ICMBio database, showed the absence of FCU on the CMS in the northern region. Thus, future studies can address how much this historical error in the database affected the protection and management of these FCU, since the ecosystems of the northern region are recognized by both the high biodiversity and the loss of sensitive natural habitats.^60,72,73

At the biome – ocean interface in the southern region, the attributes of geobiodiversity proper to the Atlantic Forest and Pampa biomes influenced the marked alteration in the geometry of the CMS. In Figure 4, it is observed on the continental strip that the beginning of the sharp enlargement of the CMS occurs exactly in the transition zone between these biomes, and thus proceeds towards the southern limit of the Pampa biome, which produced a large area of overlap. The explanation for this abrupt change on the internal limit of the CMS may be related to geological and geomorphological aspects, which are significantly different between the biomes. For example, in the ecotone zone, granites and gneisses, and the high escarpments of the coastal mountains (“Serra do Mar”) produced enormous influx of sediments and formed the extensive coastal plain of the Pampa biome.^1,74

The present study applied geospatial analyses, based on algebraic topology and Euclidean geometry, to model the spatial relationship between federal conservation units (FCU) and the new Coastal Marine System (CMS) of Brazil. The CMS represents a geographical space, meaning a subset of the two-dimensional Euclidean plane, which has attributes of geobiodiversity associated with a part of its geometry, depending on its location in the biomes. Based on the 5 spatial models created to investigate this spatial relationship, the M_5 model is the most robust to represent the real situation between the FCU overlapping the SCM. Thus, from the perspective of the efficient protection of the natural resources contained in the vast CMS domain, the study also concluded that:

1. The method, based on algebraic, geometric and topological concepts, showed the functional connectivity of landscapes and protected areas along a territorial extension of continental scale.
2. Considering the national territory, the creation of new FCU in the CMS should be prioritized in the Cerrado, Caatinga and Pampa biomes;
3. The zone of CMS which overlaps the Atlantic Forest biome and the coastal border of the Northeast Region are of central importance for the planning of geobiodiversity conservation;

The present ICMBio database does not contain adequate information to allow a robust analysis of the spatial relationship between the FCU and the CMS. This fact negatively affects the creation and maintenance of efficient government policies for the conservation of the biodiversity on a national scale. The issues discussed here can be improved in the future by integrating the entire SNUC spatial data, i.e., all federal, state, and municipal conservation units and natural heritage reserves. It is recommended to follow the theoretical-conceptual bases contained in the technical document presented by IBGE at the end of 2019, because it is important to maintain the reliability of spatial data and the interoperability of databases of the Brazilian public institutions.

The authors are grateful to the institutional support from GGEMMA Lab | UFRN, GEOQUANTT Lab | UFPE and CEPENE Marine Research Center | ICMBio. We also thank the anonymous reviewers for their accurate and constructive comments, which helped to improve the manuscript. OAS is very grateful to Sara Guimarães for the sharing her algebraic-topological modeling insights on the chessboard. PPBE is gratefully acknowledge the financial support by CAPES (Marine Sciences II Nº23038.004320/2014-11), and the post-doctoral fellowship grants (Nº88887.305531/2018-00, Nº88881.188496/2018-01, Nº9999.000098/2017-05), at Moss Landing Marine Laboratories at San Jose State University (MLML/SJSU), at the Ocean Sciences Department of the University of California at Santa Cruz (UCSC), and at the International Ocean Discovery Program (IODP) through Texas A&M University (USA). We are very grateful for the detailed English revision done by Christofer Paul Barker from www.EcoLogicProject.com, Santa Cruz, California (USA).

None.

1. IBGE. Biomas e Sistema Costeiro-Marinho do Brasil. Rio de Janeiro, RJ. 2019.
2. Anderson MG, Barnett A. Resilient Coastal Sites for Conservation in the South Atlantic US. Nat Conserv East Conserv Sci. 2019;1–169.
3. Carollo C, Allee RJ, Yoskowitz DW. Linking the coastal and marine ecological classification standard (CMECS) to ecosystem services: An application to the US Gulf of Mexico. Int J Biodivers Sci Ecosyst Serv Manag. 213;9:249–256.
4. Dillenburg, SR, Hesp PA. Geology and geomorphology of holocene coastal barriers of Brazil. Springer Berlin Heidelberg. 2008;107:1–380.
5. Junior RN, Walfirmartins P, Filho S, et al. Mapeamento da área de manguezal na zona costeira amazônica ( Pará e Maranhão ) a partir de dados multisensores e abordagem orientada a objectos. XIII Congresso da Associação Brasileira de Estudos do Quaternário ABEQUA. 2009;5–8.
6. Vasconcelos R., Gomes VDS, Lucena DR, et al. Soil organic matter and soil acidity in Mangrove areas in the river Paraiba Estuary, Cabedelo, Paraiba, Brazil. Eurasian J Soil Sci. 2014;3:157–162.
7. Gonçalves-Souza, T, Santos, AJ, Romero GQ, et al. Conservation along a hotspot rim: spiders in Brazilian coastal restingas. Biodivers Conserv. 2014;24:1131–1146.
8. Nagelkerken I, Blaber SJM, Bouillon S, et al. The habitat function of mangroves for terrestrial and marine fauna: A review. Aquat Bot. 2008;89(2):155–185.
9. Dias-Silva K, Vieira TB, Moreira FFF, et al. Protected areas are not effective for the conservation of freshwater insects in Brazil. Sci Rep. 2021;11(1):21247.
10. Relatório de Gestão Integrada. Brasília, DF. ICMBio. 2021;1–27.
11. Kleidon A, Mooney HA. A global distribution of biodiversity inferred from climatic constraints: Results from a process-based modelling study. Glob Chang Biol. 2000;6(5):507–523.
12. UNEP-WCMC, IUCN, NGS, Protected Planet Report 2018. UNEP-WCMC, IUCN and NGS: Cambridge UK, Gland, Switzerland and Washington, D.C, USA. 2018.
13. Rowland JA, Bland LM, Keith DA, et al. Ecosystem indices to support global biodiversity conservation. Conserv Lett. 2020;13(1):e12680.
14. Ferreira HM, Magris RA, Floeter SR, et al. Drivers of ecological effectiveness of marine protected areas: A meta-analytic approach from the Southwestern Atlantic Ocean (Brazil). J Environ Manage. 2022;301:113889.
15. Spalding MD, Fox HE, Allen GR, et al. Marine ecoregions of the World: a bioregionalization of coastal and shelf areas. Bioscience. 2007;57:573–583.
16. Kumar P. On the topological situations in geographic spaces. Ann GIS. 2014;20(2):131–137.
17. Clevenger AP, Wierzchowski J, Chruszcz B, et al. GIS-generated, expert-based models for identifying wildlife habitat linkages and planning mitigation passages. Conserv Biol. 2002;16(2):503–514.
18. Laffan SW, Skidmore AK, Franklin J. Geospatial analysis of species, biodiversity and landscapes : introduction to the second special issue on spatial ecology. Int J Geogr Inf Sci. 212;26(11):2003–2007.
19. Cumming GS, Bodin Ö, Ernstson H, et al. Network analysis in conservation biogeography: challenges and opportunities. Divers Distrib. 2010;16:414–425.
20. Pant R, Thacker S, Hall JW, et al. Critical infrastructure impact assessment due to flood exposure. J Flood Risk Manag. 2018;11(1):22–33.
21. Carroll C, Rohlf DJ, Li YW, et al. Connectivity conservation and endangered species recovery: a study in the challenges of defining conservation-reliant species. Conserv Lett. 2015;8(2);132–138.
22. Ferdaña Z, Patton J. Geospatial conservation at the nature conservancy: 2019 annual report and map book. Arlington, VA. 2019.
23. Mazziotta A, Triviño M, Tikkanen OP, et al. Applying a framework for landscape planning under climate change for the conservation of biodiversity in the Finnish boreal forest. Glob Chang Biol. 2015;21(2):637–651.
24. Gray A. Euclidean Spaces, in: Modern Differential Geometry of Curves and Surfaces with Mathematica. CRC Press, Boca Raton, FL, 1997;2–5.
25. Worboys MF. Metrics and topologies for geographic space. In: Kraak MJ, Molenaar M. Ed, Advances in GIS Research II. Taylor and Francis, Abington, Delft, NE. 1996:365–375.
26. Bishop MJ, Mayer-pinto M, Airoldi L, et al. Effects of ocean sprawl on ecological connectivity : impacts and solutions. J Exp Mar Bio Ecol. 2017;492:7–30.
27. Lecours V, Devillers R, Schneider DC, et al. Spatial scale and geographic context in benthic habitat mapping: Review and future directions. Mar Ecol Prog Ser. 2015;535:259–284.
28. Bishop MP, James LA, Shroder JF, et al. Geospatial technologies and digital geomorphological mapping: concepts, issues and research. Geomorphology. 2012;137(1):5–26.
29. Iverson LR, Mckenzie D. Tree-species range shifts in a changing climate : detecting, modeling, assisting. Landscape Ecol. 2013;28(5):879–889.
30. Miloslavich P, Klein E, Díaz JM, et al. Marine biodiversity in the Atlantic and Pacific coasts of South America: knowledge and gaps. PLoS One. 2011;6(1):e14631.
31. Schiavetti A, Manz J, Zapelini dos Santos C, et al. Marine Protected Areas in Brazil: An ecological approach regarding the large marine ecosystems. Ocean Coast Manag. 213;76:96–104.
32. Williams BA, Watson JEM, Beyer HL, et al. The global rarity of intact coastal regions. Conserv Biol. 2022;36(4):e13874.
33. ICMBio. Mapa Temático e Dados Geoestatísticos das Unidades de Conservação Federais- Português (Brasil). Unidades Conserv Fed. 2022.
34. IBGE. Biomas e Sistema Costeiro-Marinho do Brasil - PGI. Mapas Temáticos. 2022.
35. Câmara, G, Monteiro A, Vieira M, et al. Towards a unified framework for spatial data models. J Braz Comput Soc. 2000;7(1):17–25.
36. Egenhofer MJ. A model for detailed binary topological relationships. Geomatica. 1993;47(3):261–273.
37. Shekhar S, Xiong H, Zhou X. Encyclopedia of GIS, 2nd Ed, Springer International Publishing. Springer, Cham, Switzerland. 2017.
38. Ross F, Ross WT. The Jordan Curve Theorem is non-trivial. J Math Arts. 2011;5(4):213–219.
39. Tverberg H. A proof of the Jordan Curve Theorem. Bull London Math Soc. 1980;12(1):34–38.
40. Clementini E, Di Felice P, Oosterom PV. A small set of formal topological relationships suitable for end-user interaction. Adv Spatial Databases. 1993;277–295.
41. Egenhofer MJ, Sharma J, Mark DM. et al. A critical comparison of the 4-intersection and 9-intersection models for spatial relations: formal analysis. Proc 11th Autocarto Conf. 1993;1–12.
42. Clementini E, Di Felice P. A comparison of methods for representing topological relationships. Inf Sci Appl. 1995;3(3):149–178.
43. Egenhofer MJ, Franzosa RD. Point-set topological spatial relations. Int J Geogr Inf Syst. 1991;5(2):161–174.
44. Kumar GN, Bangi M. An extension to winding number and point-in-polygon algorithm. IFAC-PapersOnLine. 2018;51(1):548–553.
45. Smith MJ, Goodchild MF, Longley PA. Geospatial Analysis. A comprehensive guide to principles techniques and software tools. 6th Ed. 2018.
46. United Nations Oceans and Law of the Sea. Div Ocean Aff Law Sea. 2020.
47. Meirelles PM, Amado-Filho GM, Pereira-Filho GH, et al. Baseline assessment of mesophotic reefs of the Vitória-Trindade Seamount Chain based on water quality, microbial diversity, benthic cover and fish biomass data. PLoS One. 2015;10(6):e0130084.
48. Pinheiro HT, Mazzei E, Moura RL, et al. Fish biodiversity of the Vitória-Trindade seamount chain, southwestern Atlantic: an updated database. PLoS One. 2015;10(3):e0118180.
49. Selig ER, Turner WR, Troeng S, et al. Global priorities for marine biodiversity conservation. PLoS One. 2014;9(1):e82898.
50. Sutherland WJ, Butchart SHM, Connor B, et al. A 2018 horizon scans of emerging issues for global conservation and biological diversity. Trends Ecol Evol. 2018;33(1):47–58.
51. Álvares-Da-Silva O, Eichler PPB, Barbosa JA. Federal conservation units of Brazil’s coastal-marine system. 2023;2.
52. Rodrigues MT. Herpetofauna da Caatinga. In: Leal IR, Tabarelli M, Silva JMC. da (Ed), Ecologia e Conservação Da Caatinga Recife: Ed. Universitária Da UFPE. Ed. Universitária da UFPE, Recife, PE. 2003;181–236.
53. Andrade-Lima D. The caatingas dominium. Rev Bras Botânica. 1981;4(2):149–163.
54. ICMBio. Planos de Manejo. 2021.
55. Elfes CT, Longo C, Halpern BS, et al. A regional-scale ocean health index for Brazil. PLoS One. 2014;9(4):e92589.
56. Amaral DD, Prost MT, Bastos M, et al. Amazonian coastline candy coastal in the Amapá and Pará States, Brazil. Bol Mus Para Emílio Goeldi. 2008;3:35–67.
57. De Menezes MPM, Berger U, Mehlig U. Mangrove vegetation in Amazonia: A review of studies from the coast of Pará and Maranhão States, north Brazil. Acta Amaz. 2008;38(3):403–419.
58. Rossetti DF, Bezerra FHR, Dominguez JML. Late Oligocene-Miocene transgressions along the equatorial and eastern margins of Brazil. Earth-Science Rev. 2013;123:87–112.
59. Rossetti DF, Souza LSB, Prado R, et al. Neotectonics in the northern equatorial Brazilian margin. J South Am Earth Sci. 2012;37: 175–190.
60. Azevedo TR, Rosa MR, Shimbo JZ, et al. Annual Deforestation Report of Brazil. São Paulo, SP. 2020.
61. Loyola RD, Oliveira-Santos LGR, Almeida-Neto M, et al. Integrating economic costs and biological traits into global conservation priorities for carnivores. PLoS One. 2009;4(8):e6807.
62. Pivello VR, Vieira I, Christianini AV, et al. Understanding Brazil’s catastrophic fires: causes, consequences and policy needed to prevent future tragedies. Perspect Ecol Conserv. 2021;19(3):233–255.
63. Morais AR, Siqueira MN, Freitas-Oliveira R, et al. Analyzing temporal and spatial trends in management plans of federal protected areas in Brazil. Oecologia Aust. 2021;25(4):846–854.
64. Powell GVN, Barborak J, Rodriguez S. Assessing representativeness of protected natural areas in Costa Rica for conserving biodiversity: A preliminary gap analysis. Biol Conserv. 2000;93(1):35–41.
65. Bridge TCL, Luiz OJ, Coleman RR, et al. Ecological and morphological traits predict depth-generalist fishes on coral reefs. Proc Biol Sci. 2016;283(1823):20152332.
66. Pimm SL, Jenkins CN, Abell R, et al. The biodiversity of species and their rates of extinction, distribution, and protection. Science. 2014;344(6187):1246752.
67. Magris RA, Mills M, Fuentes MMPB, et al. Analysis of progress towards a comprehensive system of marine protected areas in Brazil. Nat Conserv. 2013;11(1):81–87.
68. Fletcher RJ, Didham RK, Banks-Leite C, et al. Is habitat fragmentation good for biodiversity? Biol Conserv. 2018;226:9–15.
69. Pe’er G, Tsianou M, Franz KW, et al. Toward better application of minimum area requirements in conservation planning. Biol Conserv. 2014;170:92–102.
70. Myers N, Mittermeier RA, Mittermeier CG, et al. Biodiversity hotspots for conservation priorities. Nature. 2000;403(6772):853–858.
71. Rezende CL, Scarano FR, Assad ED, et al. From hotspot to hopespot: An opportunity for the Brazilian Atlantic Forest. Perspect Ecol Conserv. 2018;16(4):208–214.
72. IPBES. Global assessment report on biodiversity and ecosystem services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. IPBES. 2019.
73. Silva Junior CHL, Pessôa ACM, Carvalho NS, et al. The Brazilian Amazon deforestation rate in 2020 is the greatest of the decade. Nat Ecol Evol. 2021;5(2):144–145.
74. Robaina LE, Trentin R, Sccoti AAV. Geomorphological description of the biome Pampa (Brazil) with support of digital elevation model and geographic information system. Revista Do Departamento De Geografia. 2021;41(1):e169605.