It is shown that a non-uniform scaling transformation group represents a particular class of the exact solution of the nonlinear shallow water equations corresponding to the two-dimensional atmospheric waves within a circular geometry. The obtained solution has a Fibonacci spiral-like form. We have used the parameters of the model to associate to obtained solutions with the Fibonacci spiral. It is shown that the physically relevant part of the solution matches exactly the Fibonaccy spiral.

Keywords: atmospheric waves, Fibonacci sequence, shallow water theory, exact solutions

Probably, the most known relationship that occurs in the smallest, to the largest objects in nature is the Fibonacci sequence of numbers $F_n$  is defined by using the recursive relation $F_n=F_{n-1}+F_{n-2}$  with the assumed values $F_0=F_1=1$ . It can be observed in shells of snails, in the pattern found on the wings of dragonflies or galaxies, as shown in Figure 1. The symmetry and appearance of Fibonacci spiral patterns in nature attracted scientists, but a mathematical or physical explanation for their common occurrence in nature is still known.¹

Figure 1 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

In this paper we observe some correlation between two-dimensional atmospheric equatorial waves and the Fibonacci spiral. It is known that equatorial waves play an important role in the climate system as well as in the weather and climate changes. Equatorial waves are being associated with large-scale perturbations of the atmospheric motion extending around an equator.^2–6 Also, it is believed that the equatorial waves can be an important component of the long-term mean upwelling at the tropical tropopause, widespread changes in the climate system and in absorbing harmful solar ultraviolet radiation.^3,7–13 Also, equatorial waves can be an important component in the controlling the stratospheric temperature via atmospheric radiative heating¹⁴ and in improving seasonal weather forecasting, as pointed out in.^8,12,15–21

Various methods of method of visualizing the atmospheric equatorial waves are discussed in.^5,6

In this paper, we aim to visualize atmospheric equatorial waves that are being described by the particular class of the solution that is deduced as the similarity solution of the nonlinear shallow water equations representing the free boundary of two-dimensional model describing the nonstationary motion of an incompressible perfect fluid propagating around a solid circle of a sufficiently large radius with the gravity directed to it’s center. The solution of the interest was obtained by means of Lie symmetries first reported in.²² Acquaintance with group analysis is important for constructing and investigating nonlinear mathematical models of natural and engineering problems. Numerous physical phenomena can be investigated using Lie symmetries to unearth various group invariant solutions and conservation laws that provide significant physical insight into the problem. Moreover, models of natural phenomena can often be described directly in group theoretic terms. Differential equations, conservation laws, solutions to boundary value problems, and so forth can be derived from the group invariance principle.

We consider a two dimensional motion of an incompressible perfect fluid which has a free boundary η and a solid bottom represented by a circle of radius . The fluid is propagating within a curricular domain bounded below by a sufficiently large solid circle and above by a free boundary. It is assumed that the motion is irrotational and the pressure on a free boundary is constant. It is also assumed that the distance from the origin of the circle to the unperturbed free boundary is small compared to the radius of the circle, as shown schematically in Figure 2.

Figure 2 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

The model is described by means of polar coordinates $x=r\text{cos}\theta$ , $y=r\text{sin}\theta$ , in which $\theta$ is a polar angle, $r$  is the distance from the origin of the circle and $R$  is the radius of the circle representing the radius of a planet, $h\left(t,\theta \right)=h_0+\eta \left(t,\theta \right)$ , where $t$  is time, $h_0$  is a constant undisturbed level of the equatorial atmospheric layer from the center of the planet, and $\eta \left(t,\theta \right)$ is the unknown level of disturbance of a free boundary. Hence, irrotational motion of a perfect fluid is confined in the domain ${\text{Ω}}_{\eta }=\left\{\left(r,\theta \right):0⩽\theta ⩽2\pi ,R⩽r⩽R+h\left(t,\theta \right)\right\}$ , which is bounded by a solid circular boundary $r=R$ and a perturbed free boundary $r=R+h\left(t,\theta \right)$ . As mentioned above, it s assumed that the unperturbed level of atmospheric level $h_0$  is small compared to the radius and the homogeneous gravity field is given by the vector $\overleftarrow{g,}$  which is assumed to be a constant and directed to the center of the circle.

Shallow water approximation: In what follows, it is assumed that the fluid motion is potential in the domain of the motion which allows to introduce the stream function $\psi \left(t,r,\theta \right)$ via

$v_r=-\frac{1}{r}\frac{\partial \psi }{\partial \theta }, v_{\theta }=\frac{\partial \psi }{\partial r}$     (1)

Notice that $\psi$ is a harmonic function in ${\text{Ω}}_{\eta }$ , since we assumed that the flow is irrotational. Next, we define the average velocity $u\left(\theta ,t\right)$ in terms of the stream function $\psi$ as

$u\left(\theta ,t\right)=\frac{1}{h}\stackrel{R+h}{\underset{R}{{{\displaystyle \int }}^{\text{}}}}{v}_{\theta }\left(r,\theta ,t\right)dr=\frac{1}{h}\psi \left(R+h,\theta ,t\right)$     (2)

In order to reduce the number of parameters, we introduce dimensionless variables:

$\theta =\widehat{\theta }, r=R+h_0\widehat{r}, h=h_0\widehat{h}, t=\frac{R\widehat{t}}{\sqrt{g{h}_0}}$   ,(3)

$\psi =h_0\sqrt{g{h}_0}\widehat{\psi }, u=\sqrt{g{h}_0}\widehat{u}$

We next introduce the parameter

$\epsilon =\frac{h_0}{R}$     (4)

The hypothesis that water is "shallow" is based on the assumption that the parameter  is "small".

In particular the relation between the boundaries of the dimensional and nondimensional variables can be summarized in the Table 1 below Equ_(5)

Hereafter the symbol "hat" is omitted.

So, in the nondimensional variables, the free boundary is given by $r\left(=1+\epsilon 1+h\right)$ and thus the functions $h\left(\theta ,t\right)$ and $\psi \left(r,\theta ,t\right)$ are two unknown functions whereas is a given parameter. Although shallow water theory is usually related to the case when the water depth is small relative to the wavelengths of the waves, we find it more appropriate to choose the radius as a natural physical scale since, in the frame of the present model, we consider waves with wavelengths of the order of the radius of a planet.

Representing the stream function $\psi$ by the series expansion: $\psi =\underset{n}{{{\displaystyle \sum }}^{\text{}}}{\epsilon }^n{\psi }^{\left(n\right)}$  and application of the Lagrange’s method allows one to write the boundary problem as the following nondimensional system of nonlinear shallow water equations, which are a higher-order analogue of the Su - Gardner equations:²³

 $u_t+u{u}_{\theta }+h_{\theta }+\frac{\epsilon }{2}\left(3h{u}_t-u{h}_t-u^2{h}_{\theta }+2h{h}_{\theta }\right)=0$  ,(6)

 $h_t+u{h}_{\theta }+h{u}_{\theta }+\epsilon h{h}_t=0$  ,(7)

where the subscripts denote partial derivatives in which independent variables $t$ and $\theta$ denote the time and the polar angle, respectively, the dependent variables are the average velocity $u$ and the level $h>0$ of the atmosphere perturbed from $h_0$ , whereas $\epsilon \ll 1$  is a small parameter.

Due to the fact that $\epsilon$ is a small parameter, the terms of order $0\left(\epsilon \right)$  can be considered as small perturbation to the zeroth order terms (unperturbed model). Our main concern is a simplified version of the model, in which the perturbations (nonlinear terms at $\epsilon$ , are ignored and we consider the following unperturbed system. As has been shown in,^24,25 elimination of $u_t$  and $h_t$  from the terms of the equations (6)-(7) and ignore the terms with $\epsilon$ . This leads to the following unperturbed system:

 $u_t+u{u}_{\theta }+h_{\theta }=0$  ,(8)

 $h_t+u{h}_{\theta }+h{u}_{\theta }=0$  .(9)

It can be checked by direct substitution that one particular exact solution of the unperturbed shallow water system (8)-(9) is

 $h^0=\epsilon ,$  $u^0=-\frac{\text{Γ}}{2\pi \epsilon }\text{ln}\left(1+\epsilon \right)$ (10)

where $\text{Γ}=\text{const}$  is the intensity of the vortex (source) localized at the center of the planet and is related with the the rotation rate of the planet (for example, the angular velocity of the earth is $\text{Ω}=2\pi \text{rad}/\text{day}\approx 0.73\times {10}^{-4}{s}^{(-1)})$ by the equation $\text{Γ}=2\pi \text{Ω}{R}^2$  Since the solution (10) corresponds to the constant flow with an undisturbed circular free surface, we call it a trivial solution. At certain extent, the above ansatz (10) can be associated with the polar vortex, which represents a very powerful whirlpool swirling steadily around the planet’s poles at all times.

Understanding and predicting break downs and overall dynamic structure of the polar vortex is important for improving seasonal forecasting.²¹ If the undulating path of the west to east atmospheric flow generated by the polar vortex could be predicted, then weather could be predicted too – not just for a week or two, but for an entire season.²⁶ However, as pointed out in,²⁷ until now understanding of a such correlation has been based on observations and statistical modeling only rather than on the knowledge of its physical foundation. Because of the periodic seasonal breakdowns of the polar vortex and the lack of continuous data for the input of such interactions, statistical approach generally cannot provide the weather patterns accurately enough.^28,29

Up to the present days, our knowledge of gravity wave sources and properties in the polar region is very much limited because collecting the observations is generally difficult because of harsh natural environments.³⁰

Detailed presentations of the theory of symmetries and invariant solutions of differential equations can be found elsewhere.^31–38 For convenience, we summarize the basic notation from calculus of Lie group analysis in Appendix, which represents a simplified version of the overview of basic concepts of Lie symmetry groups.

A simple inspection shows that the system (8)-(9) admits the infinite-dimensional Lie algebra composed by the operators

$\begin{array}{l}{X}_1=t\frac{\partial }{\partial \theta }+\frac{\partial }{\partial u} , X_2=\theta \frac{\partial }{\partial \theta }+2h\frac{\partial }{\partial h}+u\frac{\partial }{\partial u} , X_3=t\frac{\partial }{\partial t}+\theta \frac{\partial }{\partial \theta }\\ X_4=\left(2\theta -6tu\right)\frac{\partial }{\partial t}+\left(6th-3t{u}^2\right)\frac{\partial }{\partial \theta }+4hu\frac{\partial }{\partial h}+\left(u^2+4h\right)\frac{\partial }{\partial u}\end{array}$   (11)

In particular, the operator $X_1$  is admitted due to the invariance of the system (8) - (9) under the Galilean transformation group

$\overline{\theta }=\theta +t{a}_1 , \overline{u}=u+a_1$   (12)

With an arbitrary parameter $a_1$ . The operator $X_2$  indicates that the system (8) - (9) is invariant under the non-uniform scaling transformation group.

 $\overline{\theta }=\theta {\text{e}}^{a_{{}_2}}, \overline{h}=h{\text{e}}^{2a_{{}_2}}, \overline{u}=u{\text{e}}^{a_{{}_2}},$  (13)

where $a_2$  is another arbitrary parameter and the operator  is responsible for a specific non-scaling symmetry of the one-dimensional shallow water model (8) - (9).

The term similarity solution refers to invariant solutions based on scaling transformations (12). It can be checked by direct substitution that the shallow water model (8)-(9) is invariant under the transformation (12). One calculates the invariant $J\left(t,\theta ,u,h\right)$ of the group $X_2$  by solving the first-order linear partial differential equation

 $X_{2}J=0$  (14)

The latter equation (14) gives three functionally independent invariants corresponding to the transformation (12):

$J_1=t, J_2=\frac{u}{\theta } , J_3=\frac{h}{{\theta }^2}.$

Accordingly, we look for the invariant solution of the (8) - (9) in the form

$u=\theta U\left(t\right), h={\theta }^{2}H\left(t\right).$   (15)

Direct substitution of the presentation (15) in the system (8) - (9) yields the following nonlinear ordinary differential equations:

$\frac{dU}{dt}+U^2+2H=0,$   (16)

$\frac{dH}{dt}+3UH=0.$   (17)

In case when $H\ne 0,$ the equation (17) can be written as the following coupled equations

$H={\text{e}}^{-3W},U=\frac{dW}{dt}$   (18)

where $W$ satisfies the nonlinear differential equation of the second order,

$\frac{d^{2}W}{d{t}^2}+{\left(\frac{dW}{dt}\right)}^2+2e^{-3W}=0.$   (19)

Integration of the equation (19) yields

$\frac{dW}{dt}=2e^{-\frac{3W}{2}}\sqrt{1+k {\text{e}}^W}$   (20)

where $k$ is a constant and so $W$ is given implicitly by equation

${{\displaystyle \int }}^{\text{}}\frac{{\text{e}}^{3W/2}}{\sqrt{1+k {\text{e}}^W}} dW=\pm 2\left(t-t_0\right) ,$   (21)

where $t_0$  is an arbitrary constant.

In particular, if the function $H$ is known, the function $u$ can be expressed in terms of $H$ as

$u=\pm 2\theta \sqrt{H}\sqrt{1+k{H}^{-1/3}}$   (22)

The equation (21) provides an implicit representation of the function $W\left(t\right)$ and hence the functions $U\left(t\right)$ and $H\left(t\right)$ is (15) due to the equations (18). We calculate the integral and distinguish the following three cases:

Case k=0

When k=0 the equation (21) has the form

$F_0\left(W\right):={\text{e}}^{\frac{3W}{2}}=\pm 3\left(t-t_0\right).$   (23)

In this case, the equations (15) provide us with the solution

$H=\frac{1}{9{(t-t_0)}^2} , U=\frac{2}{3\left(t-t_0\right)}$   (24)

and thus the exact solution of the system (8) - (9) is given by

$u=\frac{2\theta }{3\left(t-t_0\right)}, h=\frac{{\theta }^2}{9{(t-t_0)}^2}$   (25)

Case k>0

When $k>0$ , the functions $U$ and $H$ are given by

$U=\pm 2 {\text{e}}^{-\frac{3W}{2}}\sqrt{1+k{\text{e}}^W} , H={\text{e}}^{-3W} ,$   (26)

where $k>0$ and $W$ is given implicitly by equation

$F_{+}\left(W\right):={\text{e}}^{\frac{W}{2}}\sqrt{\frac{1}{k}+{\text{e}}^W}-\frac{1}{k}\text{ln}\left({\text{e}}^{\frac{W}{2}}+\sqrt{\frac{1}{k}+{\text{e}}^W}\right)=\pm 2\left(t-t_0\right).$   (27)

Case k<0

When $k<0$ the functions $U$ and $H$ are given by

$U=\pm 2 {\text{e}}^{-\frac{3W}{2}}\sqrt{1+k{\text{e}}^W} , H={\text{e}}^{-3W} ,$   (28)

where $k<0$ and $W$ is given implicitly by equation

$F_{-}\left(W\right):=-{\text{e}}^{\frac{W}{2}}\sqrt{-\frac{1}{k}-{\text{e}}^W}-\frac{1}{k}\text{arcsin}\left(\sqrt{-k}{\text{e}}^{\frac{W}{2}}\right)=\pm 2\left(t-t_0\right).$   (29)

The function $F_{-}\left(W\right)$  is defined subject to constraint

$\left|k\right|<e^{-W}.$   (30)

For example, the function $F_{-}\left(W\right)$  is not defined for $k=\mathrm{0.1.}$  

We will approximate the functions $F_{\pm }\left(W\right)$  for large and small values of $W$ and also for large and small values of $k.$

We will analyze the asymptotic behavior of the similarity solution (15) for large and small $W$ as well as for large and small values $k.$

Approximation of the similarity solution for large and small W

We next approximate the function $F_{+}\left(W\right)$  given by equation (27) in the limit $W\to \pm \infty .$ We start with $F_{+}\left(W\right)=f\left(W\right)+g\left(W\right),$  where

$f\left(W\right)=e^{\frac{W}{2}}\sqrt{\frac{1}{k}+e^W}, g\left(W\right)=-\frac{1}{k}\text{ln}\left(e^{\frac{W}{2}}+\sqrt{\frac{1}{k}+e^W}\right).$   (31)

First, we consider the limiting behavior of $f\left(W\right):$

$\underset{W\to -\infty }{\text{lim}}f\left(W\right)=0$   (32)

and for $W>>0,$ since $f\left(W\right)\sim e^W,$ we look for $\underset{W\to +\infty }{\text{lim}}f\left(W\right)-e^W.$  Using $\frac{1}{u}=e^{\frac{W}{2}},$  we find

$\underset{W\to +\infty }{\text{lim}}f\left(W\right)-e^W=\underset{u\to +\infty }{\text{lim}}\frac{1}{u}\sqrt{\frac{1}{k}+\frac{1}{u^2}}-\frac{1}{u^2}=\underset{u\to +\infty }{\text{lim}}\frac{u\sqrt{\frac{u^2}{k}+1}-u}{u^3}.$   (33)

After applying the L’Hopital’s rule 3 times, we get

$\underset{W\to +\infty }{\text{lim}}f\left(W\right)=\frac{1}{2k}.$   (34)

Next, with the limiting behavior of $g\left(W\right):$

$\underset{W\to -\infty }{\text{lim}}g\left(W\right)=\frac{\text{ln}k}{2k}.$   (35)

For $W>>0,$ since $g\left(W\right)\sim -\frac{1}{k}\text{ln}\left(2e^{\frac{W}{2}}\right),$ we get

$\underset{W\to +\infty }{\text{lim}}g\left(W\right)+\frac{\text{ln}2}{k}+\frac{W}{2k}=0.$   (36)

Using this, we can find two approximations for $F_{+}\left(W\right):$

$W<<0: F_{+}\left(W\right)\approx \frac{\text{ln}k}{2k},$   (37)

since

$\underset{W\to -\infty }{\text{lim}}\left(f\left(W\right)+g\left(W\right)-\left[\frac{\text{ln}k}{2k}\right]\right)=0.$   (38)

$W>>0: F_{+}\left(W\right)\approx e^W+\frac{1}{k}\left(\frac{1}{2}-\text{ln}2-\frac{W}{2}\right),$   (39)

since

$\underset{W\to +\infty }{\text{lim}}\left(f\left(W\right)+g\left(W\right)-\left[e^W+\frac{1}{k}\left(\frac{1}{2}+\text{ln}2-\frac{W}{2}\right)\right]\right)=0.$   (40)

This analysis shows that there are two approximations for $F_{+}\left(W\right),$  for very large $W$ and for very small $W$ In particular, $\underset{W\to -\infty }{\text{lim}}{F}_{-}\left(W\right)=0$ but $\underset{W\to +\infty }{\text{lim}}{F}_{-}\left(W\right)$  does not exist since $F_{-}\left(W\right)$  is subject to the constraint $W<-\text{ln}\left(-k\right).$ (Figure 3).

Figure 3 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

Approximation of the similarity solution for large and small

Approximation of $F_0\left(W\right)$  by $F_{+}\left(W\right)$  and $F_{-}\left(W\right)$  for larger and small values of $\left|k\right|.$  We observe that $\underset{k\to \infty }{\text{lim}}{F}_{+}=F_0,$  as illustrated in panel (a) and $\underset{k\to 0}{\text{lim}}{F}_{-}=F_0,$  as illustrated in panel (b). Panel (c) is used to compare the curves $F_{+}$  and $F_{-}$  with $F_0$  for the value of $k=\mathrm{0.02.}$

We note that the function $F_{+}\left(W\right)$  represents a better approximation of $F_0\left(W\right)$  for larger values of $\left|k\right|$  whereas the function $F_{-}\left(W\right)$  represents a better approximation of $F_0\left(W\right)$  for smaller values values of $\left|k\right|,$  which is demonstrated in Figure ??. In particular, the panel (a) shows the curve $F_0$  and $F_{+}$  for $k=0.1$ and $k=10.$ It can be shown that $\underset{k\to \infty }{\text{lim}}{F}_{+}=F_0.$  The panel (b) compares the curve $F_0$  and v for $k=0.04$ and $k=\mathrm{0.020.}$ It can be shown that $\underset{k\to 0}{\text{lim}}{F}_{-}=F_0,$  subject to the constraint (30). Finally, the panel (c) is used to compare $F_0$  with $F_{+}$  and $F_{-}$ for $k=\mathrm{0.02.}$  For this reason we call the exact solution (15) an attractor solution in the sense that $F_0$  is defined as the smallest unit which cannot be itself decomposed into two or more attractors with distinct basins of attraction. This restriction is necessary since, in general, a dynamical system may have multiple attractors, each with its own basin of attraction.

We start with analyzing the exact attractor solution $h\left(\theta ,t\right)$ representing the deviation of the free boundary (see equation (15)) form the unperturbed boundary $r=1+\epsilon$ for the case $k=0$ at different values of time $t.$ As shown in Figure 4, the attractor solution is decreasing function of $t.$  for a fixed values of $\theta$ but it is increasing function of $\theta$ for a fixed values of time $t.$ We will also apply the numerical technique to compare the attractor solution

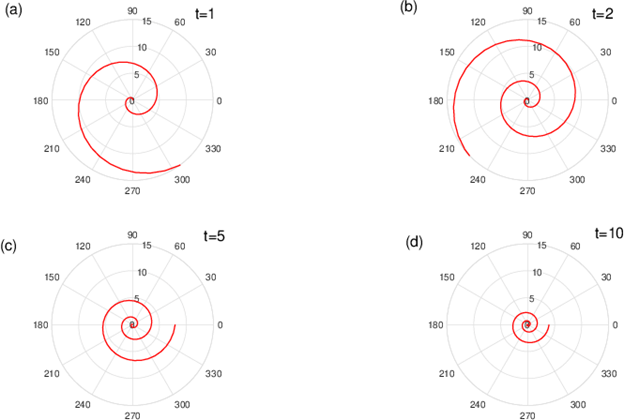
Figure 4 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

$h=\frac{{\theta }^2}{9{(t-t_0)}^2}$   (41)

with the exact solution

$h\left(\theta ,t\right)={\theta }^2{e}^{-3W\left(t\right)}$   (42)

 the both cases when $k>0$ and $k<0.$ The results are shown in Figures 5,6. Attractor solution $h=\frac{{\theta }^2}{9{(t-t_0)}^2}$  for the case $k=0$  and differentt valaues of time $t=1,t=2,t=5$  and $t=10.$

Comparison of the solution $h\left(\theta ,t\right)$  for $k>0$  with the attractor solution $h=\frac{{\theta }^2}{9{(t-t_0)}^2}$  at $t=1$  and different values of $k.$  Panel (a) shows the attractor solution (red line) and the solution $h\left(\theta ,t\right)$  evaluated at $k=10$  (blue line) and $h\left(\theta ,t\right)$ evaluated at $k=1$  (green line) and panel (a) compares these solutions for the $k=10$  and 1 as well, but evaluated at $t=2.$

In particular, the Figure 5 is used to compare the solution $h\left(\theta ,t\right)$  given by (42) for $k>0$  with the attractor solution given by (41) at $t=1$  and different values of $k.$  Panel (a) shows the attractor solution (red line) and the solution $h\left(\theta ,t\right)$ given by (41) evaluated at $k=10$ (blue line) and $k=1$  (green line). We can observe that the attractor solution represents a betterb approximation of the exact solution given by (41) at $k=10$ then at $k=1,$  as expected from the asymptotic analysis showing that $\underset{k\to \infty }{\text{lim}}{F}_{+}=F_0.$  A similar conclusion holds for larger values of time t, as illustrated in Panel (b) of this figure, showing the solutions evaluated at $t=2.$

Figure 5 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

Similarly, the Figure 6 is used to compre the nonlinear solution $h\left(\theta ,t\right)={\theta }^2{e}^{-3W\left(t,k\right)}$  given by (42) for $k<0$  with the attractor solution $h=\frac{{\theta }^2}{9{(t-t_0)}^2}$  given by (41) at $t=1$  and different values of $k.$  In this plot, the attractor solution is plotted by the red line and the solution $h\left(\theta ,t\right)$  evaluated at $k=-0.4$  is shown by the blue line where as $h\left(\theta ,t\right)$  evaluated at $k=-0.1$  is shown by the green line. We note that the similarity solution $h\left(\theta ,t\right)$  is defined for $k<0$  and $0<t<-\frac{\pi }{4k}$ , which covers the whole range of $F_{\_}\left(W\right).$

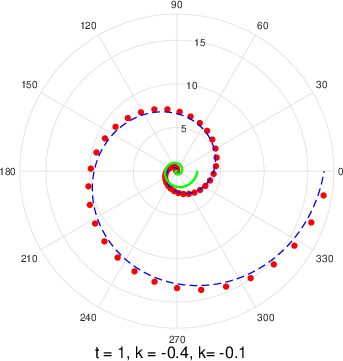
Figure 6 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

We associate the parameter k with the Fibonacci sequence $\left\{k_n\right\}$  defined by $k_n=k_{n-1}-k_{n-2}$  with $k_0=1$  and $k_1=1.$  Here each value $k_n$  corresponds to the circular arc $\theta \in \left[\frac{m\pi }{2},\frac{\left(m+1\right)\pi }{2}\right],$  where $m=0,1,2,\mathrm{...}$  so that $k_1=1$  corresponds to the circular arc $\theta \in \left[0,\frac{\pi }{2}\right]$  with $m=0.$  Also $k_2=1$  corresponds to the circular arc $\theta \in \left[\frac{\pi }{2},\pi \right]$  with $m=1$  and $k_3=2$  corresponds to the circular arc $\theta \in \left[\pi ,\frac{3\pi }{2}\right]$  with $m=2$  and so on. Next, the parameter $t_0$  is chosen for each value of $k$ such that the endpoints of the arc segments $\theta \in \left[\frac{m\pi }{2},\frac{\left(m+1\right)\pi }{2}\right]$  connect smoothly with the next circular segment $\theta \in \left[\frac{\left(m+1\right)\pi }{2},\frac{\left(m+2\right)\pi }{2}\right],$  for any given value of time $t,$  so that $t-t_0={\text{Δ}}_{k}t,$ where we call ${\text{Δ}}_{k}t$  model hypermarameter and it is tuned for the given predictive model represented by the Fibonacci spiral. We are tuning the hypermarameter in order to discover how the parameters $k_n$  and $t_0$  of the model result in the given prediction.

For example, for $t=1,$  the values of ${\text{Δ}}_{k}t$  corresponding to the first seven terms of Fibonacci sequence $\left\{k_n\right\}$  are approximated by the values shown in Table 2 Equ_(43).

Table 2

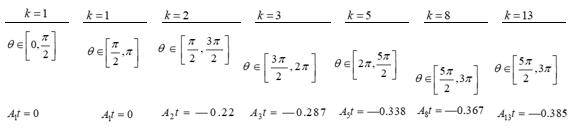
The values of ${\text{Δ}}_{k}t$  are also shown in Figure 7 and the corresponding few circular arcs are shown in Figure 8. We observe that

${\underset{k\to \infty }{\text{lim}}{\text{Δ}}_k|}_{t=1}=-0.41,$   (44)

which is also seen from the Figure 7.

Figure 7 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

In particular, based on the results for the hyperparameter ${\text{Δ}}_{k}t$  as shown in Table 2, we visualize our exact solution (15) for $h\left(\theta ,t\right)={\theta }^2{e}^{-3W\left(t\right)}$  for $t=1$  in Figure 8 as the sequence of circular arcs plotted at the values of time given by $t+{\text{Δ}}_{k}t$ . For example, when $k=2,$  we evaluate our exact solution as a function of $\theta$  at the value of time $1+0.22=\mathrm{1.22.}$  Similarly, when $k=3,$  we evaluate our exact solution as a function of $\theta$  at the value of time $1+0.287=1.287$  and so forth.

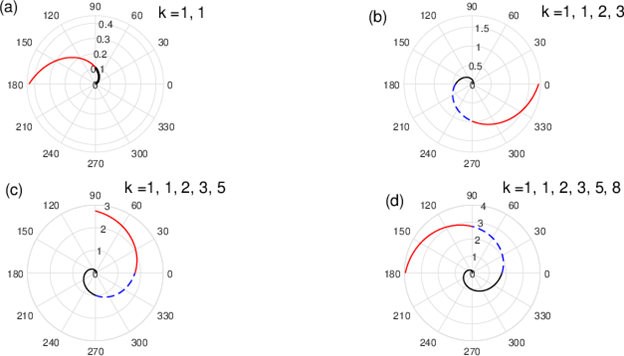
Figure 8 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

Figure 9 is used to compare the attractor solution $h=\frac{{\theta }^2}{9{(t-t_0)}^2}$  with the numerical approximation of the perturbation $h\left(\theta ,t\right)={\theta }^2{e}^{-3W\left(t\right)}$  for $k=1$  and $\theta =\frac{\pi }{8}$  and $\theta =\frac{\pi }{4}$  as the function of time $t.$  We note that $h\left(\theta ,t\right)$  represents the deviation of the free boundary from the unperturbed state $r=1+\epsilon ,$  so the feasible domain of $h$  is given by

${\text{Φ}}_h=\left\{h:0⩽h⩽\epsilon \right\},$   (45)

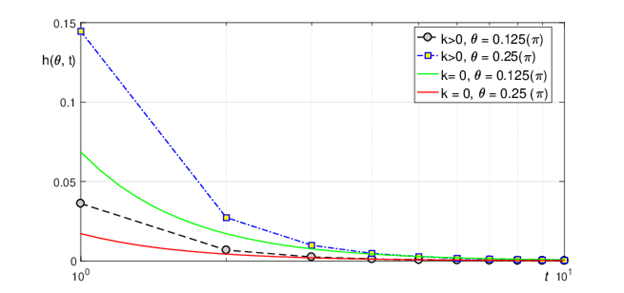
Figure 9 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

where $\epsilon <1$  is a small parameter since it is assumed that the unperturbed level of atmospheric “depth” is small compared to the radius of the Earth. As Figure ?? shows, $h$  is decreasing function of time $t,$  but it is increasing function of a polar angle $\theta ,$  which means that our nontrivial solution is valid for only very small values of $\theta .$

Comparison of the free boundary $\eta =1+\epsilon h\left(\theta ,t\right)$  and the Fibonacci spiral for the first three values of $k.$  

Figure 10 is used to compare the free boundary given by $\eta =1+h\left(\theta ,t\right)$  and the Fibonacci spiral for the first four values of $k,$  namely, for $k=1,1,2,3.$ According to the values chosen as shown in Table 2, panel (a) shows the segment of the Fibonacci spiral (green circles) and the free boundary (blue solid line) evaluated at the values of $k=1,$   $t=1$  and $t_0=0.$  Panel (b) compares the segment of the Fibonacci spiral and the free boundary evaluated at the values of $k=1,$   $t=1$  and $t_0=0.$  Panel (c) compares the segment of the Fibonacci spiral and the free boundary evaluated at the values of $k=2,$   $t=1.22$  and $t_0=-\mathrm{0.22.}$  Finally, panel (d) compares the segment of the Fibonacci spiral and the free boundary evaluated at the values of $k=3,$   $t=1.287$  and $t_0=-\mathrm{0.287.}$

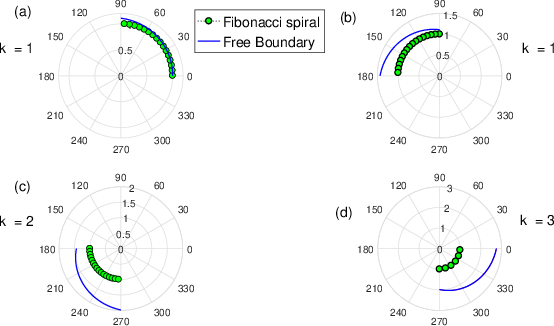
Figure 10 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

As it was discussed earlier, the solution for the free boundary perturbation $h\left(\theta ,t\right)$  is only valid in the domain ${\text{Φ}}_h$  defined by (45), i.e. in a very narrow band $\left|h\right|⩽\epsilon <1.$  For example, if $\epsilon =0.15,$  we can see from Figure (??) that our solution is valid for a very small values of $\theta$  bounded by $\theta \in \left(0,\frac{\pi }{4}\right).$  Thus, for example, if $\theta =\frac{\pi }{4},$  the solution is bounded by $\left|h\right|⩽\mathrm{0.15.}$  So, in this domain, the Fibonacci spiral corresponding to $k=1$  is a very good approximation of the nontrivial solution $\eta ,$  as shown in panel (a) of the Figure (??). For larger values of $k,$  we observe that the solution $\eta$  diverges from the Fibonacci spiral.

In this paper, we have analyzed and visualized the exact invariant solution of the nonlinear simplified version of the shallow water equations (8) - (9)

$\begin{array}{l}{u}_t+u{u}_{\theta }+h_{\theta }=0,\\ h_t+u{h}_{\theta }+h{u}_{\theta }=0,\end{array}$   (46)

which are being used to simulate equatorial atmospheric waves of planetary scales. Our model is represented by the Cauchy–Poisson free boundary problem on the nonstationary motion of a perfect incompressible fluid circulating around a vortex field approximated by a circle of a large radius and the gravity is directed to the center of the circle. The solution for the free boundary perturbation $h\left(\theta ,t\right)$  is only valid in a very narrow band $\left|h\right|⩽\epsilon <1,$  as also shown schematically in Figure 12. We have shown that within this band, Fibonacci spiral corresponding to $k=1$  is a very good approximation of the nontrivial solution $\eta ,$  as shown in Figure 11. However, we observe that the solution $\eta$  diverges from the Fibonacci spiral for increasing values of $k$ . In other words, the physically relevant part of the solution matches exactly the Fibonaccy spiral.

Figure 11 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

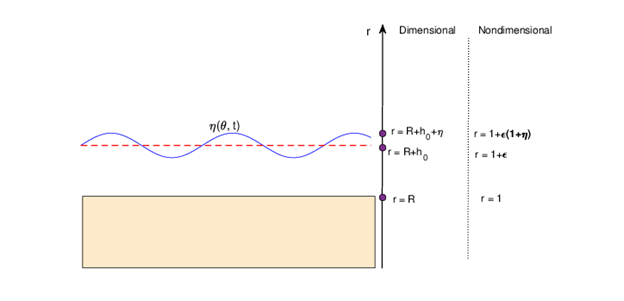
Figure 12 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion.

We also remark that the higher order of the shallow water equations can be derived for our free boundary model and the higher-order approximation has the following form:

$u_t$   (47)

$h_t+u{h}_{\theta }+h{u}_{\theta }-\epsilon h\left(u{h}_{\theta }+h{u}_{\theta }\right)=0$   (48)

It is one of our goals for further studies to study the higher-order approximation (47) - (48) and see if the Fibonacci spiral can be a better approximation of the free boundary model for larger values of $k.$

We also note that the model (8) - (9) is invariant under the group of transformations

$X^{\infty }={\xi }^1\left(h,u\right)\frac{\partial }{\partial t}+{\xi }^2\left(h,u\right)\frac{\partial }{\partial \theta } ,$   (49)

where the functions ${\xi }^1\left(h,u\right), {\xi }^2\left(h,u\right)$  solve the system of first-order equations

${\xi }_h^2+{\xi }_u^1-u{\xi }_h^1=0 , {\xi }_u^2-u{\xi }_u^1+h{\xi }_h^1=0.$   (50)

If we write the operator (49) as an infinitesimal transformation

$\overline{t}\approx t+{\xi }^1\left(h,u\right), \overline{\theta }\approx \theta +{\xi }^2\left(h,u\right).$   (51)

The equations (50) show that the infinitesimal transformation (51) changes the variables $\left(t,\theta \right)$  by adding to them an arbitrary solution of the system of linear differential equations

${\theta }_h+t_u-u{t}_h=0, {\theta }_u+h{t}_h-u{t}_u=0$   (52)

and that the system (52) admits the infinitesimal transformation (51).

Hence the operator (49) is admitted both by the nonlinear system (8) - (9) and by the linear system (52). This fact predicts a possibility to map the nonlinear equations (8) - (9) to the linear system (52) by an appropriate change of variables. It is important to note that the linear system is homogeneous, i.e. invariant under the uniform dilation $\overline{t}=t{\text{e}}^{a_{{}_5}}, \overline{\theta }=\theta {\text{e}}^{a_{{}_5}}$ produced by the operator $X_3$  from (11).

We conclude that the operator (49) and the operator $X_3$  from (11) are responsible for the possibility of mapping of the nonlinear system (8) - (9) to the linear homogeneous system (52). Mapping the nonlinear model (8) - (9) to a linear system will be studies in the forthcoming paper.

We would like to thank the Dean of STEM & Social Sciences at Wenatchee Valley College, Holly Bringman and Electronic Media Producer Lead, Brett McGinnis for providing us with all the necessary facilities for the research, great support, and encouragement.

Basic concepts from Lie group analysis of differential equations that are used in the present paper are assembled here.For further information regarding Lie groups and their applications to the theory of differential equations, the reader should consult the various classical and modern texts in the field, such as.^31–38

Definition of one-parameter groups: Let

${\overline{z}}^i=f^i\left(z,a\right), i=1,\mathrm{...}N,$   (A1)

be a one-parameter family of invertible transformations of points $z=\left(z^1,\mathrm{...},z^N\right)\in {ℝ}^N$  into points $\overline{z}=\left({\overline{z}}^1,\mathrm{...},{\overline{z}}^N\right)$ $\in {ℝ}^N.$  

Here $a$  is a real parameter from a neighborhood of $a=0,$  and we impose the condition that Transformation (A1) is an identity if and only if $a=0,$  i.e.,

$f^i\left(z,0\right)=z^i, i=1,\mathrm{...},N.$   (A2)

The set $G$  of transformations (A1) satisfying Condition (A2) is called a (local) one-parameter group of transformations in ${ℝ}^N$  if the successive action of two transformations is identical to the action of a third transformation from $G,$  i.e., if the function $f=\left(f^1,\mathrm{...},f^N\right)$  satisfies the following group property:

$f^i\left(f\left(z,a\right),b\right)=f^i\left(z,c\right), i=1,\mathrm{...},N,$   (A3)

where

$c=\phi \left(a,b\right)$ b  (A4)

With a smooth function $\phi \left(a,b\right)$  defined for sufficiently small $a$  and $b.$  The group parameter $a$  in the transformation (A1) can be changed so that the function (A4) becomes $c=a+b.$  In other words, the group property (A3) can be written, upon choosing an appropriate parameter $a$  (called a canonical parameter) in the form

$f^i\left(f\left(z,a\right),b\right)=f^i\left(z,a+b\right).$   (A5)

Group Generator. Let $G$  be a group of transformations (A1) satisfying the condition (A2) and the group property (A5). Expanding the functions $f^i\left(z,a\right)$  into Taylor series near $a=0$  and keeping only the linear terms in $a,$  one obtains the infinitesimal transformation of the group $G:$

${\overline{z}}^i\approx z^i+a{\xi }^i\left(z\right),$   (A6)

where

${\xi }^i\left(z\right)={\frac{\partial f^i\left(z,a\right)}{\partial a}|}_{a=0}, i=1,\mathrm{...},N.$   (A7)

The first-order linear differential operator

$X={\xi }^i\left(z\right)\frac{\partial }{\partial z^i}$   (A8)

is known as the generator of the group $G.$

Invariants: A function $J\left(z\right)$  is said to be an invariant of the group $G$ if for each point $z=\left(z^1,\mathrm{...},z^N\right)\in {ℝ}^N$  is is constant along the trajectory determined by the totality of transformed points $\overline{z}:J\left(\overline{z}\right)=J\left(z\right).$

The function $J\left(z\right)$  is an invariant of the group $G$  with Generator (A8) if and only if

$X\left(J\right)\equiv {\xi }^i\left(z\right)\frac{\partial J}{\partial z^i}=0.$   (A9)

Hence any one-parameter group has exactly $N-1$  functionally independent invariants (basis of invariants). One can take them to be the left-hand sides of $N-1$ first integrals $J_1\left(z\right)=C_1,\mathrm{...},J_{N-1}\left(z\right)=C_{N-1}$  of the characteristic equations for linear partial differential equation (A9). Then any other invariant is a function of $J_1\left(z\right),\mathrm{...},J_{N-1}\left(z\right).$

Invariant equations: We say that a system of equations

$F_k\left(z\right)=0, k=1,\mathrm{...},s$   (A10)

Is invariant with respect to the group $G$  (or admits the group $G$ ) if the transformations (A1) of the group $G$  map any solution of Eqs. (A10) into a solution of the same equations, i.e.,

$F_k\left(\overline{z}\right)=0, k=1,\mathrm{...},s$   (A11)

whenever $z$  solves Eqs. (A10). The group $G$  with the generator (A8) is admitted by Eqs. (A10) if and only if

${X\left(F_k\right)|}_{\left(A10\right)}=0, k=1,\mathrm{...},s,$   (A12)

where the symbol ${|}_{\left(A10\right)}$  means evaluated on the solutions of Eqs. (A10).

If $z$  is a collection of independent variables $x=\left(x^1,\mathrm{...},x^n\right),$  dependent variables $u=\left(u^1,\mathrm{...},u^m\right)$  and partial derivatives $u_{\left(1\right)}=\left\{u_i^{\alpha }\right\},u_{\left(2\right)}=\left\{u_{ij}^{\alpha }\right\},\mathrm{...},$  of $u$  with respect to $x$  up to certain order, where

$u_i^{\alpha }=\frac{\partial u^{\alpha }}{\partial x^i}, u_{ij}^{\alpha }=\frac{{\partial }^2{u}^{\alpha }}{\partial x^i\partial x^j},\mathrm{...}$

then (A10) is a system of partial differential equations

$F_k\left(x,u,u_{\left(1\right)},\mathrm{...}\right)=0, k=1,\mathrm{...},s.$   (A13)

Furthermore, if the transformations (A1) are obtained by the transformations of the independent and dependent variables

$\overline{x}=f\left(x,u,a\right), \overline{u}=g\left(x,u,a\right)$   (A14)

and the extension of (A14) to all derivatives $u_{\left(1\right)},$  etc. involved in the differential equations (A13), then Eqs. (A11) define a group $G$  of transformations (A14) admitted by the differential equations (A13). In other words, an admitted group does not change the form of the system of differential equations (A13). The generator of the admitted group $G$  is termed an infinitesimal symmetry (or simply symmetry) of the differential equations (A13). Equations (A12) serve for obtaining the infinitesimal symmetries and are known as the determining equations. These equations are linear and homogeneous and therefore the set $L$  of its solutions is a vector space. integration of determining equations often provides several linearly independent infinitesimal symmetries. Moreover, the determining equations have a specific property that guarantees that the set $L$  is closed with respect to the commutator $\left[X_1,X_2\right]=X_1{X}_2-X_2{X}_1.$  Due to this property $L$  is called a Lie algebra. If the dimension of the vector space $L$  is equal to $r,$  the space is denoted by $L_r$  and is called an $r-$  dimensional Lie algebra. An $r-$  dimensional Lie algebra $L_r$  generates a group depending on $r$  parameters which is called an v parameter group.

Invariant solutions. Let the differential equations (A13) admit a multi-parameter group $G,$  and let $H$  be a subgroup of $G.$  A solution

$u^{\alpha }=h^{\alpha }\left(x\right), \alpha =1,\mathrm{...},m$   (A15)

of Eqs. (A13) is called an $H-$  invariant solution (termed for brevity an invariant solution) if Eqs. (A15) are invariant with respect to the subgroup $H.$  If $H$  is a one-parameter group and has the generator $X,$  then the $H-$  invariant solutions are constructed by calculating a basis of invariants $J_1,J_2,\mathrm{....}$ ^39,40

1. Li C, Ji A, Cao Z. Stressed Fibonacci spiral patterns of definite chirality. Applied Physics Letters. 2007;90:164102.
2. Ibragimov R, Mohazzabi P, Roembke R, et al. Asymptotic stability of the polar vortex perturbed by harmonic waves describing atmospheric gravity waves circulating in an equatorial plane of a spherical planet. Math Model Nat Phenom. 2018;13(4).
3. Holton J, Haynes P, McIntyre M, et al. Stratosphere–troposphere exchange. Rev Geophys. 1995;33(4):403–439.
4. Newman P. Chemistry and dynamics of the Antarctic ozone hole, in the stratosphere:  Dynamics, fransport, and Ghemistry. Geophys Monogr. 2010.
5. Ibragimov R. Nonlinear viscous fluid patterns in a thin rotating spherical domain and applications. Phys Fluids. 2011:23(12):123102.
6. Ibragimov R, Gunag L. Splitting phenomenon of a higher-order shallow water theory associated with a longitudinal planetary wave. Dynam Atmos Ocean. 2015;69:1–11.
7. Yulaeva E, Wallace J. The signature of ENSO in global temperatures and pre- cipitation fields derived from the Microwave Sounding Unit. J Glimate. 1994;7(11):1719–1736.
8. Zhang Y, Li J, Zhou J. The Relationship between Polar Vortex and Ozone Depletion in the Antarctic Stratosphere during the Period 1979–2016. Advances in Meteorology. 2017:1–12.
9. Ibragimov R, Lauren D, Stimmel M, et al. Visualization of Exact Invariant Solutions Associated with Atmospheric Waves in a Thin Circular Layer. Journal of Applied Mathematics and Physics. 2003;9(5):1321–1328.
10. Newman P. Chemistry and dynamics of the Antarctic ozone hole, in the stratosphere:  Dynamics, fransport, and Ghemistry. Geophys Monogr. 2010.
11. Shindell DT, Schmidt GA. Southern hemisphere climate response to ozone changes and greenhouse gas increases. Geophys Res Gett. 2004.
12. Lubin D, Jensen E. Effects of clouds and stratospheric ozone depletion on ultraviolet radiation trends. Nature. 2002;377:710–713.
13. Chipperfield M, Dhomse S, Feng W, et al. Quantifying the ozone and ultraviolet benefits already achieved by the Montreal Protocol. Nat Commun. 2015;6:7233.
14. Baldwin M, Dunkerton T. Stratospheric Harbingers of Anomalous Weather Regimes. Science. 2001;294(5542):581–584.
15. El Niño, La Niña. New Zealand’s National Institute of Water and Atmospheric Research. 2016.
16. Becker J. How Much Do El Niño and La Niña Affect Our Weather? Scientific American. 2016.
17. Angell J, Korshover J. Variation in size and location of the 300 mb north circumpolar vortex between 1963 and 1975. Monthly Weather Review. 1977;105(1)19–25.
18. Sun L, Wu H, Li X. Visualization of Exact Invariant Solutions Associated with Atmospheric Waves in a Thin Circular Layer. Journal of Applied Mathematics and Physics. 2006;9(5):52–62.
19. McCreary J. Eastern tropical ocean response to changing wind systems: with Applications to El Niño. J Phys Oceanogr. 1976;6(5)632–645
20. Murray F. Dynamic stability in the stratosphere. J Geophys Res. 1960;65(10):3273–3305.
21. Alexander M, Tsuda T, Vincent R. Latitudinal Variations Observed in Gravity Waves with Short Vertical Wavelengths. J Atmos Sci. 2002;59:1394–1404.
22. Dickson LE. Differential equations from the group standpoint. Ann Math. 1924;25(4):287–378.
23. Vassada A, Horst S, Kennedy M, et al. Cassini imaging of Saturn: Southern hemisphere winds and vorticities. J Geophys Res. 2006;111:5004–5017.
24. Su C, Gardner C. Derivation of the Korteweg-de Vries equations and Burgers equations. J Math Phys. 1968;10(3):536–539.
25. Schoeberl M, Hartmann D. The dynamics of the stratospheric polar vortex and its relation to springtime ozone depletions. Science. 1991;251:46–52.
26. Yang X. Variability of the northern circumpolar vortex and its association with climate anomaly in China. Acta Meteorologica Sinica. 2016;26(2):135–142.
27. Sigmond M, Scinocca J, Kharin V, et al. Enhanced seasonal forecast skill following stratospheric sudden warmings. Nat Geosci. 2013;6:98–102.
28. Shi C, Xu T, Guo D, et al. Modulating effects of planetary wave 3 on a stratospheric sudden warming event in 2005. J Atmos Sci. 2017;74(5):1549–1559.
29. Shi C, Xu T, Li H, et al. 2017: The Role of Rossby-Wave Propagation in a North American Extreme Cold Event. Advances in Meteorology. 2017: 4635849.
30. Cohen A. An Introduction to the Lie Theory of One-Parameter Groups With Applications to the Solution of Differential Equations. DC Heath. New York; 1911.
31. Dickson LE. Differential equations from the group standpoint. Ann Math. 1924;25(4):287–378.
32. Ovsyannikov LV. Group Properties of Differential Equations, Siberian Branch, USSR Academy of Sciences. Novosibirsk. 1962.
33. Olver PJ. Applications of Lie Groups to Differential Equations. Springer-Verlag: New York; 1986.
34. Bluman G, Kumei S. On invariance properties of the wave equations. J Math Phys. 1987;28(2):307.
35. Stephani H. Differential Equations: Their Solution Using Symmetries. Cambridge Univ Press: Cambridge; 1989.
36. Cantwell BJ. Introduction to Symmetry Analysis. Cambridge University Press: Cambridge; 2002.
37. Bluman GW, Anco SC. Symmetry and Integration Methods for Differential Equations. Springer-Verlag: New York; 2002.
38. Kovalev V, Pustovalov V, Senashov S. Lie-Bäcklund group for the nonlinear geometrical optics equations. Differential equations. 1993;29(10):1751–1764.
39. Yulaeva E, Wallace J. The signature of ENSO in global temperatures and pre- cipitation fields derived from the Microwave Sounding Unit. J Glimate. 1994;7(11):1719–1736.
40. Zhang Y, Li J, Zhou J. The Relationship between Polar Vortex and Ozone Depletion in the Antarctic Stratosphere during the Period 1979–2016. Advances in Meteorology. 2017:1–12.