The purpose of this study was to develop a novel seabed-surveying AUV with a spatial control system which is consisted manages depth, attitude, and line tracing, simultaneously. Our novel AUV, named SASSY, equipped the vector thrusters to generate appropriate thrust force for task demands. In this study, we demonstrate the basic specifications of attitude, depth, and line-trace control based on the PID controller with limit sensitivity detection methods. To measure the depth control capability, step and frequency responses had been measured to construct the plant model of SASSY using a Bode diagram. To trace the guide rope set on the seabed, the attitude angle of the yaw direction was controlled using incline deviations between SASSY’s direction and the center of the guide rope. To verify the depth and attitude controller of SASSY, two video-transect experiments had been conducted: (1) in a simulated environment with static water conditions, and (2) in real sea of Ofunato Bay. The mosaicing images were constructed in each experiment, suggesting that SASSY’s depth and attitude controller was able to record photographs of the seabed purposely.

Keywords: seabed surveying, autonomous underwater vehicle, video-transect, depth control, attitude control, line-trace control

In order to efficiently and sustainably use the high commercial value of marine resources, it is necessary to detect their amounts and distribution. Recent studies had proposed new camera configurations to census moving fish and benthic fauna; such as a stereo-vision system¹ and a simultaneous down- and forward-looking camera system.² Traditional ways for managing marine resources, however, the video-transect method had been used by divers following a rope equipped with underwater video cameras,³ as shown in Figure 1.

This method involves recording photographs and/or movies of the coastal area at around 3 to 10m deep from the surface, and to survey the growth of coral reef and marine resources.⁴ Generally, divers move to the survey area and go to the depth to be investigated, and then move approximately 10 to 50m along a guide rope set on the seabed. The ocean floor is photographed with a video camera, and the distribution and quantity of marine resources are analyzed from the images. In order to unify the analysis conditions, it is necessary to maintain an angle of view around the guide rope where a width of 2m can be photographed.

Completing the video transect by underwater robots instead of divers is desirable, since the physical burden imposed on divers is high. Briefly, the video-transect method involves tracing the line, since this method requires following a guide rope set on the seabed. Considerable research concerning line-trace experiments have been conducted on land.^5,6 Although the movement of line-trace experiments on land had been constrained to a two-dimensional plane, it would have to control the depth and/or the altitude of the vehicle, the attitude of the vehicle, and the angle of the video camera’s view while working in the sea. According to the research on line tracing in deep sea area, there are the cable tracking system for cable surveying task.^7–9 However, in general, submarine cables are placed at depths of more than 1500m, and this area has little influence of waves and current velocity.¹⁰ There is also a research on line tracing in the breakwater area,¹¹ but this is only used for pilot assistance of the remotely operated vehicle (ROV). Hence, the purpose of this study was to develop a novel autonomous underwater vehicle (AUV) for the video-transect method. In section IV, we demonstrate our AUV’s concepts and its design. In section V, the design and the validation of the spatial control system are demonstrated. In section VI, the processes of achieving the video-transect method using our AUV and the results of the experiments conducted in the real environment are discussed, and concluding remarks are made in section VII.

Figure 1 Schematic figure of the video-transect method by diver.

In order to implement the video transect on behalf of the diver, the AUV must achieve the following three points simultaneously: (1) autonomous navigation in the breakwater area, (2) autonomous control of attitude and altitude (or depth) which is named as a “spatial control system” in this study, and (3) line tracing is possible. Figure 2A shows the overview of our novel seabed-surveying AUV with a spatial control system, named “SASSY”: the total length is 0.7m, the full width is 0.6m, the total height is 0.3m, and the dry weight is 8.1kg. SASSY is capable of operating within 5degrees of freedom surge, heave, roll, pitch, and yaw directions using four main screw-propeller thrusters and two vector thrusters,^12,13 as shown in Figure 2B. Two vector thrusters generate the thrust force in the travelling direction where the rotational direction of the motors is constant (clockwise direction). Figure 2C shows the installed vector thruster when the angle A_i=0⁰ (i=1, 2) formed by the axis of motor and the X axis of SASSY coordinate system (surge direction) is in parallel and the range of motion of A_i was set at -45≤A_i≤90⁰.The heave motion was controlled using thrusters nos. 1 to 4; the roll and pitch motion was controlled by thrusters nos. 3 and 4, and the yaw motion was achieved by thrusters nos. 5 and 6.

The attitude angle of the roll Φdeg, the pitch θdeg, and the yaw Ψdeg were measured using the inertial measurement unit (IMU; MPU 9150, Inven Sense). The depth was detected by a pressure sensor (MS 5803-14 BA, TE). The sampling frequency of the IMU was set at 50Hz, and the depth sensor was 12.5Hz. In order to acquire the altitude of SASSY, an ultrasonic sensor (transducer; record unit: PICO 2204, Pico Technology) was situated in the vertical axis of the SASSY coordinate system, and the data were sampled at a frequency of 40Hz. The altitude was calculated using the time of flight (TOF) method following UNESCO's equation¹⁴ for determining the speed of sound in water. For taking photographs of the seabed, we installed a complementary metal oxide semiconductor (CMOS) camera (BFLY - PGE - 13E4C - CS, Blackfly; secures a horizontal angle of view approximately 62deg; acquires photographs of 360×240pixels) with a wide-angle lens (HHF 6M, Blackfly) enclosed in a pressure hull at a frame rate of 30fps. Control signals from the PC were transmitted to the microcomputer board (Arduino Uno, Arduino) inside the pressure hull. The pulse width modulation controller was then used to control all of the thrusters.

Figure 2 (A) Overview of SASSY, (B) number assignments of thrusters, (C) overview of vector thruster.

Spatial control system and its validation

The spatial control system regulated the attitude and altitude of SASSY by generating the thrust forces. The direction of the thrust force was controlled by a vector thruster in the heave direction so as to be parallel with the Z axis of the SASSY coordinate system. The equipped camera should always face the ocean floor to detect the guide rope while moving. Figure 3 shows the block diagram for spatial control system; the equipped camera’s angle of view was stabilized to control the attitude of SASSY using the IMU information.

The thrust force generation was based on the PID controller as follows:

$F_j=\frac{U_n{F}_{jmax}}{P_n}$ (1),

$U_n=K_{Pn}\left(e_n+\frac{1}{T_{In}}{{\displaystyle \int }}^{\text{}}{e}_{n}dt+T_{Dn}\frac{d}{dt}{e}_n\right)$ (2),

where F_j (j=1,2,…,6) [N] is the generated force, F_{j max} (j=1,2,…,6) N is the maximum force for each thruster (8.5N),¹⁵P_n(n=Φ,θ,ψ,h) is the deviation between the target value and the sensor value at the start time while the heave motion is controlled; also, P_n(n=Φ,θ,ψ,h) denotes the maximum allowable angle in each direction (Φ,θ,ψ) while the attitude is controlled, and U_n(n=Φ,θ,ψ,h) is the gain matrix of the PID controller for each direction. The PID gain matrix used for this controller was determined by trial and error based on the limit of sensitivity detection method. The feedback gains of the PID controller were tuned at K_P=4.0, K_I=4000, and K_D=4E-05 for heave motion control; at K_P=0.4, K_I=400, and K_D=4E-6 for roll and pitch motion control; and at K_P=3, K_I=600, and K_D=3E-4 for yaw motion control.

To check the validation of the spatial control system, the experiment of step responses was conducted under static conditions in the water (the water tank was 1.57m deep×1.2m wide×1.27m high). The target depth was set at 0.5m from the surface, where the initial attitude of SASSY was in contact with the water’s surface. During the experiment, SASSY was controlled to maintain the initial attitude. The pressure and the attitude information were smoothed with a 4th order Butterworth filter with a cutoff frequency of 5Hz. Figure 4A & Figure 4B show the typical results of the pressure and the attitude of SASSY. SASSY reached the target depth 10 [sec] from the start position. After the convergence, the averaged deviation was 0.0003m(less than 1.0 % of SASSY’s total height), and the maximum deviation was 0.0153m (less than 5.0 % of SASSY’s total height). Also, the averaged deviations in the roll and yaw motions were less than 1.0deg. Based on these results, we decided that the PID gains were appropriate for further experiments.

System identification by frequency response experiments

Previously, system identifications of the underwater robot had been conducted to clarify the unknown parameters,¹⁶ since the underwater robot has many black boxes due to its complicated shape. In this study, we conducted experiments regarding frequency responses to identify the simulation model of SASSY’s spatial control system in the same water tank. The center of the amplitudes of the depth was set at 0.5m, and the PID gains were the same as those of the step-response experiment. When SASSY reached the target depth (0.5m), a sine wave with an amplitude of 0.15m was used as an input, and the frequency was set from 0.01Hz to 0.25Hz with 0.01Hz steps. Each frequency condition was conducted three times, and a total of 15 cycle data was measured. Figure 5A shows a typical example of the depth changes at the 0.08Hz condition. The periodic pattern can be confirmed; however, there are phase lag, amplitude, and steady-state deviations. Thus, we constructed a Bode diagram of the depth control of SASSY as follows:

$G=20\log \left|\frac{A_{out}}{A_{in}}\right|$ (3),

$P=\frac{360{{\displaystyle \sum }}_{k=1}^j\left(I_{out,k}-I_{in,k}\right)}{jT}$ (4),

where GdB is the gain, P deg is the phase lag, A_inm is the amplitude of the input, A_outm is the amplitude of the output, T s is the cycle of the input, I_out,k s(k=1,…,j) is the time when the kth peak value of the measuring depth had appeared, and I_in,ks(k=1,…, j) is the time when the kth peak value of the target depth had appeared. Figure 5B shows the Bode diagram of the frequency responses during spatial control. To identify the spatial control model, we determined that SASSY could be approximated by a time lag system of the second order. From the results of the step responses, frequency responses, and the Bode diagram, we estimated the transfer function of SASSY’s spatial control system using MATLAB’s R2016b System Identification Toolbox (MathWorks, Inc.), and the estimated transfer function is as follows:

$\text{G}\left(\text{s}\right)\text{=}\frac{\text{0}\text{.4638}\left(\text{s+0}\text{.13176}\right)}{\left(\text{s+0}\text{.439861}\right)\left(\text{s+0}\text{.138839}\right)}{\text{e}}^{\text{-0}\text{.29s}}$ (5)

Figure 3 Diagram of the spatial control system.

Figure 4 (A) Typical result of depth control, (B) typical result of attitude control.

Figure 5 (A) Results of depth control at a frequency of 0.08 [Hz], (B) Bode diagram of the frequency response of the depth control

System configuration and line detection by image processing

Figure 6 shows the flow of the video-transect executed by SASSY. To follow the guide rope set on the seabed, control of the travelling direction (surge) and the depth was achieved simultaneously to maintain the angle of view. Previous study had demonstrated the optimal method of detecting the guide rope set on the seabed, which selects the image plane where the guide rope is most emphasized with respect to the seabed, and then generates a histogram of the image, determines the threshold of the Canny filter using the discriminant analysis method, and, finally, detects the guide rope.¹⁴ In this study, we used the same method to detect the guide rope set on the seabed, and then applied the Hough transform to calculate the angle of deviation  deg between the guide rope and the travelling direction, as shown in Figure 7A and Figure 7B.

In addition, the sway deviation  [pixel] between the center of the guide rope and the center of the camera is also calculated, as shown in Figure 7A and Figure 7B. SASSY’s travelling direction controller was constructed by spatial control system and disturbance observer based on Equation 5 as shown in Figure 7C; the input is the travelling direction, the feedback signal is the angle deviation  the yaw angle is calculated to control SASSY’s direction from the deviation of these two, and the sway deviation is controlled to be zero simultaneously.

For spatial control, we first set the target altitude and then switched to the depth control when the difference from the current altitude became the setting range. The altitude was measured using an ultrasonic sensor, converting it to the target depth using the following equation after processing with the median filter:

$D_t=D_r+h_r-h_t$ (6),

Where D_tm is the target depth, D_rm is the present depth from the pressure sensor, h_rm is the present altitude, and h_tm is the target altitude.

Video-transect experiment I: simulated environment with static water conditions

To validate SASSY’s travelling direction and spatial control system, we conducted the line-trace experiment in a two-dimensional water tube with a total length of 26m, a width of 0.8m, and a height of 1.0m, as shown in Figure 8A. The water height was set at 0.8m. The guide rope was set on the bottom of the tube with a total length of 3.7m and a width of 0.013m. Travelling direction and depth control commands were executed simultaneously along the guide rope; the target depth was set at 0.4m. SASSY was set at the starting point, where the guide rope could be photographed beforehand in the angle of view, and then the line-trace experiment was started. To follow the guide rope, certain inputs were sent to the thruster nos. 5 and 6. The PID gain for the vector thruster was set at K_P=90, the other PID gains were the same as in the experiment of spatial control system. In addition, the PID gains for correcting the deviation in the sway direction and the yaw direction are K_P=1.0 and K_I=1000, respectively.

Figure 8 shows a typical result of SASSY’s tracking the set section of 3.7m to the guide rope. Figure 8A shows the state of SASSY during the experiment. Figure 8B is the mosaic image processed using Microsoft Image Composite Editor 2 (Microsoft Corp.). Regarding the depth control, as shown in Figure 8C, the input value of 0.4m deep was maintained once SASSY had reached this set value, validating that SASSY’s depth controller could reasonably achieve the line trace. Figure 8D shows the typical results of the angle deviation (-2.9±2.3 deg) and the sway deviation(5.7±10.6pixels) while line tracing. The result of the sway deviation  was less than 20% of the angle of view, since the window size of image processing is set to 80×60pixels. Further research and/or tuning of the feedback gains are needed for more precise control in moving along the guide rope; however, the ability to follow the guide line could be improved by weighting according to the angular difference in the traveling direction and the magnitude of the deviation. The photographing range is calculated from the created mosaic image, as shown in Figure 8B, and the result is shown in Figure 8E. The averaged sway deviation on the left was 5.4±0.9cm and 3.8±0.8cm for the right side. When achieving the video transect in the actual environment, it is necessary to photograph a range of 1.0m on each side from the center of the line. Therefore, it was suggested that the SASSY could utilize the video-transect method by maintaining an altitude of about 9.0m from the bottom of the sea.

Video-transect experiment II: real sea at Ofunato Bay

We conducted the video-transect experiment in a real situation on November 16, 2016, at Ofunato Bay, Iwate. The weather was fine, the temperature was 6.0 degrees Celsius, and the water temperature was 14degrees Celsius. A video transect was performed with the rail tracing, which was 7.0cm wide, already installed in Ofunato Bay as the target. SASSY was operated at an average depth of 0.3m, and a section of about 12m was photographed. As shown in Figure 9, the photographing range is calculated from the created mosaic image; the averaged sway deviation  in the left was 0.33±0.17m and was 0.31±0.15m for the right side. The spread of the photographing range has been confirmed, as shown in the profiles of sway deviations, since the distance between the ocean floor and SASSY increased while maintaining a constant depth offshore. Further modification will be needed to complete a video transect using SASSY in real situations, e.g., conducting a survey further off the coast and/or installing a wide-angle lens.

The coordinates are the image coordinate system, and the SASSY had moved from the start point to the end point in the direction defined as the X axis. (A) Experimental environment, (B) mosaic image, (C) typical result of depth, (D) typical results of the angle deviation  and the sway deviation , (E) photographing range calculated from the mosaic image.

Figure 6 Video transection flow for SASSY.

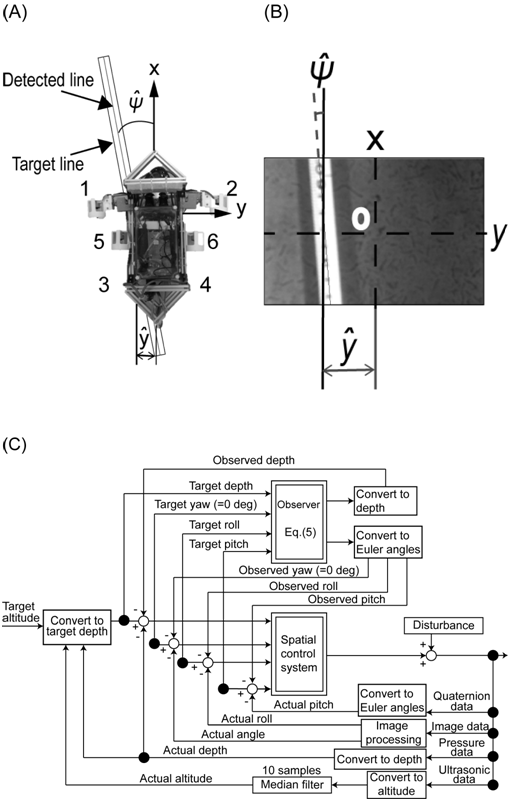
Figure 7 (A) Definition of the control parameters for guide-rope tracking, (B) control parameters for guide-rope tracking projected to the AUV coordinate system, (C) control diagram of the spatial control system with guide-rope tracking.

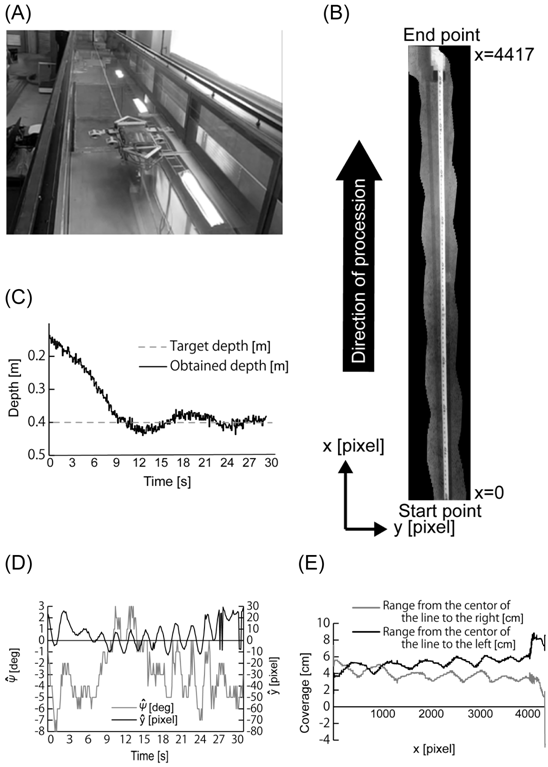
Figure 8 Line-trace experiment in static water conditions. The coordinates are the image coordinate system, and the SASSY had moved from the start point to the end point in the direction defined as the X axis. (A) Experimental environment, (B) mosaicing image, (C) typical result of depth, (D) typical results of the angle deviation and the sway deviation y ̂, (E) photographing range calculated from the mosaic image.

Figure 9 Mosaicing image in real sea, recorded at Ofunato Bay, Nov. 16, 2016. The photographing ranges were calculated from the mosaic image.

In this study, we had constructed a novel seabed-surveying AUV, “SASSY,” with a spatial control system, including a depth and line-trace controller, to utilize the video-transect method. Two experiments were conducted in a static water tube and a real situation (Ofunato Bay), and managed to record movies about the seabed and make the mosaic images.

Part of this work was supported by JSPS KAKENHI Grant Number 17K08029 and Soft-Path Science andEngineering Research Center, Iwate University.

We thank Yuriko Matsubayashi, Wataru Satoh, Tomoka Shimizu and AkiyoshiYamaoi for their preparation of the experiments, and Ofunato Dock Co., Ltd. for their help with the experiments at Ofunato Bay.

Author declares that there is no conflict of interest.

1. Bernard ATF, Götz A, Parker D, et al. New possibilities for research on reef fish across the continental shelf of South Africa. S Afr J Sci .2014;110:9–10.
2. Auster P, Lindholm J, Plourde M, et al. Camera Configuration and Use of AUVs to Census Mobile Fauna. Marine Tech Soc J. 2007;41(4):49–52.
3. Hart AM, Fabris FP. Digital video techniques for assessing population size structure and habitat of Greenlip and Roe’s abalone. Fisheries Research Report. 2007;167.
4. Hill J, Wilkinson C. Methods for Ecological Monitoring of Coral Reefs. Australian Institute of Marine Science, Townsville. 2004; p.38–40.
5. Wang Y, Shen D, Teoh KE. Lane detection using spline model. Patt Recog Lett. 2000;21:677–689.
6. Aufrere R, Chapuis R, Chusse F. A model–driven approach for real–time road recognition. Machine Vision and Applications. 2001;13:95–107.
7. Antich J, Ortiz A. A behavior–based control architecture for visually guiding an underwater cable tracker. IFAC Proceed Vol. 2003;36:67–72.
8. Antich J, Ortiz A. Experimental evaluation of the control architecture of an underwater cable tracker. IFAC Proceed Manoeuvr Cntl Marine Craft. 2003;121–126.
9. Ortiz A, Antich J, Oliver G. Experimental evaluation of a particle filter–based approach for visually tracking undersea cables. IFAC Proceed Vol. 2009;42:140–145.
10. Nguyen TD. Boundary stabilization of marine structure. IFAC Proceed Vol. 2008;41(2):1839–1844.
11. Chen HH, Chuang WN, Wang CC. Vision–based line detection for underwater inspection of breakwater construction using an ROV. Ocean Eng. 2015;109:20–33.
12. Huang Y, Yang P, Gong H, et al. Mathematical modeling of thruster vectored AUV based on the single rotating object.3rd Int Conf Mech Robot Automation. 2015;613–619.
13. Cavallo E, Michelini CR, Filaretov FV. Conceptual Design of an AUV Equipped with a Three Degrees of Freedom Vectored Thruster. J Intel Robot Sys. 2004;39(4):365–391.
14. Chen AC, Millero JF. Speed of sound in seawater at high pressures. J Acoust Soc of Am. 1997;5:1129–1135.
15. Takagi M, Mori H, Yimit A, et al. Development of a Small Size Underwater Robot for Observing Fisheries Resources-Underwater Robot for Assisting Abalone Fishing. Robot Mech. 2016;28(3):397–403.
16. Avila JPJ, Donha DC, Adamowski JC. Experimental model identification of open–frame underwater vehicles. Ocean Eng. 2013;60(1):81–94.