The mechanism of mycobacterium tuberculosis macrophage interactions was studied using surface energetics tool in determining the interaction processes. The surface interfacial energies were explained using van der Waals concept of particle interactions. Twenty samples each of infected and uninfected sputum were collected and screened to determine the infection status using GeneXpert and Ziehl-Neelsen staining method. The absorbance, ā, values of each specimen, for wavelength range of 230-950nm were measured using digital Ultraviolet Visible Spectrophotometer. Matlab software tools were used in the mathematical analysis of the data generated from the absorbance values. The combined Hamaker coefficients were obtained using the values of the dielectric constant with the Lifshitz Equation. The harmonized Hamaker coefficients A_132har and the absolute combined Hamaker coefficients A_132abs of infected samples were deduced. The values of A_132abs for mtb infected sputum and Ã_132abs for mtb/HIV co-infected sputum are 0.21631x10^-21Joule and 0.18825x10^-21Joule respectively. This result reveals that the surface energy of the macrophage is less than the surface energy of the mtb, mtb/HIV while the surface energy of the mtb/HIV macrophage is less than that of mtb macrophage. HIV has the tendency to reduce the interaction energy with the consequences of increased viral loads and decreased immune systems. The interaction energy is reduced by 13% confirming adverse effects observed in HIV patients suffering from Tb. Negative Hamaker coefficient of -0.22669x10^-19mJ/m² was calculated indicating that separation of mtb is practical. The effect of the infection can only be abated if additive(s) in form drug is added that can render A₁₃₂ negative. Thus, the value of Hamaker constant of the sputum A₃₃ was required for repulsion to occur mathematically derived as A₃₃≥0.9527x10^-21Joule which satisfies this condition for negative A_132abs.

Keywords: absorbance, energetics, hamaker coefficient, macrophage, mycobacterium tuberculosis, van der waals forces, wavelength

In the world today, tuberculosis (tb) is the leading cause of death due to its interaction with other infectious diseases such as the Human Immunodeficiency Virus (HIV), which is the AIDS causative agent.¹ The HIV impact on tb is quite overwhelming prior to the fact that tb would already be declining worldwide if not for HIV which is contributing approximately 10% of all global mortality cases.² Individual who are latently infected have a 10% risk of developing the disease in their life time, although HIV is a strong risk factor for developing active tb.^3-5 About 14 million people are estimated worldwide with active tb infection. However, the vast majority of tb-related deaths occur in the developing part of the world.⁶ About 9.4 million new tb cases were reported in 2009, and about 22.5% of 1.7 million deaths reported were related to tb among people with HIV.⁶ About 8.7 million people suffered from tb-related illness, including 1.1 million cases among people with HIV, leading to 1.4 million deaths in 2011.⁷ The bacterial pathogen that causes tb mycobacterium tuberculosis (mtb) latently infects one third of the world’s population and is responsible for the highest mortality rate of any single bacterial pathogen.^3,4 The lung is typically the primary site of the bacterial infection, where it is engulfed by macrophages during an innate immune response.¹ Mycobacterium tb has a slow doubling time of about 15-20 hours, and prefers to live within macrophages. Bacteria are then transported by dendritic cells to the closest draining lymph nodes (LN) where the host’s adaptive immune response is mounted against infection.

A T-cell mediated immune response rather than an antibody mediated immune response is necessary to combat infection since mtb generally resides within macrophages. These take up the bacteria together with the dendritic cells at the site of infection and transport them or bacterial antigen to the draining LN where a specific immune response can be developed. $C{D}_4^{+}$ T-cells and macrophages are critical to our immune system response and HIV is a virus that specially infects them,¹ thus compromising the host ability to control interaction(s). HIV weakens the immune system; tb thrives in a weakened immune system. Each disease increases the other’s progress.^8,9 Surface property determination of interacting particles lead to the further understanding of the mechanism of interactions; whereby a common area of contact is established once two particles meet each other leading to a displacement of a certain portion of each particle. The consecutive impact on the surface is called surface thermodynamic effects. From surface thermodynamic point of view, related works are in the phagocytic engulfment and cell adhesiveness as cellular surface phenomena and bacteria platelets highly developed by.^10-12 Neumann et al.¹⁰ considered the relationship between free energy of engulfment and number of bacteria ingested. In this research, it is of interest to understand how the mtb interacts with the macrophage. The process involves the bacterium modeled as a particle in a liquid medium (sputum) attaching itself on the surface of the macrophage (another particle), penetrating and probably destroying it. The condition under which bacterium attachment on the surface of the macrophage does not take place will be sought, even in the presence of HIV with its destructive effect. The free energy for the condition where no adhesion should occur is to be predicted from the concept of negative Hamaker coefficient. It is also desired to determine quantitatively the mechanism of interactions between the mtb and macrophages using the concept of surface energetics.

The methodology of this research work involved sputum sample collection, mycobacterium and macrophages structural studies, mycobacterium tuberculosis screening, and the study of the mechanism of interaction of the bacterium and the macrophage. Twenty samples each of infected, uninfected and mtb/HIV co-infected sputum was collected. Each specimen was screened to determine the infection status using GeneXpert and Ziehl-Neelsen staining method. The slides were prepared and the absorbance, ā, values of each specimen, for wavelength range of 230-950 nm were measured using digital Ultraviolet Visible Spectrophotometer. The data generated and the various Equation s governing the relationship among the variables were used in calculating values for the reflectance, R, transmittance, T, refractive index, n, and the dielectric constant, ε. Matlab software tools were employed in the mathematical analysis of the data generated from the absorbance values.

Thermodynamics particle-particle interaction mechanisms

Presume in a certain case, the bacterium, mtb has been considered as a particle coming in the vicinity of the macrophage which is further considered as another particle. In the successive step, one particle (the bacterium) attaches itself on the surface of the other (the macrophage) under a specific condition where the macrophage is dispersed in sputum medium (Figure 1). Expression of the thermodynamic free energy associated with adhesion process $\Delta F_{pls}^{adh}$ provided in Figure 1 is represented as follows:^13,14

$\Delta F_{pls}^{adh}\left(d_o\right)={\gamma }_{ps}-{\gamma }_{pl}-{\gamma }_{sl}$ . (1)

Where, $\Delta F_{pls}^{adh}$ = The integrated free energy of adhesion considered from infinity to the equilibrium
d_o= separation distance
P & S= Bacteria and macrophage respectively
L= sputum
γ_ps= Expresses the interfacial free energy between P and S
γ_pl= Expresses the interfacial free energy between P and L
γ_sl= Expresses the interfacial free energy between S and L

Successful bacterial penetration in the macrophage cells will occur through the engulfment of the bacteria requiring net free energy, represented as:^13,15

$\Delta F_{NET}={\gamma }_{ps}-{\text{γ}}_{\text{pl}}<0$ . (2)

In Equation 2, rejection of the bacteria by the macrophage will be represented, if $\Delta F_{NET}$ becomes greater than zero. For the interaction between the individual components, similar Equation s can be written also:^13,14

$\Delta F_{ps}^{adh}\left(d_1\right)={\gamma }_{ps}-{\gamma }_{pv}-{\gamma }_{sv}$ . (3)

Figure 1 Conceptual representation of mtb-macrophage adhesion process.

$\Delta F_{sl}^{adh}\left(d_1\right)={\gamma }_{sl}-{\gamma }_{sv}-{\gamma }_{lv}$ . (4)

$\Delta F_{pl}^{adh}\left(d_1\right)={\gamma }_{pl}-{\gamma }_{pv}-{\gamma }_{lv}$ .(5)

For a liquid, the force of cohesion, which is the interaction with itself, is described by:

$\Delta F_{ii}^{coh}\left(d_1\right)=-2{\gamma }_{lv}$ . (6)

∆F^adh can be determined by several approaches, apart from the above surface free energy approach. The classical work of¹⁶ is very appropriate.

A system containing two planes could be considered for computing the free energy of interaction. This can be done for semi-infinite, parallel bodies belonging to material 1 and 2 isolated by material 3, bearing thickness ‘d’ (Figure 2) provided in the following section.¹⁶ This is calculated by the following Equation:

$\Delta F_{132}\left(d_o\right)=\left[-\frac{A_{132}}{12\pi d_o^2}\right]$ . (7)

Figure 2 Representation of interaction of two solid bodies, depicted by 1 and 2 which are eventually isolated by d, liquid 3.

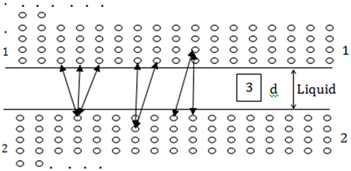
In this, ${\text{A}}_{132}$ = Hamaker coefficient for a respective system.

Considering nominal isolation distance d0, and Equation 7 as valid for such a small distance, the Hamaker coefficient should be expressed as:¹⁶

$A_{132}=-12\pi d_o^2\Delta F^{adh}\left(d_o\right)$ . (8)

The Hamaker coefficient A132 for the interactions between two different bodies in a liquid can be calculated from Equation 8 once the free energy of adhesion between the two bodies is known or through the pair-wise additivity approach as originally proposed by Hamaker¹⁶ or by the macroscopic approach of Lifshitz.¹⁷ As the actual material atomic structures are overlooked, the Lifshitz method is suitable in certain cases. In this method, bulk material properties are considered for calculation of interactions between the macroscopic bodies. Properties like refractive indices and dielectric permittivity $\epsilon \left(i\zeta \right)$ are considered for such calculations. Dielectric permittivity represents the microscopic polarizability as a manifested macroscopic property for the constant atoms belonging to certain materials. The Hamaker coefficient represents the macroscopic resultant for the interactions which happened due to the atom polarizations in a material.¹⁸ Following Lifshitz theory, the Hamaker coefficient is represented as follows:¹⁷

$A_{ikj}=\frac{3}{4}\pi \hslash {\displaystyle \underset{0}{\overset{\infty }{\int }}\left[\frac{{\epsilon }_i\left(i\zeta \right)-{\epsilon }_k\left(i\zeta \right)}{{\epsilon }_i\left(i\zeta \right)+{\epsilon }_k\left(i\zeta \right)}\right]\left[\frac{{\epsilon }_j\left(i\zeta \right)-{\epsilon }_k\left(i\zeta \right)}{{\epsilon }_j\left(i\zeta \right)+{\epsilon }_k\left(i\zeta \right)}\right]d\zeta }$ . (9)

Where, ${\epsilon }_j\left(i\zeta \right)$ refers to the dielectric constant of a specific material j, this is considered through the imaginary i, frequency axis, $\left(i\zeta \right)$ , $ђ$ is planck’s constant. In this context, the evaluation of Equation 9 should result in equivalent value with the thermodynamic free energy of adhesion, provided in Equation 1. The molecular contact was maintained at (d=0). Interestingly, constituent molecule numbers are of finite size and for that it is not possible to attain d=0 for two macroscopic surfaces. Therefore, whenever the surfaces attain a distance do, molecular contacts are considered. The divergences according to Lifshitz theory are eliminated by the parameter do. Thus, the Hamaker coefficient or the Lifshitz-van der Waals constant A132 may result in negative. In certain condition, the contact between the interacting particles will be hampered due to the repulsive (electrostatic) force originated. The resultant effect in certain cases remains as repulsion instead of attraction for the considered particles. The Hamaker coefficient and the interfacial free energies are connected through the following Equation:

$A_{pls}=-12\pi d_o^2\left({\gamma }_{ps}-{\gamma }_{pl}-{\gamma }_{sl}\right)$ . (10)

This Equation has been derived through combining Equation 8 with Equation 1. For the issue of self-interaction of a particle Equation 11 should be considered:

$A_{ij}=\frac{3}{4}\pi \hslash {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left[\frac{{\epsilon }_i\left(i\zeta \right)-{\epsilon }_j\left(i\zeta \right)}{{\epsilon }_i\left(i\zeta \right)+{\epsilon }_j\left(i\zeta \right)}\right]}^{2}d\zeta }$ . (11)

To be able to use the absorbance data to calculate the Hamaker coefficients using the Lifshitz theorem of Equation 9, there is a need to evaluate the dielectric constant ε of the Equation. From the information of light absorbance, reflection and transmittance, it could be seen that:

$ā+T+R=1$ . (12)

Where; ā is absorbance, T is transmittance, and R is reflectance. Also, from the information of light absorbance and transmittance:

$T=ex{p}^{-ā}$ . (13)

With the values of ā determined from absorbance experimental results and substituting the values of ā into Equation 13 to obtain T, R could easily be derived by substituting the values of ā and T into Equation 12. To find a value for the refractive index, n employing the mathematical relation:¹⁹

$n=\left[\frac{1-R^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1+R^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right]$ . (14)

A value for the extinction coefficient, k is obtained from the Equation:

$k=\left[\frac{\alpha \lambda \times {10}^{-9}}{4\pi }\right]$ . (15)

Where; a is the absorption coefficient defined as follows:

$\alpha =\left[\frac{\overline{a}}{\lambda \times {10}^{-9}}\right]$ . (16)

Substituting the value, α of Equation 16 into Equation 15:

$k=\left[\frac{\overline{a}}{4\pi }\right]$ . (17)

The dielectric constant, ε could thus be given by the formula,²⁰ for the real part:

${\epsilon }_1=n_1^2-k^2$ . (18)

For the imaginary part:

${\epsilon }_2=2n_{2}k$ . (19)

With these values, it is possible to determine $A_{ij}$ using the relevant Equation s to determine A11:

$A_{11}=2.5{\left[\frac{{\epsilon }_{10}-1}{{\epsilon }_{10}+1}\right]}^2=2.5{\left[\frac{n_1{}^2-1}{n_1{}^2+1}\right]}^2$ . (20)

This gives a value to the Hamaker constant A11, and by extension to other Hamaker constantsA22 and A₃₃. For combination of two different materials 1 and 2 in approximation:

$A_{12}=\sqrt{A_{11}{A}_{22}}$ . (21)

For a combination of two dissimilar materials (i.e. macrophage, 1 and the bacteria, 2) with the gap between 1 and 2 filled with sputum as the medium 3, the combined Hamaker coefficient will be given by:

$A_{132}=A_{12}+A_{33}-A_{13}-A_{23}$ . (22)

$A_{131}=A_{11}+A_{33}-2A_{13}$ . (23)

Therefore, the system under consideration follows Equations 22 and 23. Rewriting these Equations will give:

$A_{132}=\left(\sqrt{A_{11}}-\sqrt{A_{33}}\right)\left(\sqrt{A_{22}}-\sqrt{A_{33}}\right)$ . (24)

$A_{131}={\left(\sqrt{A_{11}}-\sqrt{A_{33}}\right)}^2$ . (25)

Equation 24 shows that, for a three-component system involving three different materials, 1, 2 and 3, A132 can become negative:

$A_{132}<0$ . (26)

When,

$\sqrt{A_{11}}>\sqrt{A_{33}}$ and $\sqrt{A_{22}}<\sqrt{A_{33}}$ . (27)

A₃₃= Hamaker constant for sputum; A13= Hamaker constant between both materials (i.e. mtb and sputum); A23= Hamaker constant between both materials (i.e. macrophage and sputum). Thus the Hamaker Coefficient A132 becomes:

$A_{132}=\frac{3}{4}\pi \hslash {\displaystyle \underset{0}{\overset{\infty }{\int }}}\left[\frac{{\epsilon }_1\left(i\zeta \right)-{\epsilon }_3\left(i\zeta \right)}{{\epsilon }_1\left(i\zeta \right)+{\epsilon }_3\left(i\zeta \right)}\right]\left[\frac{{\epsilon }_2\left(i\zeta \right)-{\epsilon }_3\left(i\zeta \right)}{{\epsilon }_2\left(i\zeta \right)+{\epsilon }_3\left(i\zeta \right)}\right]d\zeta$ . (28)

Integrating all the values of the combined Hamaker coefficient, A132 gives an absolute value for the coefficient denoted by A_132abs and applying Lifshitz derivation for van der Waals forces as in Equation 28.

The absolute value for the Hamaker coefficient could be derived by obtaining the mean of all the A132 values got from the Lifshitz relation:²¹

$A_{132abs}=\frac{{\displaystyle \sum _{i=1}^N\left(A_{132}i\right)}}{N}$ . (29)

Also

$A_{131abs}=\frac{{\displaystyle \sum _{i=1}^N\left(A_{131}i\right)}}{N}$ . (30)

And

$A_{232abs}=\frac{{\displaystyle \sum _{i=1}^N\left(A_{232}i\right)}}{N}$ .(31)

The absorbance values were obtained as a function of wavelength and summarized in Table 1. It could be seen that the peak absorbance values of the various sputum samples and components vary in magnitude revealing the notable effect of the bacteria on them. The comparison between the positive and negative samples of the macrophages is imperative to this research. This is because Mtb actually attacks the macrophages by attaching itself to the macrophage cells.

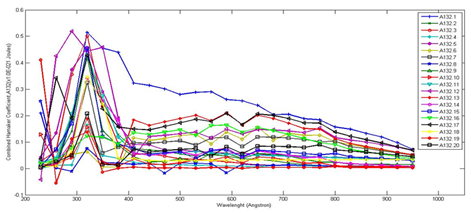
Table 1 reveals also the degree of variation between similar infected and uninfected sputum components at a glance for a clearer understanding. Equation 11 was used to obtain for each interacting system; $A_{ij} \left(A_{11}, A_{22}, A_{33}, A_{12}, A_{13}, A_{23}\right)$ by approximate change of variables using MatLab computation tools. This involved the numerical integration of Equation 11 for each wavelength from 230nm to 950nm for all the twenty samples in each category. Analysis based on the particle-particle interaction mechanisms of the mathematical formulations outlined yielded values for the needed variables (such as the transmittance T, reflectance R, refractive index (real and imaginary) n, extinction coefficient k, absorption coefficient α, dielectric constants (real and imaginary) ${\epsilon }_{ij}$ , Hamaker Constants $A_{ij}$ , and Hamaker Coefficients A132 were calculated and presented in Figure 3-5.

Figure 3 Variation of Combined Hamaker Coefficient, A₁₃₂ with Wavelength, λ (nm) for the mtb infected Sputum Samples.

Figure 4 Variation of Combined Hamaker Coefficient, A₁₃₁ with Wavelength, λ (nm) for the mtb uninfected Sputum Samples.

Figure 5 Variation of Combined Hamaker Coefficient, A₂₃₂ with Wavelength, λ (nm) for the mtb infected Sputum Samples.

The difference between the peak absorbance values of mtb positive, mtb/HIV co-infected and negative sputum components respectively is an indication of how the bacteria affects the properties of the macrophage cells. The trend is such that the mean absorbance peak values of mtb negative sputum samples are reduced by infection from 0.6244± 0.3545 to 0.4588± 0.1468 by a factor of about 26.5%. In mtb macrophage samples, the reduction is from 0.0784± 0.0206 to 0.0496± 0.0116, a factor of about 36.7%. While in mtb/HIV co-infected macrophage samples, the reduction is from 0.0784± 0.0206 to 0.0456± 0.0106 by a factor of about 41.8%. Comparing the mean absorbance peak values of mtb positive sputum samples and the mean absorbance peak values of mtb/HIV co-infected sputum samples; the results of the mean absorbance peak values reveal that the mean absorbance peak value of the mtb/HIV co-infected samples is generally reduced as compared to that of the mean absorbance peak values of the mtb positive sputum samples (Table 1).

The macrophages are of particular interest to this research since the bacteria attacks this T-cells component which serves as receptor cells. Comparing the mean absorbance peak values of mtb positive macrophage samples and the mean absorbance peak values of mtb/HIV co-infected macrophage samples; the results of the mean absorbance peak values reveal that the mean absorbance peak values of the mtb/HIV co-infected samples is generally reduced by infection from 0.0784± 0.0206 to 0.0456± 0.0106 by a factor of about 41.8% as compared to that of the mean absorbance peak values of the mtb positive macrophage sample with a factor of about 36.7%. It could be seen that the reduction between the peak values absorbance (mean) of the sputum component is such that the macrophages reduced from mtb to mtb/HIV by a factor of about 8.1%. The reduction in the absorbance of the mtb/HIV infected sputum samples reveals the role of the bacteria in drastically affecting the surface properties of the infected macrophage cells and specimens.

Figure 3-5 reveal the pattern of the combined Hamaker coefficients for the infected sputum samples with clear maxima and minima values occurring at various wavelengths. Harmonized values of the combined Hamaker coefficient became necessary to streamline the findings. This involves the integration of all the Hamaker coefficients first over each wavelength, secondly with each sputum sample in view to give the harmonized combined Hamaker coefficients, A_132har.

Ultimately a single value of the Hamaker coefficient is essential in determining the final outcome. This is known as the absolute combined Hamaker coefficient, A_132abs (Figure 3), A_131abs (Figure 4) and A_232abs (Figure 5). It is obtained by integrating all the values of the Hamaker coefficient to give a single value. Not much meaning could be made out of Figure 3-5. To generate more meaningful plot, average value for the given Hamaker coefficients of a given wavelength was determined from the data for the twenty samples. These results are given in Figure 6.

Figure 6 Variation of Average Combined Hamaker Coefficients, A132 A131 and A232 with Wavelength, λ (nm) for the mtb infected Sputum Samples.

Figure 6 reveals the pattern of the average combined Hamaker coefficients, A132, A131 and A232 for the sputum samples with clear peak values occurring at various wavelengths. The peak average values of A132 and A232 occur at wavelength of 320 nm with values of 0.30968 x 10-21 J and 0.18609 x 10-21 J respectively, while the peak average value of A131 occurs at wavelength of 290nm with value of 0.03074 x 10-21 J. Energy level increases in average combined Hamaker coefficients, A132 and A232 which is the infected Hamaker coefficients as against the decreased energy level of the uninfected average combined Hamaker coefficient, A131. This is quite a significant phenomenon which explains away the fact of the effect of co-infection.

Table 2 reveal that the surface energy of the macrophages as computed in terms of Hamaker coefficients is less than the surface energy of the Mtb, Mtb/HIV. This result also shows that the surface energy of the Mtb/HIV macrophage is less than that of Mtb macrophage. HIV has the tendency to reduce the energy with the consequence of increased viral loads and decreased immune systems. tb is an opportunistic disease and in presence of HIV, the consequence is dreadful. Hence for A132˃ 0, A131(macropage)< A232(M-TB/HIV).

The mean of all values of A11 and A22 could be obtained and substituted into Equation 24 in order to derive a value for A₃₃ at which A132 is equal to zero in agreement with the earlier stated reasons. Rearranging Equation 24 and making A₃₃ subject of the formula:

$A_{33}={\left[\frac{2\sqrt{A_{11}}\sqrt{A_{22}}-A_{132}}{\sqrt{A_{11}}+\sqrt{A_{22}}}\right]}^2$ . (32)

The mean of all the values of A11 and A22 respectively gave the absolute values of the Hamaker constants as: A11= 0.94188x 10-21 Joule and A22= 0.96068x 10-21 Joule (for mtb); Ã11= 0.94188x 10-21 Joule and Ã22= 0.97862x 10-21 Joule (for mtb/HIV co-infection). Thus, inserting these values into Equation 29 and rendering A132 ≤ 0 will give the critical value of A₃₃C that satisfies the condition for the combined Hamaker coefficient to be equal to or less than zero. Hence any value of A₃₃ greater than the critical would be the desired value necessary to attain a negative combined Hamaker coefficient.

Thus, the critical absolute Hamaker constant A₃₃C for the sputum which renders the A132 negative is given as: A₃₃C= 0.9527 x 10-21 Joule (for mtb) and Ã33C= 0.9598 x 10-21 Joule (for mtb/HIV co-infection). Thus for negative combined Hamaker coefficient A132, Ã132 of the infected mtb, mtb/HIV sputum to be attained respectively, the combined Hamaker constant of the sputum as the intervening medium A₃₃, Ã33 respectively should be of the magnitude: A₃₃C≥ 0.9527 x 10-21 Joule and Ã33C≥ 0.9598 x 10-21 Joule respectively. Inserting the above values of A₃₃, Ã33C into Equation 24 would yield negative values for A132, Ã132 respectively as follows: A132= -0.22669x 10-25 Joule (when A₃₃ = 0.9527x 10-21Joule) and Ã132= -0.08786x 10-25 Joule (when A₃₃= 0.9598x 10-21 Joule). A mathematical expression for harmonized Hamaker coefficients was given as follows:²²

$A_{132har}={\phi }_t{A}_{132\max }$ . (33)

Where

${\phi }_t={\displaystyle \underset{0}{\overset{\infty }{\int }}}\left(A_{132\max }-A_{132har}\right)d\lambda$ . (34)

Where Фt = the integral of the difference between A132max and A_132hars.

Thus, from the deductions made from this work the following result was got;

$A_{132har}\approx 0.4725\left(A_{132max}\right)$ . (35)

Hence

$A_{132\max }\approx \frac{1}{0.4725}\left(A_{132har}\right)$ . (36)

It could easily be seen that in finding a solution for the absolute Hamaker coefficient, the maxima and harmonized values of Hamaker coefficient could be used. This approximate method thus serves as an alternative method for obtaining a reliable value for the absolute combined Hamaker coefficient for human sputum systems and could well be relevant to other biological and particulate systems. This latter statement needs verification and could be taken up as a new research area in this field. The single value of the Hamaker coefficient is necessary in determining the final conclusion. Harmonized values of the combined Hamaker coefficient is required to rationalize the findings. This involves the integration of all the Hamaker coefficients over each wavelength, with each sputum sample in view to give the harmonized combined Hamaker coefficients, A_132har for both mtb and mtb/HIV co-infection. The harmonized values of the combined Hamaker coefficient for each infected and uninfected sputum samples are shown in Table 3 alongside with that of the absolute combined Hamaker coefficient for both mtb and mtb/HIV co-infection. The interaction systems of mtb with the HIV sputum samples gave a positive absolute combined Hamaker coefficient, A132 which entails attractive van der Waals forces.

The positive sense of the absolute combined Hamaker coefficient obtained is in agreement with the statement of Achebe et al.²² However, the positive values of the absolute combined Hamaker coefficient A₁₃₁ for mtb interacting with HIV negative sputum samples as shown in Table 3 indicate that there is an attraction between the interacting bodies. This is so because the positive sense of the absolute combined Hamaker coefficient shows that the van der Waals forces of the interacting systems are attractive. A comparison in Table 3 of the maxima A_132max and the harmonized A_132har values of the combined Hamaker coefficient shows a direct association between the two. Difference in terms of the magnitude only was recorded. However, this research work is limited to the role the van der Waals forces play in the process and progress of mtb/HIV co-infection, the mechanism involved and the contribution its study could offer in the chase for a feasible solution to the overwhelming condition.

The prediction of the interactions that occur between mtb and HIV co-infections was based on the concept of van der Waals attractive forces and absolute Hamaker coefficient whose negative and positive values respectively indicate attraction. The absolute Hamaker coefficient A₁₃₁= 0.10165x10^-21 Joule gives the interaction energy among the macrophage cells in the sputum while A₂₃₂ is the interaction energy among the mtb particles in the sputum. A₂₃₂ for mtb/HIV co-infection is less than that for mtb alone. Reduction in energy in the presence of HIV confirms the adverse effect when mtb and HIV occur simultaneously in a patient. Reduction in energy leads to reduction in CD4 in HIV patient and hence greater prospect for death. This is so since a positive Hamaker value for any interacting system implies an attraction between the interacting bodies or particles while a negative Hamaker coefficient means repulsive van der Waals forces hence the interacting bodies would repel each other. The importance of negative Hamaker coefficient (-0.2267x 10^-19 mJ/m²) indicated that separation of bacteria is realistic. The desired outcome is that the bacteria do not adhere to the macrophage cells to avoid penetration, in which case a condition for rendering combined Hamaker coefficient negative is required. Thus, a condition was required for repulsion to occur and that condition was based on the value of A₃₃ that would render the absolute combined Hamaker coefficient A_132abs negative. A model for the infection mechanism was built-up employing the principle of particle interaction. Mathematically, it was derived as A₃₃≥ 0.9527x 10^-21 Joule which satisfies this condition for negative A_132abs. To achieve the condition of A₃₃ above, possible additive(s) to the system (in form of drugs) to the sputum as intervening medium should be required.

None.

The author declares no conflict of interest.

1. Bauer AL, Hogue IB, Marino S, et al. The effects of HIV-1 infection on latent tuberculosis. Math Model Nat Phenom. 2008;3(7):229–266.
2. Paul Nunn, Brian Williams, Katherine Floyd, et al. Tuberculosis control in the era of HIV. Nature Reviews Immunology. 2005;5(10):819–826.
3. World health organization. Global tuberculosis control. Geneva, Switzerland: WHO report; 2010.
4. Aandahl RZ, Reyes JF, Sisson SA, et al. A model-based bayesian estimation of the rate of evolution of vntr loci in mycobacterium tuberculosis. PLoS Comput Biol. 2012;8(6):e1002573.
5. Chukwuneke JL, Chukwuneke PC, Okolie PC, et al. Hamaker coefficient concept: the application to the mycobacterium tuberculosis-macrophage interactions mechanism. Advances in Bioscience and Bioengineering. 2016;4(1):1–20.
6. Gyasi Agyei KA, Agyei AG, Obeng Denteh W. Mathematical modelling of the epidemiology of tuberculosis in the ashanti region of Ghana. British Journal of Mathematics & Computer Science. 2014;4(3):375–393.
7. World health organization. Global tuberculosis. Geneva, Switzerland: WHO report; 2012.
8. World health organization. Tuberculosis. Geneva, Switzerland: WHO information: Fact Sheets; 2005.
9. Tsai MC, Chakravarty S, Zhu G, et al. Characterization of the tuberculous granuloma in murine and human lungs: cellular composition and relative tissue oxygen tension. Cell Microbiol. 2006;8(2):218–232.
10. Van Oss CJ, Visser J, Absolom DR, et al. The concept of negative hamaker coefficients, II. Thermodynamics, experimental evidence and applications. Advances in Colloid and Interface Science. 1983;18(3-4):133–148.
11. Stuart AE. Phagocytic engulfment and cell adhesiveness as surface phenomena. J Clin Pathol. 1977;30(6):592.
12. Absolom DR, Francis DW, Zingg W, et al. Phagocytosis of bacteria by platelets: surface thermodynamics. Journal of Colloid and Interface Science. 1982;85(1):168–177.
13. Omenyi SN. Attraction and Repulsion of particles by Solidification Fronts. PhD Dissertation, Canada: University of Toronto; 1978. p. 33–34.
14. Visser J. The concept of negative hamaker coefficients. 1. History and present status. Advances in Colloid and Interface Science. 1981;15(2):157–169.
15. Achebe CH, Sinebe JE, Chukwuneke JL, et al. Surface energetics of mycobacterium tuberculosis -macrophage interactions. Journal of Biomedical Engineering and Medical Imaging. 2015;2(6):49–61.
16. Hamaker HC. The London-van der Waals attraction between spherical particles. Physica. 1937;4(10):1058–1072.
17. Lifshitz, EM. The theory of molecular attractive forces between solids. Soviet Phys. JETP. 1956;2(1):73.
18. David B Hough, Lee R White. The calculation of Hamaker constants from Liftshitz theory with applications to wetting phenomena. Advances in Colloid and Interface Science. 1980;14(1):3–41.
19. Robinson TS. Optical constants by reflection. Proceedings of the physical society. Section. 1952;B 65(11):B910.
20. Kittel Charles. Introduction to Solid State Physics. 7th ed. New York, USA: John Willey and sons Inc; 1996. 308 p.
21. Achebe CH. Human Immunodeficiency Virus (HIV)-Blood Interactions: Surface Thermodynamics Approach. Nigeria: Nnamdi azikiwe university; 2010. p. 1–120.
22. Achebe CH, Omenyi SN, Manafa OP, et al. Human Immunodeficiency Virus (HIV)-Blood Interactions: Surface Thermodynamics Approach. Proceedings of the international multi-conference of engineers and computer scientists, Hong Kong: IMECS; 2012. p. 136–141.