The boomerang flight is presented in the known publications by the action of aerodynamic forces and gyroscopic precession torque. This solution does not give a true answer because gyroscopic effects are expressed by the action of the eight interrelated inertial torques generated by the rotating objects. The publications with numerical modeling do not describe the physics of the boomerang flight. Today, the solution of this problem is presented by the mathematical model with the action of the lift forces and inertial torques generated by the rotating boomerang. The boomerang flight is described by the methods of theories of aerodynamics and gyroscopic effects that express the kinetic energy of the boomerang motion and rotation. The mathematical model for the boomerang flight contains multifunctional and interrelated expressions of two theories, which manual solution is sophisticated, but solved by computer software without numerical modeling. The analytical solution for the boomerang flight describes its physics and presents a good example for the educational process of engineering mechanics and aerodynamics.

Keywords: aerodynamics; boomerang; gyroscopic effects; inertial torque, kinetic energy

The boomerang is the hunting tool of specific designs was one of the oldest flying inventions of ancient civilizations. Hunters threw the boomerangs to bludgeon a target and, in case of a miss, they returned to them by the curvilinear trajectory of their flights. In such a situation, hunters did not lose time for the search of the flown-away boomerang. This specific effect of a throwing object by hand attracted scientists to describe the physics of flight and properties of the boomerang.^1–3 Analysis of the return boomerang designs, starting from ancient to modern sport one, shows most of them contain from two to four airfoiled blades. Figure 1 shows some typical designs of the boomerang.

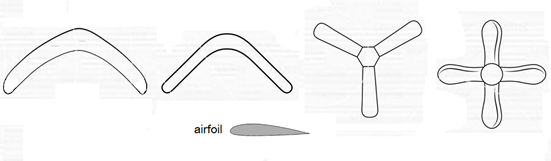
Figure 1 Typical boomerang designs.

The two blade's boomerangs are designed with curved forms, other ones have rectilinear. All blades have aerofoil cross-sections that produce aerodynamic lift forces. Any boomerang designs of airfoiled blades will manifest the curvilinear trajectory of flights. The studies of the specificity of boomerang flight show the combined action of its aerodynamic forces and gyroscopic inertial torques. The known publications contain this conclusion but with action only gyroscopic precession inertial torque that does not describe the full picture of the boomerang flight. ^4,5

The aerodynamics component of the boomerang flight is based on well-developed aerodynamic theory. The flight of the boomerang is going on by the action of the lift force generated by the rotation of airfoiled blades.^6–8 The gyroscopic effects express the action of the eight interrelated inertial torques on the rotating boomerang. These two components are described separately and presented in several publications.^9–11 The curvilinear flight of the rotating boomerang and the turn of its plane around the diametral line is the result of the combined action of gyroscopic effects and the action of the aerodynamic thrust force.

The new theory of the gyroscopic effects for rotating objects enables supplementing and describing the physics of boomerang flight completely. Gyroscopic effects are formulated by mathematical models, and their physics is described by the principle of classical mechanics.^12–14 The spinning object is subjected to the action of the system of torques generated by the centrifugal and Coriolis forces of the distributed mass of the rotating object and the torque of the change in the angular momentum.^15,16 The expressions of inertial torques depend on the geometry of the rotating object that has many designs. The mathematical models of gyroscope motions include the interrelation of all torques about two axes by the principle of mechanical energy conservation and are represented for the boomerang with three blades in Table 1.¹⁵

The physics of gyroscope inertial torques and motions are explained in detail and confirmed by practice. The unique designs of the boomerang will produce different gyroscopic inertial torques, the aerodynamic thrust force, and the trajectory of its flight. This work presents a detailed description of the physics of the curvilinear flight of returning boomerangs based on two theories of aerodynamics and gyroscopic effects. The known publications do not contain the action of the system of the interrelated inertial torque generated by the rotating boomerang. The mathematical model for the boomerang flight is considered after the action of the initial impulse force that gives the rotation to the boomerang and its linear velocity in space. The mathematical model for the motions around three axes of the Cartesian 3D coordinate system is presented in the Euler differential equations. The analytical solution for the boomerang flight presents a good example for the educational process of engineering mechanics and aerodynamics.

The known publications dedicated to the boomerang flight contain the mathematical models based on the action of aerodynamic forces and gyroscopic precession torque generated by the rotating boomerang. This solution does not give a true answer because gyroscopic effects are the manifestation of the action of the system of interrelated inertial torques of the rotating object. The boomerang flight is described by the aerodynamic lift forces of its blades and the system of interrelated inertial torques of the rotating boomerang that is presented below. The forces and torques produced by the boomerang blades are variable, which action generates a fluctuated flight around two axes that is described by the theory of vibration. Naturally, a fluctuated flight produces additional forces acting on the boomerang and changes its curvilinear motion in space. The mathematical model of the boomerang flight with the action of all physical components will be very sophisticated and difficult to solve. Analysis of the vibratory forces shows their action depends on the speed of the boomerang rotation. The amplitude of vibration is relatively high, the time of the action of the forces is short that does not change too much the boomerang flight. This section does not consider the aspect of the boomerang vibratory flight and is limited by the action of two initial components that are aerodynamic lift forces and the system of interrelated inertial torques.

The physical model for the boomerang flight is considered for the three blades design. This design is similar to an aircraft propeller with known expressions of inertial torques generated by the mass of its blades.¹⁵ The boomerang launches horizontally for the vertical disposition of its plane with linear velocity V of its center mass and rotates with the angular velocity ω of counterclockwise. The spinning boomerang acts like a simple propeller and produces the thrust force that pushes the boomerang to the side that is perpendicular to the line of the linear velocity V of its center mass. The linear velocity of the boomerang and its rotation manifests more thrust force in the upper part $F_u$  than in the down part $F_d$ of the blades because of a difference in the resultant linear velocities $V_u=V+V_b$ and $V_d=V_b -V$ , respectively. Where $V_u$ , $V_d$  and $V_b$  are the linear velocity of the upper part, the down part, and the blades, respectively. This difference in the forces shifts the aerodynamic resultant force $F_a=F_u+F_d$ upwards above the center of gravity and created the aerodynamic torque $T=\left(F_u–F_d\right)k$  (k is the centroid) that turns the boomerang about axis ox (Figure 2). The value of the aerodynamic torque T is fluctuated and changed by sine law because of the rotation of the blades. The known equation presented in publications of aerodynamic expresses the value of aerodynamic force.^3–6 The action of the torque T on the spinning boomerang produces the system of the inertial torques generated by its rotating mass that manifest gyroscopic effects. As described above, motions, velocities, forces, and torques of the spinning boomerang are demonstrated in Figure 2 at the Cartesian 3D system coordinates $\Sigma oxyz$ .

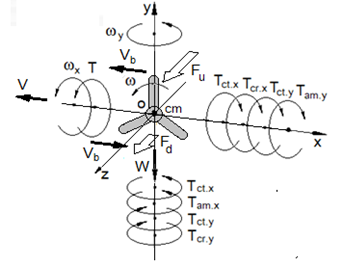
Figure 2 The thrust forces and inertial torques act on the vertical disposition of the boomerang and its motions.

The boomerang motion is considered for the actions of its weight W, the aerodynamic torque T that produces gyroscopic effects, and the linear velocity V about axes ox and oy. The action of the gyroscopic torques on rotating objects and the dependency of the angular velocity of their rotation around axes are well described in publications and will not be repeated for the boomerang rotation.^15,16

Inertial torques generated the boomerang with three blades and the dependency of angular velocities about axes of rotation are presented in Table 1.¹⁵ The spin of the boomerang is variable because of the drag force acting on the three blades. The mathematical model for the boomerang flight with its variable angular velocity of rotation is not a critical engineering problem. For solution is accepted the aerodynamic components of the boomerang flight with its constant spin that presented by the strip theory. The aerodynamic lift force is normal to the relative velocity of the boomerang blades aerofoil. The drag force is in the direction of the relative velocity of the aerofoil. The pitching moment is due to offsetting between the center of pressure and the aerodynamic center of the airfoil. This moment creates the internal stress of the boomerang blades, does not change its flight, and is omitted from consideration.

The motions of the boomerang about axis ox and oy are presented by the known equations for the spinning objects.¹⁴ The action of resistance force of the air on the boomerang turn around axes oy and ox is omitted because of the small value of the high order.

$J_x\frac{d{\omega }_x}{dt}=T-T_{ct.x}-T_{cr.x}-T_{am.y}$   (1)

$J_y\frac{d{\omega }_y}{dt}=T_{ct.x}+T_{am.x}-T_{cr.y}$   (2)

${\omega }_y=-1,645(\pi +\text{2,608)}{\omega }_x$   (3)

where ${\omega }_x$  and ${\omega }_y$  is the angular velocity of the boomerang about axes ox and oy, respectively; $T_{ct.x}$ , $T_{cr.x}$ , $T_{cr.y}$ , $T_{am.x}$  and $T_{am.y}$ are inertial torques generated by the centrifugal, Coriolis, and the change in the angular momentum acting about axes ox and oy, respectively; $J_x=J_y$  is the moment of inertia of the boomerang about axes ox and oy, respectively. The inertial torques $T_{ct.y}$ acting about axes ox and oy are removed because of mutual subtraction.¹⁶

The combined action of the weight, gyroscopic inertial torques, and motion of the boomerang produce dynamical changes of its flight that are traced by the following steps presented below.

1. The vertically rotating boomerang begins to move along the axis ox (Figure 3, position 1). The action of the resulting load torque, $T_r=T-T_{ct.x}-T_{cr.x}-T_{am.y}$ turns the boomerang about axis oy and generates the precession torque $T_p=T_{ct.x}+T_{am.x}–T_{cr.y}$ that turns the boomerang about axis oy in a counter-clockwise direction.
2. The boomerang begins to move curvilinearly to the left side on the plane $xoz$ under the action of the thrust force $F_a$ . The intensive turn of boomerang about axis oy (Eq. (4)) under the action of the precession torque $T_p$  produces new resulting resistance torque $T_r*>T_r$  that bigger the initial load torque. (Figure 3, position 2).
3. The intensive turn of the boomerang about axis ox in a clockwise direction changes the direction of the thrust force $F_a$  and lifts it. At this condition, the boomerang moves by a line of small radius of curvature. The value of the precession torque $T_p$  decreases because the value of the resulting load torque $T_r$  decreases (Figure 3, positions 4 - 5).
4. The intensive turn of the boomerang about axis ox inclines it from the vertical to the horizon. The value of the aerodynamic torque T is counterbalanced to the value of the resistance gyroscopic inertial torques. The value of the precession torque $T_p$ decreases, $T_p=\left(T_{ct.x}+T_{am.x}\right)cos\phi –T_{cr.y}$ and the value of resulting resistance torque $T_r*=T_r$ comes to the dynamic balance with the initial load torque. The boomerang flies by the line of the increased radius of curvature motion. The angular velocity ω of the boomerang decreases and decreases the value of the thrust force $F_a$ . The plane of the spinning boomerang is almost horizontal and its flight is going by gliding curve (Figure 3, positions 6 - 7).

The trajectory of the typical flight of the boomerang under the action of the forces and torques described in paragraphs a) – d) is demonstrated in Figure 3.

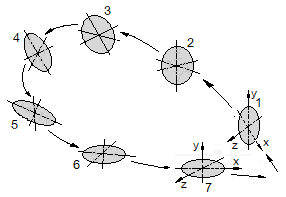
Figure 3 Change in the curvilinear flight and the disposition of the plane of the spinning boomerang.

The acting forces and inertial torques on the horizontal disposition of the boomerang and its motions are demonstrated in Figure 4.

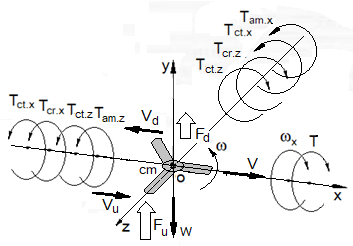
Figure 4 The thrust forces and inertial torques act on the horizontal disposition of the boomerang and its motions.

The curvilinear aerodynamic flight of the spinning boomerang in space is going on under the action of the starting impulse force, its weight, thrust force, and gyroscopic inertial torques. At the process of flight, the vertically disposed boomerang begins to change its orientation in space. The mathematical model for the flight of the spinning boomerang is presented by the system of equations at the permanent system of the Cartesian 3D coordinates, but its gyroscopic motions at the movable one (Figure 5).

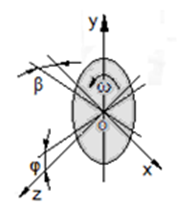
Figure 5 The common disposition of the boomerang at the 3D coordinate system.

The differential equations of the boomerang linear velocities along the coordinates are presented by the Euler form:

-  along with the axes ox, oz, and oy:

$\begin{array}{l}m\frac{d{V}_x}{dt}=(F_x-F_{dr.b})\cos \beta -F_a\sin \beta \cos \phi =\\ [F_x-\left(1/2\right)\rho V_b^{2}c{C}_d{A}_c]\cos ({\omega }_{y}t)-\left(1/2\right)\rho V_b^{2}c{C}_L\sin ({\omega }_{y}t)\cos ({\omega }_{x}t)\end{array}$   (4)

$\begin{array}{l}m\frac{d{V}_y}{dt}=-W-F_{dr.b}\cos \phi +F_a\sin \phi =\\ -W-\left(1/2\right)\rho V_b^{2}c{C}_d\cos ({\omega }_{x}t)+\left(1/2\right)\rho V_b^{2}c{C}_L\sin ({\omega }_{x}t)\end{array}$   (5)

$m\frac{d{V}_z}{dt}=F_a\cos \phi \cos \beta =\left(1/2\right)\rho V_b^{2}c{C}_L\cos ({\omega }_{x}t)\cos ({\omega }_{y}t)$   (6)

where m is the mass of the boomerang; $V_x$ , $V_z$ , and $V_y$ , are the linear velocity along with the axis ox, oz, and oy respectively; $F_x$  is the impulse force of short-time action that launched the boomerang; $F_a{}_{ }=\left(1/2\right)\rho V_b{}^{2}c{C}_L$  is the thrust force ($V_b$  is the tangential velocity of the blade; c is the aerodynamic aerofoil chord; $C_L$  is the lift coefficient); $F_{dr.b}=\left(1/2\right)\rho V_b{}^2{C}_{d.}{A}_c$  is the drag force of the air ($\rho$  is the mass density of air, $C_d$  is the drag coefficient for the linear motion, $A_c$  is the integer cross-section of the longitudinal area of the boomerang); $\phi$  and $\beta$  is the angle inclination of the boomerang axle to the axis oz on the plane zoy and ox on the plane xoy, respectively; ${\omega }_x$  and ${\omega }_x$  is the angular velocity of the boomerang about axis ox ad oy, respectively; t is the time; W is the boomerang weight, other parameters are as specified above.

Separating variables of Eqs. (4) – (6) and presentation by the integral forms gives:

${\displaystyle \underset{V_{in}}{\overset{V_x}{\int }}d{V}_x}=\frac{1}{m}{\displaystyle \underset{0}{\overset{t}{\int }}[F_x-\left(1/2\right)\rho V_b^{2}c{C}_d{A}_c]\cos ({\omega }_{y}t)-\left(1/2\right)\rho V_b^{2}c{C}_L\sin ({\omega }_{y}t)\cos ({\omega }_{x}t)dt}$   (7)

${\displaystyle \underset{0}{\overset{V_{y.}}{\int }}d{V}_y}=\frac{1}{m}{\displaystyle \underset{0}{\overset{t}{\int }}[-W-\left(1/2\right)\rho V_b^{2}c{C}_d\cos ({\omega }_{x}t)+\left(1/2\right)\rho V_b^{2}c{C}_L\sin ({\omega }_{x}t)]dt}$   (8)

${\displaystyle \underset{0}{\overset{V_z}{\int }}d{V}_z}=\frac{1}{m}{\displaystyle \underset{0}{\overset{t}{\int }}\left(1/2\right)\rho V_b^{2}c{C}_L\cos ({\omega }_{x}t)\cos ({\omega }_{y}t)dt}$   (9)

The solutions of the integral Eqs. (7) – (9) are tabulated and presented by the following:

$V_{x.}-V_{in}=\frac{1}{m}\left\{[F_{x}t-\frac{1}{2{\omega }_y}\rho V_b^{2}c{C}_d{A}_c]\sin ({\omega }_{y}t)+\frac{1}{2}\rho V_b^{2}c{C}_L\left[\frac{\cos ({\omega }_y+{\omega }_x)t}{2({\omega }_y+{\omega }_x)}+\frac{\cos ({\omega }_y-{\omega }_x)t}{2({\omega }_y-{\omega }_x)}\right]\right\}$   (10)

where $V_{x.1}{}_{}$  is the initial linear velocity

$V_y=\frac{1}{m}\left[-Wt-\frac{1}{2{\omega }_x}\rho V_b^{2}c{C}_d\sin ({\omega }_{x}t)-\frac{1}{2{\omega }_x}\rho V_b^{2}c{C}_L\cos ({\omega }_{x}t)\right]$   (11)

$V_z=\frac{1}{m}\left[\frac{1}{4}\rho V_b^{2}c{C}_L\left(\frac{\sin ({\omega }_x-{\omega }_y)t}{{\omega }_x-{\omega }_y}+\frac{\sin ({\omega }_x+{\omega }_y)t}{{\omega }_x+{\omega }_y}\right)\right]$   (12)

Where the linear velocities $V_i$  give the ability to define the distances of the boomerang motions at the system of coordinates $\Sigma oxyz$ .

The differential equation of the boomerang gyroscopic angular velocity about axis ox is presented by the Euler form. Substituting expressions of the inertial torques (Table 1), $\omega$ , and expression ${\omega }_y$  (Eq. (3)) into Eq. (1) yields the following:

$J_x\frac{d{\omega }_x}{dt}=T-0,933\pi J\omega {\omega }_x-1,866J\omega {\omega }_x-1,645(\pi +\text{2,608)}J\omega {\omega }_x$   (13)

were $J_x$  is the moment of inertia of the boomerang around axis ox.

Separating variables of Eq. (13), transformation and presenting by the integral forms gives:

$\frac{J_x}{\text{2,578(}\pi \text{+1,664)}J\omega }{\displaystyle \underset{0}{\overset{{\omega }_x}{\int }}\frac{d{\omega }_x}{\frac{T}{\text{2,578(}\pi \text{+1,664)}J\omega }-{\omega }_x}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}$   (14)

The left integral of Eq. (14) is tabulated and represented the integral ${\displaystyle \int \frac{dx}{a-x}}=-\ln x+C$ . The right integral is simple. Solving of integrals yields the following equation:

that gave rise to the following

$\ln \left[\frac{T}{\text{2,578(}\pi \text{+1,664)}J\omega }-{\omega }_x\right]|{}_0^{{\omega }_x}=-\frac{\text{2,578(}\pi \text{+1,664)}J\omega }{J_x}t|{}_0^t$   (15)

${\omega }_x=\frac{T}{\text{2,578(}\pi \text{+1,664)}J\omega }\left(1-e^{-\frac{\text{2,578(}\pi \text{+1,664)}J\omega t}{J_x}}\right)$

The angular velocity around axis oy is defined by substituting Eq. (15) into Eq. (3) and simplification yields:

${\omega }_y=\frac{1,645(\pi +\text{2,608)}{\omega }_{x}T}{\text{2,578(}\pi \text{+1,664)}J\omega J\omega }\left(1-e^{-\frac{\text{2,578(}\pi \text{+1,664)}J\omega t}{J_x}}\right)=\frac{T}{J\omega }\left(1-e^{-\frac{\text{2,578(}\pi \text{+1,664)}J\omega t}{J_x}}\right)$   (16)

Substituting expressions ${\omega }_x$  and ${\omega }_y$  (Eqs. (16) and (15)) into Eqs. (10) – (12) yields the dependency from a time of the linear velocities of the boomerang at the system of coordinate $\Sigma oxyz$ . The distance of motions and disposition of the boomerang at the coordinate system $\Sigma oxyz$  is defined by the timely dependency $S_i=V_{i}t$ , where $S_i$  is presented by distances X, Y, and Z. The sophisticated flight of the boomerang at the condition of its variable rotation and the resistance of air is described by the multifunctional and interrelated equations at the 3D coordinates system (Eqs. (10)- (12) and Eqs. (16) and (15)). These equations can be solved manually but it will be very labor-intensive work. The computer modeling for the boomerang flight and solution of equations is preferable.

The boomerang flight is related to the most complex examples of the motions in space. The flight of the rotating objects of complex form with airfoil blades involves the combined action of the aerodynamic forces and gyroscopic effects. The known publications describe the boomerang flight by the action of the aerodynamic force and only the precession torque of the change in the angular momentum that do not give the true solution. The application of the new system of gyroscopic inertial torques generated by the spinning boomerang gives a correct solution for its flight. The sophisticated flight of the boomerang at the condition of its variable rotation and the resistance of air is described by the multifunctional and interrelated equations at the 3D coordinates system. These equations can be solved manually but it will be very labor-intensive work. The computer modeling for the boomerang flight and solution of equations is preferable.

The new theory of gyroscopic effects for rotating objects enables solving many problems related to the dynamics of their motions. The boomerang flight presents an example of the combined physical process of the action of the aerodynamic force and gyroscopic effects that are described by these two analytical approaches. The computer mathematical models can implement the solution of the complex analytical models for boomerang flight. Today practically, the boomerang flight presents an interest for researchers in entertaining games and presents a good example for the educational process. The numerical modeling of the curvilinear boomerang flight can be removed from consideration because there is a mathematical model.

A, $A_c$  – cross-section of the longitudinal area of the boomerang three blades and an integer

$c_{d.b}$  - drag coefficient for the boomerang rotation

$c_{d.r}$  - drag coefficient for the boomerang rotation

$c_l$  - drag coefficient for the boomerang thrust force

$F_a$ , $F_u$ , $F_d$  - thrust force of the center, the upper and the down part of the boomerang, respectively

$F_{dr}{}_{.}$  – drag force of the rotating boomerang

$F_{dr.b}{}_{}$  - drag force of the boomerang blades

$F_x$  - impulse force of short-time action

J, $J_x$  –moment of inertia the boomerang about the axle and axis ox, respectively

m – mass of the boomerang

r - radius of the drag force action

S - boomerang blades planform area

T – load torque of the boomerang about axis ox

$T_r$ , $T_p$  – resulting and precession torques, respectively

$T_{ct}$ , $T_{cr.}$ , $T_{am}$  – torque generated by centrifugal, Coriolis, and a change in the angular momentum, respectively

t – time

$V_x$ , $V_y$ $V_z$   - linear velocity of the boomerang by coordinate axes ox, oy, and oz, respectively

V, $V_u$ $V_d$   - linear velocity of the center, the upper and the down part of the boomerang

$v_b$  – tangential velocity of the boomerang blade

W - boomerang weight

$\beta$ , $\phi$  - angle of the boomerang inclination to axes ox ad oz, respectively

$\rho$  - mass density of air

$\omega$ , ${\omega }_{in}$ , ${\omega }_x$ , ${\omega }_y$ , ${\omega }_z$  – angular velocity of the boomerang about its axle general and initial, and about axes ox, oy, ad oz, respectively

The manuscript was prepared for publication without financial support and recommended by the Kyrgyz State Technical University after I. Razzakov.

The authors declare there are no conflicts of interest.

None.

1. Barceló G. Theory of Dynamic Interactions: The Flight of the Boomerang II. Journal of Applied Mathematics and Physics. 2015;3:545–555.
2. Azuma A, Beppu G, Ishikawa H, et al. Flight Dynamics of the Boomerang, Part 1: Fundamental Analysis. Journal of Guidance, Control, and Dynamics. 2004;27(4):545–554.
3. Vassberg J. Boomerang flight dynamics. IEEE American Institute of Aeronautics and Astronautics. 2012;1:1–43.
4. Pakalnis S. Aerodynamics of Boomerang. Research Support Technologies. 2006.
5. Cross J. Performance Boomerangs. 2nd edition. In: Michael Siems, editor. New Ultimate Boomerang Book. 2012.
6. Collicott SH, Valentine DT, Houghton EL, et al. Aerodynamics for Engineering Students. 7th ed. London: Elsevier; 2015.
7. Burgers P. A thrust equation treats propellers and rotors as aerodynamic cycles and calculates their thrust without resorting to the blade element method. International Journal of Aviation, Aeronautics, and Aerospace. 2019;6(5):1–22.
8. Wright JR, Cooper JE. Introduction to Aircraft Aeroelasticity and Loads. John Wiley & Sons, Ltd., 2007.
9. Cordeiro FJB. The Gyroscope, CreateSpace. NV, USA. 2015.
10. Greenhill G. Report on Gyroscopic Theory. CA, USA: Relink Books, Fallbrook; 2015.
11. Scarborough JB. The Gyroscope Theory and Applications. London: Nabu Press; 2014.
12. Gregory DR. Classical Mechanics. New York: Cambridge University Press; 2006.
13. Taylor JR. Classical Mechanics. California, USA: University Science Books; 2005.
14. Aardema MD. Analytical Dynamics. Theory and Application. New York: Academic/Plenum Publishers; 2005:340.
15. Usubamatov R. Inertial Forces Acting on Gyroscope. Journal of Mechanical Science and Technology. 218;32(1):101–108.
16. Usubamatov R. Theory of gyroscope effects for rotating objects. Singapore: Springer; 2020.