New studies of the dynamics of rotating objects have shown the origin of their gyroscopic effects is more sophisticated than presented in publications. Their rotating mass acting on bodies generates the system of the kinetically interrelated inertial torques. The method for developing mathematical models for inertial torques of the spinning objects shows their dependencies on geometries. The inertial torques generated by the disc, ring, paraboloid, and others have confirmed this statement. The derived analytical method presents a new direction for the dynamics of classical mechanics. The several inertial torqueses acting on any movable spinning objects in space were unknown until recent times. The gyroscopic effects of rotating objects in engineering and a new method for computing their inertial torques are the challenges for researchers. The novelty of this manuscript is the mathematical models for the inertial torques generated by the rotating mass acting on the spinning solid and hollow sphere.

Keywords: inertial torques; gyroscope theory; spinning sphere

In engineering, all spinning objects manifest gyroscopic effects manifested by the action of their inertial torques that are not well-described.^1–4 Beginning with the Industrial Revolution, mathematicians and physicists studied the gyroscopic effects. Only famous L. Euler derived the mathematical foundation for the one torque that expresses the change in the angular momentum. His mathematical model did not describe all gyroscopic effects. Intensification processes in engineering forced to development of the theory of dynamics in classical mechanics. Scientists determined the gyroscopes and dynamics of rotating objects are a significant area in engineering science.^5–8 The textbooks of engineering mechanics contain a chapter on the dynamics of mechanisms with simple analytical approaches in solutions to gyroscopic effects.^9–11 Many publications described the original properties of the gyroscopic devices, which remain an unsolved problem and present a challenge for researchers.^12–14

Recent studies in gyroscopic effects showed their physics are sophisticated than could imagine researchers of engineering mechanics. The inertial torques generated by the rotating mass of the spinning objects are kinetically interrelated .¹⁵ The mathematical models of inertial torques for the rotating bodies are different and depend on their geometries. The inertial torques of the spinning sphere at known publication contain errors in the graphical presentation and mathematical processing.¹⁶ Practitioners of engineering need the method for deriving correct inertial torques of spinning objects to design the perfect machines. The known method for deriving the inertial torques for the spinning disc enables developing the mathematical models for any rotating bodies.^15,16 The novelty of this manuscript is the inertial torques generated by rotating masses of the solid and hollow spheres.

Inertial torques of a spinning sphere

The rotating mass of the spinning solid and hollow sphere generates inertial torques of the centrifugal and Coriolis forces that are acting simultaneously about axes of motions. The mathematical modeling of the action of the inertial forces on the sphere is the same as for the spinning disc.¹⁵ The mass elements are disposed on the surface of the 2/3 radius for the solid sphere and the middle radius for the thin hollow sphere. The rotating mass elements produce the centrifugal forces that are disposed on the random plane that is parallel to its plane of the maximal diameter of the sphere Figure 1.

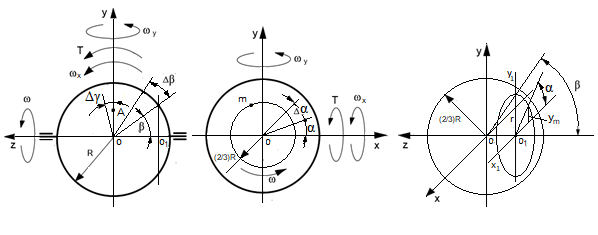
Figure 1 Schematic of the spinning sphere.

The inclination of the spinning sphere on the angle $\Delta \gamma$ gives the change in the vector’s forces $f_{ct.z}$ that is parallel to the sphere axis oz. The integrated product of a change in the forces $f_{ct.z}$ acts about axes ox and oy by sine and cosine laws and presents the resistance torque $T_{ct,x}$ and precession torque $T_{ct,x}$ respectively. The scheme of acting centrifugal forces and torques of the solid sphere’s plane with rotating mass elements about axis ox (a) and axis oy (b) is presented in Figure 2. Below is considered the action of the resistance torque, which expression is the same as for precession torque. The mass element m is disposed on the radius $R_i$  of the sphere, where i indicate the solid ss and hollow hs spheres $\left(R_{ss}=\left(2/3\right)R\right)$  for the solid sphere and $R_{hs}=R$  for the hollow sphere). The sphere rotates with an angular velocity $\omega$ in the counter-clockwise direction.

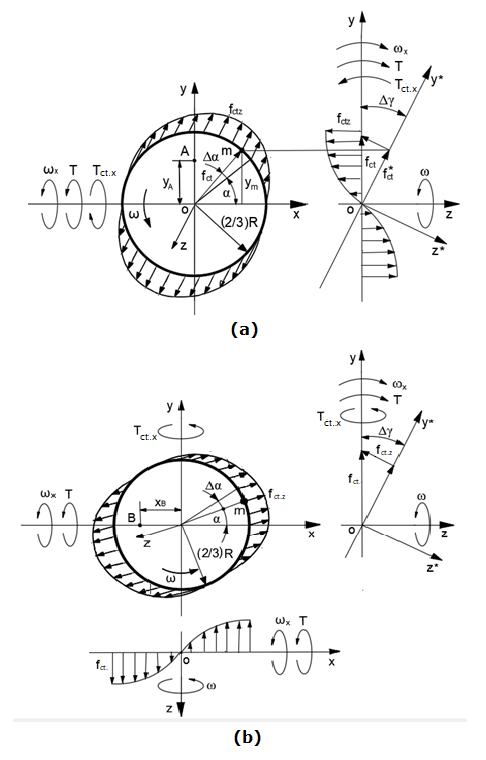
Figure 2 Schematic of acting centrifugal forces and torques of the sphere’s plane with rotating mass elements about axis ox (a) and axis oy (b).

The expression of the resistance torque $\Delta T_{ct}$  of the centrifugal force $f_{ct.z}$ is:

$\Delta T_{ct.}=f_{ct.z}{y}_m$   (1)

where $y_m=R_{i}sin\beta sin\alpha$  is the normal to axis o₁x₁, other components are as specified above.

The change of the centrifugal force $f_{ct.z}$ for arbitrarily chosen plane is:

$f_{ct.z}=f_{ct}\sin \Delta \gamma =mr{\omega }^2\sin \Delta \gamma$   (2)

where $f_{ct}=mr{\omega }^2$  is the centrifugal forceof the mass element m;, $m=\frac{M}{4\pi R_i^2}\Delta \delta R_i^2=\frac{M}{4\pi }\Delta \delta$ ,

M is the mass of the sphere; 4π is the spherical angle;$\Delta \delta$ is the spherical angle of the mass element; r is the radius of the mass element rotation at the plane o₁x₁y₁; α and β is the angle of the mass element’s disposition on the plane x oy and y oz, respectively; Δγ is the angle of turn for the sphere around axis ox ($sin\Delta \gamma =\Delta \gamma$ for the small values of the angle), other parameters are as specified above and in Figure 2.

The defined parameter is substituted into Eq. (1) that yields:

-for the solid sphere

$f_{ct.z}=-\frac{M}{4\pi }{\omega }^2\Delta \delta \Delta \gamma \frac{2}{3}R\sin \beta \sin \alpha =-\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha$   (3)

-for the hollow sphere

$f_{ct.z}=-\frac{M}{4\pi }{\omega }^2\Delta \delta \Delta \gamma \times R\sin \beta \sin \alpha =-\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha$   (4)

The integrated torque is the product of the forces $f_{ct.z}$  and the centroid $y_A$ (point A, Figure 1). The latter one is as follows:^5–7

-for the solid sphere

$\begin{array}{l}{y}_A=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{ct.z}{y}_{m}d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{ct.z}d\alpha d\beta }}}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha \times \frac{2}{3}R\sin \beta \sin \alpha d\alpha d\beta }}}{{\displaystyle \underset{\alpha =}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha d\beta d\alpha }}}=\\ \frac{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \times \frac{2}{3}R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta \sin \alpha \sin \beta \sin \alpha dd\beta }}}{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma {\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta \sin \alpha d\beta d\alpha }}}=\\ \frac{\frac{2}{3}R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{\sin }^2\beta {\sin }^2\alpha d\beta d\alpha }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta \sin \alpha d\beta d\alpha }}}\end{array}$   (5)

-for the hollow sphere

$\begin{array}{l}{y}_A=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{ct.z}{y}_{m}d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{ct.z}d\alpha d\beta }}}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha \times R\sin \beta \sin \alpha d\beta d\alpha }}}{{\displaystyle \underset{\alpha =}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha d\beta d\alpha }}}=\\ \frac{\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \times R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta \sin \alpha \sin \beta \sin \alpha d\beta d\alpha }}}{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma {\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta \sin \alpha d\beta d\alpha }}}=\\ \frac{R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{\sin }^2\beta {\sin }^2\alpha d\beta d\alpha }}}{{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta d\beta }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}\end{array}$   (6)

where the component $\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma$  and $\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma$  is accepted at this stage of computing as constant for Eqs. (5) and (6), respectively.

Defined parameter y_m is substituted into Eqs. (3) and (4), where $\sin \alpha ={\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }$ , $\sin \beta ={\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta d\beta }$ , ${\sin }^2\alpha =\frac{1}{2}(1-\cos 2\alpha )$ , ${\sin }^2\beta =\frac{1}{2}(1-\cos 2\beta )$  and represented by the integral forms with limits for the hemisphere., Then the following equations emerge:

-for the solid sphere

${\displaystyle \underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}}=-\frac{MR{\omega }^2}{6\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\delta }{\displaystyle \underset{0}{\overset{\gamma }{\int }}d\gamma }{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta }d\beta {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha }d\alpha \times \frac{\frac{2}{3}R\times \frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\beta )d\beta \times \frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\alpha )d\alpha }}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha }d\alpha {\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \beta d\beta }}$   (7)

-for the hollow sphere

${\displaystyle \underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}}=-\frac{MR{\omega }^2}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\delta }{\displaystyle \underset{0}{\overset{\gamma }{\int }}d\gamma }{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta }d\beta {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha }d\alpha \times \frac{\frac{1}{2}R{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\beta )d\beta \times \frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}(1-\cos 2\alpha )d\alpha }}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \beta }d\beta {\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}$   (8)

 Solution of integral Eqs. (7) and (8) yield:

-for the solid sphere

$T_{ct}|{}_0^{T_{ct}}=-\frac{MR{\omega }^2}{6\pi }\times \left(\delta |{}_0^{2\pi }\right)\times \left(\gamma |{}_0^{\gamma }\right)\times 2\sin \beta |{}_0^{\pi /2}\times 2\sin \alpha |{}_0^{\pi /2}\times \frac{\frac{1}{6}\times R\left(\beta -\frac{1}{2}\sin \beta \alpha \right)|{}_0^{\pi }\times \left(\alpha -\frac{1}{2}\sin 2\alpha \right)|{}_0^{\pi }}{(-\cos \beta )|{}_0^{\pi }\times (-\cos \alpha )|{}_0^{\pi }}$

that giving the rise to the following

$\begin{array}{l}{T}_{ct}=-\frac{MR{\omega }^2}{6\pi }\times (2\pi -0)\times (\gamma -0)\times 2(1-0)\times 2(1-0)\times \frac{\frac{1}{6}R\left[\left(\pi -0\right)-0\right]\times \left[\left(\pi -0\right)-0\right]}{[-(-1-1)]\times [-(-1-1)]}=\\ -\frac{M{R}^2{\pi }^2{\omega }^2}{18}\gamma \end{array}$   (9)

-for the hollow sphere

$\begin{array}{l}{T}_{ct}|{}_0^{T_{ct}}=-\frac{MR{\omega }^2}{4\pi }\times \left(\delta |{}_0^{2\pi }\right)\times \left(\gamma |{}_0^{\gamma }\right)\times 2\sin \beta |{}_0^{\pi /2}\times 2\sin \alpha |{}_0^{\pi /2}\times \\ \frac{R\times \frac{1}{2}\left(\beta -\frac{1}{2}\sin 2\beta \right)|{}_0^{\pi }\times \frac{1}{2}\left(\alpha -\frac{1}{2}\sin 2\alpha \right)|{}_0^{\pi }}{(-\cos \beta )|{}_0^{\pi }\times (-\cos \alpha )|{}_0^{\pi }}\end{array}$

that giving the rise to the following

$\begin{array}{l}{T}_{ct}=-\frac{MR{\omega }^2}{4\pi }\times (2\pi -0)\times (\gamma -0)\times 2(1-0)\times 2(1-0)\times \frac{\frac{R}{4}\left[\left(\pi -0\right)-0\right]\times \left[\left(\pi -0\right)-0\right]}{[-(-1-1)]\times [-(-1-1)]}=\\ -\frac{M{R}^2{\pi }^2{\omega }^2}{8}\gamma \end{array}$   (10)

where the change of the limits is taken for half of the sphere.

The variable angle γ of Eqs. (9) and (10) depend on the angular velocity ${\omega }_x$ of the sphere.

The differential equation of change in the torque $T_{ct}$  per time is:

-for the solid sphere 

$\frac{d{T}_{ct}}{dt}=-\frac{M{R}^2{\pi }^2{\omega }^2}{18}\frac{d\gamma }{dt}$   (11)

-for the hollow sphere

$\frac{d{T}_{ct}}{dt}=-\frac{M{R}^2{\pi }^2{\omega }^2}{8}\frac{d\gamma }{dt}$   (12)

where $t=\alpha /\omega$  is the time taken relative to the angular velocity of the spinning sphere.

The differential of time and the angle is: $dt=\frac{d\alpha }{\omega };\frac{d\gamma }{dt}={\omega }_x$  is the angular velocity of the sphere about axis ox.

The defined components is substituted into Eqs. (11) and (12), separated variables, and presented by the integral forms with defined limits:

-for the solid sphere

$\begin{array}{l}\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\pi }^2{\omega }^2}{18}{\omega }_x,d{T}_{ct}=-\frac{M{R}^2{\pi }^2\omega {\omega }_x}{18}d\alpha ,\\ {\displaystyle \underset{0}{\overset{T_{}}{\int }}d{T}_{ct}}=-{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{M{R}^2{\pi }^2\omega {\omega }_x}{18}d\alpha },T_{ct}=-\frac{1}{18}M{R}^2{\pi }^3\omega {\omega }_x\end{array}$   (13)

-for the hollow sphere

$\begin{array}{l}\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\pi }^2{\omega }^2}{8}{\omega }_x,d{T}_{ct}=-\frac{M{R}^2{\pi }^2\omega {\omega }_x}{8}d\alpha ,\\ {\displaystyle \underset{0}{\overset{T_{}}{\int }}d{T}_{ct}}=-{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{M{R}^2{\pi }^2\omega {\omega }_x}{8}d\alpha },T_{ct}=-\frac{1}{8}M{R}^2{\pi }^3\omega {\omega }_x\end{array}$   (14)

The torque acts on the upper and lower sides of the sphere. Then the total resistance torque $T_{ct}$  of Eq. (13) and (14) is multiplied by two.

-for the solid sphere

$T_{ct}=\pm \frac{2}{18}M{R}^2{\pi }^3\omega {\omega }_x=\pm \frac{5}{18}{\pi }^{3}J\omega {\omega }_x$   (15)

-for the hollow sphere

$T_{ct}=\pm \frac{2}{8}M{R}^2{\pi }^3\pi \omega {\omega }_{ч}=\pm \frac{3}{8}{\pi }^{3}J\omega {\omega }_x$   (16)

where $J=2M{R}^2/5$ and $J=2M{R}^2/3$  are the moment of inertia for solid and hollow spheres, respectively.

The expression for the precession torque generated by the centrifugal forces of the mass element (Eqs. (3) and (4)) is almost the same as for the resistance torque of the sphere considered above. The difference is in the change by the cosine law. The direction of the resistance (sign (-)) and the precession torque (sign (+)) are in the clockwise and the counter- clockwise direction, respectively.

Coriolis torques of a spinning sphere

The mathematical modeling of the action Coriolis torques generated by the mass elements of the spinning sphere is the same as presented for the centrifugal forces (Section 2.1). The scheme of acting Coriolis forces and torques of the sphere’s plane with rotating mass elements about axis ox is presented in Figure 3.

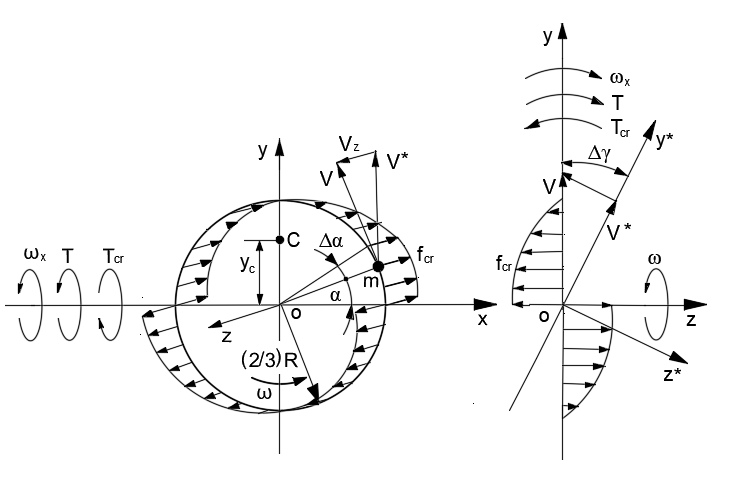
Figure 3 Schematic of acting Coriolis forces and torques of sphere’s plane with rotating mass elements about axis ox.

The expression for the inertial torque $\Delta T_{cr}$  of Coriolis forces of the mass elements for the sphere is:

$\Delta T_{cr}=-f_{cr}{y}_m=-m{a}_z{y}_m$    (17)

where y_m is represented by Eq. (1).

The expression for a_z is as follows: 

${\alpha }_z=-\frac{d{V}_z}{dt}=\frac{d(V\cos \alpha \sin \Delta \gamma )}{dt}=-V\cos \alpha \frac{d\gamma }{dt}=-R_i\sin \beta \cos \alpha \omega {\omega }_x$   (18)

where $a_z=d{V}_z/dt$  is

Coriolis acceleration of the mass element along axis oz;$V_z=Vcos\alpha sin\Delta \gamma =R_i\omega cos\alpha cos\beta sin\Delta \gamma$  is the change in the tangential velocity V of the mass element;$sin\Delta \gamma =\Delta \gamma$ for the small angle; other components are as specified above.

Defined parameters are substituted into the expression $f_{cr}$ (Eq. (17))that brings:

-for the solid sphere

$f_{cr}=\frac{M\Delta \delta }{4\pi }\frac{2}{3}R\omega {\omega }_x\sin \beta \cos \alpha =\frac{MR\Delta \delta }{6\pi }\omega {\omega }_x\sin \beta \cos \alpha$   (19)

-for the hollow sphere

$f_{cr}=\frac{M\Delta \delta }{4\pi }R\omega {\omega }_x\sin \beta \cos \alpha =\frac{MR\Delta \delta }{4\pi }\omega {\omega }_x\sin \beta \cos \alpha$   (20)

Then, the defined parameters are substituted into Eq. (17) that yields:

-for the solid sphere

$\Delta T_{cr}=\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\sin \beta \cos \alpha \times y_m$   (21)

for the hollow sphere

$\Delta T_{cr}=\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\sin \beta \cos \alpha \times y_m$   (22)

The disposition of the resultant torque is the centroid C of the Coriolis torque’s curve calculated by Eq. (5).

-for the solid sphere

$\begin{array}{l}{y}_C=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{cr}{y}_{m}d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{cr}d\alpha d\beta }}}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\sin \beta \cos \alpha \times \frac{2}{3}R\sin \alpha \sin \beta d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\sin \beta \cos \alpha d\alpha d\beta }}}=\\ \frac{\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\frac{2}{3}R\sin \beta \cos \alpha d\alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \beta \cos \beta d\beta }}}{\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\sin \beta d\beta \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }}}=\frac{\frac{2}{3}R{\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\beta d\times {\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha \cos \alpha d\alpha }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\sin \beta d\beta \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }}}\end{array}$   (23)

-for the hollow sphere

$\begin{array}{l}{y}_C=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{cr}{y}_{m}d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}{f}_{cr}d\alpha d\beta }}}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\sin \beta \cos \alpha \times R\sin \alpha \sin \beta d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi }{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\sin \beta \cos \alpha d\alpha d\beta }}}=\\ \frac{\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}R\sin \alpha \cos \alpha d\alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\beta d\beta }}}{\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}\sin \beta d\beta \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }}}=\frac{R{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\beta d\beta }}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \beta d\beta \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }}}\end{array}$   (24)

where the components $\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }$  and $\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }$  are accepted as constant. The expressions of $y_C$ (Eqs. (23) and (24)) are substituted into Eqs. (21) and (22), respectively. Where $\cos \alpha ={\displaystyle \underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha }$ , $\sin \beta ={\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta d\beta }$  are presented by the integral forms:

-for the solid sphere

${\displaystyle \underset{0}{\overset{T_{cr}}{\int }}d{T}_{cr}}=\frac{MR\omega {\omega }_x}{6\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\delta }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta d\beta }{\displaystyle \underset{0}{\overset{\pi }{\int }}-\sin }\alpha d\alpha \times \frac{\frac{2}{3}R{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\beta d\beta }}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \beta d\beta \times {\displaystyle \underset{\begin{array}{l}0\\ \end{array}}{\overset{\pi }{\int }}\cos \alpha d\alpha }}}$   (25)

-for the hollow sphere

${\displaystyle \underset{0}{\overset{T_{cr}}{\int }}d{T}_{cr}}=\frac{MR\omega {\omega }_x}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\delta }\times {\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \beta d\beta }{\displaystyle \underset{0}{\overset{\pi }{\int }}-\sin }\alpha d\alpha \times \frac{R{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\beta d\beta }}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \beta d\beta }}}$   (26)

where the limits of integration for the trigonometric expressions are taken for the hemisphere.

Solving of integrals Eq. (25) and (26) yield:

-for the solid sphere

$T_{cr}|{}_0^{T_{cr}}=\frac{MR\omega {\omega }_x}{6\pi }\times \left(\delta |{}_0^{2\pi }\right)\times (2\sin \alpha |{}_0^{\pi /2})\times \left(\cos \beta |{}_0^{\pi }\right)\times \frac{\frac{2}{3}R\times 2\frac{{\sin }^2\alpha }{2}|{}_0^{\pi /2}\times \frac{1}{2}\left(\beta -\frac{\sin 2\beta }{2}\right)|{}_0^{\pi }}{2\sin \alpha |{}_0^{\pi /2}(-\cos \beta )|{}_0^{\pi }}$

that giving the rise to the following:

$T_{cr}=\frac{MR\omega {\omega }_x}{6\pi }\times (2\pi -0)\times 2(1-0)\times (-1-1)\times \frac{\frac{2}{3}R(1-0)\times \frac{1}{2}\left(\pi -0\right)}{2(1-0)]\times (-)(-1-1)}=-\frac{M{R}^2\pi \omega {\omega }_x}{9}$    (27)

-for the hollow sphere

$T_{cr}|{}_0^{T_{cr}}=\frac{MR\omega {\omega }_x}{4\pi }\times \left(\delta |{}_0^{2\pi }\right)\times (2\sin \beta |{}_0^{\pi /2})\times \left(\cos \alpha |{}_0^{\pi }\right)\times \frac{R\times 2\frac{{\sin }^2\alpha }{2}|{}_0^{\pi /2}\times \frac{1}{2}\left(\beta -\frac{\sin 2\beta }{2}\right)|{}_0^{\pi }}{2\sin \alpha |{}_0^{\pi /2}(-\cos \beta )|{}_0^{\pi }}$

that giving the rise to the following:

$T_{cr}=\frac{MR\omega {\omega }_x}{4\pi }\times (2\pi -0)\times 2(1-0)\times (-1-1)\times \frac{R(1-0)\times \frac{1}{2}\left(\pi -0\right)}{2(1-0)(-)(-1-1)}=-\frac{1}{4}M{R}^2\pi \omega {\omega }_x$   (28)

Coriolis torque acts on the upper and lower sides of the hemisphere. Then the total resistance torque $T_{cr}$ is obtained when the result of Eqs. (27) and (28) is multiplied by two.

-for the solid sphere

$T_{cr}=-2\times \frac{M{R}^2\pi \omega {\omega }_x}{9}=-\frac{5}{9}\pi J\omega {\omega }_x$   (29)

-for the hollow sphere

$T_{cr}=-2\times \frac{M{R}^2\pi \omega {\omega }_x}{4}=-\frac{3}{4}\pi J\omega {\omega }_x$   (30)

where $J=2M{R}^2/5$ and $J=2M{R}^2/3$ is the sphere moment of inertia for solid and hollow sphere,^5–8 respectively; the sign (-) means the action of the torque in the clockwise direction; other parameters are as specified above.

The torque of the change in the angular momentum is:^5–7

$T_{am}=J\omega {\omega }_x$   (31)

The analysis of Eqs. (17) and (31) shows the torques of the centrifugal and Coriolis forces of the spinning sphere’s mass elements present the resistance torques acting opposite to the load torque. The torques of the centrifugal forces and the change in the angular momentum present the precession load torques.

Attributes of the inertial torques acting on the spinning sphere

The derived mathematical models for the inertial torques of the solid and hollow sphere should be used for computing their gyroscopic effects. The inertial torques of the centrifugal, Coriolis forces, and the torque of the change in the angular momentum are active physical components of the spinning sphere. These torques are the components of the total resistance and precession torques acting about axes ox and oy of the spinning sphere. The mathematical models for internal torques of the spinning sphere are represented in Table 1. The inertial torques of the spinning solid and hollow sphere should be used for the formulation of their gyroscopic effects. New studies of the inertial torques have shown that their values depend on the geometry of the spinning objects that can be different designs in engineering. The equality of the kinetic energies of its motions defined the kinematic dependency of the angular velocities of the spinning sphere.¹⁵ This kinematic dependency for the solid and hollow spheres is as follows:

-The solid sphere

$-\frac{5}{18}{\pi }^{3}J\omega {\omega }_x-\frac{5}{9}\pi J\omega {\omega }_x-\frac{5}{18}{\pi }^{3}J\omega {\omega }_y-J\omega {\omega }_y=\frac{5}{18}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x-\frac{5}{18}{\pi }^{3}J\omega {\omega }_y-\frac{5}{9}\pi J\omega {\omega }_y$   (32)

Transformation of Eq. (32) yields:

${\omega }_y=\left(\frac{5{\pi }^3+5\pi +9}{5\pi -9}\right){\omega }_x$   (33)

For the hollow sphere

$-\frac{3}{8}{\pi }^{3}J\omega {\omega }_x-\frac{3}{4}\pi J\omega {\omega }_x-\frac{3}{8}{\pi }^{3}J\omega {\omega }_y-J\omega {\omega }_y=\frac{3}{8}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x-\frac{3}{8}{\pi }^{3}J\omega {\omega }_y-\frac{3}{4}\pi J\omega {\omega }_Y$   (34)

Transformation of Eq. (34) yields:

${\omega }_y=\left(\frac{3{\pi }^3+3\pi +4}{3\pi -4}\right){\omega }_x$   (35)

The ratio of the angular velocities of the spinning spheres should be used for the mathematical models for their rotation about axes ox and oy.

Working example

The sphere of a mass of 0.5 kg, a radius of 0.08 m, and spinning at 2000 rpm. The sphere rotates with an angular velocity of 0.02 rpm under the action of the external torque. The values of the inertial torques acting on the spinning sphere should be determined Figure 1. Substituting the initial data into equations of Table 2 and computing yields.

The known publications with the mathematical models for the inertial torques generated by the rotating mass of the spinning sphere contained errors in the graphical presentation of the acting forces and processing of the integral equations. The issues had the wrong title of the precession torque generated by the rotating mass of the sphere. The new graphical scheme and vectorial diagrams of the acting forces derived the corrected mathematical models for the inertial torques of the centrifugal and Coriolis forces of the spinning sphere. The corrected inertial torques and the ratio of the angular velocities of the sphere about axes of rotation enable getting the exact solutions in computing the gyroscopic effects and present the novelty for the dynamics of rotating objects.

The modified method of graphical and analytical approaches for deriving the inertial torques generated by the rotating mass of the spinning sphere developed their correct mathematical models. The expressions of inertial torques and the ratio of the angular velocities of the sphere about axes of rotation enable planning mathematical models for its motion in space. The analytical models for the kinetically interrelated inertial torques of the spinning sphere describe its physics of gyroscopic effects and yield a high accuracy of computing. This analytical solution for inertial torques opens new possibilities for solving gyroscopic problems of spherical objects.

$f_{ct},f_{cr}$ , – centrifugal and Coriolis forces, respectively, generated by mass elements of a spinning sphere

J – mass moment of inertia of a sphere

M – mass of a sphere

m – mass element of a sphere

R – radius of a sphere

T – external torque

$T_{ct},T_{cr},T_{am}$  – torque generated by centrifugal, Coriolis, and a change in the angular momentum, respectively

t – time

$y_A,y_m$  – centroid and distance of disposition of mass element along axis

$\Delta \alpha ,\alpha$ – increment angle and angle of the turn for a sphere around axis of spinning, respectively

β – angle of disposition the mass element of a sphere

$\Delta \delta$  – spherical angle of the mass element

$\Delta \gamma$  – angle of inclination of a sphere

ω – angular velocity of a sphere

${\omega }_x,{\omega }_y$  – angular velocity of precession around axes ox and oy, respectively

None.

The authors declare that they have no conflicts of interest.

None.

1. Muller D. The bizarre behavior of rotating bodies, explained. Veritasium. 2020.
2. Jin J, Hwang I. Attitude control of a spacecraft with single variable-speed control moment gyroscope. Journal of Guidance, Control, and Dynamics. 2011;34:1920–1925.
3. Liang WC, Lee SC. Vorticity, gyroscopic precession, and spin- curvature force. Physical Review D. 2013;87:044024.
4. Weinberg H. Gyro mechanical performance: the most important parameter. Analog Devices, Technical Article MS-2158. 2011;1–5.
5. Cordeiro FJB. The gyroscope. Createspace, NV, USA. 2015.
6. Greenhill G. Report on gyroscopic theory. Relnk Books, Fallbrook, CA, USA. 2015.
7. Scarborough JB. The gyroscope theory and applications. Nabu Press, London. 2014.
8. Aardema MD. Analytical dynamics. theory and application. Academic/Plenum Publishers, New York. 2005.
9. Hibbeler RC, Yap KB. Mechanics for engineers-statics and dynamics. 13th ed. Prentice Hall, Pearson, Singapore. 2013.
10. Gregory DR. Classical mechanics. Cambridge University Press, New York. 2006.
11. Taylor JR. Classical mechanics. University Science Books, California, USA. 2005.
12. Crassidis JL, Markley FL. Three-axis attitude estimation using rate-integrating gyroscopes. Journal of Guidance, Control, and Dynamics. 2016;39:1513–1526.
13. Nanamori Y, Takahashi M. An integrated steering law considering biased loads and singularity for control moment gyroscopes. AIAA Guidance, Navigation, and Control Conference. 2015.
14. Sands T, Kim JJ, Agrawal BN. Nonredundant single-gimbaled control moment gyroscopes. Journal of Guidance, Control, and Dynamics. 2012;35(2):578–587.
15. Usubamatov R. Inertial forces acting on gyroscope. Journal of Mechanical Science and Technology. 2018;32(1):101-108.
16. Usubamatov R. Theory of gyroscopic effects for rotating objects. Springer, Singapore. 2020.