Sol-gel is a modern technological process that is widely used in production of inorganic sorbents, catalysts and catalyst carriers, synthetic zeolites, inorganic binders, ceramics with select physical, optical, magnetic, and electrical properties, glass, glass ceramics, fibers, etc. The creation of models of this process will make it possible to fine-tune the properties of the resulting materials. The sol-gel transition is a process of sol particle association accompanied by the formation of "an infinite aggregate". Two ways of constructing mathematical models are suggested. The first approach is based on the methods of statistical thermodynamics, and the second one is hydrodynamical. Both methods make it possible to obtain the inter- consistent equations describing the relationship between the gelation time and the macroscopic parameters.

Keywords: sol-gel transition, aggregation, coagulation, fractals, fractal dimension, modeling

The coagulation of colloidal particles plays an essential role during various processes, including the production of materials for structural and functional purposes, water purification by reagent methods, and the implementation of nanotechnology processes. The sol-gel process is used in the production of inorganic sorbents, catalysts and catalyst carriers, synthetic zeolites, inorganic binders, ceramics with select physical, optical, magnetic, and electrical properties, glass, glass ceramics, fibers, etc.The sol-gel process is one aspect of nanotechnology. It describes the preparation of nanoscale objects like e.g., particles and their processing of nanostructured materials. One process step, thereby, includes the solidification of a liquid nanoparticle dispersion (sol) by inter particulate forces to a gel. The creation of models of this process will make it possible to fine-tune the properties of the resulting materials.

An aggregate is a collection of particles with strong interparticle bonds. These bonds can be covalent or even necked between individual particles. In this case, the resulting surface area of the formed aggregates can be significantly less than the sum of the surface areas of the particles that formed it. The purpose of this work is to obtain results that allow a direct approach to the physical and mathematical modeling of colloidal processes associated with coagulation and aggregation of nanoparticles. Let us consider the possible mechanisms that promote or prevent the coagulation of particles in solution. It should be borne in mind that they often proceed together.One of the main processes leading to the interaction of colloidal particles with each other is Brownian coagulation. Colloidal particles react to random molecular fluctuations in the density and average velocity of solvent molecules; therefore, they remain in irregular (Brownian) motion all the time. Brownian wandering leads to their mutual collision; therefore, it is one of the main consistently acting mechanisms that contribute to the coagulation of colloidal particles.

Brownian diffusion is another process that determines the interaction of colloidal particles. The Brownian walk of particles leads to the so-called Brownian diffusion and the interaction of particles with each other. It also promotes their deposition on the surface of various materials. However, large particles and their aggregates are flown around by the solvent due to sedimentation. Consequently, simultaneously with the convective transfer of small particles and Brownian diffusion, convective Brownian diffusion can be observed.During the sedimentation of large aggregates of colloidal particles, the "engagement" effect can be observed. The particles have a finite size; therefore, at a distance of the order of the particle radius from the surface of the aggregate, the standard component of the solvent velocity is finite; during convective transfer, additional "engagement" of the particle with a large aggregate is possible. The engagement effect plays a significant role in the formation of precipitation, especially under the additional action of gravitational and centrifugal forces, when convective Brownian diffusion is no longer sufficient.All the processes discussed above act together in the gravitational coagulation of particles of comparable sizes. Gravitational coagulation is one of the main microphysical mechanisms of sediment formation. Convective transport of particles by the solvent always results in less deposition because it is directed against gravity. Sol-gel transition and sedimentation are mutually different processes. Therefore, a sol-gel change is observed only when the growth rate of aggregates significantly exceeds the rate of their deposition, and the formation of an infinite aggregate stops the sedimentation process altogether.

The sol-gel transition is observed in the processes of colloidal particle association. It is accompanied by the formation of the so-called “endless aggregate”, i.e., unit comparable to the size of the entire system. There are several approaches to the modeling of kinetics and structure formation at sol-gel transition the construction of mathematical models of the aggregation process and the computer simulation. Nonlinear equations for aggregates growth rate, like the nonlinear Boltzmann equation, are usually used to construct mathematical models of the aggregation process. The equations of chain growth rate were first obtained by Smoluchowski ¹ in a discrete form and by Schuman² in a continuous way. The essential difference between the Boltzmann equation and the equation for the rate of fragmentation and growth of aggregates lies in the difference in the conservation laws that are embedded in these equations. In the equations for the rate of fragmentation and growth of aggregates, the total mass of aggregates is constant, and their total number is not conserved. This difference also provokes a significant difference in the behavior of their decisions. For example, some solutions are used to describe the kinetics of the gelation process. Such an equation corresponds to the conditions under which the total mass of aggregates of finite size and colloidal particles is retained until a certain critical point in time (gelation point). After reaching the gel point, the total mass of such particles begins to decrease. This behavior of the system corresponds to the emergence of mass flow from aggregates of limited size to an "infinite aggregate" - a gel.³ The equation of aggregates growth and fragmentation rate is expressed in a continuous form:

${\partial }_{t}c\left(x\right)=\frac{1}{2}\underset{0}{\overset{x}{{\displaystyle \int }}}k\left(x-y,y\right)c\left(x-y\right)c\left(y\right)dy-c(x)\underset{0}{\overset{\infty }{{\displaystyle \int }}}k\left(x,y\right)c\left(y\right)dy+\underset{0}{\overset{\infty }{{\displaystyle \int }}}F\left(x,y-x\right)c\left(y\right)dy-\frac{1}{2}c(x)\underset{0}{\overset{x}{{\displaystyle \int }}}F\left(y,x-y\right)dy (1)$

When a variable characterizing the mass or sizes of an aggregate takes the discrete values, the equation of the rate of aggregates formation reaction in a unit volume may be written as follows:

$c_K=\frac{1}{2}{\displaystyle \sum }_{j=1}^{k-j}{\displaystyle \sum }_{i=1}^{k-i}{K}_{ij}{c}_i{c}_j-c_k{\displaystyle \sum }_{j=1}^{\infty }{K}_{ij}{c}_j+{\displaystyle \sum }_{j=1}^{\infty }{F}_{kj}{c}_j-\frac{1}{2}{c}_k{\displaystyle \sum }_{j=1}^{k-j}{\displaystyle \sum }_{i=1}^{k-i}{F}_{ij}$      (2)

For the analysis of the solutions of equations (1) and (2), the corresponding moments of distribution functions are the most interesting:

$M_g\left(t\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{x}^{g}c\left(x,t\right)dx={\displaystyle \sum }_{k=0}^{\infty }{x}^g{c}_k(t)$      (3)

Here: $M_0\left(t\right)$  is the overall number of aggregates, $M_1\left(t\right)$  is the total mass of aggregates, and $M_2\left(t\right)$  - is the second moment of the distribution; its value is proportional to the degree of aggregation.All these quantities are referred to as the unit volume. For some models of growth and fragmentation of aggregates with specially chosen functions $K$  and $F$ , the closed equations may be obtained directly from the functions $M_k\left(t\right)$ . These equations are called the equations of macroscopic rates. In general, their consequence is the conservation equation of the total mass $M_1\left(t\right)$ .

The described equations are used for modeling the processes of the polycondensation polymerization and in the meteorology, and for the calculation of the process of atmospheric precipitation formation.⁴ Let us construct a model of aggregation rate in terms of statistical thermodynamics. For colloidal particles having a two-hole potential and a certain energy barrier, the expression for the rate constant may be written:

$K=\frac{2k_{B}T}{3\eta }\left(i+j\right){\left(ij\right)}^{\frac{i}{i+j}}{j}^{\frac{j-1}{i+j}}{e}^{-\left(\frac{E}{k_{B}T}\right)}$      (4)

Where η is the viscosity of the medium. If $j=m.i$ , for rather large aggregates, we will obtain from eq. (4) a ratio of the interaction processes rate constants for aggregate-aggregate and aggregate-particle:

$U(m,i)=\frac{3\eta K}{2k_{B}T}{e}^{\left(\frac{E}{k_{B}T}\right)}=i\left(m+1\right){\left(i^2.m\right)}^{\frac{1}{m+1}}{(m.i)}^{\frac{m.i-1}{i(m+1)}}$      (5)

The parameter m  shows the magnitude of the difference between the reacting aggregates. The value m=1 corresponds to the case of the interaction of identical aggregates. If m >1, then this means that j >1, that is, the primary aggregate i interacts with a large aggregate j. For m <1, the opposite situation arises. Figure 1 shows the behavior of function ⁵depending on the parameter m and the number of particles in the primary aggregate. It can be assumed that there should be some symmetry in the behavior of the function $U(m,i)$  for the value m =1. However, from Figure 1, this symmetry is not explicitly observed. For a more detailed understanding of the current situation, let us analyze the behavior of the partial derivative of the function $U(m,i)$  concerning m:

$\frac{\partial }{\partial m}U(m,i)=\frac{1}{\left(m+1\right)m}\left(2{\left(i^{2}m\right)}^{\frac{1}{m+1}}\left(-\frac{\ln \ln \left(i^{2}m\right)im}{2}+\frac{\left(i+1\right)\ln \ln \left(mi\right)m}{2}+\left(m+1\right)\left(mi+\frac{1}{2}i-\frac{1}{2}\right)\right)m{i}^{\frac{mi-1}{i\left(m+1\right)}}\right)$      (6)

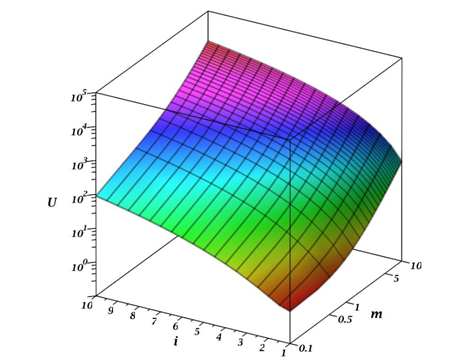
Figure 1 Graph of the behavior of equation (5) of the function $U\left(m,i\right)$ depending on the parameter m and $i$ - the number of particles in the primary aggregate.

Figure 2 shows a graph of the equation (6) behavior depending on the parameter m and the number of particles in the primary aggregate. Analysis of this dependence shows that $\frac{\partial }{\partial m}U(m,i)$  has some symmetry concerning m =1, although it is not ideal. Hence, we can conclude that the aggregation process has a greater tendency to collect individual colloidal particles and small aggregates by a large aggregate than vice versa, although both processes take place.As is known from the laws of chemical kinetics, the speed of a complex multistage process is determined by the limiting stage rate, that is, the stage with the minimum rate. From equation (4) and Figures 1&2, such a stage is the interaction of primary particles, that is when the value of $i$  is minimal. Thus, to estimate the rate of aggregation, one can use the equality condition i =1. In the case when i =1, equation (5) describes the case of aggregate-particle interaction. In this case, the m value indicates the number of particles in the aggregate:

$U_{i=1}(m)=\left(m+1\right)m^{\frac{m}{m+1}}$      (7)

Figure 2 The graph of the behavior of the equation (6) of the partial derivative $\frac{\partial }{\partial m}U\left(m,i\right)$ depending on the parameter m and i - the number of particles in the primary unit.

The analysis of the equation (7) shows that when the differences in aggregates sizes are small in a system, the aggregation rate is a weakly dependent on m. The aggregates differing much in sizes exhibit a drastic growth of aggregation rate, which is proportional to m²:

$\underset{m\to \infty }{\lim }\underset{m\to \infty }{\lim }{U}_{i=1}\left(m\right)=m^2$      (5.2)

Thus, the occurrence of particles with many different sizes will lead to a sharp increase in aggregation rate, i.e., the aggregates "pick up" on themselves the separate particles into the small aggregates. Figures 1&2 clearly show that in the case of aggregate-aggregate interaction, the speed of their interaction grows especially rapidly with an increase in the size of the aggregates participating in the process. However, the total rate of this process is determined by the rate of interaction between primary particles and small aggregates.

The gelation time will be determined by the size distribution functions of the primary aggregates. Therefore, to determine the gelation time, it is most convenient to use the functions corresponding to the moments of the aggregate size distribution. The most suitable of these moments is the moment corresponding to the variance of the distribution $M_2\left(t\right)$ , which is the value proportional to the aggregation degrees. To determine the time of infinite cluster formation, let us study the asymptotic properties of size distribution functions of aggregates for a model with the nucleus k =i.j For this purpose, we write a set of equations for the moment $M_2$ , which simply follows from equations (1) and (3):

$\frac{d{M}_2}{dt}=2M_2^2$      (8)

In this model, at a time moment $t=t_c$  a super particle - "infinite aggregate" is formed. The quantity $t_c$  is determined from the condition of tending to ∞ of moment $M_2\left(t\right)$. Moment $M_2\left(t\right)$  is the second moment of the distribution; its value is proportional to the degree of aggregation. Solving equation (8), we get:

$M_2(t)=\frac{M_2(0)}{1-2M_2(0).t}$      (9)

Fromequation (9) wefind:

$t_c=\frac{1}{2M_2(0)}$      (10)

Further examination will be made for the model of monodispersed particles of the unit size ($g=1$ ) since the limiting stage of the aggregation process is the stage of attachment of primary particles to the forming aggregate. The particle size distribution for this case can be represented as the Dirac δ-function:

$c\left(g\right)=\delta (g-g_0)$      (11)

Following the filtering property of the δ-function, the moment $M_2\left(0\right)$  will be equal to:

$M_2\left(0\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{g}^2\delta (g-g_0)dg=g_0^2$      (12)

From here for $g_0=1$ , we have $t_c=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ . For the transition from dimensionless to real-time, we introduce the aggregation time ${\tau }_{agr}$ . This parameter represents the time interval between individual events in the aggregation process:

${\tau }_{agr}=\frac{1}{kN}$      (13)

Where: N is the number of particles in a unit volume.

From equation (4), we can get the apparent aggregation time under the condition $i=j=1$ :

${\tau }_c=t_c{\tau }_{agg}=\frac{3\eta }{8k_{B}TN}{e}^{\frac{E}{k_{B}T}}$      (14)

The analysis of equation (14) shows that the gelling time is directly proportional to the viscosity of the medium and inversely proportional to the temperature and the concentration of particles. The increase in potential barriers during the interaction of particles leads to a rise in gelling time. To elucidate the effects of hydrodynamic flows, let us consider the case where the aggregate grows by the conservative attachment of separate particles. Two mechanisms drive the aggregation process. One of the mechanisms of this process is the diffusion motion of the reacting particles. The second mechanism is due to the movement of aggregates under the influence of existing hydrodynamic flows. In the latter case, the aggregate rate is little compared to the heat rate of particles, so that the attachment of particles ultimately occurs due to their diffusion.

The balance equation has the following form for the total number of particles  in the aggregate, considering the flow of both processes:

$\frac{dn}{dt}=v_d+v_m$      (15)

Where  is the rate of adherence of colloidal particles to the aggregate in the diffusive motion of particles, and  is the rate of adherence of particles to the aggregate due to the occurrence in the aggregate motion band when it moves along by linear path.Usually, the aggregate is rather large ($R>>r_0$ ) and base a fractal geometry (Figure 3), i.e., the number of particles in it is equal to:

$n={\left(\frac{R}{r_0}\right)}^d$      (16)

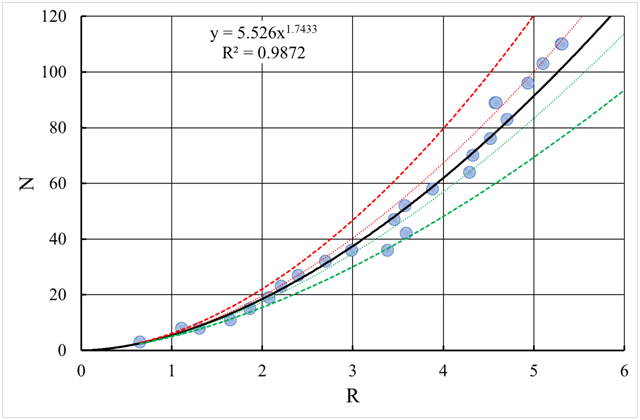
Figure 3 Correlation of the number of particles N in a fractal and its size R (obtained by the method of simulation modeling). The dotted and dashed lines correspond to the confidence intervals and respectively. (Note to the equation $y=N$ : and $x=R$ , $R^2$ - coefficient of determination).

Where: $d$  - is the fractal dimension.

From equation (15), we have:

$\frac{dn}{dt}={\vartheta }_D{n}^{\frac{1}{d}}+{\vartheta }_G{n}^{\frac{2}{d}}$      (17)

Where: ${\vartheta }_D=4\pi D{r}_{0}N$  aggregation rate coefficient for diffusion transfer of reacting particles; ${\vartheta }_G=\pi r_0^{2}vN$  - aggregation rate coefficient for hydrodynamic transfer of reacting particles; D - is the diffusion coefficient of particles;  - is the concentration of particles, and $N$  - is the speed of aggregates motion under the action of the hydrodynamic flow.For the convenience of analyzing the behavior of solutions to the differential equation (17), we bring it to a dimensionless form:

$\frac{dn}{d\stackrel{�}{t}}=\frac{{\vartheta }_D}{{\vartheta }_G}{n}^{\frac{1}{d}}+n^{\frac{2}{d}}=a.n^{\frac{1}{d}}+n^{\frac{2}{d}}$      (18)

Where: $\stackrel{}{\tilde{t}}={\vartheta }_G.t$  – adjusted time; a= ϑ_D/ϑ_G  – the ratio of aggregation rate coefficients for diffusion and hydrodynamic transfer of reacting particles. In the case when $a>1$, the diffusion transfer of particles due to Brownian motion prevails. In the case when $a<1$ , the hydrodynamic transfer of particles predominates due to the movement of a liquid medium to which these particles are dispersed. The behavior of solutions to equation (18) is shown in Figure 4.

Figure 4 The total number of particles in the resulting aggregate by equation (18). 1-3 - Influence of fractal dimension $d.$ 4-6 - Influence of the ratio of the aggregation rate coefficients during diffusion and hydrodynamic transfer of reacting particles $a=\frac{{\vartheta }_D}{{\vartheta }_G}.$ The image numbers correspond to the following values of the initial parameters used in the numerical solution of equation (18): 1 - $a=4.0$ . 1 - $a=0.72$ . 1 - $a=0.01$ . 4 - $d=1.3$ . 5 - $d=1.7$ . 6 - $d=2.1$ .

The analysis of the numerical solutions of equation (18) presented in Figure 4 showed that a decrease in the fractal dimension of the forming aggregate sharply increases the rate of its growth and, accordingly, the rate of formation of an infinite aggregate, that is, reduces the time of gel formation during the sol-gel transition. If a≪1, that is, the hydrodynamic transfer of particles due to the movement of a liquid medium prevails, then there is a simple process of particle aggregation followed by the formation of a gel, which is elegantly seen from Figure 4. In this case, with the formation of aggregates with a high value of the fractal dimension approaching d→3, the aggregate growth process simply slows down. The value  is a critical value, above which there is a change in the mechanisms of the behavior of aggregates with small and large fractal dimensions. With a sizeable fractal dimension, the aggregates stop forming and are removed from the system due to sedimentation. This phenomenon is visible in Figures 1–4. In this case, with an increase in the fraction of the diffusion component in the growth rate of aggregates, the critical value of the fractal dimension shifts towards lower values. At the same time, the growth rate of aggregates is overgrowing. Such a breakdown of the aggregation rate for a sizeable fractal dimension of aggregates is visible from Figures 4–6. In this case, the critical value of the fractal dimension is approximately $d\approx 2.1$ . These calculations were carried out by the method of numerical solution of the differential equation (18). To assess the influence of other factors on the aggregation process, we carried out a qualitative assessment of the gelation time, which was estimated as the time required to collect all particles into a single endless aggregate. Determine now the time when all sol particles combine into a single aggregate, which is equal by sizes to the entire system:

${\tau }_c=\underset{1}{\overset{\infty }{{\displaystyle \int }}}\frac{dn}{{\vartheta }_D{n}^{\frac{1}{d}}+{\vartheta }_G{n}^{\frac{2}{d}}}\propto \frac{B{\vartheta }_0^{d-2}}{{\vartheta }_1{}^{d-1}}$      (19)

Where  is a composite quantity that weakly depends on the fractal dimension .As compared to equation (14), the equation (19) gives overstated results of gelling times, because it does not consider the coalescence of aggregates. However, the analysis of the asymptotic behavior of equation (19) shows that it will give the results that are like equation (14). Substituting into equation (19) the values of the parameters indicated in equation (17), we obtain:

${\tau }_c=\frac{B{.2}^{2d-3}{D}^{d-2}}{D_p^d{V}^{d-1}N}=\frac{\stackrel{}{\tilde{B}}}{D_p^d{V}^{d-1}N}$      (20)

Where $D_p=2r_0$  – particle diameter.

So, from equation (20), it follows that the gelation time is inversely proportional to the number concentration of particles:

${\tau }_c\propto \frac{1}{N}$      (21)

Accordingly, for the speed of movement of the units, there is the following proportionality with the gelation time:

${\tau }_c\propto \frac{1}{V^{d-1}}$      (22)

The nature of the gelation time dependence on the particle size is determined by the influence of other factors on this dependence, for example, such as the diffusion coefficient $D$ . The diffusion coefficient of particles depends on the average speed of movement of particles and their free path.^6,7 Considering the mean free path $\lambda$  of a colloidal particle and the mean square velocity  of motion of colloidal particles,⁷ the equation for the diffusion coefficient will have the form:

$D=\frac{1}{3}v\lambda =\frac{1}{6m\sqrt{\pi }}\sqrt{\frac{kT\rho }{D_p}}\propto D_p{}^{-\frac{1}{2}}$      (23)

Where k – Boltzmann constant; T – absolute temperature; – mass concentration of colloidal solution [kg/m³];  is the density of the substance of the colloidal particle [kg/m³].

Considering the above factor, for the size of the first particles, we have the following proportionality, if the concentration of the sol is constant and expressed in counting units:

${\tau }_c\propto d^{1-\frac{3}{2}d}$      (24)

If a constant mass concentration is maintained in the experiments, then this formula will change its form and will look like this:

$\tau \propto d^{4-\frac{3}{2}{D}_f}$      (25)

The shape of the aggregate and its fractal dimension  can be different. It depends on the nature of aggregation, and according to the literature, it takes values from 1.75 to 2.5 ÷ 3.0.^8,9 A significant difference between the two models is that the first version includes only the material balance in the system. In contrast, the second model considers the structural feature of the forming gel. This feature is due to the fractal geometry of gel formation and its relationship with the kinetics of aggregation.

Experiments were carried out to study the effect of the particle size of a colloidal solution of silicon oxide on the time of its gelation to check the obtained dependences. In all tests, a constant mass concentration of the colloidal solution was maintained. The resulting dependencies are shown in Figure 5.

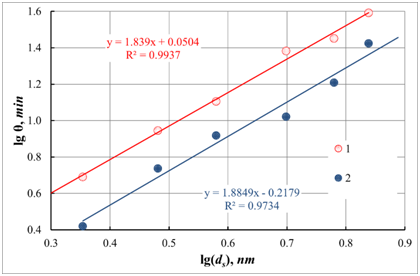
Figure 5 Dependence of gelation time $\theta$ on the size $d_s$ of colloidal particles in sol at different temperatures. The axes in the picture are plotted in logarithmic coordinates. 1 - 80 ; 2- 100 (Note to the equation $y=\lg \theta$ : and $x=\lg d_s$ , $R^2$ - coefficient of determination)

Figure 5 shows that the obtained dependences fit well into a linear correlation. In this case, using relation (25), one can calculate the fractal dimension of the resulting gels. So, for a temperature of 80 ℃, it is $d=1.44\pm 0.06$ , and for a temperature of 100 ℃ - $d=1.41\pm 0.09$ . Under the method developed by us earlier [10], from the data on the fractal dimension, we calculated the mean value of the coordination number for colloidal particles of silicon oxide in the gel formed in these experiments. Accordingly, the calculated values of the coordination numbers ($CN$ ) were: for temperature 80 ℃ - $CN=2.88\pm 0.06$ , and for a temperature of 100 ℃ - $CN=2.82\pm 0.09$ .

Considering the measurement error of the fractal dimension, we can conclude that the structure of the forming gel practically weakly depends on the temperature in the experimental region. Also, it can be seen from the data obtained that an increase in the process temperature leads to the formation of a more delicate gel structure. This phenomenon is associated with an increase in the rate of gelation. Accordingly, it is related to a decrease in the possibility of penetration of sol particles into the inner part of the unit. During the interaction of colloidal particles with each other, the average coordination number of colloidal particles in the aggregate decreases. Also, such small values of the fractal dimension of the formed gels indicate their very delicate structure. The reason for such significant differences in the value of the fractal dimension, in comparison with the literature data, can only be explained by the fact that the published works studied gels that had already been dried and underwent syneresis processes, that is, compaction.

The use of computer simulation techniques makes it possible to obtain the results, which describe well both kinetics and geometry of forming aggregate — the most widespread and like the real state is the model of diffusion-limited aggregation.⁵ An example of diffusion-limited aggregation is the modeling of the concentration dependence of gelling time given in Figure 6. The results are obtained using statistical averaging of gelling time. For comparison, Figure 6 also presents experimental data on the dependence of the gelation time on the concentration of a colloidal solution of silicon oxide SiO₂. Figure 6 presents the comparison of experimental and simulation results. The equation describes both dependencies:

$t_c=a{c}^{-b}$      (26)

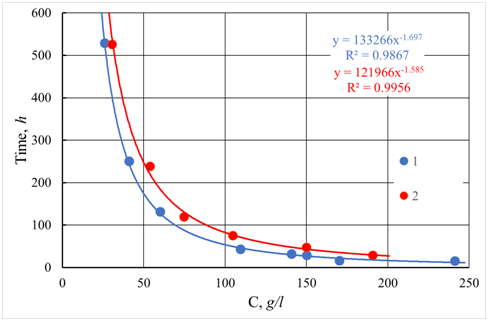
Figure 6 Dependence of gelling time on concentration C. 1 - Experimental data for silica sol with particle size 2.4 nm and pH = 2.2. 2 - Results of computer simulation. (Note to the equation: $y=h$ and $x=C$ ; $R^2$ - coefficient of determination).

The values of parameters b in equation (26) for the experiment (e) and simulation (s) model coincide within the statistical error: $b_e=1.70\pm 0.16$ , $b_s=1.59\pm 0.08$ . By comparing equation (26) to equations (14) and (19), it may be concluded that they coincide by the value of the exponent of power dependence of gelling time on the concentration.¹⁰

The sol-gel transition is a process of sol particle association accompanied by the formation of "an infinite aggregate". Two ways of constructing mathematical models are suggested. The first approach is based on the methods of statistical thermodynamics, and the second one is hydrodynamical. Both methods make it possible to obtain the inter- consistent equations describing the relationship between the gelation time and the macroscopic parameters. As a result of the simulation of the sol-gel process, adequate results were obtained, which make it possible to predict the behavior of the colloidal dispersion in the process of gelation. The study of the obtained models made it possible to reveal the regularities of the gelation process and determine the factors that determine the rate of this process and the structure of the forming gel.

We also carried out experimental verification of the proposed models. We investigated the formation of a primary gel containing all the water that was part of the initial colloidal solution - sol. The critical point is that at the point of gelation, an endless aggregate is formed, but at the same time, only a part of the sol particles participates in its formation. The rest of the particles enter their structure after the point of gelation. Thus, the fractal dimension of an infinite aggregate should increase as its creation is completed, after passing the gelation point. The data obtained showed that an increase in the temperature of the process leads to the formation of a somewhat more delicate structure in the forming gel. Accordingly, an increase in the rate of gelation leads to a decrease in the possibility of penetration of colloidal particles into the interior of the growing aggregate. These restrictions also reduce the average coordination number of particles in the forming aggregate.

Of course, one cannot discount the fact that the theoretical premises proposed above are based on several approximations and assumptions. Therefore, for this reason, specific errors are also possible in assessing specific parameters in such complex systems as colloidal solutions. Under these results, further research in this area should be aimed at finding factors that additionally affect the nature of the sol-gel processes, as well as studying the means and methods of structure formation in the forming gels.

None.

There are no conflicts of interest.

None.

1. Smoluchowski M. Attempt of a mathematical theory of the coagulation kinetics of colloidal solutions. Zeitschrift für Physikalische Chemie. 1917;92:129–168.
2. Schumann TEW. Theoretical aspects of the size distribution of fog particles. QJR Meteorol Soc. 1949;661:95–208.
3. Ziff RM, Stell G. Kinetics of polymer gelation. J Chem Phys. 1980;73(7):3492.
4. Vinokurov LI, Kats AV. Power-law solutions of the kinetic equation for stationary coagulation of aerosols. Proceedings of the USSR Academy of Sciences. Physics of the atmosphere and ocean. 1980;16(6):601–607.
5. Mandelbrot Benoît B. The Fractal Geometry of Nature. San Francisco; 1983.
6. Lifshitz EM, Pitaevskii LP. Physical Kinetics. Course of Theoretical Physics. Pergamon Press; 1981.
7. Kudryavtsev P, Figovsky O. Simulation of Hardening Processes in Silicate Systems. Journal Scientific Israel: Technological Advantages. 2015;17(1–2):122–159.
8. Jullien R. Fractal Aggregates. Comm. Mod. Phys. Pt B. 1987;13(4):177–205.
9. Smirnov BM. Properties of a fractal aggregate. Physics-Uspekhi (Advances in Physical Sciences).1989;32(1):181–182.
10. Kudryavtsev P. Pore System in the Structure of Solid Porous Bodies. Journal Scientific Israel- Technological Advantages. 2019;21(2–3):41–66.