The intense process of deforestation in tropical regions has resulted in the fragmentation of most native forests. The effects of fragmentation on genetic diversity and effective population size of tree species depends in large part on the level of gene flow among remnant populations. The main objective of this study was to use microsatellite loci to investigate the impact of spatial isolation caused by forest fragmentation on pollen and seed flow in a population of the tropical tree Genipa americana. We also investigate the genetic diversity, inbreeding, and spatial genetic structure (SGS) in adults, regenerants, and open-pollinated seeds. In the studied fragment, all adult trees were mapped, sexed, and sampled. We also mapped and sampled regenerants and collected open-pollinated seeds during two reproductive events. Using parentage analysis, we detected a minimum immigration of pollen at 6% and seeds at 4% and pollen and seeds were dispersed in a pattern of isolation by distance. We found variation in female and male fertility, with the largest females mothering more regenerants and the largest males fathering more seeds. We found significant SGS for adults and regenerants; the SGS in adults resulted in regenerants and seeds produced through mating among relatives (20-40%), which explains the inbreeding detected in all samples. Our results indicate genetic connectivity between the fragment and other populations, possibly due to insect pollination and seed dispersal vectors (barochory, hydrochory, and zoochory by mammals). We discuss our results in terms of in and ex situ conservation.

Highlights

1. The population spatial isolation by forest fragmentation not resulted in genetic isolation.
2. Seed and pollen flow can reduce the negative impacts of genetic drift.
3. Pollen and seeds are dispersal in a pattern of isolation by distance.
4. Largest female and male trees generate more descendants.
5. Adults and regenerants are spatially genetic structured.
6. The population can be a source for seed collection for ex situ genetic conservation and environmental reforestation programs.

Keywords: forest fragmentation, gene flow, microsatellite loci, parentage analysis, tropical trees

Tropical forests contain some of the greatest diversity of tree species in the world, making them vital for the maintenance of the planet’s biodiversity. In tropical ecosystems, the diversity of tree species provides habitats and environmental conditions necessary for the survival of thousands of species of animals and plants.¹ As a result of indiscriminate harvesting, the advancement of agriculture, and urban sprawl, these ecosystems are among the most devastated in the world; the destruction of this habitat has become synonymous with species loss.² The survival of tropical species is thus dependent on their ability to persist in fragmented landscapes or isolated nature reserves.

Pollen and seed flow are among the most important factors that influence the genetic structure of tree species.^3-5 Forest fragmentation spatially isolates the remaining stands which may result in decreased pollen and seed flow among tree populations.^3,6-9 Furthermore, genetic diversity may be reduced due to restricted gene flow, genetic drift, and increased rates of correlated mating and mating among related trees.^7,10 Thus, mitigating the genetic effects of forest fragmentation depends critically on gene flow; if limited, it can be highly detrimental in the long term for remaining populations¹¹ because the genetic connectivity conferred by gene flow maintains the levels of genetic diversity⁴ and the effective size of spatially isolated populations.^7,9 As such, there has been an increased interest in quantifying the consequences of forest fragmentation on plant population genetics. Restricted gene flow and loss of genetic diversity resulting from forest fragmentation has been reported in many studies on tree species.^7,12-17

Molecular genetic studies have become an integral part of forest fragmentation analyses as they provide crucial information for a detailed understanding of the impact of fragmentation on remaining populations. This, in turn, allows for the definition of appropriate strategies for in situ and ex situ conservation, as well as seed collection strategies for environmental restoration.¹⁴ Parentage analysis based on data from microsatellite loci is a direct method for inferring contemporary gene flow mediated by pollen and seeds in plants, allowing us to estimate pollen and seed immigration, dispersal distance and patterns, pollination neighbor area, variations in male and female fertility, and the out crossing rate in a population, among other parameters ^5,18-20. Such studies based on samples from regenerants, such as seedlings and juveniles, allow us to estimate the realized pollen and seed flow and dispersal patterns, and based on open pollinated seeds, the effective pollen dispersal distance.^18,21

In this context, we investigated a small Genipa Americana L. (Rubiacea) population to determine the effects of spatial isolation on genetic diversity, inbreeding, spatial genetic structure (SGS), pollen and seed flow and dispersal distance and patterns. There is no information about distance pollen and seed dispersal patterns in the species, which are important factors in predicting the dynamics of plant populations and are the basis for designating conservation strategies in fragmented environments.²² The analysis focused on microsatellite markers in order to propose strategies for conservation of the studied remnant. We specifically answered the following questions:

1. Has the spatial isolation of the population due to forest fragmentation resulted in pollen and seed flow isolation?
2. What are the distance and patterns of pollen and seed dispersal within the forest fragment?
3. Are the distance and patterns of effective pollen dispersal different between reproductive events?
4. Are there differences in the levels of genetic diversity, inbreeding, and SGS in the pre-fragmentation (adults) and post-fragmentation generations (seeds and regenerants)?

Study Species

Genipa Americana is a slow growing, semi-deciduous, dioecious tree, that is found throughout tropical America.²³ Adult individuals can reach 8 to 14 m in height and up to 60 cm in diameter at breast height (dbh). Pollination occurs by bees, such as Bombus morio, Epicharis rustica flava, Apis mellifera, Trigona truculent, Augochlora sp, and Tetragonisca augustula.^23-25 Seed dispersal occurs by barochory, hydrochory, and zoochory by mammals, such as the monkeys Cebus epetku and Callicebus personatus.^23-25 Female trees produce large quantities of viable seeds annually (> 100 seeds per fruit) and the species presents a high population density in the study area (> 1 tree/ha).

Study Site

The study was conducted in the Mata da Figueira (22º16' S, 47º11' W, mean altitude 600 m), a small forest fragment (7.2 ha) of riparian semi-deciduous, mesophytic plateau forest (Figure 1), in São Paulo State, Brazil. Currently, the forest is surrounded by agriculture (sugarcane, Eucalyptus) and pasture. The soils are classified as flood plain types LVa and LE (hydromorphic), and are subject to periodic flooding. The climate is Cwa and characterized as humid and mesothermal, with mean monthly temperatures varying from 14.3 to 24.6º C [26].

Figure 1 Spatial distribution of adult trees and regenerants of Genipa americana in the Mata da Figueira.

Sampling

All 187 adult trees (density of 25 trees/ha) found in the forest fragment were sampled (cambial tissue), mapped (using a GPS-III, USA), sexed, and measured for dbh (11-70 cm, mean of 31.2±12.4 cm ±standard deviation, SD). Based on their dbh, it is likely that many of the adult trees are remnants of the pre-fragmentation population as fragmentation occurred about 30 years ago. Female and male trees were identified during the fruiting period, creating a sample of 138 males and 49 females. We also sampled (leaf tissue), mapped, and measured the total height (H) of 143 regenerants (0.4-10 m, mean ± SD: 2.4 ± 2.2 m). The regenerants represent individuals that were established post-fragmentation. Additionally, open-pollinated seeds were collected from 13 seed trees during the reproductive event in 2010 and 12 seed trees during the reproductive event in 2011. We collected four fruits per tree, one at each of the cardinal points (North, South, East, and West). Seeds were germinated separately by fruit and seed tree and 15 to 25 seeds per fruit were obtained for genetic analysis, totalling 936 and 967 seeds in 2010 and 2011, respectively.

Microsatellite Genotyping

DNA was extracted from the cambial tissue of adult trees using the method described by.²⁷ From regenerants and germinated seeds, DNA was extracted from leaf tissue using the method described by.²⁸ Six primers developed for the species were used in the study: Gam01, Gam02, Gam06, Gam11, Gam24, and Gam41.²⁹ These primers present Mendelian segregation and are not linked.³⁰ In the statistical analysis, we only used individuals genotyped for at least five loci (187 adults, 108 regenerants, 870 seeds from 2010, and 956 seeds from 2011).

Analysis of Genetic Diversity and Inbreeding

Genetic diversity for adults, regenerants, and seeds from the two reproductive events were averaged across all loci for the following indexes: allelic richness$(R)$ , observed$(H_o)$ and expected heterozygosity according to Hardy-Weinberg equilibrium$(H_e)$ . The presence of private alleles was determined by comparing all sample types: adults, regenerants, and seeds from 2010 and 2011. The presence of inbreeding was assessed using the fixation index, $F=1-(H_o/H_e)$  ³¹. The statistical significance of $(F)$  values was tested using 1,000 Monte Carlo permutations of alleles between individuals. All analyses were performed using the FSTAT program.³² Because each plant within a family receives at least one maternal allele, the fixation index within families$(F)$ can be biased due to an overestimation of gene frequencies of maternal alleles in comparison to the true gene frequencies of these alleles in the parental population. An overestimation of gene frequencies results in an overestimation of the expected heterozygosity under Hardy-Weinberg equilibrium $H_e=1-{\displaystyle {\sum }_{i=1}^k{p}_i^2}$ , where $p_i^2$  is the frequency of the $i-th$  allele ³¹, because alleles with a high frequency contribute more to the estimate of $H_e$  than alleles with low frequencies. Thus,$H_e$ was estimated using the gene frequencies of the pollen parents, calculated using MLTR.³³ The observed heterozygosity$(H_o)$  was calculated by family with the FSTAT program.³² The frequency of null alleles$(Null)$ was estimated for adults, regenerants, and seeds using the INEST program.³⁴

Analysis of Spatial Genetic Structure (SGS)

We assessed the SGS for adults and regenerants separately based on the co ancestry coefficient $({\theta }_{xy})$  between pairs of trees, as described in,³⁵ for ten distance classes of 25m (ranging from 0 to 250m). To obtain the statistical significance of the co ancestry coefficient ${\theta }_{xy}$ we compared the limits of the confidence interval at 95% probability (95% CI) of the mean ${\theta }_{xy}$  for each distance class, calculated by 1,000 Monte Carlo permutations of individuals between distance classes. The co ancestry coefficient and the standard error were estimated using the SPAGEDI 1.3 program.³⁶ To compare SGS between adults and regenerants, we calculated the $Sp$  statistic:³⁷ $Sp=-b_k/(1-{\theta }_1)$ , where ${\theta }_1$  is the co ancestry coefficient calculated between all pairs of individuals in the first distance class, and $b_k$ is the regression slope of the coancestry coefficient on the logarithm of spatial distance between individuals (0-150m). To test the statistical significance of the SGS, the spatial position of each individual was permutated 1,000 times to obtain the frequency distribution of $b_k$  under the null hypothesis that ${\theta }_1$  and in$(d_{xy})$  are not correlated.

Analysis of Variance Effective Population Size of Adults

We calculated the variance effective population size $(N_e)$ of the adults following.³⁸ The sample variance in gene frequencies between generations from genetic drift in a population is${\sigma }_{p_i}^2=p_i(1-p_i)\Theta$ , where $p_i$  is the frequency of i-th allele and $\Theta$  is the group co ancestry of the population. The sample variance in gene frequencies of a population without inbreeding and relatedness is ${\sigma }_{p_i}^2=p_i(1-p_i)/2N_e$ . Thus, $N_e$  can be estimated using a reference population in which there is no inbreeding and relatedness, making both equations for ${\sigma }_{p_i}^2$  equal, one in a population with inbreeding and relatedness among individuals and the other without:

$p_i(1-p_i)\Theta =\frac{p_i(1-p_i)}{2N_e}$ ,

$N_e=\frac{p_i(1-p_i)}{2p_i(1-p_1)\Theta }$ ,

Thus, $N_e=0.5/\Theta$  .
The mean group co ancestry$(\Theta )$ was estimated as $\Theta ={\displaystyle {\sum }_{x=1}^{n_f}{\displaystyle {\sum }_{y=1}^{n_f}{\theta }_f/4n_f^2+{\displaystyle {\sum }_{x=1}^{n_m}{\displaystyle {\sum }_{}^{n_m^{}}{\theta }_m/4n_m^2+{\displaystyle {\sum }_{x=1}^{n_f}{\displaystyle {\sum }_{y=1}^{n_m}{\theta }_{fm}}}/2n_f{n}_m}}}}$ , where ${\theta }_f$ ,${\theta }_m$  and ${\theta }_{fm}$  are the co ancestry coefficient between females, males, and females and males, respectively; and $n_f$  and $n_m$  are the number of female and male trees ³⁹. The pair wise co ancestry coefficients were also calculated using SPAGEDI. We estimated the relation between $N_e$  and the number of sampled individuals$(n)$ as$N_e/n$ .

Parentage Analysis

The parentage analysis of regenerants and seeds from reproductive events in 2010 and 2011 were carried out using CERVUS 3.0.⁴⁰ This program was also used to determine the theoretical power of non-exclusion of the parent pair$(P_p)$ , and combined probability of genetic identity$(Q_i)$ , using only the adults in the calculations. The cryptic gene flow for regenerants $(C_{gf})$ , or the probability of finding a mother and father within the population when the true male and female parents are outside of the population, was calculated as:$C_{gf}=1-{(1-P_p)}^n$ , where n is the number of candidates for father and mother.⁴¹ The cryptic pollen flow of open-pollinated seeds, or the probability of finding a father within the population when the true father is outside the population, was calculated from the probability of detecting immigrant pollen grains $(d)$ , given a local population of candidate pollen donors:$({\Theta }_{mf})$  ^.42 The parameter $d$  was calculated as $d=1-{\displaystyle {\sum }_{i=1}^t{h}_i}$ , using the Pollen Flow program,⁴² where $h_i$  is the frequency of local pollen grain $i$  in the background population (the idealized population in which all reproductive trees could pollinate any of the seed trees of the sampled population), and $t$  is the total number of distinct local pollen grains.⁴³ The parentage analysis was based on the multilocus genotype of 187 adult trees, including 49 females and 138 males, 108 regenerants, and 870 and 956 open-pollinated seeds collected in 2010 and 2011, respectively. To determine the putative mother and father of the regenerants, all female and male trees were considered candidates for maternal and paternal parents. To determine the putative fathers of the open-pollinated seeds, only male trees were included in the analysis. The paternity and maternity of the regenerants and the paternity of the open-pollinated seeds was determined based on a simple parentage exclusion test, and did not include regenerants and seeds genotyped for less than five loci. The parentage analysis was estimated using only the estimated allelic frequencies for adults, as suggested by.⁴⁴ Regenerants and seeds with more than one possible parent pair were considered as non-immigrants, but excluded from the estimation of pollen and seed dispersal distance to avoid bias in the estimates. To confirm if the assigned parents of regenerants were true relatives, we used the SPAGEDI to estimate the co ancestry coefficient between regenerants and their putative mothers and regenerants and putative fathers. The expected co ancestry between an offspring and mother or father is 0.25. We also used SPAGEDI to estimate the co ancestry between the assigned mother and father $({\Theta }_{mf})$ of regenerants and seeds $({\Theta }_{mf})$ . A value of ${\Theta }_{mf}\ge 0.125$  was assumed to indicate mating among relatives, with the out crossing rate between relatives estimated as: $t_r=n_r/n$ , where $n_r$  is the number of regenerants and seeds originating from mating among related individuals, and $n$  is the number of sampled genotypes for at least five loci. For regenerate and seeds assigned as originating from mating among relatives, we used SPAGEDI to estimate the fixation index $(F_r)$ .

Seed flow $(b)$  was calculated as the proportion of regenerate that had no determined female and male parents within the population, while pollen flow was the proportion of regenerate that had no determined male parent within the population: $b=n_i/n$ , where is $n_i$  is the number of immigrant seeds or pollen and $n$  is the total number of regenerants sampled. For open pollinated seeds, the pollen flow was calculated as the proportion of seeds that had no determined pollen parent within the population in relation to total seeds sampled. For these seeds, the estimate of the non-biased immigration rate of pollen was calculated from the probability of detecting one immigrant pollen grain $(d)$  in paternity analysis, based on a local population of candidate pollen donors: $m=b/d$  ^.42 The standard error of pollen immigration $[SE(m)]$  was estimated as $SE(m)=\sqrt{(1-b)/(bn)}$  ^.43 As all regenerants and male and female adults sampled were mapped (coordinates x and y), the mean, median, minimum, maximum distance and standard deviation $(SD)$ of seed dispersal, were calculated as the distance between regenerants and their putative mothers, determined by parentage analysis. The mean, median, minimum, maximum distance and standard deviation of pollen dispersal was calculated as the distance between the mother and the father, as determined by paternity analysis. The distance of pollen and seed dispersal $(D)$  was calculated by the Euclidean distance between two points. To determine if reproductive success was a function of the distance between the female and male trees, we compared the frequency distribution of the effective pollen dispersal distances from 2010 and 2011 with the frequency distribution of the distances between male and female trees using the Kolmogorov-Smirnov test.⁴⁵ This test was also used to verify if the pattern of dispersal of pollen in the reproductive event of 2010 was different than in 2011. The effective pollination neighbor area $(A_{ep})$  was calculated assuming a circular area around a central seed-tree as $A_{ep}=2\pi {\sigma }_p^2$  ^,46 where ${\sigma }_p^2$  is the axial variance of pollen dispersal, which corresponds to the area where 63% of pollen donors who crossed with a seed tree are located. The Spearman ranking coefficient of correlation $(r)$ , estimated with the SAS program.⁴⁷ was used to verify if the distance among the assigned parents is associated with the frequency of generated seeds or regenerants. We also used $(P_p=0.00468)$  to verify whether fertility of female and male trees, represented by the frequency of regenerants or seeds, was associated with dbh.

Genetic Diversity and Fixation Index

From the total sample of 2,121 individuals (adults, regenerants, and seeds from 2010 and 2011), we detected 72 alleles. The total number of alleles $(k)$  ranged among samples from 38 to 62 alleles (Table 1). Comparing adults and regenerants, and adults and seeds from 2010 and 2011, 18 alleles were private to regenerants, 5 were private to seeds of 2010, and 10 to seeds of 2011, suggesting pollen and/or seed immigration. Based on the t-test, allelic richness $(R)$  was significantly higher (P= 0.006) in adults than regenerants. The fixation index $(F)$  was significantly greater than zero for all samples (ranging from 0.14 to 0.32), suggesting inbreeding in all generations. Null alleles $(Null)$  were detected at low frequencies in all loci of adults, regenerants, and seeds of 2010 and 2011, ranging among loci and samples from 0.001 to 0.133 (data not show). The low frequency suggests that null alleles did not significantly bias our estimates of $F$ and parentage analysis. The $F$ value was significantly lower in adults than regenerants (P= 0.017), seeds from 2010 (P= 0.050), and seeds from 2011 (P= 0.022).

Intrapopulation Spatial Genetic Structure (SGS)

We found significant SGS up to approximately 125m for adults and 75m for regenerants, with values falling to non-significant or significantly (P< 0.05) lower than zero in the other distance classes; a typical pattern of isolation by distance (Figure 2). The co ancestry coefficient $({\theta }_1)$  estimated in the first distance class (0-25m) was significantly higher than zero in adults (0.0162, P< 0.01) and regenerants (0.0327, P< 0.01). The regression slope for the co ancestry coefficient between pairs of individuals on the logarithm of spatial distance between individuals $(b_k)$  was significantly lower (P< 0.01) than zero in adults (mean ± standard error: -0.0054 ± 0.0031) and regenerants (-0.0152 ± 0.0073), which confirms the dispersal pattern of isolation by distance. The intensity of SGS was lower in adults (Sp = 0.0060) than regenerants (Sp = 0.0157).

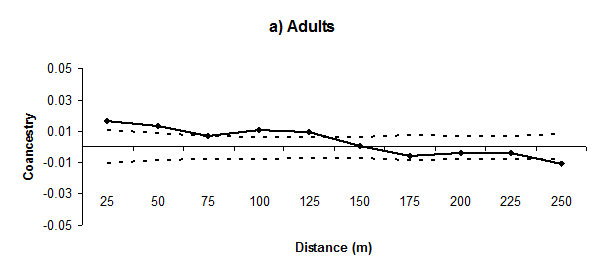
Figure 2 Correlograms of the mean co ancestry coefficient $({\theta }_{xy})$ for eleven distance classes of Genipa americana adults (a) and regenerants (b). The continuous line represents the mean estimated coancestry coefficient. The dashed lines represent the confidence interval at 95% of the distribution of the mean${\theta }_{xy}$ .

Effective Population Size for Adults

The mean pair wise co ancestry coefficient among pair wise females$({\Theta }_f)$ , males $({\Theta }_m)$ , and males and females $({\Theta }_{fm})$  was 0.0028, 0.0494, and 0.0001, respectively, resulting in a low group co ancestry $(\Theta =0.0122)$ . The 187 adult trees correspond to an effective population size of 41 unrelated and non-inbred individuals$(N_e/N=41/187=0.22)$ .

Realized Pollen and Seed Flow and Dispersal Distance and Patterns for Regenerants

The combined probability of genetic identity for adults $(Q_i=0.0000498)$  and the combined non-exclusion probability of the parent pair$(P_p=0.00468)$  were low, indicating that the genotypes are unique and that the set of loci used is sufficient to determine parentage of the regenerants. Of the 108 regenerants, at least one maternal tree was found for 104 individuals and a paternal tree for 101 individuals, indicating a limited rate of realized seed (0.04) and pollen (0.06) flow (Table 2). However, the estimate of cryptic seed and pollen flow $(C_{gf})$  was 0.20 and 0.48, respectively, suggesting that some regenerants may have been incorrectly assigned parentage within the fragment. To confirm the maternal and paternal assignments, we estimated the mean pair wise co ancestry coefficient between assigned mothers and regenerants (0.289 ± 0.166, ±standard deviation) and fathers and regenerants (0.332 ± 0.145, ±standard deviation). These values are higher than the minimum expected value between parents and offspring (0.25), suggesting that the assigned parents are correct. The regenerants with assigned parentage originated from 26 of the 49 female trees (53%) and 43 of the 138 male trees (31%). No significant association (P> 0.05) was detected between dbh of females determined as mother trees and frequency of regenerants produced $(r=0.09)$ , nor between the dbh of males determined as putative fathers and frequency of regenerants produced $(r=0.00)$ .However, when the frequencies of adults were grouped within four dbh classes (20, 30, 40, and > 40cm), the coefficient of correlation $(r=0.93,P<0.05)$ detected that larger females produced more regenerants. In contrast, the dbh of the males is not associated with fertility$(r=0.18,P>0.05)$ . Assuming $(m)$  as an indicator of mating among related parents $({\Theta }_r)$ , we found 43 related parent pairs assigned by parentage analysis and a rate of mating among relatives of 40%. The mean co ancestry between related parents (0.265) suggests that they are likely to be full-sibs (0.25). However, the estimate of the fixation index of inbred regenerants $(F_r=0.40)$  was higher than that expected (0.265). The mean realized seed dispersal distance (203 m) was similar to the mean realized pollen dispersal distance (213 m); however, both the median seed (180 m) and pollen (196 m) dispersal distances were lower than the mean, suggesting an isolation by distance pattern of gene dispersal (Table 2, Figure 3). Using a Spearman ranking correlation, the correlation $(r)$  between distance from the assigned mother tree and regenerants (-0.71, P< 0.05) and distance between the assigned mother and father and regenerants (-0.78, P< 0.05) were significantly negative and high. These results indicate that seeds were established near to the mother and mating generally occurred between near neighbor trees. Using the Kolmogorov-Smirnov test, the comparison between the frequency distribution curve of realized pollen dispersal and the frequency distribution curve of the distance between all female and male trees suggests that these are not statistically different ($D=0.034;P>0.05$ , Figure 3). Thus, the distance between males and females explains the realized pollen dispersal.

Figure 3 Realized pollen and seed dispersal distance (a), and effective pollen dispersal distance (b) for the reproductive events in 2010 and 2011.

Effective Pollen Flow, Dispersal and Pattern For Open-Pollinated Seeds

Of the 870 and 956 genotyped seeds sampled from the reproductive events in 2010 and 2011, 63 and 256 seeds, respectively, were not assigned to any male within the forest fragment, indicating a pollen immigration rate $(b)$  of 0.07 and 0.27, respectively (Table 2). Of the remaining 803 and 700 seeds from 2010 and 2011, 700 and 550 seeds were assigned to a single male tree as pollen donor within the forest fragment. Of the 138 identified male trees, 97 (70%) produced seeds in 2010 and 87 (63%) in 2011. However, the mean probability that an immigrant pollen grain has a detectable father genotype inside the fragment $(C_{gf})$  was 0.508 for seeds from 2010 and 0.766 for seeds from 2011, resulting in a mean cryptic pollen flow $(C_{gf})$  of 0.49 and 0.23, respectively. These results indicate that $C_{gf}$  may have biased the pollen flow estimates found using the CERVUS. The mean unbiased rate of pollen flow into the fragment $(m)$ in seed trees from 2010 was 0.14 and a seed of 2011 was 0.35. Using a Spearman correlation $(r=0.59,P<0.05)$ , no significant association (P> 0.05) was detected between the dbh of the assigned fathers and the frequency of seeds they produced in 2010 (0.12) and 2011 (0.11). However, when the frequencies of seeds were grouped in four dbh classes of the putative fathers (20, 30, 40, and > 40 cm), the correlation detected that larger males generated more seeds in both 2010 $(r=0.60,P<0.05)$  and 2011 $(r=0.59,P<0.05)$ .

Assuming $(D=0.041;P=0.250)$  as an indicator of mating among related parents $({\Theta }_r)$ , the mean co ancestry between the seed trees and assigned fathers in 2010 was 0.236 and in 2011 was 0.271, indicating a rate of mating among relatives of 0.38 and 0.28, respectively. The fixation index of inbred seeds $(F_r)$  from 2010 (0.21) and 2011 (0.36) was similar to that expected in 2010 (0.236) and lower than expected in 2011 (0.271). The mean distance of pollen dispersal in 2010 (207 m) and 2011 (166 m) was lower than the median (200 and 157 m, respectively), again indicating a pattern of isolation by distance. Similarly, the correlation coefficient $(r)$  for the distance between seed trees and putative fathers was significantly negative (P< 0.05) and high in 2010 (-0.86) and 2011 (-0.90), indicating that mating occurred predominantly among female and male trees located in close proximity. The comparison between the distribution curve of frequencies of pollen dispersal and the frequency curve of distance between the female and male trees, using the Kolmogorov-Smirnov test, was not statistically different in 2010 $(D=0.041;P=0.250)$ , but was statistically different in 2011 ($(N_e=41)$ , Figure 3b). Therefore, the distance between female and male trees explains the pollen dispersal pattern in the population in 2010, but not in 2011. Furthermore, the comparison between the frequency distribution curve of pollen dispersal in 2010 and 2011 indicate that these are statistically different ($D=0.179;P<0.001$ , Figure 3b). The effective pollination neighbor area$(A_{ep})$  estimated for regenerants was higher (11.2 ha) than that estimated for the seeds from 2010 (9.2 ha) and 2011 (5.1 ha).

Genetic Diversity and Inbreeding

The studied population presents higher allelic richness $(R)$  and lower fixation index $(F)$  in adults than regenerants. Furthermore, although inbreeding was detected in all samples, it was lower in adults than in the post-fragmentation ontogenetic stages (regenerants and seeds). These results suggest that not only did regenerants suffer a decrease in genetic diversity likely due to genetic drift, but mating among relatives also produced more inbreeding in post fragmentation generations than the pre-fragmentation stage (adults). Increases in inbreeding in post-fragmentation stages have been detected in other tree species, such as Fagus sylvatica,⁴⁸ Araucaria angustifolia,⁴⁹ and Copaifera langsdorffii.¹⁵ However, the significantly lower level of inbreeding in adults than subsequent generations suggests selection against inbred individuals between early developmental and adult life stages. Thus, due to the fact that inbreeding can result in inbreeding depression, leading to lower survival of inbred individuals, the observed inbreeding in post-fragmentation generations will likely diminish when the regenerants reach adulthood. Inbreeding depression has been well documented in tree species,^50-52 and likely occurs in G. americana.

Spatial Genetic Structure (SGS)

The spatial distribution of adult genotypes (125 m) in the fragment reflects historic seed and pollen dispersal, while the regenerants (75 m) represent the movement of genes in the recent past (< 30 years). Our results for SGS suggest that seeds were dispersed and established near to mother trees, in a typical dispersal pattern of isolation by distance (Figure 2). The regeneration of seeds near to the mother tree due to short distance seed dispersal by barochory is likely the main cause of SGS. The high frequency of mating between proximal male and female trees may also contribute to SGS due to the fact that seed and pollen dispersal distances measured in regenerants were similar (Table 2). However, the $({\Theta }_{fm}=0.0001)$  statistic indicates that the extent of SGS is lower in adults (0.0060) than regenerants (0.0157), with a lower mean pair wise co ancestry coefficient in the first distance class (0-25 m) for adults $({\theta }_1=0.0162)$ than regenerants $({\theta }_1=0.0327)$ , suggesting an increase in relatedness in new generations of the population. The higher co ancestry among regenerants may be explained by the fact that they represent recent seed and pollen dispersal and adults represent historical dispersal that occurred more than 30 years ago. Therefore, stochastic factors such as predation, disease, and random mortality, and deterministic factors such as natural selection, may influence the difference between SGS across life stages. Similar results were observed in other tropical tree populations occurring in forest fragments, including Myracroduon urundeuva,¹² C. langsdorffii,¹⁴ and Castanopsis sclerophylla.¹⁷

Effective Population Size

The low mean co ancestry coefficient estimated between male and female trees $({\Theta }_{fm}=0.0001)$  indicates that if mating is random, low levels of inbreeding would be expected in descent generations (juveniles and seeds) from mating among relatives. However, mating was not random as it occurred at high frequencies between near-neighbor individuals that are related due to SGS, thus resulting in substantial mating among relatives (minimum $t_r$  of 0.28). Using the MLTR program, we also found high rates of mating among relatives $\left(t_m-t_s\right)$  for seeds from 2010 (0.24) and 2011 (0.37).⁵³ Thus, non-random mating, resulting in out crossing among related individuals, can explain these levels of inbreeding. Due to inbreeding in the adult population $(F=0.14)$ and SGS, the effective population size of the adults was lower than the census number$(N_e/N=0.22)$ . Consequently, the reproductive population has a low effective population size $(N_e=41)$ . This value is much lower than that required (50) for short term genetic conservation.⁵⁴ The $({\Theta }_r)$  can be increased by gene flow because immigrant seeds and pollen introduce genotypes and alleles from individuals that are likely unrelated to those in the present population, thus decreasing relatedness. Genetic interconnection with other populations through gene flow is therefore necessary to increase the $N_e$ of future generations of this population for in situ conservation.

Gene Flow

The studied G. americana population is not genetically isolated due to both pollen (6-27%) and seed flow (4%) from outside populations. Furthermore, these values are likely underestimates due to the high probability of cryptic gene flow. Gene flow through pollen and seeds results in the introduction of new alleles and genotypes into populations, as detected here in the regenerants and seeds. It is a critical factor in increasing genetic diversity and effective population size, which can improve the evolutionary potential of the population, since these immigrant allele and genotypes are likely not identical by descent to the receiving population. The immigration of pollen and seeds into the study area can be explained by the existence of other populations located along the river (at a distance of approximately 1.5 km) and the fact that this species is pollinated mostly by bees, which have the potential to transport nectar and pollen over long distances (up to 2 km).^55,56

Our results also show lower levels of seed than pollen flow and annual variation in pollen flow. Lower seed than pollen immigration in tree populations occurring in forest fragments has been reported in other studies with tropical tree species.^3,7 Thus, seed immigration in general is more restricted than pollen immigration in forest fragment populations.

Distance and Patterns of Realized Seed Dispersal

Our results showed a high frequency of seed dispersal at short distances from the maternal tree (mean of 203 m), in a typical pattern of isolation by distance (IBD): 58% of seeds were dispersed up to 200 m, although the maximum dispersal distance reached up to 547 m (Table 2). Besides seed dispersal by barochory, G. americana seeds are also dispersed by monkeys,²⁵ bats, and some rodents.²³ Our results suggest that these vectors disperse seeds in close proximity to the seed trees, which explains the significant SGS detected in both adults and regenerants of the population. The seeds may also be dispersed by hydrochory, due to the occurrence of floods in the populations along the Mogi Guaçú River during the rainy season,²⁴ which may also explain seed immigration. Seed dispersal following the IBD pattern seems to be consistent across several tropical tree species.

Distance and Patterns of Pollen Dispersal

The estimated pollen dispersal distance was different between reproductive events. The mean pollen dispersal distance was similar between regenerants (213 m) and seeds from 2010 (207 m), but different from the 2011 seeds (166 m). The Kolmogorov-Smirnov test also showed that the pattern of pollen dispersal was different between the studied reproductive events. The effective pollination neighbor area $(A_{ep})$ was also higher in regenerants (11.2 ha) and seeds of 2010 (9.2 ha) than seeds from 2011 (5.1 ha). The pollen dispersal distance and $A_{ep}$  are obviously underestimated due to the rate of pollen immigration from outside the population, especially for the reproductive event in 2011 (35%). The difference between the pattern of realized pollen dispersal in the regenerants and seeds from 2011 may be explained by stochastic factors, such as predation and mortality, and deterministic factors, such as natural selection eliminating inbred individuals. The difference in the pattern of effective pollen dispersal between seeds in 2010 and 2011 could be explained by the individual annual variation in flowering penology between male and female trees, behavior of pollinators, deterministic factors, and/or all of these factors combined.

The pollen dispersal pattern identified in the regenerants and seeds tended toward IBD, since the mean pollen dispersal distance was always lower than the median and there is a strong association between the distance frequency among maternal and paternal trees. This pattern of pollen dispersal is common in high density, animal pollinated tropical tree species.^3,7 Thus, mating is not random and in general occurs between near neighbor trees. This pollen dispersal pattern, associated with SGS in the adults, results in mating among related individuals (28-40%) and can explain the inbreeding $(F_r)$  detected in the regenerants (0.40) and seeds from 2010 (0.21) and 2011 (0.36).

The coefficient of inbreeding generated by mating among relatives is equal to the co ancestry coefficient between crossed parents.³⁹ The mean co ancestry coefficients between the maternal and paternal trees identified as related parents $({\Theta }_r)$  of the regenerants (0.27) and seeds from 2010 (0.24) and 2011 (0.27), were similar to that expected for full-sibs (0.25), but different from$F_r$ . The difference between the observed $(F_r)$  and expected (${\Theta }_r$ ) inbreeding likely occurred because inbreeding was not assessed using genealogical analysis of the pedigree of the parents, but estimated using genetic markers. Estimations of inbreeding and relatedness using genetic markers is not easy because their accuracy is affected by polymorphism of the loci in terms of number of loci, number of alleles, and gene frequencies.⁵⁷ The indices $F_r$  and ${\Theta }_r$  were estimated from only six microsatellite loci and are therefore subject to plant genome sampling errors.

Variation in Male and Female Fertility

Our results showed that more regenerants originated from females with higher dbh and more seeds from the two reproductive events were produced by males with higher dbh. It is possible that the female trees with larger dbh produce more fruits and males with larger dbh produce more flowers, thus increasing the likelihood that offspring of the largest female trees become established in the population and large male trees fertilize more female trees. The effect of dbh on male fertility may be associated with the fact that larger tree canopies provide insects with easier access to the flowers.⁵⁸ The increased male reproductive success of larger trees has also been detected in other studies on tree species.^41,59

Implications for Conservation Genetics

Genipa americanais a tropical species that is under threat of extinction and analyses of pollen and seed dispersal are crucial in developing strategies aimed at the in situ and ex situ conservation of the species. Our results indicate that while the population is spatially isolated, it is not genetically isolated. We found immigration of seeds and pollen, which may help reduce the negative impacts of genetic drift, increase the genetic diversity through immigration of new alleles and genotypes, and consequently increase the effective population size. Thus, our results suggest that this population may be a source for seed collection for ex situ genetic conservation and environmental reforestation programs. To reduce the likelihood of seed collection from related female trees, we suggest that seeds are collected from trees located at least 125 m apart, which is the maximum distance of significant SGS for adults. However, this will not avoid collection of seeds from related male trees, due to the fact that a male tree may fertilize many different seed trees, resulting in paternal half-sibs among the progeny arrays. Thus, seed must be also collected in other populations, to increase the effective size of progeny arrays.

This study was supported by the Fundação de Amparo à Pesquisa do Estado da São Paulo (FAPESP; 2010/19613-4) and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq; 473677/2010-5). Ricardo O. Manoel would like to thank FAPESP for a PhD fellowship (scholarship nº 2011/01518-8). Research fellowships were provided by CNPq for Alexandre M. Sebbenn, Enes Furlani Júnior, Mário LT. Moraes, and Miguel L.M. Freitas. Finally, we thank Dr. Evelyn Nimmo for editing the English of the manuscript.

Author declare that there is no conflict of interest.

1. Primack RB, Rodrigues E. Biologia da conservação. Londrina: Planta. 2001.
2. Laurance W. Big trees in trouble: How the mighty are falling. New Science. 2012;39:39–41.
3. Dick CW, Hardy OJ, Jones FA, et al. Spatial scales of pollen and seed-mediated gene flow in tropical rain forest trees. Tropical Plant Biology. 2008;1(1):20–33.
4. Sork VL, Smouse PE. Genetic analysis of landscape connectivity in tree populations. Landscape Ecology. 2006;21(6):821–836.
5. Ellstrand NC. Is gene flow the most important evolutionary force in plants? American Journal of Botany. 2014;101(5):737–753.
6. Braga AC, Collevatti RG. Temporal variation in pollen dispersal and breeding structure in a bee-pollinated Neotropical tree. Heredity. 2011;106:911–919.
7. Degen B, Sebbenn AM. Genetic and tropical forest. In: Pancel L, Kölh M, editors. Tropical Forestry Handbook. 2nd ed. Germany, Berlin Heidelberg: Springer Verlag; 2014.
8. Lowe AJ, Cavers S, Boshier D, et al. The resilience of forest fragmentation genetics—no longer a paradox—we were just looking in the wrong place. Heredity. 2015;115:97–99.
9. Tambarussi EV, Boshier D, Vencovsky R, et al. Paternity analysis reveals significant isolation and near neighbor pollen dispersal in small Cariniana legalis Mart. Kuntze populations in the Brazilian Atlantic Forest. Ecology and Evolution. 2015;5:5588–5600.
10. Cuartas-Hernández S, Núñez-Farfán J, Smouse PE. Restricted pollen flow of Dieffenbachia Seguine populations in fragmented and continuous tropical forest. Heredity. 2010;105(2):197–204.
11. Bacles CFE, Ennos RA. Paternity analysis of pollen-mediated gene flow for Fraxinus excelsior L. in a chronically fragmented landscape. Heredity. 2008;101(4):368–380.
12. Gaino APSC, Silva AM, Moraes MA, et al. Understanding the effects of isolation on seed and pollen flow, spatial genetic structure and effective population size of the delicious tropical tree species Myracrodruon urundeuva. Conservation Genetics. 2010;11:1631–1643.
13. Lander TA, Boshier DH, Harris SA. Fragmented but not isolated: Contribution of single trees, small patches and long distance pollen flow to genetic connectivity for Gomortega keule, and endangered tree. Biological Conservation. 2010;143:2383–2590.
14. Sebbenn AM, Carvalho ACM, Freitas MLM, et al. Low levels of realized seed and pollen gene flow and strong spatial genetic structure in a small, isolated and fragmented population of the tropical tree Copaifera langsdorffii Desf. Heredity. 2011;106(1):134–145.
15. Manoel RO, Alves P, Dourado C, et al. Contemporary pollen flow, mating patterns and effective population size inferred from paternity analysis in a small fragmented population of the Neotropical tree Copaifera langsdorffii Desf. (Leguminosae-Caesalpinioideae). Conservation Genetics. 2012;13(3):613–623.
16. Millar MA, Coates DJ, Byrne M. Genetic connectivity and diversity in inselberg populations of Acacia woodmaniorum, a rare endemic of the Yilgarn Craton banded iron formations. Heredity. 2013;111(5):437–444.
17. Wang R, Compton SG, Shi Y, et al. Fragmentation reduces regional-scale spatial genetic structure in a wind-pollinated tree because genetic barriers are removed. Ecology and Evolution. 2012;2(9):2250–2261.
18. Burczyk J, Difazio SP, Adams WT. Gene flow in forest trees: how far do genes really travel. Forest Genetics. 2004;11(3–4):179–192.
19. Ashley MV. Plant parentage, pollination, and dispersal: How DNA microsatellites have altered the landscape.Critical Review Plant Science. 2010;29:148–161.
20. Leonarduzzi C, Leonardi S, Menozzi P, et al. Towards an optimal sampling effort for paternity analysis in forest trees: what do the raw numbers tell us? iForest. 2012;5:18–25.
21. Hamrick JL. Response of forest trees to global environmental changes. Forest Ecology and Management. 2004;197:323–335.
22. Austerlitz F, Smouse PE. Two-generation analysis of pollen flow across a landscape. II. Relation between Φft, Pollen dispersal and interfemale distance. Genetics. 2001;157(2):851–857.
23. Carvalho PER. Espécies arbóreas brasileiras. Brasília: Embrapa InformaçãoTecnológica; 2003.
24. Crestana CSM, Batista EA, Mariano G. Fenologia de Frutificação de Genipa americana L. (Rubiaceae) em Mata Ciliar do Rio Moji Guaçú, SP. Revista IPEF. 1992;45:31–34.
25. Vieira ICG, Galvão N, Rosa NA. Morphological characterization of fruits and seed germination of native Amazon tree species. Bulletin of the Museu Paraense Emílio Goeldi. 1996;12:271–288.
26. Köppen W. Climatologia: con un estudio de los climas de la tierra. Fondo de Cultura Econômica, Mexico; 1948.
27. Novaes RML, Rodrigues JG, Lovato MB. An efficient protocol for tissue sampling and DNA isolation from the stem bark of Leguminosae trees. Genetic Molecular Resources. 2009;8(1):86–96.
28. Doyle JJ, Doyle JL. Isolation of plant DNA from fresh tissue. Focus. 1990;12:13–15.
29. Manoel RO, Freitas MLM, Barreto MA, et al. Development and characterization of 32 microsatellite loci in Genipa americana (Rubiaceae). Applied Plant Science. 2014;2(3):1300084.
30. Manoel RO, Freitas MLM, Tambarussi EV, et al. Study of Mendelian inheritance, genetic linkage and genotypic disequilibrium at six microsatellite loci of Genipa americanaL. (Rubiaceae). Genetic and Molecular Resources. 2015;14(3):8161–8169.
31. Nei M. F-statistics and analysis of gene diversity in subdivided populations. Annual Human Genetics. 1977;41(2):225–233.
32. Goudet J. Fstat (Version 2.9.3.2.): a computer program to calculate F-statistics. Heredity. 1995;86:485–486.
33. Ritland K. Extensions of models for the estimation of mating systems using n independent loci. Heredity. 2002;88(4):221–228.
34. Chybicki IJ, Burczyk J. Simultaneous estimation of null alleles and inbreeding coefficients. Journal of Heredity. 2009;100(1):106–113.
35. Loiselle BA, Sork VL, Nason J, et al. Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae). American Journal of Botany. 1995;82(11):1420–1425.
36. Hardy OJ, Vekemans X. SPAGeDI: a versatile computer program to analyze spatial genetic structure at the individual or population levels. Molecular Ecology Notes. 2002;2:618–620.
37. Vekemans X, Hardy OJ. New insights from fine-scale spatial genetic structure analysis in plant populations. Molecular Ecology. 2004;13(4):921–935.
38. Cockerham CC. Variance of gene frequencies. Evolution. 1969;23(1):72–84.
39. Lindgren D, TJ Mullin TJ. Relatedness and status number in seed orchard crops. Canadian Journal of Forest Resources. 1998;28(2):276–283.
40. Kalinowski ST, Taper ML, Marshall TC. Revising how the computer program CERVUS accommodates genotyping error increases success in paternity assignment. Molecular Ecology. 2007;16(5):1099–1106.
41. Dow BD, Ashley MV. High levels of gene flow in bur oak revealed by paternity analysis using microsatellites. Journal of Heredity. 1998;89(1):62–70.
42. Slavov GT, Howe GT, Gyaourova AV, et al. Pollen Flow (PFL): a computer program for estimating pollen flow using highly variable markers and paternity exclusion. Oxford: PNWTIRC Publ. 2004.
43. Slavov GT, Howe GT, Gyaourova AV, et al. Estimating pollen flow using SSR markers and paternity exclusion: accounting for mistyping. Molecular Ecology. 2005;14(10):3109–3121.
44. Meagher TR, Thompson E. Analysis of parentage for naturally established seedlings of Chamaelirim luteum (Liliaceae). Ecology. 1987;68(4):803–812.
45. Sokal RR, Rohlf FJ. Biometry: principles and practices of statistics in biological research. 3rd ed. New York, USA: WH Freeman and Company; 1995.
46. Levin DA. The paternity pool plants. American Naturalist. 1988;132(2):309–317.
47.  SAS Institute. SAS procedures guide: Version 8 (TSMO). North Carolina, Cary: SAS Institute; 1999.
48. Jump AS, Penuelas J. Genetic effects of chronic habitat fragmentation in a wind-pollinated tree. Proceedings of National Academy of Science USA. 2006;103(21):8096–8100.
49. Bittencourt JM, Sebbenn AM. Patterns of pollen and seed dispersal in a small fragmented population of a wind pollinated Araucaria angustifolia in southern Brazil. Heredity. 2007;99(6):580–591.
50. Naito Y, Konuma A, Iwata YS, et al. Selfing and inbreeding depression in seeds and seedlings of Neobalanocarpus heimii (Dipterocarpaceae). Journal of Plant Resources. 2005;118(6):423–430.
51. Hedrick PW, Hellsten U, Grattapaglia D. Examining the cause of high inbreeding depression: analysis of whole-genome sequence data in 28 selfed progeny of Eucalyptus grandis. New Phytologist. 2016;209(2):600–611.
52. Tambarussi EV, Boshier DH, Vencovsky R, et al. Inbreeding depression from selfing and mating between relatives in the Neotropical tree Cariniana legalis Mart. Kuntze. Conservation Genetics. 2017;18(1):225–234.
53. Manoel RO, Freitas MLM, Furlani Junior E, et al. Individual, fruit, and annual variation in correlated mating in a Genipa americana population. Silvae Genetica. 2015;69:108–116.
54. Frankel OH, Soulé MS. Conservation and evolution. Cambridge, UK: Cambridge University Press; 1981.
55. Pierrot LM, Schlindwin C. Variation in daily flight activity and foraging patterns in colonies of uruçu – Meliponascutellaris Latreille (Apidae, Meliponini). Revista Brasileira de Zoologia. 2003;20(4):565–571.
56. Araujo ED, Costa M, Chaud-Netto J, et al. Body size and flight distance in stingless bees (Hymenoptera: Meliponini): inference of flight range and possible ecological implications. Brazilian Journal of Biology. 2004;64(3B):563–568.
57. Wang J. Triadic IBD coefficients and applications to estimating pairwise relatedness. Genetic Resources. 2007;89(3):135–153.
58. Plowright RC, Galen C. Landmarks or obstacles: the effects of spatial heterogeneity on bumble bee foraging behavior. Oikos. 1985;44:459–464.
59. Klein EK, Desassis N, Oddou-Muratorio S. Pollen flow in the wild service tree, Sorbus torminalis(L.) Crantz. IV. Whole interindividual variance of male fecundity estimated; jointly with the dispersal kernel. Molecular Ecology. 2008;17(14):3323–3336.