Hourly, daily and monthly evapotranspiration of Peechi-Vazhani Wildlife Sanctuary (WLS), Western Ghats, Kerala, India was estimated for a sample day using GIS and Remote sensing techniques (SEBAL model). The WLS is covered by a variety of different vegetation types forming the living habitats for several tropical mammals including the elephants. The resources used were hourly weather data measured on ground and single Land sat ETM+ imagery. It was found that Normalized Difference in Vegetation Index and Leaf Area Index were highest in areas with good vegetation cover. Evapotranspiration was highest in large water bodies. The efficacy of the method was impaired when the gradients were not steep. This provides key pointers towards water conservation and management in the context of land use patterns and can be used to study the water relation of crops especially in different seasons in terms of vegetation types, biomass and surface energy balance. This can be further applied for the management of wild animal population in the area as well as providing potable and irrigation water from the two reservoirs located in this WLS.

Keywords: energy balance, evapotranspiration, et, gis, leaf area index, peechi-vazhani wls, remote sensing, sebal, water relations

ET, evapotranspiration; ETM, enhanced thematic mapper; EVI, enhanced vegetation index; FAO, the food and agriculture organization of the united nations; LAI, leaf area index; MODIS, moderate resolution imaging spectroradiometer (it is attached to Terra a sun synchronous satellite); NDVI; normalized difference in vegetation index; SAVI, soil adjusted vegetation index; SEBAL, surface energy balance algorithms for land; TM, thematic mapper; WLS, wildlife sanctuary

Evapotranspiration (ET) can be determined using weighing lysimeters and by other micro-meteorological and energy balance methods (1). However, one of the limitations of the above methods is that they give only point values of ET of a relatively small area and fails to estimate ET on a regional scale. They have indeed much value when the purpose is to analyze the water relations of a watershed. At the same time, when the area is occupied by a variety of different forest types or vegetation, there is a need for estimations rather than direct measurements. Using remote sensing techniques, we can estimate ET over vast areas from satellite images. It is highly advantageous because ET can be computed without quantifying other complex hydrological processes and ET estimation can be done for large land surface areas with multiple vegetation types using a minimal amount of ground data.

ET is highly variable in both space and time.^1,2 It is variable in space due to the wide spatial variability of precipitation, hydraulic characteristics of soils, and vegetation types and densities. It is variable in time due to variability of weather conditions and seasons. Satellite images provide an excellent means for determining and mapping the spatial and temporal structure of ET. There are varieties of methods to compute the actual evapotranspiration particularly based on energy balance methods (1), however the more modern remote sensing methods deserve special mention.

Studies³ on the actual evapotranspiration of central Punjab in Pakistan by SEBAL model using Landsat ETM+ images found that SEBAL model is very effective to estimate the actual evapotranspiration at regional scale. Remote sensing techniques using data from Landsat 5 TM images was used to estimate the daily evapotranspiration fluxes over the semi-arid Catania, Eastern Sicily.⁴ Air temperature and actual evapotranspiration and correlation between were estimated using SEBAL model and Land sat 5 TM data.⁴ The daily crop evapotranspiration of Mandria and Kokkinochoria area of Cyprus was estimated using FAO Penman- Monteith method using satellite data ((MODIS – TERRA) and auxiliary meteorological parameters.⁵ The energy balance method was used to estimate the evapotranspiration of lake Naivasha of Kenya from Landsat TM imagery using remote sensing techniques.⁶ The evapotranspiration of Dobrogea area of Romania was estimated using remote sensing data and grid computing technique from Landsat ETM+ imageries.⁷ The Enhanced Vegetation Index (EVI) from MODIS sensors on the Terra satellite was used to estimate evapotranspiration of agricultural and riparian areas of Lower Colorado River in the southwestern U.S.⁸ Thus the SEBAL model has been widely tested against standard methods in different countries and presently it is being used at the application level.^10,11

In this study we estimate leaf area index, surface temperature and actual evapotranspiration by remotely sensed data using Surface Energy Balance Algorithms for Land (SEBAL) model.^9-11 SEBAL uses seven bands of the Landsat7-ETM+ satellite sensor and reference evapotranspiration taken from nearby weather station to estimate actual evapotranspiration pixel by pixel of the study area, Peechi - Vazhani Wild Life Sanctuary (WLS) with several different types of vegetation. While similar studies have been conducted all over the world, this is a pioneering study from this tropical region of India. We also study the correlation of Leaf Area Index (LAI) and surface temperature with actual evapotranspiration (ET) of study area.

Study area

Peechi-Vazhani WLS is located between 76.302777º to 76.419024° E and 10.464535º to 10.663871° N in the Western Ghats, in the central part of Kerala State and covers a total area of 125.5km². This protected area is located in Thrissur District in Kerala State, about 20km from Thrissur city. Peechi-Vazhani WLS was formed by combining some portions of Peechi, Pattikad and Machad ranges of Thrissur Forest Division in 1958 (Figure 1).

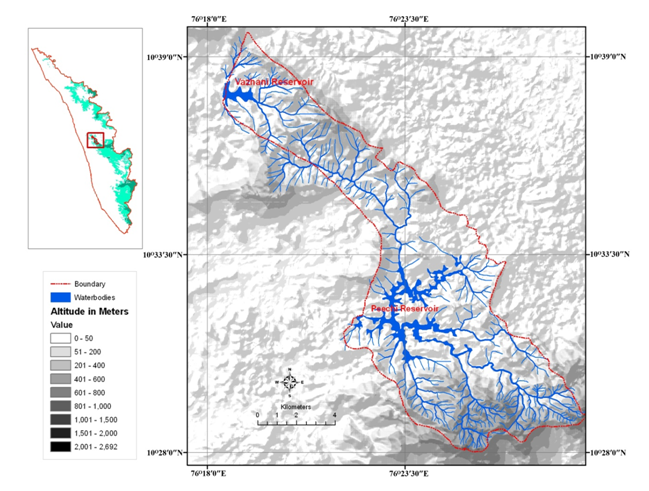
Figure 1 Map of Kerala State with study area in inset and the study area of Peechi -Vazhani WLS enlarged.

The study area has two prominent monsoonal rainfall periods- South-West and North-East monsoons. The South-West monsoon is the major contributor towards precipitation in this area, nearly 75 per cent of the total annual rainfall. The annual rainfall in this location ranges between 2500 to 3000 mm. Usually humid and warm climate prevails in this location. A major mountain gap in the Western Ghats range of hills, the Palakkad gap, is situated very close to the sanctuary. There is an easterly dry wind blowing in this region during November-January. The dry months are from January to March. March is the warmest month when the temperature reaches up to 35°C. During November-December the temperature falls to 15°C in the early morning in some regions of the sanctuary. The terrain is highly rugged, undulating; the altitude ranges from 100m to 926m. The area has two west flowing rivers, Wadakkancherry River and Manali River. There are two reservoirs, one in Peechi and the other Vazhani, which supply for irrigation and potable water needs.

Geology

The major rock types in this area are of metamorphic rocks of the gneissic series, weathering in large sheet, especially on the upper elevations. However, the rocks tend to become lateritic. Owing to active weathering, the ground is characterized by the presence of many boulders, especially in the moist deciduous forest areas. The soil is blackish or reddish and loamy.¹²

Vegetation

Vegetation consists mainly of moist deciduous and semi-evergreen natural forests and some plantations. The main tree species in the natural forests are Albizia odoratissima, Bombax ceiba, Dalbergia latifolia, Dillenia pentagyna, Grewia tiliaefolia, Haldina cordifolia, Lagerstroemia microcarpa, Pterocarpus marsupium, Tectona grandis, Terminalia bellerica, Terminalia paniculata and Xylia xylocarpa. The lower canopy consists of species such as Bridelia retusa, Careya arborea, Cassia fistula, Erythrina stricta, Schliechera oleosaandSterculia urens.Trees are deciduous during dry season, in February-March, and regain leaves from April-May after the summer rainfall.

Landsat ETM+7 images dated November 11, 1999 were downloaded for the full scene of the path and row 144/53 from global land cover facility of the University of Maryland website. The raw images acquired had file formats as GeoTIF format with UTM Zone 44 N projection and WGS 84 datum.

Pre-processing such as geometric, radiometric and atmospheric corrections which are a prerequisite for analysis of energy fluxes and land cover parameters were done. All the operations from importing the data to analysis of the data were carried out in the GIS & RS software Erdas. Enhanced Thematic Mapper Plus (ETM+), bands 1-5 and 7 provide data for the visible and near infrared bands. The pixel size for these bands is 30m by 30m. TM band 6 provides data for long wave (thermal) radiation. The pixel size for this band is 60m by 60m. Information such as satellite overpass date and time, latitude and longitude of the center of the image, sun elevation angle (β) at the overpass time, Gain and Bias levels for each band obtained from the header file of image, are very important for the SEBAL process.

SEBAL requires a weather study area, within the 50km around the study location. This was available at the Kerala Forest Research Institute, which maintains hourly weather data using automated weather stations. Hourly Weather data such as wind speed, precipitation, humidity, solar radiation and air temperature are used for calculating hourly and daily reference ET. A land-use map is useful in estimating the surface roughness parameter (z_om). The land-use map divides the area of interest into various general classes of land-use such as agriculture, forest, grassland, etc. Land-use of study area with different vegetation types are shown in the Table 1.

Evapotranspiration (ET)

In SEBAL model, ET is computed from satellite images and weather data using the surface energy balance. Since the satellite image provides information for the overpass time only, SEBAL computes an instantaneous ET flux for the image time. The ET flux is calculated for each pixel of the image as a “residual” of the surface energy budget equation:

$\text{λET}={\text{R}}_{\text{n}}-\text{G}-\text{H} \left(1\right)$

Where is the latent heat flux ( $W{m}^{-2}$ ), is the net radiation flux at the surface ( $W{m}^{-2}$ ), G is the soil heat flux ( $W{m}^{-2}$ ), and is the sensible heat flux to the air ( $W{m}^{-2}$ ).

Net surface radiation flux is computed by subtracting all outgoing radiant fluxes from all incoming radiant fluxes. This is given in the surface radiation balance equation:

$R_n=R_{S\downarrow }-\alpha R_{S\downarrow }+R_{L\downarrow }-R_{L\uparrow }-\left(1-{\epsilon }_o\right)R_{L\downarrow }{}_{ }\left(2\right)$

Figure 2 Diagrammatic representation of Net Surface Radiation $(R_n)$ calculation.

Latent heat flux ( $\text{λET}$ ) is computed for each pixel, an equivalent amount of instantaneous $ET\left(mm/hr\right)$ is readily calculated by using equation

$E{T}_{inst}=\raisebox{1ex}{$3600\text{λET}$}\!\left/ \!\raisebox{-1ex}{$\text{λ}$}\right. \left(3\right)$

$ET$ Fraction ( $E{T}_{r }\text{F}$ ) is defined as the ratio of the computed instantaneous $ET \left(E{T}_{inst}\right)$ for each pixel to the reference $ET\left(E{T}_r\right)$ .

$E{T}_{r }\text{F}=\raisebox{1ex}{${\text{ET}}_{\text{inst}}$}\!\left/ \!\raisebox{-1ex}{${\text{ET}}_{\text{r}}$}\right. { }_{ }\left(4\right)$

$E{T}_r={\frac{0.4808\Delta \left(R_{n }– G\right)+ \frac{\gamma \left(900\right)}{T+273} {\mu }_2 \left(e_s-e_a\right)}{\Delta +\gamma \left(1+0.34{\mu }_2\right)}}_{ }\left(5\right)$

Where,

$E{T}_{r }$ = reference evapotraspiration (mm/day^-1)

$R_{n }$ = net radiation at the crop surface (MJ m^-2 day^-1)

$G$ > = soil heat flux density (MJ m^-2 day^-1)

$T$ = mean daily temperature at 2 m height (ºC)

$e_s$ = saturation vapour pressure at Tc (kPa),

$e_a$ = actual vapour pressure (kPa),

$e_s-e_a$ = saturation vapour pressure deficit (kPa),

$\Delta$ = slope of the saturation vapour pressure and temperature relationship (kPa◦C⁻¹),

${\mu }_2$ = wind speed at 2 m height (m s^>−1)

Daily values of $ET(E{T}_{24})$ are very useful in transpiration studies. $E{T}_{24}{}_{ }\left(mm/day\right)$ can be computed as:

$E{T}_{24}=E{T}_{r }\text{F}\times {\text{ET}}_{\text{r}-2}{}_{4 }\left(6\right)$

Where, is the cumulative 24-hour for the day of the image. This is calculated by adding the hourly values over the day of the image. Evapotranspiration for the period of one month (November 1999) was calculated by using the following formula:

$E{T}_{period}=E{T}_r{F}_{period}{\displaystyle \sum }_1^{n}E{T}_{r-24} \left(7\right)$

Where ${}_{\text{r}-24}$ is the representative $E{T}_{r}F$ for the period, $E{T}_{r-24}$ is the daily $E{T}_r$ , and n is the number of days in the period. Advanced Training and Users Manual (12) was used for reference in different steps of SEBAL processing.

NDVI, LAI and Surface temperature

The NDVI is the ratio of the differences in reflectivity for the near-infrared band (ρ4) and the red band (ρ3) to their sum.

$NDVI=\raisebox{1ex}{$\left({\rho }_4-{\rho }_3\right)$}\!\left/ \!\raisebox{-1ex}{$\left({\rho }_4+{\rho }_3\right)$}\right. \left(8\right)$

Where ${\rho }_4$ ${\rho }_3$ and ${\rho }_3$ are reflectivity for bands 4 and 3. Leaf area index (LAI) is calculated by using empirical equation.

$\text{LAI}=\frac{\text{ln}\left[\frac{0.69-\text{SAVI}}{0.59}\right]}{0.91} \left(9\right)$

Where SAVI is the soil adjusted vegetation index of study area. SAVI was calculated using the formula:

$SAVI=\raisebox{1ex}{$\left(1+L\right)\left({\text{ρ}}_4-{\text{ ρ}}_3\right)$}\!\left/ \!\raisebox{-1ex}{$\left(L+{\rho }_{{}_4}+{\rho }_{{}_3}\right)$}\right. \left(10\right)$

Where L is a constant for SAVI. Where ${\text{ρ}}_4$  and ${\text{ρ}}_3$ are reflectivity’s for bands 4 and 3.

Surface temperature retrieved from thermal band by using following formula:

${\text{T}}_{\text{s}}=\frac{{\text{K}}_2}{\text{ln}\left[\frac{{\text{ε}}_{\text{NB }}{\text{K}}_1}{{\text{R}}_{\text{c}}}+1\right]} \left(11\right)$

Where ${\text{R}}_{\text{c}}$ is the corrected thermal radiance from the surface using $L_6$ . ${\text{K}}_1$ and ${\text{K}}_2$ are constants for Landsat images $\left(K_1=666.09,K_2=1282.71\right)$ . ${\text{ε}}_{\text{NB }}$ is the narrow band surface emissivity.

Normalized Difference in Vegetation Index (NDVI)

The NDVI is a sensitive indicator of live green vegetation. Values for NDVI range between -1 and +1. The NDVI values in the present study area ranges from -0.31 to 0.68, the mean value is 0.54. Values of NDVI of different Land-use types are given in the Table 2. NDVI map of study area is shown in Figure 3.

Figure 3 Normalized difference in vegetation index (NDVI) of study area.

Leaf Area Index (LAI)

The LAI is the ratio of the total area of all leaves on a plant to the ground area occupied by the plant. It is an indicator of biomass and canopy resistance. Leaf area index of the study area ranges between 0.34 and 5.17, the highest LAI was recorded from evergreen and semi evergreen forests. LAI map of study area is shown in Figure 4. The LAI range of different land-use types of Peechi-Vazhani WLS is given in the Table 3.

Figure 4 Leaf area Index (LAI) map of study area.

The surface temperature (T_s)

Surface temperature was retrieved from thermal band of Landsat 7 ETM+imagery. The land surface temperature map of the study area is shown in the Figure 5. The temperature range in the study area ranges from 24-35°C. The mean temperature of the study area is 26°C. The temperature range of various land-use types is given in the Table 4.

Figure 5 Surface temperature map of study area.

Daily evapotranspiration

Instantaneous ET (mm h^-1) is calculated by SEBAL method from Landsat 7 ETM+ imgery. Instantaneous $ET$ in the study area ranges between 0.75 and 0.95mm h^-1. Daily values of $ET(E{T}_{24})$ are very useful in transpiration studies. Daily ET map of the study area is shown in the Figure 6. Daily evapotranspiration in the study area ranges between 4.12 and 5.24 mm day^-1. Daily evapotranspiration values of different land-use types are tabulated in Table 5 and shown in Figure 7. The reservoirs show the highest evaporation rates.

Figure 6 Map of Daily ET in the study area.

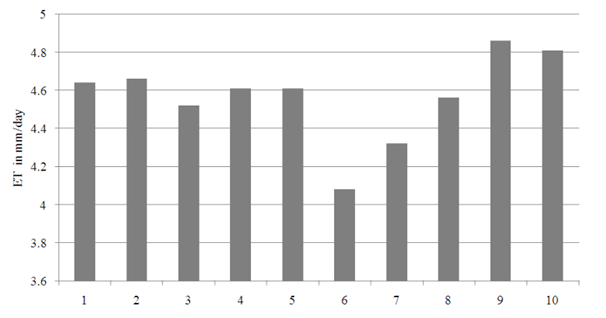
Figure 7 Graph of Daily ET (mm) of the study area.

Land use type

1. Paddy field, 2. Deciduous forest, 3. Degraded land, 4. Evergreen/semi evergreen, 5. Forest plantation,

6. Land use scrub, 7. Land without scrub, 8. Plantation, 9. Reservoir, 10. River

Seasonal evapotranspiration (ET_seasonal)

Monthly evapotranspiration map of the study area is shown in Figure 8. Monthly evapotranspiration in the study area ranges between 120 and 157mm. Monthly evapotranspiration values of different landuse types are given in (Table 6) (Table 7), Figure 9.

Figure 8 Map of Monthly ET in the study area.

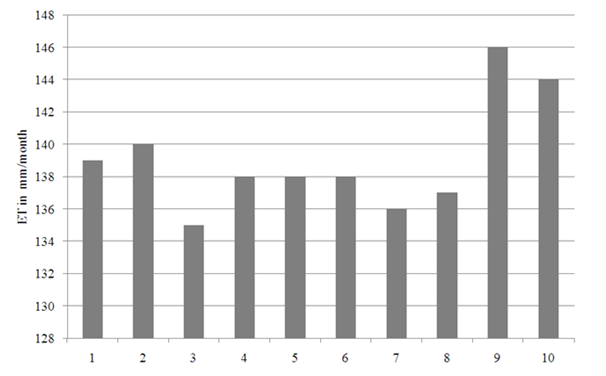
Figure 9 Graph of Monthly ET (mm) of the study area.

Land use type

1. Paddy field, 2. Deciduous forest, 3. Degraded land, 4. Evergreen/semi evergreen, 5. Forest plantation, 6. Land use scrub, 7. Land without scrub, 8. Plantation, 9. Reservoir, 10. River

Relationship between temperature, LAI and ET

On examining mean values of temperature (°C) and evapotranspiration from the study location, it was seen that the temperature and corresponding evapotranspiration are perfectly correlated $(R^2=0.999)$ . The relation is linearly represented as where is evapotranspiration and x is temperature in degree Celsius (Figure 10).

Figure 10 Relation between surface Temperature and daily ET, LAI and NDVI.

The mean values of LAI and corresponding evapotranspiration of the study area are also perfectly correlated , the relation is linearly represented as $y=0.74x+3.325,$ where $y$ is evapotranspiration and $x$  is leaf area index (Figure 9). NDVI and temperature too show a similar relation $(R^2=0.999)$ with $y=0.014x+0.320$ . Preeyaphorn¹³ mentions a similar relation between $ET$  and surface temperature. In that study the R value is 0.987.

SEBAL model for evapotranspiration has been shown to have an average accuracy of 85 to 96 percent on field and seasonal scales. The model has been tested and found successful in more than 30 countries with the method presently at the application level (10). Since SEBAL has been tested under a wide variety of conditions and found to be very reliable, we have used this model in understanding the evapotranspiration under different land-use conditions in a WLS. Hence, we have not validated the satellite data against other energy balance methods at this site. However, comparing with studies done on very similar weather, vegetation and soil conditions¹² in the nearby locations validates the accuracy of the SEBAL model at our WLS site.^14,15

Several micrometeorological and energy balance methods exist for estimating the evapotranspiration of a vegetated area or catchment. However, these methods become very cumbersome when the catchment has different types of vegetation as in the WLS under study. In such a landscape, the SEBAL model seems to be the most ideal to get a near reliable estimate of the evaporation data from a spatial distribution of vegetation. The daily value of ET of the reservoir, river, deciduous forest, paddy field, evergreen forest, forest plantation, other plantations, degraded land, land without scrub and land with scrub in the descending order is very sensible. In a WLS, understanding the spatial and temporal distribution of evaporative depletion is very important in the management of wildlife, especially when the sanctuary is surrounded by agricultural land. In the Peechi-Vazhani WLS, there are two reservoirs which are meant to provide both water for potable needs and agricultural purposes. Here also, the modelling of ET using SEBAL will have important applications. In a future climate change scenario also, the modelling of ET will gain a lot of importance as many animals including wild elephants need substantial quantity of water.

Another important issue is the water use of different types of vegetation. For example, in this part of the world, the exotic tree species such as eucalypts and acacias have been wildely planted for pulpwood purposes. However, this has been criticized by many environmental groups alleging that these trees consume excessive quantities of water compared to the native tree species.^16,17 Previous studies on these problems have been done using energy balance methods and also sapflow methods. The forest tree plantations mentioned in the Peechi-Vazhani WLS belong to eucalypts and acacias. Using the SEBAL model, it may be noted that their evapotranspiration is not significantly different from the natural forests which appear side by side to these plantations. Although this need more long term studies, the present study is very indicative for future research.¹⁸

The high values for correlation seen in the relations between temperature versus LAI, NDVI and ET certainly looks artificial in a biological system. There could be some autocorrelations in these relations. The original proponent of the SEBAL model predicts 85 to 96 accuracy in this remote sensing method. However, in spite of the various drawbacks and criticisms, this method is definitely a useful one in predicting the ET of a differently vegetated area such as the one presented in this study.

It was anticipated by previous workers (10,11,12) that SEBAL can help in establishing (1) the relationship between land use and water use for river basin planning; (2) studying impact of water conservation projects on real water savings; (3) irrigation performance; (4) environmental impact assessment due to groundwater extractions; (5) assessing the effect of water transfer design; (6) water-rights compliance; (7) hydrological modelling; (8) monitoring degradation of native vegetation systems; (9) forest vitality; and (10) assessing crop water productivity, to name a few applications (12,14). When considering large landmasses as in the case of the present study, the estimation of evapotranspiration using remote sensing techniques is very effective in the management of a Wildlife Sanctuary. The advantage of this method is estimation of pixel by pixel evapotranspiration which when compared with other methods is cost effective, time and labour saving, but its efficacy is impaired when the gradients are not steep. The intermediate estimations from this study, such as NDVI, SAVI, LAI, net surface radiation flux, soil heat flux, sensible heat flux, latent and heat flux, etc. are useful parameters in vegetation, biomass and surface energy balance studies. NDVI and LAI were found to be highest in areas with good vegetation cover and evapotranspiration was highest in large water bodies. This provides key pointers towards water conservation and management in the context of land use patterns.

The study is part of a project which was funded by the Council of Scientific and Industrial Research (CSIR), New Delhi. We thank CSIR for an Emeritus Fellowship to JK and a Senior Fellowship to TJR. We are grateful to Dr. K. V. Sankaran, Director KFRI for encouragement and support. We thank Dr. C. K. Somen and Dr. K. K. Seethalakshmi for providing weather data and other infrastructure respectively. We acknowledge Dr. Joyce Jose for her assistance in statistical help and editing. We thank the Kerala State Forest Department for co-operation by giving data on land use.

Author Declare there is no conflict of interest.

1. Lu J, Sun G, McNulty SG, et al. A comparison of six potential evapotranspiration methods for regional use in the southeastern United States. Journal of the American Water Resources Association. 2005;41(3):621‒633.
2. Kustas WP, Perry EM, Doraiswamy PC, et al. Using satellite remote sensing to extrapolate evapotranspiration estimates in time and space over a semiarid rangeland basin. Remote Sensing Environment. 1994;49(3):275‒286.
3. Sultan S, Ahmad I. Determination of daily regional scale actual evapotranspiration for Indus sub-basin using Landsat ETM +. Pakistan Journal of Meteorology.2008;4(8):49‒58.
4. Salvatore B, Consoli S, Russo A. A one-Layer satellite surface energy balance for estimating evapotranspiration rates and crop water stress indexes. Sensors. 2009;9(1):1‒21.
5. Papadavid G, Hadjimitsis D, Michaelides S, et al. Crop evapotranspiration estimation using remote sensing and the existing network of meteorological stations in Cyprus. Advances in Geosciences. 2011;30:39‒44.
6. Ahamed A, Bastiaanssen WGM. Estimating evapotranspiration from Lake Naivasha Kenya, using remotely sensed landsat thematic mapper (TM) spectral data. Journal of civil Engineering.2000;28(2):189‒203.
7. Cristina S, Maftei C, Barbulescu A. Estimation of evapotranspiration using remote sensing data and grid computing: A case study in dobrogea, Romania.Proceedings of the 14th WSEAS international conference on Computers. Greece: Part of the 14th WSEAS CSCC multiconference held at Corfu Island; 2010. p. 596‒601.
8. Murray RS, Pamela LN, Kiyomi M, et al. An empirical algorithm for estimating agricultural and riparian evapotranspiration using MODIS enhanced vegetation index and ground measurements of ET. II. Application to the Lower Colorado River, U.S. Remote Sensing. 2009;1(4):1125‒1138.
9. Bastiaanssen WGM, Menenti M, Feddes RA, et al. A remote sensing surface energy balance algorithm for land (SEBAL) 1. Formulation. Journal of Hydrology. 1998:198‒213.
10. Bastiaanssen WGM, Noordman EJM, Pelgrum H, et al. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. Journal of Irrigation and Drainage Engineering. 2005;131:85‒93.
11. Waters R, Allen R, Bastiaanssen WGM, et al. Surface Energy Balance Algorithms for Land, Idaho Implementation, Advanced Training and Users Manual, Version 1.0. USA: The Idaho Department of Water Resources; 2002.
12. Anitha V, Muraleedharan PK. Study of social and economic dependencies of the local communities on protected areas- a case of Peechi - Vazhani and Chimmoni wildlife sancturaies. Kerala: KFRI Research Report 240. KFRI, Peechi; 2002.
13. Preeyaphorn. Air temperature and actual evapotranspiration correlation using landsat 5 TM satellite imagery. Kasetsart Journal. 2009;43(3):605‒611.
14. Allen RG, Pereira LS, Raes D, et al. Crop evapotranspiration: guidelines for computing crop water requirements. Rome: FAO Irrigation and Drainage Paper 56, FAO; 1998. 1‒15p.
15. Smith M, Allen RG, Pereira LS, et al. Revised FAO methodology for crop water requirements. San Antonio, Texas: Proc of the international conference on evapotranspiration and irrigation scheduling; 1996. p. 116‒123.
16. Kallarackal J, Somen CK. Water loss from tree plantations in the tropics. Current Science.2008;94(2):201‒210. 
17. Kallarackal J, Somen CK. Water use of Eucalyptus tereticornis stands of differing density in southern India. Tree Physiology. 1997;17(3):195‒204.
18. Kallarackal J, Somen CK. An ecophysiological evaluation of the ecophysiological suitability of Eucalyptus grandis for planting in the tropics. Forest Ecology and Management. 1997;95(1):53‒61.